1 Introduction

Acoustic emissions (AE), or as well called high frequency elastic wave emissions, have over the past decade become increasingly popular in the application of nondestructive testing and condition monitoring. This technique has been proven in the separation of failure modes [2], the monitoring of wear [4, 21], the specification of contaminated systems [16, 20] and to differentiate lubricants [17] and lubrication regimes [7]. However, most of the investigations use simple signal processing methods such as root mean square (RMS) [7, 20] and activation counts (AC) [2, 16, 17, 21]. All these investigations use relative measurement methods, and signals are acquired using piezoelectric transducers, which limits investigations without further calibration to measure relatively. This use of relative measurement methods also limits the extraction of information of the acoustic wave.

The authors hypothesize that condition monitoring techniques could be improved by improving processing of the signal. A fuller understanding of the relation between the source of the wave and the actual measured signal would improve the processing of the signal. Being able to calculate the force function of the initial source based on sensor signals would increase the possibility to distinguish between different failure types and failure sizes. However, absolute measurement would therefore be required so that the relation between the signal and the wave source could be ascertained. Both McLaskey and Glaser [15] and Jacobs and Woolsey [10] have presented methods for absolute calibration of piezoelectric transducers. However, there are no evaluations of the validity of the methods which are independent of the system. McLaskey’s and Glaser’s method for absolute calibration of piezoelectric transducers is used. The method is evaluated for boundary restricted systems using a Laser–Doppler vibrometer (LDV) and Green's function based on an FEM simulation as a comparison. The term “boundary restricted systems” is used for systems where reflections of all dimensions are taken into account (in this investigation disc samples), whereas systems which are boundary free in one or two dimension are not included in this definition (calibration plate—reflection is only considered in one dimension).

An absolute measurement is required to improve condition monitoring capability of high frequency emissions. However, a better understanding of the relation between source and signal is as well an essential knowledge for improving condition monitoring by acoustic emission. Several researchers have successfully connected source and signal for high frequency emissions. McLaskey and Glaser [14] have, for example, related a signal of a piezoelectric transducer to the actual force function by using a Green’s function approach. Kundu et al. [12] have presented a mathematical method to locate Hertzian impacts by minimizing error functions. The impact of cracks on wave propagation in plates was studied by Liu and Datta [13] with FEM based on a Green’s function for transfer of the initial source. Glaser et al. [5] were able to calculate the wave propagation in an isotropic half space with a viscoelastic propagator and compared it to actual measurements. All these investigations either have used thin plates in order to minimize the problem to two dimensions or have used huge geometries in comparison with the measurement time to avoid reflections. In both cases, the boundary restrictions are simplified. However, in industrial applications boundary restrictions often comprise a great part of contribution to the measured signal.

Fig. 1
figure 1

Schematic drawings of the experimental setups. a AE transducer setup. b LDV setup

Full size image

Other researchers have taken boundary restrictions into account by using smaller geometries with limited sizes, where reflection could not be neglected, but have focused on linking physical properties to the measured signal rather than the actual source. Han et al. [8], for example, related the yield stress in tensile tests with wave forms, while Niknam et al. [18] related AE signals with a statistical approach to lubrication conditions. However, in these investigations absolute measurement is not used nor do they relate signal and source directly to each other.

Investigations with boundary restricted systems which relate wave source and signal are rare. One of the few that do is an investigation about crack propagation in brittle amorphous materials, where Gross et al. [6] link the spectra of the excitation to the speed of the crack propagation. However, investigations of Hertzian contact excited, boundary restricted systems, could not be found, even though such systems are fundamental for condition monitoring of rolling element bearings. Understanding the relation between AE source and AE signals in a rolling element bearing would enable new opportunities for improved signal processing. This article therefore describes a experimental analysis of Hertzian contacts in boundary restricted systems and compares the results to previous investigations without boundary restrictions.

2 Experimental Setup

Steel balls (SKF) with diameters from \({\varnothing}1.5\) to \({\varnothing}10\,\hbox {mm}\) were used as Hertzian excitation for all experiments. The balls were dropped from different heights onto different plates (Table 1). Impact positions were identical for all experiments so as to obtain repeatable measurements. To achieve as identical impact positions as possible, a hemispherical magnetic holder was developed (Fig. 1). With a magnetic force just enough to overcome gravity, the ball samples were self-aligning by positioning at lowest potential energy, right centred beneath the half sphere. Any redirection problem due to residual magnetism was minimized due to the minimization of contact area. This repeatability is visualized in Fig. 2. It shows repeated drops onto a pressure sensitive paper from various heights. The spread of contact points increases with increasing drop height. However, the results demonstrate an acceptable repeatability, especially considering that the ball penetrates the 0.1-mm-thick pressure sensitive paper.

Fig. 2
figure 2

Drop tests for evaluation of repeatability with pressure sensitive paper. a 350 mm drop height, b 250 mm drop height, c 150 mm drop height

Full size image

Another adjustment of the test setup was the position of sensors (LDV and AE transducer, respectively) relative to the position of the impact. Using a Green’s function approach, it is important to have impact point and sensor point vertically aligned to each other (according to Fig. 3, points \(\xi \) and x). To achieve this setup, the laser was aligned vertically by aligning the reflection of a water bath. If the laser was reflected back to its source by the water surface, the laser hit the water surface at a \(90^{\circ }\) angle and was thereby vertically aligned. Once the laser was vertically aligned, the magnetic holder was centred to the laser. Therefore was the effect used that the reflection right back to the laser source is maximized, when the laser hit the centre point of the sphere.

Table 1 Test setup
Full size table

As shown in Fig. 1, the various samples (discs) are clamped between two rubber o-ring seals. In this investigation, five different discs were used and excited by different Hertzian impacts as shown in Table 1. The discs samples only differ in material and thickness. Both diameter (\({\varnothing}103.8\,\hbox {mm}\)) and a \(30^\circ \) chamfer on one side were identical for all samples. Several combinations of disc and ball samples were tested and measured with both the Laser–Doppler vibrometer and the piezoelectric AE transducer. Each measurement was repeated eight times. All samples and test equipment, except pre-amplifier and acquisition computer, were mounted on an optical table to minimize disturbances of the surrounding.

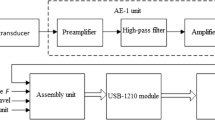
AE transducer measurements were executed with the same broadband flat-response sensor (Physical acoustics WS\(\alpha \)) used with the calibration measurements. As a pre-amplifier, a Physical Acoustic 2/4/6C was used with an inbuilt bandpass filter of 100–1200 kHz. The sensor was attached using beeswax. Therefore, beeswax was both the attachment and the couplant. A small portion was heated to \(75\,^\circ \)C. Then the sensor was pressed with dead weights onto the discs, while waiting until both disc and couplant reached room temperature again. Beeswax was chosen following tests with various methods for the attachments prior to the investigation. Additionally, several other researchers have in previous tests used beeswax as a couplant for acoustic measurements [3, 11].

The laser measurement was executed with a device called OFV056 from Polytec. The OFV056 is a laboratory type Laser–Doppler vibrometer (LDV) which uses a red laser. The LDV measures the velocity of a single point on the surface of the discs (Fig. 1a), which was by the provided software converted into displacement. In this investigation, a sensitivity of (125 mm/s)/mV was used in combination with a measurement range of 1 Hz–1 MHz. The laser head was used in combination with a matching controller and pre-amplifier box (Polytec OFV3001S). As shown in Fig. 1, it was necessary to redirect the laser by an optical mirror (Thorlabs PF20-03-P01).

The signals of both the LDV and the AE transducer are stored with a 14-bit digitizer PCI-card (GaGe OSC-432-007). A sample rate of 10 MS/s was used and in total 10000 samples per signal were recorded, which resulted in a measurement time of 1ms. However, limited to a measurement time of \(100\,\upmu \)s, all signals were triggered on a positive flank with a pretrigger storage of \(1\,\upmu \)s.

3 Green’s Function Approach

Both the calibration and simulation are based on a Green’s function approach, where a single function describes the time-dependent relation between two physical measures at two points within the system boundaries. Usually, the Green’s function g is a matrix which describes the relationship between points (x, \(\xi \)) for given directions (k, j) at specific times (t, \(\tau \)):

$$\begin{aligned} u_k(x,t)=\iint f_j(\xi ,\tau ) \times g_{kj}(x,t,\xi ,\tau )\,\hbox {d}\xi \,\hbox {d}\tau \end{aligned}$$
(1)

However, in this paper a simplified case is used, such as that which McLaskey and Glaser suggest [14]. It is assumed that the major contribution is the pressure wave through the material and therefore the simplified Green's function is only dependent on a single direction. As shown in Fig. 3, the two points of interest are only separated in direction 1 by the distance h. For all other directions, the distance between x and \(\xi \) is zero. All exciting forces f are assumed to be perpendicular to the plate, and forces therefore only act along direction 1. The same applies for the displacement u. If these assumptions are made, Green’s function may be simplified according to Eq. (2) as shown by McLaskey and Glaser [14]:

$$\begin{aligned} u_1(x,t)=f_1(\xi ,\tau ) *g_{11}(x,t,\xi ,\tau ) \end{aligned}$$
(2)

Equation (2) allows determination of the displacement (\(u_1(x,t)\)) in the perpendicular direction to the plate at the sensor position, by convolution of Green’s function (\(g_{11}(x,t,\xi ,\tau )\)) and given force functions (\(f_1(\xi ,\tau )\)). The Green’s function approach presented in this report requires independence between force function and Green’s function. Therefore, calculations are only valid for contact times (\(t_\mathrm{c}\)) shorter than any reflection time back to the point of force initiation (\(\xi \)). This is especially important for the boundary restricted systems (in this investigation small discs) and reflection times are therefore defined as follows:

$$\begin{aligned} t_{\mathrm{reflection}\,H}&=2\frac{h}{c_{\mathrm{p}}} \end{aligned}$$
(3)
$$\begin{aligned} t_{\mathrm{reflection}\,R}&=2\frac{r_\mathrm{disc}}{c_{\mathrm{p}}} \end{aligned}$$
(4)

where \(t_{\mathrm{reflection}\,H}\) and \(t_{\mathrm{reflection}\,R}\) are reflection times across the disc and radial, respectively. The variables h and \(r_\mathrm{disc}\) are height and radius of the disc, and \(c_{\mathrm{p}}\) is the speed of the pressure wave in the given material.

Fig. 3
figure 3

Schematic for declaration of experimental setup

Full size image

The Green’s function approach as used in this investigation is based on two point assumptions: One assumption is that the global force of a Hertzian elastic contact model as shown in Eq. (8) acts on a single point (in this investigation \(\xi \)). This assumption requires a small contact area and a deformation that is as homogeneous as possible across the contact area. The second point assumption used in this investigation is that calculated displacements of a single point (in this investigation x) represent measured acoustic waves by a sensor with a finite contact area. This assumption requires a ratio between sensor diameter and distance of the measurement point (x) to source point (\(\xi \)) as small as possible.

4 Calibration

As seen in Fig. 4, even high quality AE transducers with flat-response characteristic are not perfectly flat. These small variations within the bandwidth of the sensor, in case of the WS \(\alpha \) 0.1–1 MHz, do have an influence once the sensor is used for absolute measurement instead of relative measurement. Additionally, the amplitude needs to be related to a physical measure once absolute measurements are carried out. Therefore, a calibration is necessary once the sensor is used for absolute measurements and once signals will be compared to simulations.

Fig. 4
figure 4

Frequency response function of the AE transducer provided by the supplier

Full size image

McLaskey’s and Glaser’s [15] method was used for calibration of the AE transducer. As a calibration system a steel plate (Toolox40) with dimensions of \(1\,\times \,0.5\,\times \,0.051\) m was used. The huge dimensions of the steel plate were necessary in order to avoid reflections from the side walls during the measurement time of 80 \(\upmu \)s. Being able to neglect reflections allowed the use of Hsu’s [9] script for calculating Green’s function, which uses only material properties and the thickness of the plate as input parameters. The source for the wave was a glass capillary tube (\(D={\varnothing}1.4\,\hbox {mm}\) and \(d={\varnothing}1\,\hbox {mm}\)) which was compressed until it burst on the surface of the plate. A glass capillary burst was chosen as a source because of its good excitation of high frequencies due to the rapid release of force [1] and that the following equation may be used:

$$\begin{aligned} f(\tau )&= \frac{f_\mathrm{amp}}{2\times (1-\cos (\pi \tau /t_\mathrm{rise}))},&0 \le |\tau | \le t_\mathrm{rise} \\ f(\tau )&=0,&\tau < 0\\ f(\tau )&=f_\mathrm{amp},&\tau > t_\mathrm{rise} \end{aligned}$$
(5)

The calibration was carried out in a tensile test machine, where the steel plate was positioned under a steel cylinder and pressed against it with the glass capillary in between. With a speed of 0.01mm/s, the plate was elevated towards the steel cylinder and the force on the glass capillary as a result increased successively. During the whole calibration, the force on the steel cylinder, and thereby the force on the glass capillary, was measured continuously with a sample rate of 50 Samples/s. With the force measurement, the force, at which the glass capillary burst, was identified by the force maximum. This force maximum was the input value for \(f_\mathrm{amp}\) of Eq. (5). The released elastic wave was measured with an AE transducer (Physical acoustics WS\(\alpha \)), which was positioned centred to the source underneath the steel plate (positions comparable to x in Fig. 3). By transforming the measured AE transducer signal s(x, t) and the calculated theoretical displacement \(u_1(x,t)\) to the frequency plane, the sensor function is calculated by simple division [15]:

$$\begin{aligned} s(x,t)=&u_1(x,t)*i_1(t) \end{aligned}$$
(6)
$$\begin{aligned} I_1(\omega ) =&S(x,\omega ) / U_1(x,\omega ) \end{aligned}$$
(7)

While in the time domain the sensor signal (s(x, t)) is the result of the convolution of the actual displacement (\(u_1(x,t)\)) and the sensor function (\(i_1(t)\)), the convolution will transform into simple multiplication. Therefore, the sensor function (\(I_1(\omega )\)) in the frequency domain can be extracted by dividing sensor signal (\(S(x,\omega )\)) and displacement (\(U_1(x,\omega )\)).

The sensor function is the function transforming displacement of the surface to the sensor signal, including both sensor and amplifier. This transfer function can be called as well frequency response function. However, due to the definition of the used calibration method [15] it is called sensor function throughout the article. Directions of force and displacement as well as relative positions of source and measurement point were kept constant for all experiments. The extracted sensor function was therefore valid for all measured signals with the AE transducer. Further signals compensated with the sensor function represent spectra of the displacement of the point of measurement. Therefore, compensated spectra represent absolute values and enable comparison with spectra of simulated signals. This calibration method does not only allow absolute measurement, it also influence the definition of AE. In this article, AE is defined as a movement over time of a measurement point with a frequency higher than 20 kHz, regardless source.

5 Simulation

A simulation was carried out to be compared with experimental findings. Therefore, the spectra of the displacement \(U_1(x,\omega )\) were studied. First \(u_1(x,t)\) was calculated by convolution of \(f_1(\xi , \tau )\) and \(g_{11}(x, t, \xi , \tau )\)(Eq. 2). For the force function, an equation based on Hertz elastic contact mechanics derived by Reed [19] was used:

$$\begin{aligned} f(\tau )&= f_{\mathrm{max}}\sin (\pi \tau /t_c)^{3/2}&,&\,0\le \tau \le t_c \\ f(\tau )&=0&,&\tau < 0\,\hbox {and}\, \tau > t_c \end{aligned}$$
(8)

Maximum force (\(f_{\mathrm{max}}\)) and contact time (\(t_c\)) are calculated based on geometrical and physical properties according to the following equations:

$$\begin{aligned} f_{\mathrm{max}}&= 1.917\rho _1^{3/5}(\delta _1+\delta _2)^{-2/5}R_1^2v_0^{6/5}\end{aligned}$$
(9)
$$\begin{aligned} t_c&=4.53(4\rho _1 \pi (\delta _1+\delta _2)/3)^{2/5}R_1v_0^{-1/5}\\ \hbox {where}\, \delta _i&=\frac{1-\nu _i^2}{\pi E_i} \end{aligned}$$
(10)

The indexes in Eqs. (9) and (10) refer to the ball (index 1) and the disc (index 2), while index 0 refers to the velocity at the time 0 (initial impact velocity \(v_0\)).

Knowing materials and geometrical properties of the samples allows the calculation of an analytical solution for the force function. However, a solution for Green’s function (\(g_{11}(x, t, \xi , \tau )\)) of the used samples where reflections could not be neglected was neither solvable analytically nor by the Hsus [9] script used for calibration. Therefore, a finite element method (FEM) analysis was carried out to generate Green’s functions for disc samples used in this investigation. The FEM analysis was based on an LS DYNA solver for rotational symmetry. The element size of the rectangular elements was 50 \(\upmu \)m. Time steps are usually connected to element size and material properties in LS DYNA, which results in 3.6 ns for steel and 3.7 ns for aluminium. However, in this investigation a storage interval of 10 ns was used to artificially increase the time step and thereby to homogenize the time step for all samples.

Fig. 5
figure 5

Schematic drawing of the FEM model with the symmetry axis and nodes for loading (F), response extraction (M) and constraint (B)

Full size image

Figure 5 shows a schematic drawing of the FEM model with the red symmetry axis on the left side. The three yellow marked nodes on the top (marked with F) of the disc in Fig. 5 represent the nodes for the force initiation. The nodes were exposed to a step force with a rise time of 100ns. The three nodes form a circular area with a radius of 100 \(\upmu \)m, where the maximum force applied is 1N over this circular area. Usually Green’s function approaches are transfer functions between two points. However, to obtain convergence, the FEM model uses three points for the force initiation. The stored output of the model is the displacement in y-direction of a single node on the lower side of the disc positioned on the symmetry axis (Yellow node marked with M, Fig. 5). A boundary constrain was introduced to take the fixation of the discs into account. A single node with a distance to the symmetry axis equivalent to the radius of the rubber seals was tied in the y- and the z-direction (Yellow node marked with B, Fig. 5). By taking the derivative of the FEM-result (displacement in y-direction of node M), Green’s function for specific samples was obtained. In combination with the equation for the force function (8), it enabled the calculation of the spectra for various Hertzian impacts. However, simulated results were only valid as long as the force and elastic wave do not interact(\(t_c<t_{\mathrm{reflection}\,H}, t_{\mathrm{reflection}\,R}\)).

6 Zero Frequencies

Zero frequencies according to McLaskey and Glaser [14] are calculated by using Eq. (11). McLaskey and Glaser [14] have shown acoustic waves excited by a Hertzian contact have local minima in the signal spectra (Fig. 6—\(f_{\mathrm{zero}, 1}, f_{\mathrm{zero}, 2}, f_{\mathrm{zero}, 3}\)) which they call zero frequencies. These zero frequencies are determined by the contact time (\(t_c\)) and have different orders(\(N=[1,2,3,4,...]\)) which are in theory infinite.

$$\begin{aligned} f_{\mathrm{zero}, N} = \frac{N+0.75}{t_\mathrm{c}} \end{aligned}$$
(11)

However, in practice measurement of zero frequencies at higher orders is difficult due to higher dam** of higher frequencies. This study therefore also focuses, as do McLaskey and Glaser [14], on zero frequencies up to the third order.

7 Results and Discussion

Results are divided in two sections. After repeating earlier results [14] to confirm that the calibration, by McLaskey’s and Glaser’s [15] method, was correctly executed, the calibration method was evaluated for boundary restricted systems. Therefore, measured spectra of acoustic waves in disc samples were compared to FEM simulated spectra and LDV measured spectra. In the second section, results on the behaviour of Hertzian excited elastic waves in boundary restricted systems will be shown. For cases where source and wave interact with each other, LDV measured spectra are presented and analysed. In the case of independent source and wave, AE transducer measured spectra are shown, analysed and compared to FEM simulations with respect to zero frequencies.

Fig. 6
figure 6

Schematic replication of results obtained by McLaskey and Glaser [14]

Full size image

7.1 Evaluation of Absolute Calibration for Boundary Restricted Systems

As mentioned in Sect. 4, a calibration method by McLaskey and Glaser [15] was used to extract the sensor function \(I_1(\omega )\). To confirm that the calibration was executed correctly, McLaskey’s experiment with Hertzian contacts was repeated. Figure 6 shows the results to be repeated, and Fig. 7 shows the repeated experiment for control of the calibration. The theoretical signal (green) is calculated with Hsus script and Eqs. (2)–(10). In Fig. 7a, a clear difference between the measured raw signal and the calculated theoretical signal can be seen. However, after compensating for the sensor function \(I_1(\omega )\) (7), the measured AE transducer signal (red) and the theoretical signal (green) show a good agreement (Fig. 7b) between 20 kHz and 1.2 MHz. Even the zero frequencies (\(f_{\mathrm{zero}, n}\)) of the theoretical signal and the measured AE transducer signal match each other. Comparing to McLaskey’s and Glaser’s experiments, the zero frequencies are positioned at similar positions considering plate material and ball sample. Both the overall agreement and the agreement of the zero frequencies (Fig. 7b) indicate a successful calibration and extraction of the sensor function and are in line with the earlier result of McLaskey and Glaser (Fig. 6). The difference in zero frequencies between the two results is caused by different plate materials (aluminium vs. steel) and ball sizes (1 vs. 1.5 mm) which results in different contact times \(t_c\). Therefore, the difference is expected and does not affect the conclusion of a successful calibration.

The extracted and controlled sensor function was then used for compensation of AE transducer signals recorded from Hertzian excitations in boundary restricted systems. These compensated signals were then compared to FEM simulation and LDV measured signals. For cases where source and wave do not interact with each other, the FEM simulated signal was used as a reference, while LDV measured signals were the reference for cases where source and wave do interact. The use of two different references was necessary, because for thick discs the displacement was too small to be detected by the LDV and the interaction of wave and source in thin discs could not be managed by the FEM simulation. Figure 8a shows both the LDV measured and compensated AE transducer measured signal of a Hertzian impact (\({\varnothing}8\,\hbox {mm}\) Ball) on a 5-mm-thick aluminium disc. Geometrical dimensions lead to multiple reflections (\(t_{\mathrm{reflection}\,H }= 1.575\,\upmu \)s and \(t_{\mathrm{reflection}\,R}=16.346\,\upmu \)s) within the disc in all directions during the contact time of \(31.96\,\upmu \)s. Therefore, excitation force and resulting wave are interacting with each other. As a result, the Hertzian impact excites resonances of the plate rather than enhancing zero frequencies. For this case, the calibration method shows weaknesses (Fig. 8a). While the LDV measured signal (purple) clearly shows the excitation of the resonances, the compensated AE transducer signal represents these resonances only poorly. Even though the signals show some similarities, the compensated AE transducer signal would not be enough to identify the resonances on its own. A possible explanation for the weak agreement, beside the calibration, can be the sensor itself. In comparison with the calibration plate, the sensor does change the system for the small discs by adding additional weight. The sensor rather is large (\({\varnothing}19\,\hbox {mm}\)) and therefore violates the point assumption of the Green’s function approach.

The absolute calibration seems more promising in boundary restricted systems if the exciting force and wave reflections do not interact with each other (Fig. 8b). For measurements shown in Fig. 8b, a ball of the size of \({\varnothing}1,5\hbox {mm}\) was dropped onto a steel plate with a thickness of 29 mm. By reducing the ball size and increasing the thickness, contact time was reduced (5.1 \(\upmu \)s) and reflection times were increased(\(t_{\mathrm{reflection}\,H}=9.831\,\upmu \)s and \(t_{\mathrm{reflection}\,R}= 17.59\,\upmu \)s). In this case, both excitation of the resonances and enhancing of zero frequencies was expected according to the calculated theoretical signal (green). Comparing the calculated signal and the compensated AE transducer signal (red), a good agreement of the zero frequencies can be observed. The dashed lines in Fig. 8b are indicating the zero frequencies of first, second and third order. Local minimum of simulated and measured signals agree with these zero frequency positions. However, the excited resonances indicated by the theoretical signal are not clearly represented by the compensated AE transducer signal.

Sensor function compensated AE transducer signals is capable of identifying zero frequencies in boundary restricted systems. However, the method in combination with the used equipment is not able to identify the excited resonances, even though theory would suggest otherwise. Possible explanations could be as mentioned a violation of the point assumption. While the assumption is decent for the Hertzian contact, the used sensor head with a diameter of 19 mm violates this assumption. Another explanation could be nonlinearities in the sensor function. The calibration method assumes the sensor function (\(I_1(\omega )\)) to be linear for a given frequency across the excitation amplitude, which might not be the case.

Fig. 7
figure 7

Calibration evaluation a raw signal, b calibrated signal

Full size image
Fig. 8
figure 8

Calibrated AE transducer measurements on boundary restricted systems. a Comparison of LDV measurement and AE transducer signal, b comparison of theoretical signal and AE transducer signal

Full size image

7.2 Hertzian Contacts in Boundary Restricted Systems

For boundary restricted systems, a finite element model was for this investigation developed to replace Hsus script which did not take any reflections into account. In combination with the Green’s function approach, this model is also only valid for excitations which do not interact with the excited elastic wave. Comparing the calculated spectra (green solid line) in Fig. 8b with the compensated AE transducer signal (red dashed line) shows that both are able to identify the zero frequencies. Zero frequencies according to McLaskey and Glaser [14] were calculated (11) and are indicated with the dashed vertical lines in both Figs. 8b and 9. In Fig. 8b both calculated and measured signals match the zero frequencies to a good degree. However, some deviation exists. This error gets more clearly in Fig. 9 where zero frequencies of the first three orders were extracted of all experiments and normalized by the contact time of the different impacts.

Fig. 9
figure 9

Normalized frequencies of the first three zero frequencies for different balls and drop heights on a boundary restricted system (steel plate 29 mm thickness and \({\varnothing}103.8\,\hbox {mm}\))

Full size image
Fig. 10
figure 10

Comparison of LDV measurements of different impact energies and contact times on a Steel 2511 plate of 5 mm thickness by changing drop height and ball size. a Drop height, b ball size

Full size image

By normalization of the zero frequencies over the contact time (\(t_\mathrm{c}\)), experiments with different ball sizes and drop heights are comparable. Figure 9 shows a visualization of normalized zero frequencies of several combinations of drop height and ball size. Each marker represents the mean value of eight measurements, and the error bars represent the standard deviation of the eight measurements. The results show that the identification of zero frequencies is clearly possible in boundary restricted systems. However, the failure margin increases in comparison with the case of an infinite plate [14].The failure margin shows a clear increasing trend with increased ball size. The reason for the increase is most probably the increase in contact time. For balls with a diameter of 3 mm, the contact time (\(t_\mathrm{c}\)) is almost as long as the reflection time (\(t_{\mathrm{reflection}\,H}\)). The contact time increases as well with a decrease in drop height. However, the results show a decreased failure margin. This is most likely caused by the increased spread of the impacts from increased heights as shown in Fig. 2.

By decreasing the reflection time (\(t_c>t_{\mathrm{reflection}\,H}\)) by decreasing plate thickness, zero frequencies could neither be detected by measurements nor by the FEM model based Green’s functions approach. As the results indicate, elastic wave responses in a boundary restricted system turn into a pure resonance problem once the contact time exceeds the reflection times. As Fig. 10 shows, neither a change in drop height nor a change in ball size has an effect on the excited resonances. However, a change in contact time by changing ball size does change the cut-off as Fig. 11 indicates. Therefore, matches the first zero frequency \(f_{\mathrm{zero}, 1}\) (indicated as a dotted line in Fig. 11) to a good degree matches a \(-20\) dB cut-off.

Fig. 11
figure 11

Spectra of signals with normalized amplitude for different ball sizes

Full size image
Fig. 12
figure 12

Comparison of resonances calculated and measured

Full size image
Fig. 13
figure 13

Degree of agreement between resonances calculated and measured by the LDV

Full size image

Even though the Green’s function approach is not valid for cases where initiating force and elastic wave interact, it still provides information about the location of the resonances. In Fig. 12 both the normalized spectra of an aluminium plate 5mm obtained by calculation and by measurement are shown. The theoretical location and the measured location of the resonances are not identical, but show good agreement. Comparing calculated and measured resonances one to five (as indicated in Fig. 12) for different plates and ball sizes (\({\varnothing}8\,\hbox {mm}\) to \({\varnothing}3\,\hbox {mm}\)) results in Fig. 13. Except for resonance one, the agreement between calculated location and measured location is good considering the simplicity of the FEM model and the accuracy of the experiments. The larger deviation for the location of the first resonance can be partly explained by the larger percentage difference between spectral lines at low frequencies and the short time obtained by calculation and by measurement of 1 ms.

8 Conclusions

After evaluating calibration based on Green’s functions, it can be concluded that the approach is also valid for boundary restricted systems with respect to zero frequencies. The calibration is, however, not accurate enough to detect resonances. This might be explained by violation of the assumptions of the Green’s function approach by the sensor system or by a summation of measurement inaccuracy. The evaluation is, however, promising enough to investigate more accurate sensor systems which violate the assumptions of the Green’s function approach to a lesser degree.

The investigation shows a clear difference between excitation times shorter than reflection times and excitation times longer than reflection times. In cases of independence of elastic waves and excitation force, the spectra contain both zero frequencies and resonances. Therefore, the zero frequencies follow Reed’s [19] contact model, as suggested by McLaskey and Glaser [14]. However, if elastic wave and excitation force do interact, zero frequencies are not detectable anymore and the measured spectra exclusively contain resonances. Even though zero frequencies are not detectable in this case, the first zero frequency does affect the spectral signal by determining the -20dB cut-off frequency. Additionally, it was shown that the Green’s function approach does provide partial information about the resonance location and is in line with measurements.