1 Introduction

In a quantum system, two spatially separated parties can be correlated in a nonclassical way, so that a local measurement on one party may affect the state of the other at faster-than-light speed. This nonlocal effect, usually called “quantum correlation”, cannot be interpreted by any local hidden variable theory and plays the vital role in quantum information processing, such as better-than classical communication and information protocols [1, 2], quantum computing without entanglement [3], and no-local-broadcasting [4]. Furthermore, many evidences show that quantum correlation is more robust than entanglement against decoherence, so that quantum algorithms based on quantum correlation may be more robust than those based on entanglement [5–7]. In many circumstances, we need to know whether a state can be used in a quantum information task or to what extent a quantum state can help do it. Thus the measure of quantum correlation becomes very important.

For a good measure of bipartite quantum correlation, two basic conditions have to be satisfied: (i) It presents zero result for a tensor product state, and a positive result for an entangled state; (ii) the measuring result is invariant under local unitary transformations on each one of the two subsystems [8]. In addition, two optional conditions are usually suggested. Firstly, quantum correlation coincides with quantum entanglement for pure states. Secondly, the maximum quantum correlation of a quantum state should not exceed one. Some other properties, such as convexity [9], monogamy [10–12], non-increasing under local operations and classical communication [13], which are required for the measures of quantum entanglement, need not to be satisfied by the measures of quantum correlation [14, 15].

During the last decade, much effort has been made for quantifying the bipartite quantum correlation. The most widely used measure of quantum correlation is quantum discord proposed by Ollivier and Zurek [16]. Henderson and Vedral proposed a similar measure based on the positive-operator-valued measurements [17]. Horodecki group combines the quantum correlation theory and quantum thermodynamics to measure the quantum correlation of a bipartite state through the work extracted from a heat bath [18–20]. The realism in classical physics tells us that a measurement can in principle reveal the properties of a classical system without disturbing it. However, this is not allowed in quantum systems. Based on this idea, Luo and co-workers proposed the measurement-induced disturbance [21] and nonlocality [22, 23] to measure the quantum correlation. Another way to measure the quantum correlation of a quantum state is through the “distance” between the quantum state under consideration and the closest classical state with zero quantum correlation, and such kind of measures are usually called geometric measures [24–27]. Most of the above measures coincide with the quantum entanglement of relative entropy for bipartite pure states, and none of them coincides with the widely used entanglement measure, Wootters concurrence [28]. Furthermore, to satisfy the second basic condition for a good measure mentioned above, an optimization is required in the definition of the above measures, which makes it very hard to analytically evaluate the quantum correlation of a mixed state [29, 30], even for the simplest two-qubit system [31–33]. A related discussion on the optimization over positive-operator-valued measurements can be found in Ref. [34]. At present, even the numerical evaluation of quantum correlation is found to be reliable only in low-dimensional systems [35]. In this paper, we introduce a new measure of quantum correlation, which coincides with Wootters concurrence for two-qubit pure states. More importantly, no optimization is involved in this measure, which makes it very easy to compute, no matter what dimension the bipartite state has.

2 Measure of quantum correlation

We begin the discussion on the new measure of quantum correlation with the widely used measure of quantum correlation, quantum discord [16]. By imposing a local projective measurement on one of two subsystems, called apparatus \(\mathcal{A}\), the quantum discord is defined as the “distance”  between the bipartite states, composed of the system \(\mathcal{S}\) and the apparatus \(\mathcal{A}\), before and after the local projective measurement, where the “distance” is quantified through mutual information,

$$\begin{aligned} \delta (\mathcal{S:A})_{\{\varPi ^\mathcal{A}_j\}}= & {} I(\mathcal{S:A})-J(\mathcal{S:A})_{\{\varPi ^\mathcal{A}_j\}} \nonumber \\= & {} H(\mathcal{A})-H(\mathcal{S,A})+H(\mathcal{S}|{\{\varPi ^\mathcal{A}_j\}}). \end{aligned}$$
(1)

Here \(I(\mathcal{S:A})\) (\(J(\mathcal{S:A})_{\{\varPi ^\mathcal{A}_j\}}\)) is the mutual information of the bipartite state before (after) the local measurement, \(H(\rho )\) denotes von Neumann entropy of the state \(\rho \), and \(H(\mathcal{S}|{\{\varPi ^\mathcal{A}_j\}})\) is the conditional entropy of the system \(\mathcal{S}\) given the result of local projective measurement \(\{\varPi ^\mathcal{A}_j\}\). The final quantum discord is then defined as the minimum one among the above result (1) over all possible measurements \(\{\varPi ^\mathcal{A}_j\}\) on the apparatus \(\mathcal{A}\). It is this minimization that makes it very hard to analytically evaluate the quantum discord of a bipartite state.

In a typical computational basis of a \(\mathcal{SA}\) bipartite system with dimension \(N_\mathcal{S}\otimes M_\mathcal{A}\), \(\{|i_\mathcal{S}l_\mathcal{A}\rangle \}\) (\(i=1,2,\ldots ,N\) and \(l=1,2,\ldots ,M\)), sequentially arranged as \(\{|1_\mathcal{S}1_\mathcal{A}\rangle ,\ldots ,|1_\mathcal{S}M_\mathcal{A}\rangle ,|2_\mathcal{S}1_\mathcal{A}\rangle ,\ldots , |N_\mathcal{S}M_\mathcal{A}\rangle \}\), a quantum state can be described by a \((NM)\times (NM)\) non-negative Hermitian matrix,

$$\begin{aligned} \rho =\left( \begin{array}{lll} \rho _{11} &{}\quad \cdots &{}\quad \rho _{1(NM)}\\ \vdots &{} \quad \ddots &{}\quad \vdots \\ \rho _{(NM)1} &{} \quad \cdots &{} \quad \rho _{(NM)(NM)}\\ \end{array} \right) . \end{aligned}$$
(2)

According to the definition of quantum discord introduced in Eq.(1), a bipartite state described by the density matrix (2) has zero quantum correlation if and only if it, after a certain local unitary transformation \(U_\mathcal{A}\) on the apparatus \(\mathcal{A}\), i.e. \(\rho ^{\prime }=U_\mathcal{A} \rho U_\mathcal{A}^{\dag }\), can be transferred into the following form [16],

$$\begin{aligned} \rho ^{\prime }=\left( \begin{array}{lll} \rho ^{\prime (11)} &{}\quad \cdots &{} \quad \rho ^{\prime (1N)}\\ \vdots &{} \quad \ddots &{}\quad \vdots \\ \rho ^{\prime (N1)} &{}\quad \cdots &{} \quad \rho ^{\prime (NN)}\\ \end{array} \right) , \end{aligned}$$
(3)

where all block matrices \(\rho ^{\prime (ij)}\) (\(i,j=1,2,\ldots ,N\)) with dimension \(M\times M\) are diagonal. In order to get more knowledge about the density matrix (2) for a zero-quantum-correlation state, we partition it, analogue to its transformation (3), into \(N^2\) blocks,

$$\begin{aligned} \rho =\left( \begin{array}{lll} \rho ^{(11)} &{}\quad \cdots &{}\quad \rho ^{(1N)}\\ \vdots &{}\quad \ddots &{} \quad \vdots \\ \rho ^{(N1)} &{}\quad \cdots &{}\quad \rho ^{(NN)}\\ \end{array} \right) , \end{aligned}$$
(4)

with each block being an \(M\times M\) matrix, and

$$\begin{aligned} \rho ^{(ij)}=\left( \begin{array}{lll} \rho _{((i-1)M+1)((j-1)M+1)} &{} \quad \cdots &{} \quad \rho _{((i-1)M+1)(jM)}\\ \vdots &{}\quad \ddots &{}\quad \vdots \\ \rho _{(iM)((j-1)M+1)} &{}\quad \cdots &{} \quad \rho _{(iM)(jM)}\\ \end{array} \right) . \end{aligned}$$
(5)

Due to the relation between the two density matrices (3) and (4), i.e. \(\rho ^{\prime }=U_\mathcal{A} \rho U_\mathcal{A}^{\dag }\), the block matrix \(\rho ^{(ij)}\) in the density matrix (4) is connected to the corresponding block matrix \(\rho ^{\prime (ij)}\) in its transformation (3) through the relation, \(\rho ^{\prime (ij)}=U_\mathcal{A} \rho ^{(ij)} U_\mathcal{A}^{\dag }\). Since all blocks \(\rho ^{\prime (ij)}\) are diagonal matrices, the block matrices \(\rho ^{(ij)}\) in the density matrix (4) are diagonalized by the same unitary transformation, and such matrices commute with each other [36]. That is to say, if a bipartite state has zero quantum correlation, all block matrices in the form (4) of its density matrix should commute with each other, which is a necessary and sufficient condition for zero quantum correlation [37].

Now we use the commutation relations among the \(N^2\) blocks \(\rho ^{(ij)}\) in the density matrix (4) to define a new measure of quantum correlation. Firstly, we number the \(N^2\) block matrices \(\rho ^{(ij)}\) in the way \(k=i\cdot N-N+j\), so that the block matrix located in the ith row and jth column of the matrix (4) is the kth block, denoted as \(B^{(k)}\) hereafter. Secondly, a test matrix with dimension \((N^2M)\times (N^2M)\), denoted as T hereafter, is constructed through \(N^4\) block matrices. The block matrix, \(T^{(k,k^{\prime })}\), located in the kth row and \(k^{\prime }\)th column (\(k,k^{\prime }=1,2,\ldots ,N^2\)) of T is defined as the commutation between the two block matrices \(B^{(k)}\) and \(B^{(k^{\prime })}\), i.e. \(T^{(k,k^{\prime })}=[B^{(k)},B^{(k^{\prime })}]\). So all the commutation results among the \(N^2\) blocks \(\rho ^{(ij)}\) are included in the test matrix T. If T is a zero matrix, all block matrices \(\rho ^{(ij)}\) commute with each other, which means the bipartite state described by the density matrix (4) has zero quantum correlation. On the contrary, a nonzero test matrix T implies nonzero quantum correlation. This inspires us to measure the quantum correlation through Frobenius norm of the test matrix T, which is the square root of the sum of the absolute squares of its elements, i.e. \(\Vert T\Vert _F=\sqrt{\sum _{ij}|T_{ij}|^2}\) [36]. Recently, a class of computable measures of quantum correlation are proposed through the Schatten p-norms of the correlation matrix of the state [38]. However, a minimization has to be included in their definitions to meet the requirements for a good measure, which makes the evaluation of these measures very hard. In the present case, if we directly use the Frobenius norm of the test matrix, \(\Vert T(\rho )\Vert _F\), to quantify the quantum correlation of a bipartite state \(\rho \), it already satisfies the two basic conditions for a good measure of quantum correlation, mentioned in the Sect. 1. But the two optional conditions are not satisfied. Fortunately, this problem can be perfectly solved by defining the quantum correlation of the bipartite state \(\rho \) as a simple function of \(\Vert T(\rho )\Vert _F\),

$$\begin{aligned} C(\rho )=\sqrt{2-2\sqrt{1-\Vert T(\rho )\Vert _F^2}}, \end{aligned}$$
(6)

This measure satisfies all necessary conditions for a good measure of quantum correlation. Since no optimization is included in the definition, this quantum correlation is very easy to compute, no matter what dimension the bipartite state under consideration has. Some examples will be illustrated in the next section.

3 Discussion and examples

Just as we mentioned above, commutation results among the blocks of the density matrix (4) are included in the test matrix \(T(\rho )\), so a classical state with zero quantum correlation has a zero test matrix with vanishing Frobenius norm. In other words, the present measure of quantum correlation is in agree with quantum discord for verifying zero quantum correlation. Accordingly, the condition (i) mentioned in the Sect. 1 is satisfied by the present measure.

The measure proposed here is invariant under local unitary transformations. Here we briefly discuss the influence of the local unitary transformation \(U_\mathcal{A}\) on the measuring result. The block of the test matrix, \(T^{(k,k^{\prime })}=[B^{(k)},B^{(k^{\prime })}]\), turns to \(T^{\prime (k,k^{\prime })}=[B^{\prime (k)},B^{\prime (k^{\prime })}]=U_\mathcal{A}[B^{(k)},B^{(k^{\prime })}]U_\mathcal{A}^{\dag }=U_\mathcal{A}T^{(k,k^{\prime })}U_\mathcal{A}^{\dag }\), after the local unitary transformation \(U_\mathcal{A}\) on the apparatus \(\mathcal A\). As is well known, Frobenius norm is invariant under unitary transformation. That is to say, every block of the test matrix \(T(\rho )\) does not change its Frobenius norm after the local unitary transformation \(U_\mathcal{A}\) and thus keeps the Frobenius norm of the whole matrix \(T(\rho )\) invariant. As for the local transformation \(U_\mathcal{S}\) on the subsystem \(\mathcal{S}\), it does not affect the Frobenius norm of the test matrix \(T(\rho )\), too.

Just as we mentioned above, the present quantum correlation is in accord with Wootters concurrence [28] for two-qubit pure states. To prove this statement, we can first consider the pure state \(|\phi \rangle =\alpha |00\rangle +\beta |11\rangle \), with \(|\alpha |^2+|\beta |^2=1\). It is not hard to work out the Frobenius norm of the test matrix of such a two-qubit pure state, \(\Vert T(|\phi \rangle )\Vert _F=2|\alpha \beta |\sqrt{1-|\alpha \beta |^2}\), and the final quantum correlation of this two-qubit state is then equal to its concurrence, i.e. \(C(|\phi \rangle )=2|\alpha \beta |\). The conclusion for the above pure state \(|\phi \rangle \) can be generalized to an arbitrary two-qubit pure state \(|\psi \rangle =\alpha ^{\prime }|00\rangle +\gamma ^{\prime }|01\rangle +\eta ^{\prime }|10\rangle +\beta ^{\prime }|11\rangle \), with \(|\alpha ^{\prime }|^2+|\gamma ^{\prime }|^2+|\eta ^{\prime }|^2+|\beta ^{\prime }|^2=1\), because the former one can be regarded as the Schmidt decomposition of the later one, and they can be transformed to each other through local unitary transformation. As is mentioned above, local unitary transformations change neither the quantum correlation measured here, nor Wootters concurrence.

For the case of mixed states, as an example we consider a Werner state of the form [39],

$$\begin{aligned} \rho =p|\phi \rangle \langle \phi |+\frac{1-p}{4}I_4, \end{aligned}$$
(7)

with \(0\le p \le 1\). Such a two-qubit state, mixed by the maximally entangled state \(|\phi \rangle =\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )\), and the completely mixed state \(\frac{1}{4}I_4\) (\(I_N\) stands for N-order unity matrix hereafter), is entangled for \(\frac{1}{3}< p \le 1\), with concurrence \(E(\rho )=\frac{3p-1}{2}\), and separable for \(0< p \le \frac{1}{3}\). Here we see that a sudden change occurs at the point \(p=\frac{1}{3}\), if we plot the concurrence as a function of the parameter p. Based on definition introduced above, the quantum correlation of the above two-qubit state can be manually worked out, which is \(C(\rho )=\sqrt{2-\sqrt{4-3p^4}}\). It is a smooth function of the parameter p. More importantly, the present measure can be used to calculate the quantum correlation of high-dimensional bipartite states. As another example, we consider a \(2\otimes 3\) bipartite state of the form,

$$\begin{aligned} \rho =p|\psi \rangle \langle \psi |+\frac{1-p}{6}I_6, \end{aligned}$$
(8)

which is a mixture of an entangled pure state \(|\psi \rangle =\frac{1}{\sqrt{3}}(|00\rangle +|11\rangle +|12\rangle )\) and a mixed state represented by \(\frac{1}{6}I_6\). According to the Peres–Horodecki criterion [40, 41], this state is entangled for \(\frac{2\sqrt{2}-1}{7}<p\le 1\), with quantum entanglement of Negativity [42] \(N(\rho _{AB})=\frac{1}{3}(2\sqrt{2}p+p-1)\), and separable for \(0\le p\le \frac{2\sqrt{2}-1}{7}\). To calculate the quantum correlation of the above state (8), we first partition its density matrix into four blocks and get

$$\begin{aligned} B^{(1)}=\frac{1}{6}\left( \begin{array}{lll} 1+p &{}\quad 0 &{}\quad 0\\ 0 &{} \quad 1-p &{}\quad 0 \\ 0 &{} \quad 0 &{}\quad 1-p \end{array} \right) ,~B^{(2)}=\frac{1}{3}\left( \begin{array}{lll} 0 &{}\quad p &{} \quad p\\ 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 \end{array} \right) , \nonumber \\ B^{(3)}=\frac{1}{3}\left( \begin{array}{lll} 0 &{} \quad 0 &{} \quad 0\\ p &{}\quad 0 &{}\quad 0\\ p &{}\quad 0 &{}\quad 0 \end{array} \right) , ~B^{(4)}=\frac{1}{6}\left( \begin{array}{lll} 1-p &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1+p &{}\quad 2p \\ 0 &{} \quad 2p &{}\quad 1+p \end{array} \right) . \end{aligned}$$
(9)

There are 16 commutation relations among these block matrices, where the 10 nonzero ones are,

$$\begin{aligned} \left[ B^{(1)},B^{(2)}\right]= & {} -\left[ B^{(2)},B^{(1)}\right] =\frac{1}{9}\left( \begin{array}{lll} 0 &{} \quad p^2 &{}\quad p^2\\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{} \quad 0 &{}\quad 0 \end{array} \right) , \nonumber \\ \left[ B^{(1)},B^{(3)}\right]= & {} -\left[ B^{(3)},B^{(1)}\right] =-\frac{1}{9}\left( \begin{array}{lll} 0 &{} \quad 0 &{} \quad 0\\ p^2 &{}\quad 0 &{}\quad 0 \\ p^2 &{} \quad 0 &{} \quad 0 \end{array} \right) , \nonumber \\ \left[ B^{(2)},B^{(3)}\right]= & {} -\left[ B^{(3)},B^{(2)}\right] =\frac{1}{9}\left( \begin{array}{lll} 2p^2 &{}\quad 0 &{} \quad 0\\ 0 &{}\quad -p^2 &{}\quad -p^2 \\ 0 &{} \quad -p^2 &{} \quad -p^2 \end{array} \right) , \nonumber \\ \left[ B^{(2)},B^{(4)}\right]= & {} -\left[ B^{(4)},B^{(2)}\right] =\frac{1}{9}\left( \begin{array}{lll} 0 &{} \quad 2p^2 &{} \quad 2p^2\\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{array} \right) , \nonumber \\ \left[ B^{(3)},B^{(4)}\right]= & {} -\left[ B^{(4)},B^{(3)}\right] =-\frac{1}{9}\left( \begin{array}{lll} 0 &{}\quad 0 &{} \quad 0\\ 2p^2 &{}\quad 0 &{}\quad 0 \\ 2p^2 &{}\quad 0 &{}\quad 0 \end{array} \right) . \end{aligned}$$
(10)

All the 16 commutation results, including the above 10 nonzero matrices and the other 6 zero matrices, compose of the test matrix of the bipartite state (8), whose Frobenius norm is \(\Vert T(\rho )\Vert _F=\frac{2\sqrt{14}}{9}p^2\). The final quantum correlation of the bipartite state (8), based on the definition (6), is then \(C(\rho )=\frac{1}{3}\sqrt{18-2\sqrt{81-56p^4}}\), which is a monotonically increasing function of the parameter p, ranging from the minimum value \(C_\mathrm{min}=0\) for \(p=0\) to the maximum value \(C_\mathrm{max}=\frac{2\sqrt{2}}{3}\) for \(p=1\). In the case of \(p=1\), the above state (8) turns to a pure state \(|\psi \rangle \), whose quantum correlation is equal to its quantum entanglement of Negativity.

An entangled state has nonzero quantum correlation, no matter what kind of entanglement, free or bound [43], is contained. For example, the following bipartite \(3\otimes 3\) state,

$$\begin{aligned} \rho _{\alpha }= \frac{2}{7}|\varPsi _{+}\rangle \langle \varPsi _{+}| + \frac{\alpha }{7}\sigma _{+}+ \frac{5-\alpha }{7}\sigma _{-}, \ \ 2\le \alpha \le 5, \end{aligned}$$
(11)

where

$$\begin{aligned} |\varPsi _{+} \rangle= & {} \frac{1}{\sqrt{3}}(|00\rangle +|11\rangle +|22\rangle ) \nonumber \\ \sigma _{+}= & {} {1 \over 3}(|01\rangle \langle 0 1| + |12\rangle \langle 1 2|+ |20\rangle \langle 2 0|) \nonumber \\ \sigma _{-}= & {} {1 \over 3}(|10\rangle \langle 1 0| + |21\rangle \langle 21|+ |02\rangle \langle 0 2|), \end{aligned}$$
(12)

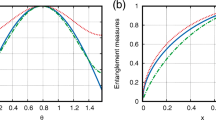
is separable for \(2\le \alpha \le 3\), bound entangled for \(3<\alpha \le 4\), and free entangled for \(4 <\alpha \le 5\) [44]. It is not easy to derive the analytical result of its geometric discord, due to the minimization involved in its definition, and the bound on its geometric discord is studied in Ref. [45]. The density matrix of this state can be partitioned into 9 blocks, and the 81 communication results between these blocks construct a test matrix with Frobenius norm \(\Vert T(\rho )\Vert _F=\frac{4}{441}\sqrt{18\alpha ^2-90\alpha +138}\). According to the definition in Eq. (6), the quantum correlation of this \(3\otimes 3\) state (11) is \(C(\rho )=\frac{1}{21}\sqrt{882-2\sqrt{192273+288\alpha (5-\alpha )}}\), which is a smooth function of the parameter \(\alpha \), and remains positive for \(2\le \alpha \le 5\). Furthermore, the minimum quantum correlation is located at the point \(\alpha =2.5\), where minimum geometric discord and minimum quantum Fisher information [46] is also located [45, 47].

Similar to quantum discord, the present measure of quantum correlation is not symmetric under the interchange of the apparatus \(\mathcal{A}\) and the system \(\mathcal{S}\), owing to the fact that the “apparatus” and the “system” play different roles in the present definition. Given an \(\mathcal{SA}\) bipartite quantum state, especially a mixed state, the present measure might give out two different results if the two subsystems \(\mathcal{S}\) and \(\mathcal{A}\) are interchanged; especially, an AB bipartite quantum state with zero quantum correlation, measured under the apparatus A, may have nonzero quantum correlation if we choose the other subsystem B as the apparatus. For example, we consider a quantum state \(\rho _{AB}=0.5|0\rangle _A\langle 0|\otimes \rho _B^{(1)}+0.5|1\rangle _A\langle 1|\otimes \rho _B^{(2)}\), with \(\rho _B^{(1)}=\frac{1}{3}\left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 2 \\ \end{array} \right) \) and \(\rho _B^{(2)}=\frac{1}{3}\left( \begin{array}{cc} 1 &{} 1 \\ 1 &{} 2 \\ \end{array} \right) \),which has zero quantum correlation under the apparatus of the subsystem A. However, if we choose the subsystem B as the apparatus, its quantum correlation, measured by the method introduced in this paper, is \(C(\rho _{AB})=\frac{1}{3}\sqrt{18-\sqrt{323}}\).

4 Conclusions

Different from quantum entanglement, the quantum correlation provides another angle of view to describe a bipartite state, which has many potential applications in quantum information processing. To measure quantum correlation, an optimization is usually required, which brings an obstacle for many theoretical investigations on quantum correlation. For example, an analytical result is usually very hard to obtain for the quantum correlation of a high-dimensional bipartite state. In this paper, we propose a new measure of quantum correlation, where no optimization is involved in the definition. This measure, which satisfies all the required conditions for a good measure and coincides with Wootters concurrence for two-qubit pure states, can be computed efficiently and even calculated manually, no matter what dimension the corresponding Hilbert space has.

Both quantum entanglement and quantum correlation play their own role in quantum information processing. Although we know that an entangled state must have nonzero quantum correlation, it is far from fully understanding the relationship between the two concepts. Since the present measure of quantum correlation is easy to compute and can even be calculated manually, it may be a useful tool for many related issues.