SpringerLink
Log in

A numerical approach for nonlinear time-fractional diffusion equation with generalized memory kernel

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

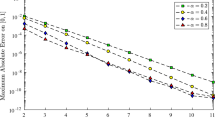
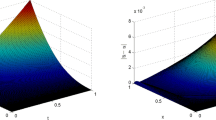
In this manuscript, a nonlinear time-fractional diffusion equation with a generalized memory kernel is studied. Initially, the original model problem is linearized by implementing the Newton’s quasilinearization technique. In the time-fractional term, a generalized Caputo derivative is considered and approximated using the non-uniform L1-scheme as the solution has a singularity at \(t=0\). The main contribution of this work is to develop a generalized discrete fractional Grönwall inequality. Thereafter, permitting its use to establish the stability and analyze the error estimate, under a proper regularity condition in the \(L^2\)-norm, and an optimal convergence order \(\mathcal {O}\left( N^{-(2-\zeta )}\right) \) is obtained for the L1-scheme with respect to the graded mesh. Numerical results are inserted to corroborate the effectiveness of the theoretical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data availability

All data generated or analyzed during this study are included in this article.

References

  1. Alikhanov, A.A.: A time-fractional diffusion equation with generalized memory kernel in differential and difference settings with smooth solutions. Comput. Methods Appl. Math. 17(4), 647–660 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  2. Alikhanov, A.A., Asl, M.S., Huang, C., Khibiev, A.: A second-order difference scheme for the nonlinear time-fractional diffusion-wave equation with generalized memory kernel in the presence of time delay. J. Comput. Appl. Math. 438, 115515 (2024)

    Article  MathSciNet  MATH  Google Scholar 

  3. Atman, K.G., Şirin, H.: Nonlocal phenomena in quantum mechanics with fractional calculus. Rep. Math. Phys. 86, 263–270 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  4. Axtell, M., Bise, M.E.: Fractional calculus application in control systems. in IEEE Conference on aerospace and electronics, IEEE, 563–566 (1990)

  5. Bagley, R.L., Torvik, P.: A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 27, 201–210 (1983)

    Article  MATH  Google Scholar 

  6. Boltzmann, L.: Theory of elastic aftereffect [zur theorie der elastischen nachwirkung]. Ann. Der Phys. Und Chem. Erganz. 7, 624–654 (1876)

    Google Scholar 

  7. Boltzmann, L.: Zur theorie der elastischen nachwirkung. Ann. Phys. 241, 430–432 (1878)

    Article  Google Scholar 

  8. Carpinteri, A., Cornetti, P., Sapora, A.: Nonlocal elasticity: an approach based on fractional calculus. Meccanica. 49, 2551–2569 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  9. Carpinteri, A., Mainardi, F.: Fractals and fractional calculus in continuum mechanics, Springer, 378 (2014)

  10. Gu, X.M., Huang, T.Z., Zhao, Y.L., Lyu, P., Carpentieri, B.: A fast implicit difference scheme for solving the generalized time-space fractional diffusion equations with variable coefficients. Numer. Methods Partial Differ. Equ. 37, 1136–1162 (2021)

    Article  MathSciNet  Google Scholar 

  11. Hardy, G., Littlewood, J., Pólya, G.: Inequalities. Cambridge University Press, Cambridge (1934)

    MATH  Google Scholar 

  12. Kalaba, R., S**arn, K.: On the rate of convergence of the quasi-linearization method. IEEE Trans. Automatic Control 28, 798–799 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kedia, N., Alikhanov, A.A., Singh, V.K.: Stable numerical schemes for time-fractional diffusion equation with generalized memory kernel. Appl. Numer. Math. 172, 546–565 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  14. Khibiev, A., Alikhanov, A.A., Huang, C.: A second-order difference scheme for generalized time-fractional diffusion equation with smooth solutions. Comput. Methods Appl, Math (2023)

    Book  MATH  Google Scholar 

  15. Liao, H.L., Li, D., Zhang, J.: Sharp error estimate of the nonuniform L1 formula for linear reaction-subdiffusion equations. SIAM J. Numer. Anal. 56, 1112–1133 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  16. Lin, Y., Xu, C.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225, 1533–1552 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  17. Mainardi, F.: On the advent of fractional calculus in econophysics via continuous-time random walk. Mathematics 8, 641 (2020)

    Article  Google Scholar 

  18. Sandev, T., Chechkin, A., Kantz, H., Metzler, R.: Diffusion and Fokker-Planck-Smoluchowski equations with generalized memory kernel. Fract. Calc. Appl. Anal. 18, 1006–1038 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  19. Saqib, M., Khan, I., Shafie, S.: Application of fractional differential equations to heat transfer in hybrid nanofluid: modeling and solution via integral transforms. Adv. Differ. Equ. 2019, 1–18 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  20. Stynes, M., O’Riordan, E., Gracia, J.L.: Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 55, 1057–1079 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  21. Tarasov, V.E.: On history of mathematical economics: application of fractional calculus. Mathematics 7, 509 (2019)

    Article  Google Scholar 

  22. Yan, Y., Khan, M., Ford, N.J.: An analysis of the modified L1 scheme for time-fractional partial differential equations with nonsmooth data. SIAM J. Numer. Anal. 56, 210–227 (2018)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The first author would like to express the thanks to Indian Institute of Technology Guwahati, India for funding this project. The authors wish to acknowledge the referees for their valuable comments and suggestions, which helped to improve the presentation.

Funding

This work was supported by the Indian Institute of Technology Guwahati, India.

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati, Assam, 781039, India

    Aniruddha Seal & Srinivasan Natesan

Authors
  1. Aniruddha Seal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Srinivasan Natesan
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.S. implemented the method, prepared the first draft of the manuscript, and implemented the computer codes. S.N. provided the concept, methodology, correcting the manuscript, etc.

Corresponding author

Correspondence to Srinivasan Natesan.

Ethics declarations

Ethics approval and consent to participate

Not applicable

Consent for publication

Not applicable

Conflict of interest

The authors declare no competing interests.

Human and animal ethics

Not applicable

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Seal, A., Natesan, S. A numerical approach for nonlinear time-fractional diffusion equation with generalized memory kernel. Numer Algor (2023). https://doi.org/10.1007/s11075-023-01714-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11075-023-01714-7

Keywords

Mathematics Subject Classification (2010)

Search

Navigation