Mathematical modeling the dynamics of SARS-CoV-2 infection with antibody-dependent enhancement

Abstract

The advent and swift global spread of the novel coronavirus (COVID-19) transmitted by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) have caused massive deaths and economic devastation worldwide. Antibody-dependent enhancement (ADE) is a common phenomenon in virology that directly affects the effectiveness of the vaccine, and there is no fully effective vaccine for diseases. In order to study the potential role of ADE on SARS-CoV-2 infection, we establish the SARS-CoV-2 infection dynamics model with ADE. The basic reproduction number is computed. We prove that when $R_0<1$, the infection-free equilibrium is globally asymptotically stable, and the system is uniformly persistent when $R_0>1$. We carry out the sensitivity analysis by the partial rank correlation coefficients and the extended version of the Fourier amplitude sensitivity test. Numerical simulations are implemented to illustrate the theoretical results. The potential impact of ADE on SARS-CoV-2 infection is also assessed. Our results show that ADE may accelerate SARS-CoV-2 infection. Furthermore, our findings suggest that increasing antibody titers can have the ability to control SARS-CoV-2 infection with ADE, but enhancing the neutralizing power of antibodies may be ineffective to control SARS-CoV-2 infection with ADE. Our study presumably contributes to a better understanding of the dynamics of SARS-CoV-2 infection with ADE.

1 Introduction

The pandemic coronavirus disease 2019 (COVID-19) resulting from severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is spreading swiftly around the world. SARS-CoV-2 was firstly notified on December 1, 2020, and then confirmed to be a formerly unidentified beta coronavirus [1, 2]. As of May 31, 2022, the cumulative reported number of confirmed cases of COVID-19 reaches over 529 million and the cumulative number of deaths reaches over 6.28 million worldwide [3]. Many countries have launched mass vaccination campaigns to control COVID-19. Currently, 63.6% of the world’s population have received at least one dose of the COVID-19 vaccine and 57% are fully vaccinated [4].

Antibody-dependent enhancement (ADE) is a significant increase in the replication or infectivity of certain viruses treated with corresponding antibodies [5]. Several studies [6,7,8] provide evidence that SARS-CoV-2 antibodies can cause ADE phenomenon in vitro. Through the study of the rhesus monkey model, Wang et al. [6] gave the first evidence that certain SARS-CoV-2 monoclonal antibodies lead to the ADE phenomenon in vitro. Through the cellular and structural biology analysis, Wu et al. [7] discovered that some monoclonal antibodies could enhance infection of SARS-CoV-2 in vitro. At the same time, these antibodies are still able to neutralize SARS-CoV-2. Liu et al. [8] discovered that some antibodies reinforce the binding ability of spike protein to ACE-2, and the infectivity of SARS-CoV-2 increases. As a result, the mechanism of ADE on SARS-CoV-2 indicates that SARS-CoV-2 can infect target cells more easily.

Mathematical modeling is an important method for quantitative and qualitative research on COVID-19 [9,10,11,12,13,14,15]. Several modeling studies contributed to the spread dynamics of COVID-19. Song et al. [11] used Baidu migration data and a mathematical model to assess the epidemic size of COVID-19 spread in Wuhan as of 23 January 2020. Tang et al. [13] estimated the risk of COVID-19 spread and displayed the influence of interventions on COVID-19 spread in China. At the same time, there are some studies about the within-Host dynamics of SARS-CoV-2. Wang et al. [14] used a model to characterize the SARS-CoV-2 infection by the interaction between viral duplication and host immune response. Perelson et al. [15] modeled the viral dynamics of SARS-CoV-2 infection and fitted it to the data to evaluate key parameters within the host.

There are several types of research on infectious disease models with ADE. Tang et al. [16] developed a dynamic model of COVID-19 incorporating vaccination and waning immunity, and they found that declining immunity, ADE, relaxation of interventions and higher transmissibility of variants make COVID-19 more difficult to control. Using the mathematical model with a dynamic switch, Gujarati et al. [17] analyzed humoral host response to primary and secondary dengue infection with ADE. Ceron et al. [18] established a dengue virus model with ADE, and evaluated the effect of the ADE phenomenon on heterologous dengue infection. Based on infection-neutralizing and infection-enhancing antibody competition scenarios, Camargo et al. [19] modeled the dynamics of secondary infection induced by two different serotypes of dengue virus, and calculated the time when the maximum enhancing activity for the infection occurs. By extending the basic model of viral dynamics, Danchin et al. [20] established neutralizing and weakly neutralizing scenarios, and they found that both weakly neutralizing antibodies and ADE could lead to eventual viral clearance or disease progression. The models in these articles focus on the perspective of cells and viruses. However, there is little research on the dynamic model describing the process of ADE infection with SARS-CoV-2 in detail.

The basic reproduction number is defined as the expected number of secondary cases caused by a single infection in a completely susceptible population [21, 22]. If $R_0<1$, the disease will decline and eventually die out. If $R_0>1$, the disease will spread and there may be an epidemic.

In this paper, to study the potential role of ADE on the SARS-CoV-2 infection, we establish the SARS-CoV-2 infection dynamics model with ADE including antibodies and immune complexes. The basic reproduction number is calculated. The stability of equilibria and the uniform persistence of the system are analyzed. In addition, the partial rank correlation coefficients (PRCCs) and the extended version of the Fourier amplitude sensitivity test (eFAST) are used to carry out the sensitivity analysis to study the effect of ADE on the SARS-CoV-2 infection. Numerical simulations are implemented to indicate the theoretical results and complex dynamics. The potential effect of ADE on the SARS-CoV-2 infection is also assessed.

This paper is organized as follows. In Sect. 2, we establish the SARS-CoV-2 dynamics model with ADE. The nonnegativity and ultimate boundedness of solutions are given. In Sect. 3, we calculate the basic reproduction number. In addition, we prove the global stability of the infection-free equilibrium and the local stability of the infection equilibrium, and the uniform persistence of the system is analyzed. In Sect. 4, sensitivity analysis and numerical simulations are carried out. The potential impact of ADE on SARS-CoV-2 infection is evaluated. Finally, a brief discussion completes the paper.

2 Mathematical modeling the dynamics of SARS-CoV-2 infection with antibody-dependent enhancement

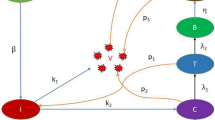
Based on the ADE phenomenon caused by SARS-CoV-2 antibodies [6,7,8, 23] and the detection of SARS-CoV-2 [24,25,26], we assume that the immune response has eradicated the initial SARS-CoV-2 infection. However, the immune memory is retained to deal with the fresh attack. When the re-infection of SARS-CoV-2 variants (V) occurs, antibodies (A) can partially neutralize the virus by forming immune complexes without complete neutralization (B) due to cross-immunity. At the same time, the target cells (T) are infected as a result of the immune complexes, and thus infected target cells (I) occur. Since the target cells contain a class of leukocytes, then we assume that the infected target cells can recover [6]. The infected target cells release the viruses through exocytosis or cell death [27]. The flowchart is shown in Fig. 1.

Fig. 1

The flowchart of SARS-CoV-2 infection dynamics with ADE

Based on the above discussion and the previous work [14, 18], SARS-CoV-2 infection dynamics model with ADE is given as

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle {\frac{\mathrm {d}A(t)}{\mathrm {d}t}}&=r_1-\theta A(t)V(t)-d_AA(t),\\ \displaystyle {\frac{\mathrm {d}B(t)}{\mathrm {d}t}}&=\theta A(t)V(t)-d_BB(t),\\ \displaystyle {\frac{\mathrm {d}T(t)}{\mathrm {d}t}}&=r_2-\beta cB(t)T(t)-d_TT(t)+\gamma I(t),\\ \displaystyle {\frac{\mathrm {d}I(t)}{\mathrm {d}t}}&=\beta cB(t)T(t)-\gamma I(t)-d_II(t),\\ \displaystyle {\frac{\mathrm {d}V(t)}{\mathrm {d}t}}&=\alpha I(t)+Nd_II(t)-\theta A(t)V(t)-d_VV(t), \end{aligned}\right. \nonumber \\ \end{aligned}$$

(1)

with the nonnegative initial values

$$\begin{aligned} \begin{aligned}&A(0)>0, B(0)\ge 0, T(0)>0, I(0)\ge 0\\&\mathrm{and} \ \ V(0)\ge 0. \end{aligned} \end{aligned}$$

(2)

Where all parameters are positive. $r_1$ is the recruitment rate of antibodies, and $r_2$ is the recruitment rate of target cells. We assume that $d_A$ is the clearance rate of antibodies, $d_B$ is the removal rate of immune complexes, $d_T$ is the natural death rate of target cells, and $d_I$ represents the death rate of infectious target cells due to infection with $d_I\ge d_T$ and $d_V$ represents the clearance rate of viruses. $\theta$ denotes the binding rate between antibodies and viruses, and c denotes the engulfment rate of immune complexes. Let $\beta$ be the infection rate of target cells and $\gamma$ be the recovery rate of infectious target cells. The parameter $\alpha$ is the releasing rate of viruses and N is the releasing rate of viruses by the target cells’ death. The details of parameters are shown in Table 1.

Table 1 Parameters and descriptions

Theorem 2.1

The solutions of the model (1) with nonnegative initial values (2) is nonnegative and ultimately bounded.

Proof

From model (1) with nonnegative initial values (2), we can get

$$\begin{aligned} \begin{aligned} A(t)&=\,e^{-\int _{0}^{t}(\theta V(s)+d_A)\mathrm {d}s}(A(0)\\&\quad +\int _{0}^{t}r_1e^{\int _{0}^{s}(\theta V(\gamma )+d_A)\mathrm {d}\gamma }\mathrm {d}s)\\&>0 \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} B(t)&=B(0)e^{-\int _{0}^{t}d_B\mathrm {d}s}+\int _{0}^{t}\theta A(s)V(s)e^{\int _{s}^{t}d_B\mathrm {d}\epsilon }\mathrm {d}s, \\ T(t)&=T(0)e^{-\int _{0}^{t}(\beta cB(s)+d_T)\mathrm {d}s}\\&\quad +\int _{0}^{t}(r_2+\gamma I(s))e^{\int _{s}^{t}(\beta cB(\epsilon )+d_T)\mathrm {d}\epsilon }\mathrm {d}s,\\ I(t)&=I(0)e^{-\int _{0}^{t}(\gamma +d_I)\mathrm {d}s}\\&\quad +\int _{0}^{t}(\beta cB(s)T(s))e^{\int _{s}^{t}(\gamma +d_I)\mathrm {d}\epsilon }\mathrm {d}s,\\ V(t)&=V(0)e^{-\int _{0}^{t}(\theta A(s)+d_V)\mathrm {d}s}+\int _{0}^{t}(\alpha I(s)\\&\quad +Nd_II(s))e^{\int _{s}^{t}(\theta A(\epsilon )+d_V)\mathrm {d}\epsilon }\mathrm {d}s \end{aligned} \end{aligned}$$

with $B(0)\ge 0, T(0)>0, I(0)\ge 0\ \text {and}\ V(0)\ge 0$.

Firstly, we prove that $B(t), I(t), V(t), T(t)\ge 0$ ($\forall t\ge 0$) always hold. If not, we choose an $t_0>0$ such that $\{B(t_0), T(t_0), I(t_0), V(t_0)\}<0$, and then $\{B(t), T(t), I(t), V(t)\}\ge 0$ for $\forall t\in [0,t_0)$. Without loss of generality, let $B(t_0)<0$. Since $A(t)>0$, $B(t)\ge 0$ and $V(t)\ge 0 (\forall t\in [0,t_0))$, then

$$\begin{aligned} B(0)e^{-\int _{0}^{t_0}d_B\mathrm {d}s}+\int _{0}^{t_0}\theta A(s)V(s)e^{\int _{s}^{t_0}d_B\mathrm {d}\epsilon }\mathrm {d}s \ge 0, \end{aligned}$$

which contradicts with $B(t_0)<0$. Then $B(t)\ge 0$. Similarly, $I(t)\ge 0$, $V(t)\ge 0$ and $T(t)>0$. Therefore, the nonnegativity of solutions is proved.

Now, we prove the boundedness of solutions. From model (1),

$$\begin{aligned} \frac{\mathrm {d}A(t)}{\mathrm {d}t}\le r_1-d_AA(t), \end{aligned}$$

Thus $\limsup _{t\rightarrow \infty }A(t)\le r_1/d_A$, and then A(t) is ultimately bounded. Due to $d_I\ge d_T$, then

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}(T(t)+I(t))}{\mathrm {d}t}&=\,r_2-d_TT(t)-d_II(t)\\&\le r_2-d_T(T(t)+I(t)). \end{aligned} \end{aligned}$$

According to the comparison theorem [28], $\limsup _{t\rightarrow \infty }(T(t)+I(t))\le r_2/d_T$. Thus, T(t) and I(t) are ultimately bounded. From the fifth equation in model (1),

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}V(t)}{\mathrm {d}t}&=\,\alpha I(t)+Nd_II(t)-d_VV(t)\\&\le \frac{(\alpha +Nd_I)r_2}{d_T}-d_VV(t), \end{aligned} \end{aligned}$$

then $\limsup _{t\rightarrow \infty }V(t)\le \frac{(\alpha +Nd_I)r_2}{d_Vd_T}$. Similarly, $\limsup _{t\rightarrow \infty }B(t)$ $\le \frac{\theta r_1r_2(\alpha +Nd_I)}{d_Ad_Bd_Td_V}$. Then V(t) and B(t) are ultimately bounded. Therefore, the nonnegativity and boundedness of solutions of model (1) are proved.

$\square$

Therefore, the feasible region

$$\begin{aligned} \begin{aligned} \Gamma&=\left\{ (A,B,T,I,V)\in R^4_+: A\le \frac{r_1}{d_A},\right. \\&T+I\le \frac{r_2}{d_T}, V \le \frac{(\alpha +Nd_I)r_2}{d_Vd_T}, \\&\left. B \le \frac{\theta r_1r_2(\alpha +Nd_I)}{d_Ad_Bd_Td_V}\right\} \end{aligned} \end{aligned}$$

is positively invariant in model (1).

3 Threshold dynamics

3.1 The basic reproduction number and equilibria

From model (1), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} r_1-\theta A(t)V(t)-d_AA(t)=0,\\ \theta A(t)V(t)-d_BB(t)=0,\\ r_2-\beta cB(t)T(t)-d_TT(t)+\gamma I(t)=0,\\ \beta cB(t)T(t)-\gamma I(t)-d_II(t)=0,\\ \alpha I(t)+Nd_II(t)-\theta A(t)V(t)-d_VV(t)=0. \end{array}\right. } \end{aligned}$$

(3)

System (1) always has an infection-free equilibrium $E_{0}=(A^0,0,T^0,0,0),$ where $A^0=r_1/d_A$ and $T^0=r_2/d_T$.

Let $X=(I,V,B)$, and the model (1) can be expressed as

$$\begin{aligned} \frac{\mathrm {d}X(t)}{\mathrm {d}t}={\mathscr {F}}-{\mathscr {V}}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&{\mathscr {F}}=\begin{pmatrix} \beta cB(t)T(t)\\ 0\\ 0 \end{pmatrix},\\&{\mathscr {V}}=\begin{pmatrix} \gamma I(t)+d_II(t)\\ \theta A(t)V(t)+d_VV(t)-\alpha I(t)-Nd_II(t)\\ d_BB(t)-\theta A(t)V(t) \end{pmatrix}. \end{aligned} \end{aligned}$$

Obviously, ${\mathscr {F}}$ and ${\mathscr {V}}$ satisfy the conditions (A1)-(A5) in [22].

The Jacobi matrix of ${\mathscr {F}}$ and ${\mathscr {V}}$ at $E_0$ is

$$\begin{aligned} \begin{aligned}&F=\begin{pmatrix} 0 &{} 0 &{} \beta cT^0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix},\\&V=\begin{pmatrix} \gamma +d_I &{} 0 &{} 0 \\ -Nd_I-\alpha &{} \theta A^0+d_V &{} 0 \\ 0 &{} -\theta A^0 &{} d_B \end{pmatrix}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} FV^{-1}=\begin{pmatrix} \frac{(\alpha +Nd_I)\beta cT^0\theta A^0}{d_B(\theta A^0+d_V)(\gamma +d_I)} &{} \frac{\beta cT^0\theta A^0}{d_B(\theta A^0+d_V)} &{} \frac{\beta cT^0}{d_B}\\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix}. \end{aligned}$$

Then the basic reproduction number

$$\begin{aligned} R_0=\frac{\alpha +Nd_I}{\gamma +d_I}\frac{\theta A^0}{\theta A^0+d_V}\frac{\beta c}{d_B}T^0. \end{aligned}$$

(4)

From (3), A(t), B(t), T(t) and I(t) can be denoted as a function of V(t), and then

$$\begin{aligned} V(t)(a_1V^2(t)+a_2V(t)+a_3)=0, \end{aligned}$$

(5)

where

$$\begin{aligned} a_1&=-\beta cd_Id_Vr_1\theta ^2-d_Bd_Td_Id_V\theta ^2\\&\quad -d_Bd_Td_V\gamma \theta ^2, \\ a_2&=N\beta cd_Ir_1r_2\theta ^2+\alpha \beta cr_1r_2\theta ^2\\ {}&\quad -\beta cd_Ad_Id_Vr_1\theta -\beta cd_Ir_1^2\theta ^2\\&\quad -2d_Ad_Bd_Td_Id_V\theta -2d_Ad_Bd_Td_V\gamma \theta \\ {}&\quad -d_Bd_Td_Ir_1\theta ^2-d_Bd_T\gamma r_1\theta ^2 ,\\ a_3&=N\beta cd_Ad_Ir_1r_2\theta +\alpha \beta cd_Ar_1r_2\theta \\&\quad -d_A^2d_Bd_Td_Id_V-d_A^2d_Bd_Td_V\gamma \\ {}&\quad -d_Ad_Bd_Td_Ir_1\theta -d_Ad_Bd_T\gamma r_1\theta . \end{aligned}$$

Denote $X(t)=a_1V^2(t)+a_2V(t)+a_3$. When $V(t)=0$ and $R_0>1$, $X(t)>0$. When $V(t)=\frac{(\alpha +Nd_I)r_2}{d_Vd_T}$ and $d_I>d_T$, $X(t)<0$. According to the intermediate value theorem and the properties of quadratic functions, and using $a_1<0$, we have $V^*\in (0,\frac{(\alpha +Nd_I)r_2}{d_Vd_T})$ for $X(t)=0$. Therefore, there is an infection equilibrium $E^*=(A^*,B^*,T^*,I^*,V^*)$.

3.2 The local stability of equilibria

Theorem 3.1

If $R_0<1$, then the infection-free equilibrium $E_0$ of model (1) is locally asymptotically stable in $\Gamma$. If $R_0>1$, the infection-free equilibrium $E_0$ is unstable.

Proof

The Jacobian matrix of model (2.1) at the infection equilibrium $E_0$ is

$$\begin{aligned} J_1=\begin{pmatrix} -d_A &{} 0 &{} 0 &{} 0 &{} -\theta A^0\\ 0 &{} -d_B &{} 0 &{} 0 &{} \theta A^0\\ 0 &{} -\beta cT^0 &{} -d_T &{} \gamma &{} 0\\ 0 &{} \beta cT^0 &{} 0 &{} -\gamma -d_I &{} 0\\ 0 &{} 0 &{} 0 &{} Nd_I+\alpha &{} -\theta A^0-d_I \end{pmatrix}. \end{aligned}$$

Then the characteristic equation corresponding to the Jacobian matrix $J_1$ is

$$\begin{aligned} (d_T+\lambda )(d_A+\lambda )(\lambda ^3+K_1\lambda ^2+K_2\lambda -K_3)=0, \end{aligned}$$

(6)

where

$$\begin{aligned} K_1=\,&\theta A^0+d_B+d_I+d_V+\gamma , \\ K_2=\,&(\theta A^0+d_I+d_V+\gamma )d_B+(\gamma +d_I)(\theta A^0+d_V), \\ K_3=\,&(\alpha +Nd_I)\beta cT^0\theta A^0-d_B(\theta A^0+d_V)(\gamma +d_I). \end{aligned}$$

Obviously, $K_3<0$ when $R_0<1$. When $R_0<1$, Eq. (6) has two negative roots $-d_T$ and $-d_A$, and the other roots are decided by

$$\begin{aligned} \lambda ^3+K_1\lambda ^2+K_2\lambda -K_3=0. \end{aligned}$$

(7)

Apparently, $-K_3>0, K_1>0, K_2>0$ and $K_1K_2+K_3>0$. Using the Routh–Hurwitz criteria [28], all roots of Eq. (6) have negative real parts. Thus, the infection-free equilibrium is locally asymptotically stable. When $R_0>1$, $-K_3<0$, and then the infection-free equilibrium is unstable. $\square$

Theorem 3.2

If $R_0>1,$ then the infection equilibrium of model (1) is locally asymptotically stable in $\Gamma$.

Proof

The Jacobian matrix of the system (1) at the infection equilibrium $E^*$ is

$$\begin{aligned} \begin{aligned} J_2=\begin{pmatrix} {\begin{matrix} -\theta V^*-d_A &{} 0 &{} 0 &{} 0 &{} -\theta A^*\\ \theta V^* &{} -d_B &{} 0 &{} 0 &{} \theta A^*\\ 0 &{} -\beta cT^* &{} -\beta cB^*-d_T &{} \gamma &{} 0\\ 0 &{} \beta cT^* &{} \beta cB^* &{} -\gamma -d_I &{} 0\\ -\theta V^* &{} 0 &{} 0 &{} Nd_I+\alpha &{} -\theta A^*-d_I \end{matrix}} \end{pmatrix}. \end{aligned} \end{aligned}$$

The characteristic equation corresponding to the Jacobian matrix $J_2$ is

$$\begin{aligned} \begin{aligned} G(\lambda )&=\lambda ^5+G_4\lambda ^4+G_3\lambda ^3\\&\quad +G_2\lambda ^2+G_1\lambda +G_0=0, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} G_4&=\,B^*\beta c+A^*\theta +V^*\theta +d_A+d_B\\ {}&\quad +d_T+d_I+d_V+\gamma ,\\ G_3&=\,A^*B^*\beta c\theta +B^*V^*\beta c\theta +B^*\beta cd_A\\&\quad +B^*\beta cd_B+B^*\beta cd_I+B^*\beta cd_V\\&\quad +A^*d_A\theta +A^*d_B\theta +A^*d_T\theta \\&\quad +A^*d_I\theta +A^*\gamma \theta +V^*d_B\theta +V^*d_T\theta \\&\quad +V^*d_I\theta +V^*d_V\theta +V^*\gamma \theta +d_Ad_B \\&\quad +d_Ad_T+d_Ad_I+d_Ad_V+d_A\gamma \\&\quad +d_Bd_T+d_Bd_I+d_Bd_V\\&\quad +d_B\gamma +d_Td_I+d_Td_V+d_T\gamma \\&\quad +d_Id_V+d_V\gamma , \\ G_2&=\,A^*B^*\beta cd_A\theta +A^*B^*\beta cd_B\theta +A^*B^*\beta cd_I\theta \\&\quad +B^*V^*\beta cd_B\theta +B^*V^*\beta cd_I\theta \\&\quad +B^*V^*\beta cd_V\theta +B^*\beta cd_Ad_B+B^*\beta cd_Ad_I\\&\quad +B^*\beta cd_Ad_V+B^*\beta cd_Bd_I+B^*\beta cd_Bd_V\\&\quad +B^*\beta cd_Id_V +A^*d_Ad_B\theta +A^*d_Ad_T\theta \\&\quad +A^*d_Ad_I\theta +A^*d_A\gamma \theta +V^*d_T\gamma \theta \\&\quad +A^*d_Bd_T\theta +A^*d_Td_I\theta +A^*d_T\gamma \theta \\&\quad +V^*d_Bd_T\theta +V^*d_Bd_I\theta +V^*d_Bd_V\theta \\&\quad +V^*d_Td_I\theta +V^*d_Td_V\theta +V^*d_B\gamma \theta \\&\quad +V^*d_Id_V\theta +V^*d_V\gamma \theta +d_Ad_Bd_T\\&\quad +d_Ad_Bd_I+d_Ad_Bd_V+d_Ad_B\gamma \\&\quad +d_Ad_Td_I+d_Ad_Td_V +d_Ad_T\gamma \\&\quad +d_Ad_Id_V+d_Ad_V\gamma +d_Bd_Td_I\\&\quad +d_Bd_Td_V+d_Bd_T\gamma +d_Td_Id_V+d_Td_V\gamma , \\ G_1&=\,A^*B^*\beta cd_Ad_B\theta +A^*B^*\beta cd_Ad_I\theta \\&\quad +A^*B^*\beta cd_Bd_I\theta +B^*V^*\beta cd_Bd_I\theta \\&\quad +B^*V^*\beta cd_Bd_V\theta +B^*V^*\beta cd_Id_V\theta \\&\quad +B^*\beta cd_Ad_Bd_I+B^*\beta cd_Ad_Bd_V\\&\quad +B^*\beta cd_Ad_Id_V\\&\quad +B^*\beta cd_Bd_Id_V +A^*d_Ad_Bd_T\theta \\&\quad +A^*d_Ad_Td_I\theta +A^*d_Ad_T\gamma \theta +V^*d_Bd_Td_I\theta \\&\quad +V^*d_Bd_Td_V\theta +V^*d_Bd_T\gamma \theta \\&\quad +V^*d_Bd_Id_V\theta +V^*d_Bd_V\gamma \theta +V^*d_Td_Id_V\theta \\&\quad +V^*d_Td_V\gamma \theta +d_Ad_Bd_Td_I+d_Ad_Bd_Td_V \\&\quad +d_Ad_Bd_T\gamma +d_Ad_Td_Id_V+d_Ad_Td_V\gamma , \\ G_0&=\,A^*B^*\beta cd_Ad_Bd_I\theta +B^*V^*\beta cd_Bd_Id_V\theta \\&\quad +B^*\beta cd_Ad_Bd_Id_V+V^*d_Bd_Td_Id_V\theta \\&\quad +V^*d_Bd_Td_V\gamma \theta . \end{aligned}$$

According to the Routh–Hurwitz criteria [28], when

$$\begin{aligned}&G_4>0, \nonumber \\&G_4G_3-G_2>0, \nonumber \\&G_4G_3G_2+G_4G_0-G)2^2-G_4^2G_1>0, \\&G_1(G_4G_3G_2+G_4G_0-G_2^2-G_4^2G_1)\nonumber \\&-G_0(G_4G_3^2+G_0-G_4G_1-G_2G_3)>0, \nonumber \\&G_0>0, \nonumber \end{aligned}$$

(8)

the infection equilibrium is locally asymptotically stable. Using Maple, we can get that the conditions hold in (8). Thus, the infection equilibrium is locally asymptotically stable when $R_0>1$. $\square$

3.3 Global stability of the infection-free equilibrium

Denote $F(x)=x-1-\ln x (x>0)$. It is obviously that $F(x)\ge 0$ when $x>0$, and $F_{\min }(x) = F(1) = 0$.

Theorem 3.3

If $R_0<1,$ the infection-free equilibrium $E_0$ of model (1) is globally asymptotically stable in $\Gamma$.

Proof

Define the Lyapunov function

$$\begin{aligned}&L_0(t) \\&= A^0F\bigg (\frac{A(t)}{A^0}\bigg ) +\frac{(\theta A^0+d_V)d_B}{d_V\beta cT^0}T^0F\bigg (\frac{T(t)}{T^0}\bigg )\\&\quad +\frac{\theta A^0+d_V}{d_V}B(t) +\frac{(\alpha +Nd_I)\theta A^0}{d_V(\gamma +d_I)}I(t)\\&\quad +\frac{\theta A^0}{d_V}V(t). \end{aligned}$$

Calculating the derivative of $L_0(t)$ along the solutions of system (1), we obtain

$$\begin{aligned}&\frac{\mathrm {d}L_0(t)}{\mathrm {d}t}\bigg |_{(2.1)}\\&=(1-\frac{A(t)}{A^0})(r_1-\theta A(t)V(t)-d_AA(t))\\&\quad +\frac{\theta A^0+d_V}{d_V}(\theta A(t)V(t)-d_BB(t)) \\&\quad +\frac{(\theta A^0+d_V)d_B}{d_V\beta cT^0}(1-\frac{T^0}{T(t)})(r_2-\beta cB(t)T(t)\\&\quad -d_TT(t)+\gamma I(t))+\frac{(\alpha +Nd_I)\theta A^0}{d_V(\gamma +d_I)}\\&(\beta cB(t)T(t)-\gamma I(t)-d_II(t)) \\&\quad +\frac{\theta A^0}{d_V}(\alpha I(t)+Nd_II(t)\\&\quad -\theta A(t)V(t)-d_VV(t). \end{aligned}$$

Since $r_1=d_AA^0$ and $r_2=d_TT^0$, then

$$\begin{aligned} \frac{\mathrm {d}L_0(t)}{\mathrm {d}t}\bigg |_{(2.1)}&=-\frac{d_A}{A(t)}(A(t)-A^0)^2\\&\quad -\frac{(\theta A^0+d_V)d_B}{d_V\beta cT^0}\frac{d_T}{T(t)}(T(t)-T^0)^2 \\&\quad -(\frac{T^0}{T(t)}-1)\gamma I(t)\\&\quad -\frac{(\theta A^0+d_V)d_B}{d_V\beta cT^0}(1-R_0)\beta cB(t)T(t). \end{aligned}$$

When $R_0<1$, $L'_0(t)\le 0$. On the basis of the above discussions, we deduce that the largest compact invariant set in $\{(A(t),B(t),T(t),I(t),V(t))|V'_0(t)=0\}$ is the singleton $\{E_0\}.$ According to the LaSalle’s invariance principle [29], we conclude that $E_0$ is globally asymptotically stable when $R_0<1$. $\square$

3.4 Uniform persistence

Theorem 3.4

When $R_0>1,$ there exists an $\varepsilon >0,$ such that any solution of the system (1) with $B(0)> 0, I(0)> 0\ \text {and}\ V(0)> 0$ satisfies $\liminf _{t\rightarrow \infty }A(t)\ge \varepsilon , \liminf _{t\rightarrow \infty }B(t)\ge \varepsilon , \liminf _{t\rightarrow \infty }T(t)\ge \varepsilon , \liminf _{t\rightarrow \infty }$ $I(t)\ge \varepsilon ,$ and $\liminf _{t\rightarrow \infty }V(t)\ge \varepsilon ,$ and then the system (1) is uniformly persistent.

Proof

Denote

$$\begin{aligned} X&=\{\varphi =(A(t),B(t),T(t),I(t),V(t)):\\&\varphi _2(0)\ge 0,\varphi _4(0)\ge 0,\varphi _5(0)\ge 0\}, \\ X_1&=\{\varphi \in X:\varphi _2(0)>0,\varphi _4(0)>0,\\&\varphi _5(0)>0\}, \\ \partial X_1&=\{\varphi \in X:\varphi _2(0)=0,\varphi _4(0)=0,\\&\varphi _5(0)=0\}. \end{aligned}$$

Clearly, $X_1$ and $X_2$ are relatively closed in X. According to Theorem 2.1, there is a compact set W such that all solutions of (1) remain in W with initial values in X. And W satisfies the condition ($C_{4.2}$) in [30].

Now, we show that $X_1$ is positively invariant with respect to system (1). Let $P(t)(t > 0)$ is the set of solution operators related to the system (1). A sequence $t_n\rightarrow \infty$ when $n\rightarrow \infty$ exits, and $P(t_n)x\rightarrow y$, $y\in X$ when $n\rightarrow \infty .$

From model (1), we have

$$\begin{aligned}&\frac{\mathrm {d}B(t)}{\mathrm {d}t}\ge -d_BB(t), \frac{\mathrm {d}I(t)}{\mathrm {d}t}\ge -\gamma I(t)-d_II(t), \\&\frac{\mathrm {d}V(t)}{\mathrm {d}t}\ge -\theta A(t)V(t)-d_VV(t). \end{aligned}$$

Since $B(0,\varphi )=\varphi _2(0)>0,I(0,\varphi ) =\varphi _4(0)>0,V(0,\varphi )=\varphi _5(0)>0,$ then

$$\begin{aligned}&B(0,\varphi )\ge \varphi _2(0)e^{-d_Bt}>0,\\&I(0,\varphi )\ge \varphi _4(0)e^{-(\gamma +d_it)}>0,\\&V(0,\varphi )\ge \varphi _5(0)e^{-(\theta A(t)-d_Vt)}>0,(\forall t\ge 0). \end{aligned}$$

Thus, $X_1$ is positively invariant. Theorem 2.1 and Theorem 2.9 in [31] imply that P(t) generates a global attractor A.

Denote $\Omega =\bigcup _{x\in \partial X_1}\omega (x).$ We can claim that $\Omega =\{E_0\}.$ From the first and third equations of system (1), we obtain that $\lim _{t\rightarrow \infty }A(t)=r_1/d_A$ and $\lim _{t\rightarrow \infty }T(t)=r_2/d_T.$ Therefore, $\{E_0\}$ is an isolated invariant set and acyclic (since there exists no solution in $\partial X_1$ which connects $E_0$ with itself).

Now, we prove that $W^s(E_0)\cap X_1=\emptyset .$ Suppose not, then there exists a solution $(A(t),B(t),T(t),I(t))\in X_1$ such that

$$\begin{aligned}&\lim _{t\rightarrow \infty }A(t)=\frac{r_1}{d_A}, \lim _{t\rightarrow \infty }B(t)=0, \lim _{t\rightarrow \infty }T(t)=\frac{r_2}{d_T},\nonumber \\&\lim _{t\rightarrow \infty }I(t)=0, \lim _{t\rightarrow \infty }V(t)=0. \end{aligned}$$

(9)

For any small enough constant $\varepsilon _1>0,$ there is a positive constant $T_0=T_0(\varepsilon _1)$ such that $0<r_1/d_A-\varepsilon _1\le A(t)\le r_1/d_A+\varepsilon _1, T(t)\ge r_2/d_T-\varepsilon _1>0, \forall t\ge T_0.$ Since $R_0=\frac{(\alpha +Nd_I)\beta cT^0\theta A^0}{d_B(\theta A^0+d_V)(\gamma +d_I)}>1,$ then we have

$$\begin{aligned} \frac{(\alpha +Nd_I)\beta c(T^0-\varepsilon _1)\theta (A^0-\varepsilon _1)}{d_B(\theta (A^0+\varepsilon _1)+d_V)(\gamma +d_I)}>1. \end{aligned}$$

From model (1), we have

$$\begin{aligned} \begin{aligned} {\frac{\mathrm {d}B(t)}{\mathrm {d}t}}\ge&\theta (A^0-\varepsilon _1)V(t)-d_BB(t),\\ {\frac{\mathrm {d}I(t)}{\mathrm {d}t}}\ge&\beta cB(t)(T^0-\varepsilon _1)\\&-\gamma I(t)-d_II(t),\\ {\frac{\mathrm {d}V(t)}{\mathrm {d}t}}\ge&\alpha I(t)+Nd_II(t)\\&-\theta (A^0+\varepsilon _1)V(t)-d_VV(t). \end{aligned} \end{aligned}$$

(10)

Define an auxiliary system

$$\begin{aligned} \begin{aligned} {\frac{\mathrm {d}B(t)}{\mathrm {d}t}}&=\theta (A^0-\varepsilon _1)V(t)-d_BB(t),\\ {\frac{\mathrm {d}I(t)}{\mathrm {d}t}}&=\beta cB(t)(T^0-\varepsilon _1)\\&\quad -\gamma I(t)-d_II(t),\\ {\frac{\mathrm {d}V(t)}{\mathrm {d}t}}&=\alpha I(t)+Nd_II(t)\\&\quad -\theta (A^0+\varepsilon _1)V(t)-d_VV(t). \end{aligned} \end{aligned}$$

(11)

The Jacobian matrix of (11) is

$$\begin{aligned} \begin{aligned} J_1=\begin{pmatrix} -d_B &{} 0 &{} \theta (A^0-\varepsilon _1)\\ \beta c(T^0-\varepsilon _1) &{} -\gamma -d_I &{} 0\\ 0 &{} \alpha +Nd_I &{} -\theta (A^0+\varepsilon _1)-d_V \\ \end{pmatrix}. \end{aligned} \end{aligned}$$

Obviously, $\mathrm {{tr}(J^1)<0}$ and $\det (J^1)=R_0-1>0$. Since the numbers on the off-diagonal line of matrix $J^1$ are positive, the solution (B(t), I(t), V(t)) of the system (10) with $(B(0), I(0), V(0)) \in X_1$ satisfies

$$\begin{aligned} (B(t), I(t), V(t))\rightarrow (+\infty ,+\infty ,+\infty ),t\rightarrow +\infty , \end{aligned}$$

which contradicts with (9). Thus $W^s(E_0)\cap X_1=\emptyset .$

Theorem 1.3.3 in [32] implies that the solutions of system (1) are uniformly persistent with respect to $(X_1, \partial X_1).$ Then there exists an $\varepsilon _2>0$ such that any solution (B(t), I(t),  V(t)) of system (1) satisfies $\liminf _{t\rightarrow \infty }(B(t), I(t)$, V(t)) $\ge (\varepsilon _2, \varepsilon _2, \varepsilon _2).$ Theorem 2.1 shows that $\liminf _{t\rightarrow \infty } A(t)\ge \varepsilon _3,$ $\liminf _{t\rightarrow \infty } T(t)\ge \varepsilon _4$ for some constants $\varepsilon _3>0$ and $\varepsilon _4>0$. Define $\varepsilon =\min \{\varepsilon _2, \varepsilon _3, \varepsilon _4\}.$ Therefore, $\liminf _{t\rightarrow \infty }A(t)\ge \varepsilon$, $\liminf _{t\rightarrow \infty }B(t)\ge \varepsilon$, $\liminf _{t\rightarrow \infty }T(t)\ge \varepsilon$, $\liminf _{t\rightarrow \infty }I(t)\ge \varepsilon$, and $\liminf _{t\rightarrow \infty }V(t)\ge \varepsilon$. The proof is completed. $\square$

4 Numerical simulations

In this section, we calculate the sensitivity indexes of the basic reproduction number $R_0$ and the state variables I and V. These indexes tell us the most crucial parameters to SARS-CoV-2 infection with ADE. Then numerical simulations are implemented to illustrate our theoretical results. Finally, we assess the impact of ADE on controlling SARS-CoV-2 infection. All simulations are implemented by MATLAB.

The removal of immune complexes mainly contributes to the continued neutralization of antibodies. The faster the antibody is produced, the more immune complexes are removed. $d_B$ can be expressed as $kr_1$, where k indicates the factor of influence of antibody production on the removal of immune complexes [33]. The details of parameters and variables are shown in Tables 1, 2 and 3.

Table 2 Summary of the model variables

Table 3 Related parameter values and sources

4.1 Sensitivity analysis

There are two very different model properties which are measured by PRCCs and eFAST. Based on sampling and rank transforms, PRCCs provide a measure of the monotonicity of the linear effect on one variable and no other variables. In comparison, based on variance decomposition, eFAST obtains a measure of the size of the effects of a single variable and the sum size of effects on its interactions with other variables, but the monotonicity of the effect is not obtained [42]. To have a complete and informative uncertainty and sensitivity (US) analysis, we calculate PRCCs and eFAST sensitivity indexes of $R_0$, I and V.

4.1.1 Sensitivity indexes of $R_0$

The PRCCs and eFAST sensitivity analysis for $R_0$ are described in Fig. 2. The PRCCs show the correlation direction among the input and output variables. The value $+\,1$ denotes a positive linear relationship of perfection, the value $-\,1$ denotes a negative linear relationship of perfection, and the value 0 denotes no relationship. Considering only $p<0.01$, sensitivity indexes of PRCCs for all the parameters except $\alpha$ and $d_V$ are significantly different from zero.

Fig. 2

a PRCCs sensitivity indexes of $R_0$; b eFAST sensitivity indexes of $R_0$

In Fig. 2b, the blue bar represents the sensitivity of the independent effects of a single parameter, denoted as $S_i$ (first-order sensitivity index), and the red bar represents the sum of the effects of a single parameter and the interactions between it and other parameters, denoted as $S_{Ti}$ (total-order sensitivity index). Considering only $p<0.01$, the size relationship of $S_i$ is $r_1\gg d_T>c\ge r_2>\beta$ and the size relationship of $S_{Ti}$ is $r_1\gg r_2>c>\beta >d_T$, and these parameters have significant effect on $R_0$.

From Fig. 2, we conclude that the parameters with high sensitivity in Fig. 2a and b are consistent. $r_2$, $\beta$ and c have significantly positive affect on $R_0$, while $r_1$ and $d_T$ have significantly negative effect on $R_0$. However, parameters including $\theta$, $d_A$, $\gamma$, $d_I$ and N have high PRCCs sensitivity indexes and conversely their eFAST sensitivity indexes are low.

4.1.2 Sensitivity indexes of I and V

Figure 2 shows the effect of parameters on $R_0$. To gauge if the significance of the parameters emerged over the entire duration of the viral dynamics process, we focus on the state variables I and V. We choose the time range from 0 to 90 for PRCCs and eFAST, and parameters are shown in Table 3. Using MATLAB, we calculate the PRCCs and eFAST ($S_i$) indexes at multiple time points and plot the time series diagram for state variables I and V. The gray area in the figure indicates that there is no significant difference from zero.

From Fig. 3a, the parameters are divided into five categories. The PRCCs index values of the first category including $\gamma$, $d_A$ and $d_I$ firstly change to a value over time, and then gradually rise or fall until they are not significantly different from zero. The second category including $\beta$, c and $r_1$ remains linearly correlated to the state variable. The third category including $\alpha$ and $d_T$ does not affect the state variable. The influence of the fourth category including $r_2$ and N gradually increases and eventually stabilizes. The last category including $\theta$ and $d_V$ gradually changes from correlated to uncorrelated with state variable. From Fig. 3b, we can see that $r_1$ maintains the maximum influence on I throughout the period. Between 50 and 70 days, $r_2$ suddenly has a significant effect on I. The other parameters gradually do not affect I. Combining Fig. 3, $r_1$ has the strongest sensitivity and keeps a negative relationship.

Fig. 3

a Time-varying PRCCs sensitivity indexes of I; b Time-varying first-order sensitivity indexes $S_i$ of I

From Fig. 4a, the PRCCs curve of the most specific parameter $d_I$ firstly drops from a positive maximum, and then crosses the gray area to a negative value, and finally stabilizes until it is not significantly different from zero. Similarly, no parameters belong to the first category. The second category includes $r_1$, $\beta$, c and N. $d_A$, $\alpha$, $\gamma$, $\theta$ and $d_T$ are in the third category. The fourth category covers $r_2$. The last category contains $d_V$. From Fig. 4b, we know that $r_1$ is the only parameter that maintains influence on V throughout the period. From Fig. 4, we get that $r_1$ is the crucial parameter to V and negatively associated with V.

Fig. 4

a Time-varying PRCCs sensitivity indexes of V; b Time-varying first-order sensitivity indexes $S_i$ of V

Finally, we find that only one parameter $r_1$ has a significant effect on these state variables over time. Compared with Sect. 4.1, we obtain the change in parameter sensitivity over time.

4.2 Numerical simulations

Figure 5 shows that the dynamics of the system (1) are completely determined by the basic reproduction number $R_0$. Simulations are carried out to verify Theorems 3.3 and 3.4.

Firstly, we choose the parameters $\beta =1.6\times 10^{-6}$, $c=1.8\times 10^{-10}$, $r_1=1.5\times 10^{10}$, $\theta =2.9\times 10^{-11}$, $d_A=0.02$, $\alpha =2.81\times 10^{4}$, $d_I=0.21$, $d_T=0.0152$, $d_V=3.41$, $\gamma =0.281$, $N=7\times 10^{10}$, $r_2=1.8\times 10^{4}$ and the initial values $A(0)=1\times 10^{10}$, $B(0)= 0$, $T(0)=1\times 10^{6}$, $I(0)= 0$, $V(0)=1\times 10^{5}$. We can calculate that the basic reproduction number $R_0<1$. Then the infection-free equilibrium of model (1) is stable and the virus dies out (see Fig. 5a).

Similarly, setting the parameters $\beta =5.2\times 10^{-6}$, $c=7.6\times 10^{-10}$, $r_1=6.0\times 10^{8}$, $\theta =2.9\times 10^{-11}$, $d_A=0.02$, $\alpha =2.81\times 10^{4}$, $d_I=0.21$, $d_T=0.0152$, $d_V=3.41$, $\gamma =0.281$, $N=7\times 10^{10}$ and $r_2=1.8\times 10^{4}$. We can obtain that the basic reproduction number $R_0>1$. Then the infection equilibrium of model (1) is stable and the virus persists uniformly (see Fig. 5b).

Fig. 5

The solution behavior of model (2.1). a When $R_0<1$, the infection-free equilibrium $E_0$ is stable; b When $R_0>1$, the infection equilibrium $E^*$ is stable

4.3 The effect of ADE on the SARS-CoV-2 infection

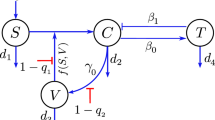
To study the possible influence of ADE on the dynamics of SARS-CoV-2 infection, we reconstruct a SARS-CoV-2 infection dynamics model. Based on the findings of SARS-CoV-2 infection [43, 44]. We assume the infection of SARS-CoV-2 without ADE. Antibodies (A) and Target cells (T) are recruited with a constant rate $r_1$ and $r_2$. $d_A$ is the inactivation rate of the antibodies. Target cells die with a death rate $d_T$ and are infected by SARS-CoV-2 (V), and then become infected cells (I). The infected cells recover at a rate $\gamma$, and die with a death rate $d_I$, and then release SARS-CoV-2 through exocytosis at a rate $\alpha$ or cell death at a rate N. The viruses are cleared at rate $\theta$ by antibodies or inactivated at rate $d_V$. The parameters $r_1$, $\theta$, $d_A$, $r_2$, $\beta$, $d_T$ $\gamma$, $d_I$, $\alpha$, N and $d_V$ are same with model (1). The SARS-CoV-2 infection dynamics model without ADE is given as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\frac{\mathrm {d}A(t)}{\mathrm {d}t}}&{}=r_1-\theta A(t)V(t)-d_AA(t),\\ \displaystyle {\frac{\mathrm {d}T(t)}{\mathrm {d}t}}&{}=r_2-\beta c_1T(t)V(t)-d_TT(t)\\ &{}+\gamma I(t),\\ \displaystyle {\frac{\mathrm {d}I(t)}{\mathrm {d}t}}&{}=\beta c_1T(t)V(t)-\gamma I(t)-d_II(t),\\ \displaystyle {\frac{\mathrm {d}V(t)}{\mathrm {d}t}}&{}=\alpha I(t)+Nd_II(t)-\theta A(t)V(t)\\ &{}-d_VV(t), \end{array}\right. \end{aligned}$$

(12)

We can compute the basic reproduction number

$$\begin{aligned} R_1=\frac{N\beta _1c_1d_Ad_Ir_2 + \alpha \beta c_1d_Ar_2}{d_Ad_Td_Id_V + d_Ad_Td_V\gamma +d_Td_Ir_1\theta +d_T\gamma r_1\theta }. \end{aligned}$$

4.3.1 Comparison of $R_0$ and $R_1$

We can increase the binding rate $\theta$ between antibodies and viruses and the recruitment rate $r_1$ of antibodies by drugs [33, 45, 46]. Therefore, we use three-dimensional graphs to study the effect of parameters $r_1$ and $\theta$ to $R_0$ and $R_1$. According to [8, 47], we set the parameters $c>c_1$, and other parameter values are the same as the model (1).

Fig. 6

a The effect of $r_1$ and $\theta$ on $R_0$; b The effect of $r_1$ and $\theta$ on $R_1$

From Fig. 6, we can see that the parameters $r_1$ and $\theta$ are positively correlated with $R_1$, but the parameter $\theta$ is negatively correlated with $R_0$. Within the range of values, $R_0$ and $R_1$ can range from 0 to 6, 2, respectively. We make a comparison between Fig. 6a and b, and can intuitively get that it is easier to reduce $R_1$ to below 1, while it is more difficult to reduce $R_0$ to below 1. Similarly, we obtain that $R_1$ can be reduced by increasing $r_1$ and $\theta$, whereas $R_0$ can only be reduced by increasing $r_1$. These findings suggest that it might be difficult to control the SARS-CoV-2 infection with ADE.

4.3.2 Comparison of sensitivity indexes of I and V

Fig. 7

a Time-varying PRCCs sensitivity indexes of I; b Time-varying PRCCs sensitivity indexes of V

Similarly to Sect. 4.1, we focus on the change in the curve during 60 days. From Fig. 7a, all parameters also can be divided into five categories. N and $\gamma$ belong to the first category, the second category contains $\beta$, $r_2$, $r_1$, $d_I$ and $\theta$, the third category includes $d_T,\alpha$ and $d_A$, and the fourth category does not cover parameters. $c_1$ and $d_V$ are in the last category. Thus, $\beta , N$ and $r_2$ are positively correlated with I, while $r_1, \theta , \gamma , d_V$ and $d_I$ are negatively correlated with I.

From Fig. 7b, the PRCCs curve of the specific parameter $d_I$ firstly drops from a positive maximum, and then crosses the gray area to a negative value, and finally stabilizes. The first category includes $r_2$ and $\gamma$. $r_1$ and $\theta$ belong to the second category. The third category contains $d_T, d_A, c_1$ and $\alpha$. There are no parameters in the fourth category. The last category covers $\beta , N$ and $d_V$. $\beta , N, r_2$ keep positive relationship with V, while $r_1, \gamma , \theta$ and $d_I$ keep negative relationship with V.

Compared with Sect. 4.1, we find that $r_1$ and $\theta$ keep a negative relationship with I and V in model (12), and they have a significant effect on I and V. In model (1), it is noticed that before 40 days, $\theta$ is positively correlated with I, and only $r_1$ remains negatively correlated with I and V. It is possible to control the SARS-CoV-2 infection without ADE by increasing $r_1$ and $\theta$, while controlling the SARS-CoV-2 infection with ADE only by $r_1$.

4.3.3 Comparison of solution behaviors between models (1) and (12)

According to [8] , we set the parameter $c_1=2.7\times 10^{-11}$, and other parameters values are the same as Fig. 5b. We can calculate the basic reproduction number $R_1>1$ and show the probable effect of ADE on SARS-CoV-2 infection from Fig. 8.

Fig. 8

The comparison between models (1) and (12). When $R_1>1$ and $R_0>1$, a the behaviors of I; b the behaviors of V, where the solutions of models (1) and (12) are represented by blue and red lines, respectively

Figure 8 shows that when $R_1>1$, the viruses and infected target cells increase acutely and then reach their peak more quickly in SARS-CoV-2 infection with ADE. Petersen et al. [48] experimented on coronavirus infection, and they found that antibody-positive targets had an earlier onset of disease and died more quickly. Subsequently, the similar conclusions in [49, 50] are obtained, and the potential effect of ADE on infection described above is similar to our results.

In summary, our results find that the impact of ADE on SARS-CoV-2 infection may be twofold. Firstly, it is likely that ADE makes SARS-CoV-2 infection more difficult to control. Secondly, SARS-CoV-2 infection with ADE may be more rapid, and then the viruses and infected target cells can increase rapidly and reach their peak in a short period.

5 Discussion and conclusion

The antibodies prevent the viruses from adhering to the surface of the host cells and render the viruses to infect the cells. But sometimes the antibodies assist the viruses to enter the target cells and increase the infection rate (ADE phenomenon). A series of studies [6,7,8, 24,25,26, 51,52,53] in vivo and vitro confirm that the antibodies of some viruses including SARS-CoV-2 [6,7,8] could cause the ADE phenomenon and enhance the infectivity of the virus. Yao et al. [24] detected SARS-CoV-2 in macrophages from the lungs by immunofluorescence staining. Feng et al. [25] detected SARS-CoV-2 in CD68+ and CD169+ macrophages from the spleen by autopsy of deceased COVID-19 patients. Grant et al. [26] detected SARS-CoV-2 transcripts in 67% of alveolar macrophages from COVID-19 patients’ samples, and SARS-CoV-2 transcripts were consistently detected in 40% of COVID-19 patients. Since vaccine efficiency is directly affected by ADE, ADE becomes a risk factor to consider in vaccine development. To study the dynamics of SARS-CoV-2 infection with ADE and estimate the potential effect of ADE on the SARS-CoV-2 infection, we develop a mathematical model of SARS-CoV-2 infection with ADE.

The dynamics of the SARS-CoV-2 infection model with ADE are analyzed. We calculate the basic reproduction number $R_0$. We prove that when $R_0<1$, the infection-free equilibrium is globally asymptotically stable and the virus dies out, and the system is uniformly persistent and the virus persists when $R_0>1$.

The results show that the recruitment rate of antibodies has a significant effect on SARS-CoV-2 infection in the model with ADE. For a complete and informative US analysis, PRCCs and eFAST (based on different principles) are used to evaluate the effect of parameters on $R_0$, I and V. PRCCs can reveal the monotonicity relation between input and output factors, while eFAST can compare with the magnitude of parameter sensitivity. Firstly, we find that the most sensitive parameters of $R_0$ are $r_1$, $\beta$, $r_2$, c and $d_T$. Secondly, the sensitivity indexes at multiple time points are calculated to observe the change of effect of parameters on I and V over time. It is noted that only the recruitment rate $r_1$ of antibodies has a significant effect on I and V over time. Time-varying sensitivity indexes show that parameters can be improved for different periods to control virus multiplication. Finally, we perform some numerical simulations to confirm our theoretical results.

Our findings indicate that ADE probably has a significant effect on the SARS-CoV-2 infection. Our results show that SARS-CoV-2 infection with ADE may be more difficult to be contained. The sensitivity indexes of I and V about all parameters at multiple time points are calculated. We investigate the effect of $r_1$ on SARS-CoV-2 infection with ADE, and effect of $r_1$ and $\theta$ on SARS-CoV-2 infection without ADE. Our results find that increasing antibody titers could reduce the viral load and infectious cell load in SARS-CoV-2 infection with ADE, while enhancing the neutralizing ability of antibodies could reduce the virus load in SARS-CoV-2 infection without ADE. In [54], serum samples collected from patients with acute or recovering COVID-19 were investigated, and the results show a predominance of neutralizing activity under high neutral conditions, which is counteracted by ADE under subneutral conditions. Thus, our results are consistent with the conclusions in [54]. Also, the SARS-CoV-2 infection dynamics with ADE and without ADE are compared. The results find that the impact of ADE on SARS-CoV-2 infection may be twofold. Firstly, the SARS-CoV-2 infection caused by ADE may be more difficult to control. Secondly, there is every probability that SARS-CoV-2 infection with ADE is more rapid, and then the viruses and infected target cells increase rapidly and reach their peak in a short period. The results in [49] found that the preinjection of study subjects with antibodies develop the disease earlier and suffer earlier death after infection. In [50], the researchers performed the same manipulation and ended up with the same results. Therefore, our findings about the potential role of ADE on infection are similar to the results in [49, 50].

It is of great interest to prove the global stability of infection equilibrium of the system (1) when $R_0>1$. For future work, the suitable Lyapunov function would be constructed to prove the global stability of infection equilibrium. Our findings probably contribute to understanding the SARS-CoV-2 infection dynamics with ADE, which may be applied to other diseases such as Zika and Dengue with ADE.