SpringerLink
Log in

Analytical derivatives of flexible multibody dynamics with the floating frame of reference formulation

  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

Abstract

In this paper, the analytical derivatives of flexible multibody dynamics with the floating frame of reference formulation are derived in a new way using the invariants and their sensitivities. This enables the decoupling of the sensitivity analysis of flexible multibody dynamics from the finite-element solver and guarantees high accuracy and efficiency of the sensitivity computations. The invariants are shown with both consistent and lumped mass approaches. The latter allows generality towards the formulation of a finite-element type, including beams, shells, and solids. The expressions are fully derived with lumped masses, showing for the first time the compensation term of inertia due to the non-consideration of the mass distribution with this approach. It is then shown that the expressions of the system parameters in the lumped case with the newly introduced inertia compensation term correspond to the general case, and, therefore, the derived approach and equations are of general nature. Crucial for the decoupling of the sensitivity analysis are the analytical derivatives of the system parameters that contain the derivatives of the invariants and whose analytical expressions are derived and provided here for the first time. The partial derivatives arise in the sensitivity analysis with both the direct differentiation method and the adjoint variable method, and the former is shown here. In addition, the partial derivatives arise in the Jacobian matrix of the nonlinear solver for the transient solution of flexible multibody systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Germany)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Abbreviations

:

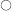zeroth-order tensor or scalar

:

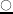first-order tensor or vector

:

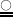second-order tensor or matrix

:

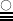third-order tensor or 3D matrix

:

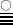fourth-order tensor or 4D matrix

:

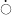first time derivative

:

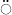second time derivative

:

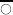expressed in floating coordinates

:

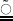skew symmetric matrix

:

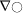total derivative of 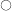w.r.t. \(\underline{\mathsf{x}}\)

:

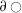partial derivative of 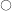w.r.t. \(\underline{\mathsf{x}}\)

:

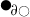partial derivative of 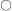w.r.t.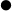

:

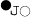Jacobian of 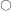w.r.t.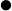

\(\underline{\underline{d}}\) :

dam** matrix

\(\underline{e}\) :

unit vector

\(\underline{\underline{e}}\) :

unit matrix (identity matrix)

\(\underline{\underline{k}}\) :

stiffness matrix

\(m\) :

mass

\(\underline{\underline{m}}\) :

mass matrix

\(\underline{q}\) :

generalized position vector

\(\underline{\dot{q}}\) :

generalized velocity vector

\(\underline{\ddot{q}}\) :

generalized acceleration vector

\(\underline{r}\) :

position vector to inertial frame expressed in intertial coordinates

\(t\) :

time

\(\underline{\overline{u}}\) :

position vector to floating frame expressed in floating coordinates

\(\underline{u}\) :

position vector to floating frame expressed in inertial coordinates

\(\underline{\mathsf{x}}\) :

vector of design variables

\(\underline{\underline{A}}\) :

rotation matrix

\(\underline{\underline{B}}\) :

Boolean matrix

:

function of

\(\underline{\underline{G}}\) :

angular velocity matrix that relates \(\underline{\omega}\) and \(\underline{\dot{\theta}}\)

\(\underline{\underline{\mathcal{I}}}\) :

invariant (inertia shape integral)

\(K\) :

kinetic energy

\(\underline{Q}{}_{\mathrm{e}}\) :

generalized external force vector

\(\underline{Q}{}_{\mathrm{v}}\) :

quadratic velocity force vector

\(\underline{\underline{\overline{S}}}\) :

matrix of shape functions expressed in floating coordinates

\(V\) :

volume

\(\underline{\zeta}\) :

vector of modal coordinates

\(\underline{\theta }\) :

vector of orientation coordinates

\(\underline{\lambda }\) :

vector of Lagrange multipliers

\(\rho \) :

density

\(\underline{\tau }\) :

position vector of floating frame

\(\underline{\chi}{}_{\mathrm{o}}\) :

center of mass of undeformed body

\(\underline{\omega }\) :

angular velocity vector

\(\underline{\underline{\Theta}}{}_{\mathrm{o}}\) :

inertia tensor of undeformed body

\(\underline{\Phi }\) :

vector of kinematic constraints

\(\underline{\underline{^{q}\hspace {-2pt}\mathtt{J}\Phi }}\) :

Jacobian matrix of kinematic constraints

\(\underline{\underline{\overline{\Psi}}}\) :

modal matrix expressed in floating coordinates

References

  1. Baier, H., Seeßelberg, C., Specht, B.: Optimierung in der Strukturmechanik. LSS Verlag, Dortmund (2006)

    Google Scholar 

  2. Bestle, D.: Analyse und Optimierung Von Mehrkörpersystemen. Springer, Berlin (1994). https://doi.org/10.1007/978-3-642-52352-6

    Book  Google Scholar 

  3. Bestle, D., Eberhard, P.: Analyzing and optimizing multibody systems. Mech. Struct. Mach. 20(1), 67–92 (1992). https://doi.org/10.1080/08905459208905161

    Article  Google Scholar 

  4. Boopathy, K., Kennedy, G.J.: Adjoint-based derivative evaluation methods for flexible multibody systems with rotorcraft applications. In 55th AIAA Aerospace Sciences Meeting. American Institute of Aeronautics and Astronautics, Reston (2017). https://doi.org/10.2514/6.2017-1671

    Chapter  Google Scholar 

  5. Craig, R.R., Bampton, M.C.C.: Coupling of substructures for dynamic analyses. AIAA J. 6(7), 1313–1319 (1968). https://doi.org/10.2514/3.4741

    Article  Google Scholar 

  6. Dias, J.M.P., Pereira, M.S.: Sensitivity analysis of rigid-flexible multibody systems. Multibody Syst. Dyn. 1(3), 303–322 (1997). https://doi.org/10.1023/A:1009790202712

    Article  Google Scholar 

  7. Fanghella, P., Galletti, C., Torre, G.: An explicit independent-coordinate formulation for the equations of motion of flexible multibody systems. Mech. Mach. Theory 38(5), 417–437 (2003). https://doi.org/10.1016/s0094-114x(02)00131-3

    Article  MathSciNet  Google Scholar 

  8. FunctionBay: Multi flexible body dynamics (2022). URL https://functionbay.com/documentation/onlinehelp/default.htm. RecurDyn ducumentation V9R4

  9. Gufler, V., Wehrle, E., Achleitner, J., Vidoni, R.: Flexible multibody dynamics and sensitivity analysis in the design of a morphing leading edge for high-performance sailplanes. In: ECCOMAS Thematic Conference on Multibody Dynamics (2021). https://doi.org/10.3311/ECCOMASMBD2021-203

    Chapter  Google Scholar 

  10. Gufler, V., Wehrle, E., Vidoni, R.: Multiphysical design optimization of multibody systems: application to a Tyrolean Weir cleaning mechanism. In: Mechanisms and Machine Science, pp. 459–467. Springer, Berlin (2021). https://doi.org/10.1007/978-3-030-55807-9_52

    Chapter  Google Scholar 

  11. Gufler, V., Wehrle, E., Vidoni, R.: Sensitivity analysis of flexible multibody dynamics with generalized-\(\alpha \) time integration and Baumgarte stabilization. In: Mechanisms and Machine Science, pp. 147–155. Springer, Berlin (2022). https://doi.org/10.1007/978-3-031-10776-4_18

    Chapter  Google Scholar 

  12. Gufler, V., Wehrle, E., Zwölfer, A.: A review of flexible multibody dynamics for gradient-based design optimization. Multibody Syst. Dyn. 53(4), 379–409 (2021). https://doi.org/10.1007/s11044-021-09802-z

    Article  MathSciNet  Google Scholar 

  13. Haftka, R.T., Gürdal, Z.: Elements of Structural Optimization, 3rd Edn. Kluwer, Dordrecht (1992). https://doi.org/10.1007/978-94-011-2550-5

    Book  Google Scholar 

  14. Haug, E.J., Arora, J.S.: Design sensitivity analysis of elastic mechanical systems. Comput. Methods Appl. Mech. Eng. 15(1), 35–62 (1978). https://doi.org/10.1016/0045-7825(78)90004-X

    Article  Google Scholar 

  15. Haug, E.J., Arora, J.S.: Applied Optimal Design: Mechanical and Structural Systems. Wiley, New York (1979)

    Google Scholar 

  16. Held, A., Knüfer, S., Seifried, R.: Structural sensitivity analysis of flexible multibody systems modeled with the floating frame of reference approach using the adjoint variable method. Multibody Syst. Dyn. 40, 287–302 (2017). https://doi.org/10.1007/s11044-016-9540-9

    Article  MathSciNet  Google Scholar 

  17. Hurty, W.C.: Dynamic analysis of structural systems using component modes. AIAA J. 3(4), 678–685 (1965). https://doi.org/10.2514/3.2947

    Article  Google Scholar 

  18. MacNeal, R.H.: A hybrid method of component mode synthesis. Comput. Struct. 1(4), 581–601 (1971). https://doi.org/10.1016/0045-7949(71)90031-9

    Article  Google Scholar 

  19. Martins, J.R.R.A., Hwang, J.T.: Review and unification of methods for computing derivatives of multidisciplinary computational models. AIAA J. 51(11), 2582–2599 (2013). https://doi.org/10.2514/1.J052184

    Article  Google Scholar 

  20. Martins, J.R.R.A., Ning, A.: Engineering Design Optimization. Cambridge University Press, Cambridge (2021). https://mdobook.github.io/

    Book  Google Scholar 

  21. MSC Software Corporation: Theory of flexible bodies (2020). URL https://help.mscsoftware.com/bundle/adams_2020/page/adams_help/Adams_Advanced_Package/flex/flex_theory/flex.theory.xhtml. Adams 2020 - Online Help (HTML)

  22. Nachbagauer, K., Oberpeilsteiner, S., Sherif, K., Steiner, W.: The use of the adjoint method for solving typical optimization problems in multibody dynamics. J. Comput. Nonlinear Dyn. 10(6), 061011 (2015). https://doi.org/10.1115/1.4028417

    Article  Google Scholar 

  23. Nejat, A.A., Moghadasi, A., Held, A.: Adjoint sensitivity analysis of flexible multibody systems in differential-algebraic form. Comput. Struct. 228, 106–148 (2020). https://doi.org/10.1016/j.compstruc.2019.106148

    Article  Google Scholar 

  24. Orzechowski, G., Matikainen, M.K., Mikkola, A.M.: Inertia forces and shape integrals in the floating frame of reference formulation. Nonlinear Dyn. 88(3), 1953–1968 (2017). https://doi.org/10.1007/s11071-017-3355-y

    Article  Google Scholar 

  25. Pi, T., Zhang, Y., Chen, L.: First order sensitivity analysis of flexible multibody systems using absolute nodal coordinate formulation. Multibody Syst. Dyn. 27, 153–171 (2012). https://doi.org/10.1007/s11044-011-9269-4

    Article  MathSciNet  Google Scholar 

  26. Rubin, S.: Improved component-mode representation for structural dynamic analysis. AIAA J. 13(8), 995–1006 (1975). https://doi.org/10.2514/3.60497

    Article  Google Scholar 

  27. Shabana, A.A.: Dynamics of Multibody Systems, 5th edn. Cambridge University Press, Cambridge (2020). https://doi.org/10.1017/9781108757553

    Book  Google Scholar 

  28. Sherif, K., Nachbagauer, K.: A detailed derivation of the velocity-dependent inertia forces in the floating frame of reference formulation. Journal of Computational and Nonlinear Dynamics 9(4), 044501 (2014). https://doi.org/10.1115/1.4026083

    Article  Google Scholar 

  29. Wehrle, E., Gufler, V.: Lightweight engineering design of nonlinear dynamic systems with gradient-based structural design optimization. In: Proceedings of the Munich Symposium on Lightweight Design 2020, pp. 44–57. Springer, Berlin Heidelberg (2021). https://doi.org/10.1007/978-3-662-63143-0_5

    Chapter  Google Scholar 

  30. Wehrle, E., Gufler, V.: Analytical sensitivity analysis of dynamic problems with direct differentiation of generalized-\(\alpha\) time integration. Submitted for publication (2022). https://doi.org/10.31224/osf.io/2mb6y

  31. Zhang, M., Peng, H., Song, N.: Semi-analytical sensitivity analysis approach for fully coupled optimization of flexible multibody systems. Mech. Mach. Theory 159, 104256 (2021). https://doi.org/10.1016/j.mechmachtheory.2021.104256

    Article  Google Scholar 

  32. Zwölfer, A., Gerstmayr, J.: Co-rotational formulations for 3D flexible multibody systems: A nodal-based approach. In: Contributions to Advanced Dynamics and Continuum Mechanics, pp. 243–263. Springer, Berlin (2019). https://doi.org/10.1007/978-3-030-21251-3_14

    Chapter  Google Scholar 

  33. Zwölfer, A., Gerstmayr, J.: A concise nodal-based derivation of the floating frame of reference formulation for displacement-based solid finite elements. Multibody Syst. Dyn. 49, 291–313 (2020). https://doi.org/10.1007/s11044-019-09716-x

    Article  MathSciNet  Google Scholar 

  34. Zwölfer, A., Gerstmayr, J.: Consistent and inertia-shape-integrals-free invariants of the floating frame of reference formulation. In: Proceedings of the ASME 2020 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (2020). https://doi.org/10.1115/DETC2020-22293

    Chapter  Google Scholar 

  35. Zwölfer, A., Gerstmayr, J.: The nodal-based floating frame of reference formulation with modal reduction. Acta Mech. (2020). https://doi.org/10.1007/s00707-020-02886-2

    Article  Google Scholar 

  36. Zwölfer, A., Gerstmayr, J.: State of the art and unification of corotational formulations for flexible multibody dynamics systems. J. Struct. Dyn. (2022). Submitted for publication

Download references

Acknowledgements

This work is supported by the project CRC 2017 – TN2091 doloMULTI \(\underline{D}\)esign \(\underline{o}\)f \(\underline{L}\)ightweight \(\underline{O}\)ptimized structures and systems under \(\underline{MULTI}\)disciplinary considerations through integration of \(\underline{MULTI}\)body dynamics in a \(\underline{MULTI}\)physics framework funded by the Free University of Bozen-Bolzano.

Author information

Authors and Affiliations

  1. Faculty of Science and Technology, Free University of Bozen-Bolzano, Universitätsplatz-Piazza Università 1, 39100, Bozen-Bolzano, South Tyrol, Italy

    Veit Gufler & Erich Wehrle

  2. TUM School of Engineering and Design, Department of Mechanical Engineering, Chair of Applied Mechanics, Technical University of Munich, 85748, Garching bei München, Germany

    Veit Gufler & Andreas Zwölfer

  3. Collins Aerospace, Applied Research and Technology, Munich, Germany

    Erich Wehrle

Authors
  1. Veit Gufler
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andreas Zwölfer
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Erich Wehrle
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

V.G.: conceptualization, data curation, formal analysis, investigation, methodology, resources, software, validation, visualization, writing – original draft, writing – review & editing. A.Z.: conceptualization, formal analysis, investigation, methodology, supervision, validation, writing – original draft, writing – review & editing. E.W.: conceptualization, funding acquisition, methodology, project administration, supervision, writing – original draft, writing – review & editing.

Corresponding author

Correspondence to Veit Gufler.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gufler, V., Zwölfer, A. & Wehrle, E. Analytical derivatives of flexible multibody dynamics with the floating frame of reference formulation. Multibody Syst Dyn 60, 257–288 (2024). https://doi.org/10.1007/s11044-022-09858-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11044-022-09858-5

Keywords

Search

Navigation