SpringerLink
Log in

Convolution based quadratic-phase Stockwell transform: theory and uncertainty relations

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

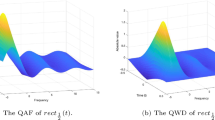
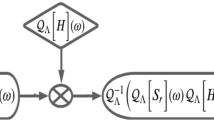
Abstract

In the field of optics and signal processing, the novel quadratic-phase Fourier transform (QPFT) has emerged as a powerful tool. However, it has a drawback as it fails in locating the quadratic-phase domain frequency contents which is much needed in numerous applications, where a joint information of time and quadratic-phase Fourier domain frequency is needed. On the other hand the Stockwell transform (ST), which is a time-frequency representation tool known for its local spectral phase properties in signal processing, uniquely combines elements of wavelet transforms and the short-time Fourier transform (STFT). However, its signal analysis ability is restricted in the time-frequency plane. In order to rectify the limitations of the QPFT and the ST, we in this paper proposed the quadratic-phase Stockwell transform (QPST) by employing the convolution structure of quadratic-phase Fourier transforms. Firstly, we examined the resolution of the QPST in the time and QPFT domains and then derived some of its basic properties, such as Rayleigh’s energy theorem, inversion formula and characterization of the range. Besides, we also derived a direct relationship between the well-known Wigner-Ville distribution and the proposed QPST. In the sequel, we introduced discrete version of the QPST, together with its reconstruction formula. Further , we are successful in establishing the well known Heisenberg’s and logarithmic uncertainty principles associated with the proposed QPST. Towards the culmination of this paper, we presented applications of the proposed QPST in detection of chirp signals in presence of echo. The simulation results lucidly demonstrate that the QPST performs exceptionally well in comparison with the conventional ST.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability

The data is provided on the request to the authors.

References

  1. Abdoush Y, Pojani G, Corazza GE, Garcia-Molina JA (2019) Controlled-coverage discrete S-transform (CC-DST): Theory and applications. Digit Signal Process 88:207–222

    Article  MathSciNet  Google Scholar 

  2. Akila L, Roopkumar R (2016) Quaternionic Stockwell transform. Integ Transf Spec Funct 27(6):484–504

    Article  MathSciNet  Google Scholar 

  3. Ali ST, Antoine JP, Gazeau JP (2015) Coherent States, Wavelets, and Their Generalizations. Springer

    Google Scholar 

  4. Battisti U, Riba L (2016) Window-dependent bases for efficient representations of the Stockwell transform. Appl Comput Harmon Anal 40:292–320

    Article  MathSciNet  Google Scholar 

  5. Battle G (1997) Heisenberg inequalities forwavelet states. Appl Comput Harmon Anal 4:119–146

    Article  MathSciNet  Google Scholar 

  6. Bayram I, Selesnick IW (2011) A dual-tree rational-dilation complex wavelet transform. IEEE Trans Signal Process 59:6251–6256

    Article  ADS  MathSciNet  Google Scholar 

  7. Beckner W (1995) Pitt’s inequality and the uncertainty principle. Proc Am Math Soc 123:1897–1905

    MathSciNet  Google Scholar 

  8. Bhat MY, Dar AH (2022) Quaternion linear canonical S-transform and associated uncertainty principles. International Journal of Wavelets, Multiresolution and Information Processing 2250035

  9. Bhat MY, Dar AH (2023) Quadratic phase S-Transform: Properties and uncertainty principles. e-Prime-Advances in Electrical Engineering, Electronics and Energy 100162

  10. Bhat MY, Dar AH, Urynbassarova D, Urynbassarova A (2022) Quadratic-phase wave packet transform. Optik - International Journal for Light and Electron Optics

  11. Bhat MY, Dar AH (2022) The 2-D Hyper-complex Gabor Quadratic-Phase Fourier Transform and Uncertainty Principles. J Anal. https://doi.org/10.1007/s41478-022-00445-7

    Article  Google Scholar 

  12. Bhat MY, Dar AH, Nurhidaya I, Pinelas S (2022) Uncertainty principles for the two-sided quaternion windowed quadratic-phase fourier transform. Symmetry, Accepted

    Book  Google Scholar 

  13. Candés E, Donoho D (1999) Ridgelets: A key to higher-dimensional intermittency? Philos Trans R Soc Lond A 357:2495–2509

    Article  ADS  MathSciNet  Google Scholar 

  14. Candés E, Donoho D (2003) Continuous curvelet transform-I: resolution of the wavefront set. Appl Comput Harmon Anal 19:162–197

    Article  MathSciNet  Google Scholar 

  15. Castro LP, Haque MR, Murshed MM, Saitoh S, Tuan NM (2014) Quadratic Fourier transforms. Ann Funct Anal AFA 5(1):10–23

  16. Castro LP, Minh LT, Tuan NM (2018) New convolutions for quadratic-phase Fourier integral operators and their applications. Mediterr J Math 15:1–17

    Article  MathSciNet  Google Scholar 

  17. Clapson MB, Bizouard MA, Brisson V, Cavalier F, Davier M, Hello P, Kreckelberg S, Varvella M (2005) A gravitational wave burst search method based on the S-transform. Classical Quant Grav 22:S1381–S1390

    Article  Google Scholar 

  18. Dahlke S, Maass P (1995) The affine uncertainty principle in one and two dimensions. Comput Math Appl 30:293–305

    Article  MathSciNet  Google Scholar 

  19. Dar AH, Bhat MY (2022) Electron Optics. Scaled ambiguity function and scaled Wigner distribution for LCT signals. Optik - International Journal for Light and Electron Optics 267, 169678

  20. Bhat MY, Dar AH (2023) Towards Quaternion Quadratic-phase Fourier transform. Math Methods Appl Sci. https://doi.org/10.1002/mma.9126

  21. Dar AH, Bhat MY (2023) Wigner distribution and associated uncertainty principles in the framework of octonion linear canonical transform. Optik - International Journal for Light and Electron Optics 272:170213

    Article  Google Scholar 

  22. Djurovic I, Sejdic E, Jiang J (2008) Frequency-based window width optimization for S-transform. AEÜ. Int J Electron Commun 62:245–250

    Article  Google Scholar 

  23. Drabycz S, Stockwell RG, Mitchell JR (2009) Image texture characterization using the discrete orthonormal S-transform. J Digit Imaging 22:696–708

    Article  PubMed  Google Scholar 

  24. Du J, Wong MW, Zhu H (2007) Continuous and discrete inversion formulas for the Stockwell transform. Integral Transforms Spec Funct 18:537–543

    Article  MathSciNet  Google Scholar 

  25. Duabechies I (1992) Ten Lectures on Wavelets. SIAM, Philadelphia

    Book  Google Scholar 

  26. Durak L, Arikan O (2003) Short-time Fourier transform: two fundamental properties and an optimal implementation. IEEE Trans Signal Process 51:1231–42

    Article  ADS  MathSciNet  Google Scholar 

  27. Folland GB, Sitaram A (1997) The uncertainty principle: A mathematical survey. J Fourier Anal Appl 3:207–238

    Article  MathSciNet  Google Scholar 

  28. Hutníková M, Mišková A (2015) Continuous Stockwell transform: coherent states and localization operators. J Math Phys

  29. Jhanwar D, Sharma KK, Modani SG (2014) Generalized fractional S-transform and its application to discriminate environmental background acoustic noise signals. Acoust Phys 60:466–473

    Article  ADS  Google Scholar 

  30. Kutyniok G, Labate D (2009) Resolution of the wavefront set using continuous shearlets. Trans Amer Math Soc 361:2719–2754

    Article  MathSciNet  Google Scholar 

  31. Lone WZ, Shah FA (2022) Weighted convolutions in the quadratic-phase Fourier domains: Product theorems and applications. Optik - International Journal for Light and Electron Optics 270:169978

    Article  Google Scholar 

  32. Moukadem A, Bouguila Z, Ould Abdeslam D, Dieterlen A (2015) A new optimized Stockwell transform applied on synthetic and real non-stationary signals. Digit Signal Process 46:226–238

    Article  MathSciNet  Google Scholar 

  33. Pinnegar CR, Mansinha L (2003) The S-transform with windows of arbitrary and varying shape. Geophysics 68:381

    Article  ADS  Google Scholar 

  34. Prasad A, Sharma PB (2020) The quadratic-phase Fourier wavelet transform. Math Methods Appl Sci. https://doi.org/10.1002/mma.6018

    Article  MathSciNet  Google Scholar 

  35. Prasad A, Sharma PB (2022) Convolution and product theorems for the quadratic-phase Fourier transform. Georgian Mathematical Journal 29(4):595–602

    Article  MathSciNet  Google Scholar 

  36. Prasad A, Manna S, Mahato A, Singh VK (2014) The generalized continuous wavelet transform associated with the fractional Fourier transform. J Comput Appl Math 259:660–671

    Article  MathSciNet  Google Scholar 

  37. Ranjan R, **dal N, Singh AK (2020) Fractional S-Transform and Its Properties: A Comprehensive Survey. Wireless Personal Communications. https://doi.org/10.1007/s11277-020-07339-6

    Article  Google Scholar 

  38. Riba L, Wong MW (2015) Continuous inversion formulas for multi-dimensional modified Stockwell transforms. Integral Transforms Spec Funct 26:9–19

    Article  MathSciNet  Google Scholar 

  39. Rioul O, Vetterli M (1991) Wavelets and signal processing. IEEE Signal Process Mag 8:14–38

    Article  ADS  Google Scholar 

  40. Saitoh S (2010) Theory of reproducing kernels: Applications to approximate solutions of bounded linear operator functions on Hilbert spaces. Amer Math Soc Trans Ser 230(2):107–134

    Google Scholar 

  41. Bhat MY, Dar AH (2023) Linear Canonical Hankel domain based Stockwell transform and associated Heisenberg’s uncertainty principle. J Anal. https://doi.org/10.1007/s41478-023-00624-0

  42. Wei D, Zhang Y, Li YM (2022) Linear canonical Stockwell transform:theory and applications. IEEE Trans Signal Process. https://doi.org/10.1109/TSP.2022.3152402

  43. Bhat MY, Dar AH, Zayed M (2023) Convolution, Correlation and Uncertainty Principle in the One-Dimensional Quaternion Quadratic-Phase Fourier Transform Domain. Mathematics. https://doi.org/10.3390/math11133002

  44. Dar AH, Bhat MY, Rahman M (2023) Generalized wave packet transform based on convolution operator in the quaternion quadratic-phase Fourier domain. Optik—Int. J. Light Electron Opt. 286:171029

  45. Sharma PB (2022) The Wigner-Ville distribution associate with quadratic-phase Fourier transform. AIP Conferenc Proceeding 2435(1)020028

  46. Singh SK (2012) The S-transform on spaces of type S. Integral Transforms Spec Funct 23:481–494

    Article  ADS  MathSciNet  Google Scholar 

  47. Srivastava HM, Khatterwani K, Upadhyay SK (2019) A certain family of fractional wavelet transformations. Math Methods Appl Sci 42:3103–3122

    Article  MathSciNet  Google Scholar 

  48. Stern A (2008) Uncertainty principles in linear canonical transform domains and some of their implications in optics. J Opt Soc Am A-Opt Image Sci Vis 25(3):647–652

    Article  ADS  MathSciNet  PubMed  Google Scholar 

  49. Stockwell RG (2007) A basis for efficient representation of the S-transform. Digit Signal Process 17:371–393

    Article  Google Scholar 

  50. Stockwell RG, Mansinha L, Lowe RP (1996) Localization of the complex spectrum: The S-transform. IEEE Trans Signal Process 44:998–1001

    Article  ADS  Google Scholar 

  51. Wei D, Zhang Y (2021) Fractional Stockwell transform: Theory and applications. Digital Signal Processing 115:103090

    Article  Google Scholar 

  52. Wilczok E (2000) Newuncertainty principles for the continuous Gabor transform and the continuouswavelet transform. Doc Math 5:201–226

    Article  MathSciNet  Google Scholar 

  53. Xu GL, Wang XT, Xu XG (2009) The logarithmic, Heisenberg’s and short-time uncertainty principles associated with fractional Fourier transform. Signal Process 89:339–343

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by the Research Grant (No. JKST &IC/SRE/J/357-60) provided by JKSTIC, Govt. of Jammu and Kashmir, India.

Funding

No funding was received for this work.

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Islamic University of Science and Technology, Kashmir, India

    Aamir H. Dar & M. Younus Bhat

Authors
  1. Aamir H. Dar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Younus Bhat
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Both the authors equally contributed towards this work.

Corresponding author

Correspondence to M. Younus Bhat.

Ethics declarations

Competing interests

The authors have no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dar, A.H., Bhat, M.Y. Convolution based quadratic-phase Stockwell transform: theory and uncertainty relations. Multimed Tools Appl 83, 20117–20147 (2024). https://doi.org/10.1007/s11042-023-16331-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-023-16331-8

Keywords

Mathematics Subject Classification (2010)

Search

Navigation