SpringerLink
Log in

Estimation of the Largest Lyapunov Exponent for a Model of Cross-Shaped Waves in a Rectangular Channel of Finite Size

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

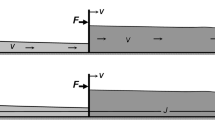
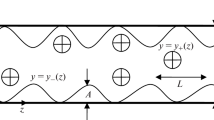
The largest Lyapunov exponent characterizes the degree of exponential divergence of close trajectories of a dynamical system. The presence of a positive Lyapunov exponent in the system reveals rapid divergence of any two arbitrarily close trajectories with time and sensitivity to the values of the initial conditions. Therefore, as a result of determination of the Lyapunov exponent, it becomes possible to identify the system in a sense of chaotic dynamics. We propose a method for increasing the accuracy of the Benettin numerical algorithm aimed at the evaluation of the largest Lyapunov exponent in the case of a dissipative dynamical system. The results of calculations are presented for the hydrodynamic model of cross-shaped waves in a rectangular channel of finite size.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. Bergé, Y. Pomeau, and C. Vidal, Order Within Chaos: Towards a Deterministic Approach to Turbulence, J. Wiley & Sons, New York (1984).

    Google Scholar 

  2. V. A. Golovko, “Neural network methods for processing chaotic processes”, in: Scientific Session of MIFI-2005, VII All-Russian Scientific and Technical Conference “Neuroinformatics–2005”: Lectures in Neuroinformatics, Yu. V. Tyumentsev (ed.), MIFI, Moscow (2005), pp. 43–91.

  3. T. S. Krasnopol’skaya and A. Y. Shvets, “Properties of chaotic fluid oscillations in cylindrical basins,” Prikl. Mekh., 28, No. 6, 52–61 (1992; English translation: Int. Appl. Mech., 28, No. 6, 386–394 (1992); https://doi.org/10.1007/BF00847097.

  4. T. S. Krasnopol’skaya and A. Y. Shvets, “Chaotic oscillations of a spherical pendulum as an example of interaction with an energy source”, Prikl. Mekh., 28, No. 10, 61–68 (1992); English translation: Int. Appl. Mech., 28, No. 10, 669–674 (1992); https://doi.org/10.1007/BF00846923.

  5. S. P. Kuznetsov, Dynamical Chaos, Fizmatlit, Moscow (2001).

    Google Scholar 

  6. F. Moon, Chaotic Vibrations: An Introduction for Applied Scientists and Engineers”, J. Wiley & Sons, New York, etc. (1987).

  7. V. I. Oseledets, “A multiplicative ergodic theorem. Lyapunov characteristic numbers for dynamical systems”, Tr.. Mosk. Mat. Obshch., 19, 179–210 (1968); English translation: Trans. Moscow Math. Soc., 19, 197–231 (1968).

  8. A. Yu. Shvets and V. A. Sirenko, “Scenarios of transitions to hyperchaos in nonideal oscillating systems”, Nelin. Kolyv., 21, No. 2, 284–292 (2018); English translation: J. Math. Sci., 243, No. 2, 338–346 (2019); https://doi.org/10.1007/s10958-019-04543-z.

  9. G. Benettin, L. Galgani, A. Giorgilli, and J. M. Strelcyn, “Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems; a method for computing all of them. Part 1: Theory”, Meccanica, 15, No. 1, 9–20 (1980); https://doi.org/10.1007/BF02128236.

    Article  Google Scholar 

  10. G. Benettin, L. Galgani, and J. M. Strelcyn, “Kolmogorov entropy and numerical experiments”, Phys. Rev. A, 14, No. 6, 2338–2342 (1976); https://doi.org/10.1103/PhysRevA.14.2338.

    Article  Google Scholar 

  11. J. P. Crutchfield, J. D. Farmer, N. H. Packard, and R. S. Shaw, “Chaos”, Sci. Am., 255, No. 6, 46–57 (1986); https://doi.org/10.1038/scientificamerican1286-46.

    Article  Google Scholar 

  12. T. S. Krasnopolskaya, “Acoustic chaos caused by the Sommerfeld effect”, J. Fluid Struct., 8, No. 7, 803–815 (1994); https://doi.org/10.1016/S0889-9746(94)90300-X.

    Article  Google Scholar 

  13. T. S. Krasnopolskaya, “Chaos in acoustic subspace raised by the Sommerfeld–Kononenko effect”, Meccanica, 41, No. 3, 299–310 (2006); https://doi.org/10.1007/s11012-005-5899-z.

    Article  MathSciNet  Google Scholar 

  14. T. S. Krasnopolskaya and G. J. F. Heijst, “Wave pattern formation in a fluid annulus with a radially vibrating inner cylinder”, J. Fluid Mech., 328, 229–252 (1996); https://doi.org/10.1017/S0022112096008701.

  15. T. S. Krasnopolskaya, V. V. Meleshko, G. W. M. Peters, and H. E. H. Meijer, “Mixing in Stokes flow in an annular wedge cavity”, Eur. J. Mech. B-Fluids, 18, No. 5, 793–822 (1999); https://doi.org/10.1016/S0997-7546(99)00119-3.

    Article  MathSciNet  Google Scholar 

  16. T. S. Krasnopolskaya and E. D. Pechuk, “Peculiarities of parametric resonances in cross-waves”, Chaotic Modeling and Simulations, No. 3, 377–385 (2016).

    Google Scholar 

  17. J. Laskar, C. Froeschlé, and A. Celletti, “The measure of chaos by the numerical analysis of the fundamental frequencies. Application to the standard map**”, Physica D: Nonlinear Phenomena, 56, Nos. 2-3, 253–269 (1992); https://doi.org/10.1016/0167-2789(92)90028-L.

    Article  MathSciNet  Google Scholar 

  18. V. Meleshko, T. Krasnopolskaya, G. W. M. Peters, and H. E. H. Meijer, “Coherent structures and scales of Lagrangian turbulence”, Advances in Turbulence. VI. Fluid Mechanics and Its Applications, S. Gavrilakis, L. Machiels, and P. A. Monkewitz (eds.), Vol. 36., Springer, Dordrecht (1996), pp. 601–604; https://doi.org/10.1007/978-94-009-0297-8_171.

  19. A. Y. Shvets and T. S. Krasnopolskaya, “Hyperchaos in piezoceramic systems with limited power supply”, IUTAM Symposium on Hamiltonian Dynamics, Vortex Structures, Turbulence, A. V. Borisov, V. V. Kozlov, I. S. Mamaev, and M. A. Sokolovskiy (eds.), IUTAM Bookseries, Vol. 6, Springer, Dordrecht (2008), pp. 313–322; https://doi.org/10.1007/978-1-4020-6744-0_27.

  20. A. Shvets and S. Donetskyi, “Transition to deterministic chaos in some electroelastic systems”, 11th Chaotic Modeling and Simulation International Conference. CHAOS 2018, C. H. Skiadas and I. Lubashevsky (eds), Springer Proceedings in Complexity, Springer, Cham (2019), pp. 257–264; https://doi.org/10.1007/978-3-030-15297-0_23.

  21. F. Takens, “Detecting strange attractors in turbulence”, D. Rand and L. S. Young (eds)., Dynamical Systems and Turbulence, Lecture Notes in Mathematics., Vol. 898, Springer, Berlin–Heidelberg (1981), pp. 366–381; https://doi.org/10.1007/BFb0091924.

  22. A. Wolf, J. B. Swift, H. L. Swinney, and J. A. Vastano, “Determining Lyapunov exponents from a time series”, Physica D: Nonlinear Phenomena, 16, No. 3, 285–317(1985); https://doi.org/10.1016/0167-2789(85)90011-9.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Kyiv National University of Construction and Architecture, Kyiv, Ukraine

    V. D. Pechuk

  2. Institute of Hydromechanics, National Academy of Sciences of Ukraine, Kyiv, Ukraine

    T. S. Krasnopolska

Authors
  1. V. D. Pechuk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. S. Krasnopolska
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to T. S. Krasnopolska.

Additional information

Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 65, No. 1-2, pp. 209–215, January–June, 2022.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pechuk, V.D., Krasnopolska, T.S. Estimation of the Largest Lyapunov Exponent for a Model of Cross-Shaped Waves in a Rectangular Channel of Finite Size. J Math Sci 282, 862–869 (2024). https://doi.org/10.1007/s10958-024-07221-x

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-024-07221-x

Keywords

Search

Navigation