An Extremal Property of the Hexagonal Lattice

Abstract

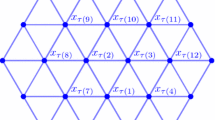
We describe an extremal property of the hexagonal lattice $\Lambda \subset \mathbb {R}^2$. Let p denote the circumcenter of its fundamental triangle (a so-called deep hole) and let $A_r$ denote the set of lattice points that are at distance r from p

$$\begin{aligned} A_r = \left\{ \lambda \in \Lambda : \Vert \lambda - p \Vert = r\right\} . \end{aligned}$$

If $\Gamma$ is a small perturbation of $\Lambda$ in the space of lattices with fixed density and $C_r$ denotes the set of points in $A_r$ shifted to the new lattice, then

$$\begin{aligned} \sum _{\mu \in C_r}{ \Vert p - \mu \Vert } - \sum _{\lambda \in A_r}{ \Vert p - \lambda \Vert } > rsim r \, \# A_r \, d(\Lambda , \Gamma )^2, \end{aligned}$$

where $d(\Lambda , \Gamma )$ denotes the distance between the lattices: the hexagonal lattice has the property that “far away points are closer than they are for nearby lattices”. This has implications in the calculus of variations: assume

$$\begin{aligned} g_\Gamma (z) = \sum _{\gamma \in \Gamma } f( \Vert z - \gamma \Vert ) \quad \text { satisfies } \quad \min _{z \in \mathbb {R}^2} g_\Lambda (z) = g_\Lambda (p). \end{aligned}$$

For a certain class of compactly supported functions f, the hexagonal lattice $\Lambda$ is then a strict local maximizer of

$$\begin{aligned} \max _{\Gamma } \min _{z \in \mathbb {R}^2} \sum _{\gamma \in \Gamma }{f( \Vert z - \gamma \Vert )}, \end{aligned}$$

where the maximum runs over all lattices of fixed density.