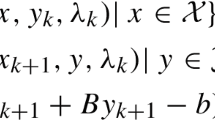SpringerLink
Log in

A Superlinearly Convergent Splitting Feasible Sequential Quadratic Optimization Method for Two-Block Large-Scale Smooth Optimization

  • Published:
Acta Mathematica Scientia Aims and scope Submit manuscript

Abstract

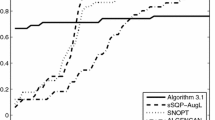
This paper discusses the two-block large-scale nonconvex optimization problem with general linear constraints. Based on the ideas of splitting and sequential quadratic optimization (SQO), a new feasible descent method for the discussed problem is proposed. First, we consider the problem of quadratic optimal (QO) approximation associated with the current feasible iteration point, and we split the QO into two small-scale QOs which can be solved in parallel. Second, a feasible descent direction for the problem is obtained and a new SQO-type method is proposed, namely, splitting feasible SQO (SF-SQO) method. Moreover, under suitable conditions, we analyse the global convergence, strong convergence and rate of superlinear convergence of the SF-SQO method. Finally, preliminary numerical experiments regarding the economic dispatch of a power system are carried out, and these show that the SF-SQO method is promising.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Börgens E, Kanzow C. Regularized Jacobi-type ADMM-methods for a class of separable convex optimization problems in Hilbert spaces. Comput Optim Appl, 2019, 73(3): 755–790

    Article  MathSciNet  MATH  Google Scholar 

  2. Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn, 2011, 3(1): 1–122

    Article  MATH  Google Scholar 

  3. Douglas J, Rachford H H. On the numerical solution of heat conduction problems in two and three space variables. Trans Amer Math Soc, 1956, 82(2): 421–439

    Article  MathSciNet  MATH  Google Scholar 

  4. Eckstein J. Splitting Methods for Monotone Operators with Applications to Parallel Optimization[D]. Cambridge: Massachusetts Institute of Technology, 1989

    Google Scholar 

  5. Fukushima M. A successive quadratic programming algorithm with global and superlinear convergence properties. Math Program, 1986, 35(3): 253–264

    Article  MathSciNet  MATH  Google Scholar 

  6. Gertz E M, Wright S J. Object orientated software for quadratic programming. ACM Trans Math Software, 2003, 29, 58–81

    Article  MathSciNet  MATH  Google Scholar 

  7. Glowinski R, Le Tallec P. Augmented Lagrangian and Operator-Splitting Methods in Nonlinear Mechanics. SIAM Philadelphia: Society for Industrial and Applied Mathematics, 1989

    Book  MATH  Google Scholar 

  8. Goldfarb D, Ma S Q, Scheinberg K. Fast alternating linearization methods for minimizing the sum of two convex functions. Math Program, 2013, 141(1–2): 349–382

    Article  MathSciNet  MATH  Google Scholar 

  9. Goldstein T, O’Donoghue B, Setzer S, Baraniuk R. Fast alternating direction optimization methods. SIAM J Imaging Sci, 2014, 7(3): 1588–1623

    Article  MathSciNet  MATH  Google Scholar 

  10. Han D R, Sun D F, Zhang L W. Linear rate convergence of the alternating direction method of multipliers for convex composite programming. Math Oper Res, 2018, 43(2): 622–637

    Article  MathSciNet  MATH  Google Scholar 

  11. He B S, Liu H, Wang Z R, Yuan X M. A strictly contractive Peaceman-Rachford splitting method for convex programming. SIAM J Optim, 2014, 24(3): 1011–1040

    Article  MathSciNet  MATH  Google Scholar 

  12. He B S, Ma F, Yuan X M. Convergence study on the symmetric version of admm with larger step sizes. SIAM J Imaging Sci, 2016, 9(3): 1467–1501

    Article  MathSciNet  MATH  Google Scholar 

  13. He B S, Yuan X M. On the O(1/n) convergence rate of the Douglas-Rachford alternating direction method. SIAM J Numer Anal, 2012, 50(2): 700–709

    Article  MathSciNet  MATH  Google Scholar 

  14. He B S, Yuan X M. On non-ergodic convergence rate of Douglas-Rachford alternating direction method of multipliers. Numer Math, 2015, 130(3): 567–577

    Article  MathSciNet  MATH  Google Scholar 

  15. Hong M Y, Luo Z Q, Razaviyayn M. Convergence analysis of alternating direction method of multipliers for a family of nonconvex problems. SIAM J Optim, 2016, 26(1): 337–364

    Article  MathSciNet  MATH  Google Scholar 

  16. Jian J B. A superlinearly convergent implicit smooth SQP algorithm for mathematical programs with nonlinear complementarity constraints. Comput Optim Appl, 2005, 31(3): 335–361

    Article  MathSciNet  MATH  Google Scholar 

  17. Jian J B. Fast Algorithms for Smooth Constrained Optimization—Theoretical Analysis and Numerical Experiments. Bei**g: Science Press, 2010

    Google Scholar 

  18. Jian J B, Chao M T, Jiang X Z, Han D L. On the convexity and existence of solutions to quadratic programming problems with convex constraint. Pac J Optim, 2019, 15(1): 145–155

    MathSciNet  MATH  Google Scholar 

  19. Jian J B, Lao Y X, Chao M T, Ma G D. ADMM-SQP algorithm for two blocks linear constrained nonconvex optimization. Oper Res Trans, 2018, 22(2): 79–92

    MathSciNet  MATH  Google Scholar 

  20. Jian J B, Ma G D. A globally convergent QP-free algorithm for inequality constrained minimax optimization. Acta Math Sci, 2020, 40B: 1723–1738

    Article  MathSciNet  MATH  Google Scholar 

  21. Jian J B, Tang C M, Hu Q J, Zheng H Y. A new superlinearly convergent strongly subfeasible sequential quadratic programming algorithm for inequality-constrained optimization. Numer Func Anal Optim, 2008, 29(3/4): 376–409

    Article  MathSciNet  MATH  Google Scholar 

  22. Jian J B, Zhang C, Yin J H, Yang L F, Ma G D. Monotone splitting sequential quadratic optimization algorithm with applications in electric power systems. J Optim Theory Appl, 2020, 186: 226–247

    Article  MathSciNet  MATH  Google Scholar 

  23. Jian J B, Liu P J, Yin J H, Zhang C, Chao M T. A QCQP-based splitting SQP algorithm for two-block nonconvex constrained optimization problems with application. J Comput Appl Math, 2021, 390: 113368

    Article  MathSciNet  MATH  Google Scholar 

  24. Kellogg R B. A nonlinear alternating direction method. Math Comput, 1969, 23(105): 23–27

    Article  MathSciNet  MATH  Google Scholar 

  25. Li G Y, Pong T K. Global convergence of splitting methods for nonconvex composite optimization. SIAM J Optim, 2015, 25(4): 2434–2460

    Article  MathSciNet  MATH  Google Scholar 

  26. Lions P L, Mercier B. Splitting algorithms for the sum of two nonlinear operators. SIAM J Numer Anal, 1979, 16(6): 964–979

    Article  MathSciNet  MATH  Google Scholar 

  27. Marchuk G I. Splitting and alternating direction methods// Lions J L. Handbook of Numerical Analysis. Vol I. Amsterdam: North-Holland, 1990: 197–462

    Chapter  Google Scholar 

  28. Monteiro R D, Svaiter B F. Iteration-complexity of block-decomposition algorithms and the alternating direction method of multipliers. SIAM J Optim, 2013, 23(1): 475–507

    Article  MathSciNet  MATH  Google Scholar 

  29. OOQP solver for Quadratic Program. https://www.inverseproblem.co.nz/OPTI/index.php/Solvers/OOQP

  30. Panier E R, Tits A L. A superlinearly convergent feasible method for the solution of inequality constrained optimization problems. SIAM J Control Optim, 1987, 25(4): 934–950

    Article  MathSciNet  MATH  Google Scholar 

  31. Passty G B. Ergodic convergence to a zero of the sum of monotone operators in hilbert space. J Math Anal Appl, 1979, 72(2): 383–390

    Article  MathSciNet  MATH  Google Scholar 

  32. Robinson S M. A quadratically-convergent algorithm for general nonlinear programming problems. Math Program, 1972, 3(1): 145–156

    Article  MathSciNet  MATH  Google Scholar 

  33. Shefi R, Teboulle M. Rate of convergence analysis of decomposition methods based on the proximal method of multipliers for convex minimization. SIAM J Optim, 2014, 24(1): 269–297

    Article  MathSciNet  MATH  Google Scholar 

  34. Solodov M V. Global convergence of an SQP method without boundedness assumptions on any of the iterative sequences. Math Program, 2009, 118(1): 1–12

    Article  MathSciNet  MATH  Google Scholar 

  35. Theerthamalai A, Maheswarapu S. An effective non-iterative “λ-logic based” algorithm for economic dispatch of generators with cubic fuel cost function. Int J Electr Power Energy Syst, 2010, 32(5): 539–542

    Article  Google Scholar 

  36. Wang Y, Luo L, Freedman M T, Kung S Y. Probabilistic principal component subspaces: a hierarchical finite mixture model for data visualization. IEEE Trans Neural Net, 2000, 11(3): 625–636

    Article  Google Scholar 

  37. Wilson R B. A Simplicial Method for Concave Programming[D]. Cambridge: Harvard University, 1963

    Google Scholar 

  38. Xu Z B, Chang X Y, Xu F M, Zhang H. L1/2 regularization: a thresholding representation theory and a fast solver. IEEE Trans Neural Netw Learn Syst, 2012, 23(7): 1013–1027

    Article  Google Scholar 

  39. Yang L F, Luo J Y, Xu Y, Zhang Z R, Dong Z Y. A distributed dual consensus ADMM based on partition for DC-DOPF with carbon emission trading. IEEE Trans Ind Inform, 2020, 16(3): 1858–1872

    Article  Google Scholar 

  40. Zhang C, Yang L F, Jian J B. Two-stage fully distributed approach for unit commitment with consensus ADMM. Electr Pow Syst Res, 2020, 181(106180): 1–12

    Google Scholar 

  41. Zhu Z B, Jian J B. An efficient feasible SQP algorithm for inequality constrained optimization. Nonlinear Anal Real, 2009, 10(2): 1220–1228

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Mathematics and Physics, Guangxi Key Laboratory of Hybrid Computation and IC Design Analysis, Center for Applied Mathematics and Artificial Intelligence, Guangxi Minzu University, Nanning, 530006, China

    **bao Jian

  2. School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai, 200093, China

    Chen Zhang

  3. School of Mathematics, China University of Mining and Technology, Xuzhou, 221116, China

    Pengjie Liu

Authors
  1. **bao Jian
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chen Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Pengjie Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to **bao Jian.

Additional information

This work was supported by the National Natural Science Foundation of China (12171106), the Natural Science Foundation of Guangxi Province (2020GXNSFDA238017 and 2018GXNSFFA281007) and the Shanghai Sailing Program (21YF1430300).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jian, J., Zhang, C. & Liu, P. A Superlinearly Convergent Splitting Feasible Sequential Quadratic Optimization Method for Two-Block Large-Scale Smooth Optimization. Acta Math Sci 43, 1–24 (2023). https://doi.org/10.1007/s10473-023-0101-z

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10473-023-0101-z

Key words

2010 MR Subject Classification

Search

Navigation