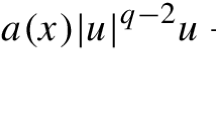Abstract
In this paper, by extending the notions of harmonic transplantation and harmonic radius in the Heisenberg group, we give an upper bound for the first eigenvalue for the following Dirichlet problem:
where \( \Omega \) is a regular bounded domain of \( \mathbb {H}^1\) and \(\Delta _{\mathbb {H}^1}\) is the Kohn–Laplace operator. Using a result of Pansu which gives a relation between the volume of \(\Omega \) and the perimeter of its boundary, we prove that
where \(l_{11} \) is the first strictly positive zero of the Bessel function of first kind and order 1, \( C_{\Omega } \) is a constant depending of \( \Omega \), and \(r_{\Omega }(\xi ) \) is the harmonic radius of \( \Omega \) at a point \(\xi \) of \(\Omega .\)
Similar content being viewed by others
References
Hersch, J.: Transplantation harmonique, transplantation par modules et théorèmes isopérim étriques. Comment. Math. Helv. 44–3, 354–366 (1969)
Polya, G., Schiffer, M.: Convexity of functionals by transplantation. J. Anal. Math. 3, 245–345 (1954)
Polya, G., Szego, G.: Isoperimetric Inequalities in Mathematical Physics. Princeton University Press, Princeton (1951)
Bandle, C., Flucher, M.: Harmonic radius and concentration of energy, hyperbolic radius and Liouvilles equations. SIAM 38–2, 191–238 (1996)
Bandle, C., Brillard, A., Flucher, M.: Grenn’s function. Harmonic transplantation, and best Sobolev constant in spaces of constant curvature. Trans. Am. Math. Soc. 350–3, 1103–1128 (1998)
Pansu, P.: Une inégalité isopérimétrique sur le groupe de Heisenberg. C. R. Acad. Sci. Paris. I Math. 295–2, 127–130 (1982)
Pansu, P.: An isoperimetric inequality on the Heisenberg group. In: Conference on Differential Geometry on Homogeneous Spaces (Turin, 1983). Rend. Sem. Mat. Univ. Politec. Torino, Special Issue (1983)
Ritore, M., Rosales, C.: Area-stationary surfaces in the Heisenberg group \( {\mathbb{H}}^1 \). Adv. Math. 219–2, 633–671 (2008)
Leonardi, G.P., Rigot, S.: Isoperimetric sets on Carnot Groups. Houston J. Math. 29–3, 609–637 (2003)
Luo, X., Niu, P.: Eigenvalue problems for square sum operators consisting of vector fields. Math. Appl. 10–4, 101–104 (1997)
Luo, X., Niu, P.: On the eigenvalues of the operator sum of squares of vector fields. Chin. Bull. Sci. 43, 263 (1998)
Luo, X., Niu, P.: On the Dirichlet eigenvalue problem of the Folland-Stein operator in the Heisenberg group. Acta Math. Sci. 17, 70–75 (1997)
Kohn, J.J.: Boundaries of complex manifolds, pp. 81–94. Minneapolis, Proc. Conf. on complex manifolds (1964)
Franchi, B., Serapione, R., Serra Cassano, F.: Rectifiability and perimeter in the Heisenberg group. Math. Ann. 321, 479–531 (2001)
Ritore, M., Rosales, C.: Rotationally invariant hypersurfaces with constant mean curvature in the Heisenberg group. J. Geom. Anal. 16–4, 703–720 (2006)
Gamara, N., Guemri, H.: Estimates of the Green’s function and its regular part on Heisenberg group domains. Adv. Nonlinear Stud. 11, 593–612 (2011)
Krantz, G.S., Parks, R.H.: Geometric Integration Theory, Springer Science and Business Media (2008)
Chavel, I.: Riemaniann Geometry. Cambridge University Press, Cambridge (1995)
Korenev, B.G.: Bessel Functions and Their Applications. CRC Press, Boca Raton (2003)
Capogna, L., Danielli, D., Garofalo, N.: An isoperimetric inequality and the geometric Sobolev embedding for vector fields. Math. Res. Lett. 1–2, 203–215 (1994)
Monti, R., Rickly, M.: Convex isoperimetric sets in the Heisenberg group. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 8(2), 391–415 (2009)
Danielli, D., Garofalo, N., Nhieu, D.-M.: Sub-Riemannian calculus on hypersurfaces in Carnot groups. Adv. Math. 215–1, 292–378 (2007)
Bony, J.M.: Principe du maximum, inégalite de Harnack et unicité du problème de Cauchy pour les opérateurs elliptiques dégénerés. Ann. Inst. Fourier 19–1, 277–304 (1969)
Hansen, W., Hueber, H.: The Dirichlet problem for sub-Laplacians on nilpotent Lie groups-geometric criteria for regularity. Math. Ann. 276, 537–547 (1987)
Acknowledgements
The authors would like to thank P. Pansu for his suggestions and advices.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gamara, N., Makni, A. The First Eigenvalue of the Kohn–Laplace Operator in the Heisenberg Group. Mediterr. J. Math. 14, 60 (2017). https://doi.org/10.1007/s00009-017-0851-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00009-017-0851-8
Keywords
- Kohn–Laplace operator
- first eigenvalue
- harmonic radius
- harmonic transplantation
- Green’s function
- Heisenberg group