1 Introduction

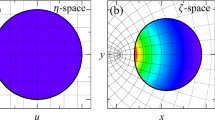
Whispering-gallery-mode (WGM) cavity is an intriguing platform for intensely enhancing light-matter interaction, which lays the foundations for ultra-low threshold lasers [1, 2], ultra-sensitive sensing [28,29,30,37,38,39,40,

2 Results and discussions

Let’s start by reviewing the TIR at the planar interface between two dielectric media as shown in Fig. 1a, considering a light beam with incident angle \(\theta _i\) im**ing on the boundary from a denser medium (\(n_1\)). When \(\theta _i\) is greater than the critical angle \(\theta _c\) (\(\theta _c\) = arcsin\((\frac{n_0}{n_1}))\), only the decaying evanescent field exists in the less dense medium (\(n_0\)). Based on the TO theory, wave propagation in physical (z) space with homogeneous index (\(n_z\)) could be equivalent to that in the virtual (w) space with inhomogeneous index distribution. Thus, a two-dimensional (2D) OBH cavity in virtual space (\(w = u+iv\)) is constructed by implementing an exponential transformation: \(w = {w_0}{e^{z/{z_0}}}\) as shown in Fig. 1b, where \(z = x +iy\) is complex variables of the physical space, \(w_0\) and \(z_0\) are the constants in w space and z space, respectively. The refractive index profile of OBH cavity is derived as:

$$\begin{aligned} n(r) = \left\{ \begin{array}{ll} n_z\Big |\frac{\mathrm {d} z}{\mathrm {d} w}\Big | = \frac{n_0}{r/R} &\quad r > R\\ n_1 & \quad r \le R \end{array}\right. \end{aligned}$$
(1)

Note that we only conformally map the index distribution in the claddings (\(r>R\)) and keep the core region (\(r\le R\)) intact to avoid the divergence of index in the cavity center (see Additional file 1) [45]. As a consequence, the evanescent wave in w-space with polar coordinates can be obtained directly from the TIR-field transformation (see Additional file 1) [45]:

$$\begin{aligned} E(r,\varphi ) = A{({\textstyle {R \over r}})^\alpha }{e^{im_w\varphi } } \end{aligned}$$
(2)

where A is field amplitude, \(\alpha = \sqrt{m_w^2-{(n_0k_0R)^2}}\), \(m_w = \beta R\), \(\beta\) and \(k_0\) are the propagation wave vector in z-space and vacuum, respectively, and \(\varphi\) is the azimuthal angle. Therefore, the optical field in the cladding of the OBH cavity should follow the fast decay rule (\(\sim 1/r^\alpha\)), which is radically different from the Hankel-function distributions (asymptotic \(\sqrt{1/r}\)) of a homogeneous cavity. Further, a group of conformal OBH cavities, such as single-core and multi-core shapes, are engineered based on the form invariance of Maxwell’s equations under coordinate transformations. Specifically, the map** of \({w^2} = {\chi ^2} - 1\) is performed on the circular OBH cavity [equation (1)], where \(\chi = \xi +i\eta\), and the quadrupole (peanut-like) OBH cavity is constructed with \(\left| R_w \right|\) = 1.55 (\(\left| R_w \right|\) = 1) as shown in Fig. 1c\(_1\) (Fig. 1c\(_2\)). The optical properties of these non-circular cavities are discussed later.

Fig. 1
figure 1

Conformal transformation for optical black hole (OBH) cavity. Map** the homogeneous refractive index distribution in the original straight space (a) to a circular OBH cavity (b) with gradient index. The black and orange straight lines in (a) are transformed into the interior and exterior circle. The core region of OBH cavity is truncated as homogeneous index. The quadrupole cavity (c\(_1\)) and peanut-like cavity (c\(_2\)) are transformed from the circular OBH cavity under different structural parameters, \({{R}_{\text {w}}} = \sqrt{{{u}^{2}}+{{v}^{2}}}\). The black curve is the cavity boundary

Full size image
Fig. 2
figure 2

Optical properties of whispering-gallery-mode (WGM) in OBH cavity and homogeneous cavity. Analytical standing wave pattern of WGM in OBH cavity (a) and homogeneous cavity (b), where the resonant mode-number m is 3 and eigen-frequency is \(\sim\) 1.93 GHz. Inset: normalized electric field amplitude in the radial direction. c Comparison of skin depth of WGM field in the OBH cavity and homogeneous cavity with various azimuthal mode numbers. d Effective potential of OBH cavity (red curve) and homogeneous cavity (black curve)

Full size image
Fig. 3
figure 3

Experimental characterizations of OBH cavity. a Experimental setup of the microwave near-field scanning system. Inset: photograph of the fabricated sample. b Design aperture size distributions in OBH layered structures. c Comparison of simulated Q-factor in continuous and discrete OBH cavity with various azimuthal mode numbers. d Experimental normalized resonant spectra of OBH cavity and homogeneous cavity with mode number m = 3 and m = 4. The solid curves are Lorentz fittings. Measured WGM field pattern with mode number (e\(_1\)) m = 3 and (e\(_2\)) m = 4 . Simulated WGM field pattern with mode number (f\(_1\)) m = 3 and (f\(_2\)) m = 4. The white curves are the core and cladding material boundary of OBH cavity device

Full size image
Fig. 4
figure 4

Comparison of WGM in a face-shaped deformed OBH cavity and homogeneous cavity. Simulated WGM field of (a) deformed OBH cavity, and (b) deformed homogeneous cavity. White solid (dashed) curve is the deformed (circular) cavity boundary. c Comparison of Q-factor for a deformed OBH cavity (black curve) and homogeneous cavity (red curve) with various deformations. The resonant mode number is m = 5. d Comparison of Q-factor of deformed OBH (black curve) and homogeneous cavity (red curve) with different mode numbers

Full size image
Fig. 5
figure 5

WGM fields in the conformal OBH cavity and homogeneous cavity. The refractive index distribution for (a\(_1\)) the quadrupole OBH cavity and (a\(_2\)) the peanut-like OBH cavity. The maximal refractive index of quadrupole and peanut-like cavity is truncated as 27 to avoid index divergence in the core region. The typical WGM field patterns with resonant mode-number m = 4 of (b\(_1\)) the quadrupole OBH cavity and (b\(_2\)) the peanut-like OBH cavity. Typical WGM field patterns of (c\(_1\)) the homogeneous quadrupole cavity and (c\(_2\)) peanut-like cavity. The resonant frequency is \(\sim\) 4.8 GHz and \(\sim\) 7.3 GHz for quadrupole cavity and peanut-like cavity, respectively

Full size image

Now we analyze the WGM of a circular OBH cavity via the direct solution of Maxwell’s equations in the cylindrical coordinates. Since the transverse electric (TE) and transverse magnetic (TM) polarizations are decoupled, we consider the TE polarization without the loss of generality. Employing the method of separating variables with the boundary continuity, the WGM fields in the cladding region of OBH cavity is derived (see Additional file 1) [45], which is nearly the same as equation (2). The eigen-equation of OBH cavity is as following:

$$\begin{aligned} {k_0}{n_1}R{J'_m}({n_1}{k_0}R) = -\sqrt{{m^2}-{{({n_0}{k_0}R)}^2}} {J_m}({n_1}{k_0}R) \end{aligned}$$
(3)

where m is an integer, \(J_m\)(\(n_{1}k_{0}R\)) is the m-order Bessel function. It is found that equation (3) has the real eigen-value under certain conditions (see Additional file 1: Fig. S1) [45], which is completely different from the homogeneous cavity with complex eigenfrequency. Thus the radiation loss caused by the curved boundary is completely inhibited in OBH cavity [46].

The analytical results of WGM fields in OBH cavity are shown in Fig. 2a. Here, the structural parameters of circular OBH cavity are as following: R = 3 cm, \(n_1\) = 4, \(n_0\) = 2, which facilitates the experimental verification. In this study, only the lowest radial mode numbers are considered, due to their optical fields being closely confined to the cavity boundary and having the smallest radial extent. As a comparison, the WGM fields of a homogeneous cavity with the constant refractive index (\(n_1'\) = 4, \(n_0'\) = 2) is calculated as shown in Fig. 2b. The WGM fields in the OBH cavity are tightly confined near the boundary, by contrast, there is a considerable part of optical fields leaking into the cavity surroundings in the homogeneous cavity as shown in Fig. 2a, b (Additional file 1: Fig. S2) [45]. To quantitatively characterize the field confinement, we define a skin depth (SD) \(\delta\), i.e., the distance between the cavity boundary and the position with 1/e field-amplitude maximum. The SD of OBH cavity is always smaller than that of the homogeneous cavity as shown in Fig. 2c. Since the optical field confinement is enhanced with the increase of resonant mode number, SD is decreased with the mode number as well.

To more clearly elucidate the functions of the OBH refractive index profile, the radial cylindrical Bessel equation is modified as the analog of the Schrödinger equation [47]. The central potential function V(r) of light propagation in OBH cavity is:

$$\begin{aligned} V(r) = k_0^2[1-n^2(r)]+\frac{(m+1/2)(m-1/2)}{r^2} \end{aligned}$$
(4)

In particular, the potential function in the cladding region (\(r>R\)) is V(r) = \(k_0^2\)+\(({m^2}-{n_0^2}{k_0^2}{R^2}-1/4)/{r^2}\) as shown in Fig. 2d. Obviously, the OBH cladding relaxes the change of the potential barrier, and the eigen-energy (\(k_0^2\)) of WGM in OBH cavity is always smaller than the potential under the aforementioned cavity parameters. Thus, the WGM field is tightly confined within the potential well, and the classical radiation loss is completely inhibited theoretically. On the contrary, light always tunnels out of the open boundary in a homogeneous cavity since the eigen-energy of WGM is larger than the effective potential when \(r\gg R\) (Fig. 2d black curve), and the radiation loss is not zero in all the WGMs. Note that in a conventional homogeneous cavity, the radiation loss predominates and the Q-factor is significantly decreased when the cavity geometry is comparable to the resonant wavelength (small resonant mode-number). Although an OBH cavity with a finite shell model has been theoretically studied to realize broadband light trap**/absorption and field penetration enhancement [15, 48], in this work we reveal the total radiation inhibition with infinite radiation Q-factor and the unique field decay rule in an ideal OBH cavity based on TO theory.

From Eq. (1), it demonstrates that a perfect OBH cavity requires an infinite region for gradient-index cladding that ranges from \(n_0\) to 0. This is challenging to realize in conventional materials [37, 49,50,51]. Here, as an executable alternative, by truncating the area in the OBH cavity with an index of less than 1, we reserve the range of cladding index from \(n_0\) to 1. Note that the index truncation breaks the ideal potential barrier and causes regenerated radiation loss (Additional file 1: Fig. S4) [45]. Nevertheless, the Q/S (S is the effective mode area for 2D cavities) enhancement of OBH cavity is still considerably high compared with a homogeneous cavity (Additional file 1: Fig. S5) [45]. Following that, the continuous OBH cladding is discretized into 9 layers with various effective index (Additional file 1: Fig. S6) [45], and the refractive index of the outermost layer (\(r>\) 5.4 cm) is simply set as air. Based on effective medium theory, the discrete layered index profile is achieved by drilling air holes with different diameters in two homogeneous dielectric slabs (Fig. 3a, b, Additional file 1). Here, three TF-2 dielectric plates with different permittivity are employed, which are 16, 4.4 and 2.2 from inside to outside. In Fig. 3c, a numerical simulation is used to evaluate the effectiveness of this discontinuous multi-layer cavity construction. Finally, the fabricated sample, with 5.4 cm in radius and 2 cm in height (Fig. 3a inset), were constructed by precision machining of dielectric plates.

In microwave experiments, a point source was utilized to excite the WGM, and a near-field scanning device, as illustrated in Fig. 3a, was employed to retrieve the resonant field. The scanning system was controlled by a three-axis motion controller with a sampling step of 2 mm. As comparison, a homogeneous cavity with a core of index \(n_1'\) = 4 and a cladding of index \(n_0'\) = 2 (6 cm in radius and 2 cm in height) was fabricated and measured. From the resonant spectra of OBH cavity (red curve) and homogeneous cavity (black curve) in Fig. 3d, the extracted Q-factor of WGM mode \(m = 3\) (\(m = 4\)) is \(\sim\) 49 (\(\sim\) 241) for OBH cavity, as for homogeneous cavity, the Q-factor of WGM mode \(m = 3\) (\(m = 4\)) is \(\sim\) 25 (\(\sim\) 30). The maximized Q-factor enhancement is \(\sim\) 8 for mode m = 4, which is smaller than the simulated Q-factor enhancement of \(\sim\) 12. The discrepancy between experimental and theoretical results are caused by the strong light scattering in the drilling air hole and the limited precision of mechanical machining for OBH cavity sample. Besides, the vertical radiation loss due to the air gap between samples and metal plate in the measurement also reduces the ultimate Q-factors (Additional file 1: Fig. S7) [45]. Figure 3e plots the measured field patterns for WGM modes (\(m = 3,4\)), which are in good agreement with the simulation results shown in Fig. 3f. They unambiguously demonstrate the stronger field confinement than that of the homogeneous cavity (Additional file 1: Fig. S8) [45]. Furthermore, we theoretically investigate the light trap** effect in the truncated OBH cavity. It is found that the trapped light fields are bent and directed to the inner cavity boundary and are tightly confined in the OBH cavity with clearly regular field patterns (Additional file 1: Figs. S12, S13) [45], which shows the potential of remote excitations of WGMs in OBH cavities.

In addition to demonstrating radiation Q-factor enhancement and field confinement in a circular cavity, our designed device can be generalized to the deformed cavity with directional emission [\({w^2} = {\chi ^2}-1\) for circular OBH cavity, we have obtained quadrupole OBH cavity and peanut-like (dual cores) OBH cavity with gradient index both in the core and cladding regions, as shown in Fig. 5(a\(_1\), a\(_2\)). It can be found that WGM fields in these conformal OBH cavities (Fig. 5b\(_1\), b\(_2\)) are tightly confined in the boundary compared with the homogeneous cavity (Fig. 5c\(_1\), c\(_2\)). Besides, the Q-factor of conformal quadrupole cavity (peanut-like cavity) is boosted by 7 (4) orders of magnitude compared with a homogeneous one (see Additional file 1) [45]. The different Q-factor enhancement can be attributed to the various cavity structures in the virtual w-space for the conformal map**. Given the ingenious conformal transformation, theoretically the OBH cavity with arbitrary boundary shapes can be constructed, which may provide a new avenue to cavity optics for fundamental physics and photonic applications.

3 Conclusions

In summary, we have reported a group of conformal OBH cavities based on transformation optics. The universal radiation loss in a conventional homogeneous cavity is completely inhibited in the ideal OBH cavity by an infinite wide potential barrier. The WGM fields in the OBH cavity are revealed to follow an unconventional \(1/r^{\alpha }\) decay rule based on the conformal map**. We demonstrate both the Q-factor enhancement and strongly confined WGM fields for a truncated OBH cavity in the microwave spectra. Furthermore, we show that the designed OBH cavity of circular shape can be applied to arbitrary-shaped cavities, which might find applications for chaotic photon transport and non-Hermitian physics with high-Q factor. For optical frequency band applications, the OBH cavity can be realized by using the gradient-thickness waveguide structures [37, 55] or gradient-size nanostructures [56]. Note that the absorption/scattering loss in the aforementioned platforms can be a serious issue, thus it is still challenging to realize high-Q OBH cavity in the optical frequency band.