1 Background

The time fractional partial differential equations have grown more attention outstanding to several real-life applications in electrical network systems, signal processing, optics, mathematical biology, financial evaluation and prediction, material science, electromagnetic control theory, multidimensional fluid flow, acoustics, pre-predator modeling in biological systems, and many more [2, 3, 5,6,7,8]. The delayed time fractional predator–prey model with feedback control has been studied by Hopf bifurcation [10, 11]. For better accuracy in real-life models, the applications of fractional models are growing and indicate significant requirements for better fractional mathematical models. Radial basis functions and Laplace transformation are used for the approximation of fractional anomalous sub-diffusion equation [12]. This process's advantage is handling many matrix data efficiently and accurately. Padder et al. [32] recently performed a dynamical analysis of a generalized tumor model via the Caputo fractional-order derivative. The Caputo fractional-order derivative is being employed to model biological systems, including tumor growth. Tumor growth models are extensively used in biomedical research to understand tumor development dynamics and evaluate potential treatments.

Various analytical approaches are accessible for the numerical simulation of fractional partial differential equations. Typically, these types of equations are complicated to handle analytically. Thus, numerical approaches play a massive role in numerical approximations. For example, existing collocation methods based on Jacobi–Gauss–Lobatto have been generalized in [15]. Chebyshev polynomials in spectral collocation have been used to compute the space-fractional KdV–Burgers' equation [16], where Caputo–Fabrizio treats the space-fractional derivative. The spectral Pell collocation technique for approximating the TFNB equation has been used in [17]. The authors of [18] used the Hermite cubic spline collocation technique for the computational approximation of Helmholtz and Burgers’ equations. The authors of [19, 21, 35, 36] used the quadratic B-spline Galerkin (QBSG) method, balanced space–time Chebyshev spectral collocation method, finite element method based on the cubic B-spline collocation method, and trigonometric tension B-spline collocation method, respectively, for TFNB equations. A practical and accurate technique based on the shifted Gegenbauer polynomials has been presented in [24] to simulate the multidimensional space-fractional coupled Burgers’ equations. The residual power series method was utilized for time fractional BBM Burgers by Zhang et al. [25] and found that it is in good arrangement with the exact solution. Different fractional differential operators are applied for the analytical result of the TFNB equation [26]. Analytical approaches for approximating the fractional Burger’s equation are presented in [27, 28].

A cubic B-spline FEM is applied in [13] to estimate time fractional Fisher’s as well as Burgers’ equations, while the authors of [14] used a collocation method based on Fibonacci polynomial and finite difference method to solve coupled fractional Burgers' equations. The authors of [22, 23] developed computational techniques based on cubic trigonometric B-splines (CTBS) and cubic parametric splines (CPS) to approximate the TFNB equation. Recently, Shafiq et al. [9] represented a numerical technique based on cubic B-spline (CB-spline) functions for the TFNB equation with the Atangana–Baleanu derivative. In addition, the authors of [1] discussed a numerical scheme for the Riemann–Liouville fractional integral. Further, they suggested two numerical schemes for the Caputo–Fabrizio and the Atangana–Baleanu integral operators. They analyzed that the Riemann–Liouville fractional integral yields smaller errors and an intense significant experimental convergence order in most functions, especially when the fractional order \(\alpha \to\) 0. A new adaptive numerical technique is proposed in [2] to solve nonlinear, singular, and stiff initial value problems frequently challenged in real life.

The arrangement of the paper is structured as follows. The discretization of the TFNB equation is given in Sect. 2. In Sect. 3, the von Neumann stability is discussed. Section 4 presents numerical results, while Sect. 5 presents its discussion. Finally, Sect. 6 highlights the conclusions.

2 Methods

2.1 Problem formulation

We establish a new hybrid B-spline collocation technique for following the Caputo TFNB equation.

$$\frac{{\partial^{\alpha } v}}{{\partial t^{\alpha } }} + v\frac{\partial v}{{\partial x}} - \hat{\nu }\frac{{\partial^{2} v}}{{\partial x^{2} }} = f(x,t), \, a \le x \le b, \, 0 < \alpha < 1,$$
(1)

Along with

$$v(x,0) = \phi (x),$$
(2)
$$v(a,t) = \psi_{1} (t), \, v(b,t) = \psi_{2} (t),$$
(3)

where the \(\frac{{\partial^{\alpha } v}}{{\partial t^{\alpha } }}\) denotes the Caputo time fractional derivative as follows:

$$\frac{{\partial^{\alpha } v}}{{\partial t^{\alpha } }} = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\int\limits_{0}^{t} {\left( {t - \varsigma } \right)^{ - \alpha } } \frac{{\partial v\left( {x,\varsigma } \right)}}{\partial \varsigma }d\varsigma , \, 0 < \alpha < 1.$$
(4)

Now, let us specify the definitions of Caputo fractional integral and derivatives.

Definition 2.1

The Caputo integral of the function \(g(t)\in {\mathbb{R}}\) of order \(\alpha \ge 0\) is defined as follows:

$${}^{c}J_{0,t}^{\alpha } g(t) = \frac{1}{\Gamma (\alpha )}\int\limits_{0}^{t} {\left( {t - \chi } \right)^{\alpha - 1} g(\chi )d\chi , \, \alpha } > 0, \, t > 0.$$

Definition 2.2

The Caputo derivative of \(g\left(t\right)\in {\mathbb{R}}\) is defined as follows:

$${}^{c}D_{0,t}^{\alpha } g\left( t \right) = \frac{1}{{\Gamma \left( {\hat{l} - \alpha } \right)}}\int\limits_{0}^{t} {\left( {t - \chi } \right)^{{\hat{l} - \alpha - 1}} } g^{{\left( {\hat{l}} \right)}} \left( \chi \right)d\chi , \, t > 0, \, \hat{l} - 1 < \alpha < \hat{l} \in {\mathbb{Z}}^{ + } .$$

2.2 Discretization of the problem

This part performs the procedure to discretize the Caputo TFNB equation using the cubic HB-spline collocation technique.

2.2.1 Caputo time fractional derivative

First, we do a uniform partition in [0, T] with length \(\Delta t = \frac{T}{N}\). Here \(N\) is the number of partitions in the time mesh. Now, the discretization of fractional derivatives \(\frac{{\partial^{\alpha } v}}{{\partial t^{\alpha } }}\) for \(0 < \alpha < 1\) at \(t = t_{j + 1}\) is given by L1 formula [20, 29, 30] as follows:

$$\frac{{\partial^{\alpha } v_{i}^{j + 1} }}{{\partial \tau^{\alpha } }} = a_{0} \sum\limits_{k = 0}^{j} {P_{k} \left( {v_{i}^{j - k + 1} - v_{i}^{j - k} } \right) + \hat{r}^{j + 1} } ,\;j = 0,1,2 \ldots N,$$
(5)

where \(a_{0} = \frac{{\Delta t^{ - \alpha } }}{{\left| \!{\overline {\, {2 - \alpha } \,}} \right. }}\), \(p_{j} = \left( {j + 1} \right)^{1 - \alpha } - j^{1 - \alpha }\), \(j = 0,1,2....N\), and truncate error represented as \(\hat{r}^{j + 1}\) which is described by \(\hat{r}^{j + 1} \le k_{v} \Delta t^{2 - \alpha }\), where \(k_{v}\) is a constant only related to dependent variable \(v\).

Lemma 2.1

The factor \(p_{k}\), occurring in Eq. (5), satisfies the following properties:

$$\left\{ \begin{gathered} p_{k} > 0, \, k = 0,1,...,N, \hfill \\ 1 = p_{0} > p_{1} > p_{2} > ... > p_{N} , \, p_{N} \to 0{\text{ as }}N \to \infty , \hfill \\ \end{gathered} \right.$$

Proof

For proof of Lemma, see references [20, 29].

2.2.2 Spatial derivatives

Now, we use the HB-spline collocation technique for discretizing the spatial derivatives. The domain [a, b] is partitioned uniformly with the space size \(h = \Delta x = \frac{b - a}{M}\) by the knots \(x_{i} = a + ih\), \(i = 0,1, \ldots M\), so that we possess \(a = x_{0} < x_{1} < x_{2} < \ldots < x_{M} = b\). Now, we specify the HB-spline functions \(Hb_{i} (x)\) for \(i = - 1, \, 0, \, ..., \, M + 1\) as follows:

$$Hb_{i} \left( x \right) = \frac{1}{{h^{3} }}\left\{ {\begin{array}{*{20}l} {\sigma \left( {x - x_{i - 2} } \right)^{3} + (1 - \sigma )b_{2} \left\{ { - \frac{1}{{\hat{p}}}\left( {\sinh \left( {\left( {x_{i - 2} - x} \right)\hat{p}} \right)} \right) + \left( {x_{i - 2} - x} \right)} \right\}, \, x \in \left[ {x_{i - 2} ,x_{i - 1} } \right),} \\ \begin{gathered} \sigma \left\{ {h^{3} + 3h^{2} \left( {x - x_{i - 1} } \right) + 3h\left( {x - x_{i - 1} } \right)^{2} - 3\left( {x - x_{i - 1} } \right)^{3} } \right\} + \hfill \\ (1 - \sigma )\left\{ {a_{1} } \right. + b_{1} \left( {x_{i} - x} \right) + c_{1} {\text{e}}^{{\hat{p}\left( {x_{i} - x} \right)}} + d_{1} \left. {{\text{e}}^{{\hat{p}\left( {x - x_{i} } \right)}} } \right\}, \, x \in \left[ {x_{i - 1} ,x_{i} } \right), \hfill \\ \end{gathered} \\ \begin{gathered} \sigma \left\{ {h^{3} + 3h^{2} \left( {x_{i + 1} - x} \right) + 3h\left( {x_{i + 1} - x} \right)^{2} - 3\left( {x_{i + 1} - x} \right)^{3} } \right\} + \hfill \\ (1 - \sigma )\left\{ {a_{1} } \right. + b_{1} \left( {x - x_{i} } \right) + c_{1} {\text{e}}^{{\hat{p}\left( {x - x_{i} } \right)}} + d_{1} \left. {{\text{e}}^{{\hat{p}\left( {x_{i} - x} \right)}} } \right\}, \, x \in \left[ {x_{i} ,x_{i + 1} } \right), \hfill \\ \end{gathered} \\ {\sigma \left( {x_{i + 2} - x} \right)^{3} + (1 - \sigma )b_{2} \left\{ { - \frac{1}{p}\left( {\sinh \left( {\hat{p}\left( {x - x_{i + 2} } \right)} \right)} \right) + \left( {x - x_{i + 2} } \right)} \right\}{, }x \in \left[ {x_{i + 1} ,x_{i + 2} } \right),} \\ {0,{\text{ otherwise,}}} \\ \end{array} } \right.$$
(6)

where

$$a_{1} = \frac{{\hat{p}h\hat{\varsigma }_{1} }}{{\hat{p}h\hat{\varsigma }_{1} - \hat{\varsigma }_{2} }}, \, b_{1} = \frac{{\hat{p}}}{2}\left( {\frac{{\hat{\varsigma }_{1} \left( {\hat{\varsigma }_{1} - 1} \right) + s^{2} }}{{\left( {ph\hat{\varsigma }_{1} - \hat{\varsigma }_{2} } \right)\left( {1 - \hat{\varsigma }_{1} } \right)}}} \right), \, c_{1} = \frac{1}{4}\left( {\frac{{{\text{e}}^{{ - \hat{p}h}} \left( {1 - \hat{\varsigma }_{1} } \right) + \hat{\varsigma }_{2} \left( {{\text{e}}^{{ - \hat{p}h}} - 1} \right)}}{{\left( {\hat{p}h\hat{\varsigma }_{1} - \hat{\varsigma }_{2} } \right)\left( {1 - \hat{\varsigma }_{1} } \right)}}} \right)$$
$$d_{1} = \frac{1}{4}\left( {\frac{{e^{{\hat{p}h}} \left( {\hat{\varsigma }_{1} - 1} \right) + \hat{\varsigma }_{2} \left( {e^{{\hat{p}h}} - 1} \right)}}{{\left( {\hat{p}h\hat{\varsigma }_{1} - \hat{\varsigma }_{2} } \right)\left( {1 - \hat{\varsigma }_{1} } \right)}}} \right), \, b_{2} = \frac{{\hat{p}}}{{2\left( {\hat{p}h\hat{\varsigma }_{1} - \hat{\varsigma }_{2} } \right)}}, \, \hat{\varsigma }_{1} = \cosh (\hat{p}h), \, \hat{\varsigma }_{2} = \sinh (\hat{p}h).$$

The HB-spline functions are obtained by using \(Hb_{i} (x) = \sigma B_{i} (x) + (1 - \sigma )EB_{i} (x)\), where \(B_{i} (x)\) and \(EB_{i} (x)\) are cubic B-spline basis functions [4, 31] and cubic exponential B-spline basis functions [3, 33, 34], and \(\sigma\) is a hybrid parameter. The term \(\hat{p}\) is a free parameter which acquires various forms of cubic exponential B-spline basis functions. The HB-spline functions are piecewise basis functions with non-negativity, \(C^{2}\) continuity, unity partition property, and form a basis in \(\left[ {a, \, b} \right]\). The values of \(Hb_{i} (x)\), \(Hb^{\prime}_{i} (x)\), and \(Hb^{\prime\prime}_{i} (x)\) are presented in Table 1.

Table 1 The values of \(Hb_{i} (x)\) and its derivatives at the knots
Full size table

We define the approximate solution as

$$u\left( {x,t_{j} } \right) \approx \sum\limits_{i = - 1}^{M + 1} {Hb_{i} \left( x \right)C_{i} \left( {t_{j} } \right)} ,$$
(7)

where \(C_{i} \left( {t_{j} } \right)\) is unknown quantities.

The variation of the \(v\left( {x,t_{j} } \right)\) is stated as follows:

$$v\left( {x,t_{j} } \right) = \sum\limits_{k = i - 1}^{i + 1} {Hb_{k} \left( x \right)C_{k} \left( {t_{j} } \right)} .$$
(8)

Using above equation, we get the approximate values of \(v\), \(v_{x}\), and \(v_{xx}\) as

$$v_{i}^{n} = \tau_{1} C_{i - 1}^{j} + \tau_{2} C_{i}^{j} + \tau_{1} C_{i + 1}^{j} ,$$
(9)
$$\left( {v_{x} } \right)_{i}^{j} = - \tau_{3} C_{i - 1}^{j} + \tau_{3} C_{i + 1}^{j} ,$$
(10)

and

$$\left( {v_{xx} } \right)_{i}^{j} = \tau_{4} (C_{i - 1}^{j} - 2C_{i}^{j} + C_{i + 1}^{j} ).$$
(11)

At \(t = t_{j + 1}\), using Eq. (5) for the time fractional derivative, the problem (1) is discretized as follows:

$$a_{0} \sum\limits_{k = 0}^{j} {p_{k} \left( {v_{i}^{j - k + 1} - v_{i}^{j - k} } \right)} + v_{i}^{j + 1} \left( {v_{x} } \right)_{i}^{j + 1} - \hat{\nu }\left( {v_{xx} } \right)_{i}^{j + 1} = f_{i}^{j + 1} , \, i = 0,1,...,M, \, j = 0,1,...,N.$$
(12)

For linearizing the nonlinear term, we use the Rubin–Graves technique as follows:

$$\left( {vv_{x} } \right)_{i}^{j + 1} = v_{i}^{j} \left( {v_{x} } \right)_{i}^{j + 1} + v_{i}^{j + 1} \left( {v_{x} } \right)_{i}^{j} - v_{i}^{j} \left( {v_{x} } \right)_{i}^{j}$$
(13)

By Eqs. (12) and (13), we have

$$a_{0} \sum\limits_{k = 0}^{j} {p_{k} \left( {v_{i}^{j - k + 1} - v_{i}^{j - k} } \right)} + v_{i}^{j} \left( {v_{x} } \right)_{i}^{j + 1} + v_{i}^{j + 1} \left( {v_{x} } \right)_{i}^{j} - v_{i}^{j} \left( {v_{x} } \right)_{i}^{j} - \hat{\nu }\left( {v_{xx} } \right)_{i}^{j + 1} = f_{i}^{j + 1} .$$
(14)

We can rewrite above equation as follows:

$$a_{0} \left[ {v_{i}^{j + 1} - \sum\limits_{k = 0}^{j - 1} {\left( {p_{k} - p_{k + 1} } \right)v_{i}^{j - k} - p_{j} v_{i}^{0} } } \right] + v_{i}^{j} \left( {v_{x} } \right)_{i}^{j + 1} + v_{i}^{j + 1} \left( {v_{x} } \right)_{i}^{j} - v_{i}^{j} \left( {v_{x} } \right)_{i}^{j} - \hat{\nu }\left( {v_{xx} } \right)_{i}^{j + 1} = f_{i}^{j + 1} .$$
(15)
$$\Rightarrow$$
$$\left( {a_{0} + \left( {v_{x} } \right)_{i}^{j} } \right)v_{i}^{j + 1} + v_{i}^{j} \left( {v_{x} } \right)_{i}^{j + 1} - \hat{\nu }\left( {v_{xx} } \right)_{i}^{j + 1} = a_{0} \sum\limits_{k = 1}^{j - 1} {\left( {\left( {p_{k} - p_{k + 1} } \right)v_{i}^{j - k} + p_{j} v_{i}^{0} } \right)} + v_{i}^{j} \left( {v_{x} } \right)_{i}^{j} + f_{i}^{j + 1} ,\,i = 0,1,...,M,\;j = 0,1,...,N.$$
(16)

Now, using Eqs. (9)–(10) in above equation, we get

$$A_{i}^{j} C_{i - 1}^{j + 1} + B_{i}^{j} C_{i}^{j + 1} + D_{i}^{j} C_{i + 1}^{j + 1} = R_{i}^{j} \;\;i = 1,2, \ldots ,M + 1,j = 0,1,...,N,$$
(17)

where

$$A_{i}^{j} = \left( {a_{0} + \left( {v_{x} } \right)_{i}^{j} } \right)\tau_{1} - v_{i}^{j} \tau_{3} - \hat{\nu }\tau_{4} , \, B_{i}^{j} = \left( {a_{0} + \left( {v_{x} } \right)_{i}^{j} } \right)\tau_{2} + 2\hat{\nu }\tau_{4} , \, D_{i}^{j} = \left( {a_{0} + \left( {v_{x} } \right)_{i}^{j} } \right)\tau_{1} + v_{i}^{j} \tau_{3} - \hat{\nu }\tau_{4} ,$$
$$R_{i}^{j} = a_{0} \sum\limits_{k = 1}^{j - 1} {\left( {\left( {p_{k} - p_{k + 1} } \right)v_{i}^{j - k} + p_{j} v_{i}^{0} } \right)} + v_{i}^{j} \left( {v_{x} } \right)_{i}^{j} + f_{i}^{j + 1} .$$

Equation (17) forms a system of linear equations with \(M + 1\) equations and \(M + 3\) unknows. For unique solution, we treat the boundary conditions \(v\left( {a,t} \right) = \psi_{1} \left( t \right)\) and \(v\left( {b,t} \right) = \psi_{2} \left( t \right)\) as

$$\left( {\tau_{1} C_{ - 1}^{j} + \tau_{2} C_{0}^{j} + \tau_{1} C_{1}^{j} } \right) = \psi_{1}^{j} ,$$
(18)

and

$$\left( {\tau_{1} C_{M - 1}^{j} + \tau_{2} C_{M}^{j} + \tau_{1} C_{M + 1}^{j} } \right) = \psi_{2}^{j} ,$$
(19)

Solving Eqs. (18) and (19), we get

$$C_{ - 1}^{j} = - \frac{{\tau_{2} }}{{\tau_{1} }}C_{0}^{j} - C_{1}^{j} + \frac{1}{{\tau_{1} }}\psi_{1}^{j} \,{\text{and}}\,C_{M + 1}^{j} = - C_{M - 1}^{j} - \frac{{\tau_{2} }}{{\tau_{1} }}C_{M}^{j} + \frac{1}{{\tau_{1} }}\psi_{2}^{j} .$$
(20)

For \(i = 0\) and \(i = M\), using (20) in (17), we have

$$\left( { - \frac{{\tau_{2} }}{{\tau_{1} }}A_{0}^{j} + B_{0}^{j} } \right)C_{0}^{j + 1} + \left( { - A_{0}^{j} + D_{0}^{j} } \right)C_{1}^{j + 1} = R_{0}^{j} - \frac{{A_{0}^{j} }}{{\tau_{1} }}\psi_{1}^{j + 1} ,$$
(21)

and

$$\left( {A_{M}^{j} - D_{M}^{j} } \right)C_{M - 1}^{j + 1} + \left( {B_{M}^{j} - \frac{{\tau_{2} }}{{\tau_{1} }}D_{M}^{j} } \right)C_{M}^{j + 1} = R_{M}^{j} - \frac{{D_{M}^{j} }}{{\tau_{1} }}\psi_{2}^{j + 1} .$$
(22)

Equations (21), (22), and (17) form a system of linear equations as follows:

$$\left[ {\begin{array}{*{20}c} { - \frac{{\tau_{2} }}{{\tau_{1} }}A_{0}^{j} + B_{0}^{j} } & { - A_{0}^{j} + D_{0}^{j} } & 0 & 0 & 0 & \cdots & 0 \\ {A_{0}^{j} } & {B_{0}^{j} } & {C_{0}^{j} } & 0 & 0 & \cdots & 0 \\ 0 & {A_{1}^{j} } & {B_{1}^{j} } & {D_{1}^{j} } & 0 & \cdots & 0 \\ \vdots & \ddots & \ddots & \ddots & \ddots & \vdots & \vdots \\ 0 & \cdots & 0 & {A_{M - 2}^{j} } & {B_{M - 2}^{j} } & {D_{M - 2}^{j} } & 0 \\ 0 & \cdots & 0 & 0 & {A_{M - 1}^{j} } & {B_{M - 1}^{j} } & {D_{M - 1}^{j} } \\ 0 & \cdots & 0 & 0 & 0 & {A_{M}^{j} - D_{M}^{j} } & {B_{M}^{j} - \frac{{\tau_{2} }}{{\tau_{1} }}D_{M}^{j} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {C_{0}^{0} } \\ {C_{1}^{0} } \\ {C_{2}^{0} } \\ \vdots \\ {C_{M - 2}^{0} } \\ {C_{M - 1}^{0} } \\ {C_{M}^{0} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{0}^{j} - \frac{{A_{0}^{j} }}{{\tau_{1} }}\psi_{1}^{j + 1} } \\ {R_{1}^{j} } \\ {R_{2}^{j} } \\ \vdots \\ {R_{M - 2}^{j} } \\ {R_{M - 1}^{j} } \\ {R_{M}^{j} - \frac{{D_{M}^{j} }}{{\tau_{1} }}\psi_{2}^{j + 1} } \\ \end{array} } \right].$$

To solve above system, we require to determine the initial vector \(\left( {C_{0}^{0} ,C_{1}^{0} ,...,C_{M - 1}^{0} ,C_{M}^{0} } \right)\) from the initial condition which delivers \(M + 1\) equations with \(M + 3\) unknowns. To remove the \(C_{ - 1}^{0}\) and \(C_{M + 1}^{0}\), we use the first derivative of the initial condition at the boundaries which gives:

$$C_{ - 1}^{0} = C_{1}^{0} - \frac{1}{{\tau_{3} }}\left( {\phi_{x} } \right)_{0} \,{\text{and}}\,C_{M + 1}^{0} = C_{M - 1}^{0} + \frac{1}{{\tau_{3} }}\left( {\phi_{x} } \right)_{M} ,$$
(23)

Now using Eqs. (23) and (9), we have the following system of linear equations:

$$\left[ {\begin{array}{*{20}c} {\tau_{2} } & {2\tau_{1} } & 0 & {} & {} & {} & {} \\ {\tau_{1} } & {\tau_{2} } & {\tau_{1} } & {} & {} & {} & {} \\ 0 & {\tau_{1} } & {\tau_{2} } & {\tau_{1} } & {} & {} & {} \\ {} & \ddots & \ddots & \ddots & {} & {} & {} \\ {} & {} & {} & {\tau_{1} } & {\tau_{2} } & {\tau_{1} } & 0 \\ {} & {} & {} & {} & {\tau_{1} } & {\tau_{2} } & {\tau_{1} } \\ {} & {} & {} & {} & 0 & {2\tau_{1} } & {\tau_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {C_{0}^{0} } \\ {C_{1}^{0} } \\ {C_{2}^{0} } \\ \vdots \\ {C_{M - 2}^{0} } \\ {C_{M - 1}^{0} } \\ {C_{M}^{0} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\phi_{0} + \frac{{\tau_{1} }}{{\tau_{3} }}\left( {\phi_{x} } \right)_{0} } \\ {\phi_{1} } \\ {\phi_{2} } \\ \vdots \\ {\phi_{M - 2} } \\ {\phi_{M - 1} } \\ {\phi_{M} - \frac{{\tau_{1} }}{{\tau_{3} }}\left( {\phi_{x} } \right)_{M} } \\ \end{array} } \right].$$

3 Stability analysis

The stability analysis of the discretized system of the TFNB equation based on the von Neumann method [22, 36, 39] is established in this section. According to Duhamels’ principle [40], it is assumed that the stability analysis of an inhomogeneous problem is an instantaneous consequence of the stability analysis for the subsequent homogeneous problem. So, for convenience and without loss of generality, we consider \(f = 0\), and we linearize the term \(vv_{x}\) by taking \(v_{x} = \hat{k}_{1}\) as locally constants. Using above assumptions and some manipulation, Eq. (12) can be rewritten as follows:

$$A^{*} C_{i - 1}^{j + 1} + B^{*} C_{i}^{j + 1} + D^{*} C_{i + 1}^{j + 1} = a_{0} \sum\limits_{k = 0}^{j - 1} {\left( {P_{k} - P_{k + 1} } \right)\left( {\tau_{1} C_{i - 1}^{j - k} + \tau_{2} C_{i}^{j - k} + \tau_{1} C_{i + 1}^{j - k} } \right) - } a_{0} p_{j} \left( {\tau_{1} C_{i - 1}^{0} + } \right.\tau_{2} C_{i}^{0} + \left. {\tau_{1} C_{i + 1}^{0} } \right) - a_{0} p_{j} \left( {\tau_{1} C_{i - 1}^{0} + \tau_{2} C_{i}^{0} + \tau_{1} C_{i + 1}^{0} } \right),\,i = 0,1,...,M,j = 0,1,...,N,$$
(24)

where

$$A^{*} = D^{*} = \left( {a_{0} + \hat{k}_{1} } \right)\tau_{1} - \hat{\nu }\tau_{4} , \, B^{*} = \left( {a_{0} + \hat{k}_{1} } \right)\tau_{2} + 2\hat{k}_{1} \tau_{4} .$$

Now, we take a Fourier mode as \(C_{i}^{j} = \delta^{j} e^{{\hat{i}i\mu h}}\), where \(\hat{i} = \sqrt { - 1}\), \(\delta\) is the time-dependent constraint. Applying it into above equation and simplifying it, we get

$$\left( {2A^{*} \cos \left( {\mu h} \right) + B^{*} } \right)\delta^{j + 1} = \left( {a_{0} \sum\limits_{k = 0}^{j - 1} {\left( {P_{k} - P_{k + 1} } \right)\delta^{j - k} - a_{0} p_{j} \delta^{0} } } \right)\left( {2\tau_{1} \cos \left( {\mu h} \right) + \tau_{2} } \right).$$
(25)
$$\Rightarrow \left[ {\left( {2(a_{0} + \hat{k}_{1} )\tau_{1} - 2\hat{\nu }\tau_{4} } \right)\cos \left( {\mu h} \right) + (a_{0} + \hat{k}_{1} )\tau_{2} + 2\hat{\nu }\tau_{4} } \right]\delta^{j + 1} = \left( {a_{0} \sum\limits_{k = 0}^{j - 1} {\left( {P_{k} - P_{k + 1} } \right)\delta^{j - k} } - } \right.\left. {a_{0} p_{j} \delta^{0} } \right)\left( {2\tau_{1} \cos \left( {\mu h} \right) + \tau_{2} } \right).$$
(26)

Now, we define

$$\delta_{\max }^{j} = \mathop {\max }\limits_{0 \le i \le j} \left| {\delta^{j} } \right|.$$
(27)

Using in above equation, we get

$$\left[ {\left( {2(a_{0} + \hat{k}_{1} )\tau_{1} - 2\hat{\nu }\tau_{4} } \right)\cos \left( {\mu h} \right) + (a_{0} + \hat{k}_{1} )\tau_{2} + 2\hat{\nu }\tau_{4} } \right]\delta^{j + 1} = \left( {a_{0} \sum\limits_{k = 0}^{j - 1} {\left( {P_{k} - P_{k + 1} } \right) - } } \right.\left. {a_{0} P_{j} } \right)\delta_{\max }^{j} \left( {2\tau_{1} \cos \left( {\mu h} \right) + \tau_{2} } \right),$$
(28)

Simplifying it, we have

$$\delta^{j + 1} = \frac{{a_{0} \left( {2\tau_{1} \cos \left( {\mu h} \right) + \tau_{2} } \right)}}{{\left( {2(a_{0} + \hat{k}_{1} )\tau_{1} - 2\hat{\nu }\tau_{4} } \right)\cos \left( {\mu h} \right) + (a_{0} + \hat{k}_{1} )\tau_{2} + 2\hat{\nu }\tau_{4} }}\delta_{\max }^{j} .$$
(29)

The discretized system of the TFNB equation is unconditionally stable when \(\left| \delta \right| \le 1\) which is obvious from above equation. One can see the alternative proof in [22].

4 Results

This section considers examples of TFNB equation to test the performance and efficacy of the established procedure. The rate of convergence (ROC) is analyzed by:

\({\text{ROC}} = \frac{{\log \left( {E^{{h_{1} }} /E^{{h_{2} }} } \right)}}{{\log \left( {{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {h_{2} }}} \right. \kern-0pt} {h_{2} }}} \right)}}\), where \(E^{{h_{1} }}\) and \(E^{{h_{2} }}\) signify the errors with \(h_{1}\) and \(h_{2}\), respectively. The error analysis is done in terms of \(L_{2}\), \(L_{\infty }\) and RMS errors, defined by:

\(L_{2} = \left( {\sum {|U_{j} - u_{j} |^{2} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} {\text{; L}}_{\infty } = \max |U_{j} - u_{j} |{\text{ ; RMS = }}\left( {\sum {\frac{{|U_{j} - u_{j} |^{2} }}{n}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}\).

Example 1

Consider the TFNB Eq. (1) for \(f(x,t) = \frac{{2t^{2 - \alpha } e^{x} }}{{\left| \!{\overline {\, {3 - \alpha } \,}} \right. }} + t^{4} e^{2x} - \hat{\nu }t^{2} e^{x}\) with \(v\left( {x,t} \right) = t^{2} e^{x}\) in [0,1].

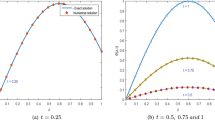
We fix free parameter \(\hat{p}\) = 5 for all computations of Example 1. First, we approximate it with \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1 for grids \(M\) = 10, 20, 40, and 80. The numerical solutions are presented in Table 2, while Table 3 compares \(L_{2}\) and \(L_{\infty }\) errors of the proposed method with those available in Ref. [19] with \(\alpha\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1 for hybrid parameters \(\sigma\) = 0.1, 0.5, 0.9, and grids \(M\) = 10, 20, 40, and 80. Now, we solve this example with the parameters \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(M\) = 80, \(\hat{\nu }\) = 1 at \(t\) = 1 for different \(\Delta t =\) 0.002, 0.001, 0.0005, and 0.00025. The numerical solutions are presented in Table 4, while Table 5 compares \(L_{2}\) and \(L_{\infty }\) errors of the proposed method with those available in Ref. [19]. The comparison of the proposed method with QBSG method [19] together with the convergence rate of the proposed method is shown in Table 6 for \(\alpha\) = 0.5, \(\sigma\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1. It is obvious that the proposed method is second-order accurate in space variable. The \(L_{2}\) and \(L_{\infty }\) error norms with \(\Delta t\) = 0.00025 and \(\hat{\nu }\) = 1 at \(t\) = 1 for fractional order \(\alpha\) = 0.1 with hybrid parameters \(\sigma =\) 0.1, 0.5, and 0.9 are demonstrated in Table 7. Figures 1 and 2 show the comparison of the exact and numerical solutions graphically with \(\sigma =\) 0.5, \(\alpha\) = 0.5, \(M\) = 10, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 for different times. Figure 2 demonstrates the exact and numerical solutions along with absolute errors for \(\sigma =\) 0.5, \(\alpha\) = 0.5, \(M\) = 80, \(\Delta t\) = 0.05, and \(\hat{\nu }\) = 1 at \(t\) = 0.5, while Fig. 3 shows it for \(\sigma =\) 0.9, \(\alpha\) = 0.1, \(M\) = 80, \(\Delta t\) = 0.05, and \(\hat{\nu }\) = 1 at \(t =\) 1.

Table 2 The comparison of present and existing numerical solutions with exact solutions for \(\alpha\) = 0.5, \(\sigma\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1
Full size table
Table 3 The \(L_{2}\) and \(L_{\infty }\) errors with \(\alpha\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1
Full size table
Table 4 The numerical solutions with \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(M\) = 80, and \(\hat{\nu }\) = 1 at \(t\) = 1
Full size table
Table 5 The comparison of the proposed and existing methods in terms of \(L_{2}\) and \(L_{\infty }\) with \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(M\) = 80, and \(\hat{\nu }\) = 1 at \(t\) = 1
Full size table
Table 6 The comparison of error norms together with the convergence rate of the present method for \(\alpha\) = 0.5, \(\sigma\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1
Full size table
Table 7 The \(L_{2}\) and \(L_{\infty }\) errors with \(\alpha\) = 0.1, \(\sigma\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1
Full size table
Fig. 1
figure 1

The exact and approximate \(v(x,t)\) with \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(\Delta t\) = 0.00025, \(\hat{\nu }\) = 1, and \(M\) = 10 at \(t\) = 0.2, 0.4, 0.6, 0.8, and 1 for Example 1

Full size image
Fig. 2
figure 2

The exact and approximate \(v(x,t)\) along with abs. errors for \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(\Delta t\) = 0.05, v = 1, and \(M\) = 80 at \(t\) = 0.5 for Example 1

Full size image
Fig. 3
figure 3

The exact and approximate \(v(x,t)\) along with abs. error for \(\sigma\) = 0.9, \(\alpha\) = 0.1, \(\Delta t\) = 0.05, \(\hat{\nu }\) = 1, and \(M\) = 80 at \(t\) = 1 for Example 1

Full size image

Example 2

Now, we consider the TFNB Eq. (1) with the following initial and boundary conditions

$$v\left( {x,0} \right) = 0, \, 0 \le x \le 1,$$

and

$$v\left( {0,t} \right) = t^{2} , \, v\left( {1,t} \right) = - t^{2} , \, t \ge 0.$$

The exact solution is \(v\left( {x,t} \right) = t^{2} \cos (\pi x)\), and the function \(f\left( {x,t} \right)\) is

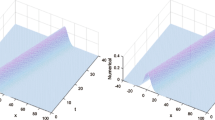
$$f\left( {x,t} \right) = \left( {\frac{{2t^{2 - \alpha } }}{{\left| \!{\overline {\, {3 - \alpha } \,}} \right. }} + \pi t^{2} \left( {\hat{\nu }\pi - t^{2} \sin (\pi x)} \right)} \right)\cos (\pi x).$$

Table 8 shows the comparison of \(L_{2}\) and \(L_{\infty }\) error norms for \(\hat{p}\) = 0.015, \(\sigma\) = 0.5, \(\alpha\) = 0.5 \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1 for \(M\) = 10, 20, 40, and 80. This table also establishes that the proposed method is second-order accurate in space variable. The error norms \(L_{2}\) and \(L_{\infty }\) are calculated for \(\hat{p}\) = 0.015, \(\sigma\) = 0.5, \(\alpha\) = 0.5 \(M\) = 80, and \(\hat{\nu }\) = 1 at \(t\) = 1 for various time mesh sizes in Table 9. Now, Table 10 shows the comparison of error norms with \(\sigma\) = 0.5, \(M\) = 80, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1 for various values of fractional orders \(\alpha\) = 0.1, 0.25, 0.75, and 1. Figure 4 exhibits that absolute error norms are very less (\(\approx 10^{ - 5}\)) for parameters \(\alpha = 0.5\), \(\hat{p}\) = 0.015, \(\sigma\) = 0.5, \(M\) = 80, \(\Delta t\) = 0.0005, and \(\hat{\nu }\) = 1 at \(t\) = 0.2, 0.4, 0.6, 0.8, and 1. Figure 5 shows the comparison of the exact and numerical solutions for \(\alpha = 0.5\), \(\hat{p}\) = 0.015, \(\sigma\) = 0.5, \(\hat{\nu }\) = 1, \(M\) = 20, and \(\Delta t\) = 0.001 at various times, while Fig. 6 shows the surface behavior of the solutions for \(\alpha = 0.5\), \(\hat{p}\) = 0.015, \(\sigma\) = 0.5, \(M\) = 80, \(\Delta t\) = 0.0005, and \(\hat{\nu }\) = 1.

Table 8 The comparison of error norms together with the convergence rate of the present method for \(\alpha\) = 0.5, \(\sigma\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1 for Example 2
Full size table
Table 9 The comparison of error norms for \(\alpha\) = 0.5, \(\sigma\) = 0.5, \(M\) = 80, and \(\hat{\nu }\) = 1 at \(t\) = 1 for Example 2
Full size table
Table 10 The comparison of error norms with \(\sigma\) = 0.5, \(M\) = 80, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1 for various values of fractional order \(\alpha\) for Example 2
Full size table
Fig. 4
figure 4

Absolute error norms for \(\alpha = 0.5\), \(\hat{p}\) = 0.015, \(\sigma\) = 0.5, \(M\) = 80, \(\Delta t\) = 0.0005, and \(\hat{\nu }\) = 1 for Example 2

Full size image
Fig. 5
figure 5

The comparison of the exact and numerical solutions for \(\alpha = 0.5\), \(\hat{p}\) = 0.015, \(\sigma\) = 0.5, \(\hat{\nu }\) = 1, \(M\) = 20, and \(\Delta t\) = 0.001 at various times for Example 2

Full size image
Fig. 6
figure 6

Surface behavior of the exact and numerical solutions for \(\alpha = 0.5\), \(\hat{p}\) = 0.015, \(\sigma\) = 0.5, \(M\) = 80, \(\Delta t\) = 0.0005, and \(\hat{\nu }\) = 1 for Example 2

Full size image

Example 3

Finally, we consider the TFNB Eq. (1) for

\(f\left( {x,t} \right) = \left( {\frac{{2t^{2 - \alpha } }}{{\left| \!{\overline {\, {3 - \alpha } \,}} \right. }} + 2\pi t^{2} \left( {2\hat{\nu }\pi + t^{2} \cos (2\pi x)} \right)} \right)\sin (2\pi x)\) with \(v\left( {x,t} \right) = t^{2} \sin (2\pi x)\).

Finally, Example 3 is approximated for free parameter \(\hat{p}\) = 0.5. Table 11 shows the comparison of present, existing [19], and exact solutions with \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 for different grid sizes \(M\) = 40 and 80, while Table 12 determines it with \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(M\) = 120, and \(\hat{\nu }\) = 1 at \(t\) = 1 for \(\Delta t\) = 0.0025, 0.002, 0.001, and 0.0005. Figure 7 shows the graphical comparison of exact and approximated solutions with \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(\Delta t\) = 0.001, \(\hat{\nu }\) = 1, and \(M\) = 20 at \(t\) = 0.2, 0.4, 0.6, 0.8, and 1, while Fig. 8 depicts exact and approximate solutions along with absolute errors for \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(M\) = 120, \(\Delta t\) = 0.001, and \(\hat{\nu }\) = 1 at \(t\) = 1.

Table 11 The comparison of present, existing, and exact solutions with \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 for Example 3
Full size table
Table 12 The comparison of present, existing, and exact solutions with \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(M\) = 120, and \(\hat{\nu }\) = 1 at \(t\) = 1 for Example 3
Full size table
Fig. 7
figure 7

Comparison of exact and approximated solutions with \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(\Delta t\) = 0.001, \(\hat{\nu }\) = 1, and \(M\) = 20 at \(t\) = 0.2, 0.4, 0.6, 0.8, and 1 for Example 3

Full size image
Fig. 8
figure 8

The exact and approximate solutions, along with abs. errors for \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(M\) = 120, \(\Delta t\) = 0.001, and \(\hat{\nu }\) = 1 at \(t\) = 1 for Example 3

Full size image

5 Discussion

Table 2 compares obtained solutions with those solutions presented in [19] for parameters \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1 for grids \(M\) = 10, 20, 40, and 80. Table 3 compares \(L_{2}\) and \(L_{\infty }\) errors of the proposed and QBSG methods [19] with \(\alpha\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1 for hybrid parameters \(\sigma\) = 0.1, 0.5, and 0.9 and grids \(M\) = 10, 20, 40, and 80. Tables 4 and 5 exhibit the comparison of the proposed method with QBSG method [19] with the parameters \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(M\) = 80, and \(\hat{\nu }\) = 1 at \(t\) = 1 for \(\Delta t =\) 0.002, 0.001, 0.0005, and 0.00025 while Table 6 exhibits the comparison together with convergence rate with \(\alpha\) = 0.5, \(\sigma\) = 0.5, \(\Delta t\) = 0.00025, and \(\hat{\nu }\) = 1 at \(t\) = 1 for grids \(M\) = 10, 20, 40, and 80. Obviously, obtained results are closer than exact solutions, and error norms are better than error norms presented in [19], and the proposed method is second-order accurate in space variable. The \(L_{2}\) and \(L_{\infty }\) error norms in Table 7 show that solutions are more accurate for hybrid parameter 0.9. From Figs. 1–3, an excellent agreement is noticed between exact and approximate solutions with absolute error in (\(\approx 10^{ - 3}\) to \(10^{ - 4}\)).

Next, Example 2 is solved with free parameter \(\hat{p}\) = 0.015 and \(\hat{\nu }\) = 1 and for various other parameters. The \(L_{2}\) and \(L_{\infty }\) error norms depicted in Tables 8 and 9 show that the proposed method results are better than those presented in [19, 35, 36], and the proposed method is second-order accurate in space variable. It is also observed that both error norms \(L_{2}\) and \(L_{\infty }\) are decreasing on increasing the space as well as time mesh sizes. Now, Table 10 shows the error norms for fractional orders \(\alpha\) = 0.1, 0.25, 0.75, and 1. In the case of higher fractional orders, the proposed method results are more accurate than presented in [19, 35]. The small absolute error norms (\(\approx 10^{ - 5}\)) shown in Fig. 4 exhibit that solutions are very accurate, while Figs. 5 and 6 show an excellent agreement between exact and approximate solutions.

Finally, Example 3 is solved with free parameter \(\hat{p}\) = 0.5, hybrid parameter \(\sigma\) = 0.5, fractional order \(\alpha\) = 0.5, and \(\hat{\nu }\) = 1 for various space and time meshes at \(t\) = 1. Tables 11 and 12 reveal that the proposed method results are more accurate than the results presented in [19] and are very close to the exact solutions. Figures 7 and 8 compare exact and approximated solutions with \(\sigma\) = 0.5, \(\alpha\) = 0.5, \(\Delta t\) = 0.001, \(\hat{\nu }\) = 1, and \(M\) = 20 and 120, respectively. An excellent agreement is observed between exact and approximated solutions with absolute error in (\(\approx 10^{ - 4}\)).

6 Conclusions

A new cubic HB-spline collocation technique has been established for the numerical treatment of the Caputo TFNB equation. The technique is used for discretizing the spatial derivatives. The Rubin–Graves type quasi-linearization technique has been employed to linearize the nonlinear terms. The three examples have been considered to validate the accuracy and efficiency of the proposed method. It has been observed that the present method provides better results than the methods in [19, 35, 36]. The graphical results are also presented that confirm the accuracy of the proposed algorithm. As we can see, Figs. 2, 3, 6, and 8 are clear representations of the smoothness between numerical and exact solutions, while Figs. 1–3, 4, 7, and 8 expose that absolute errors are very low in (\(\approx 10^{ - 3}\) to \(10^{ - 5}\)).