1 Introduction

Since the burst of COVID-19, a good many countries have been in immense fright. It is a disease spread by contact and breathing. Infected people usually present with cough, fever, diarrhea, and other symptoms. It is highly contagious and can cause lung failure. During the outbreak of this disease, people in many cities were forced to stay at home. Moreover, another bad news is that old people and children are far more likely to become infected with this disease than adults. A feature of this epidemic is that a person may be infectious but has no symptoms, it brings a great difficulty to preventive work. Although scientists have been working tirelessly, there is no drug that can effectively treat this disease so far [1–4]. So studying the dynamic characteristics of the COVID-19 outbreak is a major means to prevent and eliminate this disease.

The mathematical model is a powerful tool that has been used by mathematicians and infectious disease scientists for many years [5]. This amazing mathematical tool can help us quickly grasp detailed information about infectious diseases in a short period of time and predict possible transmission paths. Even with very little real data, we can establish preliminary models based on experience to implement predictions. In the last several years, many epidemic models have been studied by researchers. Bohner and Stamov established an SIR model with pulse delay and obtained global stability criteria for the solution through the Lyapunov method [6]. Based on the SIR model, a nonlinear SEIRRPV model was investigated by introducing new exposed, recovered, and dead people [7]. Wanduku used the parameters that were estimated from real data to a discrete time Markov chain model to forecast the situation in the United States [8]. Wang et al. applied the basic reproductive ratio theory of the reaction-diffusion infectious disease model to numerical simulation and concluded that periodic models may overestimate actual data [9]. Elbaz and El-Awady established an epidemic model of soft drugs and analyzed the sensitivity of the model by numerical simulation [10]. Yang et al. studied an SEIR infectious disease model that can be sexually transmitted, and they believed that the incubation period has a considerable impression on the peak of the contagion [11]. A time-delay AIDS model with educational movement and information was established, and the extinction, persistence, and spread speed of the disease were studied in detail [12]. Sun et al. looked at the SVIR model with both vaccination and incubation [13]. Basnarkov built the SEAIR model by capturing two dynamic characteristics of infectious diseases: delay and absence of symptoms [14]. A new SVEIS stochastic model was proposed based on the hypothesis that parameters satisfy Ornstein–Uhlenbeck process with mean regression [15]. An improved SEIHR model was used to study the effectiveness of isolation measures in Hong Kong, and the authors concluded that the model has backward bifurcation. They also used partial rank correlation coefficients to study the influence of parameters on the model [16]. Real data from the epidemic were utilized to estimate the basic reproduction number and infection rate of the model, and effective epidemic prevention and control measures were proposed [17].

With the development of scientific theory, the ideology of fractional calculus has been widely applied in mathematics, physics, engineering, chemistry, and other scientific fields after it emerged. There are some commonly used definitions, they are Riemann–Liouville, Grünwald–Letnikov, and Caputo fractional calculus [18]. Owing to the memory, historical, and nonlocal effects of fractional operators, the essence and characteristics of the model that are not available by integer operators can be understood more deeply with fractional derivative. Therefore, more and more epidemic models are depicted by fractional derivatives [19, 20]. Balzotti et al. studied the susceptibility–infection-susceptibility fractional model under the condition that the population is unchanging [21]. The fractional order smoking model under Caputo definition was established in [22]. The differences between the differential transformation method and the homotopy transformation method were discussed. Emmanuel used the Atangana–Baleanu–Caputo definition to build a nonlinear fractional smoking model and carried out a numerical study [23]. Liu considered a fractional SIR model with multiple stages in the case of heterogeneous networks [24]. Saratha improved the Riemann–Liouville definition by the Mittag-Leffler function and verified his results with nonlinear fractional differential equations [25]. A fractional order model containing three types of infected populations was established to study the spread of avian influenza [26], and the authors believed that the solution of the model is closely related to the order. Pan and Li applied the GMMP scheme to get the numerical solution of their Ebola model, and the grid approximation method was utilized to get the best parameters; the numerical results showed that their model predicted real outbreaks well [27]. The author concluded that isolation helps to control the epidemic by conducting stability and bifurcation analysis on the proposed fractional \(SE_{1}E_{2}IQR\) model [28]. The LaSalle invariance principle and the Lyapunov functional were utilized to demonstrate the asymptotic stability at the equilibrium point of the proposed fractional order SEIR model, and the numerical results supported theoretical analysis [29]. To acquire numerical solutions of the SIQR model, Paul used the Laplace iterative transform method; he also compared the effects of different numerical methods [30]. The sensitivity of models to parameter changes under different definitions was studied in [31], and the authors found that these changes may lead to chaotic behavior in the dynamic system. The authors considered the SEIGRDP model under population mobility and showed the validity of the model based on real data [32]. The fractional ABC operator was applied to the SEIR COVID-19 model, and optimal parameters of the model were obtained by using the least square method. The simulation proved the superiority of the fractional derivative [33].

However, Caputo and Fabrizio noticed that the common definitions (C, RL, GL) have singular kernels that may cause some negative influences on mathematical models. To eliminate them, Fabrizio and Caputo proposed a new definition in their work [34], which we will use in this study. Compared with the published literature, our innovations are as follows: (a)To the best of our knowledge, the fractional order SIDARTHE infectious disease model under Caputo–Fabrizio definition is investigated for the first time in this work; (b)We use the Banach fixed point theorem to prove the existence and uniqueness of the model solution, which was not considered in [35] although we used the same model as the author.

The frame of this paper is as follows: the definitions and properties of CF fractional calculus are recommended in Sect. 2. In Sect. 3, we suggest the integer order model and the fractional order model; making use of the Banach fixed point theorem, the existence and uniqueness of the model’s solution are derived. In the subsequent section, we first derive an effective iteration scheme, then we analyze the feature of the model according to the simulation results. In the last section, the ultimate conclusion is stated.

2 The new CF fractional calculus

Definition 1

[34] Set \(m\in H^{1}(a,b)\) and \(\delta \in [0,1]\), the novel CF fractional order derivative operator is advised as follows:

$$ {}^{CF}_{a}D_{t}^{\delta} \bigl(m(t)\bigr)=\frac{Z(\delta )}{1-\delta} \int _{a}^{t} \exp \biggl[-\delta \frac{t-x}{1-\delta} \biggr] m^{\prime}(x) \,dx . $$
(1)

In Eq. (1), the symbol \(Z(\delta )\) is called normalization function by Caputo and Fabrizio, and it satisfies the condition that \(Z(0)=Z(1)=1\).

If m ∉ \(H^{1}(a,b)\), for example, \(m \in L^{1}(-\infty ,c)\), where \(c>b\), then the definition will be expressed as

$$ {}^{CF}_{a}D_{t}^{\delta}\bigl(m(t) \bigr)=\frac{\delta M(\delta )}{1-\delta} \int _{-\infty}^{c} \exp \biggl[-\delta \frac{t-x}{1-\delta} \biggr]\bigl(m(t)-m(x)\bigr) \,dx . $$
(2)

Definition 2

[34] If we consider \(\omega = \frac{1-\delta}{\delta}\) and \(\omega \in [0,+\infty ]\), then we can get that \(\delta \in [0,1]\), so Eq. (1) can be showed as follows:

$$ {}^{CF}_{a}D_{t}^{\omega}\bigl(m(t) \bigr)=\frac{X(\omega )}{\omega} \int _{a}^{t} \exp \biggl[-\frac{t-x}{\omega} \biggr]m^{\prime}(x) \,dx , $$
(3)

where the symbol \(X(\omega )\) is a normalization function that is similar to \(Z(\delta )\), and \(X(0)=X(\infty )=1\). Besides, we also have

$$ \lim_{\omega \to 0} \frac{1}{\omega} \exp \biggl[- \frac{(t-x)}{\omega} \biggr]=\psi (t-x). $$
(4)

These are the concepts of CF fractional differentiation. Moreover, Losada and Nieto moved the corresponding CF fractional order integral.

Definition 3

[36] Let us consider that \(0< \delta <1\), m is a random function, and the CF fractional integral is set as follows:

$$ {}^{CF}_{0}I^{\delta}_{t} m(t)= \frac{2(1-\delta )}{(2-\delta ) Z(\delta )} m(t)+ \frac{2 \delta}{(2-\delta ) Z(\delta )} \int _{0}^{t} m(s) \,ds , \quad t \geq 0. $$
(5)

Remark 1

[36] Nieto has noticed that the CF type fractional order integral of one function m of order \(0< \delta <1\) is the mean value of m and its integral. It means that

$$ \frac{2(1-\delta )}{(2-\delta ) Z(\delta )}+ \frac{2 \delta}{(2-\delta ) Z(\delta )}=1, $$
(6)

due to this, we can infer that \(Z(\delta )=\frac{2}{2-\delta}\), \(0< \delta <1\).

Definition 4

[36] From the point of Remark 1, the new CF type fractional derivative is revised by Losada and Nieto, and it has the following form:

$$ {}^{CF}_{a}D_{t}^{\delta }\bigl(m(t) \bigr)=\frac{1}{1-\delta} \int _{a}^{t} \exp \biggl[-\delta \frac{t-x}{1-\delta} \biggr]m^{\prime}(x) \,dx . $$
(7)

3 The new SIDARTHE fractional mathematical model of COVID-19 with the CF derivative

The integer order SIDARTHE model was introduced by Giordano et al. [37], and it can be expressed as follows:

$$ \begin{aligned} &\frac{dS}{dt}=-mSI-nSD-pSA-qSR, \\ &\frac{dI}{dt}=mSI+nSD+pSA+qSR-aI-cI-uI, \\ &\frac{dD}{dt}=aI-eD-rD, \\ &\frac{dA}{dt}=cI-bA-gA-vA, \\ &\frac{dR}{dt}=eD+bA-jR-wR, \\ &\frac{dT}{dt}=gA+jR-zT-oT, \\ &\frac{dH}{dt}=uI+rD+vA+wR+zT, \\ &\frac{dE}{dt}=oT. \end{aligned} $$
(8)

In the above system, the general population is set to eight classifications, and we express them by the capital letters S, I, R, A, D, T, E, and H. Arguments are expressed in lowercase letters and all of them are positive, their meanings and difference [35, 37] are shown in Table 1.

Table 1 Connotation of variables or parameters
Full size table

Replacing the integer order operator mentioned above by the CF fractional operator, these expressions can be inferred:

$$ \begin{aligned} &{}^{CF}_{0}D^{\delta}_{t}S=-mSI-nSD-pSA-qSR, \\ &{}^{CF}_{0}D^{\delta}_{t}I=mSI+nSD+pSA+qSR-aI-cI-uI, \\ &{}^{CF}_{0}D^{\delta}_{t}D=aI-eD-rD, \\ &{}^{CF}_{0}D^{\delta}_{t}A=cI-bA-gA-vA, \\ &{}^{CF}_{0}D^{\delta}_{t}R=eD+bA-jR-wR, \\ &{}^{CF}_{0}D^{\delta}_{t}T=gA+jR-zT-oT, \\ &{}^{CF}_{0}D^{\delta}_{t}H=uI+rD+vA+wR+zT, \\ &{}^{CF}_{0}D^{\delta}_{t}E=oT, \end{aligned} $$
(9)

the initial conditions are set as follows:

$$ \begin{aligned} &S(0)=c_{1},\qquad I(0)=c_{2},\qquad D(0)=c_{3}, \qquad A(0)=c_{4}, \\ &R(0)=c_{5},\qquad T(0)=c_{6}, \qquad H(0)=c_{7},\qquad E(0)=c_{8}. \end{aligned} $$
(10)

In addition, we find that the sum \({}^{CF}_{0}D^{\delta}_{t}S+{}^{CF}_{0}D^{\delta}_{t}I+{}^{CF}_{0}D^{\delta}_{t}D+ {}^{CF}_{0}D^{\delta}_{t}A+{}^{CF}_{0}D^{\delta}_{t}R+{}^{CF}_{0}D^{\delta}_{t}T+ {}^{CF}_{0}D^{\delta}_{t}H+{}^{CF}_{0}D^{\delta}_{t}E\) is equal to zero in this system. This means that the total population \(S+I+R+A+D+T+E+H\) is taken to be a constant. We define the norm \(\Vert (S,I,R,A,D,T,E,H) \Vert =\Vert S \Vert +\Vert I \Vert +\Vert R \Vert +\Vert A \Vert + \Vert D \Vert +\Vert T \Vert +\Vert E \Vert +\Vert H \Vert \), where \(\Vert S \Vert =\sup\{\vert S(t) \vert :t \in G\}\), and G is the Banach space [38], the other seven norms are similar to this.

4 Existence and uniqueness of the solution of the SIDARTHE model of COVID-19 epidemic

In the forth part, taking advantage of fixed point theorem [38–43], the existence of the SIDARTHE fractional order system’s solution will be proved, then we would like to show the uniqueness. At first, we will prove the existence of the solution. Applying the CF fractional order integral operation on both sides of the equal sign of Eq. (9), we can get these formulas:

$$\begin{aligned} \begin{aligned} &S(t)-S(0)={}^{CF}_{0}I^{\delta}_{t} \{-mSI-nSD-pSA-qSR\}, \\ &I(t)-I(0)={}^{CF}_{0}I^{\delta}_{t} \{mSI+nSD+pSA+qSR-aI-cI-uI\}, \\ &D(t)-D(0)={}^{CF}_{0}I^{\delta}_{t} \{aI-eD-rD\}, \\ &A(t)-A(0)={}^{CF}_{0}I^{\delta}_{t} \{cI-bA-gA-vA\}, \\ &R(t)-R(0)={}^{CF}_{0}I^{\delta}_{t} \{eD+bA-jR-wR\}, \\ &T(t)-T(0)={}^{CF}_{0}I^{\delta}_{t} \{gA+jR-zT-oT\}, \\ &H(t)-H(0)={}^{CF}_{0}I^{\delta}_{t} \{uI+rD+vA+wR+zT\}, \\ &E(t)-E(0)={}^{CF}_{0}I^{\delta}_{t} \{oT\}. \end{aligned} \end{aligned}$$
(11)

Taking into account the conception of the CF fractional order integral Eq. (5), we can rewrite Eq. (11) as follows:

$$\begin{aligned}& \begin{aligned} S(t)-S(0)&=\frac{2(1-\delta )}{(2-\delta )Z(\delta )} \bigl[-mS(t)I(t)-nS(t)D(t)-pS(t)A(t)-qS(t)R(t)\bigr] \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[-mS(s)I(s)-nS(s)D(s)-pS(s)A(s)-qS(s)R(s) \bigr]\,ds , \end{aligned} \\& \begin{aligned} I(t)-I(0)&=\frac{2(1-\delta )}{(2-\delta )Z(\delta )} \bigl\{ S(t)\bigl[mI(t)+nD(t)+pA(t)+qR(t)\bigr]- \bigl[aI(t)+cI(t)+uI(t)\bigr] \bigr\} \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl\{ S(s)\bigl[mI(s)+nD(s)+pA(s)+qR(s) \bigr]-I(s) (a+c+u) \bigr\} \,ds , \end{aligned} \\& \begin{aligned} D(t)-D(0)&=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[aI(t)-eD(t)-rD(t)\bigr] \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[aI(s)-eD(s)-rD(s)\bigr]\,ds , \end{aligned} \\& \begin{aligned}[b] A(t)-A(0)&=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[cI(t)-bA(t)-gA(t)-vA(t)\bigr] \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[cI(s)-bA(s)-gA(s)-vA(s)\bigr] \,ds , \end{aligned} \\& \begin{aligned} R(t)-R(0)&=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[eD(t)+bA(t)-jR(t)-wR(t)\bigr] \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[eD(s)+bA(s)-jR(s)-wR(s)\bigr] \,ds , \end{aligned} \\& \begin{aligned} T(t)-T(0)&=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[gA(t)+jR(t)-zT(t)-oT(t)\bigr] \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[gA(s)+jR(s)-zT(s)-oT(s)\bigr] \,ds , \end{aligned} \\& \begin{aligned} H(t)-H(0)&=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[uI(t)+rD(t)+vA(t)+wR(t)+zT(t)\bigr] \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[uI(s)+rD(s)+vA(s)+wR(s)+zT(s) \bigr]\,ds , \end{aligned} \\& \begin{aligned} E(t)-E(0)&=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[oT(t)\bigr] \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[oT(s)\bigr]\,ds . \end{aligned} \end{aligned}$$
(12)

For convenience, we explain the following functions as kernels:

$$ \begin{aligned} &B_{1}(t,S)=-mS(t)I(t)-nS(t)D(t)-pS(t)A(t)-qS(t)R(t), \\ &B_{2}(t,I)=mS(t)I(t)+nS(t)D(t)+pS(t)A(t)+qS(t)R(t)-aI(t)-cI(t)-uI(t), \\ &B_{3}(t,D)=aI(t)-eD(t)-rD(t), \\ &B_{4}(t,A)=cI(t)-bA(t)-gA(t)-vA(t), \\ &B_{5}(t,R)=eD(t)+bA(t)-jR(t)-wR(t), \\ &B_{6}(t,T)=gA(t)+jR(t)-zT(t)-oT(t), \\ &B_{7}(t,H)=uI(t)+rD(t)+vA(t)+wR(t)+zT(t), \\ &B_{8}(t,E)=oT(t). \end{aligned} $$
(13)

Theorem 1

The functions \(B_{1}\), \(B_{2}\), \(B_{3}\), \(B_{4}\), \(B_{5}\), \(B_{6}\), \(B_{7}\), and \(B_{8}\) satisfy the Lipschitz condition. Moreover, if the following inequalities hold, these functions are contractions:

$$ \begin{aligned} &0 \leq ml_{2}+nl_{3}+pl_{4}+ql_{5} < 1, \\ &0 \leq ml_{1}+a+c+u < 1, \\ &0 \leq e+r < 1, \\ &0 \leq b+g+v < 1, \\ &0 \leq j+w < 1, \\ &0 \leq z+o < 1, \\ &0 \leq c_{1} < 1, \\ &0 \leq c_{2} < 1. \end{aligned} $$
(14)

Proof

Before we start the proof, we set \(\Vert S(t) \Vert \leq l_{1}\), \(\Vert I(t) \Vert \leq l_{2}\), \(\Vert D(t) \Vert \leq l_{3}\), \(\Vert A(t) \Vert \leq l_{4}\), \(\Vert R(t) \Vert \leq l_{5}\), \(\Vert T(t) \Vert \leq l_{6}\), \(\Vert H(t) \Vert \leq l_{7}\), \(\Vert E(t) \Vert \leq l_{8}\), i.e., all of them are bounded functions. Let us first consider \(B_{1}\), we take two different functions S and Ŝ, then we estimate the norm below:

$$ \begin{aligned} & \bigl\Vert B_{1}(t,S)-B_{1}(t, \widehat{S}) \bigr\Vert \\ &\quad = \bigl\Vert -m\bigl[S(t)-\widehat{S}(t)\bigr]I(t)-n\bigl[S(t)-\widehat{S}(t) \bigr]D(t) \\ &\quad \quad {}-p\bigl[S(t)- \widehat{S}(t)\bigr]A(t)-q\bigl[S(t)-\widehat{S}(t) \bigr]R(t) \bigr\Vert \\ &\quad \leq \bigl\Vert m\bigl[S(t)-\widehat{S}(t)\bigr]I(t) \bigr\Vert + \bigl\Vert n\bigl[S(t)- \widehat{S}(t)\bigr]D(t) \bigr\Vert \\ &\quad \quad{} + \bigl\Vert p\bigl[S(t)-\widehat{S}(t)\bigr]A(t) \bigr\Vert + \bigl\Vert q\bigl[S(t)-\widehat{S}(t)\bigr]R(t) \bigr\Vert \\ &\quad \leq \bigl[m \bigl\Vert I(t) \bigr\Vert +n \bigl\Vert D(t) \bigr\Vert +p \bigl\Vert A(t) \bigr\Vert +q \bigl\Vert R(t) \bigr\Vert \bigr] \bigl\Vert \bigl[S(t)-\widehat{S}(t)\bigr] \bigr\Vert \\ &\quad \leq (ml_{2}+nl_{3}+pl_{4}+ql_{5}) \bigl\Vert \bigl[S(t)-\widehat{S}(t)\bigr] \bigr\Vert \\ &\quad =\beta _{1} \bigl\Vert \bigl[S(t)-\widehat{S}(t)\bigr] \bigr\Vert , \end{aligned} $$
(15)

where \(\beta _{1}=ml_{2}+nl_{3}+pl_{4}+ql_{5}\).

Then we get

$$ \begin{aligned} \bigl\Vert B_{1}(t,S)-B_{1}(t, \widehat{S}) \bigr\Vert \leq \beta _{1} \bigl\Vert \bigl[S(t)- \widehat{S}(t)\bigr] \bigr\Vert . \end{aligned} $$
(16)

Therefore, we have shown that \(B_{1}\) satisfies the Lipschitz condition, where \(\beta _{1}\) is the Lipschitz constant and \(B_{1}\) is the Lipschitz function for S. Similarly, the other seven functions also conform to the Lipschitz conditions given as follows:

$$ \begin{aligned} & \bigl\Vert B_{2}(t,I)-B_{2}(t, \widehat{I}) \bigr\Vert \leq \beta _{2} \bigl\Vert \bigl[I(t)- \widehat{I}(t)\bigr] \bigr\Vert , \\ & \bigl\Vert B_{3}(t,D)-B_{3}(t,\widehat{D}) \bigr\Vert \leq \beta _{3} \bigl\Vert \bigl[D(t)- \widehat{D}(t)\bigr] \bigr\Vert , \\ & \bigl\Vert B_{4}(t,A)-B_{4}(t,\widehat{A}) \bigr\Vert \leq \beta _{4} \bigl\Vert \bigl[A(t)- \widehat{A}(t)\bigr] \bigr\Vert , \\ & \bigl\Vert B_{5}(t,R)-B_{5}(t,\widehat{R}) \bigr\Vert \leq \beta _{5} \bigl\Vert \bigl[R(t)- \widehat{R}(t)\bigr] \bigr\Vert , \\ & \bigl\Vert B_{6}(t,T)-B_{6}(t,\widehat{T}) \bigr\Vert \leq \beta _{6} \bigl\Vert \bigl[T(t)- \widehat{T}(t)\bigr] \bigr\Vert , \\ & \bigl\Vert B_{7}(t,H)-B_{7}(t,\widehat{H}) \bigr\Vert \leq \beta _{7} \bigl\Vert \bigl[H(t)- \widehat{H}(t)\bigr] \bigr\Vert , \\ & \bigl\Vert B_{8}(t,E)-B_{8}(t,\widehat{E}) \bigr\Vert \leq \beta _{8} \bigl\Vert \bigl[E(t)- \widehat{E}(t)\bigr] \bigr\Vert , \end{aligned} $$
(17)

where

$$ \begin{aligned} &\beta _{2}=ml_{1}+a+c+u, \\ &\beta _{3}=e+r, \\ &\beta _{4}=b+g+v, \\ &\beta _{5}=j+w, \\ &\beta _{6}=z+o, \\ &\beta _{7}=c_{1}, \\ &\beta _{8}=c_{2}, \end{aligned} $$
(18)

and \(c_{1}\), \(c_{2}\) are arbitrary positive constants. Additionally, if Eq. (14) holds, these functions are contractions. □

In view of these eight functions, substituting Eq. (13) into Eq. (12), we obtain

$$ \begin{aligned} &S(t) =S(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{1}(t,S) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{1}(s,S)\,ds , \\ &I(t) =I(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{2}(t,I) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{2}(s,I)\,ds , \\ &D(t) =D(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{3}(t,D) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{3}(s,D)\,ds , \\ &A(t) =A(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{4}(t,A) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{4}(s,A)\,ds , \\ &R(t) =R(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{5}(t,R) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{5}(s,R)\,ds , \\ &T(t) =T(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{6}(t,T) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{6}(s,T)\,ds , \\ &H(t) =H(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{7}(t,H) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{7}(s,H)\,ds , \\ &E(t) =E(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{8}(t,E) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{8}(s,E)\,ds . \end{aligned} $$
(19)

Now we provide these recursive formulas:

$$ \begin{aligned} &S_{n}(t) = \frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{1}(t,S_{n-1}) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{1}(s,S_{n-1}) \,ds , \\ &I_{n}(t) =\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{2}(t,I_{n-1}) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{2}(s,I_{n-1}) \,ds , \\ &D_{n}(t) =\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{3}(t,D_{n-1}) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{3}(s,D_{n-1}) \,ds , \\ &A_{n}(t) =\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{4}(t,A_{n-1}) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{4}(s,A_{n-1}) \,ds , \\ &R_{n}(t) =\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{5}(t,R_{n-1}) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{5}(s,R_{n-1}) \,ds , \\ &T_{n}(t) =\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{6}(t,T_{n-1}) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{6}(s,T_{n-1}) \,ds , \\ &H_{n}(t) =\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{7}(t,H_{n-1}) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{7}(s,H_{n-1}) \,ds , \\ &E_{n}(t) =\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{8}(t,E_{n-1}) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{8}(s,E_{n-1}) \,ds , \end{aligned} $$
(20)

where these initial values are included

$$\begin{aligned}& S_{0}(t) =S(0), \\& I_{0}(t) =I(0), \\& D_{0}(t) =D(0), \\& A_{0}(t) =A(0), \\& R_{0}(t) =R(0), \\& T_{0}(t) =T(0), \\& H_{0}(t) =H(0), \\& E_{0}(t) =E(0). \end{aligned}$$
(21)

In terms of Eq. (20), let us take the difference between two adjacent terms as follows:

$$\begin{aligned}& \begin{aligned} \lambda _{n}(t)&=S_{n}(t)-S_{n-1}(t) \\ &=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[B_{1}(t,S_{n-1})-B_{1}(t,S_{n-2}) \bigr] \\ &\quad {}+\frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[B_{1}(s,S_{n-1})-B_{1}(s,S_{n-2}) \bigr]\,ds , \end{aligned} \\& \begin{aligned} \eta _{n}(t)&=I_{n}(t)-I_{n-1}(t) \\ &=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[B_{2}(t,I_{n-1})-B_{2}(t,I_{n-2}) \bigr] \\ &\quad {}+\frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[B_{2}(s,I_{n-1})-B_{2}(s,I_{n-2}) \bigr]\,ds , \end{aligned} \\& \begin{aligned} \mu _{n}(t)&=D_{n}(t)-D_{n-1}(t) \\ &=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[B_{3}(t,D_{n-1})-B_{3}(t,D_{n-2}) \bigr] \\ &\quad {}+\frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[B_{3}(s,D_{n-1})-B_{3}(s,D_{n-2}) \bigr]\,ds , \end{aligned} \\& \begin{aligned}[b] \epsilon _{n}(t)&=A_{n}(t)-A_{n-1}(t) \\ &=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[B_{4}(t,A_{n-1})-B_{4}(t,A_{n-2}) \bigr] \\ &\quad {}+\frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[B_{4}(s,A_{n-1})-B_{4}(s,A_{n-2}) \bigr]\,ds , \end{aligned} \\& \begin{aligned} \varepsilon _{n}(t)&=R_{n}(t)-R_{n-1}(t) \\ &=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[B_{5}(t,R_{n-1})-B_{5}(t,R_{n-2}) \bigr] \\ &\quad {}+\frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[B_{5}(s,R_{n-1})-B_{5}(s,R_{n-2}) \bigr]\,ds , \end{aligned} \\& \begin{aligned} \zeta _{n}(t)&=T_{n}(t)-T_{n-1}(t) \\ &=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[B_{6}(t,T_{n-1})-B_{6}(t,T_{n-2}) \bigr] \\ &\quad {}+\frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[B_{6}(s,T_{n-1})-B_{6}(s,T_{n-2}) \bigr]\,ds , \end{aligned} \\& \begin{aligned} \iota _{n}(t)&=H_{n}(t)-H_{n-1}(t) \\ &=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[B_{7}(t,H_{n-1})-B_{7}(t,H_{n-2}) \bigr] \\ &\quad {}+\frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[B_{7}(s,H_{n-1})-B_{7}(s,H_{n-2}) \bigr]\,ds , \end{aligned} \\& \begin{aligned} \kappa _{n}(t)&=E_{n}(t)-E_{n-1}(t) \\ &=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[B_{8}(t,E_{n-1})-B_{8}(t,E_{n-2}) \bigr] \\ &\quad {}+\frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[B_{8}(s,E_{n-1})-B_{8}(s,E_{n-2}) \bigr]\,ds . \end{aligned} \end{aligned}$$
(22)

We can easily find from Eq. (22) that

$$ \begin{aligned} &\sum^{n}_{i=0} \lambda _{i}(t)=S_{n}(t),\qquad \sum ^{n}_{i=0}\eta _{i}(t) =I_{n}(t), \\ &\sum^{n}_{i=0}\mu _{i}(t)=D_{n}(t),\qquad \sum^{n}_{i=0}\epsilon _{i}(t) =A_{n}(t), \\ &\sum^{n}_{i=0}\varepsilon _{i}(t)=R_{n}(t), \qquad \sum^{n}_{i=0} \zeta _{i}(t) =T_{n}(t), \\ &\sum^{n}_{i=0}\iota _{i}(t)=H_{n}(t),\qquad \sum^{n}_{i=0} \kappa _{i}(t) =E_{n}(t). \end{aligned} $$
(23)

Let us assess the value of \(\lambda _{n}(t)\). Taking the norm for the first formula in Eq. (22), we can get

$$ \begin{aligned} \bigl\Vert \lambda _{n}(t) \bigr\Vert &= \bigl\Vert S_{n}(t)-S_{n-1}(t) \bigr\Vert \\ &= \biggl\Vert \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[B_{1}(t,S_{n-1})-B_{1}(t,S_{n-2}) \bigr] \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}\bigl[B_{1}(s,S_{n-1})-B_{1}(s,S_{n-2}) \bigr]\,ds \biggr\Vert \\ &\leq \frac{2(1-\delta )}{(2-\delta )Z(\delta )} \bigl\Vert \bigl[B_{1}(t,S_{n-1})-B_{1}(t,S_{n-2}) \bigr] \bigr\Vert \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \biggl\Vert \int _{0}^{t}\bigl[B_{1}(s,S_{n-1})-B_{1}(s,S_{n-2}) \bigr]\,ds \biggr\Vert \\ &\leq \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1} \bigl\Vert S_{n-1}(t)-S_{n-2}(t) \bigr\Vert \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1} \int _{0}^{t} \bigl\Vert S_{n-1}(s)-S_{n-2}(s) \bigr\Vert \,ds \\ &=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1} \bigl\Vert \lambda _{n-1}(t) \bigr\Vert +\frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1} \int _{0}^{t} \bigl\Vert \lambda _{n-1}(s) \bigr\Vert \,ds , \end{aligned} $$
(24)

i.e.,

$$ \begin{aligned} \bigl\Vert \lambda _{n}(t) \bigr\Vert \leq \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1} \bigl\Vert \lambda _{n-1}(t) \bigr\Vert + \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1} \int _{0}^{t} \bigl\Vert \lambda _{n-1}(s) \bigr\Vert \,ds . \end{aligned} $$
(25)

We propose the following theorem on consideration of the formulas above.

Theorem 2

The fractional order SIDARTHE mathematics model for COVID-19 has solutions if there is a real number \(t_{0}\) such that

$$ \begin{aligned} \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{i}+ \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{i}t_{0} < 1, \quad \textit{where } i=1,2, \ldots ,8. \end{aligned} $$
(26)

Proof

In the previous part of this article, we have demonstrated that the kernels satisfy the Lipschitz condition, and we have assumed that these functions \(S(t)\), \(I(t)\), \(D(t)\), \(A(t)\), \(R(t)\), \(T(t)\), \(H(t)\), \(E(t)\) are bounded. Considering Eq. (25) and Eq. (26), then applying the recursive method subsequently, we can infer that

$$ \begin{aligned} \bigl\Vert \lambda _{n}(t) \bigr\Vert &\leq \biggl[\biggl( \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}\biggr)+\biggl( \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1}t \biggr)\biggr]^{n} \bigl\Vert S_{0}(t) \bigr\Vert \\ &=\biggl[\biggl(\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}\biggr)+\biggl( \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1}t\biggr)\biggr]^{n} \bigl\Vert S(0) \bigr\Vert . \end{aligned} $$
(27)

Similarly, the other seven inequalities can be deduced as follows:

$$ \begin{aligned} &\bigl\Vert \eta _{n}(t) \bigr\Vert \leq \biggl[\biggl( \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{2}\biggr)+\biggl( \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{2}t \biggr)\biggr]^{n} \bigl\Vert I(0) \bigr\Vert , \\ &\bigl\Vert \mu _{n}(t) \bigr\Vert \leq \biggl[\biggl( \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{3}\biggr)+\biggl( \frac{2\delta}{(2-\delta )Z(\delta )} \beta _{3}t\biggr)\biggr]^{n} \bigl\Vert D(0) \bigr\Vert , \\ &\bigl\Vert \epsilon _{n}(t) \bigr\Vert \leq \biggl[\biggl( \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{4}\biggr)+\biggl( \frac{2\delta}{(2-\delta )Z(\delta )} \beta _{4}t\biggr)\biggr]^{n} \bigl\Vert A(0) \bigr\Vert , \\ &\bigl\Vert \varepsilon _{n}(t) \bigr\Vert \leq \biggl[\biggl( \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{5}\biggr)+\biggl( \frac{2\delta}{(2-\delta )Z(\delta )} \beta _{5}t\biggr)\biggr]^{n} \bigl\Vert R(0) \bigr\Vert , \\ &\bigl\Vert \zeta _{n}(t) \bigr\Vert \leq \biggl[\biggl( \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{6}\biggr)+\biggl( \frac{2\delta}{(2-\delta )Z(\delta )} \beta _{6}t\biggr)\biggr]^{n} \bigl\Vert T(0) \bigr\Vert , \\ &\bigl\Vert \iota _{n}(t) \bigr\Vert \leq \biggl[\biggl( \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{7}\biggr)+\biggl( \frac{2\delta}{(2-\delta )Z(\delta )} \beta _{7}t\biggr)\biggr]^{n} \bigl\Vert H(0) \bigr\Vert , \\ &\bigl\Vert \kappa _{n}(t) \bigr\Vert \leq \biggl[\biggl( \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{8}\biggr)+\biggl( \frac{2\delta}{(2-\delta )Z(\delta )} \beta _{8}t\biggr)\biggr]^{n} \bigl\Vert E(0) \bigr\Vert . \end{aligned} $$
(28)

Equations (27) and (28) show the continuity and existence of the solution of the model. □

Next, we aim to find out a solution of Eq. (9). For this purpose, let us assume that Eq. (19) is an answer. We note that

$$\begin{aligned}& \begin{aligned} S(t)-S(0)=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{1}(t,S) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{1}(s,S)\,ds , \end{aligned} \end{aligned}$$
(29)
$$\begin{aligned}& \begin{aligned} S_{n}(t)= \frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{1}(t,S_{n-1}) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{1}(s,S_{n-1}) \,ds . \end{aligned} \end{aligned}$$
(30)

Supposing that

$$ \begin{aligned} S(t)-S(0)=S_{n}(t)+\xi _{n}(t), \end{aligned} $$
(31)

we will get

$$ \begin{aligned} \xi _{n}(t)&= \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[B_{1}(t,S)-B_{1}(t,S_{n-1}) \bigr] \\ &\quad {}+\frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t} \bigl[B_{1}(s,S)-B_{1}(s,S_{n-1}) \bigr]\,ds . \end{aligned} $$
(32)

Taking the norm for Eq. (32) and applying the triangle inequality, we can get

$$ \begin{aligned} \bigl\Vert \xi _{n}(t) \bigr\Vert &\leq \frac{2(1-\delta )}{(2-\delta )Z(\delta )} \bigl\Vert \bigl[B_{1}(t,S)-B_{1}(t,S_{n-1})\bigr] \bigr\Vert \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t} \bigl\Vert \bigl[B_{1}(s,S)-B_{1}(s,S_{n-1}) \bigr] \bigr\Vert \,ds \\ &\leq \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1} \Vert S-S_{n-1} \Vert +\frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1} \Vert S-S_{n-1} \Vert t \\ &=\biggl[\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}+ \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1}t\biggr] \Vert S-S_{n-1} \Vert , \end{aligned} $$
(33)

i.e.,

$$ \begin{aligned} \bigl\Vert \xi _{n}(t) \bigr\Vert \leq \biggl[ \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}+ \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1}t\biggr] \Vert S-S_{n-1} \Vert , \end{aligned} $$
(34)

and we have

$$ \begin{aligned} \Vert S-S_{n-1} \Vert \leq \biggl[ \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}+ \frac{2\delta}{(2-\delta )Z(\delta )} \beta _{1}t\biggr] \Vert S-S_{n-2} \Vert . \end{aligned} $$
(35)

Therefore, using this process recursively, we can deduce that

$$ \begin{aligned} \bigl\Vert \xi _{n}(t) \bigr\Vert &\leq \biggl[ \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}+ \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1}t\biggr] \Vert S-S_{n-1} \Vert \\ &\leq \biggl[\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}+ \frac{2\delta}{(2-\delta )Z(\delta )} \beta _{1}t\biggr] \\ &\quad {}\cdot \biggl[ \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}+ \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1}t\biggr] \Vert S-S_{n-2} \Vert \\ &\leq \cdots \\ &\leq \biggl[\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}+ \frac{2\delta}{(2-\delta )Z(\delta )} \beta _{1}t\biggr]^{n} \Vert S-S_{0} \Vert \\ &\leq \biggl[\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}+ \frac{2\delta}{(2-\delta )Z(\delta )} \beta _{1}t\biggr]^{n+1} \Vert S \Vert . \end{aligned} $$
(36)

It follows from Eq. (36) that

$$ \begin{aligned} \bigl\Vert \xi _{n}(t) \bigr\Vert &\leq \biggl[ \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}+ \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1}t \biggr]^{n+1}\cdot l_{1}\quad \bigl( \Vert S \Vert \leq l_{1}\bigr). \end{aligned} $$
(37)

Hence, we have the following formula at \(t_{0}\):

$$ \begin{aligned} \bigl\Vert \xi _{n}(t) \bigr\Vert &\leq \biggl[ \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}+ \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1}t_{0} \biggr]^{n+1}\cdot l_{1}. \end{aligned} $$
(38)

We have \(\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}+ \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1}t_{0} < 1\) in Theorem 2, making \(n\rightarrow \infty \), the following formula will be concluded:

$$ \begin{aligned} \bigl\Vert \xi _{n}(t) \bigr\Vert \rightarrow 0\quad (n\rightarrow \infty ). \end{aligned} $$
(39)

Then we receive

$$ \begin{aligned} S(t)-S(0)&=\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{1}(t,S) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{1}(s,S)\,ds . \end{aligned} $$
(40)

In other words, the solution is

$$ \begin{aligned} S(t)&=S(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{1}(t,S) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{1}(s,S)\,ds . \end{aligned} $$
(41)

Similarly, if we take

$$ \begin{aligned} &I(t)-I(0)=I_{n}(t)+\pi _{n}(t), \\ &D(t)-D(0)=D_{n}(t)+\varpi _{n}(t), \\ &A(t)-A(0)=A_{n}(t)+\varrho _{n}(t), \\ &R(t)-R(0)=R_{n}(t)+\varsigma _{n}(t), \\ &T(t)-T(0)=T_{n}(t)+\tau _{n}(t), \\ &H(t)-H(0)=H_{n}(t)+\phi _{n}(t), \\ &E(t)-E(0)=E_{n}(t)+\chi _{n}(t), \end{aligned} $$
(42)

in the same way, if we take \(n \rightarrow \infty \), then we can get

$$ \begin{aligned} & \bigl\Vert \pi _{n}(t) \bigr\Vert \rightarrow 0,\qquad \bigl\Vert \varpi _{n}(t) \bigr\Vert \rightarrow 0,\qquad \bigl\Vert \varrho _{n}(t) \bigr\Vert \rightarrow 0,\qquad \bigl\Vert \varsigma _{n}(t) \bigr\Vert \rightarrow 0, \\ & \bigl\Vert \tau _{n}(t) \bigr\Vert \rightarrow 0, \qquad \bigl\Vert \phi _{n}(t) \bigr\Vert \rightarrow 0, \qquad \bigl\Vert \chi _{n}(t) \bigr\Vert \rightarrow 0. \end{aligned} $$
(43)

Finally, we get the other seven formulas of the solution:

$$ \begin{aligned} &I(t) =I(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{2}(t,I) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{2}(s,I)\,ds , \\ &D(t) =D(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{3}(t,D) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{3}(s,D)\,ds , \\ &A(t) =A(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{4}(t,A) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{4}(s,A)\,ds , \\ &R(t) =R(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{5}(t,R) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{5}(s,R)\,ds , \\ &T(t) =T(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{6}(t,T) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{6}(s,T)\,ds , \\ &H(t) =H(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{7}(t,H) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{7}(s,H)\,ds , \\ &E(t) =E(0)+\frac{2(1-\delta )}{(2-\delta )Z(\delta )}B_{8}(t,E) + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t}B_{8}(s,E)\,ds . \end{aligned} $$
(44)

Namely, Eq. (19) is one solution of the system. That is the end of the proof of existence.

Now, let us consider the uniqueness, we provide the following theorem primarily.

Theorem 3

The system Eq. (9) has only solution if the following inequality is satisfied:

$$ \begin{aligned} 1-\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{i}- \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{i}t > 0,\quad \textit{where } i=1,2, \ldots ,8. \end{aligned} $$
(45)

Proof

Let us consider the solution \(S(t)\), supposing that there is another solution \(\widetilde{S}(t)\), then we have

$$ \begin{aligned} S(t)-\widetilde{S}(t)&= \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\bigl[B_{1}(t,S)-B_{1}(t, \widetilde{S})\bigr] \\ &\quad {}+\frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t} \bigl[B_{1}(s,S)-B_{1}(s, \widetilde{S})\bigr] \,ds . \end{aligned} $$
(46)

We take the norm on both sides of Eq. (46), and taking into account the triangle inequality, we have

$$ \begin{aligned} \bigl\Vert S(t)-\widetilde{S}(t) \bigr\Vert &\leq \frac{2(1-\delta )}{(2-\delta )Z(\delta )} \bigl\Vert \bigl[B_{1}(t,S)-B_{1}(t, \widetilde{S})\bigr] \bigr\Vert \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )} \int _{0}^{t} \bigl\Vert \bigl[B_{1}(s,S)-B_{1}(s, \widetilde{S})\bigr] \bigr\Vert \,ds \\ & \leq \frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1} \Vert S- \widetilde{S} \Vert \\ &\quad{} + \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1}t \Vert S- \widetilde{S} \Vert . \end{aligned} $$
(47)

Then we can get

$$ \begin{aligned} \Vert S-\widetilde{S} \Vert \leq 0 \end{aligned} $$
(48)

if

$$ \begin{aligned} 1-\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{1}- \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{1}t > 0. \end{aligned} $$
(49)

Then we can deduce that \(S=\widetilde{S}\), i.e., the solution S is unique.

Similarly, if

$$ \begin{aligned} 1-\frac{2(1-\delta )}{(2-\delta )Z(\delta )}\beta _{i}- \frac{2\delta}{(2-\delta )Z(\delta )}\beta _{i}t>0,\quad \text{where } i=2,3, \ldots ,8, \end{aligned} $$
(50)

employing the same process, we can infer that

$$ \begin{aligned} &I=\widetilde{I}, \\ &D=\widetilde{D}, \\ &A=\widetilde{A}, \\ &R=\widetilde{R}, \\ &T=\widetilde{T}, \\ &H=\widetilde{H}, \\ &E=\widetilde{E}. \end{aligned} $$
(51)

 □

Hence, the fractional SIDARTHE mathematics model Eq. (9) has a unique solution, the proof of the uniqueness is finished.

5 Numerical simulation

5.1 Numerical method

In the current section, we study several numerical simulations to observe the effects of the order δ and other parameters in the SIDARTHE mathematics model. In the last several years, many numerical techniques have been investigated and used to simulate the epidemic models. So, before we start our experiment, it is necessary to introduce one famous iterative scheme, named the three-step Adams–Bashforth scheme, which was proposed by Atangana and Owolabi [44]. With the help of it, our numerical scheme can be inferred.

Let us pay our attention to the following differential equation with the CF operator:

$$ \begin{aligned} {}^{CF}_{0}D^{\delta}_{t} \bigl(\nu (t)\bigr)=P\bigl(t,\nu (t)\bigr),\quad 0< \delta < 1. \end{aligned} $$
(52)

Here we use Caputo and Fabrizio’s definition instead of the definition proposed by Nieto and Losada [19, 45, 46]. Applying the fractional order integral to the above equation, we can obtain

$$ \begin{aligned} \nu (t)-\nu (0)= \frac{1-\delta}{Z(\delta )}P\bigl(t,\nu (t)\bigr)+ \frac{\delta}{Z(\delta )} \int _{0}^{t}P\bigl(s,\nu (s)\bigr)\,ds . \end{aligned} $$
(53)

Discretizing the interval of time \([0,t]\) with the step size h, we can get a sequence, that is, \(t_{0}=0\), \(t_{k+1}=t_{k}+h\), \(k=0, 1, \ldots , N-1\), where \(N=\frac{t}{h}\). If we take \(t=t_{k+1}\) and \(t=t_{k}\), then the following equation will be inferred:

$$ \begin{aligned} \nu (t_{k+1})-\nu (0)= \frac{1-\delta}{Z(\delta )}P\bigl(t_{k+1},\nu (t_{k+1})\bigr)+ \frac{\delta}{Z(\delta )} \int _{0}^{t_{k+1}}P\bigl(s,\nu (s)\bigr)\,ds \end{aligned} $$
(54)

and

$$ \begin{aligned} \nu (t_{k})-\nu (0)= \frac{1-\delta}{Z(\delta )}P\bigl(t_{k},\nu (t_{k})\bigr)+ \frac{\delta}{Z(\delta )} \int _{0}^{t_{k}}P\bigl(s,\nu (s)\bigr)\,ds . \end{aligned} $$
(55)

From Eq. (54) and Eq. (55) we can infer that

$$ \begin{aligned} \nu (t_{k+1})-\nu (t_{k})=\frac{1-\delta}{Z(\delta )}\bigl[P\bigl(t_{k+1},\nu (t_{k+1})\bigr)-P\bigl(t_{k}, \nu (t_{k}) \bigr)\bigr]+\frac{\delta}{Z(\delta )} \int _{t_{k}}^{t_{k+1}}P\bigl(s, \nu (s)\bigr)\,ds . \end{aligned} $$
(56)

According to Atangana and Owolabi’s opinion, the integral in Eq. (56) can be discretized with the help of the Lagrange interpolating method, i.e.,

$$ \begin{aligned} \int _{t_{k}}^{t_{k+1}}P\bigl(s,\nu (s)\bigr)\,ds = \frac{23h}{12}P\bigl(t_{k},\nu (t_{k})\bigr)- \frac{16h}{12}P\bigl(t_{k-1},\nu (t_{k-1})\bigr)+ \frac{5h}{12}P\bigl(t_{k-2},\nu (t_{k-2})\bigr). \end{aligned} $$
(57)

Substituting Eq. (57) into Eq. (56), the following iterative scheme can be deduced readily:

$$ \begin{aligned} \nu _{k+1}&=\nu _{k}+\biggl(\frac{1-\delta}{Z(\delta )}+ \frac{23\delta h}{12Z(\delta )} \biggr)P(t_{k},\nu _{k})-\biggl( \frac{1-\delta}{Z(\delta )}+ \frac{16\delta h}{12Z(\delta )}\biggr)P(t_{k-1}, \nu _{k-1}) \\ &\quad{} + \biggl(\frac{5\delta h}{12Z(\delta )}\biggr)P(t_{k-2},\nu _{k-2}), \end{aligned} $$
(58)

where \(\nu _{k+1}=\nu (t_{k+1})\), \(\nu _{k}=\nu (t_{k})\), \(\nu _{k-1}= \nu (t_{k-1})\), \(\nu _{k-2}=\nu (t_{k-2})\).

Now we apply this method to our model, writing the system Eq. (9) into vector form as follows:

$$ \begin{aligned} {}^{CF}_{0}D^{\delta}_{t} \bigl(\boldsymbol{\nu}(t)\bigr)=\boldsymbol{P}\bigl(t,\boldsymbol{\nu}(t)\bigr),\quad 0< \delta < 1, \end{aligned} $$
(59)

where

$$ \begin{aligned} \boldsymbol{\nu}(t)= \begin{bmatrix} S(t) \\ I(t) \\ D(t) \\ A(t) \\ R(t) \\ T(t) \\ H(t) \\ E(t) \end{bmatrix} , \qquad \boldsymbol{P}\bigl(t,\boldsymbol{\nu}(t) \bigr)= \begin{bmatrix} B_{1}(t,S) \\ B_{2}(t,I) \\ B_{3}(t,D) \\ B_{4}(t,A) \\ B_{5}(t,R) \\ B_{6}(t,T) \\ B_{7}(t,H) \\ B_{8}(t,E) \end{bmatrix} . \end{aligned} $$
(60)

Assuming \(\boldsymbol{\nu}(0)=[S(t_{0}),I(t_{0}),D(t_{0}),A(t_{0}),R(t_{0}),T(t_{0}),H(t_{0}),E(t_{0})]^{T}\), using the process used before, the final recursion formula can be obtained as follows:

$$ \begin{aligned} \boldsymbol{\nu}_{k+1}&= \boldsymbol{\nu}_{k}+\biggl(\frac{1-\delta}{Z(\delta )}+ \frac{23\delta h}{12Z(\delta )}\biggr)\boldsymbol{P}(t_{k},\boldsymbol{ \nu}_{k})-\biggl( \frac{1-\delta}{Z(\delta )}+\frac{16\delta h}{12Z(\delta )}\biggr) \boldsymbol{P}(t_{k-1}, \boldsymbol{\nu}_{k-1}) \\ &\quad{} + \biggl(\frac{5\delta h}{12Z(\delta )}\biggr)\boldsymbol{P}(t_{k-2}, \boldsymbol{\nu}_{k-2}). \end{aligned} $$
(61)

Now we can begin to proceed our experiment, all the programs and code are based on MATLAB 2018a. The total population is taken to be one hundred million, we expressed it by the capital letter N. According to the real statistical data in Italy [37], the initial conditions and parameters are listed in Table 2.

Table 2 The corresponding value for each parameter
Full size table

5.2 Discussion

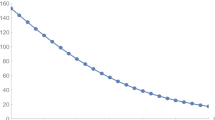
The purpose of the numerical simulation is to examine the influence of order and parameter change on the dynamic action of the system. For this reason, we use the iterative scheme of Caputo–Fabrizio derivative derived above to make Figs. 1 to 8. Figures 1 to 5 are the change curves of the eight state variables of the system when using ode45 and the order is 1, 0.8, 0.6, and 0.4, respectively. From the figures, we can see that each variable converges to its equilibrium point after a certain time, but the time is slightly different. Figure 6 is a comparison diagram of various variables under different orders. It can be seen from the photos that the system state depends on the fractional order. When the order is 1, the model shows an integer order. In addition, for different orders, each state variable shows the same change trend; however, their equilibrium points are slightly different, and the time to converge to the equilibrium point is also slightly different. With the increase of the order, the model converges to the equilibrium point faster, and with the drop of the order, the amounts of infected people decrease more obviously; that is to say, the fractional order operator shows the good properties that the integer order operator does not have, and it can predict the model more accurately. In addition, we can see that with the growth of time, the number of four types of infected people and one type of critical people will be infinitely close to zero, and the whole system will only be left with vulnerable people, cured people, and dead people, which means that the epidemic will slowly end; it is similar to the conclusion reached by Giordano [37] using the integer order model. At the same time, our theoretical results are also verified. Figure 7 is a comparison plot under different probabilities of the conversion of susceptible persons to infected persons. From the diagrams, we can see that the different infection rates have a greater impact on the model. With the decrease of the infection rate, the number of susceptible persons will increase, which means that fewer people will be infected with diseases. At the same time, the peak values of the four classes of infected human beings and the first type of critical ones will drop sharply, and the time to reach the peak values will also be delayed. Figure 8 is a diagram under different detection probabilities of asymptomatic infected persons. We can see from the subplots that the dynamic behavior is similar to Fig. 7 with changing the parameter a.

Figure 1
figure 1

Plot for all state variables in Eq. (9) under ode45

Full size image
Figure 2
figure 2

Plot for all state variables in Eq. (9) when \(\delta =1\)

Full size image
Figure 3
figure 3

Plot for all state variables in Eq. (9) when \(\delta =0.8\)

Full size image
Figure 4
figure 4

Plot for all state variables in Eq. (9) when \(\delta =0.6\)

Full size image
Figure 5
figure 5

Plot for all state variables in Eq. (9) when \(\delta =0.4\)

Full size image
Figure 6
figure 6

The behavior for each state variable in Eq. (9) when \(\delta = 1, 0.8, 0.6, 0.4\), respectively

Full size image
Figure 7
figure 7

The behavior for each state variable in Eq. (9) when \(m = 0.7, 0.6, 0.5\), and 0.4, respectively

Full size image
Figure 8
figure 8

The behavior for each state variable in Eq. (9) when \(a = 0.3, 0.25, 0.2\), and 0.15, respectively

Full size image

Tables 3 to 10 show the comparison between the integer derivative and the CF derivative. It follows from these tables that compared with the standard derivative, the Caputo–Fabrizio derivative has new properties, and the change of order has a more obvious impact on the model results. Therefore, we conclude that the quantity of infected men will be significantly diminished by formulating protective measures, such as wearing masks, limiting travel, maintaining social distancing, increasing the screening of people in close contact, and isolating infected persons. However, there are some potential limitations in our model. Like most infectious disease modeling studies of this type, our approach is based on some reasonable assumptions, but in a real-world scenario, the progress of the epidemic will largely depend on the implementation and timing of the measures described above. Moreover, because the simulation is based on real data on infections in Italy, the classification of populations in outbreaks in other countries may be different. The different measures of different countries may cause small fluctuations in model parameters, resulting in large differences in simulation results.

6 Conclusion

In this paper, the SIDARTHE fractional order epidemic model with CF fractional operator is investigated. Firstly, by taking advantage of the Banach fixed point theorem, we researched the existence and uniqueness of the system’s solution. In an effort to gain the numerical solution of the system, the three-step Adams–Bashforth scheme is exploited to infer the iterative formula. Then we compared the dynamic behavior of the model under different orders and parameters; moreover, their impacts on the model are discussed. The research shows that the Caputo–Fabrizio fractional order operator has positive memory effect, and we can observe the essence of the model more accurately with the help of it, which is unobtainable by the integer order operator. Eventually, we concluded that reducing the infection rate and increasing the detection frequency of asymptomatic infected persons can effectively prevent the spread of infectious diseases, which has important reference significance for policymakers. In future work, we will try to introduce algorithms with higher accuracy and improve the model. Some groups of people may be classified into one category, or new groups of people may be introduced to improve the accuracy of the model’s description of actual problems. In addition, incorporating real data sets of COVID-19 epidemiology into the model will help improve the applicability of the model.