Synchronization analysis for stochastic reaction-diffusion Cohen-Grossberg neural networks with Neumann boundary conditions via periodically intermittent control

Abstract

In this paper, mathematical analysis is proposed on the synchronization problem for stochastic reaction-diffusion Cohen-Grossberg neural networks with Neumann boundary conditions. By introducing several important inequalities and using Lyapunov functional technique, some new synchronization criteria in terms of p-norm are derived under periodically intermittent control. Some previous known results in the literature are improved, and some restrictions on the mixed time-varying delays are removed. The influence of diffusion coefficients, diffusion space, stochastic perturbation and control width on synchronization is analyzed by the obtained synchronization criteria. Numerical simulations are presented to show the feasibility of the theoretical results.

1 Introduction

Synchronization introduced by Pecora and Carrol [1] means two or more systems which are either chaotic or periodic and share a common dynamic behavior. Synchronization problems of Cohen-Grossberg neural networks have been widely researched because of their extensive applications in secure communication, information processing and chaos generators design. Up to now, various control methods have been introduced to achieve synchronization of neural networks including sampled data control [2], pinning control [3], adaptive control [4], sliding mode control [5], impulsive control [6], periodically intermittent control [7–10], and so on.

In the process of signal transmission, an external control should be loaded when the signal becomes weak due to diffusion, and be unloaded when the signal strength reaches the upper bound considering the cost. Hence, discontinuous control methods including impulsive control and intermittent control are more economical and effective than continuous control methods. For impulsive control, the external control is added only at certain points and the control width is zero, but the control width of the intermittent control is non-zero. Therefore, intermittent control can be seen as the transition from impulsive control to continuous control, and it has the advantages of these two methods.

Many results with respect to the synchronization of Cohen-Grossberg neural networks have been obtained based on periodically intermittent control in recent years (see, for example, [11–18]). In [15], the exponential synchronization of Cohen-Grossberg neural networks with time-varying delays was discussed based on periodically intermittent control:

$$\begin{aligned} &{\frac{\mathrm {d}u_{i}(t)}{\mathrm {d}t}=-\alpha_{i}\bigl(u_{i}(t) \bigr) \Biggl[\beta _{i}\bigl(u_{i}(t)\bigr)-\sum _{j=1}^{n}a_{ij}f_{j} \bigl(u_{j}(t)\bigr) -\sum_{j=1}^{n}b_{ij}f_{j} \bigl(u_{j} \bigl(t-\tau_{j}(t)\bigr)\bigr)+J_{i} \Biggr],} \end{aligned}$$

(1.1)

$$\begin{aligned} &{\frac{\mathrm {d}v_{i}(t)}{\mathrm {d}t}=-\alpha_{i} \bigl(v_{i}(t)\bigr) \Biggl[\beta _{i}\bigl(v_{i}(t) \bigr)-\sum_{j=1}^{n}a_{ij}f_{j} \bigl(v_{j}(t)\bigr) -\sum_{j=1}^{n}b_{ij}f_{j}\bigl(v_{j} \bigl(t-\tau_{j}(t)\bigr)\bigr)+J_{i} \Biggr]} \\ &{\hphantom{\frac{\mathrm {d}v_{i}(t)}{\mathrm {d}t}=} {}+K_{i}(t),} \end{aligned}$$

(1.2)

where $u(t)=(u_{1}(t),u_{2}(t),\ldots,u_{n}(t))^{\mathrm{T}}$ denotes the state of the drive system at time t; $v(t)=(v_{1}(t),v_{2}(t),\ldots ,v_{n}(t))^{\mathrm{T}}$ denotes the state of the response system at time t; $\alpha_{i}(\cdot)$ represents the amplification function of the ith neuron; $\beta_{i}(\cdot)$ is the appropriately behaved function of the ith neuron; $f_{j}(\cdot)$ denotes the activation function of the jth neuron; $a_{ij}$ is the connection strength between the jth neuron and the ith neuron; $b_{ij}$ is the discrete time-varying delay connection strength of the jth neuron on the ith neuron; $0<\tau_{j}(t)\leq\tau$ is the discrete time-varying delay of jth neuron and corresponds to finite speed of axonal signal transmission at time t; $J_{i}$ denotes the input from outside of the networks; $K_{i}(t)$ is a periodically intermittent controller. The exponential synchronization criteria were obtained by using some analysis techniques.

Discrete time-varying delays were considered in [15]. In fact, the neural signals propagate along a multitude of parallel pathways with a variety of axon sizes and lengths over a period of time. In order to reduce the influence of the distant past behaviors of the state, distributed delays are introduced to describe this property. In addition, stochastic effects on the synchronization should be considered in real neural networks since synaptic transmission is completed by releasing random fluctuations from neurotransmitters or other random causes [16]. Besides, dynamic behaviors of neural networks derive from the interactions of neurons, which is not only dependent on the time of each neuron but also its space position [17]. Hence, it is essential to study the state variables varying with the time and space variables, especially when electrons are moving in nonuniform electromagnetic fields. Such phenomena can be described by reaction-diffusion equations. In conclusion, more realistic neural networks should consider the effects of mixed time-varying delays, stochastic perturbation and spatial diffusion.

In [18], Gan studied the synchronization problem for Cohen-Grossberg neural networks with mixed time-varying delays, stochastic noise disturbance and spatial diffusion:

$$\begin{aligned} &{\frac{\partial u_{i}(t,x)}{\partial t} =\sum _{k=1}^{l^{\ast}}\frac{\partial}{\partial x_{k}} \biggl(D_{ik} \frac{\partial u_{i}(t,x)}{\partial x_{k}} \biggr) -\alpha_{i}\bigl(u_{i}(t,x)\bigr) \Biggl[\beta_{i}\bigl(u_{i}(t,x)\bigr)-\sum _{j=1}^{n}a_{ij}f_{j} \bigl(u_{j}(t,x)\bigr)} \\ &{\hphantom{\frac{\partial u_{i}(t,x)}{\partial t} =} {} -\sum_{j=1}^{n}b_{ij}g_{j} \bigl(u_{j} \bigl(t-\tau_{ij}(t),x\bigr)\bigr) -\sum_{j=1}^{n}d_{ij} \int^{t}_{t-\tau_{ij}^{\ast}(t)}h_{j}\bigl(u_{j}(s,x) \bigr)\,\mathrm {d}s+J_{i} \Biggr],} \end{aligned}$$

(1.3)

$$\begin{aligned} &{\mathrm {d}v_{i}(t,x)=\Biggl\{ \sum_{k=1}^{l^{\ast}}\frac{\partial }{\partial x_{k}} \biggl(D_{ik}\frac{\partial v_{i}(t,x)}{\partial x_{k}} \biggr)-\alpha_{i} \bigl(v_{i}(t,x)\bigr) \Biggl[\beta_{i}\bigl(v_{i}(t,x) \bigr)-\sum_{j=1}^{n}a_{ij}f_{j} \bigl(v_{j}(t,x)\bigr)} \\ &{\hphantom{\mathrm {d}v_{i}(t,x)=} {}-\sum_{j=1}^{n}b_{ij}g_{j} \bigl(v_{j} \bigl(t-\tau_{ij}(t),x\bigr)\bigr) -\sum_{j=1}^{n}d_{ij} \int^{t}_{t-\tau _{ij}^{*}(t)}h_{j}\bigl(v_{j}(s,x) \bigr)\,\mathrm {d}s+J_{i} \Biggr]+K_{i}(t,x)\Biggr\} \,\mathrm {d}t} \\ &{\hphantom{\mathrm {d}v_{i}(t,x)=} {} +\sum_{j=1}^{n}\sigma_{ij} \bigl(e_{j}(t,x),e_{j}\bigl(t-\tau _{ij}(t),x \bigr),e_{j}\bigl(t-\tau_{ij}^{\ast}(t),x\bigr)\bigr)\,\mathrm {d}\omega_{j}(t),} \end{aligned}$$

(1.4)

where $u(t,x)=(u_{1}(t,x),u_{2}(t,x),\ldots,u_{n}(t,x))^{\mathrm{T}}$ denotes the state of the drive system at time t and in space x; $v(t,x)=(v_{1}(t,x),v_{2}(t,x),\ldots,v_{n}(t,x))^{\mathrm{T}}$ denotes the state of the response system at time t and in space x; $\Omega=\{ x=(x_{1}, x_{2}, \ldots, x_{l^{\ast}})^{\mathrm{T}}| \vert x_{k} \vert < m_{k}, k=1,2,\ldots , l^{\ast}\}\subset R^{l^{\ast}}$ is a bound compact set with smooth boundary ∂Ω and mes $\Omega>0$; $e(t,x)=(e_{1}(t,x),e_{2}(t,x),\ldots, e_{n}(t,x))=v(t,x)-u(t,x)$ is the synchronization error signal; $d_{ij}$ is the distributed delay connection strength between the jth neuron and the ith neuron; $f_{j}(\cdot)$, $g_{j}(\cdot)$ and $h_{j}(\cdot)$ denote the activation functions; $D_{ik}>0$ is the diffusion coefficient along the ith neuron; $0<\tau_{ij}^{\ast}(t)\leq\tau^{\ast}$ is the distributed time-varying delay between the jth neuron and the ith neuron; $\sigma=(\sigma_{ij})_{n\times n}$ is the noise intensity matrix; $K_{i}(t,x)$ is an intermittent controller; $\omega(t)=(\omega _{1}(t),\omega_{2}(t),\ldots,\omega_{n}(t))^{T}\in\mathbb{R}^{n}$ is the stochastic disturbance which is a Brownian motion defined on the complete probability space $(\Omega,\mathcal{F},\mathcal{P})$ (where Ω is the sample, $\mathcal{F}$ is the σ-algebra of subsets of the sample space and $\mathcal{P}$ is the probability measure on $\mathcal{F}$), and

$$ \mathbf{E}\bigl\{ \mathrm {d}\omega(t)\bigr\} =0,\qquad\mathbf{E}\bigl\{ \mathrm {d}\omega^{2}(t)\bigr\} =0, $$

(1.5)

where $\mathbf{E}\{\cdot\}$ is the mathematical expectation operator with respect to the given probability measure $\mathcal{P}$. By using Lyapunov theory and stochastic analysis methods, sufficient conditions were given to realize the exponential synchronization based on p-norm.

The exponential synchronization criteria obtained in [18] assumed that $\dot{\tau}_{ij}(t)\leq\varrho<1$ and $\dot{\tau}^{\ast}_{ij}(t)\leq\varrho^{\ast}<1$ for all t, that is, the time-varying delays were slowly varying delays. In fact, the continuous varying of delays may be slow or fast. Hence, these restrictions are unnecessary and impractical. Furthermore, the boundary conditions in [18] are assumed to be Dirichlet boundary conditions. In engineering applications, such as thermodynamics, Neumann boundary conditions need to be considered. As far as we know, there are few results concerning the synchronization of reaction-diffusion stochastic Cohen-Grossberg neural networks with Neumann boundary conditions.

Based on the above discussion, we are concerned with the combined effects of mixed time-varying delays, stochastic perturbation and spatial diffusion on the exponential synchronization of Cohen-Grossberg neural networks with Neumann boundary conditions in terms of p-norm via periodically intermittent control to improve the previous results. To this end, we discuss the following neural networks:

$$\begin{aligned} \frac{\partial u_{i}(t,x)}{\partial t} =&D_{i} \Delta u_{i}(t,x)-\alpha_{i}\bigl(u_{i}(t,x) \bigr) \Biggl[\beta_{i}\bigl(u_{i}(t,x)\bigr)-\sum _{j=1}^{n}a_{ij}f_{j} \bigl(u_{j}(t,x)\bigr) \\ &{} -\sum_{j=1}^{n}b_{ij}g_{j} \bigl(u_{j} \bigl(t-\tau_{ij}(t),x\bigr)\bigr) -\sum_{j=1}^{n}d_{ij} \int^{t}_{t-\tau_{ij}^{\ast}(t)}h_{j}\bigl(u_{j}(s,x) \bigr)\,\mathrm {d}s+J_{i} \Biggr], \end{aligned}$$

(1.6)

where $\Delta=\sum_{k=1}^{l^{\ast}}\frac{\partial^{2}}{\partial x_{k}^{2}}$ is the Laplace operator; $D_{i}>0$ is the diffusion coefficient along the ith neuron.

The boundary conditions and the initial values of system (1.6) take the form

$$\begin{aligned} &{\frac{\partial u_{i}(t,x)}{\partial{\mathbf {n}}} := \biggl(\frac{\partial u_{i}(t,x)}{\partial x_{1}},\frac{\partial u_{i}(t,x)}{\partial x_{2}}, \ldots ,\frac{\partial u_{i}(t,x)}{\partial x_{l^{\ast}}} \biggr)^{\mathrm{T}} = {\mathbf{0}},} \\ &{\quad (t,x)\in[-\bar{\tau},+\infty)\times\partial \Omega, i\in\ell,} \end{aligned}$$

(1.7)

and

$$ u_{i}(s,x)=\phi_{i}(s,x),\quad (s,x)\in[-\bar{ \tau},0]\times\Omega, i\in\ell, $$

(1.8)

where $\bar{\tau}=\max\{\tau,\tau^{*}\}$, $\phi(s,x)=(\phi _{1}(s,x),\phi_{2}(s,x),\ldots,\phi_{n}(s,x))^{\mathrm{T}}\in\mathcal {C}\triangleq\mathcal{C}([-\bar{\tau},0)\times\Omega, \mathbb{R}^{n})$ which denotes continuous functions with p-norm:

$$\Vert \phi \Vert _{p}= \Biggl( \int_{\Omega}\sum_{i=1}^{n} \sup_{-\bar {\tau}\leq s\leq0} \bigl\vert \phi_{i}(s,x) \bigr\vert ^{p} \,\mathrm {d}x \Biggr)^{\frac {1}{p}}, \quad p\in Z^{+}. $$

System (1.6) is called drive system. The response system is described in the following:

$$\begin{aligned} \mathrm {d}v_{i}(t,x) =&\Biggl\{ D_{i}\Delta v_{i}(t,x)-\alpha _{i} \bigl(v_{i}(t,x)\bigr) \Biggl[\beta_{i}\bigl(v_{i}(t,x) \bigr)-\sum_{j=1}^{n}a_{ij}f_{j} \bigl(v_{j}(t,x)\bigr) \\ &{} -\sum_{j=1}^{n}b_{ij}g_{j} \bigl(v_{j} \bigl(t-\tau_{ij}(t),x\bigr)\bigr) -\sum_{j=1}^{n}d_{ij} \int^{t}_{t-\tau _{ij}^{*}(t)}h_{j}\bigl(v_{j}(s,x) \bigr)\,\mathrm {d}s+J_{i} \Biggr]+K_{i}(t,x)\Biggr\} \,\mathrm {d}t \\ &{} +\sum_{j=1}^{n}\sigma_{ij} \bigl(e_{j}(t,x),e_{j}\bigl(t-\tau _{ij}(t),x \bigr),e_{j}\bigl(t-\tau_{ij}^{\ast}(t),x\bigr)\bigr)\,\mathrm {d}\omega_{j}(t). \end{aligned}$$

(1.9)

The boundary conditions and initial values of the response system (1.9) are given in the following forms:

$$\begin{aligned} &{\frac{\partial v_{i}(t,x)}{\partial{\mathbf {n}}} := \biggl(\frac{\partial v_{i}(t,x)}{\partial x_{1}},\frac{\partial v_{i}(t,x)}{\partial x_{2}}, \ldots ,\frac{\partial v_{i}(t,x)}{\partial x_{l^{\ast}}} \biggr)^{\mathrm{T}} ={\mathbf{0}},} \\ &{\quad (t,x)\in[-\bar{\tau},+\infty)\times\partial \Omega, i\in\ell,} \end{aligned}$$

(1.10)

and

$$ v_{i}(s,x)=\psi_{i}(s,x),\quad (s,x)\in[-\bar{ \tau},0]\times\Omega, i\in\ell, $$

(1.11)

where $\psi(s,x)=(\psi_{1}(s,x), \psi_{2}(s,x),\ldots, \psi_{n}(s,x))\in \mathcal{C}$ is bounded and continuous.

Let $K(t,x)=(K_{1}(t,x),K_{2}(t,x),\ldots,K_{n}(t,x))$ be an intermittent controller defined by

$$ K_{i}(t,x)= \textstyle\begin{cases} -k_{i}(v_{i}(t,x)-u_{i}(t,x)), &(t,x)\in[mT,mT+\delta)\times\Omega,\\ 0, &(t,x)\in[mT+\delta,(m+1)T)\times\Omega, \end{cases} $$

(1.12)

where $m\in N=\{0,1,2,\ldots\}$, $k_{i}>0$ ($i\in\ell$) denote the control strength, $T>0$ denotes the control period and $0<\delta<T$ denotes the control width.

In this paper, the intermittent controller $K(t,x)$ is designed to achieve exponential synchronization of systems (1.6) and (1.9). The model is derived under the following assumptions.

(H1) There exist positive constants $L_{i}$, $L_{i}^{\ast}$, $M_{i}$, $M_{i}^{\ast}$, $N_{i}$, and $N_{i}^{\ast}$ such that:

$$\begin{aligned} &{\bigl\vert f_{i}(\hat{v}_{i})-f_{i}( \check{v}_{i}) \bigr\vert \leq L_{i} \vert \hat{v}_{i}-\check{v}_{i} \vert ,\qquad \bigl\vert f_{i}(\hat{v}_{i}) \bigr\vert \leq L_{i}^{\ast},} \\ &{\bigl\vert g_{i}(\hat{v}_{i})-g_{i}( \check{v}_{i}) \bigr\vert \leq M_{i} \vert \hat{v}_{i}-\check{v}_{i} \vert ,\qquad \bigl\vert g_{i}(\hat{v}_{i}) \bigr\vert \leq M_{i}^{\ast},} \\ &{\bigl\vert h_{i}(\hat{v}_{i})-f_{i}( \check{v}_{i}) \bigr\vert \leq N_{i} \vert \hat{v}_{i}-\check{v}_{i} \vert ,\qquad \bigl\vert h_{i}(\hat{v}_{i}) \bigr\vert \leq N_{i}^{\ast},} \end{aligned}$$

where $\hat{v}_{i}$, $\check{v}_{i}\in\mathbb{R}$, $i\in\ell$.

(H2) There exist positive constants $\bar{\alpha}_{i}$ and $\alpha_{i}^{\ast}$ such that

$$\bigl\vert \alpha_{i}(\hat{v}_{i})-\alpha_{i}( \check{v}_{i}) \bigr\vert \leq\bar{\alpha }_{i} \vert \hat{v}_{i}-\check{v}_{i} \vert , \quad0\leq \alpha_{i}(\hat{v}_{i})\leq \alpha_{i}^{\ast}$$

for all $\hat{v}_{i}$, $\check{v}_{i}\in\mathbb{R}$, $i\in\ell$.

(H3) There exist positive constants $\gamma_{i}$ such that

$$\frac{\alpha_{i}(\hat{v}_{i})\beta_{i}(\hat{v}_{i})-\alpha_{i}(\check{v}_{i}) \beta_{i}(\check{v}_{i})}{\hat{v}_{i}-\check{v}_{i}}\geq\gamma_{i} $$

for all $\hat{v}_{i}, \check{v}_{i}\in\mathbb{R}$, and $\hat{v}_{i}\neq \check{v}_{i}$, $i\in\ell$.

(H4) There exist positive constants $\eta_{ij}$ such that

$$\bigl\vert \sigma_{ij}(\tilde{v}_{1},\hat{v}_{1}, \check{v}_{1})-\sigma_{ij}(\tilde {v}_{2}, \hat{v}_{2},\check{v}_{2}) \bigr\vert ^{2}\leq \eta_{ij}\bigl( \vert \tilde{v}_{1}-\tilde{v}_{2} \vert ^{2}+ \vert \hat{v}_{1}-\hat {v}_{2} \vert ^{2}+ \vert \check{v}_{1}-\check{v}_{2} \vert ^{2}\bigr) $$

for all $\tilde{v}_{1},\tilde{v}_{2},\hat{v}_{1},\hat{v}_{2},\check {v}_{1},\check{v}_{2}\in\mathbb{R}$, and $\sigma_{ij}(0,0,0)=0$, $i,j\in \ell$.

The organization of this paper is as follows. In Section 2, some definitions and lemmas which will be essential to our derivation are introduced. In Section 3, by using Lyapunov functional technique, some new criteria are obtained to achieve the exponential synchronization of systems (1.6) and (1.9). Some numerical examples are given to verify the feasibility of the theoretical results in Section 4. This paper ends with a brief conclusion in Section 5.

2 Preliminaries

In this section, we propose some definitions and lemmas used in the proof of the main results.

Definition 2.1

The response system (1.9) and the drive system (1.6) are exponential synchronization under the periodically intermittent controller (1.12) based on p-norm if there exist constants $\mu>0$ and $M\geq1$ such that

$$\mathbf{E} \bigl\{ \bigl\Vert v(t,x)-u(t,x) \bigr\Vert _{p} \bigr\} \leq M\mathbf{E} \bigl\{ \Vert \psi-\phi \Vert _{p} \bigr\} e^{-\mu t},\quad(t,x)\in[0,+\infty)\times \Omega, $$

where $u(t,x)$ and $v(t,x)$ are solutions of systems (1.6) and (1.9) with differential initial functions $\phi, \varphi\in\mathcal{C}$, respectively, and

$$\bigl\Vert v(t,x)-u(t,x) \bigr\Vert _{p}= \Biggl( \int_{\Omega}\sum_{i=1}^{n} \bigl\vert v_{i}(t,x)-u_{i}(t,x) \bigr\vert ^{p} \,\mathrm {d}x \Biggr)^{\frac{1}{p}}. $$

Lemma 2.1

Wang [19] Itô’s formula

Let $x(t)$ ($t\geq 0$) be Itô processes, and

$$\mathrm {d}x(t)=f(t)\,\mathrm {d}t+g(t)\,\mathrm {d}B_{t}, $$

where $f\in\mathcal{L}^{1}(R^{+},R^{n})$ ($\mathcal{L}^{1}$ is the space of absolutely integrable function), $g\in\mathcal{L}^{2}(R^{+},R^{n\times m})$ ($\mathcal{L}^{2}$ is the space of square integrable function). If $V(x,t)\in C^{2,1}(R^{n}\times R^{+};R)$, ($C^{2,1}(R^{n}\times R^{+};R)$ is the family of all nonnegative functions on $R^{+}\times R^{n}$ which are continuously twice differentiable in x and once differentiable in t), then $V(x(t),t)$ is still Itô processes, and

$$\begin{aligned} \mathrm {d}V\bigl(x(t),t\bigr) =& \biggl[V_{t}\bigl(x(t),t \bigr)+V_{x}\bigl(x(t),t\bigr)f(t)+\frac {1}{2}\operatorname{tr} \bigl(g^{T}(t)V_{xx}\bigl(x(t),t\bigr)g(t) \bigr) \biggr]\,\mathrm {d}t \\ &{} +V_{x}\bigl(x(t),t\bigr)g(t)\,\mathrm {d}B_{t}, \end{aligned}$$

(2.1)

where

$$\begin{aligned} &{V_{t}\bigl(x(t),t\bigr)= \frac{\partial V(x(t),t)}{\partial t},} \\ &{V_{x}\bigl(x(t),t\bigr)= \biggl(\frac{\partial V(x(t),t)}{\partial x_{1}},\ldots ,\frac{\partial V(x(t),t)}{\partial x_{n}} \biggr),} \\ &{V_{xx}\bigl(x(t),t\bigr)= \biggl(\frac{\partial^{2} V(x(t),t)}{\partial e_{i}\,\partial e_{j}} \biggr)_{n\times n}.} \end{aligned}$$

Lemma 2.2

Gu[20]

Suppose that Ω is a bounded domain of $R^{l^{\ast}}$ with a smooth boundary ∂Ω. $u(x)$, $v(x)$ are real-valued functions belonging to $\mathcal{C}^{2}(\Omega\cup \partial\Omega)$. Then

$$ \int_{\Omega}u(x)\Delta v(x)\,\mathrm {d}x= \int_{\partial\Omega }u(x)\frac{\partial v(x)}{\partial\mathbf{n}}\,\mathrm {d}x- \int_{\Omega}\bigl(\nabla u(x)\bigr)^{T}\nabla v(x)\,\mathrm {d}x, $$

(2.2)

where $\nabla=(\frac{\partial}{\partial x_{1}}, \frac{\partial }{\partial x_{2}}, \ldots,\frac{\partial}{\partial x_{l^{\ast}}})^{\mathrm{T}}$ is the gradient operator.

Lemma 2.3

Let $p\geq2$ be a positive integer and Ω be a bounded domain of $R^{l^{\ast}}$ with a smooth boundary ∂Ω. $\varphi(x)\in\mathcal{C}^{1}(\Omega)$ is a real-valued function and $\frac{\partial\varphi(x)}{\partial\mathbf{n}}| _{\partial\Omega }=\mathbf{0}$. Then

$$ \int_{\Omega}\bigl\vert \varphi(x) \bigr\vert ^{p} \,\mathrm {d}x \leq\frac{p-1}{\lambda _{1}} \int_{\Omega}\bigl\vert \varphi(x) \bigr\vert ^{p-2} \bigl\vert \nabla\varphi(x) \bigr\vert ^{2} \,\mathrm {d}x, $$

(2.3)

where $\lambda_{1}$ is the smallest positive eigenvalue of the Neumann boundary problem

$$ \textstyle\begin{cases} -\Delta\vartheta(x)=\lambda\vartheta(x), &x\in\Omega,\\ \frac{\partial\vartheta(x)}{\partial\mathbf{n}}=0, &x\in\partial \Omega. \end{cases} $$

(2.4)

Proof

According to the eigenvalue theory of elliptic operators, the Laplacian −Δ on Ω with the Neumann boundary conditions is a self-adjoint operator with compact inverse, so there exists a sequence of nonnegative eigenvalues $0=\lambda_{0}<\lambda _{1}<\lambda_{2}<\cdots$ , ($\lim_{i\to\infty}\lambda_{i}=+\infty$) and a sequence of corresponding eigenfunctions $\vartheta_{0}(x), \vartheta_{1}(x), \vartheta_{2}(x), \ldots$ for the Neumann boundary problem (2.4), that is,

$$ \textstyle\begin{cases} \lambda_{0}=0, &\vartheta_{0}(x)=1,\\ -\Delta\vartheta_{m}(x)=\lambda_{m}\vartheta_{m}(x), &\mbox{in } \Omega,\\ \frac{\partial\vartheta_{m}(x)}{\partial\mathbf{n}}=0, &\mbox{on } \partial\Omega. \end{cases} $$

(2.5)

Integrate the second equation of (2.5) over Ω after multiplying by $\vartheta_{m}^{p-1}(x)$ ($m=1,2,\ldots$). Then, by Green’s formula (2.2), we obtain

$$\begin{aligned} &{\lambda_{m} \int_{\Omega}\vartheta^{p}_{m}(x)\,\mathrm {d}x} \\ &{\quad =- \int_{\Omega}\vartheta_{m}^{p-1}(x)\Delta \vartheta_{m}(x)\,\mathrm {d}x} \\ &{\quad =- \int_{\partial\Omega}\vartheta_{m}^{p-1}(x) \frac{\partial \vartheta_{m}(x)}{\partial\mathbf{n}}\,\mathrm {d}s+ \int_{\Omega}\bigl(\nabla\vartheta_{m}^{p-1}(x) \nabla\bigr)^{T} \vartheta_{m}(x)\,\mathrm {d}x} \\ &{\quad = \int_{\Omega}(p-1)\vartheta_{m}^{p-2}(x) \biggl[ \biggl(\frac{\partial \vartheta_{m}(x)}{\partial x_{1}} \biggr)^{2}+ \biggl(\frac{\partial \vartheta_{m}(x)}{\partial x_{2}} \biggr)^{2}+\cdots+ \biggl(\frac{\partial \vartheta_{m}(x)}{\partial x_{l^{\ast}}} \biggr)^{2} \biggr]\,\mathrm {d}x} \\ &{\quad =(p-1) \int_{\Omega}\vartheta_{m}^{p-2}(x) \bigl\vert \nabla\vartheta _{m}(x) \bigr\vert ^{2}\,\mathrm {d}x.} \end{aligned}$$

(2.6)

It is easy to show that (2.6) is also true for $m=0$.

The sequence of eigenfunctions $\{\vartheta_{i}(x)\}_{i\geq0}$ contains an orthonormal basis of $\mathcal{L}^{2}(\Omega)$. Hence, for any $\varphi(x)\in\mathcal{L}^{2}(\Omega)$, there exists a sequence of constants $\{c_{m}\}_{m\geq0}$ such that

$$ \varphi(x)=\sum_{m=0}^{\infty}c_{m} \vartheta_{m}(x). $$

(2.7)

It follows from (2.6) and (2.7) that

$$\begin{aligned} \int_{\Omega}\bigl\vert \varphi(x) \bigr\vert ^{p} \,\mathrm {d}x \leq& \int_{\Omega}\sum_{m=0}^{\infty} \bigl\vert c_{m}\vartheta_{m}(x) \bigr\vert ^{p}\,\mathrm {d}x \\ \leq&\frac{p-1}{\lambda_{1}} \int_{\Omega}\sum_{m=0}^{\infty } \bigl\vert c_{m}\vartheta_{m}(x) \bigr\vert ^{p-2} \bigl\vert c_{m}\nabla\vartheta_{m}(x) \bigr\vert ^{2}\,\mathrm {d}x \\ \leq&\frac{p-1}{\lambda_{1}} \int_{\Omega}\sum_{m=0}^{\infty } \bigl\vert c_{m}\vartheta_{m}(x) \bigr\vert ^{p-2}\sum_{m=0}^{\infty} \bigl\vert c_{m}\nabla\vartheta _{m}(x) \bigr\vert ^{2} \,\mathrm {d}x \\ =&\frac{p-1}{\lambda_{1}} \int_{\Omega}\bigl\vert \varphi(x) \bigr\vert ^{p-2} \bigl\vert \nabla \varphi(x) \bigr\vert ^{2}\,\mathrm {d}x. \end{aligned}$$

 □

Remark 1

If $p=2$, the integral inequality (2.3) is the Poincaré integral inequality in [21]. The smallest eigenvalue $\lambda_{1}$ of the Neumann boundary problem (2.4) is determined by the boundary of Ω [21]. If $\Omega=\{ x=(x_{1}, x_{2}, \ldots, x_{l^{\ast}})^{\mathrm{T}}| m_{k}^{-}\leq x_{k}\leq m_{k}^{+}, k=1,2,\ldots, l^{\ast}\}\subset R^{l^{\ast}}$, then

$$\lambda_{1}=\min\biggl\{ \biggl(\frac{\pi}{m_{1}^{+}-m_{1}^{-}} \biggr)^{2}, \biggl(\frac{\pi}{m_{2}^{+}-m_{2}^{-}} \biggr)^{2},\ldots, \biggl(\frac{\pi }{m_{l^{\ast}}^{+}-m_{l^{\ast}}^{-}} \biggr)^{2}\biggr\} . $$

Lemma 2.4

Mei[22]

Let $p\geq2$ and $a,b,h>0$. Then

$$\begin{aligned} &{a^{p-1}b \leq\frac{(p-1)ha^{p}}{p}+ \frac{b^{p}}{ph^{p-1}},} \\ &{a^{p-2}b^{2} \leq\frac{(p-2)ha^{p}}{p}+\frac{2b^{p}}{ph^{\frac{p-2}{2}}}.} \end{aligned}$$

3 Exponential synchronization criterion

In this section, the exponential synchronization criterion of the drive system (1.6) and the response system (1.9) is obtained by designing the suitable T, δ and $k_{i}$. For convenience, the following denotations are introduced.

Denote

$$\begin{aligned} &{w_{1} =\max_{i\in\ell}\Biggl\{ \alpha_{i}^{\ast}\sum_{j=1}^{n} \frac{N_{j} \vert d_{ij} \vert }{\rho_{j}^{p-1}}\Biggr\} ,} \\ &{w_{2}=\max_{i\in\ell}\Biggl\{ (p-1)\sum _{j=1}^{n} \frac{\eta_{ij}}{\varsigma_{j}^{\frac{p-2}{2}}}\Biggr\} ,} \\ &{w_{3}=\max_{i\in\ell}\Biggl\{ \alpha_{i}^{\ast}\sum_{j=1}^{n}\frac {M_{j} \vert b_{ij} \vert }{\zeta_{j}^{p-1}} +(p-1)\sum _{j=1}^{n}\frac{\eta_{ij}}{\epsilon_{j}^{\frac {p-2}{2}}}\Biggr\} ,} \\ &{\kappa_{i} =p\lambda_{1}D_{i}+p \gamma_{i}+p k_{i}-p\alpha_{i}^{\ast} \vert a_{ii} \vert L_{i}-(p-1)\alpha_{i}^{\ast}\sum_{j=1,j\neq i}^{n} L_{j} \vert a_{ij} \vert \xi _{j}-(p-1)\alpha_{i}^{\ast}\sum_{j=1}^{n} M_{j} \vert b_{ij} \vert \zeta_{j}} \\ &{\hphantom{\kappa_{i} =} {}-(p-1)\alpha_{i}^{\ast}\sum_{j=1}^{n} N_{j} \vert d_{ij} \vert \rho_{j}-p\bar{ \alpha }_{i}\sum_{j=1}^{n} \bigl[ \vert a_{ij} \vert L_{j}^{\ast}+ \vert b_{ij} \vert M_{j}^{*}+ \vert d_{ij} \vert N_{j}^{\ast}\tau^{\ast}+ \vert J_{i} \vert \bigr]} \\ &{\hphantom{\kappa_{i} =} {}-\alpha_{i}^{\ast}\sum _{j=1,j\neq i}^{n}\frac{L_{i} \vert a_{ji} \vert }{\xi_{i}^{p-1}} -\frac{1}{2}(p-1) (p-2)\sum_{j=1,j\neq i}^{n} \varrho_{j}\eta _{ij}-(p-1)\sum_{j=1,j\neq i}^{n} \frac{\eta_{ji}}{\varrho_{i}^{\frac {p-2}{2}}}-\frac{1}{2}p(p-1)\eta_{ii}} \\ &{\hphantom{\kappa_{i} =} {}-\frac{1}{2}(p-1) (p-2)\sum_{j=1}^{n} \epsilon_{j}\eta_{ij}-\frac {1}{2}(p-1) (p-2) \sum _{j=1}^{n}\varsigma_{j} \eta_{ij},} \end{aligned}$$

where $\xi_{i}$, $\zeta_{i}$, $\rho_{i}$, $\varrho_{i}$, $\epsilon_{i}$ and $\varsigma _{i}$ are positive constants.

Consider the following function:

$$F(\varepsilon)=\varepsilon-\kappa+we^{\varepsilon\bar{\tau}}, $$

where $\varepsilon\geq0$, $w=w_{1}\tau^{\ast}+w_{2}+w_{3}$, $\kappa=\min_{i\in\ell}\{\kappa_{i}\}$. If the following holds:

(H5) $\kappa>w$, then $F(0)<0$, and $F_{i}(\varepsilon_{i})\rightarrow+\infty$ as $\varepsilon_{i}\rightarrow+\infty$. Noting that $F(\varepsilon)$ is continuous on $[0,+\infty)$ and $F'(\varepsilon)>0$, using the zero point theorem, we obtain that there exists a unique positive constant ε̄ such that $F(\bar{\varepsilon})=0$.

Theorem 3.1

Under assumptions (H1)-(H5), the response system (1.9) and the drive system (1.6) are exponential synchronization under the periodically intermittent controller (1.12) based on p-norm, if the following condition holds:

(H6) $\theta>0$, $\bar{\varepsilon}-\frac{(T-\delta )\theta}{T}>0$, where $\theta=\kappa+\max_{i\in\ell}\{ -\kappa_{i}+pk_{i}\}$.

Proof

Subtract (1.6) from (1.9), and we obtain the error system

$$\begin{aligned} &{\mathrm {d}e_{i}(t,x) =\Biggl\{ D_{i} \Delta e_{i}- \bigl[\alpha _{i}\bigl(v_{i}(t,x) \bigr)\beta_{i}\bigl(v_{i}(t,x)\bigr) -\alpha_{i} \bigl(u_{i}(t,x)\bigr)\beta_{i}\bigl(u_{i}(t,x) \bigr) \bigr]} \\ &{\phantom{\mathrm {d}e_{i}(t,x) =} {}+\alpha_{i}\bigl(v_{i}(t,x)\bigr)\sum _{j=1}^{n} \biggl[a_{ij}f_{j}^{\ast}\bigl(e_{j}(t,x)\bigr) +b_{ij}g_{j}^{\ast}\bigl(e_{j} \bigl(t-\tau_{ij}(t),x\bigr)\bigr)} \\ &{\phantom{\mathrm {d}e_{i}(t,x) =} {}+d_{ij} \int_{t-\tau_{ij}^{\ast}(t)}^{t} h_{j}^{\ast}\bigl(e_{j}(s,x)\bigr)\,\mathrm {d}s \biggr]} \\ &{\phantom{\mathrm {d}e_{i}(t,x) =} {} + \alpha_{i}^{\ast}\bigl(e_{i}(t,x)\bigr)\sum _{j=1}^{n} \biggl[a_{ij}f_{j} \bigl(u_{j}(t,x)\bigr) + b_{ij}g_{j} \bigl(u_{j} \bigl(t-\tau_{ij}(t),x\bigr)\bigr)} \\ &{\phantom{\mathrm {d}e_{i}(t,x) =} {} + d_{ij} \int_{t-\tau_{ij}^{\ast}(t)}^{t} h_{j}\bigl(u_{j}(s,x) \bigr)\,\mathrm {d}s - J_{i} \biggr]-k_{i}e_{i}(t,x) \Biggr\} \,\mathrm {d}t} \\ &{\phantom{\mathrm {d}e_{i}(t,x) =} {} +\sum_{j=1}^{n} \sigma_{ij}\bigl(e_{j}(t,x),e_{j}\bigl(t- \tau_{ij}(t),x\bigr),e_{j}\bigl(t-\tau _{ij}^{\ast}(t),x \bigr)\bigr)\,\mathrm {d}\omega_{j}(t),} \\ &{\quad (t,x)\in[mT, mT+\delta)\times\Omega,} \end{aligned}$$

(3.1)

$$\begin{aligned} &{\mathrm {d}e_{i}(t,x)=\Biggl\{ D_{i}\Delta e_{i}- \bigl[\alpha _{i} \bigl(v_{i}(t,x)\bigr)\beta_{i}\bigl(v_{i}(t,x) \bigr) -\alpha_{i}\bigl(u_{i}(t,x)\bigr)\beta_{i} \bigl(u_{i}(t,x)\bigr) \bigr]} \\ &{\phantom{\mathrm {d}e_{i}(t,x)=} {} +\alpha_{i}\bigl(v_{i}(t,x)\bigr)\sum _{j=1}^{n} \biggl[a_{ij}f_{j}^{\ast}\bigl(e_{j}(t,x)\bigr) +b_{ij}g_{j}^{\ast}\bigl(e_{j} \bigl(t-\tau_{ij}(t),x\bigr)\bigr) } \\ &{\phantom{\mathrm {d}e_{i}(t,x)=} {} +d_{ij} \int_{t-\tau_{ij}^{\ast}(t)}^{t} h_{j}^{\ast}\bigl(e_{j}(s,x)\bigr)\,\mathrm {d}s \biggr]} \\ &{\phantom{\mathrm {d}e_{i}(t,x)=} {} +\alpha_{i}^{\ast}\bigl(e_{i}(t,x)\bigr)\sum _{j=1}^{n} \biggl[a_{ij}f_{j} \bigl(u_{j}(t,x)\bigr) +b_{ij}g_{j} \bigl(u_{j}\bigl(t-\tau_{ij}(t),x\bigr)\bigr)} \\ &{\phantom{\mathrm {d}e_{i}(t,x)=} {} +d_{ij} \int_{t-\tau_{ij}^{\ast}(t)}^{t} h_{j}\bigl(u_{j}(s,x) \bigr)\,\mathrm {d}s-J_{i} \biggr]\Biggr\} \,\mathrm {d}t} \\ &{\phantom{\mathrm {d}e_{i}(t,x)=} {} +\sum_{j=1}^{n} \sigma _{ij}\bigl(e_{j}(t,x),e_{j}\bigl(t- \tau_{ij}(t),x\bigr),e_{j}\bigl(t-\tau_{ij}^{\ast}(t),x \bigr)\bigr)\,\mathrm {d}\omega_{j}(t),} \\ &{\quad (t,x)\in \bigl[mT+\delta,(m+1)T\bigr)\times\Omega,} \end{aligned}$$

(3.2)

where

$$\begin{aligned} &{e_{i}(t,x)=v_{i}(t,x)-u_{i}(t,x),} \\ &{\alpha_{i}^{\ast}\bigl(e_{i}(\cdot,x)\bigr)= \alpha_{i}\bigl(v_{i}(\cdot,x)\bigr)-\alpha _{i} \bigl(u_{i}(\cdot,x)\bigr),} \\ &{f_{j}^{\ast}\bigl(e_{j}(\cdot,x) \bigr)=f_{j}\bigl(v_{j}(\cdot,x)\bigr)-f_{j} \bigl(u_{j}(\cdot,x)\bigr),} \\ &{g_{j}^{\ast}\bigl(e_{j}(\cdot,x) \bigr)=g_{j}\bigl(v_{j}(\cdot,x)\bigr)-g_{j} \bigl(u_{j}(\cdot,x)\bigr),} \\ &{h_{j}^{\ast}\bigl(e_{j}(\cdot,x) \bigr)=h_{j}\bigl(v_{j}(\cdot,x)\bigr)-h_{j} \bigl(u_{j}(\cdot,x)\bigr).} \end{aligned}$$

Define

$$ V(t)= \int_{\Omega}\sum_{i=1}^{n} \bigl\vert e_{i}(t,x) \bigr\vert ^{p}\,\mathrm {d}x. $$

(3.3)

For $(t,x)\in[mT, mT+\delta)\times\Omega$, by (1.5), Itô’s differential formula (2.1) and the Dini right-upper derivative, we get

$$\begin{aligned} &{D^{+}\mathbf{E}\bigl\{ V(t)\bigr\} } \\ &{\quad \leq\mathbf{E}\Biggl\{ \int_{\Omega}\sum_{i=1}^{n} \Biggl\{ p \bigl\vert e_{i}(t,x) \bigr\vert ^{p-1} \biggl[D_{i}\Delta \bigl\vert e_{i}(t,x) \bigr\vert -k_{i} \bigl\vert e_{i}(t,x) \bigr\vert } \\ &{\quad\qquad{} - \bigl\vert \alpha_{i}\bigl(v_{i}(t,x)\bigr) \beta_{i}\bigl(v_{i}(t,x)\bigr)-\alpha _{i} \bigl(u_{i}(t,x)\bigr)\beta_{i}\bigl(u_{i}(t,x) \bigr) \bigr\vert } \\ &{\quad\qquad{} + \bigl\vert \alpha_{i} \bigl(v_{i}(t,x)\bigr) \bigr\vert \sum_{j=1}^{n} \biggl[ \vert a_{ij} \vert \bigl\vert f_{j}^{\ast}\bigl(e_{j}(t,x)\bigr) \bigr\vert + \vert b_{ij} \vert \bigl\vert g_{j}^{\ast}\bigl(e_{j}\bigl(t- \tau_{ij}(t),x\bigr)\bigr) \bigr\vert } \\ &{\quad\qquad{}+ \vert d_{ij} \vert \int _{t-\tau_{ij}^{\ast}(t)}^{t} \bigl\vert h_{j}^{\ast}\bigl(e_{j}(s,x)\bigr) \bigr\vert \,\mathrm {d}s \biggr]} \\ &{\quad\qquad{}+ \bigl\vert \alpha_{i}^{\ast}\bigl(e_{i}(t,x) \bigr) \bigr\vert \sum_{j=1}^{n} \biggl[ \vert a_{ij} \vert \bigl\vert f_{j} \bigl(u_{j}(t,x)\bigr) \bigr\vert + \vert b_{ij} \vert \bigl\vert g_{j}\bigl(u_{j}\bigl(t-\tau_{ij}(t),x \bigr)\bigr) \bigr\vert } \\ &{\quad\qquad{}+ \vert d_{ij} \vert \int _{t-\tau_{ij}^{\ast}(t)}^{t} \bigl\vert h_{j}^{\ast}\bigl(u_{j}(s,x)\bigr) \bigr\vert \,\mathrm {d}s+ \vert J_{i} \vert \biggr] \biggr]} \\ &{\quad\qquad{} +\frac{1}{2}p(p-1) \bigl\vert e_{i}(t,x) \bigr\vert ^{p-2}\sum_{j=1}^{n} \sigma _{ij}^{2}\bigl(e_{j}(t,x),e_{j}\bigl(t- \tau_{ij}(t),x\bigr),e_{j}\bigl(t-\tau_{ij}^{\ast}(t),x \bigr)\bigr)\Biggr\} \,\mathrm {d}x\Biggr\} .} \end{aligned}$$

(3.4)

If (H1)-(H4) hold, it is easy to show that

$$\begin{aligned} &{D^{+}\mathbf{E}\bigl\{ V(t)\bigr\} } \\ &{\quad \leq \mathbf{E}\Biggl\{ \int_{\Omega}\sum_{i=1}^{n}\Biggl\{ p \bigl\vert e_{i}(t,x) \bigr\vert ^{p-1} \Biggl[D_{i}\Delta \bigl\vert e_{i}(t,x) \bigr\vert -\gamma _{i} \bigl\vert e_{i}(t,x) \bigr\vert -k_{i} \bigl\vert e_{i}(t,x) \bigr\vert } \\ &{\qquad {}+\alpha_{i}^{\ast}\sum_{j=1}^{n} \biggl[ \vert a_{ij} \vert L_{j} \bigl\vert e_{j}(t,x) \bigr\vert + \vert b_{ij} \vert M_{j} \bigl\vert e_{j}\bigl(t-\tau_{ij}(t),x \bigr) \bigr\vert + \vert d_{ij} \vert \int_{t-\tau_{ij}^{\ast}(t)}^{t} N_{j} \bigl\vert e_{j}(s,x) \bigr\vert \,\mathrm {d}s \biggr]} \\ &{\qquad {}+\bar{\alpha}_{i} \bigl\vert e_{i}(t,x) \bigr\vert \sum_{j=1}^{n} \bigl[ \vert a_{ij} \vert L_{j}^{\ast}+ \vert b_{ij} \vert M_{j}^{*}+ \vert d_{ij} \vert N_{j}^{\ast}\tau^{\ast}+ \vert J_{i} \vert \bigr] \Biggr]} \\ &{\qquad {} + \frac {1}{2}p(p-1) \bigl\vert e_{i}(t,x) \bigr\vert ^{p-2}\sum_{j=1}^{n} \eta_{ij} \bigl[ \bigl\vert e_{j}(t,x) \bigr\vert ^{2} + \bigl\vert e_{j}\bigl(t-\tau_{ij}(t) \bigr) \bigr\vert ^{2}} \\ &{\qquad {} + \bigl\vert e_{j}\bigl(t- \tau_{ij}^{\ast}(t)\bigr) \bigr\vert ^{2} \bigr]\Biggr\} \,\mathrm {d}x\Biggr\} .} \end{aligned}$$

(3.5)

From the boundary conditions (1.7), (1.10) and Lemma 2.3, we get

$$\begin{aligned} &{p \int_{\Omega}\bigl\vert e_{i}(t,x) \bigr\vert ^{p-1}D_{i}\Delta \bigl\vert e_{i}(t,x) \bigr\vert \,\mathrm {d}x} \\ &{\quad =p \int _{\Omega}\bigl\vert e_{i}(t,x) \bigr\vert ^{p-1}D_{i}\sum_{k=1}^{l^{\ast}} \frac{\partial }{\partial x_{k}} \biggl(\frac{\partial \vert e_{i}(t,x) \vert }{\partial x_{k}} \biggr)\,\mathrm {d}x} \\ &{\quad = p \Biggl( \int_{\partial\Omega} \bigl\vert e_{i}(t,x) \bigr\vert ^{p-1}D_{i}\sum_{k=1}^{l^{\ast}} \frac{\partial \vert e_{i}(t,x) \vert }{\partial x_{k}}\cos (x_{k},n)\,\mathrm {d}s} \\ &{\qquad{}- \int_{\Omega}\sum_{k=1}^{l^{\ast}}D_{i} \frac {\partial \vert e_{i}(t,x) \vert }{\partial x_{k}}\cdot\frac{\partial \vert e_{i}(t,x) \vert ^{p-1}}{\partial x_{k}}\,\mathrm {d}x \Biggr)} \\ &{\quad =-p(p-1)D_{i} \int_{\Omega} \bigl\vert e_{i}(t,x) \bigr\vert ^{p-2}\sum_{k=1}^{l^{\ast}} \frac{\partial \vert e_{i}(t,x) \vert }{\partial x_{k}}\cdot\frac{\partial \vert e_{i}(t,x) \vert }{\partial x_{k}}\,\mathrm {d}x} \\ &{\quad =-p(p-1)D_{i} \int_{\Omega} \bigl\vert e_{i}(t,x) \bigr\vert ^{p-2} \bigl\vert \nabla \bigl\vert e_{i}(t,x) \bigr\vert \bigr\vert ^{2}\,\mathrm {d}x} \\ &{\quad \leq-p\lambda_{1}D_{i} \int_{\Omega}\bigl\vert e_{i}(t,x) \bigr\vert ^{p} \,\mathrm {d}x.} \end{aligned}$$

(3.6)

It follows from Lemma 2.4 that

$$\begin{aligned}& \frac{1}{2}(p-1)p \bigl\vert e_{i}(t,x) \bigr\vert ^{p-2}\sum _{j=1,j\neq i}^{n} \eta _{ij} \bigl\vert e_{j}(t,x) \bigr\vert ^{2} \\& \quad \leq \frac{1}{2}(p-1) (p-2) \bigl\vert e_{i}(t,x) \bigr\vert ^{p}\sum _{j=1,j\neq i}^{n}\varrho_{j}\eta_{ij} +(p-1)\sum_{j=1,j\neq i}^{n}\frac{\eta_{ij}}{\varrho_{j}^{\frac {p-2}{2}}} \bigl\vert e_{j}(t,x) \bigr\vert ^{p}, \\& \frac{1}{2}p(p-1) \bigl\vert e_{i}(t,x) \bigr\vert ^{p-2}\sum _{j=1}^{n} \eta_{ij} \bigl\vert e_{j}\bigl(t-\tau _{ij}(t)\bigr) \bigr\vert ^{2} \\& \quad \leq\frac{1}{2}(p-1) (p-2) \bigl\vert e_{i}(t,x) \bigr\vert ^{p} \sum_{j=1}^{n} \epsilon_{j}\eta_{ij} +(p-1)\sum_{j=1}^{n}\frac{\eta_{ij}}{\epsilon_{j}^{\frac {p-2}{2}}} \bigl\vert e_{j}\bigl(t-\tau_{ij}(t)\bigr) \bigr\vert ^{p}, \\& \frac{1}{2}p(p-1) \bigl\vert e_{i}(t,x) \bigr\vert ^{p-2}\sum_{j=1}^{n} \eta_{ij} \bigl\vert e_{j}\bigl(t-\tau _{ij}^{\ast}(t) \bigr) \bigr\vert ^{2} \\& \quad \leq\frac{1}{2}(p-1) (p-2) \bigl\vert e_{i}(t,x) \bigr\vert ^{p} \sum _{j=1}^{n}\varsigma_{j}\eta_{ij} +(p-1)\sum_{j=1}^{n}\frac{\eta_{ij}}{\varsigma_{j}^{\frac {p-2}{2}}} \bigl\vert e_{j}\bigl(t-\tau_{ij}^{\ast}(t)\bigr) \bigr\vert ^{p}, \\ & \\ & \alpha_{i}^{\ast}p \bigl\vert e_{i}(t,x) \bigr\vert ^{p-1}\sum_{j=1,j\neq i}^{n} \vert a_{ij} \vert L_{j} \bigl\vert e_{j}(t,x) \bigr\vert \\& \quad \leq (p-1)\alpha_{i}^{\ast}\bigl\vert e_{i}(t,x) \bigr\vert ^{p}\sum _{j=1,j\neq i}^{n} L_{j} \vert a_{ij} \vert \xi_{j} +\alpha_{i}^{\ast}\sum_{j=1,j\neq i}^{n} \frac{L_{j} \vert a_{ij} \vert }{\xi _{j}^{p-1}} \bigl\vert e_{j}(t,x) \bigr\vert ^{p}, \\& \alpha_{i}^{\ast}p \bigl\vert e_{i}(t,x) \bigr\vert ^{p-1}\sum_{j=1}^{n} \vert b_{ij} \vert M_{j} \bigl\vert e_{j}\bigl(t- \tau _{ij}(t),x\bigr) \bigr\vert \\& \quad \leq (p-1)\alpha_{i}^{\ast}\bigl\vert e_{i}(t,x) \bigr\vert ^{p}\sum _{j=1}^{n} M_{j} \vert b_{ij} \vert \zeta_{j} +\alpha_{i}^{\ast}\sum_{j=1}^{n} \frac{M_{j} \vert b_{ij} \vert }{\zeta _{j}^{p-1}} \bigl\vert e_{j}\bigl(t-\tau_{ij}(t),x \bigr) \bigr\vert ^{p}, \\& \alpha_{i}^{\ast}p \bigl\vert e_{i}(t,x) \bigr\vert ^{p-1}\sum _{j=1}^{n} \vert d_{ij} \vert \int_{t-\tau_{ij}^{\ast}(t)}^{t} N_{j} \bigl\vert e_{j}(s,x) \bigr\vert \,\mathrm {d}s \\& \quad \leq (p-1)\alpha_{i}^{\ast}\bigl\vert e_{i}(t,x) \bigr\vert ^{p}\sum _{j=1}^{n} N_{j} \vert d_{ij} \vert \rho _{j} +\alpha_{i}^{\ast}\sum_{j=1}^{n} \frac{N_{j} \vert d_{ij} \vert }{\rho_{j}^{p-1}} \biggl[ \int_{t-\tau_{ij}^{\ast}(t)}^{t} \bigl\vert e_{j}(s,x) \bigr\vert \,\mathrm {d}s \biggr]^{p}. \end{aligned}$$

(3.7)

Substituting (3.6)-(3.7) into (3.5), we have

$$\begin{aligned} &{D^{+}\mathbf{E}\bigl\{ V(t)\bigr\} } \\ &{\quad \leq \mathbf{E}\Biggl\{ \int_{\Omega}\sum_{i=1}^{n}\Biggl\{ \Biggl[-p\lambda_{1}D_{i}-p\gamma_{i}-p k_{i}+p\alpha _{i}^{\ast} \vert a_{ii} \vert L_{i}+\alpha_{i}^{\ast}\sum _{j=1,j\neq i}^{n}\frac {L_{i} \vert a_{ji} \vert }{\xi_{i}^{p-1}}} \\ &{\qquad{} +p\bar{\alpha}_{i}\sum_{j=1}^{n} \bigl[ \vert a_{ij} \vert L_{j}^{\ast}+ \vert b_{ij} \vert M_{j}^{*}+ \vert d_{ij} \vert N_{j}^{\ast}\tau^{\ast}+ \vert J_{i} \vert \bigr]} \\ &{\qquad{} +(p-1)\alpha_{i}^{\ast}\sum_{j=1,j\neq i}^{n} L_{j} \vert a_{ij} \vert \xi _{j}+(p-1) \alpha_{i}^{\ast}\sum_{j=1}^{n} M_{j} \vert b_{ij} \vert \zeta_{j}+(p-1) \alpha _{i}^{\ast}\sum_{j=1}^{n} N_{j} \vert d_{ij} \vert \rho_{j}} \\ &{\qquad{} +(p-1)\sum_{j=1,j\neq i}^{n}\frac{\eta_{ji}}{\varrho_{i}^{\frac {p-2}{2}}}+\frac{1}{2}p(p-1)\eta_{ii}+\frac{1}{2}(p-1) (p-2)\sum _{j=1,j\neq i}^{n}\varrho_{j} \eta_{ij}} \\ &{\qquad{} +\frac{1}{2}(p-1) (p-2)\sum_{j=1}^{n} \epsilon_{j}\eta_{ij}+\frac {1}{2}(p-1) (p-2) \sum _{j=1}^{n}\varsigma_{j} \eta_{ij} \Biggr] \bigl\vert e_{i}(t,x) \bigr\vert ^{p}} \\ &{\qquad{} +\sum_{j=1}^{n} \biggl[\alpha_{i}^{\ast}\frac{M_{j} \vert b_{ij} \vert }{\zeta_{j}^{p-1}} +(p-1) \frac{\eta_{ij}}{\epsilon_{j}^{\frac{p-2}{2}}} \biggr] \bigl\vert e_{j}\bigl(t- \tau_{ij}(t),x\bigr) \bigr\vert ^{p}} \\ &{\qquad{} +(p-1)\sum_{j=1}^{n}\frac{\eta_{ij}}{\varsigma_{j}^{\frac {p-2}{2}}} \bigl\vert e_{j}\bigl(t-\tau_{ij}^{\ast}(t)\bigr) \bigr\vert ^{p}+\alpha_{i}^{\ast}\sum _{j=1}^{n}\frac{N_{j} \vert d_{ij} \vert }{\rho_{j}^{p-1}} \biggl[ \int_{t-\tau _{ij}^{\ast}(t)}^{t} \bigl\vert e_{j}(s,x) \bigr\vert \,\mathrm {d}s \biggr]^{p}\Biggr\} \,\mathrm {d}x\Biggr\} } \\ &{\quad =\mathbf{E}\Biggl\{ \int_{\Omega}\sum_{i=1}^{n} \Biggl\{ -\kappa _{i} \bigl\vert e_{i}(t,x) \bigr\vert ^{p}+\sum_{j=1}^{n} \biggl[ \alpha_{i}^{\ast}\frac {M_{j} \vert b_{ij} \vert }{\zeta_{j}^{p-1}} +(p-1)\frac{\eta_{ij}}{\epsilon_{j}^{\frac{p-2}{2}}} \biggr] \bigl\vert e_{j}\bigl(t-\tau_{ij}(t),x\bigr) \bigr\vert ^{p}} \\ &{\qquad{} +(p-1)\frac{\eta_{ij}}{\varsigma_{j}^{\frac{p-2}{2}}} \bigl\vert e_{j}\bigl(t-\tau _{ij}^{\ast}(t)\bigr) \bigr\vert ^{p}+ \alpha_{i}^{\ast}\sum_{j=1}^{n} \frac{N_{j} \vert d_{ij} \vert }{\rho_{j}^{p-1}} \biggl[ \int_{t-\tau_{ij}^{\ast}(t)}^{t} \bigl\vert e_{j}(s,x) \bigr\vert \,\mathrm {d}s \biggr]^{p} \Biggr\} \,\mathrm {d}x\Biggr\} } \\ &{\quad \leq\mathbf{E}\bigl\{ -\kappa V(t)+w\overline{V}(t)\bigr\} ,} \end{aligned}$$

(3.8)

where

$$\overline{V}(t)=\sup_{s\in[t-\bar{\tau},t]}V(s) =\sup_{s\in[t-\bar{\tau},t]} \int_{\Omega}\sum_{i=1}^{n} \bigl\vert e_{i}(s,x) \bigr\vert ^{p}\,\mathrm {d}x. $$

Similarly, for $(t,x)\in[mT+\delta, (m+1)T)\times\Omega$, we derive that

$$ D^{+}\mathbf{E}\bigl\{ V(t)\bigr\} \leq \mathbf{E}\bigl\{ \sigma V(t)+w\overline{V}(t)\bigr\} . $$

(3.9)

Denote $Q(t)=H(t)-hU$, where

$$H(t)=e^{\bar{\varepsilon} t}V(t), \qquad U=\sup_{s\in[-\bar{\tau },0]}V(s),\quad h>1, t \geq0. $$

Evidently,

$$ Q(t)< 0, \quad\forall t\in[-\bar{\tau},0]. $$

(3.10)

Now, we prove that

$$ Q(t)< 0, \quad\forall t\in[0,\delta). $$

(3.11)

Otherwise, there exists $t_{0}\in[0,\delta)$ such that

$$ Q(t_{0})=0, \qquad D^{+}\mathbf{E}\bigl\{ Q(t_{0})\bigr\} \geq0,\qquad Q(t)< 0, \quad \forall t\in[-\bar{\tau}, t_{0}). $$

(3.12)

It follows from (3.8) that

$$\begin{aligned} D^{+}\mathbf{E}\bigl\{ Q(t_{0}) \bigr\} =&\bar{\varepsilon} H(t_{0})+e^{\bar {\varepsilon} t_{0}}D^{+}\mathbf{E}\bigl\{ V(t)\bigr\} | _{t_{0}} \\ \leq&\bar{\varepsilon} H(t_{0})+e^{\varepsilon t_{0}}\bigl(-\kappa V(t_{0})+w\overline{V}(t_{0})\bigr) \\ =& (\bar{\varepsilon}-\kappa) H(t_{0})+we^{\bar{\varepsilon} t_{0}} \overline{V}(t_{0}). \end{aligned}$$

(3.13)

By (3.12), we conclude that

$$ \overline{V}(t_{0})< \sup_{s\in[t_{0}-\bar{\tau},t_{0}]} hUe^{-\bar{\varepsilon} s}\leq H(t_{0})e^{-\bar{\varepsilon} (t_{0}-\bar{\tau})}. $$

(3.14)

Hence, we know from (3.13) and (3.14) that

$$ D^{+}\mathbf{E}\bigl\{ Q(t_{0})\bigr\} < \bigl(\bar{ \varepsilon}-\kappa+we^{\bar {\varepsilon}\bar{\tau}}\bigr)H(t_{0})=0, $$

(3.15)

which contradicts (3.12). Then (3.11) holds.

Next, we show that

$$ \tilde{Q}(t)=H(t)-hUe^{(t-\delta)\theta}< 0, \quad t\in[\delta, T). $$

(3.16)

Otherwise, there exists $t_{1}\in[\delta,T)$ such that

$$ \tilde{Q}(t_{1})=0, \qquad D^{+}\mathbf{E}\bigl\{ \tilde{Q}(t_{1})\bigr\} \geq0,\qquad \tilde{Q}(t)< 0, \quad\forall t\in[ \delta,t_{1}). $$

(3.17)

By (3.17), we have

$$ V(t_{1})=e^{-\bar{\varepsilon}t_{1}}hUe^{(t_{1}-\delta)\theta},\qquad V(t)< hUe^{(t-\delta)\theta}e^{-\bar{\varepsilon}t}, \quad\forall t\in[\delta,t_{1}). $$

(3.18)

For $\bar{\tau}>0$, if $(t_{1}-\bar{\tau})\in[\delta, t_{1})$, we derive from (3.18) that

$$\overline{V}(t_{1})< \sup_{s\in[t_{1}-\bar{\tau },t_{1}]}hUe^{(s-\delta)\theta}e^{-\bar{\varepsilon}s} < e^{-\bar{\varepsilon}(t_{1}-\bar{\tau})}hUe^{(t_{1}-\delta)\theta} =e^{\bar{\varepsilon}\bar{\tau}}V(t_{1}). $$

If $t_{1}-\bar{\tau}\in[-\bar{\tau},\delta)$, by (3.11) and (3.18), we see that

$$\begin{aligned} \overline{V}(t_{1}) =&\max\Bigl\{ \sup _{s\in[t_{1}-\bar{\tau },\delta)}V(s),\sup_{s\in[\delta,t_{1}]}V(s)\Bigr\} \\ < &\max\Bigl\{ \sup_{s\in[t_{1}-\bar{\tau},\delta )}hUe^{-\bar{\varepsilon} s},\sup _{s\in[\delta ,t_{1}]}hUe^{(s-\delta)\theta}e^{-\bar{\varepsilon}s}\Bigr\} \\ \leq&\max\bigl\{ V(t_{1})e^{\bar{\varepsilon}\bar{\tau }}e^{-(t_{1}-\delta)\theta}, V(t_{1})e^{\bar{\varepsilon}(t_{1}-\delta)}\bigr\} \\ < &\max\bigl\{ V(t_{1})e^{\bar{\varepsilon}\bar{\tau}}, V(t_{1})e^{\bar{\varepsilon}(t_{1}-\delta)} \bigr\} \\ =&e^{\bar{\varepsilon}\bar{\tau}}V(t_{1}). \end{aligned}$$

Therefore, for any $\bar{\tau}>0$,

$$ \overline{V}(t_{1})< e^{\bar{\varepsilon}\bar{\tau}}V(t_{1}). $$

(3.19)

Then, we conclude from (3.9), (3.18) and (3.19) that

$$\begin{aligned} D^{+}\mathbf{E}\bigl\{ \tilde{Q}(t_{1})\bigr\} \leq&\mathbf{E}\bigl\{ \bar {\varepsilon}H(t_{1}) +e^{\bar{\varepsilon}t_{1}} \bigl(\sigma V(t_{1})+w\overline{V}(t_{1})\bigr)-\theta hUe^{(t_{1}-\delta)\theta}\bigr\} \\ < &\mathbf{E}\bigl\{ \bar{\varepsilon}H(t_{1}) +e^{\bar{\varepsilon}t_{1}}\sigma V(t_{1})+e^{\bar{\varepsilon }t_{1}}we^{\bar{\varepsilon}\bar{\tau}}V(t_{1})-\theta hUe^{(t_{1}-\delta )\theta}\bigr\} \\ =&\mathbf{E}\bigl\{ \bigl(\bar{\varepsilon}+\sigma+we^{\bar{\varepsilon }\bar{\tau}}-\theta \bigr)H(t_{1})\bigr\} \\ =&\mathbf{E}\bigl\{ \bigl(\bar{\varepsilon}-\kappa+we^{\bar{\varepsilon }\bar{\tau}} \bigr)H(t_{1})\bigr\} =0, \end{aligned}$$

which contradicts (3.17). Then equality (3.16) holds. That is, for $t\in[\delta, T)$,

$$H(t)< hUe^{(t-\delta)\theta}< hUe^{(T-\delta)\theta}. $$

On the other hand, it follows from (3.10) and (3.11) that for $t\in [-\bar{\tau}, \delta)$,

$$H(t)< hU< hUe^{(T-\delta)\theta}. $$

Therefore, for all $t\in[-\bar{\tau}, T)$,

$$H(t)< hUe^{(T-\delta)\theta}. $$

Similar to the proof of (3.11) and (3.16), respectively, we can show that

$$\begin{aligned} &{H(t) < hUe^{(T-\delta)\theta}, \quad t\in[T, T+\delta),} \\ &{H(t) < hUe^{(T-\delta)\theta}e^{(t-(T+\delta))\theta }=hUe^{(t-2\delta)\theta},\quad t\in[T+\delta, 2T)} \end{aligned}$$

Using the mathematical induction method, the following inequalities can be proved to be true for any nonnegative integer l.

$$\begin{aligned} &{ H(t)\leq hUe^{l(T-\delta)\theta},\quad t\in [lT,lT+\delta).} \end{aligned}$$

(3.20)

$$\begin{aligned} &{ H(t)\leq hUe^{(t-(l+1)\delta)\theta},\quad t\in \bigl[lT+\delta,(l+1)T\bigr).} \end{aligned}$$

(3.21)

If $t\in[lT, lT+\delta)$, then $l\leq t/T$, we derive from (3.20) that

$$H(t)< hUe^{(T-\delta)\theta t/T}. $$

If $t\in[lT+\delta,(l+1)T)$, then $l+1> t/T$, we conclude from (3.21) that

$$H(t)< hUe^{(t-t\delta/T)\theta}=hUe^{(T-\delta)\theta t/T}. $$

Hence, for any $t\in[0,+\infty)$,

$$ H(t)< hUe^{(T-\delta)\theta t/T}. $$

(3.22)

Note that

$$ \begin{aligned} & U =\sup_{s\in[-\bar{\tau},0]}V(s)= \int_{\Omega}\sum_{i=1}^{n} \sup_{-\bar{\tau}\leq s< 0} \bigl\vert e_{i}(t,x) \bigr\vert ^{p}\,\mathrm {d}x= \|\psi-\phi\|_{p}^{p}, \\ & V(t) = \int_{\Omega}\sum_{i=1}^{n} \bigl\vert e_{i}(t,x) \bigr\vert ^{p}\,\mathrm {d}x= \bigl\| v(t,x)-u(t,x)\bigr\| _{p}^{p}. \end{aligned} $$

(3.23)

From (3.22) and (3.23), we have

$$\bigl\| v(t,x)-u(t,x)\bigr\| _{p} < h^{\frac{1}{p}}\|\psi-\phi \|_{p}^{p}e^{-\mu t}, $$

where

$$\mu=\frac{1}{p} \biggl[\bar{\varepsilon}-\frac{(T-\delta)\theta }{T} \biggr]>0. $$

Hence, the response system (1.9) and the drive system (1.6) are exponential synchronization under the periodically intermittent controller (1.12) based on p-norm. This completes the proof of Theorem 3.1. □

Remark 2

In this paper, by introducing the important inequality (2.3) in Lemma 2.3 and using Lyapunov functional theory, the exponential synchronization criteria relying on diffusion coefficients and diffusion space are derived for the proposed Cohen-Grossberg neural networks with Neumann boundary conditions under the periodically intermittent control. References [23–26] also researched the synchronization of reaction-diffusion neural networks with Neumann boundary conditions. The corresponding synchronization criteria obtained in these papers are all irrelevant to the diffusion coefficients and diffusion space. The influence of the reaction-diffusion terms on the synchronization of neural networks cannot be found. Hence, our results have wider application prospects.

Remark 3

In [13, 14] and [18], the authors have obtained the exponential synchronization criteria for neural networks by assuming that $\dot{\tau}_{ij}(t)\leq\varrho<1$ and $\dot{\tau}^{\ast}_{ij}(t)\leq\varrho^{\ast}<1$ for all t. These restrictions are removed in this paper. Therefore, the synchronization criteria obtained in this paper are less conservative.

4 Numerical simulations

In this section, some examples are given to demonstrate the feasibility of the proposed synchronization criteria in Theorem 3.1.

System (1.6) with $n=2$, $k=1$ takes the form

$$\begin{aligned} \frac{\partial u_{i}(t,x)}{\partial t} =&D_{i} \frac{\partial^{2} u_{i}(t,x)}{\partial x^{2}}-\alpha _{i}\bigl(u_{i}(t,x)\bigr) \Biggl[ \beta_{i}\bigl(u_{i}(t,x)\bigr) -\sum _{j=1}^{2}a_{ij}f_{j} \bigl(u_{j}(t,x)\bigr) \\ &{} -\sum_{j=1}^{2}b_{ij}g_{j}(u_{j} \bigl(t-\tau(t),x\bigr) -\sum_{j=1}^{2}d_{ij} \int^{t}_{t-\tau^{\ast}(t)}h_{j}\bigl(u_{j}(s,x) \bigr)\,\mathrm {d}s \Biggr], \end{aligned}$$

(4.1)

where $\alpha_{1}(u_{1}(t,x))=0.7+\frac{0.2}{1+u_{1}^{2}(t,x)}$, $\alpha_{2}(u_{2}(t,x))=1+\frac{0.1}{1+u_{2}^{2}(t,x)}$, $\beta_{1}(u_{1}(t,x))=1.4u_{1}(t,x)$, $\beta_{2}(u_{2}(t,x))=1.6u_{2}(t,x)$, $f_{j}(u_{j}(t,x))=g_{j}(u_{j}(t,x))=h_{j}(u_{j}(t,x))=\mathrm{tanh}(u_{j}(t,x))$, $\tau(t)=0.55\pi+0.1\pi\cos t$, $\tau^{\ast}(t)=0.102+0.01\sin (t-0.1)$. The parameters of (4.1) are assumed to be $D_{1}=0.1$, $D_{2}=0.1$, $a_{11}=1.5$, $a_{12}=-0.25$, $a_{21}=3.2$, $a_{22}=1.9$, $b_{11}=-1.8$, $b_{12}=-1.3$, $b_{21}=-0.2$, $b_{22}=2.5$, $d_{11}=0.9$, $d_{12}=-0.15$, $d_{21}=0.2$, $d_{22}=-0.2$, $x\in\Omega=[-5,5]$. The initial conditions of system (4.1) are chosen as

$$ u_{1}(s,x)=0.1\cos \biggl(\frac{x+5}{10}\pi \biggr), \qquad u_{2}(s,x)=0.2\cos \biggl(\frac{x+5}{10}\pi \biggr), $$

(4.2)

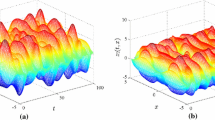
where $(s,x)\in[-0.65\pi,0]\times\Omega$. Numerical simulation illustrates that system (4.1) with boundary condition (1.7) and initial condition (4.2) shows chaotic phenomenon (see Figure 1).

Figure 1

Chaotic behaviors of Cohen-Grossberg neural networks ( 4.1 ).

The response system takes the form

$$\begin{aligned} \mathrm {d}v_{i}(t,x) =&\Biggl\{ D_{i}\frac{\partial^{2} v_{i}(t,x)}{\partial x^{2}}-\alpha_{i}\bigl(v_{i}(t,x) \bigr) \Biggl[\beta_{i}\bigl(v_{i}(t,x)\bigr) -\sum _{j=1}^{2}a_{ij}f_{j} \bigl(v_{j}(t,x)\bigr) \\ &{} -\sum_{j=1}^{2}b_{ij}g_{j}\bigl(v_{j} \bigl(t-\tau(t),x\bigr)\bigr) -\sum_{j=1}^{2}d_{ij} \int^{t}_{t-\tau^{*}(t)}h_{j}\bigl(v_{j}(s,x) \bigr)\,\mathrm {d}s \Biggr] +K_{i}(t,x)\Biggr\} \,\mathrm {d}t \\ &{} +\sum_{j=1}^{2}\sigma_{ij} \bigl(e_{j}(t,x),e_{j}\bigl(t-\tau(t),x\bigr),e_{j} \bigl(t-\tau ^{\ast}(t),x\bigr)\bigr)\,\mathrm {d}\omega_{j}(t), \end{aligned}$$

(4.3)

where

$$\begin{aligned} &{\sigma_{11}=0.1e_{1}(t,x)+0.2e_{1} \bigl(t-\tau(t),x\bigr)+0.1e_{1}\bigl(t-\tau^{\ast}(t),x\bigr), \qquad\sigma_{12}=0,} \\ &{\sigma_{21}=0,\qquad\sigma_{22}=0.1e_{2}(t,x)+0.1e_{2} \bigl(t-\tau (t),x\bigr)+0.1e_{2}\bigl(t-\tau^{\ast}(t),x\bigr).} \end{aligned}$$

The initial conditions for response system (4.3) are chosen as

$$v_{1}(s,x)=0.5\cos \biggl(\frac{x+5}{10}\pi \biggr),\qquad v_{2}(s,x)=0.6\cos \biggl(\frac{x+5}{10}\pi \biggr), $$

where $(s,x)\in[-0.65\pi,0]\times\Omega$.

It is easy to know that $L_{i}^{*}=M_{i}^{\ast}=N_{i}^{\ast}=L_{i}=M_{i}=N_{i}=1$, $i=1,2$, $\bar{\alpha}_{1}=0.2$, $\bar{\alpha}_{2}=0.1$, $\alpha_{1}^{\ast}=0.9$, $\alpha_{2}^{\ast}=1.1$, $\gamma_{1}=0.84$, $\gamma_{2}=1.52$, $\eta_{11}=0.12$, $\eta_{12}=0$, $\eta_{21}=0$, $\eta_{22}=0.03$, $\tau=0.65\pi$, $\tau^{\ast}=0.112$, $\lambda_{1}=0.0987$. Therefore, assumptions (H1)-(H4) hold for systems (4.1) and (4.3).

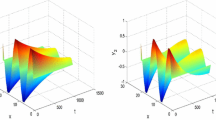
Let $p=2$, $\xi_{i}=\zeta_{i}=\rho_{i}=\varrho_{i}=\epsilon _{i}=\varsigma_{i}=1$ for $i=1,2$, $l=1,2$, and choose the control parameters $k_{1}=10$, $k_{2}=10$, $\delta=9.8$, $T=10$, then $\kappa=10.0527$, $w=3.2258$, $\theta=20.0000$. Therefore, $\bar{\varepsilon}= 0.5301$. Obviously, systems (4.1) and (4.3) satisfy assumptions (H5)-(H6). Hence, by Theorem 3.1, systems (4.1) and (4.3) are exponentially synchronized as shown in Figure 2 by numerical simulation.

Figure 2

Asymptotic behaviors of the synchronization errors.

Remark 4

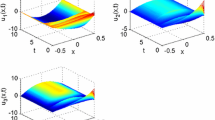
Clearly, if the control width δ increases, assumptions (H1)-(H6) can be satisfied easily. Hence, the exponential synchronization of Cohen-Grossberg neural networks with the larger control width is more easily realized. Dynamic behaviors of the synchronization errors between systems (4.1) and (4.3) with differential control width are shown in Figure 3.

Figure 3

Asymptotic behaviors of the synchronization errors with differential control width.

Remark 5

It follows from (H5) that the larger stochastic perturbation is, the more difficult (H5) can be satisfied. Hence, the exponential synchronization of Cohen-Grossberg neural networks with the smaller stochastic perturbation is more easily achieved. Dynamic behaviors of the synchronization errors between systems (4.1) and (4.3) with differential stochastic perturbation are shown in Figure 4.

Figure 4

Asymptotic behaviors of the synchronization errors with differential stochastic perturbation.

Remark 6

For the given control strength $k_{i}=k(i\in\ell)$, as long as $D_{i}$ is large enough or $\vert x_{k} \vert$ is small enough, assumptions (H5) and (H6) can always be satisfied. Hence, it is beneficial for reaction-diffusion Cohen-Grossberg neural networks to realize the synchronization by increasing diffusion coefficients or reducing diffusion space. Dynamic behaviors of the errors between systems (4.1) and (4.3) with differential diffusion coefficients and differential diffusion space are shown in Figures 5 and 6.

Figure 5

Asymptotic behaviors of the synchronization errors with differential diffusion coefficients.

Figure 6

Asymptotic behaviors of the synchronization errors with differential diffusion space.

Remark 7

In many cases, two-neuron networks show the same behavior as large size networks, and many research methods used in two-neuron networks can be applied to large size networks. Therefore, a two-neuron networks can be used as an example to improve our understanding of our theoretical results. In addition, the parameter values are selected randomly to ensure that neural networks (4.1) exhibit a chaotic behavior.

5 Conclusion

In this paper, a periodically intermittent controller was designed to achieve the exponential synchronization for stochastic reaction-diffusion Cohen-Grossberg neural networks with Neumann boundary conditions and mixed time-varying delays based on p-norm. By constructing the Lyapunov functional, the exponential synchronization criteria dependent on diffusion coefficients, diffusion space, stochastic perturbation and control width were obtained. Theory analysis revealed that stochastic reaction-diffusion Cohen-Grossberg neural networks can achieve exponential synchronization more easily by increasing diffusion coefficients and control width or reducing diffusion space and stochastic perturbation. Compared with the previous works [13, 14, 18, 23–26], the obtained synchronization criteria are less conservative and have wider application prospects.

Note that the important inequality (2.3) in Lemma 2.3 holds under the assumption that $p\geq2$. Hence, it is our future work to study the exponential synchronization of stochastic reaction-diffusion Cohen-Grossberg neural networks with Neumann boundary conditions for $p=1$ or $p=\infty$.