Microwave electrometry with bichromatic electromagnetically induced transparency in Rydberg atoms

Abstract

A scheme for measuring microwave (MW) electric (E) fields is proposed based on bichromatic electromagnetically induced transparency (EIT) in Rydberg atoms. A bichromatic control field drives the excited state transition, whose absorption shows three EIT windows. When a MW field drives the Rydberg transition, the EIT windows split and six transmission peaks appear. It is interesting to find that the peak-to-peak distance of transmission spectrum is sensitive to the MW field strength, which can be used to measure MW E-field. Simulation results show that the spectral resolution could be increased by about 4 times, and the minimum detectable strength of the MW E-field may be improved by about 3 times compared with the common EIT scheme. After the Doppler averaging, the minimum detectable MW E-field strength is about 5 times larger than that without Doppler effect. Also, we investigate other effects on the sensitivity of the system.

1 Introduction

Microwave (MW) electric (E) field measurement has great technological importance in electronic information systems, which have been widely used in radar [1, 2], communications [3–5], navigation [6, 7], remote sensing [8], etc. Traditional MW measurement is based on dipole antennas, which is limited to receiving sensitivity, self-calibration, antenna size and so on [9]. Rydberg atoms have large electric dipole moments, which are extremely sensitive to external electric field [10]. Rydberg atom-based MW metrology has been explored with quantum technology [11–13], e.g., electromagnetically induced transparency (EIT) [14–17], Autler-Townes (AT) splitting [18, 19], electromagnetically induced absorption (EIA) [20, 21], and active Raman gain (ARG) [22, 23]. At present, many promising schemes have been proposed for measuring MW fields, using frequency detuning [24], homodyne detection [25], intracavity atomic systems [26], double dark states [27, 28], dispersion [29], nonlinear effects [30] and deep learning [31], etc.

Bichromatic EIT can improve the fluorescence, absorption and transmission spectra of atoms [32–34]. Wang et al. first experimentally demonstrated bichromatic EIT in cold atoms and observed multiple absorption peaks [35]. Later, Yan et al. experimentally observed double symmetrical EIT windows instead of multiple absorption peaks in hot atomic vapors [36]. In recent years, four-wave mixing (FWM) signals in such systems has attracted great interest [37–39]. For example, multi-channel FWM process [40], phase compensation induced by anomalous dispersion [41], and high-efficiency reflection [42]. Also, bichromatic field has other important applications, such as optical nonreciprocity [43], optical bistability [44], optomechanical bichromatic wavelength switching [45], multimode circuit electromechanical systems [46], cross-phase modulation [47], and attosecond polarization [48]. While, few research involves the application of bichromatic EIT in MW E-field measurement.

Here, we present a scheme for MW E-field measurement by using bichromatic EIT in Rydberg atoms. First, a Doppler-free configuration is considered, where the probe field counter-propagates with the bichromatic control field. When the bichromatic control field drives the excited state transition, the EIT spectrum shows three transmission peaks. With coupling of a MW field, the transmission peaks split into six. The frequency splitting of the transmission peaks is linearly related to the MW field strength. This can be used to measure MW E-field. The numerical results show that the linewidth of the central transmission peaks may be narrowed to 1/4 of the common EIT scheme, and the minimum detectable strength of the MW E-field could be improved by about 3 times. Fortunately, if the probe and bichromatic control fields co-propagate through the atomic vapor, the Doppler effect greatly narrows the central transmission peaks, and the minimum detectable MW E-field strength is about 5 times larger than that without Doppler effect. The scheme may be useful for designing novel MW sensing devices.

2 Model and basic equations

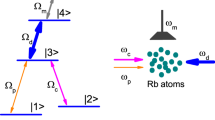
The four-level Rydberg atomic system we considered is shown in Fig. 1(a). A bichromatic control field $E_{c}(t) = (E_{c1}e^{- i\omega_{ c1}t} + E_{c2}e^{- i\omega_{c2}t})/2 + c.c{.}$ drives the transition $|2\rangle \rightarrow |3\rangle$ with frequency difference $\omega _{c2} - \omega _{c1} = \delta$. A weak probe field $E_{p}(t) = E_{p} e^{- i\omega_{p} t} /2 + c.c{.}$ drives the transition $|1\rangle \rightarrow |2\rangle$, and a MW field $E_{m}(t) = E_{m} e^{- i\omega_{m} t}/2 + c.c{.}$ drives the Rydberg transition $|3\rangle \rightarrow|4\rangle$. The relevant quantum states $|1\rangle$, $|2\rangle$, $|3\rangle$ and $|4\rangle$ correspond to the rubidium-87 atomic levels $5S_{1/2}(F = 2)$, $5P_{3/2}(F = 3)$, $53D_{5/2}$, and $54P_{5/2}$, respectively. Figure 1(c) shows the schematic configuration of the coupling fields and the atomic vapor cell. The probe and bichromatic control fields counter-propagate through the atomic vapour, which belongs to a Doppler-free scheme.

Figure 1

(a) Four-level Rydberg atomic model, (b) the corresponding dressed picture and (c) schematic diagram of the experiment

After the electric dipole approximation, the Hamiltonian of the system in the interaction picture is given by [49]

$$\begin{aligned} H =& \hbar \omega _{1} \vert 1 \rangle \bigl\langle 1 \vert + \hbar \omega _{2} \vert 2 \bigr\rangle \bigl\langle 2 \vert + \hbar \omega _{3} \vert 3 \bigr\rangle \bigl\langle 3 \vert + \hbar \omega _{4} \vert 4 \bigr\rangle \bigl\langle 4 \vert \\ &{}- \hbar \bigl[ \Omega _{p}e^{ - i\omega _{p}t} \vert 2 \bigr\rangle \bigl\langle 1 \vert + \bigl( \Omega _{c1}e^{ - i\omega _{c1}t} + \Omega _{c2}e^{ - i\omega _{c2}t} \bigr) \vert 3 \bigr\rangle \bigl\langle 2 \vert \\ &{} + \Omega _{m}e^{ - i\omega _{m}t} \bigl\vert 4 \bigr\rangle \langle 3 \bigr\vert + H.C. \bigr], \end{aligned}$$

(1)

where the Rabi frequencies of the probe, control, and MW fields are, respectively, denoted as $\Omega _{p} = E_{p} \mu _{12} /\hslash$, $\Omega _{c1(c2)} = E_{c1 (c2)} \mu _{23} /\hslash$ and $\Omega _{m} = E_{m} \mu _{34} /\hslash$. $\mu _{i j}$ and $\omega_{i j}$ are the relevant dipole moment and transition frequency from $|i\rangle$ to $|j\rangle$ ($i, j \in \{1, 2, 3, 4\}$). $E_{p}$, $E_{c1(c2)}$, and $E_{m}$ are the respective amplitudes of the laser fields. The dynamic evolution of the system can be described by solving the master equation [50]

$$ \frac{\partial \rho}{\partial t} = - \frac{i}{\hbar} [ H,\rho ] + L ( \rho ), $$

(2)

where ρ is the density operator and $L(\rho )$ denotes the decoherence processes. And then we obtain the time evolution of density matrix elements as follows:

$$\begin{aligned}& \begin{aligned} & \dot{\rho}_{21} = - \gamma _{21}\rho _{21} - i \bigl[ \omega _{21}\rho _{21} - \Omega _{p}e^{ - i\omega _{p}t} ( \rho _{22} - \rho _{11} ) + \bigl( - \Omega _{c1}e^{ - i\omega _{c1}t} - \Omega _{c2}e^{ - i\omega _{c2}t} \bigr)\rho _{31} \bigr], \\ &\dot{\rho}_{31} = - \gamma _{31}\rho _{31} - i \bigl[ ( \omega _{21} + \omega _{32} )\rho _{31} + \Omega _{m}e^{ - i\omega _{m}t}\rho _{41} + \Omega _{p}e^{ - i\omega _{p}t}\rho _{32} \\ &\hphantom{\dot{\rho}_{31} =}{} + \bigl( - \Omega _{c1}e^{ - i\omega _{c1}t} - \Omega _{c2}e^{ - i\omega _{c2}t} \bigr)\rho _{21} \bigr], \\ &\dot{\rho}_{41} = - \gamma _{41}\rho _{41} - i \bigl[ ( \omega _{21} + \omega _{32} - \omega _{43} )\rho _{41} + \Omega _{m}e^{ - i\omega _{m}t}\rho _{31} + \Omega _{p}e^{ - i\omega _{p}t}\rho _{42} \bigr], \end{aligned} \end{aligned}$$

(3)

with the closure relationship $\rho _{11} + \rho _{22} + \rho _{33} + \rho _{44} = 1$. $\gamma_{j k} = (\Gamma _{j} + \Gamma _{k})/2$, $\Gamma _{j} = \sum_{k} \Gamma _{j k}$ ($j, k = 1, 2, 3, 4$), where $\Gamma _{j k}$ is the spontaneous decay rate from state $|j\rangle$ to state $|k\rangle$. We perform a rotating-frame transformation using $\rho _{21} = \tilde{\rho}_{21}e^{ - i\omega _{p}t}$, $\rho _{31} = \tilde{\rho}_{31}e^{ - i ( \omega _{p} + \omega _{c1} )t}$ and $\rho _{41} = \tilde{\rho}_{41}e^{ - i ( \omega _{p} + \omega _{c1} - \omega _{m} )t}$. The density-matrix element $\tilde{\rho}_{ij}$ can be expanded in terms of Fourier components as

$$ \tilde{\rho}_{ij} = \sum \tilde{\rho}_{ij}^{ ( n )}e^{ - in\delta t} \quad \bigl( i,j \in \{ 1,2,3,4 \},n = 0, \pm 1, \ldots \bigr). $$

(4)

We keep the first order of the probe and all orders of the control and MW fields, and get

$$ \begin{aligned} &\tilde{\rho}_{21}^{ ( n )} = \frac{i ( \tilde{\rho}_{31}^{ ( n )}\Omega _{c1} + \tilde{\rho}_{31}^{ ( n - 1 )}\Omega _{c2} + \Omega _{p} )}{\gamma _{21} + i\Delta _{p} - in\delta}, \\ &\tilde{\rho}_{31}^{ ( n )} = \frac{ - i\tilde{\rho}_{21}^{ ( n )}\Omega _{c1} - i\tilde{\rho}_{21}^{ ( n + 1 )}\Omega _{c2}}{ - \gamma _{31} + in\delta - i ( \Delta _{p} + \Delta _{c1} ) - \frac{i\Omega _{m}^{2}}{i\gamma _{41} + n\delta + \Delta _{m} - \Delta _{p} - \Delta _{c1}}}, \\ &\tilde{\rho}_{41}^{ ( n )} = \frac{\tilde{\rho}_{31}^{ ( n )}\Omega _{m}}{i\gamma _{41} + n\delta + \Delta _{m} - \Delta _{p} - \Delta _{c1}}, \end{aligned} $$

(5)

where $\Delta _{p} = \omega _{p} - \omega _{21}$, $\Delta _{c1} = \omega _{c1}- \omega _{32}$ and $\Delta _{m} = \omega _{m} - \omega _{43}$ are the detunings of the probe, control and MW fields, respectively. The solution of $\tilde{\rho}_{21}^{ ( n )}$ is obtained from the recursion relation as

$$ \tilde{\rho}_{21}^{ ( n )} = D_{n}^{ - 1} \biggl[ - i\Omega _{p} + \frac{\tilde{\rho}_{21}^{ ( n - 1 )}\Omega _{c1}^{ *} \Omega _{c2}}{X_{n - 1}} + \frac{\tilde{\rho}_{21}^{ ( n + 1 )}\Omega _{c1}\Omega _{c2}^{ *}}{X_{n}} \biggr], $$

(6)

where $X_{n} = - \gamma _{31} + in\delta - i ( \Delta _{p} + \Delta _{c1} ) + i \Omega _{m}^{2}/ ( i \gamma _{41} + n\delta + \Delta _{m} - \Delta _{p} - \Delta _{c1} )$ and $D_{n} = - \gamma _{21} - i ( \Delta _{p} - n\delta ) - \Omega _{c1}^{2}/X_{n} - \Omega _{c2}^{2}/X_{n - 1}$. We can obtain the coherent term $\tilde{\rho}_{21}^{ ( 0 )}$ with a continued fraction method [42]

$$ \tilde{\rho}_{21}^{ ( 0 )} = \frac{ - i\Omega _{p}}{D_{0} - \frac{\Omega _{c1}\Omega _{c2}^{ *} W_{1}}{ - \gamma _{31} - i ( \Delta _{p} + \Delta _{c1} ) - \frac{i\Omega _{m}^{2}}{i\gamma _{41} + \Delta _{m} - \Delta _{p} - \Delta _{c1}}} - \frac{\Omega _{c1}^{ *} \Omega _{c2}V_{1}}{ - \gamma _{31} - i ( \Delta _{p} + \Delta _{c2} ) - \frac{i\Omega _{m}^{2}}{i\gamma _{41} + \Delta _{m} - \Delta _{p} - \Delta _{c2}}}}, $$

(7)

where $\Delta _{c2} =\Delta _{c1}- \delta$, $W_{1} = \tilde{\rho}_{21}^{ ( 1 )}/\tilde{\rho}_{21}^{ ( 0 )}$ and $V_{1} = \tilde{\rho}_{21}^{ ( 1 )}/\tilde{\rho}_{21}^{ ( 2 )}$. The susceptibility χ is found to be $\chi = N\mu _{21}^{2}\tilde{\rho}_{21}^{ ( 0 )}/\hbar \varepsilon _{0}\Omega _{p}$, where $\varepsilon _{0}$ is the permittivity of vacuum, N is the atomic density, and ħ is the reduced Planck’s constant. The transmission spectrum can be described as [51]

$$ T = \exp \bigl( - 2\pi \ell \operatorname{Im} [ \chi ] / \lambda _{p} \bigr), $$

(8)

where ℓ is the medium length and $\lambda _{p}$ is the center wavelength of probe field.

3 Results and discussion

We consider the ⁸⁷Rb atoms within a vapor cell of length 5.0 cm. The probe field, ∼780 nm, is tuned to the $|1\rangle \rightarrow |2\rangle$ transition. The control field, ∼480 nm, drives $|2\rangle \rightarrow |3\rangle$ transition. The Rydberg transition $|3\rangle \rightarrow |4\rangle$ is driven by the MW field. In the following discussion, the parameters are scaled by $\Gamma = 2\pi \times 6$ MHz for simplicity. First, let us briefly discuss the absorption spectra of common EIT scheme. If the MW field $\Omega _{m} = 0$, there is an EIT window (see red dotted line in Fig. 2(a)). With coupling of the MW field, an absorption peak appears in the EIT window, i.e., bright resonance [11] (see red dotted line in Fig. 2(b)). Here, we are interested in the absorptive features of bichromatic EIT spectra, as shown by the solid blue line in Fig. 2. Without coupling of the MW field, there are four absorption peaks in EIT spectrum (see Fig. 2(a)). When the MW field drives the Rydberg transition, the two side absorption peaks and the central EIT window split, resulting in seven absorption peaks (see Fig. 2(b)).

Figure 2

Comparison of absorption spectra driven by bichromatic control field (blue) and single control field (red). (a) $\Omega _{m} = 0$ and (b) $\Omega _{m} = 0.5\Gamma$. Other parameters are $\Omega _{c1} = \Omega _{c2} = 1\Gamma$, $\Delta _{c1} =\Delta _{m} = 0$, $\delta = 6\Gamma$, $\gamma _{21} =\Gamma = 2\pi \times 6$ MHz, $\gamma _{31} = 2\pi \times 1$ kHz and $\gamma _{41} = 2\pi \times 0.5$ kHz

The results can be interpreted in the dressed-state picture, as shown in Fig. 1(b). It is known that the central EIT window originates from inter-path interference of the transitions $|1\rangle \rightarrow |\pm 1\rangle$. The dressed-states created by the bichromatic control field consist of infinite ladders with an equal separation δ [52]. In particular, when $\Omega _{c1}$, $\Omega _{c2} < \delta$, the transition amplitude will be dominant only for a few dressed-states around $|m = 0\rangle$ [35]. The probe transitions from $|1\rangle$ to the dressed-states $|m = \pm 1, \pm 2\rangle$ lead to four absorption peaks. When the Rydberg transition $|3\rangle \rightarrow |4\rangle$ is driven by the MW field $\Omega _{m}$, five new eigenstates appear, i.e., $|0\rangle$, $|\pm a\rangle$ and $|\pm b\rangle$. So, there are seven transition channels with the coupling of the probe field, $|1\rangle \rightarrow |m = 0,\pm 1,\pm a,\pm b\rangle$, which contribute to seven absorption peaks.

Next, we focus on the bichromatic EIT transmission with the MW fields. If $\Omega _{m} = 0$, there are three transmission peaks around $\Delta _{\mathrm{p}} = 0$, $\pm 6\Gamma$ (see blue solid line in Fig. 3(a)). It is consistent with the result of Ref. [35] under the given conditions, e.g., $\Omega _{c1} = \Omega _{c2} = 0.5\Gamma$ and $\Delta _{c1} = \Delta _{c2} = \delta /2 = \Gamma$. When the MW field is applied, e.g., $\Omega _{m} = 0.5\Gamma$, the three transmission peaks split into six via the EIT-AT effect (see blue solid line in Fig. 3(b)). Figure 3(c) depicts the bichromatic EIT transmission spectra with a varying MW field strength $\Omega _{m}$. The frequency splitting of transmission peaks becomes larger with the increase of $\Omega _{m}$. It is interesting to find that the peak-to-peak distance Δf is proportional to the MW field strength, as shown in Fig. 3(d). Their linear relationship can be written as $\Delta f = 2\Omega _{m}$, and the magnitude of the applied MW E-field can be estimated by

$$ \vert E_{m} \vert = \frac{\hbar \Omega _{m}}{\mu _{34}} = \frac{\hbar \Delta f}{2\mu _{34}}. $$

(9)

Figure 3

(a) Transmission spectra with $\Omega _{m} = 0$ and (b) is the same as (a) except for $\Omega _{m} = 0.5\Gamma$; (c) bichromatic control field-driven transmission spectra with different MW fields; (d) peak-to-peak distance Δf versus MW field strength $\Omega _{m}$, and other parameters are the same as in Fig. 2

It is worth mentioning that the frequency splitting of the side peaks also has the good linear relationship with the MW E-field strength. Of course, the linear relationship between Δf and $\vert E_{m} \vert$ will fail and become nonlinear when $\Omega _{m} < 0.0025\Gamma$.

Moreover, the linewidth of the central transmission peak is much narrower than that of the common EIT transmission peak (see Fig. 3(b)). The linewidth narrowing can be understood from the high dispersion produced by the bichromatic EIT. Figure 4 shows the real ($\operatorname{Re}[\chi ]$) and imaginary ($\operatorname{Im}[\chi ]$) parts of the atomic susceptibility. The bichromatic EIT dispersion $\partial \operatorname{Re}[\chi ]/\partial \omega _{p}$ is larger than that of the common EIT scheme in Fig. 4(a). The larger dispersion, the larger frequency pulling effect, and then the resonance frequency is strongly pulled to its bichromatic EIT frequency. As a result, the two EIT windows are narrowed, resulting in two narrow peaks in the bichromatic EIT transmission (see red dashed line in Fig. 4).

Figure 4

Susceptibility as a function of probe field detuning $\Delta _{p}$. $\operatorname{Re}[\chi ]$ (blue solid line) and $\operatorname{Im}[\chi ]$ (red dash line) for (a) single and (b) bichromatic control fields. Other parameters are the same as in Fig. 2

The linewidth can be described as [14]

$$ \Delta _{\mathrm{width}} = \frac{\Omega _{c1}^{2} + \Omega _{p}^{2}}{\sqrt{\Gamma _{21}\gamma _{21}}} \frac{1}{\sqrt{\sigma N\ell}}\quad (\sigma N \ell \gg 1), $$

(10)

where $\sigma = 3\lambda _{p}^{2}/2\pi$ is the absorption cross section, N is the atomic denstiy, and ℓ is the medium length. The numerical results show that the full width at half maximum (FWHM) of the bichromatic EIT central transmission peaks is about 0.24Γ. While, the FWHM of the common EIT transmission peaks is about 0.9Γ. The linewidth is narrowed to about 1/4 of the common EIT scheme. The spectral resolution is intimately related to the EIT linewidth [21, 53]. This indicates that the spectral resolution could be increased by about 4 times under the given conditions. Moreover, the application of narrow EIT spectrum would compress the nonlinear zoom of frequency splitting and decrease the uncertainty of the MW E-field measurements [54]. So the inter-path interference leads to the narrow EIT spectrum, contributing to the sensitive measurement of MW E-fields.

The minimum detectable strength is important for the weak MW E-field measurement, which depends on the minimum detectable splitting of the transmission peak. In a weak MW field regime, the frequency splitting strongly depends on the EIT linewidth that is related to the Rabi frequency of control (probe) field (see equation (10)) [54]. The frequency splitting Δf decreases as $\Omega _{c1(p)}$ decreases. The minimum detectable strength of the MW E-field is given by [55]

$$ \vert E_{\min} \vert = \frac{\hbar \Delta _{\mathrm{width}}}{2\mu _{34}}, $$

(11)

where $\Delta _{\mathrm{width}} < \Delta f$. The linear relationship between Δf and $\vert E_{m} \vert$ from equation (9) is valid and can be used to determine the E-field strength when the EIT linewidth is small compared to the frequency splitting [15]. This means that the narrow EIT linewidth would enable the frequency splitting to be observed at a weak MW field [21, 26].

According to the Rayleigh criterion [56], the minimum detectable splitting means that the splitting of two peaks is about half maximum of its peak value. For the common EIT scheme, when $\Omega _{m} = 0.007\Gamma$, the transmission peaks overlap partly and are just discernible, as shown in Fig. 5(a). While, the bichromatic EIT transmission peaks are clearly separated from each other (see Fig. 5(b)). Under the given condition, the minimum detectable strength of the MW field is about $\Omega _{m} = 0.0025\Gamma$ from the simulation. It is about 1/3 of the common EIT scheme, ${\sim} 0.007\Gamma$. This indicates that the minimum detectable MW E-field strength could be enhanced about 3 times. In other words, the inter-path interference much narrow the EIT linewidth and improve the sensitivity of minimum MW E-field.

Figure 5

(a) Single control field-driven and (b) bichromatic control field-driven transmission spectra (inset is zoomed views of central peaks), and other parameters are the same as in Fig. 2

In addition, we consider the longitudinal motion of atoms at randomly distributed velocity v. It is instructive to examine the MW E-field measurement with Doppler effect, i.e., the probe and control fields $\Omega _{c1}$ (or $\Omega _{c1}$ and $\Omega _{c2}$) co-propagating through the atomic cell. Here, the susceptibility with atomic motion should be expressed as $\chi ( v ) = N\mu _{21}^{2}\int \tilde{\rho}_{21}^{ ( 0 )} ( v ) * D ( v )/\hbar \varepsilon _{0}\Omega _{p}\,dv$, where $\Delta _{p}$, $\Delta _{c1}$ and $\Delta _{c2}$ are replaced with $\Delta _{p} + k_{p} v$, $\Delta _{c1} + k_{c1}v$ and $\Delta _{c2}\pm k_{c2}v$ respectively (+ for the x-axis), $D ( v ) = \exp ( - v^{2}/v_{p}^{2} )/\pi ^{1/2}v_{p}$, represents the Maxwell–Boltzmann distribution of atoms, and $v_{p}$ is the most probable velocity. For simplicity, we assume that the wavevector $\vert k_{p} \vert \approx \vert k_{c1} \vert \approx \vert k_{c2} \vert \approx \vert k \vert$.

Figure 6 shows the Doppler-averaged transmission spectrum. When the control fields $\Omega _{c1}$ and $\Omega _{c2}$ counter-propagate through the atomic vapor, the central transmission peaks are much narrowed and the side peaks decrease sharply (see Fig. 6(a)). It is consistent with the result of Ref. [36] under the given conditions, e.g., $\Omega _{c1}=\Omega _{c2}=\Gamma$ and $\Delta _{c1}=\Delta _{c2}=\delta /2 = 0.05\Gamma$. This result originates from the shift of the dressed levels and the modification to the transition probability between dressed states when the Doppler effect is considered [57]. The sum of all contributions by atoms with different velocities results in the narrowed transmission spectrum. In this case, the minimum detectable MW field strength is about $\Omega _{m} = 0.00125\Gamma$, as illustrated in Fig. 6(c). Figure 6(b) depicts the transmission of the control field $\Omega _{c1}$ and $\Omega _{c2}$ co-propagating with the probe field. The central transmission peaks are further narrowed under the same conditions. The minimum detectable strength of the MW field is about $\Omega _{m} = 0.00045\Gamma$ from the simulation (see Fig. 6(d)). It is about 1/5 of that without Doppler averaging, ${\sim} 0.0025\Gamma$. This indicates that the minimal detectable MW E-field strength could be improved by more than 5 times after Doppler averaging.

Figure 6

Transmission of the bichromatic control field with Doppler effect for the counter-propagation (a) and co-propagation (b) cases; (c) is the same as (a) except for $\Omega _{m} = 0.00125\Gamma$ and (d) is the same as (b) except for $\Omega _{m} = 0.00045\Gamma$ (inset is zoomed views of central peaks). Other parameters are the same as in Fig. 2

At last, the effect of frequency detuning on the transmission of the probe field is investigated. Take control fields $\Omega _{c1}$ and $\Omega _{c2}$ counter-propagation for example, Fig. 7(a) shows the transmission peaks with a varying MW field detuning $\Delta _{m}$. The peak-to-peak distance Φf is enlarged with an increase in $\Delta _{m}$, which can be expressed as $\Phi f = ( \Delta _{m}^{2} + ( 2\Omega _{m} )^{2} )^{1/2}$. This result is consistent with Ref. [24], and indicates that frequency detuning could improve the sensitivity of MW E-field measurements. In Fig. 7(b), the central transmission peaks shift with the bichromatic control field detuning ($\Delta = \Delta _{c1}=\Delta _{c2}$), while both the linewidth and the peak-to-peak distance basically remain unchanged. The bichromatic EIT scheme shows some tunability and may allow the MW E-field measurement in a broad frequency range.

Figure 7

Transmission spectra of the probe field at different MW field detuning (a) and bichromatic control field detuning (b). Other parameters are the same as in Fig. 2

4 Conclusions

In summary, we propose a scheme for MW E-field measurement based on the bichromatic EIT in Rydberg atoms. Due to the inter-channel EIT interference, the EIT spectrum exhibits multiple narrow transmission peaks. It is interesting to find that the frequency splitting of transmission peaks shows a linear relationship with the MW field strength, which can be used to measure the MW E-field. The numerical results show that the spectral resolution may be enhanced by about 4 times, and the minimum detectable strength of the MW E-field is about 3 times larger than that of the common EIT scheme. If the Doppler scheme is adopted, the minimum detectable MW E-field strength could be further increased by about 5 times after Doppler averaging. The bichromatic EIT scheme exhibits high sensitivity, high resolution, and a broad detection range, which may help to design novel MW-sensing devices.