1 Introduction

The Black Holes (BHs) are the most fascinating objects in the universe those arise in Einstein’s General Relativity (GR), a classical theory of gravity proposed by Einstein about a century ago [1,2,3,4,5,6]. The Schwarzschild metric obtained in GR was the first unique solution to Einstein’s field equations in vacuum with a spherically symmetric matter distribution, which represents the simplest spacetime of a black hole (BH) having mass but no charge and spin [7, 8]. There are, however, other BH spacetimes emerging as solutions of Einstein’s field equations in GR having charge/or spin with mass such as the Reissner–Nordström BH [9, 10], the Kerr BH [11], and the Kerr–Newmann BH spacetimes [12] along with the BH spacetimes in alternative theories of gravity like string theory.

In GR, the curvature plays crucial role to understand the geometric effect of curved spacetime. The study of geodesics alongwith their deformations in the background of a given spacetime is an elegant way to describe the underlying geometry of that particular spacetime [1,2,3, 5, 6, 13, 30]. A number of studies related to the geodesic motion in the background of various BH spacetimes have been performed time and again mainly in view of their astrophysical importance [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29].

The observations from supernovae (Type Ia), cosmic microwave background radiation (CMBR), Baryon acoustic oscillations (BAO) and the Hubble measurements indicates that our universe appears to be expanding at an increasing rate. The driving force behind such an accelerating universe is believed to be some unknown form of energy with a large negative pressure which is known as dark energy. There are several candidates for dark energy, such as cosmological constant [30, 31], phantom [32,33,34,35], quintessence [36, 37], K-essence [38, 39] and quintom [40,41,42] with various models subjected to the different values of the equation of state (EOS) parameter (\(\varepsilon \)) which relates the energy density to the pressure. The quintessence scalar field model as an alternative to dark energy is one of the most popular models with the EOS parameter lying in the range \(-1<\varepsilon <-1/3\).

It would therefore be quite interesting to study the geodesics and their deformations in the background of a charged BH spacetime surrounded by quintessence to see the effect of dark energy, if any, on the universe locally. It is also important to look on the matter distribution which causes this spacetime such that the Einstein equations hold and to identify the interesting regions in the spacetime in view of the weak energy condition (WEC) and strong energy condition (SEC).

In the present paper, we study the geodesic flows and deformations alongwith energy conditions around a charged BH spacetime surrounded by quintessence by solving the evolution (i.e. Raychaudhuri) equations as an initial value problem for expansion scalar, shear and rotation (ESR variables) numerically. First, we briefly review the spacetime used in the next section. In Sect. 3, the nature of effective potential is discussed. Section 4 deals with the discussion of the kinematics of geodesic flows and visualisation of ESR. Finally, the results are summarized in Sect. 5.

2 The charged BH spacetime surrounded by quintessence

We consider a charged BH surrounded by quintessence with the EOS parameter \(\varepsilon = \frac{p_{\Phi }}{\rho _{\Phi }}\). For the static spherically symmetric quintessence surrounding a BH, the energy density of quintessence scalar field (\(\Phi \)) reduces to the following form [43]:

$$\begin{aligned} \rho _{\Phi } = - \frac{\alpha }{2}\frac{3\varepsilon }{r^{3(1+\varepsilon )}}, \end{aligned}$$
(1)

where the allowed values for \(\varepsilon \) lies between \(-1<\varepsilon <-\frac{1}{3}\) [43] and \(\alpha \) is the normalisation constant. The energy density of scalar field, \(\rho _{\Phi }\) is always a positive quantity so \(\varepsilon \) has a negative value while the normalisation factor \(\alpha \) should be a positive quantity. Based on such standpoints, the metric of a charged BH then reads

$$\begin{aligned} \mathrm{d}s^2 = f(r)\mathrm{d}t^2-\frac{1}{f(r)}\mathrm{d}r^2 -r^2(\mathrm{d}\theta ^2 + \sin ^2 \theta \mathrm{d}\phi ^2), \end{aligned}$$
(2)

where

$$\begin{aligned} f(r) = 1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{\alpha }{r^{3\varepsilon +1}}, \end{aligned}$$

here M and Q represent the mass and charge of the BH respectively. The above metric (2) represents a BH for \(M>Q\), an extremal BH for \(M=Q\) and a naked singularity for \(M<Q\) (for a complete discussion of the horizon structure for this spacetime see [44]). The metric reduces to a Reissner–Nordström black hole (RNBH) in the limit \(\alpha =0\), which further reduces to Schwarzschild black hole (SBH) in the absence of charge. In addition to this, with \(\varepsilon = -1\), it also reproduces the corresponding BH spacetimes with cosmological constant. The geodesic equations for the metric (2) are given by

$$\begin{aligned} \ddot{t} + \frac{ f'(r)}{f(r)}\, \dot{r} \, \dot{t} = 0, \end{aligned}$$
(3)
$$\begin{aligned} \ddot{r} + \left[ \frac{ f'(r) \, \dot{t}^2 + f^{-1}(r)' \,\dot{r}^2 - 2 r \, \dot{\theta }^2 -2 r \, \sin ^2 \theta \, \dot{\phi }^2}{2 \, f^{-1} (r)} \right] = 0, \end{aligned}$$
(4)
$$\begin{aligned} \ddot{\theta }+ \frac{2}{r}\, \dot{r} \, \dot{\theta }- \cos \theta \, \sin \theta \, \dot{\phi }^2 = 0, \end{aligned}$$
(5)
$$\begin{aligned} \ddot{\phi }+ \frac{2}{r} \, \dot{r} \, \dot{\phi }+ 2 \, \cot \theta \, \dot{\theta }\, \dot{\phi }=0, \end{aligned}$$
(6)

where the prime denotes the differentiation with respect to r. The first integral of the geodesic Eqs. (3) and (6) on equatorial plane (i.e. \(\theta = \pi /2\)) read

$$\begin{aligned} \dot{t} = \frac{E}{1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{\alpha }{r^{3\varepsilon +1}}}, \end{aligned}$$
(7)
$$\begin{aligned} \dot{\phi } = \frac{L}{r^2}, \end{aligned}$$
(8)

where E and L are the integrating constants which correspond to the conserved total energy and angular momentum per unit mass respectively for a test particle. Using the constraint \(u^{\mu }u_{\mu }=-1\), the expression for radial velocity (\(u^r\) = \(\dot{r}\)) can now be obtained:

$$\begin{aligned} {\dot{r}}^2={E}^2-V_\mathrm{eff}, \end{aligned}$$
(9)

where \(V_\mathrm{eff}\) is defined as an effective potential and is expressed as

$$\begin{aligned} V_\mathrm{eff}=\left( 1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{\alpha }{r^{3\varepsilon +1}}\right) \left( \frac{{L}^2}{r^2}+1\right) . \end{aligned}$$
(10)
Fig. 1
figure 1

The effective potential for \(M=L=1\) and \(\varepsilon =-2/3\)

Full size image

3 Nature of effective potential

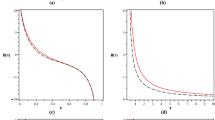
Figures 1 and 2 represent the nature of effective potential for different values of the parameters involved in. In particular, Fig. 1a–c represent the corresponding nature of effective potential for a BH, extremal BH and naked singularity respectively. It is evident from the Fig. 2 that the nature of effective potential is qualitatively similar for SBH and that of charged BH with \(\varepsilon =-1/3\). Meanwhile, for \(\varepsilon =-2/3\), there exist no minima in the radial plot of effective potential. Hence there are no stable circular orbits for charged BH surrounded by quintessence. For the circular motion of a test particle, its radial velocity vanishes. Hence using Eqs. (9) and (10) the angular momentum and energy per unit mass for the incoming test particle in circular motion is

$$\begin{aligned} PL_c^2 = -r^2_c\left( 2M{r^{3\varepsilon +2}_c}-2Q^2{r^{3\varepsilon +1}_c}+3\alpha \varepsilon {r^2_c}+\alpha {r^2_c}\right) ,\nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned} {P}\,r^2_c E_c^2= & {} 4Q^2\alpha r^2_c -8M\alpha r^3_c+4\alpha r^4_c-2{r^{3\varepsilon +5}_c}\nonumber \\&-2Q^4 {r^{3\varepsilon +1}_c}-4Q^2 {r^{3\varepsilon +3}_c}-2{\alpha }^2 {r^{-3\varepsilon +3}_c}\nonumber \\&+8M{r^{3\varepsilon +4}_c}-8M^2{r^{3\varepsilon +3}_c}+8Q^2M{r^{3\varepsilon +2}_c}, \end{aligned}$$
(12)

where \(P = 3\alpha (\varepsilon +1)r^2_c -4Q^2 {r^{3\varepsilon +1}_c} +6M{r^{3\varepsilon +2}_c}-2{r^{3\varepsilon +3}_c}\) and \(L_c\), \(E_c\) represent the specific angular momentum and energy per unit mass for massive test particle in circular motion with corresponding radius of circular orbit \(r_c\).

Fig. 2
figure 2

The effective potential with \(M = 1, Q = 0.5, L = 6.5\)

Full size image

4 Geodesic flows

4.1 The energy conditions

The Ricci scalar for the BH spacetime given by Eq. (2) is calculated to be

$$\begin{aligned} R = \frac{3\alpha \varepsilon \left( 1-3\varepsilon \right) }{r^{3\varepsilon +3}}, \end{aligned}$$
(13)

one may notice that it diverges at \(r\rightarrow 0\) and vanishes at \(r\rightarrow \infty \). The stress-energy tensor is proportional to

(14)

where

$$\begin{aligned} A= & {} 3\alpha \varepsilon -{Q^2}r^{3\varepsilon -1},\nonumber \\ B= & {} r^{3\varepsilon +1}-2Mr^{3\varepsilon }+{Q^2}r^{3\varepsilon -1}-\alpha , \\ C= & {} -\frac{3\alpha \varepsilon (1+3\varepsilon )}{2r^{3\varepsilon +5}}.\nonumber \end{aligned}$$
(15)

In order to analyse the energy conditions, it is convenient to introduce an orthonormal frame that satisfies

$$\begin{aligned} g_{\mu \nu }e_{\alpha }^{\mu }e_{\beta }^{\nu }=\eta _{\alpha \beta }, \end{aligned}$$
(16)

where \(\eta _{\alpha \beta } =\) diag\((1,-1,-1,-1)\) is the Lorentzian metric. We consider a choice of orthonormal basis for given metric as \(e_{\alpha }^{\mu }\) = diag \(\left( \frac{1}{\sqrt{g_{00}}},\frac{1}{\sqrt{-g_{11}}},\frac{1}{\sqrt{-g_{22}}},\frac{1}{\sqrt{-g_{33}}}\right) \), where the energy momentum tensor can be written in the following form:

$$\begin{aligned} T^{\mu \nu }=\rho e_{0}^{\mu }e_{0}^{\nu } + {p_1}e_{1}^{\mu }e_{1}^{\nu } + {p_2}e_{2}^{\mu }e_{2}^{\nu } + {p_3}e_{3}^{\mu }e_{3}^{\nu }. \end{aligned}$$
(17)
Fig. 3
figure 3

Evolution of X with the affine parameter \(\lambda \), where \(E=0.95, L=6.5, \alpha =0.1, M=1, Q=0.5\) for different values of \(\varepsilon \)

Full size image
Fig. 4
figure 4

The evolution of expansion scalar (\(\theta \)) with normalisation constant (\(\alpha \)) with no initial shear and rotation for different values of charge (Q)

Full size image
Fig. 5
figure 5

The evolution of expansion scalar (\(\theta \)) with the BH charge (Q) and the EOS parameter (\(\varepsilon \)) with no initial shear and rotation

Full size image
Fig. 6
figure 6

The evolution of expansion scalar (\(\theta \)) with the affine parameter (\(\lambda \)) for different values of the EOS parameter (\(\varepsilon \)) and initial conditions on ESR variables

Full size image
Fig. 7
figure 7

The evolution of expansion scalar (\(\theta \)) with normalisation constant (\(\alpha \)) without any initial shear and rotation

Full size image
Fig. 8
figure 8

The evolution of expansion scalar (\(\theta \)) with the EOS parameter (\(\varepsilon \)) and the normalisation constant (\(\alpha \)) without any initial shear and rotation for initially contracting congruences with \(\theta _0=-0.01\)

Full size image

The WEC for quintessential fields is

$$\begin{aligned} T_{\mu \nu }u^{\mu }u^{\nu }\ge 0\approx \rho \ge 0, \rho +p_{i}>0, \end{aligned}$$
(18)

and for the given spacetime (2), we have

$$\begin{aligned} T_{\mu \nu }u^{\mu }u^{\nu }=\frac{1}{r^{3\varepsilon +3}}\left( Q^2 r^{3\varepsilon -1}-3\alpha \varepsilon \right) . \end{aligned}$$
(19)

Hence the WEC simplifies as follows:

$$\begin{aligned} Q^2 r^{3\varepsilon -1}-3\alpha \varepsilon \ge 0. \end{aligned}$$
(20)

However, the SEC reads

$$\begin{aligned} T_{\mu \nu }u^{\mu }u^{\nu }\ge \frac{1}{2}T_\nu ^\mu u^{\nu }u_{\nu }, \end{aligned}$$
(21)

and for the spacetime used it can be written

$$\begin{aligned} \frac{1}{2r^{3\varepsilon +1}}\left[ 2Q^2 r^{3\varepsilon -1}-3\alpha \varepsilon (3\varepsilon +1)\right] \ge 0. \end{aligned}$$
(22)

If the WEC represented by Eq. (20) follows, Eq. (22) for the SEC reduces to the following:

$$\begin{aligned} 3\alpha \varepsilon \left( 1-3\varepsilon \right) \ge 0, \end{aligned}$$
(23)

hence for \(\alpha >0\) and \(-\frac{1}{3}<\varepsilon <-1\), the above condition is clearly violated. Both the WEC and the SEC therefore ensure that \(r\ne 0\). Hence, locally the attractive nature of gravity may exist there, but on average the quintessential fields have a repulsive nature, which can be visualised in the deformation of geodesic congruences as discussed below.

4.2 Raychaudhuri equations for ESR variables

The spacetime given by Eq. (2) can be decomposed into a transverse part i.e. a transverse metric \(h_{\mu \nu }\) on a spacelike hypersurface and a longitudinal part (\(-u_{\mu }u_{\nu }\)) as follows:

$$\begin{aligned} h_{\mu \nu }=g_{\mu \nu }+u_{\mu }u_{\nu },\quad (\mu ,\nu =0,1,2,3). \end{aligned}$$
(24)

Here \(u^{\mu }\) (a timelike vector field) satisfies the constraint \(u^{\mu }u_{\mu }=-1\). One can investigate the evolution of ESR variables on this spacelike hypersurface with \(h_{\mu \nu }\) orthogonal to \(u^{\mu }\) i.e. \(u^{\mu }h_{\mu \nu }=0\), such that it represents the local rest frame of a freely falling observer in given spacetime (2) by using a tensor \({B_{\mu \nu }}\) which is defined as \(B_{\mu \nu } = \nabla _\nu u_\mu \). For a 4 dimensional spacetime, \({B_{\mu \nu }}\) can be decomposed as

$$\begin{aligned} {B_{\mu \nu }}=\frac{1}{3} \, \theta h_{\mu \nu }+\sigma _{\mu \nu }+\omega _{\mu \nu }, \end{aligned}$$
(25)

here the quantities \(\theta \), \(\sigma _{\mu \nu }\) and \(\omega _{\mu \nu }\) are known as the expansion scalar, shear tensor and the rotation tensor of the congruence (family) of geodesics defined by \(u^{\mu }\) [3, 4]. These variables can be written explicitly as

$$\begin{aligned} \theta ={B^\mu }_\mu , \end{aligned}$$
(26)
$$\begin{aligned} \sigma _{\mu \nu }=\frac{1}{2}\left( {B_{\mu \nu }}+{B_{\nu \mu }}\right) -\frac{1}{3}\theta h_{\mu \nu }, \end{aligned}$$
(27)
$$\begin{aligned} \omega _{\mu \nu }=\frac{1}{2}\left( {B_{\mu \nu }}-{B_{\nu \mu }}\right) . \end{aligned}$$
(28)

As per their constructional properties, the shear and rotation tensors also satisfy, \(h^{\mu \nu }\sigma _{\mu \nu }=0\) and \(h^{\mu \nu }\omega _{\mu \nu }=0\) alongwith \(g^{\mu \nu }\sigma _{\mu \nu }=0\) and \(g^{\mu \nu }\omega _{\mu \nu }=0\). Since \(u^\mu \sigma _{\mu \nu }=0\) and \(u^\mu \omega _{\mu \nu }=0\), both \(\sigma _{\mu \nu }\) and \(\omega _{\mu \nu }\) are purely spatial in nature (i.e., \(\sigma ^{\mu \nu }\sigma _{\mu \nu }>0\) and \(\omega ^{\mu \nu }\omega _{\mu \nu }>0\)). The evolution equation for the spatial tensor \({B}_{\mu \nu }\) can also be written as

$$\begin{aligned} {\dot{B}_{\mu \nu }}+{B}_{\mu \gamma }{B}^\gamma _\nu =-R_{\mu \eta \nu \delta }u^{\eta }u^{\delta }, \end{aligned}$$
(29)

where \(R_{\eta \nu \mu \delta }\) is the Riemann tensor and the dot (.) represents differentiation w.r.t. the affine parameter \(\lambda \). On decomposition of \(B_{\mu \nu }\) to the trace, symmetric traceless and antisymmetric parts as in Eqs. (26)–(28), Eq. (29) leads to the Raychaudhuri equations for ESR variables in four dimensions [3, 4],

$$\begin{aligned} {\dot{\theta }}+\frac{1}{3}\theta ^2+\sigma ^2-\omega ^2+R_{\mu \nu }u^{\mu }u^{\nu }=0, \end{aligned}$$
(30)
$$\begin{aligned}&{\dot{\sigma }_{\mu \nu }}+\frac{2}{3}\theta \sigma _{\mu \nu }+\sigma _{\mu \gamma }\sigma ^\gamma _\nu +\omega _{\mu \gamma }\omega ^\gamma _\nu +\frac{1}{3}\left( \sigma ^2-\omega ^2\right) h_{\mu \nu }\nonumber \\&\quad +\,\mathscr {C}_{\mu \eta \nu \delta }u^{\eta }u^{\delta }-\frac{1}{2}\tilde{\mathscr {R}}_{\mu \nu }=0, \end{aligned}$$
(31)
$$\begin{aligned} {\dot{\omega }_{\mu \nu }}+\frac{2}{3}\theta \omega _{\mu \nu }+{{\sigma ^\gamma }_\mu }{\omega _{\gamma \nu }}+{{\omega ^\gamma }_\mu }{\sigma _{\gamma \nu }}=0. \end{aligned}$$
(32)

where \(\sigma ^2=\sigma ^{\mu \nu }\sigma _{\mu \nu }\), \(\omega ^2=\omega ^{\mu \nu }\omega _{\mu \nu }\), \(\mathscr {C}_{\mu \eta \nu \delta }\) is the Weyl tensor and \(\tilde{\mathscr {R}}_{\mu \nu }=\left( h_{\mu \gamma }h_{\nu \delta }-\frac{1}{3}h_{\mu \nu }h_{\gamma \delta }\right) {R}^{\gamma \delta }\) is the transverse trace-free part of \({R}_{\mu \nu }\).

4.3 Evolution of ESR variables

In order to represent ESR variables at any point in the geodesic congruence associated with a timelike vector field \(u^{\mu }\), let us consider a freely falling (Fermi) normal frame having the basis vectors \(E_{\eta }^\mu \), \(\eta =0,\ldots ,3\) (with \(E_{0}^\mu = \hat{u}^{\mu }\)) which are parallel-transported [45, 46]. Such frames can be constructed numerically by solving the differential equations \(u^\nu \nabla _\nu \, E_{\eta }^{\mu } =0\) (with initial conditions of an orthonormal frame) simultaneously with Eq. (29). The tensor \(B_{\mu \nu }\) in the Fermi basis may then be represented as follows:

$$\begin{aligned} B_{\mu \nu }= & {} \left( \frac{1}{3}\theta +\sigma _{11}\right) e^1_{\mu }e^1_{\nu } + \left( \frac{1}{3}\theta +\sigma _{22}\right) e^2_{\mu }e^2_{\nu }\nonumber \\&+ \left( \frac{1}{3}\theta -\sigma _{11}-\sigma _{22}\right) e^3_{\mu }e^3_{\nu } + (\sigma _{12} - \omega _3)e^1_{\mu } e^2_{\nu }\nonumber \\&+(\sigma _{21} + \omega _3)e^2_{\mu }e^1_{\nu } + (\sigma _{13} + \omega _2)e^1_{\mu }e^{3}_{\nu } \nonumber \\&+(\sigma _{31} -\omega _2) e^{3}_{\mu }e^1_{\nu }+ (\sigma _{23} - \omega _1) e^{2}_{\mu }e^{3}_{\nu } \nonumber \\&+ (\sigma _{32}+ \omega _1) e^{3}_{\mu }e^{2}_{\nu } \end{aligned}$$
(33)

where \(e^\eta _\mu \) are co-frame basis which satisfy the relation \(e^\eta _\mu E_\beta ^{\mu } = \delta ^{\eta }_{\beta }\). The ESR variables can now be constructed from the evolution tensor (33), using the basis vectors \(E_\eta ^ \mu \), as described in [45]. In order to understand the focussing and defocussing behaviour of a timelike geodesic congruence, let us further redefine the expansion scalar as \(\theta = 3{\dot{F}}/F\). Equation (32) may now be expressed in the form of the following Hill-type equation:

$$\begin{aligned} {\ddot{F}} + X \, F = 0, \end{aligned}$$
(34)

where \(X =(\sigma ^2-\omega ^2+R_{\mu \nu }u^{\mu }u^{\nu })/3\) with \(\sigma ^2= 2(\sigma _{11}^2 + \sigma _{22}^2 + \sigma _{12}^2 + \sigma _{13}^2 + \sigma _{23}^2 + \sigma _{11} \sigma _{22})\) and \(\omega ^2 = 2(\omega _1^2 +\omega _2^2 +\omega _3^2)\). One may note that the Raychaudhuri scalar \(R_{\mu \nu }u^{\mu }u^{\nu }\) is zero for the pure SBH case. It is evident from (34) that, for \(F\rightarrow 0\) in finite time, we have a finite time singularity in \(\theta \) with focussing (defocussing) if \(\dot{F}<0\) (\(\dot{F}>0\)). The signature of X is thus decisive as we examine focussing/defocussing in view of the critical values for the initial condition on expansion scalar i.e. \(\theta _0\) [45, 46]. When X is positive definite (i.e., \(\sigma ^2+R_{\mu \nu }u^{\mu }u^{\nu }>\omega ^2\)), there exist conjugate points and geodesic focussing/defocussing takes place accordingly. On the other hand, no finite time singularity exists for an initially non-contracting congruence (i.e., \(\theta _0\ge 0\)) in the case that X is negative definite. For \(\theta _0<0\), there exists a critical value below which focussing/defocussing will take place. From Fig. 3, one may easily notice the signature of X for different values of \(\varepsilon \), which in turn reflects the non-attractive behaviour of the quintessential fields in case of \(\varepsilon =-2/3\) and \(\varepsilon =-1\) without initial shear and rotation. However, in view of a positive definite value of X for the case of \(\varepsilon =-1/3\), geodesic focussing may even occur without initial shear and rotation. The exact behaviour of geodesic focussing as well as defocussing can easily be visualised in the evolution of ESR variables as presented below. Using the velocity vector field \(u_i\) = (\(\dot{t}\), \(\dot{r}\), \(\dot{\phi }\)) in Eqs. (7)–(9), the ESR variables can be represented as functions of r. It leads to the following expression for the expansion scalar:

$$\begin{aligned} \theta = \pm \,\frac{\left[ \left( 4r^2(E^2 -1)+6Mr-2Q^2\right) r^{3\varepsilon +1}-3\alpha r^2(\varepsilon -1)\right] }{2r^{3(1-\varepsilon )/2}\left[ \left( (E^2 -1)r^2+2Mr-Q^2\right) r^{3\varepsilon +1}+\alpha r^2\right] ^{1/2}}. \end{aligned}$$
(35)

The expression given in Eq. (35) for \(\theta \) accommodates the evolution of a geodesic congruence for the fixed value of E and L only. It is evident from Eq. (35) that \(\theta \rightarrow \pm \infty \) as the denominator vanishes. It is worth noticing that the denominator of RHS of Eq. (35) corresponds to the radial velocity for a test particle with zero-angular momentum and hence it does not include the case of a non-radial motion of test particles as well as the arbitrary initial conditions subjected to the ESR variables. In order to have a complete analysis of the geodesics deformations, one need to solve the Raychaudhuri equations (30–32) arbitrarily.

In the following, the evolution of the ESR variables is presented for the case of a charged BH as well as SBH surrounded with quintessence background, under the different conditions on the parameters involved. The results obtained are compared with those in the RNBH and SBH backgrounds as well as with the corresponding interesting cases having a non-zero cosmological constant.

We study the deformation in equatorial section i.e. \(\theta =\pi /2\). For further numeric computation of the evolution of expansion scalar with the affine parameter, we have considered \(E=0.95\), \(L=6.5\) as it represents the energy and angular momentum per unit mass for the test particle in the innermost circular orbit (ISCO) around a SBH with quintessence when \(\varepsilon =-2/3\). For initially diverging congruences (i.e. \(\theta _0>0\)), there exists a critical value of the expansion scalar (\(\theta _c\)) below which there is a focussing (i.e. \(\theta \rightarrow -\infty \)) when the normalisation constant (\(\alpha \)) and the EOS parameter (\(\varepsilon \)) have small magnitude while as the value of \(\alpha \) becomes more positive or the value of \(\varepsilon \) becomes more negative, no focussing is observed as depicted in subsequent figures. It is important to mention that with the change in the initial conditions on shear and rotation, the critical value of the initial expansion scalar will also change. The critical value (\(\theta _c\)) of the expansion scalar for SBH is calculated as 0.02902 with \(E=0.95, L=6.5\) without initial shear and rotation. For all the figures presented here (Figs. 4, 5, 6 and 7), we have considered \(\theta _0=0.01\) for \(\theta _0<\theta _c\) and \(\theta _0=0.1\) for \(\theta _0>\theta _c\).

Figure 4a–c represent the evolution of expansion scalar for \(\theta _0<\theta _c\) with \(\varepsilon = -2/3\) for different values of \(\alpha \), where (a–c) represent the case of BH, extremal BH and naked singularity, respectively. Without \(\alpha \) geodesics focussing is observed, which converts in defocussing as quintessence appears. The positive increment in the value of \(\alpha \) further supports this defocussing, as geodesic defocussing appears earlier with a positive increase in the value of \(\alpha \). Figure 4d–f represent the evolution of expansion scalar for initially diverging geodesics with \(\theta _0>\theta _c\) for different values of \(\alpha \). In this case, a positive increment in \(\alpha \) first delays the defocussing while if one continuously increases the value of \(\alpha \) it then supports geodesic defocussing.

Figure 5a, b depict the effect of increasing BH charge (Q) on the evolution of expansion scalar for both cases of initially diverging geodesics. It is observed that there occurs no geodesic focussing due to the presence of quintessence. The defocussing present is further delayed as one compares BH, extremal BH and naked singularity cases, as shown in Fig. 5a. Similar is the effect observed with a negative increment in the value of the EOS parameter (\(\varepsilon \)) [47] as shown in Fig. 5c, d.

Figure 6a, b represent the evolution of the expansion scalar (\(\theta \)) for the case \(\varepsilon = -1/3\), with fixed value of normalisation constant (\(\alpha \)). It clearly shows that without initial shear and rotation, the geodesics focus (defocus) as \(\theta _0 < \theta _c\) (\(\theta _0\) > \(\theta _c\)). Figures 6c–f represent the evolution of expansion scalar (\(\theta \)) for \(\varepsilon = -2/3\) and \(-1\), respectively, with fixed value of normalisation constant (\(\alpha \)). It shows that without initial shear and rotation geodesics defocus even if \(\theta _0 < \theta _c\). The presence of an initial shear assists focussing in all the above mentioned cases. As shown in Fig. 6a, where focussing is already present, the presence of an initial shear accelerates focussing. On the other hand, the presence of an initial rotation favours defocussing. As shown in Fig. 6b–f, in the cases where defocussing is already present, the presence of initial rotation assists it.

Figure 7a, b represent the comparative plots for the evolution of the expansion scalar (\(\theta \)) with the EOS parameter (\(\varepsilon \)) for SBH surrounded by quintessence. An increment in the negative value of \(\varepsilon \) plays a different role for the two cases. The cases of SBH and \(\varepsilon = -1/3\) are quite similar except that focussing and defocussing both appear earlier for later case due to the non-zero value of \(\alpha \). Figure 7c, d represent the effect of the normalisation parameter \(\alpha \) on focussing and defocussing of congruences for \(\varepsilon = -1/3\). In fact, an increment in the value of \(\alpha \) assists both focussing and defocussing. The evolution of the expansion scalar (\(\theta \)) is represented for initially contracting congruences with the EOS parameter (\(\varepsilon \)) in Fig. 8a, b and with the normalisation parameter (\(\alpha \)) in Fig. 8c, d in the background of RNBH and SBH, respectively. One can notice that the role of the negative increment in \(\varepsilon \) as well as the positive increment in \(\alpha \) is similar to that of the respective cases of initially diverging congruences.

5 Summary and conclusions

We have investigated the kinematics of timelike geodesic congruences in the background of a charged BH surrounded with quintessence. The important conclusions are summarised as follows:

  • The spacetime representing a charged BH surrounded by quintessence satisfies the WEC but violates the SEC even in the absence of BH charge.

  • The evolution of ESR variables for timelike geodesic congruences is affected qualitatively as well as quantitatively by the normalisation constant and the EOS parameter along with the BH charge and mass.

  • The presence of BH charge supports the defocussing effect of quintessence as for SBH with quintessence the evolution of \(\theta \) is similar to the SBH case for small negative values of \(\varepsilon \) while no focussing is observed in the presence of both Q and \(\alpha \). However, with the increase in negative \(\varepsilon \) value, the nature of the evolution shifts towards the corresponding de Sitter spacetimes.

  • The normalisation constant behaves like cosmological constant. For initially converging congruences, a positive increment in \(\alpha \) always assists geodesic focussing.

  • For initially diverging congruences, the positive increment in \(\alpha \) assists defocussing when the initial expansion is greater than its critical value for the SBH case. However, for the other case when the initial expansion is smaller than its critical value, a similar increment in \(\alpha \) assists geodesic focussing though the congruences defocus as \(\alpha \) value is increased further.

    The study of the accretion disk formation around the rotating analogue of the BH spacetimes used in this study would be important astrophysically in view of the permissible range of the quintessence parameters \(\varepsilon \) and \(\alpha \). Hence by looking into the future observations of ISCOs and accretion onto the BHs, this study might be helpful to constrain the various parameters involved therein from the cosmological view point. In addition to this, the study of null geodesic flows in the background of such BH spacetimes would be useful to provide a more detailed understanding of these spacetimes. We intend to report on these issues in near future.