Sizing complex networks

Abstract

Among the many features of natural and man-made complex networks the small-world phenomenon is a relevant and popular one. But, how small is a small-world network and how does it compare to others? Despite its importance, a reliable and comparable quantification of the average pathlength of networks has remained an open challenge over the years. Here, we uncover the upper (ultra-long (UL)) and the lower (ultra-short (US)) limits for the pathlength and efficiency of networks. These results allow us to frame their length under a natural reference and to provide a synoptic representation, without the need to rely on the choice for a null-model (e.g., random graphs or ring lattices). Application to empirical examples of three categories (neural, social and transportation) shows that, while most real networks display a pathlength comparable to that of random graphs, when contrasted against the boundaries, only the cortical connectomes prove to be ultra-short.

The small-world phenomenon has fascinated popular culture and science for decades. Discovered in the realm of social sciences during the 1960s, it arises from the observation that any two persons in the world are connected through a short chain of social ties¹. Since then many real networks have been found to be small-world as well^2,3,4, from natural to man-made systems. But, how small is a small-world network and how does it compare to others? In the physical world we evaluate and compare the size of objects by contrasting them to a common reference, usually a standard metric system defined and agreed by the community. In the case of complex networks the difference is that every network constitutes its own metric space. Thus, the question of whether a network is smaller or larger than another implies the comparison of two different spaces with each other, rather than the more familiar situation in which two objects are contrasted within the space they live.

The quantification of the small-world property relies on the computation of the average pathlength—the average graph distance between all pairs of nodes. As it happens for any graph metric, its outcome depends on the number of nodes and links of the network under study. Consider two empirical networks. ${G}_{1}$ is a small social network, e.g., a local sports club of ${N}_{1}=100$ members. A link between two members implies they are friends. ${G}_{2}$ is an online social network with ten million users (${N}_{2}=1{0}^{7}$) where two profiles are connected if users follow each other. If we found that the average pathlength ${l}_{1}$ of ${G}_{1}$ is smaller than the length ${l}_{2}$ of ${G}_{2}$, we would not be able to conclude that the internal topology of the local sports-club is shorter, or more efficient, than the structure of the large online network. The observation that ${l}_{1}\ <\ {l}_{2}$ could be a trivial consequence of the fact that ${N}_{1}\ll {N}_{2}$. In order to fully interpret this result we need to disentangle the contribution of the network’s internal architecture to the pathlength from the incidental influence contributed by the number of nodes and links.

In practice, the typical strategy seen in the literature to deal with this problem consists in comparing empirical networks to well-known graph models, e.g., random graphs, scale-free networks and regular lattices^2,5,6,7,8. It shall be emphasised that these architectures represent different null-models, generated upon particular hypotheses and thus useful to answer a variety of questions we may have about the data. However, their role as absolute references is restricted since they are not representative of the limits that network metrics, such as pathlength and efficiency, can take^{\(\tilde{L}=N\) arcs, all pointing in the same orientation. Finally, a complete graph is the network in which all nodes are connected to each other, thus containing ${L}_{o}=\frac{1}{2}N(N-1)$ edges or ${\tilde{L}}_{o}=N(N-1)$-directed arcs. The average pathlength of a complete graph is ${l}_{o}=1$, the shortest of all networks.}

Fig. 1

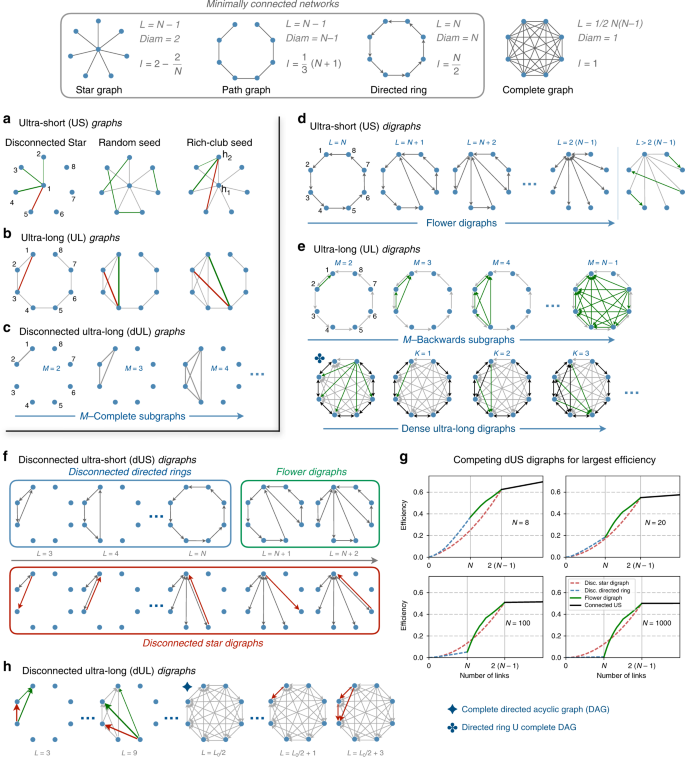
Construction of ultra-short and ultra-long (di)graphs. Star graphs, path graphs, directed rings and complete graphs serve as the starting references to construct (di)graphs of arbitrary density with extremal average pathlength. a–c Procedures to build ultra-short and ultra-long graphs, both connected and disconnected. Edge colour denotes the order of edge addition. Red edges are the last added and green links the ones in the previous steps. d–h Generation of directed graphs with extremal pathlength or efficiency. These cases are often non-Markovian and reveal novel structures. d In the sparse regime ultra-short digraphs are characterised by a collection of directed cycles converging at a single hub. We name these flower digraphs. Every arc added leads to a flower digraph with an additional “petal”. e Although several configurations may lead to digraphs with longest pathlength, we introduce here an algorithmic approximation to the upper bound: $M$-backwards subgraphs. f Up to three different digraph configurations compete for largest efficiency. g The winner depends on network density. Finally, h digraphs with smallest efficiency are achieved by constructing the densest directed acyclic graphs possible, to minimise the contribution of cycles to the path structure of the network

US and UL graphs of arbitrary $L$ can be achieved by adding edges to star and path graphs, respectively, Figs. 1a–c. In the case of digraphs, both US and UL configurations are obtained by adding arcs to a directed ring, Figs. 1d–h. The precise order of link addition differs from case to case. Two findings deserve a special mention. (1) US and UL graphs can be generated adding edges one-by-one to the initial configurations, Fig. 1a, b, but construction of extremal digraphs is often non-Markovian. That is, an US or an UL digraph with $\tilde{L}+1$ arcs cannot always be achieved by adding one arc to the extremal digraph with $\tilde{L}$ arcs. For example, Fig. 1d shows that the digraphs with shortest pathlength initially transition from a directed ring onto a star graph following unique configurations we named flower digraphs. (2) For a given size and number of links, all configurations with diameter ${\rm{diam}}(G)=2$ have exactly the same pathlength^9,10,12 and they are US, regardless of how their links are internally arranged. Their pathlength is $l=2-\rho$, where $\rho$ is the link density. See the US graph theorem (Theorems 1 and 4) in Supplementary Notes 1 and 2.

When studying large networks it is common to find that these are sparse and fragmented into many components. While the pathlength in these cases is infinite, these networks can still be characterised by their efficiency, which remains a finite quantity allowing to zoom into the sparse regime. We remind that the global efficiency $E$ of a network is defined as the average of the inverses of the pairwise distances. Thus the contribution of disconnected pairs (with infinite distance) is null. We could identify sparse configurations [$L\ <\ N-1$ or $\tilde{L}\ <\ 2(N-1)$] with the largest efficiency, whose efficiency transitions from zero (for an empty network) to that of a star graph. In the case of graphs, Fig. 1a, there is a unique optimal configuration but for digraphs we found that up to three different structures compete for the largest efficiency when $\tilde{L}\ <\ 2(N-1)$, Fig. 1f, g. See Fig. 1c, h for the graphs and digraphs with smallest possible efficiency, which equals the link density, $E=\rho$.

The length of common network models

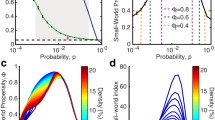
In the following we illustrate how knowledge of the US and UL boundaries frame the space of lengths that networks take, both empirical and models. We start by investigating the null-models which over the years have dominated the discussions on the topic of small-world networks: random graphs (Erdős–Rényi type), scale-free networks¹³ and ring lattices. We consider undirected and directed versions with $N=1000$ nodes and study the whole range of densities; from empty ($\rho =0$) to complete ($\rho =1$). The results are shown in Fig. 2. Find comparative results for $N=100$ and $N=10,000$ in Supplementary Note 4. Shaded areas mark the values of pathlength and global efficiency that no network can achieve. Solid lines represent the ranges in which the models are connected and dashed lines correspond to the efficiency when the networks are disconnected. The location of the original building-blocks (star graphs, path graphs, directed rings and complete graphs) are also shown over the maps for reference.

Fig. 2

Pathlength and efficiency of characteristic network models. Ring lattices (red), random (Erdős–Rényi type, green) and scale-free¹³ graphs (blue) of $N=1000$ nodes, plotted together with the corresponding upper and lower boundaries ultra-long (yellow) and ultra short (grey). Shaded areas mark values of pathlength and efficiency that no (di)graph of the same size can achieve. a The average pathlength of the three models decay towards the ultra-short limit at sufficiently large density. b Same as panel (a) with density re-scaled for visualisation. c Global efficiency of the network models. The lower boundary (ultra-long) is represented by two lines: a dashed line representing the efficiency of disconnected graphs ${E}_{dUL}\approx \rho$ and a solid line for connected graphs. d Same as panel (c) with density re-scaled for visualisation. The efficiency of random and scale-free graphs undergoes a transition from ultra-long to ultra-short centered at their percolation thresholds. e Pathlength of random and scale-free digraphs. In this case, the two boundaries emerge from the same point corresponding to a directed ring (open circle). f Efficiency of random and scale-free digraphs. Curves for random and scale-free networks are averages over 1000 realisations. Dashed lines represent ranges of density for which the models are disconnected and solid lines represent (di)graphs which are connected. Results for sizes $N=100$ and $10,000$ are shown in Supplementary Note 4

The pathlength of random, scale-free and ring networks decays with density, as expected, with the three eventually converging onto the lower boundary and becoming US, Fig. 2a, b. But, the decay rates differ across models. Scale-free networks are always shorter than random graphs in the sparser regime, where the length of both models is well above the lower boundary. However, the two models converge simultaneously onto the US limit at $\rho \approx 0.08$. On the other hand, the ring lattices decay much slower and only becomes US at $\rho \approx 0.5$.

Figure 2c, d reproduces the same results in terms of efficiency. An advantage of efficiency is that it always takes a finite value, from zero to one, regardless of whether a network is connected or not. Zooming into the sparser regime, we observe that the efficiency of both random (${E}_{r}$) and scale-free (${E}_{SF}$) graphs undergoes a transition, shifting from the UL to the US boundary, Fig. 2d. They are nearly identical except for a narrow regime in between $\rho \in (4\ \times \ 1{0}^{-4},2\ \times \ 1{0}^{-3})$. Here, ${E}_{SF}$ grows earlier than ${E}_{r}$, reaching a peak difference of ${E}_{SF}\approx 5\times {E}_{r}$ at $\rho =1{0}^{-3}$. The reason for this is that SF graphs percolate earlier than random graphs¹⁴. Indeed, the onset of a giant component in random graphs of size $N=1000$ happens at $\rho \approx 1{0}^{-3}$.

The results for the directed versions of the random and scale-free networks, Fig. 2e, f, are very similar. The main difference is that when $\tilde{L}=N$ both the upper and the lower boundaries are born from the same point corresponding to a directed ring, Fig. 2e.

Length and global efficiency of empirical networks

We now elucidate how the knowledge of the boundaries allows us to interpret the length of real networks faithfully. First, we will illustrate how different references may give rise to subjective interpretations. Then, we will show how the boundaries help framing both empirical and model networks into a unified representation.

Given two networks ${G}_{1}$ and ${G}_{2}$ with pathlength ${l}_{1}\ <\ {l}_{2}$ (the absolute values), we could affirm that ${G}_{1}$ is shorter than ${G}_{2}$. But, if ${G}_{2}$ is bigger (${N}_{1}\ <\ {N}_{2}$) then the fact that ${l}_{1}\ <\ {l}_{2}$ does not necessarily imply that the topology of ${G}_{1}$ is more efficient than the topology of ${G}_{2}$. An approach commonly followed in the literature to face this problem consists in comparing networks ${G}_{1}$ and ${G}_{2}$ with well-known network models, or null-models. For example, random graphs (Erdős–Rényi) and ring lattices are typically employed as the references to characterise the “small-worldness” of complex networks. In some cases, the relative pathlength $l^{\prime} =l/{l}_{r}$, is used which considers the length ${l}_{r}$ of random graphs as the lower boundary⁵. This measure takes $l^{\prime} =1$ when the length of the network matches that of random graphs. In other cases, a two-point normalisation using ring lattices as the upper boundary^6,7 was proposed, $l^{\prime} =(l-{l}_{r})/({l}_{latt}-{l}_{r})$. Here, $l^{\prime} =0$ if the length of the real network equals that of random graphs (the lower boundary) and $l^{\prime} =1$ if it matches the length of ring lattices (the upper boundary). Considering the US and UL boundaries, one could also propose the following re-scaling

$$l^{\prime} =\frac{l}{{l}_{US}}.$$

(1)

$$l^{\prime} =\frac{l-{l}_{US}}{{l}_{UL}-{l}_{US}}.$$

(2)

At this point, it shall be stressed that the use of relative metrics may lead to biased interpretations, depending on the question(s) we are asking about the data. Relative pathlengths such as $l^{\prime} =l/{l}_{r}$ and $l^{\prime} =l/{l}_{latt}$ are conceptually different from the ones in Eqs. (1) and (2) because ${l}_{r}$ and ${l}_{latt}$ are expectation values associated to given null-models while ${l}_{US}$ and ${l}_{UL}$ are actual limits. Thus, they are meant to answer different questions. On the one hand, null-models are constructed upon particular sets of constraints and following generative assumptions on the rules governing how nodes link with each other. The role of expectation values is thus to test whether those hypotheses explain the pathlength observed in the real networks. On the other hand, limits correspond to the extremal values (di)graphs could take and are independent of generative assumptions. The reader should keep in mind that here, our intention is neither to identify the key topological factors that “explain” the pathlength observed in real networks nor to model the real networks themselves. Our goal is to address the question “how short or how long is a given network?” This allows us to position network models in the space of reachable pathlength and to compare these models with potentially different numbers of nodes and links.

For practical illustration, we study a set of empirical datasets from three different domains: neural and cortical connectomes, social networks and transportation systems, see Table 1. These examples represent a small but diverse set of real networks with sizes ranging from $N=34$ to $4941$ and densities ranging from $\rho \approx 1{0}^{-4}$ to $0.330$. First, we show that the ranking of these networks with respect to pathlength is very much altered depending on the relative reference chosen, Fig. 3. According to the absolute pathlength, Fig. 3a, cortical and neural connectomes tend to be shorter than social and transportation networks. The network of prison inmates is directed and weakly connected, therefore it has an infinite pathlength. See Supplementary Note 5 for the results presented in terms of global efficiency. We could now ask whether these observations are a trivial consequence of the different sizes of those networks. For that, we consider the relative pathlength $l^{\prime} =l\ /\ N$, Fig. 3b. In this case, the ranking changes considerably. The short length of the cortico-cortical connectomes seems to be partly explained by their small size ($N\ <\ 100$).

Table 1 Characteristics of the sample real networks investigated: For illustrative purposes we analyse twelve networks from three different domains: neural, social and transportation. Networks marked with and asterisk (${}^{* }$) are directed

Fig. 3

Comparison of absolute and relative pathlength for selected neural, social and transportation networks. a Absolute average pathlength of the empirical networks, b–f different relative pathlength definitions. b Relative to network size $N$, c relative to equivalent random graphs, d relative to the pathlength to the ultra-short boundary. e, f Two-point normalisations considering random graphs and ring lattices as benchmarks (e), and relative to the ultra-short and ultra-long boundaries (f). Red crosses indicated cases for which all random graphs generated as benchmark were disconnected and had thus an infinite pathlength. The Prison social network is weakly connected and can thus only be studied by characterising efficiency, see Supplementary Note 5

When considering random graphs as the reference, Fig. 3c, we find that all the networks take relative values $l^{\prime} \approx 1$; with the neural networks, the Zachary karate club and the airports network being the closest to random graphs. With these results at hand we may tend to believe that, e.g., the airport transportation network is shorter than the dolphins social network. This interpretation is only part of the picture because ${l}_{r}$ is an expectation value. Here, $l^{\prime}$ provides a ranking of the networks whose pathlength is better explained by the generative assumptions of random graphs. If the US limit is taken as reference, a different scenario is found, Fig. 3d. In this case, the cortical networks (cat, macaque and human) lie marginally above $l^{\prime} =1$, meaning that they are practically US. The dolphins and the facebook circles are twice as long as the lower boundary and the transportation networks deviate even further. The comparison to random graphs was not possible for three transportation networks (London transportation, Chicago transportation and the U.S. power grid) because their densities lie below the percolation threshold for Erdős–Rényi graphs and thus no connected graphs could be constructed with the same $N$ and $L$. Calculated in terms of global efficiency, this comparison shows that these three networks are less efficient than random graphs and lie notably far from the optimal, see Supplementary Note 5. Notice that transportation networks, in reality, are embedded in space and are nearly planar. The planarity helps sparse networks to be connected¹⁵, while they would easily be disconnected if this constraint were ignored. However, here we are discarding any constraints besides $N$ and $L$ whether they concern internal features (e.g., the degree distribution) or external (e.g., spatial embedding), and focus solely on the theoretical limits the pathlength and efficiency can take.

Figure 3e shows the two-point relative pathlengths when both random graphs and ring-lattices are taken as references. With these results the Zachary Karate Club and the airports network would appear to be shorter than the brain connectomes, the collaboration network of jazz musicians and the dolphin’s network. Since ${l}_{r}$ and ${l}_{latt}$ are expectation values, the results should be seen as which of the two null-models, random graphs or ring-lattices, better explains the length of each real network. Finally, considering the US and the UL boundaries as references, Fig. 3f, it becomes clear that all the networks are closer to the US boundary than to the UL.

So far, we have evidenced that the use of relative metrics to rank networks according to their length may lead to biased interpretations because the outcome depends on whether the reference is a null-model or a limit. Therefore, a more informative solution than relying on relative metrics is to display all the relevant results, both for real networks and for null-models, into a unified representation. Figure 4 shows the global efficiency of the thirteen empirical networks (+), together with their corresponding US (grey bars) and UL (gold bars) boundaries, and the expectation values for equivalent random graphs (blue lines) and ring lattices (red lines). This representation elucidates the results reported in Fig. 3c–f. First, the space of accessible efficiencies (delimited in between the lower and the upper boundaries) differs from case to case, depending on the size and density of each network. Second, the position that both real networks and null-models take within this space is revealed. In the case of the three brain connectomes (cat, macaque and human) their equivalent random graphs match the US boundary. Thus comparing these networks to random graphs is the same as comparing them to the lower limit. However, in sparser networks this is no longer the case. For example, the efficiency of the neural network of the Caenorhabditis elegans is close to that of random graphs, but both values depart from the US boundary. In this case, the network is far from ring lattices (red lines) and from the UL boundary. The opposite is found for transportation networks: their global efficiency and the efficiency of corresponding random graphs lie closer to the UL boundary than to the US.

Fig. 4

Comparison of global efficiency for selected neural, social and transportation networks. The global efficiency of the thirteen empirical networks (+) is shown together with their ultra-short and ultra-long boundaries. The span of the boundaries very much differs from case to case because of the different sizes and densities of the networks studied. For the denser networks (e.g., cortical connectomes) the efficiency of random graphs (blue lines) lie almost on top of the largest possible efficiency (ultra-short boundary). On the contrary, for the sparser networks (e.g., the transportation systems) the efficiency of random graphs very much divert from ultra-short

In summary, the synoptic representation in Fig. 4 tells us that: (1) The pathlength (efficiency) of empirical networks is usually comparable to the length of random graphs; meaning that the random connectivity hypothesis partly explains the empirical values. But (2) the position networks take with respect to the limits very much differs from case to case, exposing how close each network—real and models—lie from the optimal efficiency or from the worst-case scenario. In future practical studies, Fig. 4 can be complemented with the results from other null-models, each accounting for specific sets of constraints, e.g., conserving the degree distribution or considering the limitations imposed by the spatial embedding. The expectation value calculated for each null-model will add one datapoint per network and thus allow to visualise the contribution of every set of constraints. Here, we restricted to random graphs and ring lattices for the illustrative purposes.

Discussion

Among the many descriptors to characterise complex networks, the average pathlength is a very important one. It lies at the heart of the small-world phenomenon and also plays a crucial role in network dynamics, as short pathlength facilitate global synchrony^4,16 or the diffusion of information and diseases^17,18. Unfortunately, the pathlength is also difficult to treat mathematically and most analytic results so far are restricted to statistical approximations on scale-free and random graphs, at the thermodynamic limit^19,20. Here, we have taken a considerable step forward by identifying and formally calculating the limits for the average pathlength and for the global efficiency in networks of any size and density. We provide results for both directed and undirected networks, whether they are sparse (disconnected) or dense (connected), thus delivering solutions that are useful for the whole range of real networks and (di)graph models studied in practice.

We have found that these boundaries are given by specific architectures which we generically named US and UL networks. The optimal configurations are not always unique and may vary according to size or density. US and UL networks are thus characterised by a collection of models as summarised in Fig. 1.

We have studied empirical networks from three scientific domains—neural, social and transportation. The comparison evidences that cortical connectomes are the shortest of the three classes. In fact, they are practically as short as they could possibly be and any alteration of their structure, e.g., a selective rewiring of their links, would only lead to negligible decrease of the pathlength. Over the last decade it has been discovered that brain and neural connectomes are organised into modular architectures with the cross-modular paths centralised through a rich-club^{21,22,23,24,25}. Recently, it has been shown that this type of organisation supports complex network dynamics as compared to the capabilities of other hierarchical architectures^26,27. Now, we find that cortical connectomes are also quasi-optimal in terms of pathlength. On the other extreme, transportation networks are more than five times longer than the corresponding lower limit. This contrast between cortical and transportation networks is rather intriguing since both are spatially embedded. While the aim of neural networks might be the rapid and efficient access to information within the network, transportation networks are planar and developed to service vast areas surrounding a city. Thus they are often characterised by long chains spreading out radially from a rather compact centre.

From a practical point of view, our theoretical findings solve the problem of assessing and comparing how short or how long a network is. Evaluating the length of a network with a single number—whether absolute or relative—has strong limitations and often involves arbitrary choices. The usual approach consists in defining relative metrics that normalise empirical observations $l$ with the pathlength from a model, e.g., random graphs, ring lattices or rewired networks which conserve the node degrees. The choice of the null-model depends on the particular question we may be asking about the data. We have stressed that relative metrics as $l^{\prime} =l/{l}_{r}$ and $l^{\prime} =l/{l}_{US}$ serve different purposes because ${l}_{r}$ is an expectation value (for a given generative assumption and conditional on a set of constraints) while ${l}_{US}$ is a limit. Thus, ${l}_{US}$ is free from assumptions on how empirical networks may have been generated. Relative metrics based on null-models are better suited to answer questions like “why does an empirical network take the observed value $l$?” or “how surprising is that a network takes pathlength $l$?” rather than to resolve how short or how long a network is. The US and the UL limits allow us to anchor the values of pathlength and efficiency into well-defined regions of the space of accessible outcomes, which depend on $N$ and $L$ alone. A more telling approach is then to display all the results (both the empirical observations and the expectation values arising from different null-models, e.g., generated by the recent nPSO model²⁸) into a unified representation together with the corresponding limits. Figure 4 offers a synoptic way to assess the position every network (real or model) takes in the space of global efficiencies, and thereby discloses the relations needed to interpret the results²⁹.

In addition to the limits, one may want to obtain the full distribution of pathlength and efficiencies for a given $N$ and $L$. Such a distribution would be instrumental in answering statistical questions such as “what is the most likely pathlength for networks of size $N$ and $L$ links?”. On the one hand, for fixed $N$ and $L$, the distribution will exist between the boundaries we have reported here. On the other hand, the description of the full distribution still depends on the choice of a generating mechanism, e.g., whether we consider non-isomorphic (non-labelled) networks alone, or isomorphic (labelled) ones. Regarding the likelihood of the US and the UL (di)graph families, for now we can only affirm that the UL limit is a very unlikely outcome in the case of undirected graphs (Fig. 1b) because the configurations are unique: the rewiring of a single link will reduce their pathlength. On the contrary, the US boundary is highly degenerate since any configuration with diameter ${\rm{diam=2}}$ is US.

The aim of the present paper was the study of the limits for average pathlength and efficiency. We have thus referred to small-world networks in its classical sense, paying attention only to the graph distance. Although the US and UL (di)graphs were not optimised for clustering, US graphs possess a rather small clustering (comparable to random graphs). On the contrary, the clustering of UL graphs grows very rapidly reaching values close to $C=1$, since most of their links are contained within a complete subgraph. See Supplementary Note 6.

The implications of our results transcend the purely structural study of networks. Given that the underlying patterns of connectivity very much influence dynamic phenomena, e.g., synchrony and diffusion, it remains an open question to investigate the emergent collective behaviour supported by the families of US and UL (di)graphs, and to assess their use as benchmarks for the study of dynamics in real systems.

The limits reported here are the solutions to the most basic optimisation problem for the average pathlength and global efficiency, restricted to the minimal set of constraints (number of nodes and links) inherent to all networks. While the analytic boundaries are well-defined and can be calculated, the configurations are usually degenerate. For example, in Fig. 1a we illustrated two different strategies to construct US graphs: (1) by randomly seeding links to a star graph or (2) by deliberately constructing a rich-club. While the pathlength of these constructs is the same, their dynamic properties may significantly differ.

A class of optimisation problems with practical and economic implications is that of network navigability, which is tightly related to the small-world phenomenon and the travelling salesman problem. In this case, the optimal solutions depend both on the network structure and the routing algorithm. Recent studies showed that navigability on empirical networks is efficient due to a hidden (hyperbolic) space many real networks are embedded in ref. ³⁰. Thus optimal navigability with Greedy Routing is achieved when packages are forwarded from the destination to its neighbours at closest hyperbolic distance.^28,31 It remains an open question whether among the diversity of US (di)graphs, some configurations optimise navigability with Greedy Routing against others. Finally, if the networks are embedded in space, e.g., transportation networks, identifying optimal structures implies considering a balance between their efficiency and the resources needed to build the infrastructures, or the costs associated with navigating them³², as well as the fact that in these cases the definition of shortest path and efficiency take euclidean distances into account^15,33.

In conclusion, network optimisation problems involve the maximisation of a variety of parameters. Our results are the solutions to the simplest case with a minimal set of constraints. They can serve as the starting point to inform more complex problems which include additional constraints beyond $N$ and $L$.

Methods

Length boundaries of complex networks

We now describe the principles behind the generation of US and UL (di)graphs. The formal mathematical results, including all definitions, propositions and theorems we refer to in this section are found in Supplementary Notes 1 and 2, together with the complete set of equations to analytically calculate the US and the UL boundaries. Supplementary Note 3 includes systematic numerical searches for some UL (di)graph configurations.

Undirected graphs

Our first goal is to generate US graphs, that is, graphs of arbitrary number of nodes and edges with the shortest possible pathlength. This can be achieved by adding edges to a star graph. Indeed, any arbitrary order followed to add edges to a star graph will result in an US graph. Figure 1a illustrates two different examples. One consists in seeding edges at random while in the other links are orderly planted favouring the creation of new hubs; a procedure that would eventually lead to the formation of a rich-club. The reason why the order in which edges are added is irrelevant for the value the average pathlength takes, is that the diameter of the star graph is $\delta =2$. Any further edge $(i,j)$ added results in converting an entry ${d}_{ij}=2$ in the distance matrix to ${d}_{ij}=1$. As a consequence, at fixed density, all graphs with diameter $\delta \ =\ 2$ are US and have the same pathlength. See the US graph theorem (Theorem 1) for a formal statement, and refs. ^9,10,12 for alternative proofs. The pathlength and efficiency of a US graph are given by

$${l}_{US}=2-\frac{L}{{L}_{o}}\ =\ 2-\rho$$

(3)

$${E}_{US}=\frac{1}{2}\left(\ 1+\frac{L}{{L}_{o}}\ \right)\ =\ \frac{1}{2}\left(\right.1+\rho \left)\right.,$$

(4)

where ${L}_{o}=\frac{1}{2}N(N-1)$ and $\rho := L/{L}_{o}$ is the density of the network.

To generate connected graphs of arbitrary $L$ with the longest possible pathlength, namely UL graphs, we consider the path graph as a starting point. Any link added to a path graph reduces its diameter, i.e., the distance between the nodes at the two ends. The key is thus to add new links, one-by-one, such that the diameter of the resulting network is minimally reduced at every step. This can be achieved by orderly accumulating all new edges at one end of the chain, Fig. 1b. The procedure creates complete subgraphs of size ${N}_{c}$ as $L$ grows, with ${N}_{c}=\lfloor \frac{1}{2}\left(3+\sqrt{9+8(L-N)}\right)\rfloor$ where $\lfloor \cdot \rfloor$ stands for the floor function. The remainder of the network consists of a tail of size ${N}_{t}=N-{N}_{c}$. The complete subgraph contains ${L}_{c}=\frac{1}{2}{N}_{c}({N}_{c}-1)$ edges and the tail ${L}_{t}={N}_{t}$. If $L\ \ne \ {L}_{c}+{L}_{t}$, the remaining edges are placed connecting the first node of the tail to the complete subgraph. We find that the average pathlength of an UL graph can be approximated as

$${l}_{UL}\approx 2+\rho -2\sqrt{\rho }+\frac{N}{3}\left(\right.1-3\rho +2\rho \sqrt{\rho }\ \left)\right..$$

(5)

The approximation improves as $N$ increases, incurring a relative error smaller than $1 \%$ for $N\ > \ 122$. See Theorem 3 and Supplementary Eqs. (7)–(9) for the exact solutions, and also ref. ⁹.

So far, we have only considered connected networks. When $L\ <\ N-1$ the shortest architecture (largest possible efficiency) consists of an incomplete star graph of size $N^{\prime} \ =\ L+1$. This leaves the remaining $N-N^{\prime}$ nodes isolated, Fig. 1a and Definition 1. We refer to these networks as disconnected US (dUS) graphs (Theorem 2). Once $L\ge N$, the solutions for the most efficient and US graphs are identical (i.e., star graphs with added links).

The construction of disconnected graphs with smallest efficiency is a non-Markovian process. Smallest efficiency is achieved by never having a pair of nodes indirectly connected. This can be realised by forming complete subgraphs which are mutually disconnected (Definition 4 and Proposition 1). In the special cases when $L=\frac{1}{2}M(M-1)$ for $M=2,3,\ldots ,N$, the network with smallest efficiency consists of a complete subgraph of size $M$, and $N-M$ isolated nodes, Fig. 1c. The distance between two nodes in the complete subgraph is ${d}_{ij}=1$ while all other distances are infinite. Therefore, the efficiency in these cases is exactly $\rho =\frac{L}{{L}_{o}}$. The efficiency can also be equal to $\rho$ in intermediate cases (Definition 5 and Proposition 2). We refer to these networks as disconnected UL (dUL) graphs. In summary, the efficiency of dUS and of dUL graphs are given by

$${E}_{dUS}=\frac{1}{4\ {L}_{o}}\left[\ {L}^{2}+3L\ \right]: L\ <\ (N-1),$$

(6)

$${E}_{dUL}=L/{L}_{o}=\rho: 0\ <\ L\ <\ {L}_{o}.$$

(7)

Directed graphs

We will denote the properties of digraphs with a tilde, e.g., $\tilde{L}$, $\tilde{l}$ and $\tilde{E}$. Following standard notation, we will refer to directed links as arcs. The identification of US and UL digraphs is more intricate because the conditions for a digraph to be connected are more flexible, distinguishing between weakly and strongly connected. We have found three major differences with the results for graphs. (1) The minimally connected digraph is a directed ring (DR) instead of star or path graphs. Thus, DRs are the origin for both US and UL connected digraph families. (2) The construction of US and UL digraphs is often a non-Markovian process. (3) In certain regimes of density more than one configuration compete for the optimal pathlength or efficiency.

The US graph theorem guarantees that any graph with diameter $\delta =2$ has the shortest possible pathlength regardless of its precise configuration. This result also applies to digraphs (Theorem 4) and thus any set of arcs added to a star graph will lead to an US digraph. The difference is that a star graph contains $\tilde{L}=2\ (N-1)$ arcs. Hence, the result holds for $\tilde{L}\ge 2(N-1)$. However, in the range $N\le \tilde{L}\ <\ 2\ (N-1)$ strongly connected digraphs exist, whose diameter is always larger than two. In this range the digraphs with the shortest pathlength consist of a set of directed cycles overlap** at a single hub, Fig. 1d. We name these networks flower digraphs (Definition 6). Notice that flower digraphs represent the natural transition between a DR and a star graph. The DR is the flower made of a unique cycle of length $N$ and a star graph is the flower digraph with $N-1$ “petals” of length $2$. Hence, in this regime US digraph generation is non-Markovian (Proposition 3).

Construction of UL digraphs turns rather intricate and we will provide a partial solution here. Numerical exploration with small networks revealed that, in general, more than one optimal configuration exist. See a summary of all the UL digraphs for networks of $N=5$ in Supplementary Note 3. The process is divided into two regimes, with a transition happening at $\tilde{L}^{\prime} =\frac{1}{2}N(N+1)-1$, or $\tilde{\rho }^{\prime} =\frac{1}{2}+\frac{1}{N}$. Given a DR with each node $i$ pointing to node $i+1$ (except the last is pointing to the first) any arc $i\to j$ added in the forward orientation ($i\ <\ j$) becomes a shortcut notably reducing the distance between several nodes. Arcs running in the opposite orientation ($i\to j$ with $i\ > \ j$) introduce cycles of length $j-i+1$ which only reduce the distance between the nodes participating in the cycle. Thus the strategy is to add arcs to a DR such that each new arc causes the shortest cycle(s) possible. Despite the intricacy of the problem, a particular subclass of digraphs could be found which are guaranteed to be US. Given an integer $M$, the optimal configuration with $\tilde{L}=N+\frac{1}{2}M(M-1)$ arcs consist of the superposition of a DR and what we name an $M$-backwards subgraph or $M$-BS. An $M$-BS is formed by the first $M$ nodes of the ring, with each node pointing to all its predecessors, Fig. 1e. Each $M$-BS contributes to reduce the pathlength of a DR by exactly $\Delta {l}_{M}=-\frac{1}{{\tilde{L}}_{0}}\frac{M\left(M-1\right)}{2}\left(N-\frac{M+4}{3}\right)$, see Lemma 3. After calculating the exact solution for these particular cases [Eqs. (S37)–(S39), and Proposition 4], we find that the pathlength ${l}_{UL}$ of UL digraphs, of arbitrary $\tilde{L}$, can be approximated by

$${\tilde{l}}_{UL}\approx 1+\frac{3\tilde{\rho }}{2}-\left(\frac{\tilde{\rho }}{3}+1\right)\sqrt{\frac{\tilde{\rho }}{2}}+N\left(\frac{1}{2}-\tilde{\rho }+\frac{\tilde{\rho }\sqrt{2\tilde{\rho }}}{3}\right).$$

(8)

This approximation is valid when $\tilde{\rho }\ <\ \frac{1}{2}+\frac{1}{N}$.

In the particular case when $M=N$ (or $\tilde{\rho }=\frac{1}{2}+\frac{1}{N}$) the first node receives inputs from all other nodes and the last sends outputs to all the network. All the arcs of the original DR have become bidirectional except for the one pointing from the last to the first node, Fig. 1e. Its pathlength is ${\tilde{l}}_{UL}=\frac{N+4}{6}$, Proposition 5. From this point, any further arc added will create a reciprocal link. Then, the longest pathlength is maintained if the arcs of the $M$-backwards subgraphs are symmetrised in the same order they were created, (Proposition 6). In the specific cases where $\tilde{L}=\frac{N(N+1)}{2}-1+\frac{K(K-1)}{2}$, it is possible to completely bilateralise an $M$-BS with a $K$-forward subgraph of $K$-FS giving (Remark 12)

$${\tilde{l}}_{UL}=\frac{4+N}{6}-\frac{K(K-1)}{2{\tilde{L}}_{o}}\left(N-\frac{2(K+1)}{3}\right).$$

(9)

Finally, we focus on the efficiency of networks which may be disconnected. Regarding the US boundary up to three different network configurations compete for the largest efficiency when $\tilde{L}\ <\ 2(N-1)$, Fig. 1f, g. One of the routes is non-Markovian. It consists in first creating DRs of growing size until $\tilde{L}=N$ which then naturally continues into flower digraphs. The second route is Markovian and corresponds to the directed version of the disconnected star procedure introduced for graphs. Both routes converge at $\tilde{L}=2(N-1)$ where a star graph is formed. Figure 1g shows the competition of the three models for largest efficiency for different network sizes. At larger densities, when $\tilde{L}\ge 2(N-1)$, the US theorem applies.

To construct digraphs with minimal efficiency, we seed arcs to an initially empty network such that it contains as many weakly connected nodes as possible. We do so by adding $M$-backward subgraphs of increasing $M$ to the empty graph, Fig. 1h. The distance matrix of such a digraph contains $\tilde{L}$ entries with ${d}_{ij}=1$ and all remaining entries are infinite. Thus, its efficiency is ${\tilde{E}}_{dUL}=\tilde{L}/{\tilde{L}}_{0}=\tilde{\rho }$, see Proposition 7. Arcs can be seeded following this procedure until $\tilde{L}={\tilde{L}}_{o}/2$, corresponding to the largest $M$-BS, with $M=N$. At this point, the network consist of the densest possible directed acyclic graph. Any subsequent arc added will introduce at least one cycle. To conserve the lowest efficiency possible, new arcs need to cause cycles with a minimal impact over the path. This is achieved, again, by bilateralising the $M$-backwards subgraphs in the forward direction (Proposition 9). In these special cases, the efficiency of the digraphs equals their link density: ${\tilde{E}}_{dUL}=\tilde{\rho }$. Intermediate values of $\tilde{L}$ which do not meet these criteria, may display small departures from ${\tilde{E}}_{dUL}=\tilde{\rho }$, with the error decreasing as $N$ grows.

Synthetic networks

Random graphs were generated following the random generator usually known as the $G(n,M)$ model, which guarantees all realisations have the same number of links. In our nomenclature $n\to N$ and $M\to L$ (or $M\to \tilde{L}$). Scale-free networks were generated following the method in ref. ¹³. A power exponent of $\gamma =3.0$ was used. The resulting SF digraphs would display correlated in- and out-degrees but not necessarily identical. The range of densities for scale-free networks was restricted to $\rho \in [0.0001,0.1]$ because for $\rho \ > \ 0.1$ the power-law scaling of the degree distribution is lost due to saturation of the hubs. For each value of density an ensemble of $1000$ realisations was generated. All synthetic networks were generated using the package GAlib: a library for graph analysis in Python (https://pypi.org/project/galib/).

Empirical datasets

The empirical networks employed are well known in the literature and have been often used as benchmarks, except for the local transportation of Chicago which we have assembled for the present manuscript. These datasets represent a heterogeneous sample of networks with a variety of sizes and densities, both directed and undirected, see Table 1 and Supplementary Note 7 for details. Those datasets are available online from different sources. We have constructed the local transportation network of Chicago for the present manuscript by combining the Chicago Transit Authority (CTA) and the METRA commuter rail systems based on the official transportation maps (http://www.transitchicago.com/). The network consists of 376 stations, of them 142 are serviced by the CTA system and 236 by the METRA railroad. We considered two station to be linked also if they were marked as accessible at a short walking distance, giving rise to a total 402 links and a density of $\rho =0.006$. Since several stations in the network are named the same, an identifier to the line they belong was added.