Abstract
The intertwining between spin, charge, and lattice degrees of freedom can give rise to unusual macroscopic quantum states, including high-temperature superconductivity and quantum anomalous Hall effects. Recently, a charge density wave (CDW) has been observed in the kagome antiferromagnet FeGe, indicative of possible intertwining physics. An outstanding question is that whether magnetic correlation is fundamental for the spontaneous spatial symmetry breaking orders. Here, utilizing elastic and high-resolution inelastic x-ray scattering, we observe a c-axis superlattice vector that coexists with the 2\(\times\)2\(\times\)1 CDW vectors in the kagome plane. Most interestingly, between the magnetic and CDW transition temperatures, the phonon dynamical structure factor shows a giant phonon-energy hardening and a substantial phonon linewidth broadening near the c-axis wavevectors, both signaling the spin-phonon coupling. By first principles and model calculations, we show that both the static spin polarization and dynamic spin excitations intertwine with the phonon to drive the spatial symmetry breaking in FeGe.
Similar content being viewed by others
Introduction
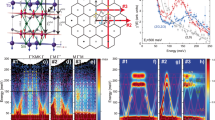
The combination of magnetism and characteristic electronic structures of the kagome lattice, including flat-band1,2,3, Dirac-fermion4,5,6,7, and van Hove singularities4) point is resolution limited in the entire temperature range, consistent with the absence of longitudinal and transverse acoustic phonon energy anomaly at the M and L point.
a and b experimental and DFT S(Q, ω) along the Γ(0, 0, 4)-M(0.5, 0, 4)-L(0.5, 0, 4.5)-A(0, 0, 4.5)-Γ(0, 0, 4) direction. As described in Methods, the IXS intensity is dominated by the lattice distortions along the crystal c-axis. The IXS data shown in a were collected at 200 K. c Extracted phonon dispersion along the M-Γ-A direction at 200 (cyan) and 420 K (orange). The dashed rectangle highlights the temperature dependent phonon energy renormalization near the A point. d and e temperature dependent IXS spectra at the M and A point. Dashed curves are fittings of the experimental data (see Methods). Blue, green and orange circles represent 110, 300 and 420 K, respectively. f Temperature dependence of the fitted phonon peak positions at the A (open purple circles) and M (open green squares) point. g Temperature dependence of the fitted phonon peak width at the A (open purple circles) and M (open green squares) point. Dashed line represents the instrumental energy resolution. h Dynamical spin-phonon coupling. Top panel shows the second-order Feynman diagram for the phonon self-energy. Dashed and solid lines represent the phonon and magnon Green’s functions, respectively. iωn and \(i{\xi }_{{{{{{\rm{m}}}}}}}\) are bosonic Matsubara frequencies. Bottom panel shows a schematic of the dynamical spin-phonon coupling in an effective 1-dimensional spin chain with A-AFM. The magnon-phonon scattering induces strong the phonon self-energy effects and yields a phonon-energy hardening and phonon-linewidth broadening near the charge dimerization A-point (see Supplementary Fig. 11). The vertical error bars shown in c–f represent 1-standard deviation from either Poissonian statistics or least-squares fitting. The vertical error bars shown in g represent the experimental step size that is about 3 times larger than the fitting error bars.
The observed phonon hardening and broadening above the TCDW in FeGe are fundamentally different from the Kohn anomaly in electron-phonon coupled CDW systems and the emergent amplitude mode below the TCDW19, 29,30,31. These phonon anomalies are, however, captured by the dynamical spin-phonon coupling picture shown in Fig. 3h. The second order Feynman diagram depicts a phonon with energy, ωn, and momentum, q, scatters into two magnons with (ξm, k) and (ωn-ξm, q-k). As we show in more details in the Supplementary Discussion and Supplementary Fig. 11, this dynamical spin-phonon interaction yields strong phonon self-energy effect, including the phonon energy hardening and phonon linewidth broadening near the A-point, in agreement with experimental observations. Interestingly, similar phonon anomalies were observed in Kondo insulator FeSi33 and spin-Peierls compound CuGeO334,35, supporting a ubiquitous phonon hardening and broadening in spin-phonon coupled systems. The observation of superlattice peaks at \({Q}_{A}^{\perp }\) and the associated giant phonon anomalies constitute our main experimental observations.
Motivated by these experimental results, we perform DFT + U calculations for the A-AFM phase of FeGe at the zero temperature to understand the interplay between static spin-polarizations and the lattice distortions in the CDW phase. Fig. 4a–c show the calculated phonon spectra of FeGe in the A-AFM phase as increasing Hubbard U. We find that the experimentally observed phonon modes shown in Fig. 3a exhibit the most dramatic change as increasing U with an energy minimum at the L point for U < 2 eV. This observation indicates that stronger electronic correlations and spin-polarizations tend to induce a lattice instability in FeGe. Interestingly, this mode corresponds to atomic vibrations that are mainly composed of out-of-phase c-axis lattice distortions between adjacent Fe-Ge kagome layers, consistent with experimentally observed superlattice peaks at \({Q}_{A}^{\perp }\). To understand the nature of the 2\(\times\)2\(\times\)2 superstructure, we take the equal phase and amplitude superpositions of the experimentally observed phonon mode at the three equivalent L-points as shown in Fig. 4d. The arrows point the movement of Fe and Ge atoms. In kagome layers, Fe and Ge atoms move out-of-plane along the c-axis. The Ge-1 atoms are divided into out-of-phase Ge-1a (blue) and Ge-1b (light blue) groups, where Ge-1a has a much larger atomic movement than that of Ge-1b, forming Ge-1 dimers along the c-axis. The honeycomb layers of Ge−2 atoms (grey) show in-plane Kekulé-type distortions36,37. Starting from this 2\(\times\)2\(\times\)2 supercell that preserves the P6/mmm space group, we relax the internal atomic positions. Fig. 4e shows the energy difference between the 2\(\times\)2\(\times\)2 superstructure and the ideal kagome phase, \(\Delta E={E}_{{Charge}-D{imer}}-{E}_{{Kagome}}\), which decreases as increasing U. Intriguingly, the 2\(\times\)2\(\times\)2 superstructure is already an energetically favored phase at U = 0 and becomes even more robust with increasing U accompanied by the increase in the static moment. These results suggest that the magnitude of the static spin-polarization is important to stabilize the 2\(\times\)2\(\times\)2 superstructure with large c-axis lattice distortions in the Kagome plane. Furthermore, as we show in Fig. 4e, by forming this 2\(\times\)2\(\times\)2 superstructure, the ordered magnetic moment is further enhanced by 0.01 ~ 0.05 \({\mu }_{B}\)/Fe at U = 0 ~ 3 eV, consistent with the previous neutron scattering study24. It is important to point out that the experimentally determined static spin moment is more consistent with DFT + U calculations at U = 0 (Fig. 4a), therefor the static spin-moment induced phonon softening effect at elevated temperature will be neglectable and the dominated phonon anomaly is expected to arise from the dynamical magnon-phonon coupling as shown in Fig. 3.
a–c, The DFT + U calculated phonon spectra of FeGe in the AFM phase as increasing Hubbard U. The phonon spectra are plotted with respect to the non-magnetic BZ of FeGe. The calculated ordered magnetic moments per Fe atom, M, are 1.50, 2.35 and 2.57 μB for U = 0, 2 and 3 eV, respectively. The calculated M at U = 0 eV is closer to the experimental value. The red curve corresponds to the experimentally observed phonon modes which show the most dramatic change as the spin-polarization is enhanced. The red circles highlight the \({B}_{1u}\) phonon mode at the L-point, which has the lowest energy along the A-L-H-A direction. The energy of the \({B}_{1u}\) mode and nearby phonon dispersion at U = 0 matches the IXS determined dynamical structure factor shown in Fig. 3a. d The equal phase and amplitude superposition of the \({B}_{1u}\) modes at the three equivalent L-points yields a charge-dimerized 2\(\times\)2\(\times\)2 superstructure. The arrows indicate the movements of Fe and Ge atoms. In kagome layers, Fe and Ge atoms move out-of-plane to form dimers along c-axis. Ge-1a (blue) and Ge-1b (light blue) have out-of-phase vibrations. Ge-1a has much larger movement than Ge-1b. The honeycomb layers of Ge−2 (grey) atoms show in-plane Kekulé-type distortions. e Left y-axis shows the DFT + U calculated energy difference between the charge-dimerized 2\(\times\)2\(\times\)2 superstructure and the ideal Kagome phase, \(\Delta E={E}_{{Charge}-{Dimer}}-{E}_{{Kagome}}\). Right y-axis shows the calculated ordered magnetic moment of the 2\(\times\)2\(\times\)2 superstructure (blue solid) and ideal Kagome (red dashed) phases, respectively. The magnetic moments are enhanced by 0.01 ~ 0.05 \({\mu }_{B}\)/Fe by forming the 2\(\times\)2\(\times\)2 superstructure.
Our experimental and numerical results support a spin-phonon coupling picture for the emergence of CDW in FeGe. Near TCDW, the energy gain by forming a 2\(\times\)2\(\times\)2 superstructure with enhanced static moment overcomes the energy cost of lattice distortions and gives rise to a weak first order phase transition38. The presence of large itinerant electrons allows additional energy gain by removing the high density-of-states near EF39. We emphasize, however, that the A-AFM induced van Hove singularity near EF may only plays a minor role for the CDW in FeGe for the following reasons: first, the conventional electron-phonon coupling tends to favor lattice distortions parallel to the nesting vectors different from the experimental and DFT observations. Second, the strong temperature dependent phonon anomaly near \({Q}_{A}^{\perp }\) and the absence of phonon anomaly at \({Q}_{M}^{//}\) are incompatible with a nesting driven CDW picture.
Methods
Sample preparation and characterizations
Single crystals of B35-type FeGe were grown via chemical vapor transport method. Stoichiometric iron powders (99.99%) and germanium powders (99.999%) were mixed and sealed in an evacuated quartz tube with additional iodine as the transport agent. The quartz tube was then loaded into a two-zone horizontal furnace with a temperature gradient from 600 °C (source) to 550 °C (sink). After 12 days growth, FeGe single crystals with typical size 1.5 × 1.5 × 3 mm3 can be obtained in the middle of the quartz tube.
Elastic X-ray scattering
The single crystal elastic X-ray diffraction was performed at the 4-ID-D beamline of the Advanced Photon Source (APS), Argonne National Laboratory (ANL). The incident photon energy was set to 11 keV, slightly below the Ge K-edge to reduce the fluorescence background. The X-rays higher harmonics were suppressed using a Si mirror and by detuning the Si (111) monochromator. Diffraction was measured using a vertical scattering plane geometry and horizontally polarized (σ) X-rays. The incident intensity was monitored by a He filled ion chamber, while diffraction was collected using a Si-drift energy dispersive detector with approximately 200 eV energy resolution. The sample temperature was controlled using a He closed cycle cryostat and oriented such that X-rays scattered from the (001) surface.
meV-resolution inelastic X-ray scattering
The experiments were conducted at beam line 30-ID-C (HERIX) at APS, ANL40. The highly monochromatic x-ray beam of incident energy Ei = 23.7 keV (λ = 0.5226 Å) was focused on the sample with a beam cross section of ∼35 × 15 μm2 (horizontal × vertical). The overall energy resolution of the HERIX spectrometer was ΔE ∼ 1.5 meV (full width at half maximum). The measurements were performed in reflection geometry. Under this geometry, IXS is primarily sensitive the lattice distortions along the crystal c-axis. This geometry selectively enhances the unstable phonon modes predicted in the DFT calculations. Typical counting times were in the range of 120 to 240 seconds per point in the energy scans at constant momentum transfer Q. H, K, L are defined in the hexagonal structure with a = b = 4.97 Å, c = 4.04 Å at the room temperature.
Curve Fitting
The total energy resolution ΔE = 1.5 meV is calibrated by fitting the elastic peak to a pseudo-voigt function:
where the energy resolution is the FWHM.
IXS directly probes the phonon dynamical structure factor, \(S({{{{{\bf{Q}}}}}},\, \omega )\). The IXS cross-section for solid angle dΩ and bandwidth dω can be expressed as:
where k and \({{{{{\boldsymbol{\epsilon }}}}}}\) represent the scattering vector and x-ray polarization and \(i\) and \(f\) denote initial and final states. r0 is the classical radius of the electron. In a typical measurement, the energy transfer ω is much smaller than the incident photon energy (23.71 keV in our study). Therefore, the term \(\frac{{{{{{{\boldsymbol{k}}}}}}}_{f}}{{{{{{{\boldsymbol{k}}}}}}}_{i}}\) ~ 1, and \(\frac{{d}^{2}\sigma }{d\Omega {{{{{\rm{d}}}}}}{{{{{\rm{\omega }}}}}}}\propto S({{{{{\bf{Q}}}}}},\, \omega )\).
\(S({{{{{\bf{Q}}}}}},\, \omega )\) is related to the imaginary part of the dynamical susceptibility, \({\chi }^{{\prime\prime}}\left({{{{{\bf{Q}}}}}},\, \omega \right)\), through the fluctuation-dissipation theorem:
Where \(\chi ^{\prime\prime}({{{{{\bf{Q}}}}}},\, \omega )\) can be described by the damped harmonic oscillator form, which has antisymmetric Lorentzian lineshape:
here i indexes the different phonon peaks.
The phonon peak can be extracted by fitting the IXS spectrum at constant-momentum transfer Q, using Eqs. (3) and (4). Due to the finite experimental resolution, the IXS intensity is a convolution of \(S\left({{{{{\bf{Q}}}}}},\, \omega \right)\) and the instrumental resolution function, R(ω):
Here R(ω) was determined by fitting of the elastic peak.
ARPES experiment
The ARPES experiments are performed on single crystals FeGe. The samples are cleaved in situ in a vaccum better than 5 × 10−11 torr. The experiment is performed at beam line 21-ID-1 at the NSLS-II. The measurements are taken with synchrotron light source and a Scienta-Omicron DA30 electron analyzer. The total energy resolution of the ARPES measurement is approximately 15 meV. The sample stage is maintained at T = 30 K throughout the experiment.
DFT + U calculations
DFT + U calculations are performed using Vienna ab initio simulation package (VASP)41. The exchange-correlation potential is treated within the generalized gradient approximation (GGA) of the Perdew-Burke-Ernzerhof variety42. The simplified approach introduced by Dudarev et al. (LDAUTYPE = 2) is used43. We used experimental lattice parameters of FeGe and FeSn24,44. Phonon calculations are performed in the A-type AFM phase with a \(2\times 2\times 1\) supercell (with respect to the AFM cell), using both the density-functional-perturbation theory (DFPT)45 and frozen phonon approaches, combined with the Phonopy package46. The two approaches yield identical results. The internal atomic positions of the charge-dimerized \(2\times 2\times 2\) superstructure is relaxed with the initial atomic distortions shown in Fig. 4d, until the force is less than 0.001 eV/Å for each atom. Integration for the Brillouin zone is done using a Γ-centered 8 × 8 × 10 k-point grids for the \(2\times 2\times 2\) supercell and the cutoff energy for plane-wave-basis is set to be 500 eV. Besides the \(2\times 2\times 2\) lattice distortion ansatz, we have also employed other lattice distortion ansatz, including \(1\times 2\times 2\), \(\sqrt{3}\times \sqrt{3}\times 2\) and \(\sqrt{5}\times \sqrt{5}\times 2\). All these ansata yield ground state energies higher than the \(2\times 2\times 2\) superstructure and the original ideal Kagome structure.
DFT + DMFT calculations
The fully charge self-consistent DFT + DMFT47 calculations are performed in the A-type AFM phase using an open-source code of DFT+embedded DMFT developed by Haule et al., based on Wien2k package48. We choose a hybridization energy window from −10 eV to 10 eV with respect to the Fermi level. All the five \(3d\) orbitals on an Fe site are considered as correlated ones, and a local Coulomb interaction Hamiltonian of Ising form is applied with varied Hubbard U and Hund’s coupling \({J}_{H}\) as shown in the main text. We use the continuous time quantum Monte Carlo49 as the impurity solver and an “exact” double counting scheme by Haule50,51. To compute the spectral function, the electron self-energy on real frequency is obtained by the maximum entropy analytical continuation method. The SOC is not included in the DFT + DMFT calculations since the SOC strength of Fe-\(3d\) orbitals is small and will rarely change the electronic correlations. All the calculations are performed at T = 80 K.
Electron-phonon vs spin-phonon driven CDW
From an energy point of view, the electron-phonon coupling driven CDW emphasizes the competing energy scales of charge condensation energy and lattice deformation energy, whereas the spin-phonon coupling highlights the magnetic energy gain by forming a CDW. To understand the spin-phonon coupling driven CDW, one can consider a simplified 1D Heisenberg model:
Here \(J\) is the antiferromagnetic exchange energy, \({{{{{{\boldsymbol{S}}}}}}}_{i}\) is the local spin. \({\Delta }_{i}={(-1)}^{i}\delta,\, \delta \ge 0\) is the lattice distortion at bond i, connecting sites i and i + 1, and \(k\) is the elastic constant. A CDW is energetically favored if the energy gain in the first magnetic term is greater than the energy cost of the second elastic term. This is rather static spin-phonon coupling. When the system is magnetically ordered, the energetics of this system is described by quasiparticles, i.e. magnons and phonons, thus the dynamical spin-phonon coupling becomes crucial. In the Supplementary Discussion (Section “Phonon lifetime by two magnon excitations”), we build a magnon-phonon coupling model on a 1D AFM Heisenberg chain. One of the consequences of such dynamical spin-phonon coupling appears as the phonon lifetime, which allows the direct comparison between experimental data and a theoretical prediction.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Tang, E., Mei, J. W. & Wen, X.-G. High-temperature fractional quantum hall states. Phys. Rev. Lett. 106, 236802 (2012).
Okamoto, S. et al. Topological flat bands in a Kagome lattice multiorbital system. Commun. Phys. 5, 198 (2022).
Kang, M. et al. Dirac fermions and flat bands in the ideal Kagome metal FeSn. Nat. Mater. 19, 163–169 (2020).
Ye, L. D. et al. Massive Dirac fermions in a ferromagnetic Kagome metal. Nature 555, 638–642 (2018).
Liu, D. F. et al. Magnetic Weyl semimetal phase in a Kagome crystal. Science 365, 1282–1285 (2019).
Yin, J.-X., Pan, S. H. & Hasan, M. Z. Probing topological quantum matter with scanning tunnelling microscopy. Nat. Rev. Phys. 3, 249 (2021).
Yin, J. X. et al. Quantum-limit Chern topological magnetism in TbMn6Sn6. Nature 583, 533–536 (2020).
Wang, W.-S., Li, Z.-Z., **ang, Y.-Y. & Wang, Q.-H. Competing electronic orders on kagome lattices at van hove filling. Phys. Rev. B 87, 115135 (2013).
Kiesel, M. L., Platt, C. & Thomale, R. Unconventional fermi surface instabilities in the kagome Hubbard model. Phys. Rev. Lett. 110, 126405 (2013).
Ortiz, B. R. et al. CsV3Sb5: A Z2 Topological Kagome Metal with a Superconducting Ground State. Phys. Rev. Lett. 125, 247002 (2020).
Feng, X., Jiang, K., Wang, Z. & Hu, J. P. Chiral flux phase in the kagome superconductor AV3Sb5. Sci. Bull. 66, 1384 (2021).
Denner, M. M., Thomaly, R. & Neupert, T. Analysis of Charge Order in the Kagome Metal AV3Sb5 (A=K, Rb, Cs). Phys. Rev. Lett. 127, 217601 (2021).
Lin, Y. P. & Nandkishore, R. M. Complex charge density waves at van Hove singularity on hexagonal lattices: Haldane-model phase diagram and potential realization in kagome metals AV3Sb5. Phys. Rev. B 104, 045122 (2021).
Park, T., Ye, M. & Balents, L. Electronic instabilities of kagome metals: Saddle points and Landau theory. Phys. Rev. B 104, 035142 (2021).
Christensen, M. H., Birol, T., Andersen, B. M. & Fernandes, R. M. Theory of the charge density wave in AV3Sb5 kagome metals. Phys. Rev. B 104, 214513 (2021).
Jiang, Y.-X. et al. Unconventional chiral charge order in kagome superconductor KV3Sb5, Nat. Mater. https://doi.org/10.1038/s41563-021-01034-y 2021.
Mielke III, C. et al. Time-reversal symmetry-breaking charge order in a kagome superconductor. Nature 502, 245–250 (2022).
Yang, S.-Y. et al. Giant, unconventional anomalous Hall effect in the metallic frustrated magnet candidate, KV3Sb5. Sci. Adv. 6, adv.abb6003, https://doi.org/10.1126/sci- (2020).
Li, H. et al. Observation of Unconventional Charge Density Wave without Acoustic Phonon Anomaly in Kagome Superconductors AV3Sb5. Phys. Rev. X 11, 031050 (2021).
Miao, H. et al. Geometry of the charge density wave in the kagome metal AV3Sb5. Phys. Rev. B 104, 195132 (2021).
Zhao, H. et al. Cascade of correlated electron states in the kagome superconductor CsV3Sb5. Nature 599, 216–221 (2021).
Nie, L. et al. Charge-density-wave driven electronic nematicity in a kagome superconductor. Nature 604, 59–64 (2022).
Li, H. et al. Discovery of conjoined charge density waves in the kagome superconductor CsV3Sb5. Nat. Commun. 13, 6348 (2022).
Teng, X. et al. Discovery of charge density wave in a correlated Kagome lattice antiferromagnet. Nature 609, 490–495 (2022).
Yin, J. X. et al. Discovery of charge order and corresponding edge state in Kagome magnet FeGe. Phys. Rev. Lett. 129, 166401 (2022).
Tranquada, J. et al. Evidence of stripe correlations of spins and holes in copper oxide superconductor. Nature 375, 561–563 (1995).
Miao, H. et al. High-temperature charge density wave correlations in La1.875Ba0.125CuO4 without spin-charge locking. Proc. Natl Acad. Sci. Usa. 114, 12430 (2017).
Hill, J., Helgesen, G. & Gibbs, D. X-ray scattering study of charge- and spin-density waves in chromium. Phys. Rev. B 51, 10336 (1995).
Hoesch, M., Bosak, A., Chernyshov, D., Berger, H. & Krisch, M. Giant Kohn Anomaly and the Phase Transition in Charge Density Wave ZrTe3. Phys. Rev. Lett. 102, 086402 (2009).
Weber, F. et al. Extended phonon collapse and the origin of the charge-density wave in 2H-NbSe2. Phys. Rev. Lett. 107, 107403 2011).
Miao, H. et al. Incommensurate phonon anomaly and the nature of charge density waves in cuprates. Phys. Rev. X 8, 011008 (2018).
Li, H. et al. Giant phonon anomalies in the proximate Kitaev quantum spin liquid α-RuCl3. Nat. Commun. 12, 3513 (2021).
Krannich, S. et al. Magnetic moments induced strong phonon renormalization in FeSi. Nat. Commun. 6, 8961 (2015).
Braden, M. et al. Spin-phonon coupling in CuGeO3. Phys. Rev. Lett. 80, 3634 (1998).
Gros, C. & Werner, R. Dynamics of the Peierls-active phonon modes in CuGeO3. Phys. Rev. B 58, R14677 (1998).
Kekulé, A. Studies on aromatic compounds. Ann. Chem. Pharm. 137, 129 (1865).
Shao, S. et al. Charge density wave interaction in a Kagome-honeycomb antiferromagnet. ar**v: 2206.12033.
Binder, K. Theory of first-order phase transitions. Rep. Prog. Phys. 50, 783 (1987).
Teng, X. et al. Magnetism and charge density wave order in Kagome FeGe. Nat. Phys. https://doi.org/10.1038/s41567-023-01985-w (2023).
Toellner, T., Alatas, A. & Said, A. Six-reflection meV-monochromator for synchrotron radiation. J. Synchrotron Radiat. 18, 605 (2011).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study. Phys. Rev. B 57, 1505 (1998).
Meier, W. R. et al. flat bands in the CoSn-type compounds. Phys. Rev. B 102, 075148 (2020).
Donze, X. & Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 55, 10355 (1997).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Georges, A. et al. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13 (1996).
Haule, K., Yee, C.-H. & Kim, K. Dynamical mean-field theory within the full-potential methods: electronic structure of CeIrIn5, CeCoIn5, and CeRhIn5. Phys. Rev. B 81, 195107 (2010).
Gull, E. et al. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 83, 349 (2011).
Haule, K. Exact double counting in combining the dynamical mean field theory and the density functional theory. Phys. Rev. Lett. 115, 196403 (2015).
Wu, X. et al., Annealing tunable charge density wave order in a magnetic kagome material FeGe. ar** Hu, H. C. Lei, Brain Sales, Jiaqiang Yan, Binghai Yan, Ming Yi, Zhida Song, and Jianzhou Zhao for stimulating discussions. This research was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division (x-ray and ARPES measurement and model analysis). This research used resources (beamline 4ID and 30ID) of the Advanced Photon Source, a U.S. DOE Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. ARPES measurements used resources at 21-ID-1 beamlines of the National Synchrotron Light Source II, a US Department of Energy Office of Science User Facility operated for the DOE Office of Science by Brookhaven National Laboratory under contract no. DE-SC0012704. T.T. Z. and S. M. acknowledge support from Tokodai Institute for Element Strategy (TIES) funded by MEXT Elements Strategy Initiative to Form Core Research Center Grants No. JPMXP0112101001, JP18J23289, JP18H03678, and JP22H00108. J.X.Y. acknowledges startup funding from the Southern University of Science and Technology. X.L.W. and A.F.W. acknowledge the support of the National Natural Science Foundation of China (Grant No. 12004056). T.T.Z. also acknowledges the support of the Japan Society for the Promotion of Science (JSPS), KAKENHI Grant No. JP21K13865. Y.L.W. acknowledges the support of the National Natural Science Foundation of China (No. 12174365). The DFT and DFT + DMFT calculations were performed on ThianHe-1A, the National Supercomputer Center in Tian**, China. R.T. acknowledges the support from The São Paulo Research Foundation, FAPESP (Grant No. 2021/11170-0).
Author information
Authors and Affiliations
Contributions
H.M., A.F.W., Y.L.W. and S.O. conceived the project. H.M., H.X.L, G.F., J.X.Y. and R.S. performed the elastic X-ray scattering measurement. H.M., H.X.L., G.F. and A.S. performed the inelastic X-ray scattering. H.M., H.X.L., H.N.L., T.Y., E.V. performed the ARPES measurement. X.L.W. and A.F.W. grew the single crystals of FeGe. T.T.Z. and S.M. calculated the phonon dynamical structure factor. Y.L.W. performed DFT+U and DFT+DMFT calculations for FeGe and FeSn. L.X.F., K.J. and S.O. performed the 1D model Analysis. H.M., T.T.Z., S.O. and Y.L.W. wrote the paper with inputs from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Meng Wang, and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Miao, H., Zhang, T.T., Li, H.X. et al. Signature of spin-phonon coupling driven charge density wave in a kagome magnet. Nat Commun 14, 6183 (2023). https://doi.org/10.1038/s41467-023-41957-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-41957-5
- Springer Nature Limited
This article is cited by
-
Competing itinerant and local spin interactions in kagome metal FeGe
Nature Communications (2024)
-
Softening of a flat phonon mode in the kagome ScV6Sn6
Nature Communications (2023)
-
Competing charge-density wave instabilities in the kagome metal ScV6Sn6
Nature Communications (2023)