On a Chirp-Like Model and Its Parameter Estimation Using Periodogram-Type Estimators

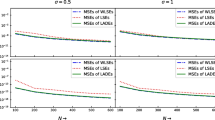
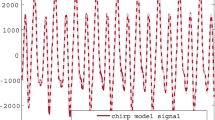
Abstract

Parametric modelling of physical phenomena has received a great deal of attention in the signal processing literature. Different models like ARMA models, sinusoidal models, harmonic models, models with amplitude modulation, models with frequency modulation and their different versions and combinations have been used to describe natural and synthetic signals in a wide range of applications. Two of the classical models that were considered by Professor C. R. Rao were one-dimensional superimposed exponential model and two-dimensional superimposed exponential model. In this paper, we consider parameter estimation of a newly introduced but related model, called a chirp-like model. This model was devised as an alternative to the more popular chirp model. A chirp-like model overcomes the problem of computational difficulty involved in fitting a chirp model to data to a large extent and at the same time provides visually indistinguishable results. We search the peaks of a periodogram-type function to estimate the frequencies and chirp rates of a chirp-like model. The obtained estimators are called approximate least squares estimators (ALSEs). We also put forward a sequential algorithm for the parameter estimation problem which reduces the computational load of finding the ALSEs significantly. Large-sample properties of the proposed estimators are investigated and the results indicate strong consistency and asymptotic normality of the ALSEs as well as the sequential ALSEs. The performance of the estimators is analysed in an extensive manner both on synthetic as well as real world signals and the results indicate that the proposed methods of estimation provide reasonably accurate estimates of frequencies and frequency rates.

Appendices

Appendices

Preliminary Results

In this section, we provide some number theory results and conjectures. These are necessary preliminary for the development of the analytical properties of the proposed sequential estimators.

Lemma 1

If $\phi \in (0, \pi )$, then the following hold true:

• (a) $\lim \limits _{N \rightarrow \infty } \frac{1}{N} \sum \limits _{t=1}^{N}\cos (\phi t) = \lim \limits _{N \rightarrow \infty } \frac{1}{N} \sum \limits _{t=1}^{N}\sin (\phi t) = 0.$

• (b) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \cos ^2(\phi t) = \lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \sin ^2(\phi t) = \frac{1}{2(k+1)};\ k = 0, 1, 2, \cdots .$

• (c) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \sin (\phi t) \cos (\phi t) = 0;\ k = 0, 1, 2, \cdots .$

Proof

Refer to Kundu and Nandi [14]. $\square$

Lemma 2

If $\phi \in (0, \pi )$, then except for a countable number of points, the following hold true:

• (a) $\lim \limits _{N \rightarrow \infty } \frac{1}{N} \sum \limits _{t=1}^{N}\cos (\phi t^2) = \lim \limits _{N \rightarrow \infty } \frac{1}{N} \sum \limits _{t=1}^{N}\sin (\phi t^2) = 0.$

• (b) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \cos ^2(\phi t^2) = \lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \sin ^2(\phi t^2) = \frac{1}{2(k+1)};\ k = 0, 1, 2, \cdots .$

• (c) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \sin (\phi t^2) \cos (\phi t^2) = 0;\ k = 0, 1, 2, \ldots .$

Proof

Refer to Lahiri [15]. $\square$

Lemma 3

If $(\phi _1, \phi _2) \in (0, \pi ) \times (0, \pi )$, then except for a countable number of points, the following hold true:

• (a) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\cos (\phi _2 t^2) =$ $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\sin (\phi _2 t^2) = 0$

• (b) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t)\cos (\phi _2 t^2) =$ $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t)\sin (\phi _2 t^2) = 0$

$k = 0, 1, 2, \cdots$

Proof

This proof follows from the number theoretic result proved by Lahiri [15] (see Lemma 2.2.1 of the reference). $\square$

Lemma 4

If X(t) satisfies Assumptions 1, 2and3, then for $k \geqslant 0$:

(a) $\sup \limits _{\phi } \bigg |\frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k X(t)e^{i(\phi t)}\bigg | \xrightarrow {a.s.} 0$            (b) $\sup \limits _{\phi } \bigg |\frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k X(t)e^{i(\phi t^2)}\bigg | \xrightarrow {a.s.} 0$

Proof

These can be obtained as particular cases of Lemma 2.2.2 of Lahiri [15]. $\square$

The following conjecture is derivative of the famous number theory conjecture of Montgomery [18]. One may refer to Lahiri [15] for details. Although these conjectures have not been proved theoretically, extensive numerical simulations indicate their validity.

Conjecture 1

If $(\phi _1, \phi _2) \in (0, \pi ) \times (0, \pi )$, then except for a countable number of points, the following hold true:

• (a) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t^2) = \lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t^2) = 0$

• (b) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\cos (\phi _2 t) =$ $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\sin (\phi _2 t) = 0$

• (c) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t)\sin (\phi _2 t) =$ $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\cos (\phi _2 t^2) = 0$

• (d) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\sin (\phi _2 t^2) =$ $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k \sqrt{N}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t)\cos (\phi _2 t^2) = 0$

• (e) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k \sqrt{N}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t)\sin (\phi _2 t^2) = 0\quad k = 0, 1, 2, \ldots$

.

Consistency of the Sequential ALSEs

To prove the consistency of the sequential ALSEs of the non-linear parameters, we need the following two lemmas:

Lemma 5

Consider the set $S_{c_1}^{(j)} = \{\alpha _j: |\alpha _j - \alpha _j^0| > c_1\}$; $j = 1, \ldots , p$. If for any $c_1 > 0$, the following holds true:

$$\begin{aligned} \limsup \sup \limits _{S_{c_1}^{(1)}} \frac{1}{N} (I_{2j-1}(\alpha _j) - I_{2j-1}(\alpha _j^0)) < 0 \text{ a.s., } \end{aligned}$$

(13)

then ${\hat{\alpha }}_j \xrightarrow {a.s.} \alpha _j^0$ as $N \rightarrow \infty$. Note that $I_{2j-1}(\alpha _j)$ can be obtained by replacing y(t) by $y_{2j-1}(t)$ and $\alpha$ by $\alpha _j$ in Eq. (6).

Proof

This proof follows along the same lines as the proof of Lemma 2A.2 in Grover [19]. $\square$

Lemma 6

Consider the set $S_{c_2}^{(k)} = \{\beta _k: |\beta _k - \beta _k^0| > c_2\}$; $k = 1, \ldots , q$. If for any $c_2 > 0$, the following holds true:

$$\begin{aligned} \limsup \sup \limits _{S_{c_2}^{(1)}} \frac{1}{N} (I_{2k}(\beta _k) - I_{2k}(\beta _k^0)) < 0 \text{ a.s., } \end{aligned}$$

then ${\hat{\beta }}_k \xrightarrow {a.s.} \beta _k^0$ as $N \rightarrow \infty$. Note that $I_{2k}(\beta _k)$ can be obtained by replacing y(t) by $y_{2k}(t)$ and $\beta$ by $\beta _k$ in Eq. (8).

Proof

This proof follows along the same lines as the proof of Lemma 2A.2 in Grover [19]. $\square$

Proof of Theorem 1

Here again, for convenience of notation, we assume $p = 2$ and $q = 2$. Now we first prove the consistency of the non-linear parameter ${\hat{\alpha }}_1$. For that we consider the following difference:

$$\begin{aligned}\begin{aligned}&\frac{1}{N} [I_1(\alpha _1) - I_1(\alpha _1^0)] \\&\quad = \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_1(t)\cos (\alpha _1 t)\bigg \}^2 + \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_1(t) \sin (\alpha _1 t)\bigg \}^2 \\&\qquad - \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_1(t)\cos (\alpha _1^0 t)\bigg \}^2- \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_1(t) \sin (\alpha _1^0 t)\bigg \}^2 \\ \end{aligned}\end{aligned}$$

where $y_1(t) = y(t) = \mu (t,\varvec{\theta })$¹$+ X(t)$, the original data.

Using lemmas 1, 2, 3 and 4 , we get:

$$\begin{aligned}&\limsup \sup _{S_{c_1}^{(1)}} \frac{1}{N}[I_1(\alpha _1) - I_1(\alpha _1^0)] = \limsup \sup _{|\alpha _1 - \alpha _1^0|> c} \frac{1}{N}[I_1(\alpha _1) - I_1(\alpha _1^0)] \\&\quad = -\frac{{A_1^0}^2}{4} - \frac{{B_1^0}^2}{4} \end{aligned}$$

From Lemma 5, it follows that:

$$\begin{aligned} {\hat{\alpha }}_1 \xrightarrow {a.s.} \alpha _1^0 \text{ as } N \rightarrow \infty . \end{aligned}$$

Let us recall that the linear parameter estimators of the first sinusoid are given by:

$$\begin{aligned} {\hat{A}}_1 = \frac{2}{N} \sum _{t=1}^{N} y(t) \cos (\hat{\alpha _1} t) \qquad {\hat{B}}_1 = \frac{2}{N} \sum _{t=1}^{N} y(t) \sin (\hat{\alpha _1} t) \end{aligned}$$

To prove the consistency of the estimators of the linear parameters, $A_1^0$ and $B_1^0$, we need the following lemma:

Lemma 7

If ${\hat{\alpha }}_1$ is the sequential ALSE of ${\hat{\alpha }}_1^0$ then

$$\begin{aligned} \begin{aligned} N({\hat{\alpha }}_1 - \alpha _1^0) \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty . \end{aligned}\end{aligned}$$

(14)

Proof

Let us denote $I_1^{\prime }(\alpha _1)$ and $I_1^{\prime \prime }(\alpha _1)$ as the first and second derivatives of the periodogram function $I_1(\alpha _1)$. Consider the Taylor series expansion of the function $I_1^{\prime }({\hat{\alpha }}_1)$ around the point $\alpha _1^0$ as follows:

$$\begin{aligned} I_1^{\prime }({\hat{\alpha }}_1) - I_1^{\prime }(\alpha _1^0) = ({\hat{\alpha }}_1 - \alpha _1^0) I_1^{\prime \prime }({\bar{\alpha }}_1) \end{aligned}$$

(15)

where ${\bar{\alpha }}_1$ is a point between ${\hat{\alpha }}_1$ and $\alpha _1^0$. Since ${\hat{\alpha }}_1$ is the argument maximiser of the function $I_1(\alpha _1)$, it implies that $I_1^{\prime }({\hat{\alpha }}_1) = 0$. Therefore, (15) can be rewritten as follows:

$$\begin{aligned}\begin{aligned}&- I_1^{\prime }(\alpha _1^0) = ({\hat{\alpha }}_1 - \alpha _1^0) I_1^{\prime \prime }({\bar{\alpha }}_1) \\&\quad \Rightarrow ({\hat{\alpha }}_1 - \alpha _1^0) = - I_1^{\prime }(\alpha _1^0)[I_1^{\prime \prime }({\bar{\alpha }}_1)]^{-1} \\&\quad \Rightarrow N({\hat{\alpha }}_1 - \alpha _1^0) = - \frac{1}{N^2}I_1^{\prime }(\alpha _1^0)[\frac{1}{N^3}I_1^{\prime \prime }({\bar{\alpha }}_1)]^{-1} \end{aligned} \end{aligned}$$

Now using simple calculations and number theory results 1, 2 and 3 , one can show that:

$$\begin{aligned}&\frac{1}{N^2}I_1^{\prime }(\alpha _1^0) \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty , \text{ and } \\&\quad \lim _{N \rightarrow \infty }\frac{1}{N^3}I_1^{\prime \prime }({\bar{\alpha }}_1) = \lim _{N \rightarrow \infty }\frac{1}{N^3}I_1^{\prime \prime }(\alpha _1^0) = \frac{-({A_1^0}^2 + {B_1^0}^2)}{24} \text{ as } N \rightarrow \infty . \\ \end{aligned}$$

Combining the above three equations, we have the desired result. $\square$

Now, let us consider ALSE ${\hat{A}}_1$ of $A_1^0$. Using Taylor series expansion, we expand $\cos ({\hat{\alpha }}_1 t)$ around the point $\alpha _1^0$ and get:

$$\begin{aligned}\begin{aligned} {\hat{A}}_1&= \frac{2}{N} \sum _{t=1}^{N} y(t) \cos ({\hat{\alpha }}_1 t) \\&= \frac{2}{N}\sum _{t=1}^{N}\bigg \{\mu (t, \varvec{\theta }) + X(t)\bigg \} \\&\quad \times \bigg \{\cos (\alpha _1^0 t) - t({\hat{\alpha }}_1 - \alpha _1^0) \sin ({\bar{\alpha }}_1 t) \bigg \} \xrightarrow {a.s.} A_1^0 \text{ as } N \rightarrow \infty . \end{aligned}\end{aligned}$$

The convergence in the last step follows on using the results from the preliminary number theory results (see lemmas 1, 2, 3 and 4 ) and Lemma 7.

One can show the consistency of ${\hat{B}}_1$ in the same manner as we proved for ${\hat{A}}_1$. Next, we show the strong consistency of the estimator ${\hat{\beta }}_1$. For that we consider the difference:

$$\begin{aligned}\begin{aligned}&\frac{1}{N} [I_2(\beta _1) - I_2(\beta _1^0)] \\&\quad = \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_2(t)\cos (\beta _1 t^2)\bigg \}^2 + \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_2(t) \sin (\beta _1 t^2)\bigg \}^2 \\&\qquad - \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_2(t)\cos (\beta _1^0 t^2)\bigg \}^2 - \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_2(t) \sin (\beta _1^0 t)\bigg \}^2 \\ \end{aligned}\end{aligned}$$

where $y_2(t) = y_1(t) - {\hat{A}}_1 \cos ({\hat{\alpha }}_1 t) - {\hat{B}}_1 \sin ({\hat{\alpha }}_1 t)$. On using lemmas 1, 2, 3 and 4 , we have:

$$\begin{aligned} \limsup \sup _{|\beta _1 - \beta _1^0|> c} \frac{1}{N}[I_2(\beta _1) - I_2(\beta _1^0)] \\ = -\frac{{C_1^0}^2}{4} - \frac{{B_1^0}^2}{4} < 0 \text{ a.s. } \end{aligned}$$

Therefore, ${\hat{\beta }}_1 \xrightarrow {a.s.} \beta _1^0$ as $N \rightarrow \infty$. This follows from Lemma 6.

To prove the consistency of linear parameter estimators of the first chirp component, that is, ${\hat{C}}_1$ and ${\hat{D}}_1$, we need the following lemma

Lemma 8

If ${\hat{\beta }}_1$ is the sequential ALSE of $\beta _1^0$, then

$$\begin{aligned} \begin{aligned} N^2({\hat{\beta }}_1 - \beta _1^0) \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty . \end{aligned}\end{aligned}$$

(16)

Proof

The proof of this lemma follows along the same lines as that of Lemma 7. $\square$

The consistency of linear parameter estimators ${\hat{C}}_1$ and ${\hat{D}}_1$ can now be shown along the same lines as that of ${\hat{A}}_1$ above.

Following the above proof, one can easily show the strong consistency of the second sinusoid component and chirp component parameter estimates. Moreover, the results can be extended for any p and q in general. $\square$

Proof of Theorem 2

Let us first consider the ALSE ${\hat{A}}_{p+1}$ of the linear parameter $A_{p+1}^0$:

$$\begin{aligned} \begin{aligned} {\hat{A}}_{p+1} = \frac{2}{N}\sum _{t=1}^{N} y_{p+q+1}(t) \cos ({\hat{\alpha }}_{p+1} t) \end{aligned}\end{aligned}$$

(17)

Now $y_{p+q+1}(t)$ is the data obtained by eliminating the effect of first p sinusoids and first q chirp components from the original data. It means that

$$\begin{aligned} \begin{aligned} y_{p+q+1}(t)&= y_{1}(t) - \sum _{j=1}^{p}\{{\hat{A}}_j \cos ({\hat{\alpha }}_j t) + {\hat{B}}_j \sin ({\hat{\alpha }}_j t)\} \\&\quad - \sum _{k=1}^{q}\{{\hat{C}}_k \cos ({\hat{\beta }}_k t^2) + {\hat{D}}_k \sin ({\hat{\beta }}_k t^2)\} \\&= X(t) + o(1), \text{ using } \text{ the } \text{ results } \text{ derived } \text{ in } \text{ the } \text{ proof } \text{ of } \text{ Theorem } \text{1 }. \end{aligned} \end{aligned}$$

(18)

Using the above equation, we get:

$$\begin{aligned} \begin{aligned} {\hat{A}}_{p+1}&= \frac{2}{N}\sum _{t=1}^{N} (X(t) + o(1)) \cos ({\hat{\alpha }}_{p+1} t) = \frac{2}{N}\sum _{t=1}^{n} X(t) \cos ({\hat{\alpha }}_{p+1} t) + o(1) \\&\xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty . \end{aligned}\end{aligned}$$

(19)

This follows from Lemma 4. Similarly, we have the following result:

$$\begin{aligned} \begin{aligned} {\hat{B}}_{p+1}&= \frac{2}{N}\sum _{t=1}^{N} y_{p+q+1}(t) \sin ({\hat{\alpha }}_{p+1} t) = \frac{2}{N}\sum _{t=1}^{N} (X(t) + o(1)) \sin ({\hat{\alpha }}_{p+1} t) \\&= \frac{2}{N}\sum _{t=1}^{n} X(t) \sin ({\hat{\alpha }}_{p+1} t) + o(1) \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty . \end{aligned}\end{aligned}$$

(20)

Analogously one can show that in case of overestimation the sequential ALSEs of the amplitudes of the chirp component converge to 0 as well, that is,

$$\begin{aligned} {\hat{C}}_{q+1} \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty \text{ and } {\hat{D}}_{q+1} \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty . \end{aligned}$$

Hence, the result. $\square$

Asymptotic Distribution of the Sequential ALSEs

Proof of Theorem 3

To prove this, theorem we will show asymptotic equivalence between the proposed sequential ALSEs and the sequential LSEs (see Grover [19]). For ease of notation, we assume $p = q = 2$ here, however the result can be extended for any p and q. First consider:

$$\begin{aligned}\begin{aligned}&\frac{1}{N} Q_1(\alpha _1) = \frac{1}{N} \sum _{t=1}^{N} \bigg ( y(t) - A_1 \cos (\alpha _1 t) - B_1 \sin (\alpha _1 t)\bigg )^2 \\&\quad = \frac{1}{N} \sum _{t=1}^{N} y^2(t) - \frac{2}{N} y(t) \bigg \{A_1 \cos (\alpha _1 t) + B_1 \sin (\alpha _1 t)\bigg \} \\&\qquad + \frac{1}{N}\sum _{t=1}^{N} \bigg \{A_1 \cos (\alpha _1 t) + B_1 \sin (\alpha _1 t)\bigg \}^2 \\&\quad = \frac{1}{N} \sum _{t=1}^{N} y^2(t) - \frac{1}{N} J_1(A_1, B_1, \alpha _1) + o(1) \end{aligned}\end{aligned}$$

where,

$$\begin{aligned} \frac{1}{N}J_1(A_1, B_1, \alpha _1) = \frac{2}{N} \sum _{t=1}^{N}y(t) \bigg \{A_1 \cos (\alpha _1 t) + B_1 \sin (\alpha _1 t)\bigg \} - \frac{{A_1}^2 + {B_1}^2}{2} \end{aligned}$$

At $A_1 = {\hat{A}}_1$ and $B_1 = {\hat{B}}_1$, one can show that:

$$\begin{aligned} J_1({\hat{A}}_1, {\hat{B}}_1, \alpha _1) = I_1(\alpha _1) \end{aligned}$$

Therefore, the estimator of $(A_1^0, B_1^0, \alpha _1^0)$ that maximises $J_1(A_1, B_1, \alpha _1)$ is equivalent to the sequential ALSE of $({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1)$. Now expanding ${\mathbf{J }}^{\prime }_1({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1)$ around the point $(A_1^0, B_1^0, \alpha _1^0)$, we have:

$$\begin{aligned}\begin{aligned}&\mathbf{J }^{\prime }_1({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1) - \mathbf{J }^{\prime }_1(A_1^0, B_1^0, \alpha _1^0) = ({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1) - (A_1^0, B_1^0, \alpha _1^0)[\mathbf{J }^{\prime }_1({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1)]^{-1}\\&\quad \Rightarrow - \mathbf{J }^{\prime }_1(A_1^0, B_1^0, \alpha _1^0)[\mathbf{J }^{\prime \prime }_1({\bar{A}}_1, {\bar{B}}_1, {\bar{\alpha }}_1)]^{-1} = ({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1) - (A_1^0, B_1^0, \alpha _1^0) \end{aligned}\end{aligned}$$

Now we compute the elements of first derivative vector $\mathbf{J }^{\prime }_1(A_1^0, B_1^0, \alpha _1^0)$ and using the preliminary lemmas 1, 2 and 3 and the Conjecture 1, we obtain:

$$\begin{aligned}&\begin{aligned} \frac{\partial J_1(A_1^0, B_1^0, \alpha _1^0)}{\partial A_1} = \frac{2}{N} \sum _{t=1}^{N} y(t) \cos (\alpha _1^0 t) - A_1^0 = \frac{2}{N} \sum _{t=1}^{N} X(t) \cos (\alpha _1^0 t) + o(\frac{1}{\sqrt{N}}) \end{aligned}\\&\begin{aligned} \text{ Similarly, } \frac{1}{N}\frac{\partial J_1(A_1^0, B_1^0, \alpha _1^0)}{\partial B_1} = \frac{2}{N} \sum _{t=1}^{N} X(t) \sin (\alpha _1^0 t) + o(\frac{1}{\sqrt{N}})\\ \end{aligned} \end{aligned}$$

Also,

$$\begin{aligned}\begin{aligned} \frac{1}{N}\frac{\partial J_1(A_1^0, B_1^0, \alpha _1^0)}{\partial B_1} = \frac{2}{N} \sum _{t=1}^{N} t X(t) \bigg \{-A_1^0 \sin (\alpha _1^0 t) + B_1^0 \cos (\alpha _1^0 t)\bigg \} + o(\sqrt{N})\\ \end{aligned} \end{aligned}$$

From the above three equations, it is easy to see that:

$$\begin{aligned} \begin{aligned}&\mathbf{Q }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0) = -\mathbf{J }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0) + \left[ {\begin{array}{*{20}l} o(\sqrt{N})&o(\sqrt{N})&o(N\sqrt{N}) \end{array} } \right] \\&\quad \Rightarrow \mathbf{Q }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 = -\mathbf{J }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 + \left[ {\begin{array}{*{20}l} o(1)&o(1)&o(1) \end{array} } \right] \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \lim _{N \rightarrow \infty }\mathbf{Q }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 = - \lim _{N \rightarrow \infty }\mathbf{J }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 \end{aligned}$$

Similarly, on computing the elements of the second derivative matrix, it can be shown that

$$\begin{aligned} \lim _{N \rightarrow \infty }\mathbf{D }_1\mathbf{Q }_1^{\prime \prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 = -\lim _{N \rightarrow \infty }\mathbf{D }_1\mathbf{J }_1^{\prime \prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 \end{aligned}$$

On combining these results, we get the asymptotic equivalence between the sequential ALSE $({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1)$ and $({\hat{A}}_{1 LSE}, {\hat{B}}_{1 LSE}, {\hat{\alpha }}_{1 LSE})$. It has been proved in Grover [19] that the sequential LSEs have the same asymptotic distribution as the LSEs of the parameters of a chirp-like model. This implies that $(({\hat{A}}_1 - A_1^0), ({\hat{B}}_1 - B_1^0), ({\hat{\alpha }}_1 - \alpha _1^0)) \mathbf{D }_1^{-1} \xrightarrow {d} {\mathcal {N}}_3(0, c \sigma ^2 {\varvec{\varSigma }^{(1)}_j}^{-1}) \text{ as } N \rightarrow \infty$.

Next to derive the asymptotic distribution of the sequential ALSEs of first chirp component parameters, that is, $({\hat{C}}_1, {\hat{D}}_1, {\hat{\beta }}_1)$, we proceed as before.

$$\begin{aligned} \frac{1}{N}Q_2(C_1, D_1, \beta _1) = \frac{1}{N} \sum _{t=1}^{N}\bigg (y_2(t) - C_1 \cos (\beta _1 t^2) - D_1 \sin (\beta _1 t^2)\bigg )^2. \end{aligned}$$

(21)

Here,

$$\begin{aligned}\begin{aligned}&y_2(t) = y(t) - {\hat{A}}_1 \cos (\alpha _1 t) - {\hat{B}}_1 \sin (\alpha _1 t)\\&\quad = A_2^0 \cos (\alpha _2^0 t) + B_2^0 \sin (\alpha _2^0 t) + \sum _{k=1}^{2}\{C_k^0 \cos (\beta _k^0 t^2) + D_k^0 \sin (\beta _k^0 t^2)\} + o(1) \end{aligned}\end{aligned}$$

Now expanding the right hand side of (21), we get:

$$\begin{aligned}\begin{aligned} \frac{1}{N}Q_2(C_1, D_1, \beta _1) = = \frac{1}{N} \sum _{t=1}^{N}y^2_2(t) - \frac{1}{N}J_2(C_1, D_1, \beta _1) + o(1), \end{aligned}\end{aligned}$$

where

$$\begin{aligned} \frac{1}{N}J_2(C_1, D_1, \beta _1) = \frac{2}{N} \sum _{t=1}^{N} y_2(t) \bigg \{C_1 \cos (\beta _1 t^2) + D_1 \sin (\beta _1 t^2)\bigg \} - \frac{{C_1}^2 + {D_1}^2}{2} \end{aligned}$$

We compute $\frac{1}{N} \mathbf{J }_2^{\prime }(C_1^0, D_1^0, \beta _1^0$ and using Conjecture 1 and lemmas 1, 2 and 3 , we get:

$$\begin{aligned}\begin{aligned}&\frac{1}{N}\frac{\partial J_2(C_1^0, D_1^0, \beta _1^0)}{\partial C_1} = \frac{2}{N} \sum _{t=1}^{N} X(t) \cos (\beta _1^0 t^2) + o(\frac{1}{\sqrt{N}}) \\&\frac{1}{N}\frac{\partial J_2(C_1^0, D_1^0, \beta _1^0)}{\partial D_1} = \frac{2}{N} \sum _{t=1}^{N} X(t) \sin (\beta _1^0 t^2) + o(\frac{1}{\sqrt{N}}) \\&\frac{1}{N}\frac{\partial J_2(C_1^0, D_1^0, \beta _1^0)}{\partial \beta _1} = \frac{2}{N} \sum _{t=1}^{N} t^2 X(t) \{ -C_1^0 \sin (\beta _1^0 t^2) + D_1^0\cos (\beta _1^0 t^2)\} + o({N\sqrt{N}})\\ \end{aligned} \end{aligned}$$

A similar equivalence can now be established between the $\mathbf{Q }_2^{\prime }(C_1^0, D_1^0, \beta _1^0)$ and $\mathbf{J }_2^{\prime }(C_1^0, D_1^0, \beta _1^0)$ and $\mathbf{Q }_2^{\prime \prime }(C_1^0, D_1^0, \beta _1^0)$ and $\mathbf{J }_2^{\prime \prime }(C_1^0, D_1^0, \beta _1^0)$. Procceding exactly the same way as for the first sinusoid estimators, it can be shown that the sequential ALSE $({\hat{C}}_1, {\hat{D}}_1, {\hat{\beta }}_1)$ and the sequential LSE $({\hat{C}}_{1LSE}, {\hat{D}}_{1LSE}, {\hat{\beta }}_{1LSE})$ have the same asymptotic distribution. The asymptotic distribution of the sequential LSE has been derived explicitly by Grover [19] in her thesis. Thus, we have:

$$\begin{aligned} (({\hat{C}}_1 - C_1^0), ({\hat{D}}_1 - D_1^0), ({\hat{\beta }}_1 - \beta _1^0))\mathbf{D }_2^{-1} \xrightarrow {d} {\mathcal {N}}_3(0, c \sigma ^2 {\varvec{\varSigma }^{(2)}_1}^{-1}) \text{ as } N \rightarrow \infty , \end{aligned}$$

the desired result. The result can now be extended for any p and q. $\square$