Abstract
A 16-degree-of-freedom dynamic model for the load contact analysis of a double helical gear considering sliding friction is established. The dynamic equation is solved by the Runge–Kutta method to obtain the vibration displacement. The method combines the friction coefficient model based on the elastohydrodynamic lubrication theory with the dynamic model, which provides a theoretical basis for the calculation of the power loss of the transmission system. Moreover, the sensitivity analysis of the parameters that affect the transmission efficiency is carried out, and an optimization method of meshing efficiency is proposed without reducing the bending strength of the gears. This method can directly guide the design of the double helical gear transmission system.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Power loss in a gear drive system includes windage loss, oil loss, bearing power loss, gear meshing power loss, and so forth, of which the gear meshing power loss is a major constituent [1]. Many domestic and foreign scholars have proposed several theoretical models to predict the gear meshing power loss. To improve calculation efficiency, the normal load model of the tooth surface and friction coefficient model is included in the meshing power loss model.
At present, the friction coefficient model of the tooth surface mainly includes: the Coulomb friction coefficient model, the Buckingham [2] friction coefficient semi-empirical formula, the Benedict and Kelly [3] friction coefficient model, and the Xu [4] EHL friction coefficient model.
Several techniques have been implemented to deal with the normal load of the tooth surface. Liang [5], Marimuthu and Muthuveerappan [6] carried out load-bearing contact analysis of internal and external meshing gear pairs based on the finite element principle. The method assumes that the load is evenly distributed on both surfaces of the double-tooth meshing and static load is used as a normal load for the tooth surface. Kolivand et al. [7] proposed a gear meshing power loss model by combining the load-bearing contact model and the hybrid elastohydrodynamic lubrication (EHL) model. Lin et al. [
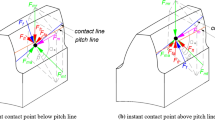
Then, the relative displacements δ12 and δ34 of the double helical gear along the mesh line can be expressed as
In the above formula, rb1, rb2, rb3, and rb4 are the base radii of each gear, while e1 and e2 are the gear meshing errors. According to the gear manufacturing accuracy level, the error is expressed as a simple harmonic function [17].
where ea is the meshing error amplitude, ω is the gear mesh engagement frequency in rad/s, and φ is the meshing phase angle.
Therefore, the elastic meshing force Flkm, Frkm and the viscous meshing force Flcm, Frkm of the left and right gear pairs can be expressed as
where Flkm, Frkm, Flcm, and Frcm are, respectively, the meshing stiffness and meshing dam** of the left and right gear pairs. The meshing stiffness value is obtained by TCA.
Based on the above analysis, the dynamic differential equation of the external meshing double helical gear pair is given by:
where mi and Ii (i = 1,2,3,4) are the mass and moment of inertia of gear i, respectively; Flf and Frf are the tooth surface friction forces of the left and right gear pairs, respectively; and Tf1, Tf2, Tf3, and Tf4 are the friction moments of the gear surface friction force on each gear.
The mass matrix M, stiffness matrix K, dam** matrix C, and excitation force matrix F can be extracted using the above formula. Since the dam** coefficient is difficult to determine, Rayleigh dam** is used in this study. The Rayleigh dam** coefficients α and β are used as reference [32].
The differential equations can be arranged as a matrix:
After eliminating the displacement of the rigid body, the displacement and velocity vectors are obtained using the Runge–Kutta method and then inserted into Eq. (4) to determine the dynamic meshing force.
2.2 Calculation of friction force and sliding friction power loss
From the dynamic equation in Sect. 2.1, it can be observed that the tooth surface meshing force and friction force are unknown, while the tooth surface friction force and friction coefficient are all dependent on the meshing force. When applying the Runge–Kutta method, the general processing method is to use the meshing force obtained from the solution of the previous loop to calculate the tooth surface friction force. The friction force is then used for the current cycle calculation in an iterative process until the two curves achieve reasonable stability.
Owing to the huge amount of finite element calculations, the meshing implemented for TCA should not be too dense. Therefore, the step size of the Runge–Kutta method will be much smaller than the step length of TCA regardless of whether a fixed-step or variable-step solver is used. To solve the data mismatch problem, it is considered that the load distribution in the vicinity of the discrete contact line has the same tendency since the discrete contact line load distribution curve is non-dimensionalized. According to the load of the current meshing position and the length of the contact line, the dimensionless load distribution curve is dimensioned such that the load distribution curve of the current meshing position is determined.
Assuming that the total meshing force is Fm at a certain time t, the expression for the friction force Fs on a single contact line is given as:
where qL(t) is the tooth-to-tooth load distribution rate at time t; qC(u, t) is the tooth surface load distribution function obtained from the loaded TCA (LTCA) model; u is the positional argument, which indicates the length from the starting point of the contact line; l is the contact line length of the current meshing position; vs(u, t) is the relative sliding speed of the tooth surface; and μ(u, t) is the friction coefficient. The above parameters are all functions of the position and time. The friction coefficient model uses the friction coefficient calculation model proposed by Xu [4] based on the theory of elastohydrodynamic lubrication. The term sgn() is a signum function whose expression is:
The friction torques of the single contact line on the driving wheel and the driven wheel are Ts1 and Ts2, respectively, and are given as:
where Rt1(u, t) and Rt2(u, t) are, respectively, the force arm of the friction force on the driving wheel and the driven wheel at any position of the contact line at time t.
If the friction force curves and friction torque curves of adjacent contact lines differ in time by a meshing period Tm, then the total friction force and friction torque of the driving wheel and the driven wheel are:
where N is the maximum number of teeth engaged in meshing at the same time.
The friction force at each point of the contact line and the relative sliding speed are different. The instantaneous power loss calculation integrates the power loss at each point along the contact line. The formula for the power loss of a single contact line is as follows:
Similarly, the total power loss at any time t is:
The average power loss is obtained by integrating the instantaneous power loss along the time axis and then averaging as given below:
The average meshing efficiency can be expressed as:
where Pin is the input power.
3 Sensitivity analysis of meshing efficiency of double helical gear parameters
Gear transmission efficiency is one of the important parameters that determine the quality of gear transmission. High-efficiency gear pairs improve energy efficiency, reduce power loss, and heat generation. Particularly in the aviation sector, improving the transmission efficiency of a gear pair is of great significance to improve the output power, increase the takeoff weight, and reduce the size of the components.
In this study, an external meshing double helical gear in a gearbox was selected for investigation. The parameters are listed in Table 1. The operating conditions and design parameters were varied using the parameters in Table 1, and the influence of the parameters on the meshing efficiency was examined.
3.1 Effect of input power, rotating speed, and transmission torque on efficiency
The gear meshing error, time-varying stiffness, tooth surface friction, and so forth will lead to vibration in the gear system and dynamic loading, which affect the gear transmission efficiency. At different input power and speed conditions, the gears have different vibration conditions; thus, it is necessary to investigate the influence of the input power, speed, and torque on the transmission efficiency. The stiffness of the support is adjusted during the calculation to avoid resonance.
Figure 2 shows the transmission efficiency variation calculated at input power condition of 1000–5000 kW and speed of 3000–8000 r/min. The efficiency distribution under constant speed, constant torque, and constant power is shown in Figs. 3, 4 and 5, respectively.
It can be observed in Fig. 3 that the efficiency increases with the increase in the input power under constant rotation speed. According to the friction coefficient calculation model proposed by Xu [4] based on the theory of elastohydrodynamic lubrication, as the input power increases, the unit normal load increases, and the friction coefficient increases, and then decreases, as shown in Fig. 6. The normal load of the working state is 0.5–5 × 10–3 GN/m, which falls to the right of the highest point of the curve. Therefore, at a constant rotational speed, the efficiency increases as the input power increases. In Fig. 4, under constant torque conditions, the efficiency decreases as the speed increases. This is because as the rotation speed increases, the entrainment velocity increases, and the friction coefficient increases. Figure 7 shows the friction coefficient curve at different entrainment velocities. In addition, as the rotational speed increases, the dynamic load due to the vibration increases, resulting in reduced efficiency. When the input power is constant, the tooth surface load decreases with the increase in the rotational speed. With comprehensive consideration of all factors, the efficiency is reduced, as shown in Fig. 5.
3.2 Effect of helix angle on efficiency
The helix angle is an important characteristic parameter of the helical gear, and it is also the main factor affecting the magnitude of the axial force and the change of the contact line. When the input power is 4500 kW and the rotation speed is 7200 r/min, the efficiency distribution with helix angle in the range of 5–35° is shown in Fig. 8. It can be observed from the figure that as the helix angle increases, the overall efficiency gradually decreases. For helix angle in the range of 10–25°, the decrease in the efficiency is small, and at helix angles greater than 25°, the efficiency drops sharply. At constant input power, the formula Fn = Ft/cosβ indicates that the introduction of the helix angle generates additional axial force, which increases the normal load of the tooth surface and further increases the power loss.
3.3 Effect of modulus on efficiency
Different moduli directly affect various geometric parameters of the gear, which in turn affect the gear's transmission efficiency. Figure 9 shows the efficiency distribution and modulus in the range of 2–4.5 at input power of 4500 kW and rotation speed of 7200 r/min.
As can be observed in Fig. 9, as the modulus increases, the transmission efficiency decreases. This is because the overall size of the gear increases as the modulus increases, when other parameters remain constant. At the same speed, the linear velocity of the gear increases and the friction power loss increases. Figure 10 shows the linear relationship between the relative sliding speed and the modulus at the meshing and recess point.
3.4 Effect of pressure angle on transmission efficiency
Figure 11 shows the efficiency distribution with pressure angle in the range of 15–25° when the input power is 4500 kW and the rotation speed is 7200 r/min. The transmission efficiency increases with the increase in the pressure angle because as the pressure angle increases, the width of the meshing surface becomes smaller, the relative sliding speed of the meshing and recess point becomes smaller, and the friction power loss decreases. Figure 12 shows the linear relationship between the relative sliding speed and the pressure angle at the meshing and recess point.
3.5 Effect of tooth widths on transmission efficiency
Figure 13 shows the efficiency distribution at different effective tooth widths when the input power is 4500 kW and the rotation speed is 7200 r/min. The transmission efficiency increases with the increase in the effective tooth width. The main reason is that as the effective tooth width increases, the unit normal load of the gear decreases, and the friction coefficient increases, resulting in increased friction loss. The relationship between the unit normal load of the gear and the friction coefficient is shown in Fig. 6.
3.6 Effect of modification coefficient on transmission efficiency
Figure 14 shows the efficiency distribution with modification coefficient in the range of −0.5 to 0.5 when the input power is 4500 kW and the rotation speed is 7200 r/min. It can be observed from the figure that the transmission efficiency is maximum when the modification coefficient is approximately zero. As shown in Fig. 15, when the modification coefficient is close to 0, the relative sliding speeds of the meshing and recess point are equal. For instance, during positive modification, as the modification coefficient increases, the meshing plane as a whole shift, the relative sliding speed of the meshing point decreases, and the relative sliding speed of the recess point increases. Compared with the modification coefficient of 0, the actual friction power loss increased so that the transmission efficiency is reduced.
In summary, the influence of relevant parameters on transmission efficiency is shown in Table 2 below. Moreover, it could be found that the influence of design parameters on meshing efficiency is followed as modulus, pressure angle > helical angle, tooth widths.
4 Optimization design method and discussion
At present, General Electric (GE), Pratt & Whitney, Pratt & Whitney's PW1000G geared fan engine(GTF), known as the advanced clean power, has become the standard for the next generation civil aero engines. The transmission system of the engine adopts star gear transmission structure, which is composed of a central gear driven by a low pressure turbine, five star gears, and one outer ring gear connected with the fan. In view of the above background, it is of great significance to study the power loss of herring tooth star gear transmission system, analyze the influence of various parameters on transmission efficiency, and summarize the design method of high efficiency herring gear for improving the efficiency of GTF engine.
4.1 Gear bending strength calculation
In addition to the modification coefficient, the gear transmission efficiency is a monotonically increasing or monotonically decreasing function of the design parameters. Therefore, it is necessary to introduce appropriate constraints so that parameter optimization is meaningful. From the above analysis, the gear transmission efficiency is closely related to the bearing capacity of the gears. This study proposes the concept of parameter optimization under constant bending strength conditions, and introduces the gear bending strength as a constraint condition. The parameters are optimized without weakening the gear strength taking the bearing capacity of the gears into account, or the allowable bending stress of the gear is determined. When optimizing the parameters, the strength always meets the design requirements.
When calculating the bending strength of the gear, the tooth root stress is calculated according to HB/Z 84.3-1984. The basic formula is as follows:
In the above formula:
- Ft:
-
Nominal tangential force, N;
- b:
-
Working tooth width, mm;
- mn:
-
Normal modulus, mm;
- YF:
-
Tooth profile coefficient when the load acts on the upper boundary of the single tooth meshing area;
- YS:
-
Stress correction factor when the load acts on the upper boundary of the single tooth meshing area;
- Yβ:
-
Helix angle coefficient.
The calculation result in this example is:
4.2 Equal bending strength optimization
Feasible domain range:
-
Modulus: The available moduli according to GB 1357–1978 are 3.25, 3.5, 3.75;
-
Pressure angle: The available pressure angles according to GB/T 1356–1988 are 20°, 22.5°, 25°;
-
Helix angle: Range 20–30°;
-
Tooth width: To ensure that the bending strength of the gears is the same, that is, the bending stress of the tooth root remains 306.36 MPa under the same load, numerical calculations are used to determine the corresponding tooth width values at the different parameters indicated above. Figures 16, 17 and 18 show the tooth width values corresponding to different pressure angles, moduli, and helix angles. It can be observed from the figures that as the helix angle increases, the tooth width gradually decreases mainly because the increase in the helix angle improves the degree of gear coincidence, and the bearing capacity of the gear is also improved. For a single pair of gears, the increase in the pressure angle is beneficial in order to improve the bending strength of the gears. However, owing to the increase in the pressure angle, the transverse contact ratio will be reduced. Under the combined effect of both, the pressure angle has a small influence on the bearing capacity of the entire meshing pair.
The meshing efficiency under various design parameters was calculated and the results are shown in Figs. 19, 20 and 21. It can be observed from the figures that under the condition of equal bending strength, the influence of various design parameters on the gear meshing efficiency is slightly different from that of the previous single factor analysis.
-
(1)
Under the conditions of equal gear bending strength, the meshing efficiency values obtained at different design parameters have a certain span, indicating that this method has room for optimization. In this case, the minimum meshing efficiency is 0.9918 and the maximum meshing efficiency is 0.9943, a difference of 0.002.
-
(2)
The meshing efficiency varies gradually with the helix angle under the condition of equal gear bending strength. This is because as the helix angle varies, the tooth width also varies, and the introduction of the tooth width plays a role in compensating for the suppression. Based on this, it can be observed that the helix angle and the tooth width have almost the same influence on the meshing efficiency.
-
(3)
Although the introduction of the tooth width plays a role in compensating for the suppression, the trend of the effect of modulus and pressure angle on efficiency is basically the same as the trend when analyzing the two separately, and the effect of modulus on efficiency is even more obvious.
-
(4)
In summary, we can determine the influence weight of each parameter on the efficiency: modulus, pressure angle > helix angle, tooth width.
The above results indicate that if the modulus and pressure angle do not change, the helix angle can be taken as 26° as shown in Fig. 20, and the corresponding tooth width is obtained by querying Fig. 17; the tooth width is determined as 60 mm. Since the efficiency (helix angle = 28°) at the original parameters is close to the maximum efficiency point, the optimization space is not large.
If the modulus and pressure angle change, the modulus and pressure angle can be selected as 3.25 and 25°, respectively according to Fig. 21. Since the meshing efficiency tends to be stable when the helix angle is in the range of 20–24°, it is preferable to select a large helix angle; on the one hand, shock vibration can be reduced, and on the other hand, the tooth width and the structural weight can be reduced. At the same time, to ensure that the center distance is an integer, the helix angle is adjusted to 23.85°, corresponding to an effective tooth width value of 73 mm. After optimizing the parameters, the meshing efficiency increased from 99.3465 to 99.3574%, an increase of 0.0109% (Table 3).
From the above analysis, it can be observed that since the modulus has the greatest influence on the efficiency, the use of a small modulus to increase the effective tooth width is preferred when applying equal gear bending strength optimization. To avoid gear eccentric load, the increase in the tooth width will be accompanied by an increase in the precision of the gear. Therefore, in the actual optimization process, the problems of gear precision and the technical aspects should also be considered.
5 Conclusion
After establishing the double helical gear dynamics model, solving method, analyzing the influence of gear design parameters and proposing the optimization scheme, the following conclusions could be drawn:
-
The gear meshing efficiency increases with the decrease in the modulus, helix angle, and effective tooth width; however, the reduction of the modulus, helix angle, and effective tooth width will weaken the bearing capacity of the gear. Under the condition that the speed is determined, the meshing efficiency increases with the input power. Therefore, under the premise of satisfying the safety factor in the design of the gear parameters, the gear strength can be appropriately reduced or the input power can be increased so that the bearing capacity of the gear can be fully utilized.
-
Under the condition of equal gear bending strength, the influence weight of each parameter on the efficiency is modulus, pressure angle > helix angle, tooth width. For the optimization, small moduli and large pressure angles can be selected. Aerospace gears are often used with 22.5° or 25° pressure angles.
-
Considering the bending strength of gears as a constraint condition, the bearing capacity of gears should be simultaneously taken into account when the parameters are optimized, which makes the optimization of the parameters practicable. The calculation results show that this method has a certain optimization space.
The actual engine power loss calculation is essential to consider the casing, the drive system structure, gear lubrication for meshing power loss in future research, more profound work would be taken into account to gradually form a more complete power loss calculation model of herring tooth star gear transmission system.