1 Introduction

The investigation of magnetohydrodynamics (MHD) flow in a duct or pipe is an interesting subject for researchers, e.g., electromagnetic pumps, generators and accelerators, flow-intake MHD devices, channels in reactors and some physiological uses [1,2,3,4,5,6,7]. The magnetic field develops the resistance Lorentz force that is dissipative in nature, so it can be used to suppress the velocity fluctuations. Therefore, well estimate of the channel’s MHD development length has a significant role to design pertinent systems and solve practical problems in many industrial and scientific fields [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Although researches about the hydrodynamic development length and suggesting the more accurate relation for development length have been studied until now [24,25,26,27,28], but the attention about the magnetohydrodynamic development length and presenting the correlation for predicting it is not noticeable.

The primary studies about the effect of magnetic field on the magnetohydrodynamic development length were done by [29,30,31,32,33,34,35,36,37]. Maciulaitis and Loeffler [34] presented a relation for magnetohydrodynamic development length. A two-dimensional flow between two flat plates was considered and the governing equations including continuity and momentum equations were transformed to the dimensionless form and solved by the momentum integral solution. However, Hwang et al. [31, 35] studied the laminar MHD entrance flow of a plane channel and computed the MHD development length at the specified values of the Hartmann number, numerically. The results were compared [38] and showed a substantial difference.

Flores and Recuero [39] presented an analysis of an MHD channel entrance flow in the Prandtl approximation. They established the correct boundary conditions for the approximation and repeated numerical calculations carried out by Hwang et al., in a few cases. The results showed that the differences were about 10%, though they increased with the augmentation of the Hartmann number.

Malekzadeh et al. [40] applied a mathematical model and a finite difference scheme to solve the governing equations of the laminar flow through a circular MHD channel. They offered an approximate mathematical expression for estimating the magnetic entrance length as a function of Hartmann number, sinus of the magnetic field angle, Reynolds number and the pipe diameter.

The focus of the mentioned researches in the field of MHD flow behavior in the entrance region in the recent years was on the pressure drop or velocity profiles variations. The development length only discussed and introduced as the length which the velocity profile does not change after that and the pressure drop becomes linear. Moreover, the correlation for the magnetohydrodynamic development length was not proposed and only the effect of flow parameters including the magnetic field, the Reynolds and Hartmann numbers on the development length has been investigated.

According to the above discussion, although a number of mathematical expressions for estimating the development length in channel flows without MHD effects have been existed in the literature [25, 27, 28, 41,42,43], but very little work has been done to present the closed-form correlation for predicting the MHD development length in MHD channel flows.

Indeed, in the previously published work of the authors’ [44], the Newtonian and power-law non-Newtonian MHD channel flow in the entrance region was investigated. An integral momentum solution was conducted to solve the governing equations. The velocity profile was approximated as sinusoidal, and analytical correlations for the development length were obtained for both Newtonian and power-law non-Newtonian MHD flows. Besides, the effect of the Hartmann number, Reynolds number, power-law index and magnetic interaction parameter on the MHD development length was discussed.

As it is obvious, in integral momentum solution, applying higher-degree approximation of the velocity profile leads to the more appropriate estimate of the flow characteristics including the development length. Thus, the purpose of this paper is to increase the accuracy of the authors’ previously proposed solution to MHD entrance flow of Newtonian electrically conducting fluids. The Pohlhausen’s fourth-degree velocity profile is applied to approximate the velocity profile, and the correlation for the development length of the MHD channel flow is obtained. Besides, the numerical finite volume method is conducted to solve the same problem. The correlation for estimating the development length is obtained numerically, and the results of the two methods are compared with each other.

2 Problem statement

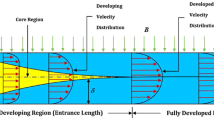
The geometric configuration of the MHD plane channel is shown in Fig. 1. A laminar, incompressible and Newtonian conducting fluid flow enters a rectangular channel with a uniform inlet velocity profile and develo**. The fluid properties are assumed constant, and a uniform magnetic field (B0) is applied in the direction normal to the flow. The channel is assumed to have a sufficiently high aspect ratio for the problem to be considered two-dimensional.

Fig. 1
figure 1

Schematic of the problem

Full size image

2.1 Governing equations for analytical method momentum integral

For analytical solution, according to the boundary layer approximations, the governing equations including continuity and momentum are defined as [44,45,46]:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(1a)
$$u\frac{\partial u}{\partial x} + v\frac{\partial v}{\partial y} = - \frac{1}{\rho }\frac{\partial P}{\partial x} + \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\sigma B_{0}^{2} u}}{\rho }\,,$$
(1b)

where ρ is the density, B0 is the applied magnetic field, P is the pressure, ν is the kinematic viscosity, σ is electrical conductivity, and u and v are the components of the velocity along and normal to the flow direction, respectively. In this study, the electrical field is neglected and the magnetic Reynolds number is assumed small enough. Also, the last term on the right-hand side of Eq. (1b) is the Lorentz body force.

As in the potential core, the viscous term vanishes, also v equals to zero, according to Eq. (1b), the pressure gradient can be related to the core velocity as [44]:

$$u_{\text{c}} \frac{{{\text{d}}u_{1b} }}{{{\text{d}}x}} = - \frac{1}{\rho }\frac{\partial P}{\partial x} - \frac{{\sigma B_{0}^{2} }}{\rho }u_{\text{c}} .$$
(2)

This equation can be named as the modified Euler equation.

Rearranging Eq. (2) and substituting to Eq. (1b), yields [44]:

$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = u_{\text{c}} \frac{{{\text{d}}u_{c} }}{{{\text{d}}x}} + \upsilon \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\sigma B_{0}^{2} }}{\rho }(u_{\text{c}} - u),$$
(3)

2.2 Governing equations for numerical solution

As well as analytical solution, the governing equations in numerical solutions are included the continuity and momentum which the continuity equation is as same [i.e., Eq. (1a)]. The momentum equations are introduced as [45, 46]:

$$\rho \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) = - \frac{\partial P}{\partial x} + \mu \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - \sigma B_{0}^{2} u,$$
(4a)
$$\rho \left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right) = - \frac{\partial P}{\partial y} + \mu \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right),$$
(4b)

where μ is the dynamic viscosity.

2.3 Boundary conditions

The boundary conditions of the problem are defined as follows:

$${\text{at:}}\quad x = 0:\quad u = U,$$
(5a)
$$y = 0:\quad u = 0,$$
(5b)
$$y = \delta \;{\text{or}}\;a:\quad u = u_{c} ,\quad \frac{\partial u}{\partial y} = 0,\quad \frac{{\partial^{2} u}}{{\partial y^{2} }} = 0,$$
(5c)

whereas U is the uniform inlet velocity, δ is the boundary layer thickness, a is the half width of the channel, and uc is the core velocity.

3 Integral momentum solution

the integral form of the momentum equation including the magnetic term (Lorentz body force) can be written as [44]:

$$\frac{{{\text{d}}u_{\text{c}}^{2} }}{{{\text{d}}x}}\int\limits_{0}^{\delta } {\left[ {\left( {1 - \frac{u}{{u_{\text{c}} }}} \right)\frac{u}{{u_{\text{c}} }}} \right]{\text{d}}y} + \frac{{{\text{d}}u_{\text{c}} }}{{{\text{d}}x}}u_{\text{c}} \int\limits_{0}^{\delta } {\left[ {\left( {1 - \frac{u}{{u_{\text{c}} }}} \right)} \right]{\text{d}}y} = \upsilon \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)_{y = 0} + \frac{{\sigma B_{0}^{2} u_{\text{c}} }}{\rho }\int\limits_{0}^{\delta } {\left[ {\left( {1 - \frac{u}{{u_{\text{c}} }}} \right)} \right]{\text{d}}y} .$$
(6)

In addition, the integral form of the mass conservation can be expressed as follows:

$$\int\limits_{0}^{\delta } {(\rho u){\text{d}}y} + \int\limits_{\delta }^{a} {(\rho u_{\text{c}} ){\text{d}}y = \rho Ua} ,$$
(7)

3.1 Velocity profile approximation

Applying Pohlhausen’s fourth-degree velocity profile, the velocity profile is defined as follows:

$$\frac{u}{{u_{\text{c}} }} = f(\eta ) = \sum\limits_{k = 0}^{4} {c_{k} \,\eta^{k} = c_{0} + c_{1} \eta + c_{2} \eta^{2} + c_{3} \eta^{3} + c_{4} } \eta^{4} ,\quad \eta = \frac{y}{\delta }$$
(8)

As it is obvious, five boundary conditions are needed to obtain the values of the five unknown coefficients (i.e., c0, c1, c2, c3 and c4) in Eq. (8). According to Eq. (5), four appropriate boundary conditions are available.

Applying the boundary condition (5b) in Eq. (1b) gives

$$u_{\text{c}} \frac{{\partial u_{\text{c}} }}{\partial x} + \upsilon \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\sigma B_{0}^{2} }}{\rho }u_{\text{c}} = 0$$
(9)

By some simple manipulation, we have

$$\frac{{\partial^{2} u}}{{\partial y^{2} }} = - \frac{{u_{\text{c}} }}{\upsilon }\left( {\frac{{\partial u_{c} }}{\partial x} + \frac{{\sigma B_{0}^{2} }}{\rho }} \right)\quad ({\text{for}}\;y = 0)$$
(10)

Therefore, the boundary conditions (5) can be rewritten as:

$$\begin{aligned} y & = 0:\quad u = 0,\;\frac{{\partial^{2} u}}{{\partial y^{2} }} = - \frac{{u_{\text{c}} }}{\upsilon }\left( {\frac{{\partial u_{\text{c}} }}{\partial x} + \frac{{\sigma B_{0}^{2} }}{\rho }} \right) \\ y & = \delta :\quad u = u_{c} ,\;\frac{\partial u}{\partial y} = 0,\;\frac{{\partial^{2} u}}{{\partial y^{2} }} = 0 \\ \end{aligned}$$
(11)

Introducing a new dimensionless parameter named Auxiliary Parameter (AP), we have

$${\text{AP}} = \frac{{\delta^{2} }}{\upsilon }\left( {\frac{{\partial u_{\text{c}} }}{\partial x} + \frac{{\sigma B_{0}^{2} }}{\rho }} \right)$$
(12)

Regarding the above equation, the different values of AP can lead to the different velocity distributions and according to Eq. (12), the value of AP depends on the magnitude of the magnetic field intensity and the core velocity gradient and consequently it depends on the magnitude of the pressure gradient [see Eq. (2)].

As well, the boundary conditions can be rewritten in dimensionless form as:

$$\begin{aligned} \eta & = 0:\quad f = 0,\quad f^{\prime \prime } = - {\text{AP}} \\ \eta & = 1:\quad f = 1,\quad f^{\prime } = 0,\quad f^{\prime \prime } = 0 \\ \end{aligned}$$
(13)

By substituting these boundary conditions (13) in Eq. (8), the velocity profile is obtained as:

$$f(\eta ) = \frac{u}{{u_{\text{c}} }} = \left( {2 + \frac{AP}{6}} \right)\eta - \left( {\frac{AP}{2}} \right)\eta^{2} + \left( {\frac{AP}{2} - 2} \right)\eta^{3} + \left( {1 - \frac{AP}{6}} \right)\eta^{4}$$
(14)

In order to obtain the theoretical range of AP, the following procedure is applied;

  • By using boundary condition \(f^{\prime } (1) = 0\), we have

    $$\begin{aligned} & \left( {2 + \frac{\text{AP}}{6}} \right) - ({\text{AP}})\eta + 3\left( {\frac{\text{AP}}{2} - 2} \right)\eta^{2} + 4\left( {1 - \frac{\text{AP}}{6}} \right)\eta^{3} = 0 \\ & 2 - 6\eta^{2} + 4\eta^{3} + \frac{\text{AP}}{6}(1 - \eta )^{3} - \frac{\text{AP}}{2}\eta (1 - \eta )^{2} = 0 \\ & \left[ {\frac{{2 - 6\eta^{2} + 4\eta^{3} }}{{(1 - \eta )^{2} }}} \right] + \frac{\text{AP}}{6}(1 - \eta ) - \frac{\text{AP}}{2}\eta = 0 \\ & \left[ {\frac{{2 - 6\eta^{2} + 4\eta^{3} }}{{(1 - \eta )^{2} }}} \right] + \frac{AP}{6}(1 - 4\eta ) = 0 \\ & 2 + 4\eta + \frac{\text{AP}}{6}(1 - 4\eta ) = 0 \\ & \eta = 1 \to {\text{AP}} = 12 \\ \end{aligned}$$

  • And using boundary condition \(f^{\prime \prime } (0) = - {\text{AP}}\) yields

    $$4 - \frac{{4{\text{AP}}}}{6} = - {\text{AP}} \to {\text{AP}} = - \;12$$

Therefore, the theoretical range of AP is obtained as:

$$- \;12 \le {\text{AP}} \le 12$$
(15)

3.2 Applying the integral momentum solution

We continue the solution with AP = − 4 and it is obvious, for the other value of AP, the solution can be obtained in the same way.

For AP = − 4, the velocity profile is obtained as:

$$f(\eta ) = \frac{4}{3}\eta + 2\eta^{2} - 4\eta^{3} + \frac{5}{3}\eta^{4} .$$
(16)

Substituting Eq. (16) in Eq. (6) gives

$$\frac{68}{567}u_{\text{c}}^{2} \frac{{{\text{d}}\delta }}{{{\text{d}}x}} + \frac{136}{567}u_{\text{c}} \delta \frac{{{\text{d}}u_{\text{c}} }}{{{\text{d}}x}} + \frac{1}{3}u_{\text{c}} \delta \frac{{{\text{d}}u_{\text{c}} }}{{{\text{d}}x}} = \frac{4}{3}\frac{{\upsilon u_{\text{c}} }}{\delta } + \frac{1}{3}\frac{{\sigma B_{0}^{2} }}{\rho }u_{\text{c}} \delta .$$
(17)

Equation (17) can be simplified as:

$$\frac{325}{756\upsilon }\delta^{2} \frac{{{\text{d}}u_{c} }}{{{\text{d}}x}} + \frac{68}{756\upsilon }u_{c} \delta \frac{d\delta }{dx} = 1 + \frac{1}{4}\frac{{\sigma B_{0}^{2} }}{\rho }\delta^{2} .$$
(18)

On the other hand, substituting Eq. (16) in Eq. (7) yields

$$\frac{\delta }{D /2} = 3\left( {1 - \frac{U}{{u_{\text{c}} }}} \right) \to \delta = \frac{3D}{2}\pi \left( {1 - \frac{U}{{u_{\text{c}} }}} \right)$$
(19)

Combining Eqs. (19) and (18) gives

$$\frac{x /D}{{Re_{D} }} = \frac{{\left[ {325\frac{{u_{\text{c}} }}{U} - 582\ln \left( {\frac{{u_{\text{c}} }}{U}} \right) - 257\frac{U}{{u_{\text{c}} }} - 68} \right]}}{{252\left[ {1 + \frac{9}{16}Ha^{2} \left( {1 - \frac{U}{{u_{\text{c}} }}} \right)^{2} } \right]}}{\mkern 1mu} ,$$
(20)

whereas \(Re = \frac{UD}{\nu }\) is the Reynolds number and \(Ha = B_{0} .D\sqrt {\frac{\sigma }{\mu }}\) is the Hartmann number.

At the end of the entrance region (xem), each boundary layer thickness can be expressed as:

$$\delta (x_{\text{em}} ) = \frac{D}{2}$$

Thus, Eq. (19) reduces as:

$$u_{\text{c}} (x_{\text{em}} ) = \frac{3}{2}U.$$
(21)

Indeed, the magnetic entrance length for the MHD channel flow with the assumed velocity profile is achieved by replacing Eq. (21) into Eq. (20) as:

$$\frac{{x_{\text{em}} /D}}{{Re_{D} }} = \frac{0.0483}{{\left[ {1 + 0.0625Ha^{2} } \right]}}.$$
(22)

3.3 Discussion

In this paper, the theoretical range of AP was determined and for several cases, some analytical closed-form correlations for estimating the magnetic development length were proposed. Table 1 presents the velocity distributions and the magnetic development length correlations for different values of AP. In addition, the velocity profiles f(η) for different values of AP are shown in Fig. 2.

Table 1 Velocity profiles and MHD development length correlations for different values of AP
Full size table
Fig. 2
figure 2

Velocity profiles for different values of AP

Full size image

Table 2 and Fig. 3 are presented to compare the obtained results with the ones attributed to the lower-degree approximations of the velocity profile. It can be seen that for the negative values of AP, the associated results are in better agreement with the ones of the second order, third order and sinusoidal assumed velocity profile, than the positive values of AP. Moreover, the results of the third order and sinusoidal velocity distributions are close together and in good agreement with the results of the fourth order velocity profiles with AP between − 4 and − 6. In addition, the results of the second order velocity distribution are matched with the results of the fourth order velocity distribution with AP = − 2.

Table 2 Different assumed velocity profiles with the attributed MHD development length correlations
Full size table
Fig. 3
figure 3

Different approximations of the velocity profile

Full size image

Some results for the magnetic development length obtained from the present work, the authors’ previous study and the other similar works have been done so far, are shown in Table 3. With the comparison between these available results from the literature and the present study, a substantial difference among some of them can be seen. That is because of the different assumed velocity profiles or different methods which were used to solve the problem.

Table 3 Comparison between some available results of entrance length from the literature and the present study
Full size table

In light of the above discussion and for the applicable uses, in Fig. 4, the variation of the non-dimensional magnetic development length versus Ha, for the different assumed velocity profiles associated with the different values of AP, is depicted for Re = 500, 1000, 1500 and 2000. It can be observed that the results of the third order and sinusoidal velocity profiles are almost matched with each other and very close to the results of the fourth order velocity profile with AP = − 4 and − 12, especially for Ha > 6. Furthermore, for a specified value of Re, with the increment of Ha, the value of the magnetic entrance length for all values of AP, reach to a specified value.

Fig. 4
figure 4

Variation of xem/D versus Ha for the different values of AP

Full size image

Figure 5 represents the variation of the non-dimensional magnetic development length versus Re, for the different assumed velocity profiles associated with the different values of AP, for Ha = 0, 4, 8 and 12. As can be seen, the results for the fourth order velocity profile with AP = − 4 and − 12 are close together and are in good agreement with the values of the MHD development length for the third order and sinusoidal velocity profiles. Indeed, in general for low Hartmann numbers, applying the fourth order velocity profile with AP = − 4, and for high Hartmann numbers, employing the fourth order velocity profile with AP = − 12 led to the more accurate estimation of the magnetic development length. It can be expected that the results for AP value between − 4 and − 8 have more compatibility with the results of the real application. But for more assurance, further investigations are required.

Fig. 5
figure 5

Variation of xem/D versus Re for the different values of AP

Full size image

The effect of Ha on the magnetic development length is plotted in Fig. 6. It is indicated as the Ha increases, the magnetic development length reduces. Ha is defined as the ratio of the Lorentz force to viscous force. Besides, Lorentz force is the resistance force and also proportional to the magnetic field intensity. Thus, when Lorentz force increases, the boundary layer thickness increases, and therefore, the magnetic development length decreases.

Fig. 6
figure 6

Effect of Ha on magnetic development length

Full size image

4 Numerical solution

This paper presents a numerical solution in order to obtain a correlation of the magnetic development length for a two-dimensional MHD channel. The numerical simulation is performed to study the liquid metal develo** flow through the MHD channel for different values of the Reynolds and the Hartmann numbers using finite volume method (FVM). The investigation is conducted with laminar flows for the Reynolds number ranging from 600 to 1200 while the Hartman number varied from 4 to 14, and 120 datasets of the magnetic development length (xem) are generated. Liquid lithium (Li) is selected for study due to its important uses in various industries [49,50,51]. The hybrid scheme and central differencing are used for the convective and diffusive terms, respectively. In addition, the SIMPLE scheme is selected for pressure–velocity coupling. The algorithm was originally put forward by Patankar and Spalding [52] and is essentially a guess-and-correct procedure for the calculation of pressure on the staggered grid. In additions, the momentum and continuity equations are solved using the Jacobi iterative method. Moreover, to obtain converged results, the residual error is selected 10−8. For all calculation, the uniform and rectangular mesh grid are considered in both directions x- and y-direction. In order to achieve valid results, the independence of the results from the mesh is checked. In Table 4, the mesh independent result is shown. It is observed that there is no variation in the results for 100 × 80 grid.

Table 4 Mesh independence for uniform inlet velocity
Full size table

Eventually, applying a surface fitted on the datasets, the correlation of the magnetic development length as a function of the Reynolds and Hartmann number is obtained as:

$$\frac{{x_{\text{em}} }}{{D{\mkern 1mu} Re_{D} }} = \frac{0.057}{1 + 0.1Ha}$$
(23)

4.1 Discussion

To validate the proposed correlations, Table 5 is presented. It can be observed that the proposed correlations have an acceptable accuracy.

Table 5 Validation of the proposed correlation
Full size table

The effect of Re and Ha on the development length of flow with the uniform inlet velocity is depicted in Fig. 7. It can be observed that with increasing of Ha and decreasing of Re, the development length decreases. As mentioned, Ha is the ratio of Lorentz force to viscous force. When Ha increases, the resistance Lorentz force also rises which leads to reduction in the development length. Further, as Re reduces, i.e., the viscous force increases, which the boundary layers’ thickness grows, and thus, the magnetic development length becomes shorter.

Fig. 7
figure 7

Effect of Ha and Re on the development length

Full size image

In order to gain insight into some of the results, the vectors of the velocity u and the Lorentz force are shown in Figs. 8 and 9. The velocity vectors along the channel are given in Fig. 8a–c. As expected, the velocity vectors change in the flow direction over the entrance region, up to the region far from entry (fully developed region) that the velocity vectors have no further change in the flow direction. As well, it can be seen that as the Hartmann number increases, the velocity vectors in the same cross section of the channel become flatten.

Fig. 8
figure 8

Velocity vectors along the channel (Re = 1400)

Full size image
Fig. 9
figure 9

Lorentz force vectors along the channel (Re = 1400)

Full size image

Figure 9a–c shows the vectors of Lorentz force along the channel. As discussed earlier, Lorentz force is proportional to the velocity directly. Thus, the variation pattern of FL in the flow direction is similar to the velocity. However, because Lorentz force is the resistance force, which affects in the opposite direction to the flow and velocity.

Eventually, in Fig. 10, the results of the analytical and numerical solution are compared. It can be seen that for AP = − 6, the results of the analytical integral momentum solution are in good agreement with the numerical FVM.

Fig. 10
figure 10

Comparison of analytical and numerical results

Full size image

5 Conclusion

In order to increase the accuracy of the authors’ previously proposed non-dimensional closed-form correlation for estimating the MHD development length of MHD channel flows, the higher-degree approximation of the velocity profile was used. Applying the appropriate boundary conditions to find the values of the unknown coefficients in the Pohlhausen’s fourth-degree velocity profile led to the appearance of a new dimensionless parameter named AP. It was shown that the value of AP depends on the magnitude of the magnetic field intensity and the pressure gradient. The theoretical range of AP was determined and for several cases, some analytical closed-form correlations of the MHD development length were proposed. Furthermore, the results were compared with that for the lower-degree approximations of the velocity profile and the effect of the governing parameters on the MHD development length was discussed. It can be concluded that for each particular application of MHD channel flows, the corresponding value of AP can be obtained via some experimental or numerical investigation. Indeed, the numerical finite volume method was conducted to solve the same problem and the correlation was computed numerically. Generally, by applying the Pohlhausen’s fourth-degree velocity profile with AP = − 6, more compatible results with numerical results can be obtained. Besides, the effect of the Reynolds and Hartmann number on the magnetic development length and velocity profile was discussed. It was demonstrated that with the augmentation of the Ha, the magnetic development length declines and the velocity profile becomes flatten. But an increase in Re leads to increase in the magnetic development length.