Analysis of P-wave propagation in filled jointed rock mass with viscoelastic properties

Abstract

Stress wave propagation in filled jointed rock mass is an important basis for the analysis of rock dynamic stability. The presence of small cracks in rock mass often causes the rock to exhibit viscoelastic behavior, resulting in the amplitude attenuation and time delay of the stress wave. In view of the incomplete understanding of stress wave propagation in viscoelastic media, this study presents an analysis on stress wave propagation in filled jointed rock mass with viscoelastic properties based on the time-domain recursive analysis method. By introducing the quality factors of stress wave in viscoelastic medium, the propagation equation of plane P-wave in filled jointed rock mass with viscoelasticity is established. Subsequently, the transmission and reflection characteristics of P-wave are accordingly analyzed. The results indicate that the transmission and reflection coefficients of P-wave through the filled joint decrease obviously due to the attenuation effect of rock viscoelasticity on wave amplitude, but the coefficients gradually stabilize as the quality factor increases. As the propagation distance of the P-wave increases in viscoelastic rock masses, the transmission and reflection coefficients decrease gradually. The normal stiffness of joint contact interface has a decisive influence on the wave propagation. Specifically, a higher normal stiffness leads to stronger transmission and poorer reflection. The larger the thickness of filled joint, the more obvious the attenuation of P-wave becomes. Additionally, the viscoelasticity of filling layer further aggravates the influence of joint thickness on the attenuation of P-wave. The study comprehensively takes into account the effect of viscoelasticity of both the rock mass and the filling layer on transmission and reflection of waves. The research results provide certain theoretical support for the dynamic response and stability analysis of rock mass containing structural planes.

Article highlights

• Theoretical analysis is conducted for wave propagation in viscoelastic filled jointed rock mass.

• Quality factors of stress wave are introduced to analyze the effect of wave propagation caused by viscoelastic medium.

• Wave propagation equation is derived when stress wave propagates in viscoelastic filled joint.

• Effect of parameters of rock mass viscoelasticity and filled joint on the wave propagation is studied.

1 Introduction

Underground energy excavation is one of the primary methods used to extract energy sources such as coal, oil, natural gas, and other resources. In recent years, the worldwide exploration of geothermal energy has been increasingly conducted due to the growing demand for energy and the wider adoption of environmental conservation principles (Singh et al. 2015; Xu et al. 2015). Whether it is the extraction of traditional mining resources or the utilization of new geothermal energy, rock mass engineering is indispensable. Blasting excavation has consistently been a crucial method in rock mass engineering for traditional resource or energy mining. When propagating through rock mass, the blast-induced stress waves will experience a certain degree of attenuation due to the viscoelastic properties of the rock. When stress wave interacts with joints which are commonly present in rock mass, there will be transmission and reflection phenomena, resulting in wave separation and energy attenuation. The stress wave propagation can induce joint deformation and even failure, which can significantly affect the safety and stability of engineering rock mass. Therefore, stress wave propagation in jointed rock mass has always been a focus of research in the field of rock dynamics. Most previous studies on stress wave propagation in jointed rock mass have treated the rock mass as a homogeneous, isotropic, linear elastic material and the joints as contact interfaces (Schoenberg 1980; Bedford and Drumheller 1994; Zhao and Cai 2001; Zhao et al. 2006; Li and Ma 2010; Chai et al. 2016, 2021; Liu et al. 2021, 2020; Li et al. 2012; Coates and Schoenberg 1995). However, these studies often overlook the thickness of joints and the presence of fillings within them. In fact, natural rock masses often contain numerous micro-cracks, impurities, and minerals, which contribute to a certain level of viscoelastic behavior in the rock. It is common for the joints in rock mass to be filled with various materials, resulting in the joints have a certain thickness. On the one hand, the viscoelasticity of rock mass and joints will cause wave attenuation. On the other hand, stress wave will undergo multiple reflections between two joint contact interfaces, making the wave propagation path more complicated. All of these factors collectively affect the propagation process of stress wave.

At present, several theoretical methods are widely used to analyze stress wave propagation in jointed rock mass, such as the method of characteristics, the time-domain recursive analysis method and the equivalent medium theory. Based on the displacement discontinuous method (Schoenberg 1980) and characteristic line theory (Bedford and Drumheller 1994), Zhao and Cai (2001) proposed a method of characteristics to analyze the transmission and reflection coefficients of stress wave at joint. Zhao et al. (2006) analyzed transmission coefficient of P-wave across nonlinear fractures with the method of characteristics. Based on the conservation of momentum at the wave front and the displacement discontinuity method, the time-domain recursive analysis method (TDRM) for the interaction between a beam of stress wave and single joint has been derived by Li and Ma (2010), so as to deduce the P- and S-wave propagation equations for linear elastic joint in time domain. Moreover, the propagation equation for P-wave interacts with two non-parallel joints with linear elastic behavior and cylindrical wave interacts with single nonlinear joint have been deduced by Chai et al. (2016, 2021) with TDRM. On the basis of TDRM, Liu et al. (2021, 2020) derived the propagation law of stress wave in in-situ stressed rock joint with different models. In order to analyze the propagation process of stress wave interacting with a group of parallel joints, Li et al. (2012) proposed a modified time-domain recursive method which can take joint spacing into account. In the equivalent medium method, the jointed rock mass is treated as an equivalent intact rock mass, and the mechanical parameters are also regarded as equivalent. Based on equivalent medium theory, Coates and Schoenberg (1995) analyzed the propagation process of stress wave in rock mass with a single fault. However, the results obtained by this approach may cause significant errors that cannot be ignored due to the simplification of the discontinuous rock mass to an equivalent medium.

In the above studies, the joints were all modeled as contact interfaces with zero thickness. For the studies that stress wave passing through the joints with a certain thickness, such simplification will inevitably lead to inaccurate results. In order to reduce this error, the stress wave propagation in a filled joint has been studied in recent years. The normal P-wave propagation across a single filled joint has been analyzed by Li et al. (2010a) based on the characteristic line theory. Ma et al. (2011) proposed the three-phase medium model to describe filled joints. Besides, Li et al. (2013, 1, the propagation distance of P-wave in rock mass is L before it reaches the left joint contact interface. The angle between the wave front and the left joint contact interface is α. The angles of the transmitted and reflected P-waves are also equal to α and the angles of the transmitted and reflected S-waves are equal to β. According to Snell’s law, the relation between α and β is:

$$\sin \beta /\sin \alpha = c_{s} /c_{p} = \sqrt {\frac{1 - 2\nu }{{2(1 - \nu )}}}$$

(1)

where c_p and c_s are, respectively, the propagation speeds of P- and S-waves.

Fig. 1

Scheme of wave propagation in viscoelastic rock mass with filled joint

2.2 Wave propagation equation in viscoelastic body

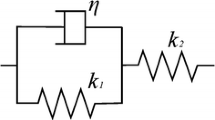
The Kelvin model is used to describe the viscoelasticity of the filled joint and the rock mass in this paper. As shown in Fig. 2, the viscoelastic Kelvin body consists of a Hooker body and a Newtonian body in parallel, that is, a spring and a damper in parallel. The constitutive equation of Kelvin model can be written as $\sigma = {\text{k}}\varepsilon + \eta \varepsilon^{{\prime }}$, where $\sigma = \sigma_{1} + \sigma_{2}$, $\varepsilon = \varepsilon_{1} = \varepsilon_{2}$.

Fig. 2

Scheme of Kelvin model

The propagation equation of P-wave in viscoelastic Kelvin model can be expressed as:

$$\rho \frac{{\partial^{2} u}}{{\partial t^{2} }} = (\lambda + 2\mu )\nabla^{2} \mu + \left( {\lambda^{{\prime }} + 2\mu^{{\prime }} } \right)\nabla^{2} \left( {\frac{\partial u}{{\partial t}}} \right)$$

(2)

where λ and μ are the Lame’s constants for isotropic body, λ′ and μ′ are the constants of the Kelvin model which are proposed by Carcione (2007) to characterize the stress and strain relationship of viscoelastic body. The harmonic solution of above motion equation can be written as

$$u(x) = A\exp ( - ax)\exp [i(\omega t - bx)]$$

(3)

$$a^{2} = \frac{{\rho E\omega^{2} }}{{2\left( {E^{2} + E^{{{\prime }2}} \omega^{2} } \right)}}\left( {\sqrt {1 + \frac{{E^{{{\prime }2}} \omega^{2} }}{{E^{2} }}} - 1} \right)$$

(4)

$$b^{2} = \frac{{\rho E\omega^{2} }}{{2\left( {E^{2} + E^{{{\prime }2}} \omega^{2} } \right)}}\left( {\sqrt {1 + \frac{{E^{{{\prime }2}} \omega^{2} }}{{E^{2} }}} + 1} \right)$$

(5)

where A is the amplitude of the initial harmonic wave; E is the elastic modulus of material and $E = \lambda + 2\mu$(for S-wave, $E = \mu$); $E^{{\prime }}$ is the viscous modulus of material and $E^{{\prime }} = \lambda^{{\prime }} + 2\mu^{{\prime }}$(for S-wave, $E^{{\prime }} = \mu^{{\prime }}$); ω is the angular frequency of P-wave.

The quality factor Q_p of P-wave is defined as (Carcione 2007)

$$Q_{p} = \frac{E}{{E^{{\prime }} }}\frac{1}{\omega }$$

(6)

The quality factor Q_s of S-wave can be obtained in the same way. This group of quality factors is used to describe the viscoelasticity of rock material in the Kelvin model in this paper. According to Eq. 6, a larger quality factor corresponds to a smaller viscous modulus relative to the elastic modulus. From Eq. 6, Eqs. 4 and 5 can be written as

$$a^{2} = \frac{{\rho \omega^{2} }}{{2E\left( {1 + \frac{1}{{Q_{p}^{2} }}} \right)}}\left( {\sqrt {1 + \frac{1}{{Q_{p}^{2} }}} - 1} \right)$$

(7)

$$b^{2} = \frac{{\rho \omega^{2} }}{{2E\left( {1 + \frac{1}{{Q_{p}^{2} }}} \right)}}\left( {\sqrt {1 + \frac{1}{{Q_{p}^{2} }}} + 1} \right)$$

(8)

According to Winkler and Nur (1982), the ratio of Q_p to Q_s decreases with the increase in depth. The values of quality factors Q_p and Q_s typically range from 5 to 70, and the approximate expression of the relationship between Q_p and Q_s in shallow rock mass is given as (Clouser and Langston 1991)

$$Q_{s} = \frac{4}{3}\left( {\frac{{c_{s} }}{{c_{p} }}} \right)^{2} Q_{p}$$

(9)

2.3 Wave propagation equation in viscoelastic rock mass with a viscoelastic filled joint

2.3.1 The three element model of viscoelastic filled joint

The three element model (TEM) of the viscoelastic filled joint comprises three components: the left joint contact interface 1, the viscoelastic filling material, and the right joint contact interface 2, as illustrated in Fig. 3. The contact interfaces between the rock material and the filling material adhere to the displacement discontinuity method (DDM), whereby stresses acting on both sides of the interface remain continuous while displacements are discontinuous. The thickness of the viscoelastic filled joint is S. The joint contact interfaces between rock and filling material can be adopted as the linear elastic model, as shown in Fig. 4, where k_n and k_s are normal stiffness and tangential stiffness of the contact interfaces, respectively. In the filled joint model utilized in previous researches in which the rock mass is always regarded as linear elasticity, stress waves are considered to directly impact contact interface 1 without taking into account the influence of the distance between the wave source and joint on incident waves. As shown in Fig. 3, to account for the amplitude attenuation and time delay effects of stress waves caused by the viscoelasticity of rock masses, it is assumed that the initial P-wave has already propagated a certain distance through the rock mass before reaching contact interface 1. The particle velocity of initial P-wave at the initial wave front is assumed to be v₀. When the P-wave first reaches the contact interface 1, the propagation distance in viscoelastic rock mass is represented by L. According to Eq. 3, the particle velocity of P-wave im**ing on filled joint will attenuate to

$$v_{rp,1}^{ - } = A\exp ( - aL)\exp \left[ {i(\omega t - bL)} \right]$$

(10)

Fig. 3

Scheme of the three element model of filled joint in viscoelastic rock mass

Fig. 4

Scheme of linear elastic model of joint contact surface

2.3.2 Wave propagation equation at joint contact interface

When the stress wave propagates through a filled joint, wave transmission and reflection take place at the joint contact interfaces. According to the modified time-domain recursive method proposed by Li et al. (2012), there are four types of stress waves at each contact interface, namely, right-running P- and S-waves at the left side of the contact interface, left-running P- and S-waves at the left side of the contact interface, right-running P- and S-waves at the right side of the contact interface and left-running P- and S-waves at the right side of the contact interface, as shown in Fig. 5.

Fig. 5

Scheme of left- and right-running P- and S-waves in joint contact interface

When a beam of right-running P-wave im**es on the contact interface from the left side, the contact interface, wave front and right-running P-wave will form a tiny element ABC, as shown in Fig. 6a. Similarly, each left- and right-running P- and S-waves will form a tiny element, as shown in Fig. 6b–h (Li et al. 2012). In Fig. 6, $\sigma_{rp}^{m}$ and $\sigma_{lp}^{m}$ denote the normal stresses of the right- and left-running P-waves on their wave fronts, $\tau_{rs}^{m}$ and $\tau_{ls}^{m}$ denote the shear stresses of the right- and left-running S-waves on their wave fronts, where m represents the symbols “−” and “+” which indicate the left- and right-hand sides of the contact interface, respectively. Since the present problem can be considered as a plane strain problem, the stresses on the plane perpendicular to each wave front are $\frac{\nu }{1 - \nu }\sigma_{rp}^{m}$ and $\frac{\nu }{1 - \nu }\sigma_{lp}^{m}$ respectively, where ν is Poisson’s ratio of the rock. Not considering the body force, according to the equilibrium condition of forces, the normal and shear stresses $\sigma_{1}^{ - }$ and $\tau_{1}^{ - }$ of the contact interface on element ABC shown in Fig. 6a must satisfy the following formula:

$$\sigma_{1}^{ - } AB - \sigma_{rp}^{ - } \cos \alpha AC - \frac{\nu }{1 - \nu }\sigma_{rp}^{ - } \sin \alpha BC = 0$$

(11)

$$\tau_{1}^{ - } AB - \sigma_{rp}^{ - } \sin \alpha AC + \frac{\nu }{1 - \nu }\sigma_{rp}^{ - } \cos \alpha BC = 0$$

(12)

Fig. 6

Scheme of stresses and right- and left-running waves on the two sides of the contact interfaces

Since $AC = AB\cos \alpha$ and $BC = AB\sin \alpha$, Eqs. 11 and 12 can be simplified as

$$\sigma_{1}^{ - } - \sigma_{rp}^{ - } \cos^{2} \alpha - \frac{\nu }{1 - \nu }\sigma_{rp}^{ - } \sin^{2} \alpha = 0$$

(13)

$$\tau_{1}^{ - } - \sigma_{rp}^{ - } \cos \alpha \sin \alpha + \frac{\nu }{1 - \nu }\sigma_{rp}^{ - } \cos \alpha \sin \alpha = 0$$

(14)

From the Snell’s law, i.e., Eq. 2, Eqs. 13 and 14 can be written as

$$\sigma_{1}^{ - } = \sigma_{rp}^{ - } \cos 2\beta ,\quad \tau_{1}^{ - } = \sigma_{rp}^{ - } \sin 2\beta \tan \beta /\tan \alpha$$

(15)

Similarly, the other $\sigma_{q}^{m}$ and $\tau_{q}^{m}$ (q = 1–4) on the left- and right-hand sides of the interface can be derived from Fig. 6b–h, that is,

$$\sigma_{1}^{m} = \sigma_{rp}^{m} \cos 2\beta ,\quad \tau_{1}^{m} = \sigma_{rp}^{m} \sin 2\beta \tan \beta /\tan \alpha$$

(16)

$$\sigma_{2}^{m} = \tau_{rs}^{m} \sin 2\beta ,\quad \tau_{2}^{m} = - \tau_{rs}^{m} \cos 2\beta$$

(17)

$$\sigma_{3}^{m} = \sigma_{lp}^{m} \cos 2\beta ,\quad \tau_{3}^{m} = - \sigma_{lp}^{m} \sin 2\beta \tan \beta /\tan \alpha$$

(18)

$$\sigma_{4}^{m} = - \tau_{ls}^{m} \sin 2\beta ,\quad \tau_{4}^{m} = - \tau_{ls}^{m} \cos 2\beta$$

(19)

The stresses on the left side of the contact interface can be expressed as

$$\sigma^{ - } = \sigma_{1}^{ - } + \sigma_{2}^{ - } + \sigma_{3}^{ - } + \sigma_{4}^{ - } ,\quad \tau^{ - } = \tau_{1}^{ - } + \tau_{2}^{ - } + \tau_{3}^{ - } + \tau_{4}^{ - }$$

(20)

The stresses on the right side of the contact interface can be expressed as

$$\sigma^{ + } = \sigma_{1}^{ + } + \sigma_{2}^{ + } + \sigma_{3}^{ + } + \sigma_{4}^{ + } ,\quad \tau^{ + } = \tau_{1}^{ + } + \tau_{2}^{ + } + \tau_{3}^{ + } + \tau_{4}^{ + }$$

(21)

According to the conservation of momentum on the wave fronts, there are

$$\sigma_{p} = z_{p} v_{p} ,\quad \tau_{s} = z_{s} v_{s}$$

(22)

where z_p and z_s are wave impedance of P- and S-waves in medium, i.e., $z_{p} = \rho c_{p}$ and $z_{s} = \rho c_{s}$, where ρ is the density of medium. By substituting Eq. 22 into Eqs. 20 and 21, the total normal stress and shear stress on left- and right-hand sides of the contact interface can be expressed as

$$\sigma^{ - } = \left( {z_{p} \cos 2\beta } \right)v_{rp}^{ - } + \left( {z_{s} \sin 2\beta } \right)v_{rs}^{ - } + \left( {z_{p} \cos 2\beta } \right)v_{lp}^{ - } + \left( { - z_{s} \sin 2\beta } \right)v_{ls}^{ - }$$

(23)

$$\begin{aligned} \tau^{ - } & = \left( {z_{p} \sin 2\beta \tan \beta /\tan \alpha } \right)v_{rp}^{ - } + \left( { - z_{s} \cos 2\beta } \right)v_{rs}^{ - } \\ & \quad { + }\left( { - z_{p} \sin 2\beta \tan \beta /\tan \alpha } \right)v_{lp}^{ - } + \left( { - z_{s} \cos 2\beta } \right)v_{ls}^{ - } \\ \end{aligned}$$

(24)

$$\sigma^{ + } = \left( {z_{p} \cos 2\beta } \right)v_{rp}^{ + } + \left( {z_{s} \sin 2\beta } \right)v_{rs}^{ + } + \left( {z_{p} \cos 2\beta } \right)v_{lp}^{ + } + \left( { - z_{s} \sin 2\beta } \right)v_{ls}^{ + }$$

(25)

$$\begin{aligned} \tau^{ + } & = \left( {z_{p} \sin 2\beta \tan \beta /\tan \alpha } \right)v_{rp}^{ + } + \left( { - z_{s} \cos 2\beta } \right)v_{rs}^{ + } \\ & \quad + \left( { - z_{p} \sin 2\beta \tan \beta /\tan \alpha } \right)v_{lp}^{ + } + \left( { - z_{s} \cos 2\beta } \right)v_{ls}^{ + } \\ \end{aligned}$$

(26)

where $v_{rp}^{m}$ and $v_{lp}^{m}$ (m =  − , +) are particle velocities of the right and left P-waves at both sides of the contact interface, respectively; $v_{rs}^{m}$ and $v_{ls}^{m}$ (m =  − , +) are particle velocities of the right and left S-waves at both sides of the contact interface, respectively.

The total normal and shear particle velocities on both sides of the contact interface can be obtained from Fig. 6, that is

$$v_{n}^{ - } = \cos \alpha v_{rp}^{ - } + \sin \beta v_{rs}^{ - } - \cos \alpha v_{lp}^{ - } + \sin \beta v_{ls}^{ - }$$

(27)

$$v_{\tau }^{ - } = \sin \alpha v_{rp}^{ - } - \cos \beta v_{rs}^{ - } + \sin \alpha v_{lp}^{ - } + \cos \beta v_{ls}^{ - }$$

(28)

$$v_{n}^{ + } = \cos \alpha v_{rp}^{ + } + \sin \beta v_{rs}^{ + } - \cos \alpha v_{lp}^{ + } + \sin \beta v_{ls}^{ + }$$

(29)

$$v_{\tau }^{ + } = \sin \alpha v_{rp}^{ + } - \cos \beta v_{rs}^{ + } + \sin \alpha v_{lp}^{ + } + \cos \beta v_{ls}^{ + }$$

(30)

The stress and displacement of contact interface satisfy the displacement discontinuous conditions, i.e.,

$$\sigma^{ - } = \sigma^{ + } = \sigma ,\quad \tau^{ - } = \tau^{ + } = \tau$$

(31)

$$u_{n}^{ - } - u_{n}^{ + } = \frac{\sigma }{{k_{n} }},\quad u_{\tau }^{ - } - u_{\tau }^{ + } = \frac{\tau }{{k_{s} }}$$

(32)

where $u_{n}^{ - }$ and $u_{n}^{ + }$ are the normal displacements on the left side and right side of the contact interface, respectively; $u_{\tau }^{ - }$ and $u_{\tau }^{ + }$ are the tangential displacements on the left side and right side of the contact interface, respectively. When Eq. 32 is differential to time t, there is

$$\begin{aligned} v_{n(i)}^{ - } - v_{n(i)}^{ + } & = \frac{1}{{k_{n} }}\frac{\partial \sigma }{{\partial t}} = \frac{1}{{k_{n} }}\frac{{\sigma_{(i + 1)} - \sigma_{(i)} }}{\Delta t} \\ \, v_{\tau (i)}^{ - } - v_{\tau (i)}^{ + } & = \frac{1}{{k_{s} }}\frac{\partial \tau }{{\partial t}} = \frac{1}{{k_{s} }}\frac{{\tau_{(i + 1)} - \tau_{(i)} }}{\Delta t} \\ \end{aligned}$$

(33)

where $\Delta t$ is a tiny interval of time.

As shown in Fig. 7, it should be noted that when stress waves im**e on a contact interface, the properties of material on both sides of the contact interface are different. Specifically, the materials on the left and right sides of contact interface 1 are rock and fillings, respectively; the materials on the left and right sides of contact interface 2 are fillings and rock, respectively. In order to distinguish easily, the wave impedances of P- and S-waves in rock material will be expressed as $z_{p}^{r} = \rho_{r} c_{p}^{r}$ and $z_{s}^{r} = \rho_{r} c_{s}^{r}$, where $\rho_{r}$ is the density of rock; $c_{p}^{r}$ and $c_{s}^{r}$ are the speeds of P- and S-waves in rock, respectively. The wave impedances of P- and S-waves in filling material will be expressed as $z_{p}^{j} = \rho_{j} c_{p}^{j}$ and $z_{s}^{j} = \rho_{j} c_{s}^{j}$, where $\rho_{j}$ is the density of joint fillings; $c_{p}^{j}$ and $c_{s}^{j}$ are the speeds of P- and S-waves in filled joint.

Fig. 7

Scheme of stress wave propagation model in the filled joint

Take contact interface 1 as an example, when the stress wave propagates to contact interface 1, Eqs. 23–26 can be rewritten as

$$\sigma^{ - } = \left( {z_{p}^{r} \cos 2\beta } \right)v_{rp}^{ - } + \left( {z_{s}^{r} \sin 2\beta } \right)v_{rs}^{ - } + \left( {z_{p}^{r} \cos 2\beta } \right)v_{lp}^{ - } + \left( { - z_{s}^{r} \sin 2\beta } \right)v_{ls}^{ - }$$

(34)

$$\begin{aligned} \tau^{ - } & = \left( {z_{p}^{r} \sin 2\beta \tan \beta /\tan \alpha } \right)v_{rp}^{ - } + \left( { - z_{s}^{r} \cos 2\beta } \right)v_{rs}^{ - } \\ & \quad { + }\left( { - z_{p}^{r} \sin 2\beta \tan \beta /\tan \alpha } \right)v_{lp}^{ - } + \left( { - z_{s}^{r} \cos 2\beta } \right)v_{ls}^{ - } \\ \end{aligned}$$

(35)

$$\sigma^{ + } = \left( {z_{p}^{j} \cos 2\beta } \right)v_{rp}^{ + } + \left( {z_{s}^{j} \sin 2\beta } \right)v_{rs}^{ + } + \left( {z_{p}^{j} \cos 2\beta } \right)v_{lp}^{ + } + \left( { - z_{s}^{j} \sin 2\beta } \right)v_{ls}^{ + }$$

(36)

$$\begin{aligned} \tau^{ + } & = \left( {z_{p}^{j} \sin 2\beta \tan \beta /\tan \alpha } \right)v_{rp}^{ + } + \left( { - z_{s}^{j} \cos 2\beta } \right)v_{rs}^{ + } \\ & \quad + \left( { - z_{p}^{j} \sin 2\beta \tan \beta /\tan \alpha } \right)v_{lp}^{ + } + \left( { - z_{s}^{j} \cos 2\beta } \right)v_{ls}^{ + } \\ \end{aligned}$$

(37)

Equation 31 can be rewritten from Eqs. 34–37 as

$$A_{1} \left[ {\begin{array}{*{20}c} {v_{rp}^{ - } } \\ {v_{rs}^{ - } } \\ \end{array} } \right] + B_{1} \left[ {\begin{array}{*{20}c} {v_{lp}^{ - } } \\ {v_{ls}^{ - } } \\ \end{array} } \right] = A_{2} \left[ {\begin{array}{*{20}c} {v_{rp}^{ + } } \\ {v_{rs}^{ + } } \\ \end{array} } \right] + B_{2} \left[ {\begin{array}{*{20}c} {v_{lp}^{ + } } \\ {v_{ls}^{ + } } \\ \end{array} } \right]$$

(38)

where

$$A_{1} = \left[ {\begin{array}{*{20}c} {z_{p}^{r} \cos 2\beta } & {z_{s}^{r} \sin 2\beta } \\ {z_{p}^{r} \sin 2\beta \tan \beta /\tan \alpha } & { - z_{s}^{r} \cos 2\beta } \\ \end{array} } \right]$$

(39)

$$B_{1} = \left[ {\begin{array}{*{20}c} {z_{p}^{r} \cos 2\beta } & { - z_{s}^{r} \sin 2\beta } \\ { - z_{p}^{r} \sin 2\beta \tan \beta /\tan \alpha } & { - z_{s}^{r} \cos 2\beta } \\ \end{array} } \right]$$

(40)

$$A_{2} = \left[ {\begin{array}{*{20}c} {z_{p}^{j} \cos 2\beta } & {z_{s}^{j} \sin 2\beta } \\ {z_{p}^{j} \sin 2\beta \tan \beta /\tan \alpha } & { - z_{s}^{j} \cos 2\beta } \\ \end{array} } \right]$$

(41)

$$B_{2} = \left[ {\begin{array}{*{20}c} {z_{p}^{j} \cos 2\beta } & { - z_{s}^{j} \sin 2\beta } \\ { - z_{p}^{j} \sin 2\beta \tan \beta /\tan \alpha } & { - z_{s}^{j} \cos 2\beta } \\ \end{array} } \right]$$

(42)

By substituting Eqs. 27–30 and Eqs. 36–37 into Eq. 33, it can be obtained

$$A_{2} \left[ {\begin{array}{*{20}c} {v_{rp}^{ + } (i + 1)} \\ {v_{rs}^{ + } (i + 1)} \\ \end{array} } \right] + B_{2} \left[ {\begin{array}{*{20}c} {v_{lp}^{ + } (i + 1)} \\ {v_{ls}^{ + } (i + 1)} \\ \end{array} } \right] = C\left[ {\begin{array}{*{20}c} {v_{rp}^{ + } (i)} \\ {v_{rs}^{ + } (i)} \\ \end{array} } \right] + D\left[ {\begin{array}{*{20}c} {v_{lp}^{ + } (i)} \\ {v_{ls}^{ + } (i)} \\ \end{array} } \right] + E\left[ {\begin{array}{*{20}c} {v_{rp}^{ - } (i)} \\ {v_{rs}^{ - } (i)} \\ \end{array} } \right] + F\left[ {\begin{array}{*{20}c} {v_{lp}^{ - } (i)} \\ {v_{ls}^{ - } (i)} \\ \end{array} } \right]$$

(43)

where

$$C = \left[ {\begin{array}{*{20}c} {z_{p}^{j} \cos 2\beta - k_{n} \Delta t\cos \alpha } & {z_{s}^{j} \sin 2\beta - k_{n} \Delta t\sin \beta } \\ {z_{p}^{j} \sin 2\beta \tan \beta /\tan \alpha - k_{s} \Delta t\sin \alpha } & { - z_{s}^{j} \cos 2\beta + k_{s} \Delta t\cos \beta } \\ \end{array} } \right]$$

(44)

$$D = \left[ {\begin{array}{*{20}c} {z_{p}^{j} \cos 2\beta + k_{n} \Delta t\cos \alpha } & { - z_{{\text{s}}}^{j} \sin 2\beta - k_{n} \Delta t\sin \beta } \\ { - z_{p}^{j} \sin 2\beta \tan \beta /\tan \alpha - k_{s} \Delta t\sin \alpha } & { - z_{{\text{s}}}^{j} \cos 2\beta - k_{s} \Delta t\cos \beta } \\ \end{array} } \right]$$

(45)

$$E = \left[ {\begin{array}{*{20}c} {k_{n} \Delta t\cos \alpha } & {k_{n} \Delta t\sin \beta } \\ {k_{s} \Delta t\sin \alpha } & { - k_{s} \Delta t\cos \beta } \\ \end{array} } \right]$$

(46)

$$F = \left[ {\begin{array}{*{20}c} { - k_{n} \Delta t\cos \alpha } & {k_{n} \Delta t\sin \beta } \\ {k_{s} \Delta t\sin \alpha } & {k_{s} \Delta t\cos \beta } \\ \end{array} } \right]$$

(47)

Equations 38 and 43 are the propagation equations of P-wave at the contact interface 1. The propagation equations of P-wave at the contact interface 2 can be obtained by the same method.

2.3.3 Transmission and reflection of stress waves in the viscoelastic filled joint

The stress wave will undergo multiple reflections within the filled joint. In order to facilitate the analysis, the propagation process of P-wave in the filled joint is divided into three steps. When the incident P-wave reaches contact interface 1 for the first time, transmission and reflection take place at the contact interface 1. As shown in Fig. 8, there are stress waves in three directions at contact interface 1, that is, right-running P-wave $v_{rp,1}^{ - }$ on the left side, left-running P-wave $v_{lp,1}^{ - }$ and S-wave $v_{ls,1}^{ - }$ on the left side and right-running P-wave $v_{rp,1}^{ + }$ and S-wave $v_{rs,1}^{ + }$ on the right side, respectively. At this time, no stress wave exists at contact interface 2 and no left-running wave exists on the right side of contact interface 1.

Fig. 8

Scheme of stress wave propagation model at contact interface 1 in the initial stage

When the right P- and S-waves on the right side of the contact interface 1 pass through the filling material and reach contact interface 2, transmission and reflection take place at the contact interface 2. As shown in Fig. 9, there are stress waves in three directions at contact interface 2, namely, the right-running P-wave $v_{rp,2}^{ - }$ and S-wave $v_{rs,2}^{ - }$ on the left side, left-running P-wave $v_{lp,2}^{ - }$ and S-wave $v_{ls,2}^{ - }$ on the left side and right-running P-wave $v_{rp,2}^{ + }$ and S-wave $v_{rs,2}^{ + }$ on the right side, respectively. No left-running wave exists on the right side of contact interface 2.

Fig. 9

Scheme of stress wave propagation model at contact interface 2

As shown in Fig. 10, when the left-running P- and S-wave on the left side of contact interface 2 pass through the filling material and back to the contact interface 1, there are stress waves in four directions at the contact interface 1.

Fig. 10

Scheme of stress wave propagation model at contact interface 1 in the final stage

Assuming that the filling material is isotropic, the stress waves in the filled joint satisfy the condition of stress and displacement continuity at any point. When the viscoelasticity of filled joint is not considered, the particle velocities of stress waves at two contact interfaces must satisfy

$$v_{rp,2}^{ - } (t) = v_{rp,1}^{ + } \left( {t - \Delta t_{p} } \right)$$

(48)

$$v_{rs,2}^{ - } (t) = v_{rs,1}^{ + } \left( {t - \Delta t_{s} } \right)$$

(49)

$$v_{lp,1}^{ + } (t) = v_{lp,2}^{ - } \left( {t - \Delta t_{p} } \right)$$

(50)

$$v_{ls,1}^{ + } (t) = v_{ls,2}^{ - } \left( {t - \Delta t_{s} } \right)$$

(51)

where $\Delta t_{p}$ and $\Delta t_{s}$ are propagation time of P- and S-waves in filled joint respectively and can be obtained by

$$\Delta t_{p} = S/\left( {c_{p}^{j} \cos \alpha } \right){,}\quad \Delta t_{s} = S/\left( {c_{s}^{j} \cos \beta } \right)$$

(52)

As we know, the joint filling layer is composed of rock weathering materials and clay, and exhibits distinct viscoelastic characteristics. The amplitude attenuation caused by the viscoelasticity of the fillings should not be ignored. Therefore, in this study, the Kelvin model is still used to characterize the viscoelasticity of the filling layer. Since the mechanical properties of filling layer are generally weaker than those of rock, to simplify the calculation, the quality factors of P- and S-waves in filling material are taken as 1/3 of the quality factors in rock material, that is, $Q_{p}^{j} = 1/3Q_{p}$ and $Q_{s}^{j} = 1/3Q_{s}$. The attenuation coefficients $a_{p}^{j}$ and $a_{s}^{j}$ of stress wave in viscoelastic filling material can be obtained by Eq. 7. The time delay effect of filling material on stress waves is not considered in this paper due to the small thickness of the filled joint. When the filling material exhibits viscoelastic behavior, Eqs. 48–51 can be rewritten as

$$v_{rp,2}^{ - } (i) = \exp \left( { - a_{p}^{j} S/\cos \alpha } \right)v_{rp,1}^{ + } \left( {i - n_{p} } \right)$$

(53)

$$v_{rs,2}^{ - } (i) = \exp \left( { - a_{s}^{j} S/\cos \beta } \right)v_{rs,1}^{ + } \left( {i - n_{s} } \right)$$

(54)

$$v_{lp,1}^{ + } (i) = \exp \left( { - a_{p}^{j} S/\cos \alpha } \right)v_{lp,2}^{ - } \left( {i - n_{p} } \right)$$

(55)

$$v_{ls,1}^{ + } ({\text{i}}) = \exp \left( { - a_{s}^{j} S/\cos \beta } \right)v_{ls,2}^{ - } \left( {i - n_{s} } \right)$$

(56)

where n_p and n_s are the smallest integers greater than the value of equations $S/(\cos \alpha \cdot c_{{\text{p}}}^{{\text{j}}} \cdot \Delta t)$ and $S/(\cos \beta \cdot c_{{\text{s}}}^{{\text{j}}} \cdot \Delta t)$, respectively, that is

$$n_{p} = {\text{int}} \left[ {S/\left( {\cos \alpha \cdot c_{p}^{j} \cdot \Delta t} \right)} \right]$$

(57)

$$n_{s} = {\text{int}} \left[ {S/\left( {\cos \beta \cdot c_{s}^{j} \cdot \Delta t} \right)} \right]$$

(58)

where $\Delta t$ is the time step. In this paper, Matlab is used to calculate the theoretical equations. In order to balance the computational efficiency of the software and the accuracy of the calculation results, $\Delta t$ is uniformly set as $1/(800{\text{f}})$.

In summary, the propagation of stress waves in a viscoelastic filled joint can be divided into three stages: firstly, the incident wave passes through the contact interface 1, generating the reflected and transmitted waves; secondly, the stress waves propagate through the viscoelastic filling material with some degree of attenuation; finally, the stress waves pass through the contact interface 2, resulting in the formation of transmitted waves. According to Eqs. 38, 43 and Eqs. 53–56, the propagation law of P-wave in a viscoelastic filled joint can be analyzed. According to Li and Ma (2010), the transmission and reflection coefficients of P-wave through a viscoelastic filled joint is defined according to the particle velocities of the waves, that is, the ratios of the maximum absolute value of the transmitted wave velocities to the maximum absolute value of the incident P-wave, and the ratios of the maximum absolute value of the reflected wave velocities to the maximum absolute value of the incident P-wave, respectively, that is,

$$T_{kc} = \frac{{\max \left| {v_{rk,2}^{ + } } \right|}}{{\max \left| {v_{rp,1}^{ - } } \right|}},\quad R_{kc} = \frac{{\max \left| {v_{lk,1}^{ - } } \right|}}{{\max \left| {v_{rp,1}^{ - } } \right|}}$$

(59)

where k = p, s, represents P-wave or S-wave.

If both the viscoelasticity of rock and the viscoelasticity of filled joint are considered, based on Eq. 59, the transmission and reflection coefficients of P-wave at filled joints can be defined as:

$$T_{k} = \frac{{\max \left| {v_{rk,2}^{ + } } \right|}}{{\max \left| {v_{0} } \right|}},\quad R_{k} = \frac{{\max \left| {v_{lk,1}^{ - } } \right|}}{{\max \left| {v_{0} } \right|}}$$

(60)

3 Special cases

In order to verify the feasibility of the proposed method, the quality factor Q_p is set as infinity and the other parameters are the same as Li et al. (\(Q_{p}^{j}\) and $Q_{{\text{s}}}^{j}$ of the filling material in Case 4 is set to 1/3, which is same as $Q_{p}^{j}$ in Case 2.

In the following special cases, referring to the laboratory test of stress wave propagation in filled jointed rock (Chai et al. 2020), the parameters of materials are as follows: rock density $\rho_{r}$ is 2430 kg/m³, joint density $\rho_{j}$ is 1912 kg/m³, P-wave speed in rock $c_{p}^{r}$ is 3368 m/s while S-wave speed $c_{s}^{r}$ is 1704 m/s, P-wave speed in the joint fillings $c_{p}^{j}$ is 2381 m/s while S-wave speed $c_{s}^{j}$ is 1205 m/s, the normal stiffness and tangential stiffness of joint contact interfaces are both 3.5 GPa/m (Li and Ma 2010). It is assumed that the initial P-waves in four cases are all half-cycle sinusoidal stress waves, with frequency f = 100 Hz, amplitude 1 m/s and duration 0.005 s. The expression is

$$V_{0} = \left\{ {\begin{array}{*{20}c} {\sin (\omega t)} & {(0 \le t \le T/2)} \\ 0 & {(t,T/2)} \\ \end{array} } \right.$$

(61)

where $\omega = 2\pi f$. In Case 1 and Case 2, the distance between wave source and filled joint along the direction of P-wave propagation is adopted as 10 m. However, in Case 3 and Case 4, this distance is considered to be zero. The incident angle α is 20°, joint thickness is 4 mm.

Figure 12a–d show the waveforms of transmitted and reflected waves of the four cases, respectively. In these figures, Region I represents the time delay of incident P-wave generated by the propagation path of initial P-wave in the rock; Region II represents the time delay of incident P-wave generated by the viscoelasticity of rock mass; Region III represents the attenuation of incident P-wave amplitude; Region IV represents the attenuation of transmitted P-wave amplitude.

Fig. 12

Transmitted and reflected waves for four cases

As shown in Fig. 12a, b, both Case 1 and Case 2 exhibit a time delay effect in the incident P-waves. In Case 1, the time delay is solely generated by the stress wave propagation path. In contrast, in Case 2, the time delay is caused by two factors: the stress wave propagation path and the viscoelasticity of the rock mass.

By comparing Fig. 12a, c, it is evident that the amplitude of the incident P-wave in Case 3 is nearly the same as that in Case 1. In other words, when the Q_p of the rock tends to infinity, the viscosity of the rock material becomes negligible, allowing the rock to be approximated as linear elastic body. Consequently, the P-wave has almost no attenuation during its propagation in rock. However, in Case 1, the propagation path of the stress wave before reaching the joint is taken into account, resulting in a certain time delay of the incident P-wave. Consequently, the waveform of the incident P-wave exhibits a slight time deviation compared to that shown in Fig. 12c.

As shown in Fig. 12c, the existence of filled joint leads to the attenuation of the amplitude of stress wave. When comparing Fig. 12b, c, it can be observed that when the Q_p of the rock is very small, the rock shows great viscosity and the amplitude of incident P-wave at the filled joint decreases significantly. As a consequence, the amplitude of transmitted P-wave, which is caused by the attenuated incident P-wave, undergoes a more obvious attenuation.

It can be seen from Fig. 12d that the viscoelasticity of filling material also contributes to the attenuation of the propagation of stress waves to a certain extent. By comparing Fig. 12b–d, it can be seen that the viscoelasticity of rock material has a more obvious effect on stress wave attenuation compared to that of filling material. This difference in effect is attributed to the small thickness of filled joints. However, despite the small thickness, the attenuation effect of viscoelasticity of filling material on stress wave cannot be ignored.

It can be concluded from above analysis that the viscoelasticity of rock, the existence of filled joint, and the viscoelasticity of filling material contribute to the attenuation of stress wave propagation. Therefore, in the next section, a parametric analysis will be conducted on the transmission and reflection coefficients of the P-wave, considering three aspects: the viscoelasticity of the rock, the characteristics of the filled joint, and the viscoelasticity of the filling material.

4 Discussion

Parametric studies include the influence of the quality factor of P-wave in viscoelastic rock, the propagation distance of P-wave in viscoelastic rock, the stiffness of joint contact interfaces and the thickness of filled joint on the transmission and reflection coefficients. The initial P-wave is represented by a half-cycle sinusoidal wave as described in Eq. 61. Unless otherwise stated, the basic parameters used will be the same as those in Sect. 3. The value of Q_s will be calculated using Eq. 9.

4.1 Limitations of the proposed method

It should be pointed out that due to some assumptions or simplifications in the establishment of the theoretical model in this study, the recursive method has certain limitations. For example, the value of quality factors is selected and calculated in a certain range according to experience, so there must be some difference with the actual engineering rock mass, and the quality factors in different ranges of rock mass may be differentiated; the joint contact interface is treated according to the simplified model, and the influence of important parameters such as joint roughness coefficient JRC and joint matching coefficient JMC is not considered; meanwhile, the tangential slip of the filled joint is not considered; only the half-cycle sinusoidal stress wave is adopted as initial P-wave, and other complex wave modes are not considered. Therefore, the approach proposed in this paper can not be used to solve practical engineering problems for the time being, but the relevant assumption and derivation can provide some reference for study on wave propagation through viscoelastic filled jointed rock mass to some extent.

4.2 Effect of the quality factor Q _p

In this study, the viscoelasticity of rock material is represented by the quality factors of waves as described in Sect. 2.2. In this section, the influence of quality factor on wave propagation characteristics is analyzed. For the analysis, the propagation distance L of P-wave in rock mass is adopted as 30 m, the range of quality factor Q_p is set from 0 to 50 based on experience. Figure 13 shows the variation of transmission and reflection coefficients with quality factor Q_p.

Fig. 13

Transmission and reflection coefficients in different Q_p

It can be seen from Fig. 13 that the transmission and reflection coefficients of P-wave increase with the increase of Q_p overall. The smaller the value of Q_p, the greater the influence it has on the transmission and reflection coefficients. In particular, when the value of Q_p is relatively small (ranging from 0 to 20), the transmission and reflection coefficients become particularly sensitive to changes in the quality factors. When Q_p tends to 0, there are no reflected and transmitted waves at filled joint since the rock mass approaches complete viscosity, and the P-wave cannot propagate to the filled joint at this situation. When Q_p is large enough, the transmission and reflection coefficients of P-wave are no longer affected by Q_p and tend to be stable. This is because the rock is approximately elastic and the amplitude of incident P-wave will not be attenuated at this situation.

4.3 Effect of the propagation distance of P-wave in rock mass

In this section, the quality factor Q_p is adopted as 20, the frequency of initial P-wave is adopted as 100 Hz and 200 Hz, respectively. Figure 14 shows the variation of the transmission and reflection coefficients with the propagation distance of P-wave in rock mass.

Fig. 14

Transmission and reflection coefficients in different L

It can be seen from Fig. 14 that with the increase of L, the transmission and reflection coefficients of P-wave decrease gradually. This observation indicates that the longer the L is, the more obvious the attenuation of rock viscoelasticity to stress wave becomes. By comparing Fig. 14a, b, it can be found that the transmission coefficients of the initial P-wave with a frequency of 100 Hz are significantly larger, while the reflection coefficients of the initial P-wave with a frequency of 200 Hz are significantly larger. These phenomena are consistent with the research results on the influence of stress wave frequency on the transmission and reflection coefficients (Li et al. 2013), that is, the higher the frequency of stress wave, the greater the attenuation caused by joint.

4.4 Effect of the stiffness of joint contact interface

In this section, the propagation distance L of P-wave in rock mass is adopted as 30 m, the quality factor Q_p is adopted as 20. When the shear stiffness k_s is 3.5 GPa/m, the variation of transmission and reflection coefficients with the normal stiffness of joint contact interface k_n is shown in Fig. 15 by the solid line. When the normal stiffness k_n is 3.5 GPa/m, the variation of transmission and reflection coefficients with the tangential stiffness of joint contact interface k_s is shown in Fig. 15 by the dotted line.

Fig. 15

Transmission and reflection coefficients in different stiffness

As can be seen from Fig. 15, when the tangential stiffness k_s is kept constant, the transmission coefficient T_p increases with the increase of the normal stiffness k_n, then gradually tends to be stable. The results indicate that the larger the normal stiffness of joint contact interface, the smaller the attenuation degree of P-wave caused by filled joints. Additionally, the transmission coefficient T_s remains within a relatively small range. The reflection coefficients R_p and R_s decrease with the increase of k_n, and the attenuation degree also decrease gradually. It can be concluded from the above analysis that the larger the normal stiffness of joint contact interface, the easier the P-wave will pass through the filled joint. When the tangential stiffness k_n is kept constant, the transmission and reflection coefficients of P-wave fluctuate slightly within a small range when k_s takes a small value, and then tends to be stable. It shows that the tangential stiffness of joint contact interface has little effect on the propagation of P-wave at filled joint.

4.5 Effect of the joint thickness

In order to clearly demonstrate the influence of joint thickness on stress wave propagation more obviously, in this section, it is assumed that the density of filling material and rock material are both 2650 kg/m³; the P- and S-wave speeds in both materials respectively are c_p = 5830 m/s and c_s = 2940 m/s, which are consistent with the reference (Li and Ma 2010). The propagation distance L of P-wave in rock mass is adopted as 30 m, the quality factor Q_p is adopted as 20, the shear and normal stiffness are both adopted as 3.5 GPa/m. With the joint thickness ranging from 4 to 16 mm, the transmission coefficients of incident P-wave with and without the viscoelasticity of joint are analyzed respectively. Figure 16 shows the variation of transmission coefficients T_p and T_s with the joint thickness, where Q_j represents the viscoelasticity of filled joint.

Fig. 16

Transmission coefficients in different S

As shown in Fig. 16, when the viscoelasticity of filling material is considered, the transmission coefficients T_p and T_s of P-wave are significantly smaller than those when the viscoelasticity of filling material is not considered. This observation indicates that the viscoelasticity of filling material has a significant attenuation effect on the propagation of P-wave.

In Fig. 15, with the increase of joint thickness, the transmission coefficient T_p decreases gradually in both cases. Moreover, when considering Q_j, the attenuation degree is slightly larger than that without consideration of Q_j. In addition, the transmission coefficient T_s of P-wave remains relatively unchanged when Q_j is not considered, while the transmission coefficient T_s of P-wave decreases gradually when Q_j is considered. This indicates that the attenuation effect of joint thickness on stress waves is caused by two reasons. On the one hand, the increase of the joint thickness will reduce the normalized normal and shear stiffness of filled joint, leading to the reduction of stress wave propagation. On the other hand, the increase of the joint thickness leads to the increase of stress wave propagation distance in viscoelastic material, thus increasing the attenuation of stress wave.

5 Conclusions

Based on the wave propagation equation in filled jointed rock mass, and by introducing the quality factors of stress wave, the formulas for calculating the transmission and reflection coefficients of P-wave in viscoelastic filled joint considering the viscoelastic properties of rock mass are derived using the time-domain recursive analysis method (TDRM), then the important parameters affecting the transmission and reflection coefficients are analyzed. The main conclusions are as follows:

• (1) The transmission and reflection coefficients of P-wave passing through filled joint decrease obviously due to the attenuation effect of rock viscoelasticity on wave amplitude. When the quality factor Q_p is small, the transmission and reflection coefficients of P-wave increase rapidly with the increase of Q_p. With the increase of Q_p, the transmission and reflection coefficients of P-wave tend to be stable gradually.

• (2) The viscoelasticity of rock mass can produce amplitude attenuation and time delay effect on P-wave propagation. With the increase of propagation distance of P-wave in viscoelastic rock mass, the transmission and reflection coefficients decrease gradually. In addition, the greater the frequency of initial P-wave, the greater the obstruction of filled joint to P-wave.

• (3) The normal stiffness of joint contact interfaces has a decisive influence on P-wave propagation, and the larger the normal stiffness is, the larger the transmitted wave intensity is and the smaller the reflected wave intensity is. The tangential stiffness of joint contact interfaces has little effect on the transmission and reflection coefficients of P-wave.

• (4) The larger the thickness of filled joint is, the more obvious the attenuation of P-wave is, and the viscoelasticity of filling layer will further aggravate the influence degree of joint thickness on the attenuation of stress wave.