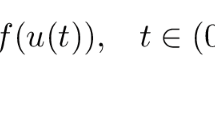A Constructive Approach About the Existence of Positive Solutions for Minkowski Curvature Problems

Abstract

In this paper, we give an existence theorem about positive solutions for the Dirichlet boundary value problem of one dimensional Minkowski curvature equations. We apply the theorem to one parameter family of problems to investigate a constructive method for numerical range of parameters where positive solutions exist. Moreover, we establish a nonexistence theorem of positive solutions for the corresponding one parameter family of problems. The coefficient function may be singular at the boundary and nonlinear term satisfies a sublinear growth condition. Main argument for the proof of existence theorem is employed by Krasnoselskii’s theorem of cone expansion and compression. We give a numerical algorithm and various examples to illustrate numerical information about ranges of the existence and nonexistence parameters which have been given only in a theoretical manner so far.

1 Introduction

We study the existence of positive solutions for the following one dimensional Minkowski curvature problem

where $\Psi (x)=\frac{x}{\sqrt{1-x^2}}$, $x\in (-1,1)$, coefficient function m satisfies $m\ge 0$, $m\not \equiv 0$ in any compact subinterval of (0, 1) and $m\in \mathcal {A}$ a class of functions given as

$$\begin{aligned} \mathcal {A}\triangleq \Big \{m\in C((0,1),{\mathbb R}_+):\int _0^1 r(1-r)m(r)\mathrm{d}r<\infty \Big \}, \end{aligned}$$

where ${\mathbb R}_+ = [0,\infty )$. As an example, let us take $m(t)=t^{-\frac{3}{2}}(1-t)^{-1},$ then $m\in \mathcal {A}$ but $m\notin L^1 (0,1)$. $f:[0,\alpha )\rightarrow {\mathbb R}_+$ with $\alpha > \frac{1}{2}$ is continuous and $f\not \equiv 0$ on $(0,\frac{1}{2})$.

We say, by definition, u a solution of problem (P) if $u\in C[0,1]\cap C^1(0,1)$, $|u'(t)|<1$ for $t\in (0,1)$, and $\Psi (u')$ is absolutely continuous in any compact subinterval of (0, 1), and u satisfies the equation and the Dirichlet boundary condition in (P). Moreover, we say a solution u positive if $u(t)>0$ for $t\in (0,1)$.

The research on problems associated with the mean curvature operator in Minkowski space is dated back to the 1960s, see [1,2,3,4,5] and the references therein. In the past decade, studies on nonexistence, existence and multiplicity of radial solutions on a bounded or an exterior domain and solutions for one-dimensional problems involving Minkowski curvature operator have attracted much attention. One may refer to [6,7,8,9,10] for radial solutions and [11,12,13,14,15,16,17] for one-dimensional problems.

Among others, Coelho-Corsato-Obersnel-Omari [13] studied positive solutions of problem

Under assumptions

$(C_1)$:

$g:[0,1] \times {\mathbb R} \rightarrow {\mathbb R}$ satisfies the $L^1$-Carathéodory conditions,

$(C_2)$:

there exists $w\in H_0 ^1 (0,1)$ with $w>0$ and $\Vert w'\Vert _{\infty } <1$ such that

$$\begin{aligned} \int _0 ^1 G(t,w)\mathrm{d}t >0, \ \ \mathrm{where} \ G(t,s)=\int _0 ^s g(t, r )\mathrm{d}r, \end{aligned}$$

$(C_3)$:

$\limsup _{s\rightarrow 0^+} \frac{G(t,s)}{s^2} \le 0$ uniformly a.e. in [0, 1], 

$(C_4)$:

$g(t,0)=0$ for a.e. $t\in [0,1],$

they proved that there is $\lambda ^* >0$ such that problem $(G_{\lambda })$ has at least two positive solutions for $\lambda > \lambda ^*.$ As an application to the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Big (\Psi (u')\Big )'=\lambda m(t)u^p, ~&{}t\in (0,1),\\ u(0)=0=u(1), \end{array}\right. } \end{aligned}$$

(1.1)

assuming $m\in C[0,1]$ and $p > 1,$ they proved that there exist $0< \lambda _* \le \lambda ^*$ such that problem (1.1) has no positive solution for $\lambda < \lambda _*$ and at least two positive solutions for $\lambda > \lambda ^*.$

Recently, Yang-Sim-Lee [17] studied nodal solutions for the following singular problem

Under assumptions $m\in \mathcal A$ and $f_0 =0,$ where $f_0\triangleq \lim \limits _{s\rightarrow 0^+}\frac{f(s)}{s},$ they proved a similar result for nodal solutions as in Coelho-Corsato-Obersnel-Omari [13].

It is interesting to notice that the studies of existence or multiple existence of positive solutions for problem (P) with condition $m\in L^1 (0,1)$ or $m\in \mathcal A$ have not been announced so far, which cannot be obtained by obvious modification from the results about one parameter family of problems $(P_{\lambda } )$ in Coelho-Corsato-Obersnel-Omari [13] or Yang-Sim-Lee [17]. We also notice that the existence and nonexistence parameters $\lambda ^*$ and $\lambda _*$ in the works of [13] or [17] were determined in a theoretical manner so that numerical information about these two parameters has not been known yet.

Thus the main goal of this paper is to introduce a new existence theorem for positive solutions of problem (P) and to obtain some numerical information about the ranges of nonexistence as well as existence of positive solutions with respect to parameters for problem $(P_{\lambda })$.

For the proof of existence theorem, we introduce newly defined integral operator on cone to apply the classical Krasnoselskii’s fixed point theorem. For numerical information, we apply the existence theorem to problem $(P_{\lambda } )$ and also investigate nonexistence of positive solutions for the problem. Modifying condition $(F_2)$ in Sect. 3 for problem $(P_{\lambda })$, we obtain some possible intervals of existence and nonexistence but the global existence interval (i.e. when $\lambda ^* =\lambda _*$) could not be answered in this work. We note that the techniques in [15] used to estimate the norm of solutions cannot be applied directly to problem (P) due to the singularity of coefficient function m and the difference of boundary conditions.

The rest of this paper is organized as follows. In Sect. 2, we introduce an integral operator which will be used as a fixed point operator for problem (P). In Sect. 3, we prove the existence of positive solutions for problem (P). In Sect. 4, we modify the existence condition given in Sect. 3 to derive numerical information about the range of existence for one parameter family of problems $(P_{\lambda } )$ including problem (1.1). In Sect. 5, we show the nonexistence of positive solutions for $(P_{\lambda } )$ and give some examples to illustrate our main results by using the proposed numerical algorithm.

2 An Integral Operator

In this section, we introduce an integral operator which corresponds to a fixed point operator for problem (P) later. For this, we first consider Poisson-type Dirichlet boundary value problem

where $\xi \in \mathcal {A}$. Let u be a solution of problem (PO). Then reminding that $\xi$ may not be integrable near 0 or 1, we fix $\sigma \in (0,1)$ in an arbitrary manner and integrate the equation in problem (PO) on the interval $(t,\sigma ]$ for $t\in (0,\sigma ]$ to obtain

$$\begin{aligned} u'(t)=\Psi ^{-1}\left( a+\int _t^\sigma \xi (r)\mathrm{d}r\right) , \end{aligned}$$

(2.1)

where we denote $a\triangleq \Psi (u'(\sigma ))$. We claim that $\Psi ^{-1}\left( a+\int _t^\sigma \xi (r)\mathrm{d}r\right) \in L^1(0,\sigma ]$. Indeed, by using changing order of integrations and $\xi \in \mathcal {A}$, we get

$$\begin{aligned}&\int _0^\sigma \Psi ^{-1}\left( a+\int _s^\sigma \xi (r)\mathrm{d}r\right) \mathrm{d}s \le \int _0^\sigma \Psi ^{-1}\left( |a|+\int _s^\sigma \xi (r)\mathrm{d}r\right) \mathrm{d}s\\ \le&\ \Psi ^{-1}(|a|)+\int _0^\sigma \Psi ^{-1}\left( \int _s^\sigma \xi (r)\mathrm{d}r\right) \mathrm{d}s \le \Psi ^{-1}(|a|)+\int _0^\sigma \int _s^\sigma \xi (r)\mathrm{d}r \mathrm{d}s \\ =&\ \Psi ^{-1}(|a|)+\int _0^\sigma r\xi (r)\mathrm{d}r<\infty . \end{aligned}$$

Thus we may integrate (2.1) on the interval (0, t) and get

$$\begin{aligned} u(t)=\int _0^t\Psi ^{-1}\left( a+\int _s^\sigma \xi (r)\mathrm{d}r\right) \mathrm{d}s,~ t\in (0,\sigma ]. \end{aligned}$$

Similarly, for $t\in [\sigma ,1)$, we obtain

$$\begin{aligned} u(t)=\int _t^1\Psi ^{-1}\left( -a+\int ^s_\sigma \xi (r)\mathrm{d}r\right) \mathrm{d}s,~ t\in [\sigma ,1). \end{aligned}$$

If we show $u(\sigma ^-)=u(\sigma ^+)$, then we see $u\in C[0,1]\cap C^1(0,1)$. For this, define a function $H:\mathbb {R}\rightarrow \mathbb {R}$ given as

$$\begin{aligned} H(a)=\int _0^\sigma \Psi ^{-1}\left( a+\int _s^\sigma \xi (r)\mathrm{d}r\right) \mathrm{d}s-\int _\sigma ^1\Psi ^{-1}\left( -a+\int ^s_\sigma \xi (r)\mathrm{d}r\right) \mathrm{d}s. \end{aligned}$$

Then by boundedness and monotone property of $\Psi ^{-1},$ we easily see that H is continuous, strictly increasing, and $H(a)<0$ as $a\rightarrow -\infty$ and $H(a)>0$ as $a\rightarrow \infty$. Therefore H has a zero, say $\alpha$ unique up to $\sigma$ and $\xi$. Define

$$\begin{aligned} T\xi (t)= {\left\{ \begin{array}{ll} \int _0^t\Psi ^{-1}\left( \alpha +\int _s^{\sigma }\xi (r)\mathrm{d}r\right) \mathrm{d}s,~&{} t\in (0,\sigma ],\\ \int ^1_t\Psi ^{-1}\left( -\alpha +\int ^s_{\sigma }\xi (r)\mathrm{d}r\right) \mathrm{d}s,~&{} t\in [\sigma ,1). \end{array}\right. } \end{aligned}$$

(2.2)

Then u a solution of problem (PO) can be equivalently written as $u=T\xi$.

Remark 2.1

Since $\alpha$ is uniquely determined, solution of problem (PO) exists uniquely.

3 An Existence Result

In this section, we study the existence of positive solutions of problem (P). For another type of function class $\mathcal {B}$ given by

$$\begin{aligned} \mathcal {B}\triangleq \left\{ m\in C((0,1),{\mathbb R}_+):\int _0^{\frac{1}{2}}\int _s^{\frac{1}{2}}m(r)\mathrm{d}r \mathrm{d}s+\int _{\frac{1}{2}}^1\int ^s_{\frac{1}{2}}m(r)\mathrm{d}r \mathrm{d}s<\infty \right\} , \end{aligned}$$

we note that $\mathcal {A}=\mathcal {B}$ mainly by Fubini’s theorem.

We now give some assumptions on nonlinear term f.

$(F_1)$:

$f_0 =0$.

$(F_2)$:

there exist $\delta \in (0,\frac{1}{2})$ and $\rho \in (0,\delta M_{\delta })$ such that

$$\begin{aligned} f(s)\ge \Psi \left( \frac{s}{\delta M_{\delta }}\right) ~\mathrm{for}~s\in [\delta \rho ,\rho ], \end{aligned}$$

where $M_{\delta }=\min \left\{ \int _\delta ^{\frac{1}{2}}\Psi ^{-1}\left( \int _s^{\frac{1}{2}}m(r)\mathrm{d}r\right) \mathrm{d}s,\int ^{1-\delta }_{\frac{1}{2}}\Psi ^{-1}\left( \int ^s_{\frac{1}{2}}m(r)\mathrm{d}r\right) \mathrm{d}s\right\}$.

Remark 3.1

We note from Theorem 2.1 in [16] that under assumption $(F_1)$, all solutions u of (P) is of $C^1[0,1]$ and $\Vert u'\Vert _\infty <1$. This implies that all solutions u of (P) satisfies $\Vert u\Vert _\infty <\frac{1}{2}.$

We now state the Krasnoselskii’s theorem of cone expansion and compression which will be used for the proof of our existence theorem.

Lemma 3.1

([18]) Let E be a Banach space and K a cone in E. Assume that $\Omega _1$ and $\Omega _2$ are bounded open in E with $0\in \Omega _1\subset \overline{\Omega _1}\subset \Omega _2$, and let $T:K\cap (\overline{\Omega _2}\setminus \Omega _1)\rightarrow K$ be completely continuous such that either

• (i) $\Vert Tx\Vert \le \Vert x\Vert$ for $x\in K\cap \partial \Omega _1$ and $\Vert Tx\Vert \ge \Vert x\Vert$ for $x\in K\cap \partial \Omega _2$, or

• (ii) $\Vert Tx\Vert \ge \Vert x\Vert$ for $x\in K\cap \partial \Omega _1$ and $\Vert Tx\Vert \le \Vert x\Vert$ for $x\in K\cap \partial \Omega _2$.

Then T has a fixed point in $K\cap (\overline{\Omega _2}\setminus \Omega _1)$.

Remark 3.2

Note that $\Psi ^{-1}(x)=\frac{x}{\sqrt{1+x^2}}$, $x\in \mathbb R$ has the property

$$\begin{aligned} \Psi ^{-1}(x)\Psi ^{-1}(y)\le \Psi ^{-1}(xy)\le xy, ~\mathrm{for}~x,y\ge 0. \end{aligned}$$

Remark 3.3

If $m\in \mathcal {A}$ and $0\le f_0 <\infty ,$ then any nontrivial solution of (P) is positive, mainly by concavity and double zero properties of solutions (see [9, 17]).

Let $E=C[0,1]$ the Banach space with supremum norm $\Vert \cdot \Vert _\infty$ and let $K=\{u\in E: u(0)=u(1)=0 \ \mathrm{and } \ u$ is concave on $(0,1) \}.$ Then K is a cone in E. For $u\in K$, replacing $\xi (t)$ with m(t)f(u(t)) in (2.2), Sect. 2, we obtain

$$\begin{aligned} (Tu)(t)= {\left\{ \begin{array}{ll} \int _0^t\Psi ^{-1}\left( \alpha +\int _s^{\sigma }m(r)f(u(r))\mathrm{d}r\right) \mathrm{d}s,~&{} t\in (0,\sigma ],\\ \int ^1_t\Psi ^{-1}\left( -\alpha +\int ^s_{\sigma }m(r)f(u(r))\mathrm{d}r\right) \mathrm{d}s,~&{} t\in [\sigma ,1), \end{array}\right. } \end{aligned}$$

where $\alpha$ satisfies

$$\begin{aligned} \int _0^\sigma \Psi ^{-1}\left( \alpha +\int _s^\sigma m(r)f(u(r))\mathrm{d}r\right) \mathrm{d}s=\int _\sigma ^1\Psi ^{-1}\left( -\alpha +\int ^s_\sigma m(r)f(u(r))\mathrm{d}r\right) \mathrm{d}s. \end{aligned}$$

We easily check that u is a solution of problem (P) if and only if $u\in K$ satisfies $u=Tu$. Moreover, we can easily check by a standard argument that $T(K)\subset K$ and T is completely continuous. For $u\in K$, Tu is concave and satisfies the Dirichlet boundary condition. Thus we may assume that there exists $t^*\in (0,1)$, a maximal point of Tu satisfying $\Vert Tu\Vert _\infty =(Tu)(t^*)$ and $(Tu)'(t^*)=0$. We note that $t^*$ need not be unique. From $(Tu)'(t^*)=0$, we obtain

$$\begin{aligned} \alpha =-\int _{t^*}^\sigma m(r)f(u(r))\mathrm{d}r. \end{aligned}$$

Since $m\in L^1(t^*-\delta ,t^*+\delta )$ for any small $\delta$, replacing $\sigma$ with $t^*$, we get $\alpha =0$ and Tu can be written as

$$\begin{aligned} (Tu)(t)= {\left\{ \begin{array}{ll} \int _0^t\Psi ^{-1}\left( \int _s^{t^*}m(r)f(u(r))\mathrm{d}r\right) \mathrm{d}s,~&{} t\in (0,t^*],\\ \int ^1_t\Psi ^{-1}\left( \int ^s_{t^*}m(r)f(u(r))\mathrm{d}r\right) \mathrm{d}s,~&{} t\in [t^*,1). \end{array}\right. } \end{aligned}$$

(3.1)

If we find a nontrivial fixed point u of T in K, then u is a positive solution of problem (P), and we now give the existence result for problem (P).

Theorem 3.1

Assume $m\in \mathcal {A}.$ Also assume $(F_1)$ and $(F_2)$. Then there exists at least one positive solution u of problem (P) satisfying $\Vert u\Vert _\infty \le \rho$.

Proof

Let $u\in K$. We know $m\in \mathcal {B}$ so let us denote $m_1$ as

$$\begin{aligned}&m_1=\max \left\{ \int _0^{\frac{1}{2}}\int _s^{\frac{1}{2}}m(r)\mathrm{d}r \mathrm{d}s,\right. \left. \int _{\frac{1}{2}}^1\int ^s_{\frac{1}{2}}m(r)\mathrm{d}r \mathrm{d}s\right\} . \end{aligned}$$

Then, by $(F_1)$, there exists $\rho _1 \in (0, \frac{1}{4}\rho )$ such that

$$\begin{aligned} f(s)\le \frac{1}{m_1}s, ~\mathrm{for}~ s\in [0,\rho _1]. \end{aligned}$$

(3.2)

Define $\Omega _1=\{u\in E:\Vert u\Vert _\infty <\rho _1\}$ and consider $u\in K \cap \partial \Omega _1.$ For $t^*$ given in (3.1), we first assume $t^*\in (0,\frac{1}{2}]$, then by using (3.2), we derive

$$\begin{aligned} \Vert Tu \Vert _{\infty }=(Tu)(t^*)&=\int _0^{t^*}\Psi ^{-1}\left( \int _s^{t^*}m(r)f(u(r))\mathrm{d}r\right) \mathrm{d}s\\&\le \int _0^{\frac{1}{2}}\Psi ^{-1}\left( \int _s^{\frac{1}{2}}m(r)f(u(r))\mathrm{d}r\right) \mathrm{d}s\\&\le \int _0^{\frac{1}{2}}\int _s^{\frac{1}{2}}m(r)f(u(r))\mathrm{d}r \mathrm{d}s\\&\le \frac{1}{m_1}\int _0^{\frac{1}{2}}\int _s^{\frac{1}{2}}m(r)\mathrm{d}r \mathrm{d}s\Vert u\Vert _\infty \le \Vert u\Vert _\infty . \end{aligned}$$

If $t^*\in (\frac{1}{2},1)$, then by an analogous argument, we also get the same inequality. Thus, $\Vert Tu\Vert _\infty \le \Vert u\Vert _\infty$ for $u\in K\cap \partial \Omega _1$.

On the other hand, define $\Omega _2=\{u\in E:\Vert u\Vert _\infty <\rho \}$ and consider $u\in K\cap \partial \Omega _2.$ If $t^*\in [\frac{1}{2},1)$, then we obtain

$$\begin{aligned} \Vert Tu \Vert _{\infty }=(Tu)(t^*)&=\int _0^{t^*}\Psi ^{-1}\left( \int _s^{t^*}m(r)f(u(r))\mathrm{d}r\right) \mathrm{d}s\\&\ge \int _{\delta }^{\frac{1}{2}}\Psi ^{-1}\left( \int _s^{\frac{1}{2}}m(r)f(u(r))\mathrm{d}r\right) \mathrm{d}s. \end{aligned}$$

Since $u\in K\cap \partial \Omega _2$, we see

$$\begin{aligned} \frac{u(t)}{\Vert u\Vert _\infty }\ge \frac{t}{t^*}>\delta , ~\mathrm{for}~t\in [\delta ,t^*]. \end{aligned}$$

Thus, $u(t)\ge \delta \Vert u\Vert _\infty$ for $t\in [\delta ,t^*]$ and this implies $u(t)\in [\delta \rho ,\rho ]$ for $t\in [\delta ,t^*]$. By applying $(F_2)$ and Remark 3.2, we get

$$\begin{aligned} \int _{\delta }^{\frac{1}{2}}\Psi ^{-1}\left( \int _s^{\frac{1}{2}}m(r)f(u(r))\mathrm{d}r\right) \mathrm{d}s&\ge \int _{\delta }^{\frac{1}{2}}\Psi ^{-1}\left( \int _s^{\frac{1}{2}}m(r)\Psi \left( \frac{u(r)}{\delta M_{\delta }}\right) \mathrm{d}r\right) \mathrm{d}s\\&\ge \int _{\delta }^{\frac{1}{2}}\Psi ^{-1}\left( \int _s^{\frac{1}{2}}m(r)\Psi \left( \frac{\Vert u\Vert _\infty }{M_{\delta }}\right) \mathrm{d}r\right) \mathrm{d}s\\&\ge \int _{\delta }^{\frac{1}{2}}\Psi ^{-1}\left( \int _s^{\frac{1}{2}}m(r)\mathrm{d}r\right) \mathrm{d}s\frac{\Vert u\Vert _\infty }{M_{\delta }} \ge \Vert u\Vert _\infty . \end{aligned}$$

By a similar argument to the case $t^*\in (0,\frac{1}{2})$, we also get

$$\begin{aligned} (Tu)(t^*)\ge \Vert u\Vert _\infty , ~\mathrm{for}~u\in K\cap \partial \Omega _2. \end{aligned}$$

This implies that $\Vert Tu\Vert _\infty \ge \Vert u\Vert _\infty$ for $u\in K\cap \partial \Omega _2.$ Therefore, by Lemma 3.1, operator T has a fixed point in $K\cap (\overline{\Omega _2}\setminus \Omega _1)$, which is a positive solution of problem (P) and the proof is complete. $\square$

Now we give an example to illustrate the applicability of Theorem 3.1.

Example 3.1

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Big (\Psi (u'(t))\Big )'=(1-t)^{-\frac{3}{2}}f(u(t)), ~&{}t\in (0,1),\\ u(0)=0=u(1), \end{array}\right. } \end{aligned}$$

(3.3)

where nonlinear term f is given by

$$\begin{aligned} f(s)= {\left\{ \begin{array}{ll} s^2,~&{} s\in [0,0.0015),\\ \mathrm{linear},~&{} s\in [0.0015,0.0025),\\ \Psi (\frac{10000s}{167}),~&{} s\in [0.0025,0.01),\\ \Psi (\frac{100}{167}),~&{} s\in [0.01, 0.5]. \end{array}\right. } \end{aligned}$$

Fix $\delta =\frac{1}{4}$. Then $M_{\delta } \approx 0.0668523.$ Take $\rho =0.01,$ then $\rho \in (0,\delta M_{\delta })$ and f satisfies $(F_1)$ and $(F_2).$ Thus from Theorem 3.1, problem (3.3) has at least one positive solution u with $\Vert u\Vert _\infty \le 0.01$.

4 Nonlinear Eigenvalue Problems

In this section, we apply Theorem 3.1 to study the existence of positive solutions for one parameter family of problems of the form

Assume $m\in \mathcal {A}$ and $g_0=0.$ For fixed $\delta \in (0,\frac{1}{2}),$ define a function ${\lambda _{\delta } }$ given by

$$\begin{aligned} {\lambda _{\delta } }(s)=\frac{\Psi \left( \frac{s}{\delta M_{\delta }}\right) }{g(s)}=\frac{s}{g(s)\sqrt{(\delta M_{\delta })^2-s^2}}, \end{aligned}$$

for $s\in (0,{\delta } M_{\delta }).$ Then ${\lambda _{\delta } } : (0,{\delta } M_{\delta }) \rightarrow (0, \infty )$ is continuous and ${\lambda _{\delta }(s) } \rightarrow \infty ,$ as $s\rightarrow 0$ or $s\rightarrow \delta M_{\delta }.$ Moreover, for each $\rho \in (0,\delta M_{\delta }),$ $\Lambda _{\delta }^{\rho }\triangleq \max \limits _{s\in [\delta \rho ,\rho ]}{\lambda _{\delta }}(s)$ is well-defined. Taking $f(s)=\lambda g(s)$, we see that f satisfies $f_0=0$ and $(F_2)$ when $\lambda \ge \Lambda _{\delta }^{\rho }.$ Therefore, we have a corollary of Theorem 3.1 as follows.

Corollary 4.1

Assume $m\in \mathcal {A}$ and $g_0=0$. Then for each $\delta \in (0,\frac{1}{2})$ and $\rho \in (0,\delta M_{\delta }),$ there exists at least one positive solution of problem $(P_\lambda )$ for all $\lambda \ge \Lambda _{\delta }^{\rho }.$ Moreover, the solution u satisfies $\Vert u\Vert _\infty \le \rho .$

Denote $\Lambda _{\delta }\triangleq \inf \limits _{\rho \in (0,\delta M_{\delta })}\Lambda _{\delta }^{\rho }.$ Since $0<\Lambda _{\delta }^{\rho }<\infty$, we see $0\le \inf \limits _{\rho \in (0,\delta M_{\delta })}\Lambda _{\delta }^{\rho }<\infty$ and $\Lambda _{\delta }$ is well-defined. Thus we see from Corollary 4.1 that problem $(P_\lambda )$ has at least one positive solution for all $\lambda > \Lambda _{\delta }.$ Furthermore, we may prove that problem $(P_\lambda )$ has at least one positive solution at $\lambda = \Lambda _{\delta }.$

Proposition 4.1

Assume $m\in \mathcal {A}$ and $g_0=0$. Then for each $\delta \in (0,\frac{1}{2}),$ there exists at least one positive solution of problem $(P_\lambda )$ at $\lambda = \Lambda _{\delta }.$

Proof

Let $\delta \in (0,\frac{1}{2})$ be given.

Claim 1. $\Lambda _{\delta }^{\rho }$ is continuous with respect to $\rho \in (0,\delta M_{\delta })$.

Indeed, let $\rho _1,\rho _2\in (0,\delta M_{\delta })$ with $\rho _1<\rho _2.$ Then by the continuity of ${\lambda _{\delta } ^{\rho }}(s)$ with respect to s, there exist $s_1\in [\delta \rho _1,\rho _1]$, $s_2\in [\delta \rho _2,\rho _2]$ such that

$$\begin{aligned} {\lambda _{\delta } }(s_1)=\max \limits _{s\in [\delta \rho _1,\rho _1]}{\lambda _{\delta } }(s) \ \mathrm{and} \ {\lambda _{\delta } }(s_2)=\max \limits _{s\in [\delta \rho _2,\rho _2]}{\lambda _{\delta } }(s). \end{aligned}$$

We now divide our claim into two cases:

Case (i) $\delta \rho _1<\rho _1< \delta \rho _2<\rho _2.$

First consider if $\Lambda _{\delta }^{\rho _2}\ge \Lambda _{\delta }^{\rho _1}$, then we get

$$\begin{aligned} 0\le |\Lambda _{\delta }^{\rho _2}-\Lambda _{\delta }^{\rho _1}|&=\max \limits _{s\in [\delta \rho _2,\rho _2]}{\lambda _{\delta } }(s)-\max \limits _{s\in [\delta \rho _1,\rho _1]}{\lambda _{\delta } }(s)\\&\le \max \limits _{s\in [\delta \rho _2,\rho _2]}{\lambda _{\delta } }(s)-{\lambda _{\delta } }(\rho _1)\\&={\lambda _{\delta } }(s_2)-{\lambda _{\delta } }(\rho _1)\rightarrow 0, \end{aligned}$$

as $0<s_2-\rho _1\le \rho _2-\rho _1\rightarrow 0$.

If $\Lambda _{\delta }^{\rho _2}<\Lambda _{\delta }^{\rho _1}$, then we similarly calculate

$$\begin{aligned} 0<|\Lambda _{\delta }^{\rho _2}-\Lambda _{\delta }^{\rho _1}|&=\max \limits _{s\in [\delta \rho _1,\rho _1]}{\lambda _{\delta } }(s)-\max \limits _{s\in [\delta \rho _2,\rho _2]}{\lambda _{\delta } }(s)\\&\le \max \limits _{s\in [\delta \rho _1,\rho _1]}{\lambda _{\delta } }(s)-{\lambda _{\delta } }(\delta \rho _2)\\&={\lambda _{\delta } }(s_1)-{\lambda _{\delta } }(\delta \rho _2)\rightarrow 0, \end{aligned}$$

as $0<\delta \rho _2-s_1\le \delta (\rho _2-\rho _1)<\rho _2-\rho _1\rightarrow 0$.

Case (ii) $\delta \rho _1< \delta \rho _2<\rho _1<\rho _2.$

$$\begin{aligned}&|\Lambda _{\delta }^{\rho _2}-\Lambda _{\delta }^{\rho _1}|=|\max \limits _{s\in [\delta \rho _2,\rho _2]}{\lambda _{\delta } }(s)-\max \limits _{s\in [\delta \rho _1,\rho _1]}{\lambda _{\delta } }(s)|\nonumber \\ \le&\underbrace{|\max \limits _{s\in [\delta \rho _2,\rho _2]}{\lambda _{\delta } }(s)-\max \limits _{s\in [\delta \rho _2,\rho _1]}{\lambda _{\delta } }(s)|}_{\triangleq \ l_1}+\underbrace{|\max \limits _{s\in [\delta \rho _2,\rho _1]}{\lambda _{\delta } }(s)-\max \limits _{s\in [\delta \rho _1,\rho _1]}{\lambda _{\delta } }(s)|}_{\triangleq \ l_2}. \end{aligned}$$

(4.1)

We consider $l_1$ first. If $s_2\in [\delta \rho _2,\rho _1]$, then $l_1\equiv 0$. And if $s_2\in [\rho _1,\rho _2]$, then

$$\begin{aligned} l_1&=\max \limits _{s\in [\rho _1,\rho _2]}{\lambda _{\delta } }(s)-\max \limits _{s\in [\delta \rho _2,\rho _1]}{\lambda _{\delta } }(s)\nonumber \\&\le {\lambda _{\delta } }(s_2)-{\lambda _{\delta } }(\rho _1) \rightarrow 0, \end{aligned}$$

(4.2)

as $0\le s_2-\rho _1\le \rho _2-\rho _1\rightarrow 0$.

Now we consider $l_2$. If $s_1\in [\delta \rho _2,\rho _1]$, then $l_2\equiv 0$. And if $s_2\in [\delta \rho _1,\delta \rho _2]$, then

$$\begin{aligned} l_2&=\max \limits _{s\in [\delta \rho _1,\delta \rho _2]}{\lambda _{\delta } }(s)-\max \limits _{s\in [\delta \rho _2,\rho _1]}{\lambda _{\delta } }(s)\nonumber \\&\le {\lambda _{\delta } }(s_1)-{\lambda _{\delta } }(\delta \rho _2)\rightarrow 0, \end{aligned}$$

(4.3)

as $0\le \delta \rho _2-s_1\le \delta (\rho _2-\rho _1)<\rho _2-\rho _1\rightarrow 0$. Thus, combining (4.1)–(4.3), we deduce $|\Lambda _{\delta }^{\rho _2}-\Lambda _{\delta }^{\rho _1}|\rightarrow 0$ as $\rho _2-\rho _1\rightarrow 0$ and Claim 1 is proved.

Denote a set $D=\{\rho \in (0,\delta M_{\delta }):$ problem $(P_\lambda )$ has at least one positive solution for all $\lambda \ge \Lambda _{\delta }^\rho \}.$ Then by the definition of $\Lambda _{\delta }$, we may choose a sequence $\{\rho _n\}\subset D$ such that $\Lambda _{\delta }^{\rho _n}\rightarrow \Lambda _{\delta }$.

Claim 2. There exists $\widetilde{\rho }\in (0,\delta M_{\delta })$ such that $\Lambda _{\delta }^{\widetilde{\rho }}=\Lambda _{\delta }$.

Thus it follows from Claim 2 and Corollary 4.1 that problem $(P_\lambda )$ has at least one positive solution at $\lambda = \Lambda _{\delta }$ and the proof of Proposition 4.1 is done. We now prove Claim 2. Since $\{\rho _n\}$ is bounded, there exists a subsequence $\{\rho _{n_k}\}$ and $\widetilde{\rho }\in [0,\delta M_{\delta }]$ such that $\rho _{n_k}\rightarrow \widetilde{\rho }$ as $k\rightarrow \infty$. By Claim 1, we see $\Lambda _{\delta }^{\rho _{n_k}}\rightarrow \Lambda _{\delta }^{\widetilde{\rho }}$ as $k\rightarrow \infty .$ Together with the fact $\Lambda _{\delta }^{\rho _n}\rightarrow \Lambda _{\delta }$ and the uniqueness of limits, we get $\Lambda _{\delta }^{\widetilde{\rho }}=\Lambda _{\delta }$. Since $\Lambda _{\delta }^{\widetilde{\rho }}=\infty$ at $\widetilde{\rho }= 0$ or $\delta M_{\delta },$ we see that $\widetilde{\rho }\ne 0$ and $\widetilde{\rho }\ne \delta M_{\delta },$ and Claim 2 is proved. $\square$

We finally denote $\Lambda ^* \triangleq \inf \limits _{\delta \in (0,\frac{1}{2})}\Lambda _{\delta }.$ Since $0\le \Lambda _{\delta }<\infty$ for $\delta \in (0,\frac{1}{2})$, we see $0\le \Lambda ^*<\infty$. Therefore, we conclude that problem $(P_\lambda )$ has at least one positive solution for all $\lambda > \Lambda ^*.$ By a similar argument in the proof of Proposition 4.1, we may prove that $(P_\lambda )$ has at least one positive solution at $\lambda =\Lambda ^*$ as well. As a consequence, we have the following corollary.

Corollary 4.2

Assume $m\in \mathcal {A}$ and $g_0=0$. Then there exists at least one positive solution of problem $(P_\lambda )$ for all $\lambda \ge \Lambda ^*.$

For more numerical information of $\Lambda ^*,$ we give the following example.

Example 4.1

Take $\lambda >0$ and $p>1$ and we deal with the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Big (\Psi (u'(t))\Big )'=\lambda t^{-\frac{3}{2}}(u(t))^p, ~&{}t\in (0,1),\\ u(0)=0=u(1). \end{array}\right. } \end{aligned}$$

(4.4)

Note that $m(t)=t^{-\frac{3}{2}} \in \mathcal A$ and $g(s)=s^p, \ p>1$ satisfies $g_0 =0.$ We check some properties of ${\lambda _{\delta } }$ to obtain a numerical information of $\Lambda ^*$.

Prop 1 From the definition of ${\lambda _{\delta } }$, we can easily see that ${\lambda _{\delta } }(s) \rightarrow \infty$ as $s\rightarrow 0^+$ or $s\rightarrow \delta M_{\delta }.$ Moreover, calculating the derivative of ${\lambda _{\delta } }$, we see that ${\lambda _{\delta } }$ is strictly decreasing on $(0,\sqrt{\frac{p-1}{p}}\delta M_{\delta })$ and strictly increasing on $(\sqrt{\frac{p-1}{p}}\delta M_{\delta }, \delta M_{\delta }).$

Prop 2 There exists unique $\rho ^* \in (0,\delta M_{\delta })$ such that ${\lambda _{\delta } }(\delta \rho ^* )={\lambda _{\delta } }(\rho ^* ).$

Indeed, let us consider a function ${\lambda _{\delta } }(\delta s )-{\lambda _{\delta } }(s )$ for $s \in (0,\delta M_{\delta }).$ Then this function is continuous and by Prop 1, we see that

$$\begin{aligned}&{\lambda _{\delta } }(\delta s )-{\lambda _{\delta } }(s )>0, \ \mathrm{for}\ s\in (0,\sqrt{\frac{p-1}{p}}\delta M_{\delta }) \triangleq I_1 \ \mathrm{and}\\&{\lambda _{\delta } }(\delta s )-{\lambda _{\delta } }(s )<0, \ \mathrm{for}\ s\in (\sqrt{\frac{p-1}{p}} M_{\delta }, \delta M_{\delta })\triangleq I_2. \end{aligned}$$

Thus by Intermediate Value Theorem, there is $\rho ^* \in (\sqrt{\frac{p-1}{p}}\delta M_{\delta },\sqrt{\frac{p-1}{p}} M_{\delta })\triangleq I_3$ such that ${\lambda _{\delta } }(\delta \rho ^* )={\lambda _{\delta } }(\rho ^* ).$

Uniqueness: If $s\in I_3,$ then $\delta s\in I_1$ and ${\lambda _{\delta } }(\delta s )$ is strictly decreasing and ${\lambda _{\delta } }(s )$ is strictly increasing. Thus ${\lambda _{\delta } }(\delta s )-{\lambda _{\delta } }(s )$ is strictly decreasing on $I_3$ and the uniqueness is guaranteed.

Prop 3 From Prop 1 and Prop 2, it is obvious to see that $\Lambda _{\delta }={\lambda _{\delta } }(\rho ^* ).$

Solving $\rho ^*$ from ${\lambda _{\delta } }(\delta \rho ^* )={\lambda _{\delta } }(\rho ^* )$ with ${\lambda _{\delta } }(s)=\frac{1}{s^{p-1}\sqrt{(\delta M_{\delta })^2-s^2}},$ we obtain

$$\begin{aligned} \rho ^*=\sqrt{\frac{1-\delta ^{2(p-1)}}{1-\delta ^{2p}}}\delta M_\delta , \ \mathrm{and} \ \ \Lambda _{\delta }={\lambda _{\delta } }(\rho ^* )=\frac{1-{\delta }^{2p}}{(\delta M_{\delta })^2\sqrt{{\delta }^{2(p-1)} (1-\delta ^{2(p-2)})(1-\delta ^2)}}. \end{aligned}$$

See Fig. 1 for the graph of $\lambda _{\delta } (s)$ and relation between $\Lambda _{\delta }^{\rho }$ and $\Lambda _{\delta }.$

Fig. 1

Graph of $\lambda _{\delta } (s)$

Algorithm for finding an approximation of $\Lambda ^*$

Step 1. For fixed $\delta \in (0,\frac{1}{2}),$ calculate

$$\begin{aligned} M_\delta =\min \left\{ \int _\delta ^{\frac{1}{2}}\frac{-2\sqrt{2}+\frac{2}{\sqrt{s}}}{\sqrt{1+\left( -2\sqrt{2}+\frac{2}{\sqrt{s}}\right) ^2}}\mathrm{d}s, \int ^{1-\delta }_{\frac{1}{2}}\frac{2\sqrt{2}-\frac{2}{\sqrt{s}}}{\sqrt{1+\left( 2\sqrt{2}-\frac{2}{\sqrt{s}}\right) ^2}}\mathrm{d}s\right\} . \end{aligned}$$

Step 2. Calculate $\rho ^*$.

$$\begin{aligned} \rho ^*=\sqrt{\frac{1-\delta ^{2(p-1)}}{1-\delta ^{2p}}}\delta M_\delta . \end{aligned}$$

Step 3. Calculate $\Lambda _{\delta }\big (={\lambda _{\delta } }(\rho ^* )\big ).$

$$\begin{aligned} \Lambda _{\delta }=\frac{1-{\delta }^{2p}}{(\delta M_{\delta })^2\sqrt{{\delta }^{2(p-1)} (1-\delta ^{2(p-2)})(1-\delta ^2)}}. \end{aligned}$$

Conclusion 1. For fixed $\delta \in (0,\frac{1}{2})$, there exists at least one positive solution u of problem (4.4) satisfying $\Vert u\Vert _\infty \le \rho ^*$ for all $\lambda \ge \Lambda _\delta$.

Step 4. Calculate $\Lambda ^* = \inf \limits _{\delta \in (0,\frac{1}{2})}\Lambda _\delta .$

Conclusion 2. There exists at least one positive solution of problem (4.4) for all $\lambda \ge \Lambda ^*$.

Use MATLAB for Step 4. The approximations of $\Lambda ^*$ with respect to $p=1.01,1.02,1.1,2,10$ are shown in Table 1.

Table 1 The approximations of $\Lambda ^*$ with respect to $p=1.01,1.02,1.1,2,10$

5 A Nonexistence Result

In this section, we study nonexistence of positive solutions for problem $(P_\lambda )$.

Theorem 5.1

Assume that there is a positive constant $c_0$ such that

$$\begin{aligned} \frac{g(s)}{s}\le c_0, \end{aligned}$$

(5.1)

for all $s\in [0,\frac{1}{2}]$. Then there is no nontrivial solution of problem $(P_\lambda )$ for all $\lambda \in (0,\Lambda _*]$ with $\Lambda _*=\frac{1}{c_0\int _0^1 t(1-t)m(t)\mathrm{d}t}$.

Proof

Let $\lambda >0.$ Suppose on the contrary that problem $(P_\lambda )$ has a nontrivial solution u at $\lambda$. Then by Remark 3.3, it is positive and by Theorem 2.1 in [16], $u\in C^1[0,1]$ and $|u'(t)|<1$ for $t\in [0,1]$. Applying the Hölder’s inequality, we obtain

$$\begin{aligned} |u(t)|\le \int _0^t|u'(r)|\mathrm{d}r\le t^{\frac{1}{2}}\left( \int _0^t|u'(r)|^2\mathrm{d}r\right) ^{\frac{1}{2}},~\forall t\in [0,1]. \end{aligned}$$

Thus

$$\begin{aligned} (1-t)|u(t)|^2\le t(1-t)\left( \int _0^t|u'(r)|^2\mathrm{d}r\right) ,~\forall t\in [0,1]. \end{aligned}$$

(5.2)

Similarly, we also obtain

$$\begin{aligned} t|u(t)|^2\le t(1-t)\left( \int _t^1|u'(r)|^2\mathrm{d}r\right) ,~\forall t\in [0,1]. \end{aligned}$$

(5.3)

Adding (5.2) and (5.3), we get

$$\begin{aligned} |u(t)|^2\le t(1-t)\left( \int _0^1|u'(r)|^2\mathrm{d}r\right) ,~\forall t\in [0,1]. \end{aligned}$$

(5.4)

Multiplying the first equation in $(P_\lambda )$ by u and then integrating on (0, 1), we have

$$\begin{aligned} \int _0^1\Big (\Psi (u'(t))\Big )u'(t)\mathrm{d}t=\lambda \int _0^1 m(t)g(u(t))u(t)\mathrm{d}t. \end{aligned}$$

(5.5)

We note that the integration on the right-hand side is well-defined by (5.1) and (5.4). Combining (5.1), (5.4) and (5.5), we get

$$\begin{aligned} \int _0^1|u'(t)|^2\mathrm{d}t&<\int _0^1\Big (\Psi (u'(t))\Big )u'(t)\mathrm{d}t \\&=\lambda \int _0^1 m(t)g(u(t))u(t)\mathrm{d}t \\&\le \lambda c_0\int _0^1 m(t)|u(t)|^2\mathrm{d}t \\&\le \lambda c_0\int _0^1 m(t)t(1-t)\mathrm{d}t\left( \int _0^1|u'(r)|^2\mathrm{d}r\right) . \end{aligned}$$

It follows that $\lambda >\Lambda _*$. Therefore, we conclude that problem $(P_\lambda )$ has no nontrivial solution for $\lambda \in (0,\Lambda _*]$ and the proof is complete. $\square$

As an immediate consequence of Corollary 4.2 and Theorem 5.1, we obtain the following result about existence and nonexistence.

Corollary 5.1

Assume $m\in \mathcal A$ and $g_0=0$. Then there exist $0<\Lambda _*<\Lambda ^*$ such that problem $(P_\lambda )$ has no nontrivial solution for $\lambda \in (0,\Lambda _*]$ and at least one positive solution for $\lambda \in [\Lambda ^*,\infty )$.

We give some examples as applications of Theorem 5.1 and Corollary 5.1.

Example 5.1

There is no nontrivial solution to problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Big (\Psi (u'(t))\Big )'=\lambda t^{-\frac{3}{2}}(1-t)^{-\frac{3}{2}}\frac{|u(t)|^2}{\sqrt{1+|u(t)|^2}}, ~&{}t\in (0,1),\\ u(0)=0=u(1), \end{array}\right. } \end{aligned}$$

for all $\lambda \in (0,\frac{\sqrt{5}}{\pi }]$. Indeed, we calculate $c_0=\frac{\sqrt{5}}{5}$ and $\Lambda _*=\frac{1}{c_0\pi }=\frac{\sqrt{5}}{\pi }$.

Example 5.2

There is no nontrivial solution to problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Big (\Psi (u'(t))\Big )'=\lambda t^{-\frac{1}{2}}(1-t)^{-\frac{3}{2}}u(t), ~&{}t\in (0,1),\\ u(0)=0=u(1), \end{array}\right. } \end{aligned}$$

for all $\lambda \in (0,\frac{2}{\pi }]$. Indeed, $c_0=1$ and $\Lambda _*=\frac{2}{c_0\pi }=\frac{2}{\pi }$.

Example 5.3

We give an example of Lane-Emden type problems with case $m\in C[0,1]$ as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Big (\Psi (u'(t))\Big )'=\lambda t^{\frac{1}{2}}(u(t))^p, ~&{}t\in (0,1),\\ u(0)=0=u(1), \end{array}\right. } \end{aligned}$$

(5.6)

where parameter $\lambda >0$ and $p>1$. By Theorem 5.1, we know $\Lambda _*=3\cdot 2^{p+1}$ and $\Lambda ^*$ can be calculated by similar computation as in Example 4.1. Thus by Corollary 5.1, we conclude that problem (5.6) has no nontrivial solution for $\lambda \in (0,\Lambda _*]$ and at least one positive solution for $\lambda \in [\Lambda ^*,\infty )$. The approximations of $\Lambda _*$ and $\Lambda ^*$ with respect to $p=1.01,1.02,1.1,2,10$ are given in Table 2.

Table 2 The approximations of $\Lambda _*$ and $\Lambda ^*$ for problem (5.6)

Example 5.4

We revisit Example 4.1. Let us consider problem (4.4) again

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Big (\Psi (u'(t))\Big )'=\lambda t^{-\frac{3}{2}}(u(t))^p, ~&{}t\in (0,1), \\ u(0)=0=u(1). \end{array}\right. } \end{aligned}$$

We calculate $c_0=\frac{1}{2^{p-1}}$ and $\Lambda _*=\frac{3}{4c_0}=3\cdot 2^{p-3}.$ Combining the results in Example 4.1 and Theorem 5.1, we conclude that problem (4.4) has no nontrivial solution for $\lambda \in (0,\Lambda _*]$ and at least one positive solution for $\lambda \in [\Lambda ^*,\infty )$. The approximations of $\Lambda _*$ and $\Lambda ^*$ with respect to $p=1.01,1.02,1.1,2,10$ are given in Table 3.

Table 3 The approximations of $\Lambda _*$ and $\Lambda ^*$ for problem (4.4)