SpringerLink
Log in

On Fractional FitzHugh-Nagumo Equation as a Transmission of Nerve Impulses Design

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

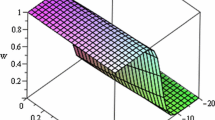
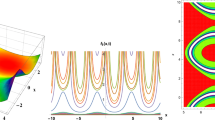
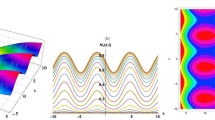
This work apprises the exact solutions of the fractional Fitzhugh-Nagumo equation as a model of transmission of nerve impulses. Two methods via the new extended direct algebraic method (EDA) and exp-function method are used to search the new exact solutions of the mentioned equation, respectively. The exp-function method is very similar to the new EDA technique. So, one of the main purposes of this study is to compare the obtained results. The other aim is to show that all findings are exceptional and new. Furthermore, it can be said that the leading advantage of the present schemes is a very simple and easy mathematical tools for obtaining the analytical solutions with nonlinear fractional partial differential equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data Availability

Not applicable.

References

  1. Oldham, K.B., Spanier, J.: The Fractional Calculus. Academic Press, New York, London (1974)

    MATH  Google Scholar 

  2. Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  3. Jumarie, G.: Table of some basic fractional calculus formulae derived from a modified Riemann-Liouville derivative for non-differentiable functions. Appl. Math. Lett. 22(3), 378–385 (2009)

    Article  MathSciNet  Google Scholar 

  4. Abdeljawad, T.: On conformable fractional calculus. J. Comput. Appl. Math. 279, 57–66 (2015)

    Article  MathSciNet  Google Scholar 

  5. Chen, W.: Fractal calculus and its geometrical explanation. Results Phys. 10, 272–276 (2018)

    Article  Google Scholar 

  6. He, J.H.: Time space fabric underlying anomalous diffusion. Chaos Solitons Fract. 28, 923–929 (2006)

    Article  Google Scholar 

  7. Singh, K.D.J., Nieto, J.J.: Analysis of an El Nino-Southern Oscillation model with a new fractional derivative. Chaos Solitons Fract. 99, 109–115 (2017)

    Article  MathSciNet  Google Scholar 

  8. Sun, H., Chen, W.: Fractal derivative multi-scale model of fluid particle transverse accelerations in fully developed turbulence. Sci. China Ser. E Techn. Sci. 52(3), 680–683 (2009)

    Article  Google Scholar 

  9. Bai, Q., Shu, J., Li, L., Li, H.: Dynamical behavior of non-autonomous fractional stochastic reaction-diffusion equations. J. Math. Anal. Appl. 485, 123833 (2020)

    Article  MathSciNet  Google Scholar 

  10. Alquran, M., Jaradat, I.: A novel scheme for solving caputo-time fractional nonlinear equations: theory and application. Nonlinear Dyn. 91(4), 2389–2395 (2018)

    Article  Google Scholar 

  11. Wang, K.L.: New variational theory for coupled nonlinear fractal schrödinger system. Int. J. Numer. Meth. Heat Fluid Flow 32(2), 589–597 (2022)

    Article  Google Scholar 

  12. Wang K.L.: Exact solitary wave solution for fractal shallow water wave model by he’s variational method. Modern Phys. Lett. B 2150602 (2022)

  13. Wang, K.L., Wang, K.J., He, C.H.: Physical insight of local fractional calculus and its application to fractional kdv-burgers-kuramoto equation. Fractals 27(07), 1950122 (2019)

    Article  MathSciNet  Google Scholar 

  14. Wang, K.L., Wang, Y.S.: He’s fractional derivative for the evalution equation. Therm. Sci. 24(4), 2507–2513 (2020)

    Article  Google Scholar 

  15. Wei, C.F.: Two-scale transform for 2-d fractal heat eqaution in a fractal space. Therm. Sci. 25(3B), 2339–2345 (2021)

    Article  Google Scholar 

  16. Guner, O., Atık, H.: Soliton solution of fractional-order nonlinear differential equations based on the exp-function method. Phys. Lett. A 127(20), 10076–10083 (2016)

    Google Scholar 

  17. He, J.H., Wu, X.H.: Exp-function method for nonlinear wave equations. Chaos Solitons Fract. 30, 700–708 (2006)

    Article  MathSciNet  Google Scholar 

  18. Taşbozan, O., Kurt, A.: The new travelling wave solutions of time fractional Fitzhugh-Nagumo equation with Sine-Gordon expansion method. Adıyaman Univ. J. Sci. 10(1), 256–263 (2020)

    Google Scholar 

  19. Karaman, B.: Analytical investigation for modified Riemann-Liouville fractional Equal-Width equation types based on \((G^{\prime }/G)\)-expansion technique. Miskolch Math. Notes 21(1), 219–227 (2020)

    Article  MathSciNet  Google Scholar 

  20. Zhang, H.: New application of the \((G^{\prime }/G)\)-expansion method. Commun. Nonlinear Sci. Numer. Simulat. 14, 3220–3225 (2009)

    Article  Google Scholar 

  21. Karaman, B.: The use of improved-F expansion method for the time-fractional Benjamin-Ono equation. Rev. Real. Acad. Cienc. Exactas. Fis. Nat. A Mat. 115(3), 1–7 (2021)

    MathSciNet  MATH  Google Scholar 

  22. Vahidi, J., Zabihi, A., Rezazadeh, H., Ansari, R.: New extended direct algebraic method for the resonant nonlinear Schrödinger equation with Kerr law nonlinearity. Optik 227, 165936 (2021)

    Article  Google Scholar 

  23. Kurt, A., Tozar, A., Tasbozan, O.: Applying the new extended direct algebraic method to solve the equation of obliquely interacting waves in shallow waters. J. Ocean Univ. China 19(4), 772–780 (2020)

    Article  Google Scholar 

  24. Hodgkin, A.L., Huxley, A.F.: A quantitive description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117(4), 500–544 (1952)

    Article  Google Scholar 

  25. Fitzhugh, R.: Impulse and physiological states in models of nerve membrane. Biophys. J . 1, 445–466 (1961)

    Article  Google Scholar 

  26. Kumar, D., Singh, J., Baleanu, D.: A new numerical algorithm for fractional fitzhugh-nagumo equation arising in transmission of nerve impulses. Nonlinear Dyn. 91, 307–317 (2018)

    Article  MathSciNet  Google Scholar 

  27. Aronson, D.G., Weinberger, H.F.: Multidimensional nonlinear diffusion arising in population genetics. Adv. Math. 30, 33–76 (1978)

    Article  MathSciNet  Google Scholar 

  28. Taşbozan, O.: A popular reaction-diffusion model fractional fitzhugh-nagumo equation: analytical and numerical treatment. Appl. Math.-A J. Chin. Univ. 36(2), 218–228 (2021)

    Article  MathSciNet  Google Scholar 

  29. Alfaqeih, S., Mısırlı, E.: On convergence analysis and analytical solutions of the conformable fractional fitzhugh-nagumo model using the conformable sumudu decomposition method. Symmetry 13, 243–257 (2021)

    Article  Google Scholar 

  30. Deniz, S.: Optimal perturbation iteration method for solving fractional Fitzhugh-Nagumo equation. Chaos Solitons Fract. 142, 110417 (2021)

    Article  MathSciNet  Google Scholar 

  31. He, J.H., Elagan, S.K., Li, Z.B.: Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys. Lett. A 376(4), 257–259 (2012)

    Article  MathSciNet  Google Scholar 

  32. He, J.H., Ain, Q.T.: New promises and future challenges of fractal calculus: from two-scale thermodynamics to fractal variational principle. Therm. Sci. 24(2), 659–681 (2020)

    Article  Google Scholar 

  33. Rezazadeh, H.: New solitons solutions of the complex Ginzburg-Landau equation with Kerr law nonlinearity. Optik 167, 218–227 (2018)

    Article  Google Scholar 

Download references

Acknowledgements

The author thank the referees for their time and comments.

Funding

There is no funding for this work.

Author information

Authors and Affiliations

  1. Department of Mathematics, Eskişehir Technical University, 26470, Eskişehir, Turkey

    Bahar Karaman

Authors
  1. Bahar Karaman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bahar Karaman.

Ethics declarations

Conflict of interest

The authors declare that they have no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Karaman, B. On Fractional FitzHugh-Nagumo Equation as a Transmission of Nerve Impulses Design. Int. J. Appl. Comput. Math 8, 95 (2022). https://doi.org/10.1007/s40819-022-01302-8

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40819-022-01302-8

Keywords

Search

Navigation