Global Dynamics of a SEIRS Epidemic Model with Saturated Disease Transmission Rate and Vaccination Control

Abstract

In this paper we take a sound approach to construct a susceptible-exposed-infected-recovered-susceptible type epidemic model with explicit vaccination control. The disease transmission from susceptible to infected class is taken in saturated form. The system is investigated both for constant control and optimal control cases. Basic reproduction number and its consequences to the system has been established. Geometric approach is used to obtain the global asymptotic stability condition of the system. Finally, with the help of some numerical illustrations, we check the validity of our theoretical results.

Introduction

From the beginning of the civil society, infectious disease has a huge effect on the lifestyle of human beings. With the invention of different control tools like vaccination, treatment etc, though the severity of the infectious diseases reduces but the total control is yet to be achieved. Moreover due to growing complexities of present lifestyle, some new diseases are included in the human society. An infectious disease can spread to a susceptible person mainly by two ways one is by direct contact and the other is via another medium. Diseases like tuberculosis, influenza, measles, different types of flues are spread by direct contact, where as diseases like dengue, malaria etc are spread by mosquito and cholera is spread by water.

Currently, not only medical practitioners but also people from other fields are now involving to achieve techniques to control the severity of the infectious diseases. Applied and computational mathematicians are now using different mathematical tools to examine some theoretical feedback on the spread of the disease. Some articles like [1, 2] considered and analyzed mathematical models on epidemiology. However, they are able to predict in particular when a disease would be controlled and what are the effective methods required to control the disease. There are various research articles like the works of [3, 9, 14, 29, 32, 36, 37] where some control measures are taken to control the disease.

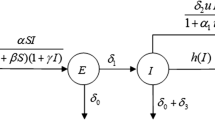
In the present work we aim to study the dynamical behaviour of an infectious disease which has some effective vaccine and can be recovered either by naturally or by some proper treatments. The infectious diseases like influenza, tuberculosis, MMR (measles-mumps-rubella) etc can be effectively controlled by some proper vaccine. The main characteristics of these diseases are that whenever the parasite of disease enter into the body of a susceptible person, he or she will be exposed for some time and then become infected. For this reason, to describe the dynamics of those diseases it is necessary to consider another intermediate compartmental class, say, exposed class between the susceptible class (S) and infected class (I). Historically some researchers also consider the exposed class in their analysis (see [9]). We divide the total human population into four time dependent classes namely susceptible class S(t),  exposed class E(t),  infected class I(t) and recovered class R(t). Let A be the recruitment rate at any time t and u be the available vaccination control which are applied to the newly recruited person. Therefore the portion uA are vaccinated and become immune from the disease (this immune may be temporary though) and move to the recovered class. The rest of the recruited individuals i.e the portion $(1-u)A$ remain susceptible for the disease. We assume that parasite of the disease spread among the susceptible population due to contact with the infected individuals and it takes some saturation time during their contact (see [9, 22, 23] etc). Hence the rate by which the portion of the susceptible individuals exposed for the disease are taken of the form $\displaystyle (\beta S I)/(1+ \eta I),\;(\beta ,\;\eta >0)$ where $\eta$ is the half saturation constant and $\beta$ is known as the parameter for force of infection. Therefore, the term $(1+\eta I)^{-1}$ is the inhibition effect of the systematic change of the susceptible populations from the crowding effects of either susceptible individuals or infected individuals or both. Obviously, one portion of the exposed class would become infected and we assume the portion $\sigma E$ become infected. It is assumed that there are both natural recovery (spontaneous recovery) or recovery due to proper treatment. Let us consider m I portion of the infected individuals recover either by naturally or by appropriate treatment and therefore these portion of the population goes to the recovered class. We assume that natural death rate is d and disease affected death rate as $\gamma .$ Moreover, we assume that the recovery is not permanent and the vaccination may be imperfect. For example the MMR vaccine is very strong but it is not $100~\%$ effective. In USA one dose of MMR vaccine is $78~\%$ effective to mumps where as two doses of MMR vaccine is $88~\%$ effective to mumps (see [13]). Therefore a portion from the recovered class would go to the susceptible class and we assume that $\alpha R$ portion of the removed class would go to the susceptible class. The flow diagram of the model is represented in Fig. 1. On the basis of the above assumptions, the mathematical model for the epidemic system is constructed as follows:

$$\begin{aligned} \begin{aligned} \frac{dS}{dt}&= (1-u)A-dS-\frac{\beta SI}{1+\eta I}+\alpha R ,\\ \frac{dE}{dt}&= -dE+\frac{\beta SI}{1+\eta I}-\sigma E,\\ \frac{dI}{dt}&= -dI+\sigma E-\gamma I-mI,\\ \frac{dR}{dt}&= Au-dR+mI-\alpha R. \end{aligned} \end{aligned}$$

(1)

The initial conditions of the system are

$$\begin{aligned} S(0)>0,E(0)>0,I(0)>0,R(0)>0. \end{aligned}$$

(2)

We have arranged the paper in the following manner : In “Analysis of the System for Fixed Control” section, we analyze the dynamics of the model with constant controls and in “Global Stability of the Endemic Equilibrium by Means of the Geometric Approach” section, we study the global asymptotic stability of the endemic equilibrium by using geometric method. “Sensitivity analysis and numerical simulation” section deals with some sensitivity analysis and numerical simulations. We compare different basic reproduction numbers in “Comparison Among Different Reproduction Numbers” section. Then we form optimal control problem and discuss the optimal control strategy in “Application of Optimal Vaccination Strategy” section and it is solved numerically in “Numerical Simulation of the Optimal Control Problem” section. Some key findings are presented in the final section.

Fig. 1

Flow diagram of the disease transmission

Analysis of the System for Fixed Control

Throughout this section we assume that the control parameter u is fixed.

First we discuss the boundedness of the system and then we find out existence criteria of different equilibria.

Boundedness of the System

Here we examine the boundedness property of the total population in the system.

Theorem 2.1

The solutions of the system (1) are uniformly bounded

Proof

Suppose

$$\begin{aligned} X=S+E+I+R. \end{aligned}$$

Then

$$\begin{aligned} \frac{dX}{dt}=\frac{dS}{dt}+\frac{dE}{dt}+\frac{dI}{dt}+\frac{dR}{dt}. \end{aligned}$$

Now putting all the values of the differential equations we get

$$\begin{aligned} \frac{dX}{dt}+dX\le A. \end{aligned}$$

(3)

Integrating both side of the above inequality and using the theory of differential inequality due to Birkhoff and Rota [5], we get

$$\begin{aligned} X \le \frac{A}{d}(1-e^{-dt})+X_0 e^{-dt}. \end{aligned}$$

Taking $t\rightarrow \infty$ we get

$$\begin{aligned} 0<X\le \frac{A}{d}. \end{aligned}$$

(4)

Hence all the solutions of (1) that initiating in $\{R_{+}^{4}\backslash 0\}$ are confined in the region

$$\begin{aligned} P=\{(S,E,I,R)\in \{R_{+}^{4}\backslash 0\}:X=\frac{A}{d}+\epsilon \} \end{aligned}$$

(5)

for any $\epsilon >0$ and for $t\rightarrow \infty$. Hence the theorem.

Since all the solutions of the system (1) are positive and bounded, we may conclude that there exist a constant $\psi _1>0$ such that

$$\begin{aligned} \psi _1<\;min\;\{\lim \;inf\;S(t),lim\;inf\;E(t),\lim \;inf\;I(t),lim\;inf\;R(t)\}. \end{aligned}$$

Basic Reproduction Number

Now we find the basic reproduction number of the system (1) by the next generation matrix approach due to [11]. Basic reproduction number in general denoted by $R_0$ and is defined as the number of newly infective individuals caused by a single infective individual (see, [11, 12]). It is easy to investigate that the system has a feasible disease free equilibrium (DFE) $E_0(S_1,0,0,R_1)$ where $S_1=\frac{A(d(1-u)+\alpha )}{d(d+\alpha )}$ and $R_1=\frac{Au}{d+\alpha }.$ To obtain basic reproduction number we write down the system (1) as follows:

$$\begin{aligned} \frac{dX}{dt}= \phi (u) - \psi (u), \end{aligned}$$

where $X=(E,I,R,S)^{T}$, $\phi (u)=\left( \frac{\beta S I}{1+\eta I},0,0,0\right) ^{T}$, and

$$\begin{aligned} \psi (u)= & {} \Bigg [(d+\sigma )E,(d+m+\gamma )I-\sigma E,(d+\alpha )R-mI-Au,dS\\&+\frac{\beta SI}{1+\eta I}-\alpha R-(1-u)A\Bigg ]^{T}. \end{aligned}$$

The Jacobian matrices of $\phi$ and $\psi$ at $E_0$ are respectively given by:

$$\begin{aligned}&J_1(\phi \mid _{E_0})= \begin{pmatrix} F &{}\quad 0 \\ 0 &{}\quad 0 \\ \end{pmatrix} \\&J_1(\psi \mid _{E_0})= \begin{pmatrix} V &{}\quad 0 \\ F_1 &{}\quad F_2 \\ \end{pmatrix} . \end{aligned}$$

Here $F=\begin{pmatrix} 0 &{} \beta S_1 \\ 0 &{} 0 \\ \end{pmatrix}$, $F_2=\begin{pmatrix} (d+\sigma ) &{} 0 \\ -\sigma &{} 0 \\ \end{pmatrix}$, $F_{1}=\begin{pmatrix} 0 &{} -m \\ 0 &{} \beta S_1 \\ \end{pmatrix}$, $V=\begin{pmatrix} (d+\alpha ) &{} 0 \\ -\alpha &{} d \\ \end{pmatrix}$.

The basic reproduction number $(R_0)$ of the system (1) is defined by the spectral radius of the matrix $(FV^{-1})$ (see [11]) and here it is given by

$$\begin{aligned} R_0=\frac{\beta \sigma A(\alpha +(1-u)d)}{d(d+\sigma )(d+\alpha )(d+\gamma +m)}. \end{aligned}$$

(6)

Equilibria and their Stability

Now our aim is to find out all the possible non negative equilibria of the system (1). We see that the system (1) has two possible non negative equilibria. The first one is the DFE $E_0(S_1,0,0,R_1)$ and the other one is $E_*(S^*,E^*,I^*,R^*)$ which is known as endemic equilibrium, where $S^*=\frac{(d+\sigma )(d+\gamma +m)(1+\eta I^{*})}{\sigma \beta }$, $E^*=\frac{(d+\gamma +m)I^*}{\sigma }$ ,$R^*=\frac{Au+mI^*}{d+\alpha }$,$I^*=\frac{(d+\sigma )(d+\alpha )(R_0-1)}{\eta (d+\alpha )(d+\sigma )+\beta (d+\alpha +\sigma )}.$ $R_0,$ is the basic reproduction number is calculated in above section.

$E_*(S^*,E^*,I^*,R^*)$ is feasible if $I^*>0$ i.e if $R_0>1.$

Also for $R_0=1$ the endemic equilibrium reduces to the disease free equilibrium and for $R_0<1$ it becomes infeasible. It is noted that when $R_0<1$ then disease dies out. Now from the above discussion we can conclude the following theorem.

Theorem 2.2

• (i) If $R_0<1,$ the system (1) has only one equilibrium, which is disease free.

• (ii) If $R_0>1,$ the system (1) has two equilibria: one is disease free and the other one is endemic equilibrium.

• (iii) If $R_0=1$, then the interior equilibrium reduces to the disease free equilibrium.

Next we shall study the stability analysis of the system around the different equilibria.

Theorem 2.3

If $R_0<1$ ($R_0>1$ ) then the disease free equilibrium is locally asymptotically stable(unstable).

Proof

The characteristic equation to the system (1) at its disease free equilibrium is given by

$$\begin{aligned} (\lambda +d)(\lambda +d+\alpha )\left( \lambda ^2+\lambda (m+\gamma +2d+\sigma )+(d+\sigma )(m+\gamma +d)-\beta \sigma S_1\right) =0. \end{aligned}$$

It is easy to show that for $R_0<1,$ all the roots of above equation has negative real parts and hence the system is locally asymptotically stable (LAS) around $E_0.$ Hence the system (1) is locally asymptotically stable (unstable) around its disease free equilibrium point if $R_0<1$ ($R_0>1$ ).

In the next theorem we discuss the local asymptotic behavior of the system around the endemic equilibrium $E_{*}.$

Theorem 2.4

The endemic equilibrium $E_*$ is LAS if $R_0>1.$

Proof

It is already shown that the endemic equilibrium $E_*$ exists for $R_0>1$ (see Theorem 2.2). Now the characteristic equation to the system (1) around $E_*$ is given by:

Clearly all the coefficients of the characteristic equation are positive.

Also on simplification we can easily show that $a_1 a_2>a_3$ and $a_1a_2a_3>a_3^2+a_1^2a_4.$

Hence by Routh-Hurwitz criterion for fourth degree polynomial equation we can conclude that the system (1) is locally asymptotically stable around its interior equilibrium.

Note 1

Since we have seen that for $R_0 > 1,$ the interior equilibrium is locally asymptotically stable but the disease free equilibrium is unstable, the system (1) will be never disease free for $R_0 > 1.$ Further we see that the disease free equilibrium passes from stable to unstable as $R_0$ increases to 1. Therefore with the help of the literature of [16], we may conclude that the system (1) undergoes a transcritical bifurcation at $R_0 = 1.$ Therefore, we use $R_0$ as bifurcation parameter for the transcritical bifurcation.

Note 2

We have already established that all the state variables associated with the system (1) are uniformly bounded and always nonnegative (see Theorem 2.1). Therefore we can de- fine the following two parameters as:

$$\begin{aligned} \Pi _1= & {} \sup \limits _{S, E, I, R}\left[ mI+\beta I \frac{S_1}{1+\eta I}+\alpha R_1 \frac{S_1}{S}\right] ,\\ \Pi _2= & {} \inf \limits _{S, E, I, R}\left[ \alpha R+dE+\sigma E +\beta \sigma I \frac{S_1}{d+\sigma }+\alpha R_1 \frac{R_1}{R}+mI \frac{R_1}{R}+\alpha R_1\right] \end{aligned}$$

In the following theorem we describe the global asymptotic stability criteria of the system (1) at the disease free equilibrium $E_0.$

Theorem 2.5

The sufficient conditions for the system (1) to be globally asymptotically stable at $E_0$ are $R_0 < 1$ and $\Pi _2 \ge \Pi _1$.

Proof

Let us define a Lyapunov function as follows:

$$\begin{aligned} V_1 = S - S_1 ln\left( \frac{S}{S_1}\right) +R - R_1 ln\left( \frac{R}{R_1}\right) +E+I. \end{aligned}$$

(7)

Now time derivative of (7) with some simplification gives,

$$\begin{aligned}&\frac{dV_1}{dt} =dS_1\left( 2-\frac{S_1}{S}-\frac{S}{S_1}\right) +dR_1\left( 2-\frac{R_1}{R}-\frac{R}{R_1}\right) +mI-\alpha R-dE-\sigma E\\&\quad -(d+\gamma +m)I+ \beta I \frac{S_1}{1+\eta I}+\alpha R_1 \frac{S_1}{S} -\alpha R_1 \frac{R_1}{R}-mI \frac{R_1}{R}-\alpha R_1. \end{aligned}$$

Using $A.M.>G.M.$ and $R_0 < 1[-(d+\gamma +m)I<- \frac{S_1 \beta \sigma I}{d+\sigma }]$, we have from the above equation,

$$\begin{aligned} \frac{dV_1}{dt} \!\le \!mI\!-\!\alpha R\!-\!dE\!-\!\sigma E \!-\!\beta \sigma I \frac{S_1}{d+\sigma }\!+\! \beta I \frac{S_1}{1+\eta I}\!+\!\alpha R_1 \frac{S_1}{S} \!-\!\alpha R_1 \frac{R_1}{R}-mI \frac{R_1}{R}-\alpha R_1. \end{aligned}$$

Again using the constructions of $\Pi _1$ and $\Pi _2$ we have,

$$\begin{aligned} \frac{dV}{dt}\le \Pi _2 -\Pi _1\le 0,\ \textit{for} \ \Pi _2\ge \Pi _1. \end{aligned}$$

Hence if $R_0 < 1$ and $\Pi _2\ge \Pi _1,$ then the disease free equilibrium $E_0$ will be globally asymptotically stable.

Global Stability of the Endemic Equilibrium by Means of the Geometric Approach

Global asymptotic stability is an important phenomenon corresponding to any epidemic system. If an endemic equilibrium will be globally asymptotic stable, then the disease would remain stable in the system forever. For this reason, some researchers like [6, 24] etc were interested to study the global asymptotic stability. So to study the way of eradication of the disease, we have to also find the condition whether there is any chance to sustain the disease in the system forever or not. However, if this occurs, i.e. if the endemic equilibrium is found to be globally asymptotic stable, then complete eradication is not possible to achieve. This is the reason for the researchers studying the globally asymptotic stability of endemic equilibrium of an epidemic system.

In Theorem 2.2 we find that for $R_0>1,$ the unique endemic equilibrium exists and locally asymptotically stable. In this section we will discuss the possible global asymptotic stability of the endemic equilibrium using the geometric approach (see [26, 27]). In our present paper we are now going to use the approach according to [7] for a STEI model of SARS epidemic. Let us consider the following autonomous dynamical system:

$$\begin{aligned} \dot{x}=f(x), \end{aligned}$$

(8)

where $f:D\rightarrow R^n,D\subset R^n$ which is an open set, simply connected and $f\in C^1(D).$ Without loss of generality we consider that the point $x=x^*$ is an equilibrium point of the dynamical system (8), i.e. $f(x^* )=0.$ Therefore, the point, $x^*$ is said to be globally asymptotically stable equilibrium point in D if it is locally asymptotically stable and all trajectories in D converge to $x^*.$

Let Q(x) be a matrix-valued function of order $\left( \begin{array}{c} \displaystyle n \\ 2 \end{array}\right)$ $\times$ $\left( \begin{array}{c} \displaystyle n \\ 2 \end{array}\right)$ that is $C^1$ on D. We also have the matrix A which is defined as: $A=Q_fQ^{-1}+Q_fMQ^{-1},$ where the matrix $Q_f$ is $(q_{ij}(x))_f=(\partial q_{ij}(x)/\partial x)^T.f(x)=\nabla q_{ij}.f(x).$

Further the Lozinski measure $\bar{\mu }$ of A with respect to a vector norm $\Vert .\Vert$ can be defined in $R^{\left( \begin{array}{c} \displaystyle n \\ 2 \end{array}\right) }$ as follows:

$$\begin{aligned} \bar{\mu }(A)=\lim _{t\in \rightarrow 0^+} \frac{\Vert I+hA\Vert }{h}. \end{aligned}$$

We will apply the following theorem according to [8, 27].

Theorem 3.1

In the interior of D,  we consider $D_1$ as a compact absorbing subset in such a way that there exists a positive constant $\gamma >0$ and a Lozinski measure $\bar{\mu }(A)\le -\gamma$ for all $x\in D_1$, then every omega limit point of system (1) in the interior of D will be an equilibrium in $D_1.$

From Theorem 2.2 we get for $R_0>1,$ there exist an unique endemic equilibrium $E_*$. Also, we know that $R_0>1$ implies that the disease free equilibrium $E_0$ is unstable. The instability of $E_0$ , together with $E_0\in \partial D,$ imply the uniform persistence of the state variables, (see [8, 15]). Therefore there exists a constant $c>0$ such that:

$$\begin{aligned} \liminf _{t\in \rightarrow \infty } x_i(t)>c, i=1,2,3,4. \end{aligned}$$

The uniform persistence, together with boundedness of $\Phi$, is equivalent to the existence of a compact set in the interior of $\Phi$ which is absorbing for (1), (see [18]). So Theorem (3.1) may be applied, with $D=\Phi$.

Remark 1

With the help of the works of [4, 7], we use an alternative approach in our work. Here, a sequence of surfaces that exist for time $\epsilon >0$ and minimizes the functional measuring surface area must be considered. The global dynamics analysis is approached in the bistability region (see [4]), for a three dimensional model.

We can evaluated the Lozinski measure in Theorem 3.1 (see [31]) as:

$$\begin{aligned} \bar{\mu }(A)=inf \{\bar{k}:D_+ \Vert z\Vert \le \bar{k}\Vert z\Vert , \hbox { for all solution of } z^{\prime }=Az \}, \end{aligned}$$

where $D_+$ is the right-hand derivative. When $R_0>1$ the endemic equilibrium is locally asymptotically stable. Hence, in order to apply Theorem 3.1 and for getting global asymptotic stability, it is necessary to find a norm $\Vert \cdot \Vert$ such that $\bar{\mu }(A)<0$ for all x in the interior of D.

Starting with the Jacobian matrix J of (1),

$$\begin{aligned} J = \left( {\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {a_{{11}} } &{}\quad {a_{{12}} } &{}\quad {a_{{13}} } &{}\quad {a_{{14}} } \\ {a_{{21}} } &{}\quad {a_{{22}} } &{}\quad {a_{{23}} } &{}\quad {a_{{24}} } \\ {a_{{31}} } &{}\quad {a_{{32}} } &{}\quad {a_{{33}} } &{}\quad {a_{{34}} } \\ {a_{{41}} } &{}\quad {a_{{42}} } &{}\quad {a_{{43}} } &{}\quad {a_{{44}} } \\ \end{array} } \right) \end{aligned}$$

the second additive compound matrix of J is given by:

$$\begin{aligned} \left( {\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {a_{{11}} + a_{{22}} } &{}\quad {a_{{23}} } &{}\quad {a_{{24}} } &{}\quad { - a_{{13}} } &{}\quad { - a_{{14}} } &{}\quad 0 \\ {a_{{32}} } &{}\quad {a_{{11}} + a_{{33}} } &{}\quad {a_{{34}} } &{}\quad {a_{{12}} } &{}\quad 0 &{}\quad { - a_{{14}} } \\ {a_{{42}} } &{}\quad {a_{{43}} } &{}\quad {a_{{11}} + a_{{44}} } &{}\quad 0 &{}\quad {a_{{12}} } &{}\quad {a_{{13}} } \\ { - a_{{31}} } &{}\quad {a_{{21}} } &{}\quad 0 &{}\quad {a_{{22}} + a_{{33}} } &{}\quad {a_{{34}} } &{}\quad { - a_{{24}} } \\ { - a_{{41}} } &{}\quad 0 &{}\quad {a_{{21}} } &{}\quad {a_{{43}} } &{}\quad {a_{{44}} + a_{{22}} } &{}\quad {a_{{23}} } \\ 0 &{}\quad { - a_{{41}} } &{}\quad {a_{{31}} } &{}\quad { - a_{{42}} } &{}\quad {a_{{32}} } &{}\quad {a_{{33}} + a_{{44}} } \\ \end{array} } \right) . \end{aligned}$$

Hence the second additive compound matrix of J is of the form

$$\begin{aligned} M = \left( {\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {M_{{11}} } &{} \quad {M_{{12}} } &{}\quad 0 &{}\quad {M_{{14}} } &{} \quad {M_{{15}} } &{} \quad 0 \\ {M_{{21}} } &{}\quad {M_{{22}} } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {M_{{26}} } \\ 0 &{}\quad {M_{{32}} } &{}\quad {M_{{33}} } &{}\quad 0 &{}\quad 0 &{}\quad {M_{{36}} } \\ 0 &{}\quad {M_{{42}} } &{}\quad 0 &{}\quad {M_{{44}} } &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {M_{{53}} } &{}\quad {M_{{54}} } &{}\quad {M_{{55}} } &{}\quad {M_{{56}} } \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {M_{{65}} } &{} \quad {M_{{66}} } \\ \end{array} } \right) ,\end{aligned}$$

where,

$$\begin{aligned} M_{11}= & {} \left( -2d-\sigma +\frac{\beta I}{1+\eta I}\right) ; M_{12}=\frac{\beta S}{(1+\eta I)^2} ; M_{14}=\frac{\beta S}{(1+\eta I)^2} ;\\ M_{15}= & {} -\alpha ; M_{21}= \sigma ; M_{22}=\left( -2d-m-\gamma -\frac{\beta I}{1+\eta I}\right) ;\\ M_{26}= & {} -\alpha ; M_{32}= m ; M_{33}=\left( -2d-\alpha -\frac{\beta I}{1+\eta I}\right) ;\\ M_{36}= & {} \frac{-\beta S}{(1+\eta I)^2} ; M_{42}=\frac{\beta I}{1+\eta I}; M_{44}=\left( -2d-\sigma -m-\gamma \right) ;\\ M_{53}= & {} \frac{\beta I}{1+\eta I}; M_{54}= m ; M_{55}=(-2d-\sigma -\alpha ); M_{56}=\frac{\beta S}{(1+\eta I)^2};\\ M_{65}= & {} \sigma ; M_{66}=(-2d-m-\gamma -\alpha ). \end{aligned}$$

Now we consider the matrix Q such that

$$\begin{aligned} Q = \left( {\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {q_{{11}} } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {q_{{22}} } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{} \quad {q_{{34}} } &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {q_{{43}} } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{} \quad {q_{{55}} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {q_{{66}} } \\ \end{array} } \right) , \end{aligned}$$

where $q_{11}=q_{22}=q_{34}=\frac{1}{I}$ and $q_{43}=q_{55}=q_{66}=\frac{1}{R}.$

Then we find the matrix A as:

$A=Q_f Q^{-1}+Q M Q^{-1},$ where $Q_f$ is the derivative of Q in the direction of the vector field f . More precisely, we have:

$$\begin{aligned} Q_f Q^{-1}=-diag\{\dot{I}/I,\dot{I}/I,\dot{I}/I,\dot{R}/R,\dot{R}/R,\dot{R}/R\} \end{aligned}$$

and

$$\begin{aligned} QMQ^{{ - 1}} = \left( {\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {M_{{11}} } &{}\quad {M_{{12}} } &{} \quad {M_{{14}} } &{} \quad 0 &{} \quad {\frac{{M_{{15}} R}}{I}} &{}\quad 0 \\ {M_{{21}} } &{}\quad {M_{{22}} } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {\frac{{M_{{26}} R}}{I}} \\ 0 &{}\quad {M_{{42}} } &{}\quad {M_{{44}} } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {\frac{{M_{{32}} I}}{R}} &{}\quad 0 &{}\quad {M_{{33}} } &{}\quad 0 &{}\quad {M_{{36}} } \\ 0 &{}\quad 0 &{}\quad {\frac{{M_{{54}} I}}{R}} &{}\quad {M_{{53}} } &{}\quad {M_{{55}} } &{} \quad {M_{{56}} } \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {M_{{65}} } &{} \quad {M_{{66}} } \\ \end{array} } \right) , \end{aligned}$$

and we have

$$\begin{aligned} \frac{\dot{I}}{I}= & {} -(d+m+\gamma )+\frac{\sigma E}{I},\\ \frac{\dot{R}}{R}= & {} \frac{u A}{R}-(d+\alpha ) + \frac{mI}{R}. \end{aligned}$$

Finally we get the matrix A as:

$$\begin{aligned} A = \left( {\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {A_{{11}} } &{}\quad {A_{{12}} } &{}\quad {A_{{13}} } &{}\quad 0 &{}\quad {A_{{15}} } &{}\quad 0 \\ {A_{{21}} } &{}\quad {A_{{22}} } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {A_{{26}} } \\ 0 &{}\quad {A_{{32}} } &{}\quad {A_{{33}} } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {A_{{42}} } &{}\quad 0 &{}\quad {A_{{44}} } &{}\quad 0 &{} \quad {A_{{46}} } \\ 0 &{}\quad 0 &{}\quad {A_{{53}} } &{}\quad {A_{{54}} } &{}\quad {A_{{55}} } &{}\quad {A_{{56}} } \\ 0 &{}\quad 0 &{}\quad 0 &{} \quad 0 &{} \quad {A_{{65}} } &{}\quad {A_{{66}} } \\ \end{array} } \right) , \end{aligned}$$

where,

$$\begin{aligned}&A_{11}=\left( -d-\sigma +m+\gamma -\frac{\beta I}{1+\eta I}-\frac{\sigma E}{I}\right) ; A_{12}=\frac{\beta S}{(1+\eta I)^2};\quad A_{13}=\frac{\beta S}{(1+\eta I)^2};\\&A_{15}=-\frac{\alpha R}{I};\quad A_{21}=\sigma ; A_{22}=\left( -2d-\gamma -m-\frac{\beta I}{1+\eta I}\right) ;\\&A_{26}=-\frac{\alpha R}{I};\quad A_{32}=\frac{\beta I}{1+\eta I}; \quad A_{33}=(-2d-\sigma -\gamma -m);\\&A_{42}=\frac{mI}{R};\quad A_{44}=\left( -2d-\alpha -\frac{\beta I}{1+\eta I}\right) ;\quad A_{46}=-\frac{\beta S}{(1+\eta I)^2};\\&A_{53}=\frac{\alpha I}{R}; \quad A_{54}=\frac{\beta I}{1+\eta I};\quad A_{55}=(-2d-\sigma -\alpha );\\&A_{56}=-\frac{\beta S}{(1+\eta I)^2};\quad A_{65}=\sigma ;\quad A_{66}=(-2d-m-\gamma -\alpha ). \end{aligned}$$

With the help of [17], we consider the following norm on $R^6$:

$$\begin{aligned} \Vert z\Vert =max\{U_1,U_2\}, \end{aligned}$$

(9)

where $z\in R^6,$ with components $z_i, i=1,2,\ldots ,6$ and $U_1{(z_1,z_2,z_3)}$ is defined as:

$$\begin{aligned} U_1{(z_1,z_2,z_3)} = \left\{ \begin{array}{c} \displaystyle max \{|z_1|,|z_2|+|z_3|\} \;\; if\;\; sgn(z_1)=sgn(z_2)=sgn(z_3) \\ max \{|z_2|,|z_1|+|z_3| \} \quad \textit{if}\;\; sgn(z_1)=sgn(z_2)=- sgn(z_3) \\ max \{|z_1|,|z_2|,|z_3|\} \quad \textit{if}\;\; sgn(z_1)=sgn(z_2)=- sgn(z_3)\\ max \{|z_1|+|z_3|,|z_2|+|z_3|\} \quad \textit{if}\;\; sgn(z_1)=sgn(z_2)=- sgn(z_3)\end{array} \right\} , \end{aligned}$$

and $U_2{(z_1,z_2,z_3)}$ is defined as:

$$\begin{aligned} U_2{(z_4,z_5,z_6)} =\left\{ \begin{array}{c} \displaystyle |z_4|+|z_5|+|z_6| \quad \textit{if}\;\; sgn(z_4)=sgn(z_5)=sgn(z_6) \\ max \{|z_4|+|z_5|,|z_4|+|z_6| \} \quad \textit{if}\;\; sgn(z_4)=sgn(z_5)=- sgn(z_6) \\ max \{|z_5|,|z_4|+|z_6| \} \quad \textit{if}\;\; sgn(z_4)=-sgn(z_5)= sgn(z_6)\\ max \{|z_4|+|z_6|,|z_5|+|z_6|\} \quad if\;\; {-}sgn(z_4)=sgn(z_5)= sgn(z_6) \end{array} \right\} . \end{aligned}$$

next we will use the following inequalities:

$$\begin{aligned} |z_2|<U_1, |z_3|<U_1, |z_2 + z_3|<U_1 \end{aligned}$$

and

$$\begin{aligned} |z_i|,|z_i + z_j|,|z_4 + z_5+z_6|\le U_2;\quad i=4,5,6 \;\;i\ne j. \end{aligned}$$

These assumptions will help us to determine $D_+ {\Vert z\Vert }$. Also some more restriction will be used in the statement of the global stability theorem later.

Further we take $d+\sigma >m+\gamma$ and let us assume

$$\begin{aligned} \phi =(d+\sigma )-(m+\gamma ). \end{aligned}$$

(10)

Case 1 $U_1>U_2,$ $z_1,z_2,z_3 >0,$ $|z_1|>|z_2|+|z_3|$ and $U_2<|z_1|.$

Then

$$\begin{aligned} \parallel z \parallel =|z_1|=z_1. \end{aligned}$$

(11)

The right hand derivative of $\Vert z\Vert$ is given by

$$\begin{aligned} D_+ \Vert z\Vert= & {} z^{\prime }_{1}\\= & {} A_{11}z_1+A_{12}z_2+A_{13}z_3+A_{15}z_5\\= & {} \left( -d-\sigma \!+\!m\!+\!\gamma \!-\!\frac{\beta I}{1+\eta I}\!-\!\frac{\sigma E}{I}\right) z_1+ \frac{\beta S}{(1+\eta I)^2}z_2+\frac{\beta S}{(1+\eta I)^2}z_3 - \frac{\alpha R}{I}z_5\\= & {} \left( -d-\sigma +m+\gamma -\frac{\beta I}{1+\eta I}-\frac{\sigma E}{I}\right) z_1+ \frac{\beta S}{(1+\eta I)^2}(z_2+z_3) - \frac{\alpha R}{I}z_5\\\le & {} \left( -d-\sigma +m+\gamma -\frac{\beta I}{1+\eta I}-\frac{\sigma E}{I}\right) |z_1|+ \frac{\beta S}{(1+\eta I)^2}(|z_2|+|z_3|) - \frac{\alpha R}{I}|z_5|. \end{aligned}$$

Using $- \frac{\alpha R}{I}|z_5|<0,$ and (11) we get

$$\begin{aligned} D_+ \Vert z\Vert\le & {} [-d-\sigma +m+\gamma -\frac{\beta I}{1+\eta I}-\frac{\sigma E}{I}+\frac{\beta S}{(1+\eta I)^2}]\Vert z\Vert \nonumber \\ D_+ \Vert z\Vert\le & {} -(d+\sigma -m-\gamma -\psi _2) \Vert z\Vert , \end{aligned}$$

(12)

where $\psi _2=max\left[ -\frac{\beta I}{1+\eta I}-\frac{\sigma E}{I}+\frac{\beta S}{(1+\eta I)^2}\right]$

Case 2 $U_1>U_2,$ $z_1,z_2,z_3 >0,$ $|z_1|<|z_2|+|z_3|.$

Then

$$\begin{aligned} \parallel z \parallel =|z_2|+|z_3|=z_2+z_3 \end{aligned}$$

(13)

and $U_2<z_2+z_3.$ Then the right hand derivative of $\Vert z\Vert$ is given by

$$\begin{aligned} D_+ \Vert z\Vert= & {} z^{\prime }_{3}+z^{\prime }_{2}\\= & {} A_{21}z_1+A_{32}z_2+A_{33}z_3+A_{44}z_4+A_{55}z_5+A_{66}z_6.\\= & {} \sigma z_1+\frac{\beta I}{1+\eta I} z_2 + (-2d-\sigma -\gamma -m)z_3+\left( -2d-\alpha -\frac{\beta I}{1+\eta I}\right) z_4\\&-(-2d-\sigma -\alpha )z_5+(-2d-\gamma -m-\alpha )z_6\\\le & {} \sigma |z_1|+\frac{\beta I}{1+\eta I} |z_2|+(-2d-\sigma -\gamma -m)|z_3|+(-2d-\alpha )|z_4|-\frac{\beta I}{1+\eta I}|z_4|\\&+(-2d-\alpha )|z_5|-\sigma |z_5| + \;\;\;(-2d-\alpha )|z_6|-(\gamma +m)|z_6| \end{aligned}$$

Now using $-\frac{\beta I}{1+\eta I}|z_4|<0, -\sigma |z_5|<0, -(\gamma +m)|z_6|<0$ and $|z_4+z_5+z_6|<U_2<|z_2|+|z_3|$ and with the help of (13) we get from the above

$$\begin{aligned}\le & {} \sigma |z_1|+\frac{\beta I}{1+\eta I}|z_2|+(-2d-\sigma -\gamma -m)|z_3|+(-2d-\alpha )(|z_4|+|z_5|+|z_6|) \\\le & {} [-4d-\alpha -\gamma -m+\frac{\beta I}{1+\eta I}]\Vert z\Vert , \end{aligned}$$

finally

$$\begin{aligned} D_+ \Vert z\Vert \le - \left[ 4d+\alpha +\gamma +m-\psi _3 \right] \Vert z\Vert , \end{aligned}$$

(14)

where $\psi _3=max\frac{\beta I}{1+\eta I}.$ The other fourteen cases are omitted for simplicity (a brief calculation is given in [6] and [8]).

Now from (12) and (14) it is clear that both of the quantities $\left( d+\sigma -m-\gamma -\psi _2\right)$ and $\left( 4d+\alpha +\gamma +m-\psi _3 \right)$ are bounded. Therefore we can assure the existence of some positive constant $\omega$ such that $-\omega$ and $\omega$ are two bounds i.e. $-\omega \le min \{\left( d+\sigma -m-\gamma -\psi _2\right) , \left( 4d+\alpha +\gamma +m-\psi _3 \right) \}$ and $max \{\left( d+\sigma -m-\gamma -\psi _2\right) , \left( 4d+\alpha +\gamma +m-\psi _3 \right) \}\le \omega .$

Now we are in a position to state the following theorem regarding to the global asymptotic stability of the endemic equilibrium of the system (1) according to [8].

Theorem 3.2

For $R_{0}>1,$ the system (1) has an unique endemic equilibrium which is globally asymptotically stable in the interior of $\Phi$ if (12) and (14) are satisfied with the condition (10), i.e. if there exists a positive constant $\omega$ such that

$$\begin{aligned} max \{\left( d+\sigma -m-\gamma -\psi _2\right) , \left( 4d+\alpha +\gamma +m-\psi _3 \right) \}\le \omega . \end{aligned}$$

Sensitivity Analysis and Numerical Simulation

Due to uncertainties associated with the estimation of certain parameter values, it is useful to carry out the sensitivity analysis to determine the model robustness as the parameter values changes. We mainly aim to determine the impact on the reproduction number $(R_0)$ when the associated parameters varies.Using the approch in Chitnis et al. [10] and [30], we analyze the reproduction number to determine whether or not treatment of infectives and mortality can lead to the effective elimination or control of the disease in the population.

Definition

The normalized forward sensitivity index of a variable, h, that depends differentially on a parameter, l, is denoted by $\Gamma ^{h}_{l}$ defined as:

$$\begin{aligned} \Gamma ^{h}_{l}=\frac{l}{h} \times \frac{\partial h}{\partial l} \end{aligned}$$

Fig. 2

Solution curves at disease free equilibrium with respect to the parameter set $P_1$

Sensitivity Indices of $R_0$

We derive the sensitivity of $R_0$ to each of the different parameters $u, \alpha , \gamma , m, \beta , \sigma .$

The sensitivity index of $R_0$ with respect to u is presented by

$$\begin{aligned} \Gamma ^{R_0}_{u}=\frac{u}{R_0} \times \frac{\partial R_0}{\partial u} =\frac{-du}{\alpha +(1-u)d}. \end{aligned}$$

Again the sensitivity indices of $R_0$ resulting from the evaluation to the other parameters of the model are shown below.

$$\begin{aligned} \Gamma ^{R_0}_{\alpha }=\frac{\alpha }{R_0} \times \frac{\partial R_0}{\partial \alpha } =\Gamma ^{R_0}_{\alpha }= \frac{\alpha du}{\alpha +(1-u)d} \end{aligned}$$

and

$$\begin{aligned} \Gamma ^{R_0}_{m}= \frac{-m}{m+\gamma +d},\quad \Gamma ^{R_0}_{\gamma }= \frac{-\gamma }{m+\gamma +d}. \end{aligned}$$

Now the analytical results are verified with the help of numerical simulations. Numeric analysis is used-due to the complexity of the analytical solutions. In this case we have some advantages that is easy to isolate the effects of the intersections between the different classes. With real world data, the prices, costs and technological factors are likely to vary from one epidemic system to another, and it would be harder to assign the causes for different results. In this paper we should consider from a qualitative, rather than a quantitative point of view. First we consider a parameter set as $P_1=\{u, A, d, \eta , \gamma , \alpha , \sigma , m\}=\{0.5, 100, 0.1, 0.9, 0.025, 0.4,0.8, 2 \}.$ Some of the parameters are taken from the published papers and some are assumed with feasible value. For this parameter set of values and for $\beta =0.001$ we have only one equilibrium which is disease free equilibrium $E_0(900, 0, 0, 20)$ and this equilibrium is locally asymptotically stable (see Fig. 2). This phenomenon is happening as the contact rate ($\beta$) is very small and so here, $R_0<1.$ Again for the same parameter set $P_1,$ with $\beta =0.01,$ we have two feasible equilibrium ; one is disease free and another is endemic and the endemic equilibrium is locally asymptotically stable (see Fig. 3). Furthermore for the parameter set $P_1,$ along with $\beta =0.01,$ the numeric value of the basic reproduction number $R_0>1$ since here the numeric value of $\beta$ is quite larger.

The parameters are arranged from the most sensitive to least. The most sensitive parameters are proportion of the maximum contact rate between susceptible and infected class is $\beta$ and transfer rate from the exposed class to infected class is $\sigma$ and the least sensitive parameter is the vector mortality rate $\gamma .$The parameters that changes $R_0$ can be considered as control parameters.

From the Table 1, $\Gamma ^{R_0}_{\beta }=1$ implying, increasing (or decreasing) the contact rate $\beta$ by $10~\%$ gives the increments (or decrements) of $R_0$ by $10~\%$ and $\Gamma ^{R_0}_{\sigma }=1$ implying, increasing (or decreasing) the transfer rate $\sigma$ by $10~\%$ gives increments (or decrements) of $R_0$ by $10~\%$. In the same way from the Table 1, increasing (or decreasing) the recovery rate m by $9.4~\%$ gives decrements (or increments) the $R_0$ by $9.4~\%.$

Shortening the lifespan of the populations reduces the basic reproductive number because more infected die before they become infectious.

Fig. 3

Solution curves at endemic equilibrium with respect to the parameter set $P_1$

Table 1 Sensitivity indices of model parameters to $R_0<1$($>$1)

In Fig. 4, it has been shown that for $R_0\le 1$ the system (1) has only one equilibrium $E_0$ where as for $R_0>1$ it has two equilibria one is the disease free $E_0$ and other is the endemic $E_*.$ Thus we can conclude that for $R_0=1$ the system (1) undergoes a transcritical bifurcation.

Fig. 4

Variation of infected population with reproduction number $R_0.$ It is showing that for $R_0 < 1,$ the disease dies out and for $R_0 > 1,$ the infection is maintained in the population

Comparison Among Different Reproduction Numbers

From (6) we have the basic reproduction number, $R_0=\frac{\beta \sigma A(\alpha +(1-u)d)}{d(d+\sigma )(d+\alpha )(d+\gamma +m)}.$ Now if we consider, the parameter u as variable parameter, then we have, $R'_{0}(u)=\frac{-\beta \sigma d A}{d(d+\sigma )(d+\alpha )(d+\gamma +m)}.$ Hence $R_0$ is a decreasing function of u. This shows that the impact of vaccination is reducing with the vaccine induced reproduction number. According to Rodrigues et al. ([34, 35]), we describe different reproduction rates for different parametric conditions.

Case 1: No vaccination

Here we consider vaccine as a control measure to the disease. If there is no vaccine, then all the recruited person at any instance would go to the susceptible class. We calculate the basic reproduction number due to [11] by the next generation matrix approach for $u=0.$ Denoting this basic reproduction number by $R_{u_0},$ we have, $R_{u_0}=\frac{\beta \sigma A}{d(d+\sigma )(d+\gamma +m)}.$ Suppose that initially, at time $t=0,$ a portion u of newborns is vaccinated with a perfect vaccine without side effects, since this portion u is now immune, then $R_{u_0}$ is reduced, creating new basic reproduction number $R_{0},$ where the basic reproduction number $R_{0}$ is calculated before. Comparing these two basic reproduction number we get $R_{0}=\frac{\alpha +(1-u)d}{\alpha +d}R_{u_0}.$ We observe that $R_{0}<R_{u_0},$ equality hold when $u=0,$ i.e when there is no vaccination. We also see that the constraint $R_0<1$ defines implicity a critical vaccination portion $(u>)u_n :=1-\frac{1}{R_{u_0}},$ that must be achieved for eradication.

Case 2: Perfect vaccination and permanent recovery

In our original model system, we consider that Au portion of the recruited individual would go to the recovered class and among infected populations, mI portion would recover either by naturally or by appropriate treatment. Now if we assume that the vaccination is perfect and recovery is permanent then no individual from the class R would go to the class S and in this case, we arrive the parametric restriction as $\alpha =0.$ As before we compute the basic reproduction number of the system for perfect vaccination and permanent recovery (i.e. when $\alpha =0$) and by denoting $R_{\alpha }$ as the basic reproduction number for this case, we have, $R_{\alpha }=\frac{\beta \sigma A(1-u)}{d(d+\sigma )(d+\gamma +m)}.$ Then, $R_{\alpha }=(1-u)R_{u_0}.$ This implies $R_{\alpha }<R_0<R_{u_0},$ where $R_{\alpha }$ is the basic reproduction number under perfect vaccination and permanent recovery.

The critical vaccination proportion will achieve eradication, $p_e$ is that for which the basic reproduction number under vaccination is just equal to 1. This yields $p_e=1-\frac{1}{R_{u_0}}.$

Case 3: If everyone is vaccinated

If everyone is vaccinated,we must have $u=1.$ Now, when $u=1$ then the basic reproduction number $R_{u_1}$ can be calculated as $R_{u_1}=\frac{\beta \sigma \alpha A}{d(d+\sigma )(d+\alpha )(d+\gamma +m)}.$

From this we get $R_{u_0}=R_{u_1}(1+(1-u)\frac{d}{\alpha }),$

i.e $R_0>R_{u_1}.$

So if $R_0<1,$ then $R_{u_1}<R_0<1.$

Then the disease free equilibrium of our model when $u=1$ is locally asymptotically stable. Again when $R_0=1,$ then $R_{u_1}\le 1,$ and in that case disease free equilibrium of the model when $u=1$ is also asymptotically stable.

Case 4: Perfect vaccination under whole vaccination strategy

If all the newly recruited are vaccinated and this vaccination is perfect, then in the model system (1), we restrict the parametric conditions as $u=1$ and $\alpha =0,$ provided the recovery is permanent. In this situation there will be no newly infected compartmental, as there is no new recruitment in susceptible class. So this situation leads to ultimate eradication of the disease from the system as from Fig. 5, it is evident that the basic reproduction number is always less than unity for this case.

Fig. 5

Variation of different basic reproduction numbers for the parameter set $P_1$ with $\beta$

In the above figure we describe the variation of different basic reproduction numbers for different parametric conditions. It is seen that for the parameter set $P_1,$ $R_{u_1}$ always remains below unity. Among the other three reproduction numbers, $R_{u_0},$ (i.e. the no vaccination case) is the greatest and vaccination under perfect vaccination strategy with permanent recovery (i.e. $R_{\alpha }$) is the lowest where as the original basic reproduction number $R_0$ lies between them.

If it is possible to vaccinated all of newly recruited populations and if the vaccination is perfect and the recovery from the disease is permanent then there will be no newly recruited infected individuals and slowly the disease would be wiped out.

Application of Optimal Vaccination Strategy

Till now we have used the control vaccination (u) as constant but originally it must be time dependent. Therefore in this section we wish to observe the behaviour of the system when the vaccination control is applied according to the necessity of the time for a given time interval. For this objective, we now form an optimal control problem using u as time dependent optimal control with simultaneous motivation of reducing infected population as much as possible.

We first construct the objective functional to be optimized as follows:

$$\begin{aligned} J\;=\; \min _{u}\int _0^{t_1}(A_1I+A_2 u^2)\;dt \end{aligned}$$

(15)

subject to the system of differential equations (1).

Our object is to find an optimal control for the vaccination, say, $u^*$ such that

$$\begin{aligned} J(u^*)\;=\;\min _{u\in \Theta }\;J(S,E,I,R,u). \end{aligned}$$

where $\Theta \;=\; \{u:~\hbox {is measurable and}~0\le u(t)\le 1~\hbox {for} ~ t \in [0,t_1] \}$ is the set for the controls.

Here $A_1$ is a positive number and it is the weight related to the infected population. The square of the vaccination control is taken to remove the severity of the side effect and overdoses of vaccination (see [20, 22]). Also here $A_2$ is the corresponding weight associated with the control u. Further the range of this weight $A_2$ is in general lies between 0 and 2N where N be the number of total populations (see [38]).

Now to solve the optimal control problem, we form the Lagrangian of this problem which is given by

$$\begin{aligned} L(I,u)=A_1I+A_2 u^2. \end{aligned}$$

(16)

The corresponding Hamiltonian H for our problem is as follows:

$$\begin{aligned} H(S,E,I,R,u,\lambda _1,\lambda _2,\lambda _3,\lambda _4)\;=\;L+\lambda _1(t)\frac{dS}{dt}+\lambda _2(t)\frac{dE}{dt} +\lambda _3(t)\frac{dI}{dt}+\lambda _4(t)\frac{dR}{dt},\nonumber \\ \end{aligned}$$

(17)

where $\lambda _i(t)$ for $i=1,\;2,\;3,\;4$ are the adjoint variables or the co state variables and can be determined by solving the following system of differential equations:

$$\begin{aligned}&\dot{\lambda }_1(t)=\;-\frac{\partial H}{\partial S}=\; -\left[ \left( -d-\frac{\beta I}{1+\eta I}\right) \lambda _1(t)+\left( \frac{\beta I}{1+\eta I}\right) \lambda _2(t)\right] ,\nonumber \\&\dot{\lambda }_2(t)=\;-\frac{\partial H}{\partial E}=\;-[(-d-\sigma )\lambda _2+\sigma \lambda _3],\nonumber \\&\dot{\lambda }_3(t)=\;-\frac{\partial H}{\partial I}=\; -\left[ A_1+(\lambda _2 -\lambda _1)\frac{\beta S}{(1+\eta I)^2}+(-d-\gamma -m)\lambda _3+m\lambda _4\right] ,\nonumber \\&\dot{\lambda }_4(t)=\;-\frac{\partial H}{\partial R}=\;-\left[ \alpha \lambda _1+(-d-\alpha )\lambda _4\right] \end{aligned}$$

(18)

satisfying the transversality conditions

$$\begin{aligned} \lambda _i(t_1)=0,\;i=1,\;2,\;3,\;4. \end{aligned}$$

(19)

Let, $\bar{S},\;\bar{I},\;\bar{R},\;\bar{V}$ are the optimum value of $S,\;I,\;R,\;V$ respectively. Also let, $\{\bar{\lambda }_1 ,\bar{\lambda }_2 ,\bar{\lambda }_3 ,\bar{\lambda }_4\}$ be solutions of system (18).

Following Lukes [28] and Zaman et al. [38] we now state and prove the following theorem.

Theorem 6.1

There is an optimal control $(u^*(t))$ such that

$$\begin{aligned} J(I(t),u^*(t))\;=\; \min _{u} \;J(I(t),u(t)) \end{aligned}$$

subject to the system of differential Eq. (1).

Proof

Here the control variable u(t) is convex since all the state and control variables are non negative. Moreover the control space $\Theta$ is closed and convex. Hence the optimal control is bounded and therefore we assure about the existence of an optimal control $u^*(t)$ which minimize (15) with the help of the system of differential Eqs. (1). Hence the theorem.

With the help of Pontryagin’s Maximum Principle (see [33]) and the theorem (6.1) we now state and prove the following theorem.

Theorem 6.2

The optimal control $(u^*)$ which minimizes J over the region $\Theta$ given by

$$\begin{aligned} \begin{array}{lcl}u^*=\;max\biggr \{0,min(\bar{u},1) \biggr \} \end{array} \end{aligned}$$

where $\bar{u}=\frac{A(\bar{\lambda }_1-\bar{\lambda }_4)}{2A_2}.$

Proof

Using the optimality conditions i.e. $\frac{\partial H}{\partial u} = 0$ we get $u=\;\frac{A(\bar{\lambda }_1-\bar{\lambda }_4)}{2A_2} \;(=\bar{u}).$ Again this control is bounded with upper and lower bounds are respectively 0 and 1 i.e. $u=0.$ This means that $u=0,$ whenever $\bar{u}\le 0$ where as $u=1,$ whenever $\bar{u}\ge 0,$ and in the rest period of time $u=\bar{u}.$ Combining these results we have the theorem.

Fig. 6

Variation of the state variables with and without control

Fig. 7

Graph for optimal vaccination control

Fig. 8

Variation for the adjoint variables

Numerical Simulation of the Optimal Control Problem

To simulate the optimal control problem numerically, we take the values of parameters as $A=100,d=0.2,\beta =0.1, \eta =0.01, \alpha =0.55, \sigma =0.05, \gamma =0.02, m=0.05.$ The time interval for which the vaccination control is applied optimally is taken as 100 units of time. One should note that this time unit will be either in days or weeks. A possible set of initial population size for susceptible, exposed, infected, removed classes are taken as 300, 100, 30, 70 respectively. We take the weight associated with vaccination control $A_2=5$ and the weight associated to the infected population $A_1=1.$ Now we solve the optimality system in the “Application of Optimal Vaccination Strategy” section by iterative method with the help of Runge–Kutta fourth order procedure (see [19, 21, 25]). First we solve the system (1) i.e. equations associated with state variables by the forward Runge–Kutta fourth order method in the time interval [0,100] and then simultaneously we use the backward Runge–Kutta fourth order method to solve the adjoint variables in the same time interval with the help of the solutions of the state variables and the transmission conditions. In Fig. 6, we present the graphs of the susceptible class, exposed class, infected class and recovered class for with and without vaccination control strategy. It is clear from the graph that the number of susceptible population decreases when there is no control. In this case most of that population goes to the infected class. However if the vaccination control is applied then the individuals from infected class would be very less where as most of the populations go to either recovered class or remains in susceptible class. Again we see that when the vaccination control is applied then the exposed class decreases and without control the exposed class increases highly. The application of vaccination control would give better result than the application of no control for both the infected class and the recovered class as optimal vaccination control would significantly reduces the amount of infected population and those populations would go to recovered class from infected class. From Fig. 7, it is evident that the control takes the highest value 1 in the starting period and towards the end of the duration of application of control, the curve slow down and finally at the end of the time interval it takes the value 0.

From the Fig. 8, we find the variation for the adjoint variables and it can be shown $\lambda _1, \lambda _2, \lambda _3$ decreasing monotonically and finally become zero as t increases to 100. The adjoint variable $\lambda _4$ first increases and then finally reduces to zero.

Conclusion

In this paper we have proposed and analyzed an infectious disease model by considering susceptible (S), exposed (E), infected (I) and recovered (R) classes of human population. Various infectious diseases which can be controlled by combined affect of vaccination and recovery (natural or treatment) like tuberculosis, influenza etc can be discussed through out this paper. Here a saturated type disease transmission rate is considered. Detailed dynamical behaviour of the model including uniform boundedness criteria, existence criteria of different equilibria and their local asymptotic stability criteria depending upon the numerical value of the basic reproduction number has been obtained. We have established that the numerical value of basic reproduction number is very much essential to sort out the characterization of the disease. Further to study the global asymptotic behaviour of the system around its endemic equilibrium, we use the geometric approach, one of the strongest methods to establish global asymptotic stability of any ecological system. Though it is quite common to observe the use of geometric method in three dimensional systems, but it is rare to apply this method in four dimensional system. Influenced by the work of [8], where the authors used this method to check the global asymptotic stability of the endemic equilibrium, we also use here this method in our present work.

Optimal control technique is another strong tool that determines the appropriate requirement of the control at a particular time interval. Here we apply the optimal control technique and Pontryagin’s maximum principle to optimize the loss occurring due to the affect of the disease in the system by considering vaccination as the control parameter.