Introduction

The dynamic matrix square root problem (DMSR) is broadly applied to engineering and research, such as power system interconnection [1], automatic control [2], signal processing [3], neural networks [4], etc. Many practical engineering applications or problems can be transformed into a potential DMSR problem, which attracted an increasing number of researchers for these topics, replacing time-independent problems. Among many works, the zeroing neural network (ZNN) is one of the most comprehensively investigated ways to resolve dynamic problems [1).

Table 1 Comparison among different neural dynamic models
Full size table

This gap motivated us to propose a more efficient activation function to improve the performance of ZNN models aided by the residual error information while maintaining the robustness even perturbed by noises. Therefore, the adaptive activation function is proposed, which can activate each component of the solution system to be activated separately in a decoupled manner and leads to better convergence and accuracy performance. After that, combining the robust evolution formula, the RDNAC model is proposed. Then the proposed RDNAC model is applied to deal with the DMSR problem for the first time to demonstrate effectiveness and potential. The most characteristic of the RNDAC model is to adopt the component information of the residual error to optimize the real-time solution effect of the model for the first time. Further, comprehensive mathematical derivation and experiments demonstrated the validity and superiority of the RNDAC model theoretically and empirically, respectively. To overview the general design and implementation process, the RNDAC model’s graphical flowchart of the RNDAC model to solve the DMSR problem is shown in Fig. 1. First, the error function is established based on the definition of the DSMR problem for monitoring the solution state. Second, the evolution formula of RNDAC is proposed to improve the convergence speed and enhance the robustness of existing models. Third, by combining the error function and substituting it with the evolution function, the RNDAC model to solve the DMSR problem is implemented. Finally, comprehensive comparison experiments are designed and conducted to verify the performance of the RNDAC model. The main contributions of this paper are listed as follows:

  1. 1.

    Different from previous work, the RNDAC model designs a new evolution formula and employs a new nonlinear adaptive activation function, which accelerates the convergence to the theoretical solution of the DMSR problem and gains a predominant performance in robustness.

  2. 2.

    Four theorems are given to verify the performance of the RNDAC model and analyze its robustness under three kinds of noises: constant, time-varying linear, and bounded random noises while solving the DMSR problem. Besides, the proof processes are given in detail.

  3. 3.

    The relevant quantitative and visual simulation experiments are carried out with a specific example to demonstrate the superior convergence and robustness of the RNDAC model under noise interference.

The rest of the structure is organized into the following six sections. “Preliminaries and related scheme formulation” shows the formulation and preliminary preparation of the DMSR problem to be solved. Next, the construction and evolution formula of the RNDAC model is given, and the corresponding analyses and proofs of the convergence of the RNDAC model are carried out in “RNDAC model construction and convergence analysis”. “Robustness of the RNDAC model”, rigorous theoretical analysis, and corresponding proof steps are given, which perfectly completes the proof of the robustness of the RNDAC model. “Simulations” provides quantitative and visual results and analyzes, which further illustrates the superiority of the RNDAC model through comparative experiments. Furthermore, the highlights and limitations of this work are discussed and presented in “Discussion”. Finally, the paper is summarized in “Conclusions”.

Preliminaries and related scheme formulation

The mathematical formula of the DMSR problem is expressed as follows:

$$\begin{aligned} X^{\text {2}}(t)=N(t), t \in [t_{0},t_{f}], \end{aligned}$$
(1)

where the matrix \(N(t)\in {\mathbb {R}}^{n\times n}\) is a known smooth dynamic matrix, and \(X(t)\in {\mathbb {R}}^{n\times n}\) is the unknown dynamic matrix to be solved with t denotes time. The superscript \(^{\text {2}}\) stands for the square operator of the matrix. It can be seen that the actual meaning of making the Eq. (1) holds is to find a suitable solution X(t). To this end, the error function is furnished as

$$\begin{aligned} \Lambda (t)=X^{\text {2}}(t)-N(t). \end{aligned}$$
(2)

Note that the condition of the Eq. (1) holds is equivalent to all components of the error function \(\Lambda (t)\) are zero. To address this problem, the original zeroing neural network (OZNN) model is adopted [2]. In light of the evolution formula of OZNN \({\dot{\Lambda }}(t)=-\gamma \Lambda (t)\) and error function (2), the following OZNN model for solving the DMSR problem (1) is presented as

$$\begin{aligned} X(t){\dot{X}}(t)+{\dot{X}}(t)X(t) -{\dot{N}}(t)=-\gamma (X^{\text {2}}(t)-N(t)), \end{aligned}$$
(3)

where \(\gamma > 0\) is a scale factor. \(\dot{X}(t)\) and \(\dot{N}(t)\) represent the time derivative of X(t) and N(t), respectively.

Fig. 1
figure 1

Graphical flowchart of the RNDAC model to solve the DMSR problem

Full size image

Noteworthy, the convergence speed and robustness of the OZNN model (3) are unsatisfactory. Given the disturbance of various noises that severely weaken the accuracy of the solution system or even make it break down. A residual-based adaptive coefficient ZNN (RACZNN) model is presented in [21]. The RACZNN model effectively avoids the problem of inflexibility in manually setting the scale factor and makes convergence faster. The RACZNN model is formulated as

$$\begin{aligned} {{\dot{\Lambda }}}(t)=-\varepsilon (\Lambda (t))\Lambda (t)-\sigma (\Lambda (t))\int _0^t\Lambda (\delta )\text {d}\delta , \end{aligned}$$
(4)

where the adaptive scale coefficient \(\varepsilon (\cdot )> 0: {\mathbb {R}}^{n \times n}\rightarrow {\mathbb {R}}\) and feedback coefficient \(\sigma (\cdot )> 0: {\mathbb {R}}^{n \times n}\rightarrow {\mathbb {R}}\). The adaptive scale coefficient \(\varepsilon (\cdot )\) is constructed as

$$\begin{aligned} \varepsilon (\Lambda (t)) = \Vert {\Lambda }(t)\Vert _\text {F}^{\pi } + e, \end{aligned}$$
(5)

where the parameter \(e > 1\) and \(\Vert \cdot \Vert _{\text {F}}\) represents the Frobenius norm. Similarly, the adaptive feedback coefficient \(\sigma (\cdot )\) is constructed as

$$\begin{aligned} \sigma ({\Lambda }(t)) = \left\| \int _0^t{\Lambda }(\delta )\text {d}\delta \right\| ^g_{\text {F}}+e, \end{aligned}$$
(6)

where the parameter \(g>0\).

RNDAC model construction and convergence analysis

To solve the DMSR problem (1) robustly under various noise interference environments and accelerate the convergence, the RNDAC model is proposed in this section.

Model formulation

Different from previous work, a new evolution formula is developed, which makes the RNDAC model perform better in the two crucial performance indicators of solution accuracy and convergence speed. The evolution formula of the RNDAC model is designed as

$$\begin{aligned} {{\dot{\Lambda }}}(t)=-\eta \kappa (\Lambda (t))-\zeta \varphi (\Lambda (t)+\eta \int _0^t\kappa (\Lambda (\delta ))\text {d}\delta ), \end{aligned}$$
(7)

where the scale coefficient \(\eta >0\) and the feedback coefficient \(\zeta >0\). Function \(\kappa (\cdot ): {\mathbb {R}}^{n \times n}\rightarrow {\mathbb {R}}^{n \times n}\) and \(\varphi (\cdot ): {\mathbb {R}}^{n \times n} \rightarrow {\mathbb {R}}^{n \times n}\) represent the adaptive control and the adaptive feedback activation function, respectively. The following expression of \(f(\cdot )\) that can be used to construct both the adaptive control \(\kappa (\cdot )\) and the adaptive feedback activation function \(\varphi (\cdot )\):

  • Power bounded adaptive function:

    $$\begin{aligned} f({\Lambda }_{ij})= {\left\{ \begin{array}{ll} \varsigma ^{+}, &{} {\Lambda }_{ij} > \varsigma ^{+}, \\ \vert {\Lambda }_{ij}\vert ^{\iota }{\Lambda }_{ij} + \varpi {\Lambda }_{ij}, &{} \varsigma ^{-}\le {\Lambda }_{ij}\le \varsigma ^{+}, \\ \varsigma ^{-}, &{} {\Lambda }_{ij} < \varsigma ^{-}, \\ \end{array}\right. } \nonumber \\ \end{aligned}$$
    (8)

  • Exponential bounded adaptive function:

    $$\begin{aligned} f({\Lambda }_{ij})= {\left\{ \begin{array}{ll} \varsigma ^{+}, &{} {\Lambda }_{ij} > \varsigma ^{+}, \\ {\text {exp}}(\vert {\Lambda }_{ij}\vert ){\Lambda }_{ij} + \varpi {\Lambda }_{ij}, &{} \varsigma ^{-}\le {\Lambda }_{ij}\le \varsigma ^{+}, \\ \varsigma ^{-}, &{} {\Lambda }_{ij} < \varsigma ^{-}, \\ \end{array}\right. }\nonumber \\ \end{aligned}$$
    (9)

where \(i, j = 1, 2,...,n,\) and parameter \(\varsigma >0\), which is adapted to limit the residual error of the solving system and enhance the robustness. Hyperparameters \(\varpi >1\) and \(\iota >1\) are utilized to control the convergence speed.

Therefore, through the combination of Eqs. (2) and (7), the RNDAC model for solving the DMSR problem (1) is formulated as

$$\begin{aligned} X(t){\dot{X}}(t)+{\dot{X}}(t)X(t){} & {} =-\eta \kappa (X^{\text {2}}(t)-N(t))+{\dot{N}}(t) \nonumber \\{} & {} -\zeta \varphi (X^{\text {2}}(t)-N(t)\nonumber \\{} & {} +\eta \int _0^t\kappa (X^{\text {2}}(\delta )-N(\delta ))\text {d}\delta ). \nonumber \\ \end{aligned}$$
(10)

In addition, the RNDAC model (10) is inevitably affected by different noises in practical application environments. Hence, here give the form of the RNDAC model (10) for solving the DMSR problem (1) under noises interference as follows:

$$\begin{aligned} X(t){\dot{X}}(t)+{\dot{X}}(t)X(t)= & {} -\eta \kappa (X^{\text {2}}(t)-N(t))+{\dot{N}}(t) \nonumber \\{} & {} -\zeta \varphi (X^{\text {2}}(t)-N(t) \nonumber \\{} & {} +\eta \int _0^t\kappa (X^{\text {2}}(\delta )-N(\delta ))\text {d}\delta )+\nu (t),\nonumber \\ \end{aligned}$$
(11)

where the noises perturbation item \({\nu }(t)\in {\mathbb {R}}^{n\times n}\).

Remark 1

Since the RNDAC model (10) is based on the continuous-time ZNN model, the “ode45“ solver in MATLAB is exploited to transfer the RNDAC model (10) into an ordinary differential equation for simulation with an approximate continuous-time from and compare with different existing ZNN models. Specifically, the RNDAC model (10) is transformed into an initial value ordinary differential equation with a mass matrix to solve the target solution X(t) in real time by using the Runge–Kutta method. The target solution X(t) obtained over time is input to the obtained error function \(\Lambda (t)\), and the residual error is generated until the accuracy reaches the requirement, and the iteration ends.

Remark 2

There are some recent works on adaptive control. First, according to the adaptive event-triggered mechanism, the sliding mode control of a class of random switching systems is realized and applied to the boost converter circuit model [33]. Second, based on the adaptive backstep** design framework incorporated with the universal online approximation capability of neural networks, Su et al. [34] realizes the probability-based asymptotic tracking control and the probability-based asymptotic tracking control. Kong et al. [35] implement an adaptive strategy based on introducing a neural network to identify unknown nonlinear functions, uses an effective hypothesis to deal with unknown system coefficients and applies it to a class of uncertain switching MIMO non-strict feedback adaptive output feedback neural tracking control problem. Compared with the three models above, the novelty of the adaptive strategy in this paper is that it is the first time to apply the adaptive strategy to the direction of the ZNN model and solves the DMSR problem (1). Unlike these works, we use the residual and integral information to guide the convergence of the model.

Convergence analysis

We provide theorem and the corresponding proof to comprehensively analyze the convergence of the RNDAC model (10).

Theorem 1

Starting from a random initial state, the RNDAC model (10) global converges to the theoretical solution of the DMSR problem (1).

Proof

Based on the evolution formula (7), the ijth element of the RNDAC model (10) is depicted as

$$\begin{aligned} {{\dot{\Lambda }}}_{ij}(t)=-\eta \kappa (\Lambda _{ij}(t))-\zeta \varphi \left( \Lambda _{ij}(t) +\eta \int _0^t\kappa (\Lambda _{ij}(\delta ))\text {d}\delta \right) . \nonumber \\ \end{aligned}$$
(12)

By introducing the Lyapunov theory [17, 36], the intermediate variable \(\vartheta (t)\) is introduced as

$$\begin{aligned} \vartheta (t)=\Lambda _{ij}(t)+\int _0^t\kappa (\Lambda _{ij}(\delta ))\text {d}\delta , \end{aligned}$$
(13)

and its derivative form \({\dot{\vartheta }}(t)={\dot{\Lambda }}_{ij}(t)+ \kappa (\Lambda _{ij}(t))\). The Eq. (12) can be rewritten in the following form to analyze the stability of the proposed RNDAC model (10) based on the Lyapunov theory mentioned in paper [17, 36]. The following Lyapunov candidate function \(Y_{1}(t)\) is offered:

$$\begin{aligned} Y_{1}(t)=\frac{1}{2}\vartheta ^{\text {T}}(t)\vartheta (t)\ge 0. \end{aligned}$$
(14)

Moreover, the derivative form of Lyapunov candidate function \(Y_{1}(t)\) is expressed as \({\dot{Y}}_{1}(t) = -\vartheta ^{\text {T}}(t)\kappa (\vartheta (t))\). In light of the definition of activation function (8) and (9), the inequality is established as follows:

$$\begin{aligned} \Vert \vartheta (t)-\kappa (\vartheta (t))\Vert ^{2}_{\text {F}} \le \Vert {\mathcal {L}}-\vartheta (t)\Vert ^{2}_{\text {F}}. \end{aligned}$$
(15)

When \({\mathcal {L}}=0\), it has \(\Vert \vartheta (t)-\kappa (\vartheta (t))\Vert ^{2}_{\text {F}} \le \Vert \vartheta (t)\Vert ^{2}_{\text {F}}\). Besides, on the basis of the definition of \(\text {F}\)-norm, we can obtained:

$$\begin{aligned} \kappa ^{\text {T}}(\vartheta (t))\kappa (\vartheta (t))-2\kappa ^{\text {T}}(\vartheta (t))\vartheta (t) \le 0. \end{aligned}$$
(16)

Further, \(0 \le \kappa ^{\text {T}}(\vartheta (t))\kappa (\vartheta (t))\le 2\kappa ^{\text {T}}(\vartheta (t))\vartheta (t)\). Hence, the following inequality is obtained:

$$\begin{aligned} {\dot{Y}}(t)\le -\alpha \kappa ^{\text {T}}(\vartheta (t))\kappa (\vartheta (t))/2\le 0. \end{aligned}$$
(17)

The time derivative of \(Y_{1}(t)\) as \({\dot{Y}}_{1}(t) \le 0\). Obviously, it can be known from Eq. (17) that the necessary and sufficient condition to satisfy \(Y_{1}(t) = 0\) and \({\dot{Y}}_{1}(t) = 0\) is if and only if \(\vartheta (t)=0\). Therefore, the \(\vartheta (t)\) is globally convergent to zero by the definition of Lyapunov stability theory.

Based on the LaSalles invariance principle [37] and \(\vartheta (t)=\Lambda (t)+\int _0^t\kappa (\Lambda (\delta ))\text {d}\delta =0\) which means \({\dot{\Lambda }}(t)=-\kappa (\Lambda (\delta ))\). Rearranging the Lyapunov candidate function as \(Y_{2}(t)=\Lambda ^{\text {T}}(t)\Lambda (t)\) is convenient for further proof steps, and the time derivative of \(Y_{2}(t)\) can be demonstrated as \({\dot{Y}}_{2}(t)=-\Lambda ^{\text {T}}(t)\kappa (\Lambda (t))\). Next, by referring to the preceding proof steps for \(Y_{1}(t)\) to prove the function \(Y_{2}(t)\), the completion that \(Y_{2}(t) \le 0\) can also be acquired. The elaborate proof steps for \(Y_{2}(t)\) are omitted here. Therefore, the RNDAC model (10) globally converges to the theoretical solution.

The proof is thus completed. \(\blacksquare \)

Computational complexity analysis

The feasibility of the RNDAC model (10) is further illustrated from the implementation and computational point of view. First, the magnitude of the variables in Eq. (10) are reviewed: \(\Lambda (t) \in {\mathbb {R}}^{n\times n}\), \(\kappa (\cdot ) \in {\mathbb {R}}^{n \times n}\) and \(\varphi (\cdot ) \in {\mathbb {R}}^{n \times n}\). Meanwhile, the addition, subtraction, multiplication, or division of two floating point numbers should be informed following to analyze the computational complexity of the RNDAC model (10).

  • The multiplication of a scalar and a vector of size \(s_1\) requires \(s_1\) floating point operations.

  • The addition or subtraction two matrices of size \(s_1 \times s_1\) requires \(s_1\) floating point operations.

  • The inverse of a square matrix of size \(s_1 \times s_1\) requires \({s_1}^3\) floating point operations.

  • For multiplication of a matrix and a vector, one of size \(s_1 \times s_2\) and another of size \(s_2\) require \(s_1(2s_2 - 1)\) floating point operations.

Based on the abovementioned preconditions, the calculation of \(X(t){\dot{X}}(t)+ {\dot{X}}(t)X(t) - {\dot{N}}(t)\) requires \(n^3+2n^2\) floating point operators; the calculation of \(\kappa (X^{\text {2}}(t)-N(t))\) requires \(n^3+6n^2-n\) floating point operators; the calculation of \(\eta \int _0^t\kappa (X^{\text {2}}(\delta )-N(\delta ))\text {d}\delta \) requires \(n^3 +8n^2+n+1\) floating point operators; the calculation of \(\Vert \cdot \Vert ^{\text {2}}_{\text {F}}\) requires \(2n^2-1\) floating point operators. The RNDAC model (10) costs \(n^3+8n^2+2n+3\) floating point operators at each time instant. It can be easily obtained that the OZNN model (3) costs \(n^3+2n^2-n\) floating point operators, the RACZNN model (4) costs \(n^3+6n^2+4n\) floating point operators.

Robustness of the RNDAC model

In this section, three theorems and corresponding proof are provided for investigating the robustness of the RNDAC model (10) under noise injected environments.

Theorem 2

The residual error \(\Vert \Lambda (t)\Vert _{\text {F}}\) of the RNDAC model (10) for solving the DMSR problem (1) globally converges to zero under the disturbance of constant noises \(\nu (t) = \nu \in {\mathbb {R}}^{n \times n}\) when the bounds of the activation function satisfy \(-\zeta \varphi (\vartheta (t))+\nu \le 0\).

Proof

First, the intermediate variable is introduced as follows:

$$\begin{aligned} \vartheta (t)=\Lambda (t)+\int _0^t\kappa (\Lambda (\delta ))\text {d}\delta . \end{aligned}$$

Referring to the defination of the intermediate variable \(\vartheta (t)\), the time-derivative of \(\vartheta (t)\) under the constant noises \(\nu \) is denoted as \({\dot{\vartheta }}(t)=-\zeta \varphi (\vartheta (t))+\nu \) and its ith subelement is expressed as

$$\begin{aligned} {\dot{\vartheta }}_{i}(t)=-\zeta \varphi (\vartheta _{i}(t))+\nu _{i}. \end{aligned}$$
(18)

For further investigating the anti-interference performance of the RNDAC model (10), we construct the following Lyapunov candidate function \(L_{i}(t)=\vartheta ^{2}_{i}(t)/2\) and its time derivative as follows:

$$\begin{aligned} {\dot{L}}_{i}(t)=\vartheta _{i}(t)(-\zeta \varphi (\vartheta _{i}(t))+\nu _{i}). \end{aligned}$$
(19)

It can be concluded from the Eq> (19) that the sign of parameter \(\vartheta _{i}(t)\) is related on the positive or negative of the \(L_{i}(t)\). Therefore, for the three different cases of the symbolic value of parameter \(\vartheta _{i}(t)\), we discuss them independently.

If \(\vartheta _{i}(t)<0\)

In accordance with the definition of the exponential bounded adaptive activation function, we can get the \(\varphi (\vartheta _{i}(t))<0\). Next, to ensure the final conclusion of \({\dot{L}}_{i}(t)<0\) is obtained. There are three different cases discussed and shown below.

  • Under the condition of \(-\zeta \varphi (\vartheta _{i}(t))+\nu _{i}>0\) and \(\vartheta _{i}(t)<0\), the Lyapunov candidate function \({\dot{L}}_{i}(t)<0\). Hence, we can get the conclusion that the system (18) converges to the theoretical solution of the DMSR problem (1) within finite time based on the Lyapunov theory [38].

  • Under the condition of \(-\zeta \varphi (\vartheta _{i}(t))+\nu _{i}=0\), by converting this equation, that is, \(\vartheta _{i}(t)=\varphi ^{-1}(\nu _{i}/\zeta )\). From the Eq. (19) can also be acquired simultaneously that the Lyapunov candidate function \({\dot{L}}_{i}(t)=0\). At this time, the system (18) converges to zero.

  • Under the condition of \(-\zeta \varphi (\vartheta _{i}(t))+\nu _{i}<0\), meanwhile, since the same signs of \(\vartheta _{i}(t)\) and \(-\zeta \varphi (\vartheta _{i}(t))+\nu _{i}\) are both less than zero, it is concluded that \({\dot{L}}_{i}(t)>0\), and the system (18) diverges. In addition, the absolute value of \(\vartheta _{i}(t)\) is proportional to the absolute value of \(\varphi (\vartheta _{i}(t))\) contemporaneously. That is to say, the absolute value of \(\varphi (\vartheta _{i}(t))\) becomes larger when the absolute value of \(\vartheta _{i}(t)\) becomes larger. The robustness of the system (18) in this case is concerned with the upper \(\varphi ^{+}\) and lower \(\varphi ^{-}\) bounds of the exponential bounded adaptive function, we divide the relationship between \(\zeta \varphi ^{-}\) and \(\nu _{i}\) into the following two subcases for further analysis. In front of \(\zeta \varphi ^{-}>\nu _{i}\), the system (18) diverges as time goes on. Inversely, in front of \(\zeta \varphi ^{-}<\nu _{i}\), the system (18) always exists a time t at which \(-\zeta \varphi (\vartheta _{i}(t))+\nu _{i}=0\) with the change of time, and the system (18) tends to be stable. Ultimately, to avoid system divergence, the scale parameter \(\zeta \) in (7) and (22) needs to be adjusted appropriately.

If \(\vartheta _{i}(t)=0\)

Distinctly, \(\varphi (\vartheta _{i}(t))=0\) and \({\dot{\vartheta }}_{i}(t)=\nu _{i}\) can be deduced from the Eq. (18) under this precondition. To ensure system stability, make constant noises \(\vartheta _{i}(t)>0\) when \(\nu _{i}>0\) or \(\vartheta _{i}(t)<0\) when \(\nu _{i}<0\). Accordingly, \(\vartheta _{i}(t)\) exists only as a transient state, and the system (18) is unstable when \(\nu _{i}(t) \ne 0\), which indicates that the situation will revert to the case of \(\vartheta _{i}(t)<0\) or \(\vartheta _{i}(t)>0\).

If \(\vartheta _{i}(t)>0\)

This part can be regarded as the opposite situation to \(\vartheta _{i}(t)<0\), which can be analyzed according to the same proof steps as \(\vartheta _{i}(t)<0\), and the detailed proof steps are omitted here.

After that, the convergence of the system (18) is analyzed in the state of \(t \rightarrow \infty \). Through mathematical derivation, we can get \(\lim \nolimits _{t \rightarrow \infty }\vartheta (t)=\varphi ^{-1}(\nu _{i}/\zeta )\) and \(\lim \nolimits _{t \rightarrow \infty }{\dot{\vartheta }}(t)=0\). When taking \(t \rightarrow \infty \) for the time t of the time derivative of the Eq. (13). That is, \({\dot{\vartheta }}(t)={\dot{\Lambda }}(t)+ \kappa (\Lambda (t))\) is reformulated as

$$\begin{aligned} {\dot{\Lambda }}(t)=-\zeta \varphi (\Lambda (t)). \end{aligned}$$
(20)

In other words, this situation corresponds to the research of Theorem 1.

All in all, the RNDAC model (10) activated by the exponential bounded adaptive function can converge to the theoretical solution of the DMSR problem (1) under constant noises \(\nu \), and the residual error \(\Vert \Lambda (t)\Vert _{\text {F}}\) of the RNDAC model (10) also globally converges to zero.

The proof is thus completed. \(\blacksquare \)

Theorem 3

In the presence of time-varying linear noises \({\bar{\nu }}(t) \in {\mathbb {R}}^{n \times n}\), the RNDAC model (10) globally converges to the theoretical solution \(X^{*} (t)\) of the DMSR problem (1). Taking the bound of the RNDAC model (10) residual error is expressed as \(\lim \nolimits _{t \rightarrow \infty }\Vert \Lambda (t)\Vert _{\text {F}} =\Vert {\bar{\nu }}\Vert _{\text {F}} /\zeta \).

Proof

According to the definition of Laplace transform [39], the ijth subsystem of the RNDAC model (10) polluted by time-varying linear noises \({\overline{\nu }}(t)\) is rewritten as

$$\begin{aligned} s\Lambda _{ij}(s) - \Lambda _{ij}(0)= & {} -\eta \kappa (\Lambda _{ij}(s))-\zeta \varphi (\Lambda _{ij}(s) \nonumber \\{} & {} +\frac{\eta }{s} \kappa (\Lambda _{ij}(s)))+\frac{{\bar{\nu }}_{ij}}{s^{2}}, \end{aligned}$$
(21)

where \(i,j = 1,2,...,n\) and it can be further derived into:

$$\begin{aligned} \Lambda _{ij}(s)=\frac{s^{2}\Lambda _{ij}(0)+{\bar{\nu }}_{ij}}{s(s^2+\eta s+\zeta s+\zeta \eta )}. \end{aligned}$$
(22)

According to the final value theorem, the Eq. (18) is formulated as

$$\begin{aligned} \lim \limits _{t \rightarrow \infty }\Vert \Lambda _{ij}(t)\Vert _{\text {F}}=\lim \limits _{s \rightarrow 0}\Vert s\Lambda _{ij}(s)\Vert _{\text {F}}=\frac{\Vert {{\bar{\nu }}_{ij}}\Vert _{\text {F}}}{\zeta \eta }. \end{aligned}$$
(23)

It can be observed from the above formula (23) that the values of \(\zeta \) and \(\eta \) are related to the value of the \(\lim \nolimits _{t \rightarrow \infty }\Vert \Lambda _{ij}(t)\Vert _{\text {F}}\). When the value of \(\zeta \eta \) as the denominator of the Eq. (23) approaches to positive infinity, the final value \(\Vert \Lambda (t)\Vert _{\text {F}}\) can be further decribed as \(\lim \nolimits _{t \rightarrow \infty }\Vert \Lambda (t)\Vert _{\text {F}}=0\).

The proof is thus completed. \(\blacksquare \)

Theorem 4

Under the interference of bounded random noises \(\nu (t)=\phi (t) \in {\mathbb {R}}^{n \times n}\), the RNDAC model (10) starts from a randomly generated initial state and eventually converges to a certain bounded range.

Proof

The activation functions \(\kappa (\cdot )\) and \(\varphi (\cdot )\) are both specified as linear activation functions for the following proof process. And then, the Eq. (7) can be denoted as

$$\begin{aligned} {{\dot{\Lambda }}}(t)=(-\eta -\zeta ){{\dot{\Lambda }}}(t)-\eta \kappa \int _0^t\Lambda (\delta )\text {d}\delta +\phi (t). \end{aligned}$$
(24)

Furthermore, adjusting the Eq. (24) to:

$$\begin{aligned} {\dot{W}} (t)= HW(t) + \textbf{p}\phi (t), \end{aligned}$$
(25)

where the above auxiliary matrices are represented as \(H=[-\eta -\zeta , -\eta \kappa ;1, 0]\), \(W_{i}(t)=[\Lambda _{i}(t);\int _0^t\Lambda _{i}(\delta )\text {d}\delta ]\) and \(\textbf{p}=[1;0]\). Moreover, its ith subelement is indicated as

$$\begin{aligned} {\dot{W}}_{i}(t)= HW_{i}(t) + \textbf{p}\phi _{i}(t). \end{aligned}$$
(26)

By solving the Eq. (26) can obtain:

$$\begin{aligned} {\dot{W}}_{i}(t)= \text {exp}(Ht)W_{i}(t) + \int _0^t\text {exp}(H(t-\delta ))\textbf{p}\phi _{i}(\delta )\text {d}\delta .\nonumber \\ \end{aligned}$$
(27)

Defined by the triangle inequality mentioned in reference [40], the following relational expression can be acquired:

$$\begin{aligned} \begin{aligned} \Vert W_{i}(t)\Vert _{\text {F}}&\le \Vert \text {exp}(Ht)W_{i}(0)\Vert _{\text {F}}\\ {}&\quad + \Vert \int _0^t\text {exp}(H(t-\delta ))\textbf{p}\phi _{i}(\delta )\text {d}\delta \Vert _{\text {F}}\\&\le \Vert \text {exp}(Ht)W_{i}(0)\Vert _{\text {F}}\\&\quad + \int _0^t\Vert \text {exp}(H(t-\delta ))\textbf{p}\Vert _{\text {F}}\vert \phi _{i}(\delta )\vert \text {d}\delta . \end{aligned} \end{aligned}$$

Next, a detailed discussion is made according to the following three different situations:

  • Under the condition of \((\eta +\zeta )^2<4\eta \zeta \). Importing the auxiliary parameters \(\Theta _{1}=(-(\eta +\zeta )+\sqrt{(\eta +\zeta )^{2}-4\eta \zeta })/2 =-\eta \) and \(\Theta _{2}=(-(\eta +\zeta )-\sqrt{(\eta +\zeta )^{2}-4\eta \zeta })/2 =-\zeta \), we can get:

    $$\begin{aligned}{} & {} \text {exp}(Ht)W_{i}(0) = \begin{bmatrix} \frac{\Lambda _{i}(0)(\Theta _{1}{\text {exp}}(\Theta _{1}t)-\Theta _{2}{\text {exp}}(\Theta _{2}t))}{\Theta _{1}-\Theta _{2}}\\ \frac{\Lambda _{i}(0)({\text {exp}}(\Theta _{1}t)-{\text {exp}}(\Theta _{2}t))}{\Theta _{1}-\Theta _{2}} \end{bmatrix}, \\{} & {} \text {exp}(Ht)p = \begin{bmatrix} \frac{\Theta _{1}{\text {exp}}(\Theta _{1}t)-\Theta _{2}{\text {exp}}(\Theta _{2}t)}{\Theta _{1}-\Theta _{2}}\\ \frac{{\text {exp}}(\Theta _{1}t)-{\text {exp}}(\Theta _{2}t)}{\Theta _{1}-\Theta _{2}} \end{bmatrix}. \end{aligned}$$

    When \(\Theta _{1}>\Theta _{2}\): Here are two inequalities satisfy that \(({\Theta _{1}{\text {exp}}(\Theta _{1}t)-\Theta _{2}{\text {exp}}(\Theta _{2}t)})/(\Theta _{1}-\Theta _{2}) < {\text {exp}}(\Theta _{1}t)\) and \(({\text {exp}}(\Theta _{1}t)-{\text {exp}}(\Theta _{2}t))<({\text {exp}}(\Theta _{1}t)/(\Theta _{1}-\Theta _{2}))\). Next, in the light of the above conditions:

    $$\begin{aligned} \begin{aligned}&\Vert \text {exp}(Ht)W_{i}(t)\Vert _{\text {F}}\le G{\text {exp}}(\Theta _{1}t)\vert \Lambda _{i}(0)\vert ,\\&\Vert \text {exp}(Ht)\textbf{p}\Vert _{\text {F}}\le G{\text {exp}}(\Theta _{1}t). \end{aligned} \end{aligned}$$

    Where the parameter \(G=\frac{\sqrt{(\eta -\zeta )^{2}+1}}{\eta -\zeta }\). In addition, we can obtain the following:

    $$\begin{aligned} \begin{aligned} \vert \Lambda _{i}(t)\vert \le \Vert W_{i}(t)\Vert _{\text {F}}&\le G\text {exp}(\Theta _{1}t)\vert \Lambda _{i}(0)\vert \\&\quad -\frac{G}{\Theta _{1}}\max \limits _{0<\delta <t}\vert \phi _{i}(\delta )\vert . \end{aligned} \end{aligned}$$

    Then, we take the limit on the residual error \(\Vert \Lambda (t)\Vert _{\text {F}}\) as

    $$\begin{aligned} \begin{aligned}&\lim _{t\rightarrow \infty }\sup \Vert \Lambda (t)\Vert _{\text {F}} \\ {}&\quad \le \max \limits _{1\le i\le r+2q}\left\{ \max _{0\le \delta \le t}\vert \phi _{i}(\delta )\vert \right\} \frac{\sqrt{r+2q}G}{\zeta }. \end{aligned} \end{aligned}$$

    The situation of \(\Theta _{1}>\Theta _{2}\) can be roughly regarded as the same situation of \(\Theta _{1}<\Theta _{2}\), and the tedious proof steps are omitted here.

  • Under the condition of \((\eta +\zeta )^2=4\eta \zeta \). We can also get the following:

    $$\begin{aligned}{} & {} \text {exp}(Ht)W_{i}(0) = \begin{bmatrix} \Lambda _{i}(0)t\Theta _{1}{\text {exp}}(\Theta _{1}t)\\ \Lambda _{i}(0)t\Theta _{1}{\text {exp}}(\Theta _{1}t)\\ \end{bmatrix}, \\{} & {} \text {exp}(Ht)\textbf{p} = \begin{bmatrix} \Theta _{1}{\text {exp}}(\Theta _{1}t)\\ t{\text {exp}}(\Theta _{1} t) \end{bmatrix}. \end{aligned}$$

    In this time, the parameter \(\Theta = \frac{-(\eta +\zeta )}{2}\). When there are two parameters \(\varrho \) and \(\Psi \) with positive values, the inequality is \(t{\text {exp}(\Theta t)}\sqrt{\Theta ^{2}+1} < \varrho {\text {exp}}(-\Psi t)\). Besides,

    $$\begin{aligned} \begin{aligned} \vert \Lambda _{i}(t)\vert \le \Vert W_{i}(t)\Vert _{\text {F}}&\le \varrho \text {exp}(\Psi t)\vert \Lambda _{i}(0)\vert \\&\quad +\frac{\varrho }{\Psi }\max \limits _{0<\delta <t}\vert \Lambda _{i}(\delta )\vert . \end{aligned} \end{aligned}$$

    The conclusion is derived as

    $$\begin{aligned} \begin{aligned} \lim \limits _{t \rightarrow \infty }\sup \Vert \Lambda (t)\Vert _{\text {F}} \le \max \limits _{1\le i\le r+2q}\left\{ \max _{0\le \delta \le t}\vert \phi (\delta )\vert \right\} \frac{\sqrt{r+2q}\varrho }{\Psi }. \end{aligned} \end{aligned}$$

To sum up, the residual error \(\Vert \Lambda (t)\Vert _{\text {F}}\) of the RNDAC model (10) is bounded when disturbed by bounded random noises \(\psi (t)\). The residual error upper bound \(\lim \nolimits _{t \rightarrow \infty }\Vert \Lambda (t)\Vert _{\text {F}}\) can be arbitrarily small if the design parameters \(\eta \) and \(\zeta \) are large enough.

Thus, the proof is thus completed. \(\blacksquare \)

Fig. 2
figure 2

The comparative results of different models to solve the DMSR problem (5.2). a Shows the residual error \(\Vert \Lambda (t)\Vert _{\text {F}}\) of different models. b The convergence performance of the RNDAC model (10) starts from different initial states

Full size image
Table 2 Comparison of experimental results
Full size table

Simulations

Experiments setup

All simulation experiments are conducted via MATLAB R2021b on a computer with Intel Core i7-12700F @2.10 GHz CPU, 64 GB memory, NVIDIA GeForce GTX 3080Ti GPU, and Windows 11 operating system. In order to realize the RNDAC model (10) and other comparison models for a fair comparison, a versatile ordinary differential equations solver “ode45” function provided in Matlab is exploited. Note that the “ode45” function is the most commonly used implementation approach for continuous-time ZNN Models [22, 41, 42] in addition more detail about this function has been introduced in Remark 1. Finally, our simulation experiments code is available on GitHub: https://github.com/cfko836/RNDAC.

Time-dependent numerical experiment

In this section, the experimental simulation is carried out in embrace of the dynamic matrix instance N(t) in the DMSR problem (1).

$$\begin{aligned} N(t)= \begin{bmatrix} \text {sin}(4t)\text {sin}(4t)+16&{} 7\text {sin}(4t)\\ 7\text {cos}(4t) &{} \text {sin}(4t)\text {cos}(4t)+9 \end{bmatrix}. \end{aligned}$$

Experiments are conducted with the dynamic matrix instance N(t) in the DMSR problem (1), and the results are shown in Figs. 2, 3 and 4. Note that the scale parameters in RNDAC and other models for comparison are \(\zeta =10\) and \(\eta =20\). The activation functions employed in the RNDAC model (10) are constructed as

  • Power bounded adaptive function:

    $$\begin{aligned} f({\Lambda }_{ij})= {\left\{ \begin{array}{ll} 2^{+}, &{} {\Lambda }_{ij} > 2_{dj}^{+}, \\ \vert {\Lambda }_{ij}\vert ^{5}{\Lambda }_{ij} + 5{\Lambda }_{ij}, &{} -2^{-}\le {\Lambda }_{ij}\le 2^{+}, \\ -2^{-}, &{} {\Lambda }_{ij} < -2^{-}, \\ \end{array}\right. } \end{aligned}$$

  • Exponential bounded adaptive function:

    $$\begin{aligned} f({\Lambda }_{ij})= {\left\{ \begin{array}{ll} 2^{+}, &{} {\Lambda }_{ij} > 2_{dj}^{+}, \\ {\text {exp}}(\vert {\Lambda }_{ij}\vert ){\Lambda }_{ij} + 5{\Lambda }_{ij}, &{} -2^{-}\le {\Lambda }_{ij}\le 2^{+}, \\ -2^{-}, &{} {\Lambda }_{ij} < -2^{-}. \\ \end{array}\right. } \end{aligned}$$

Besides, the construction approach of the corresponding models for comparison are given as

  • OZNN model [32]:

    $$\begin{aligned} X(t){\dot{X}}(t)+{\dot{X}}(t)X(t)=-\gamma (X^{\text {2}}(t)-N(t))+{\dot{N}}(t),\nonumber \\ \end{aligned}$$
    (28)

    where \(\gamma > 0\) is a scaling factor.

  • Modified ZNN (MZNN) model [24]:

    $$\begin{aligned}{} & {} X(t){\dot{X}}(t)+{\dot{X}}(t)X(t)\nonumber \\ {}{} & {} \quad =-\gamma (X^{\text {2}}(t)-N(t)) \nonumber \\{} & {} \qquad +{\dot{N}}(t)-\upsilon \int _0^t (X^{\text {2}}(\delta )-N(\delta ))\text {d}\delta , \end{aligned}$$
    (29)

    with \(\gamma > 0\) and \(\upsilon > 0\).

  • Improved zeroing neural dynamics (IZND) model [30]:

    $$\begin{aligned}{} & {} X(t){\dot{X}}(t)+{\dot{X}}(t)X(t)={\dot{N}}(t)\nonumber \\{} & {} \quad -\** \left( \left|\frac{\partial \Vert X^{\text {2}}(t)-N(t)\Vert _{\text {F}}}{\partial t}\right|\right) P_{\Pi }(X^{\text {2}}(t)-N(t)), \nonumber \\ \end{aligned}$$
    (30)

  • RACZNN model (4) for solving the DSMR (1):

    $$\begin{aligned}{} & {} X(t){\dot{X}}(t)+{\dot{X}}(t)X(t)\nonumber \\ {}{} & {} \quad =-\varepsilon (\Lambda (t))(X^{\text {2}}(t)-N(t))\nonumber \\{} & {} \qquad +{\dot{N}}(t)-\sigma (\Lambda (t))\int _0^t (X^{\text {2}}(\delta )-N(\delta ))\text {d}\delta . \end{aligned}$$
    (31)
Fig. 3
figure 3

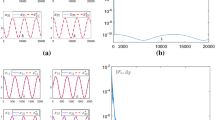
Experiments results of DMSR problem (5.2) with noise perturbed. a, d Constant noises \(\nu _{\text {c}}=[5]^{2 \times 2}\) situation. b, e Time-varying linear noises \(\nu _{\text {tv}}(t)=t\times [2]^{2 \times 2}\) situation. c, f Bounded random noises \(\nu _{\text {r}}\in [2.5, 3.5]^{2 \times 2}\) situation

Full size image

RNDAC model in noise-free environment

The comparison results of the OZNN (28), MZNN (29), IZND (30), RACZNN (31) and the RNDAC model (10) to solve the DMSR problem (5.2) in the ideal environment is illustrated in Fig. 2. As can be seen in Fig. 2a, the RNDAC model (10) is able to converge to the highest accuracy, which is the order of \(10^{-7}\), within three seconds. Meanwhile, the comparison models can only converge up to \(10^{-6}\) with the cost of prolonged convergence time consumption. Noteworthy, although the IZND model (30) is shown to possess the fastest converge speed, it can only converge to order \(10^{-4}\), which is much lower than the accuracy of the RNDAC model (30). Furthermore, Fig. 2a reveals that the RNDAC model has the ability to accurately converge to a theoretical solution from any initial state.The quantitative experiment results are shown in Table 2, which detailedly records the average steady-state residual error (ASSRE) and maximal steady-state residual error (MSSRE) when different models solve the DMSR problem (1). The mathematical description of MSSRE is defined as \(\lim \nolimits _{t \rightarrow \infty }\text {sup}\Vert \Lambda (t_m)\Vert _{\text {F}}, t_m\in [t_s,t_{\text {max}}]\) and ASSRE is defined as \(\int _{t_s}^{t_{\text {max}}} \Vert \Lambda (\delta )\Vert _{\text {F}}\text {d}\delta /(t_{\text {max}}-t_s)\), where t(s) represents the length of time in seconds. As exhibited in Table 2, booting by the adaptive activation function, the RNDAC can achieve the highest accuracy compared with other advanced models. It infers that one of the biggest advantages of the RNDAC model is the high precision. In general, in the noise free situation, the RNDAC model (10) can solve the DMSR problem (1) well, showing a competitive performance.

Fig. 4
figure 4

The comparative simulation results of different values of scale parameters \(\zeta \) and \(\eta \). a The effect of parameter \(\eta \) on RNDAC model (10). b The effect of parameter \(\zeta \) on RNDAC model (10)

Full size image

RNDAC model in noises interference environment

In this subsection, the simulations are executed to investigate the robust performance. Figure 3 demonstrates the performance of the RNDAC model (10) and compared models when solving the DMSR problem (1) in the cases of three kinds of noises.

In the case of constant noises

First, the noises in experiments are set to \([5]^{2 \times 2}\) and injected into the model as described in (11). As shown in Fig. 3d, the norm residual error of the RNDAC model (10) proposed in this paper converges in order of \(10^{-4}\), which is more accurate to the theoretical solution of the DMSR problem (5.2) than the OZNN (28), MZNN (29), IZND (30), RACZNN (31) model. At the same time, it is also observed from Fig. 3a that the RNDAC model (10) also performs well in terms of convergence speed. Furthermore, the numerical result, in this case, is also presented in Table 2. Even under the constant noise perturb, the RNDAC model can reach order \(10^{-4}\). It is to say, the performance of the RNDAC model in terms of ASSRE and MSSRE is the best in this case.

In the case of time-varying linear noises

Under the disturbance of the time-varying linear noises \(\nu _{\text {tv}}(t)= [2]^{2 \times 2}\), the solving performance compared among the RNDAC and other models is shown in Fig. 3b, e. Obviously, when solving the time-varying linear noises perturbed DMSR problem (1), the RNDAC model (10) can stably and fast converge to the order of \(10^{-2}\) and preserve the accuracy consistently. On the aspect of OZNN (28) and IZND (30) models, their residual error increases over time and then causes failure in the solution process. Further, despite the MZNN (29) and RACZNN (31) models can eliminate the influence of part of the time-varying linear noise, the cost is longer convergence time, and the accuracy is lower than the RNDAC model (10). The results provided in Table 2 further this phenomenon.

In the case of bounded random noises

It is challenging to solve the DMSR problem (1) stably under the interference of bounded random noise. In this environment, the IZND (30) model shows the best convergence performance and reaches the order of \(10^{-3}\), which is close to the accuracy generated by the RNDAC model (10). Nonetheless, the robustness performance of the RNDAC model (10) manifests the competitiveness. Specifically, except for the IZND model (30), the RNDAC model (10) is the fastest to converge. Besides, the RNDAC model (10) is the most accurate model under the perturbs of bounded random noise. Similar conclusions can be drawn from Table 2.

Different values of hyperparameter

In this subsection, we control hyper-parameters \(\eta \) and \(\zeta \) to analyze the relationship between hyper-parameters and the robustness of the RNDAC model (10). First, it can be seen from Fig. 4a that when the parameter \(\zeta \) keeps as a fixed value, meanwhile, \(\eta \) changes lead to a change in convergence time. Specifically, the RNDAC model converges faster with \(\eta \) increase but results in more computational consumption, which is limited by the practical implementation environment. Second, when the parameter \(\eta \) is set as a fixed value, the convergence speed of the RNDAC model (10) is positively correlated with the value of \(\zeta \), which the accuracy decreases with larger \(\zeta \). In addition, according to the four Theorems mentioned in this paper, it can be obtained that the accuracy and convergence performance of the RNDAC model (10) is related to the hyper-parameters. Specifically, as the parameter \(\eta \) increases and the parameter \(\zeta \) decreases, its upper and lower bounds will be more accurate under the influence of noise.

Discussion

Summary

In general, the evolution formula and activation function is the difference between our method and previous models adopted for solving the dynamic problem. The experiment results reveal that the RNDAC maintains high accuracy and faster convergence speed in the noise-free environment since it employs the proposed adaptive activation function. On the aspect of robustness, due to adopting the noise suppression evolution formula, the solution performance of the RNDAC model demonstrates enhanced robustness compared with other models, which shows reliable solution performance. In order to manifest the difference between this paper and previous works and clarify the motivation, the highlights of this paper are listed as follows:

  1. 1.

    The adaptive activation function design framework is proposed for the first time, which can effectively improve the solution system’s convergence speed and accuracy.

  2. 2.

    Based on the adaptive activation function and the novel robustness evolution formula, the RNDAC model is proposed to solve the noises perturbated DMSR problem.

  3. 3.

    Four theorems and proof process is provided for comprehensive analyze the performance of the RNDAC model.

Limitations

The limitations of the proposed model are two aspects. First, the improvement of the RNDAC model relies on the adaptive activation function, thereby needing the procedure of additional hyperparameters adjustment, which hinders the flexibility of model deployment. Second, for the way to adjust the hyperparameter and activation function to improve the RNDAN model’s performance, we have only empirically validated it in the simulation part.

Conclusions

This paper proposes a novel adaptive activation function design and constructs a framework for improving the solution model’s performance. Based on this framework and the robust evolution formula, the robust neural dynamic with adaptive coefficient (RDNAC) model is presented and applied to solving the dynamic matrix square root (DMSR) problem. Unlike the existing activation function is usually realized by a monotonically increasing odd function, our method relaxes the limitation and integrates residual information for each component to accelerate convergence. Theoretically, four theorems and proof processes are presented, which show the RNDAC model globally converges to zero in noise free and can preserve reliable solution performance in noises injected environments. Then, experiments with three metrics considered (convergence time, MSSRE, and ASSRE) are conducted to validate the effectiveness of the proposed model and investigate why it works in dealing with the problem. Under a noise free environment, our proposed model can achieve higher accuracy with faster convergence speed than previous methods. On the other hand, the RNDAC model can robustness solve the DMSR problem even perturbed by various noises, which guarantees the reliability concerns on the real-time solving system.

Considering the limitations of this paper, our future work will denote simplifying the process redundant adjustment procedure in activation functions by exploiting the dynamic bounds method. After that, we will conduct a comprehensive theoretical analysis to investigate the better implementation scheme of the proposed adaptive activation function for guiding the design and realization of the RNDAC model. Besides, we will extend the RNDAC model to the complex-valued and look for practical applications such as localization systems, filter design, algorithmic platforms for UAVs, etc.