1 Introduction

The Weibull distribution is one of the important distributions in reliability theory. It is the distribution that received maximum attention in the past few decades. Numerous articles have been written demonstrating applications of the Weibull distribution in various sciences. Furthermore, the Weibull distribution has applications in medical, biological, and earth sciences [32]. [54] discussed about efficient estimation of the Weibull shape parameter based on a modified profile likelihood. Reliability analysis using an additive Weibull model with bathtub-shaped failure rate function explained by [53]. For more discussion about Weibull distribution see, Zhang et al. [55] and [56]. A consistent method of estimation for the three-parameter Weibull distribution was discussed by [39].

We assume that the random variable X has the Weibull distribution with scale parameter \(\lambda \) and shape parameter \(\alpha \) (known) and its pdf (probability density function) is as

$$\begin{aligned} f(x)=\frac{\alpha }{\lambda }x^{\alpha -1} e^{-\frac{x^{\alpha }}{\lambda }}, \quad x>0, \quad \alpha >0, \quad \lambda >0, \end{aligned}$$
(1.1)

and so its CDF (cumulative distribution function) is

$$\begin{aligned} F(x)=1-e^{-\frac{x^{\alpha }}{\lambda }}, \quad x>0, \quad \alpha >0, \quad \lambda >0. \end{aligned}$$
(1.2)

Because of the numerous applications of the Weibull distribution, we feel the importance to investigate efficient estimation of the pdf and the CDF of the Weibull distribution. We consider several different estimation methods: uniformly minimum variance unbiased (UMVU) estimation, maximum likelihood (ML) estimation, percentile (PC) estimation, least squares (LS) estimation and weight least squares (WLS) estimation.

Similar studies have appeared in the recent literature for other distributions. For example, [6] derive estimators of the pdf and the CDF of a three-parameter generalized exponential-Poisson distribution when all but its shape parameter are assumed known. [2] derive estimators of the pdf and the CDF of a two-parameter generalized Rayleigh distribution when all but its shape parameter are assumed known. [7] derive estimators of the pdf and the CDF of a three-parameter Weibull extension model when all but its shape parameter are assumed known. Some other recent works have included: generalized exponential distribution by [3]; exponentiated Weibull distribution by [4]; exponentiated Gumbel distribution by [8].

The contents of this paper are organized as follows. The MLE and the UMVUE of the pdf and the CDF and their mean squared errors (MSEs) are derived in Sects. 2 and 3. Other estimation methods are considered in Sects. 4 and 5. The estimators are compared by simulation and real data application in Sects. 6 and 7. Finally, some discussion on the possible use of the results in the paper is provided in Sect. 8. Throughout the paper (except for Sect. 7), we assume \(\lambda \) is unknown, but \(\alpha \) is known. A future work is to extend the results of the paper to the case that all two parameters are unknown.

A future work is to extend the results of the paper to the case that all parameters of the Weibull distribution are unknown. There has been work in the literature where the pdf and the CDF have been estimated when all their parameters are unknown.

Such estimation of pdfs is considered by [33] for a trapezoidal distribution, by [31] for a log-concave distribution, and by [13] for a compound Poisson distribution. See also [16]. [31] use MLEs.

Such estimation of CDFs is considered by [44] for a three-parameter Weibull distribution, by [14] for a convex discrete distribution, and by [11] for distributions in measurement error models. [44] use MLEs and [14] use LSEs.

2 Maximum Likelihood Estimator of pdf and CDF

Let \(X_{1},\ldots ,X_{n}\) be a random sample from the Weibull distribution. The MLE of \(\lambda \) say \(\widetilde{\lambda }\) is \(\widetilde{\lambda }=n^{-1}\sum _{i=1}^{n} x_{i}^{\alpha }\). Therefore, we obtain MLEs of the pdf and the CDF as

$$\begin{aligned} \widetilde{f}(x)=\frac{\alpha }{\widetilde{\lambda }}x^{\alpha -1} e^{-\frac{x^{\alpha }}{\widetilde{\lambda }}}, \end{aligned}$$
(2.1)

and

$$\begin{aligned} \widetilde{F}(x)= 1-e^{-\frac{x^{\alpha }}{\widetilde{\lambda }}}, \end{aligned}$$
(2.2)

respectively. The probability density of \(T=\sum _{i=1}^{n} x_{i}^{\alpha }\) is

$$\begin{aligned} h^{*}(t)=\frac{ t^{n-1} ~ e^{-\frac{t}{\lambda }} }{\Gamma (n) \lambda ^n} \end{aligned}$$
(2.3)

for \(t>0.\) After some elementary algebra, we obtain the pdf of \(w=\tilde{\lambda }\) as

$$\begin{aligned} g(w)=\frac{n^n w^{n-1}}{\Gamma (n)\lambda ^n} e^{-\frac{nw}{\lambda }} \end{aligned}$$
(2.4)

for \(w > 0\).

In the following, we calculate \(E \left( {\widetilde{f}(x)}^r \right) \) and \(E\left( {\widetilde{F}(x)}^r \right) \).

Theorem 2.1

The \(E\left( {\widetilde{f}(x)}^r \right) \) and \(E\left( {\widetilde{F}(x)}^r \right) \) are given, respectively, as,

$$\begin{aligned} E \left( {\widetilde{f}(x)}^r \right)= & {} \frac{ 2 \alpha ^r n^{\frac{n+r}{2}} x^{n \alpha -r} r^{\frac{n-r}{2}}}{\lambda ^{ \frac{n+r}{2}} \Gamma (n) } K_{n-r} \left( 2 \sqrt{ \frac{r x^{\alpha } n }{\lambda } } \right) \end{aligned}$$
(2.5)
$$\begin{aligned} E \left( {\widetilde{F}(x)}^r \right)= & {} \frac{ 2 n^{\frac{n}{2}} }{ \lambda ^{ \frac{n}{2}} \Gamma (n) } \sum _{j=0}^{r} {r \atopwithdelims ()j} (-1)^j \Big (j x^{ \alpha } \Big )^{\frac{n}{2}} K_{n} \left( 2 \sqrt{ \frac{n j x^{\alpha } }{\lambda } } \right) \end{aligned}$$
(2.6)

Proof (A)

By Eq. (2.4), we can write

$$\begin{aligned} E(\widetilde{f}(x)^{r})= & {} \int _{0}^{\infty } \widetilde{f}(x)^{r} g(w)dw \nonumber \\= & {} \int _{0}^{\infty } \left[ \frac{\alpha }{w}x^{\alpha -1} e^{-\frac{x^{\alpha }}{w}} \right] ^r~ \frac{n^n w^{n-1}}{\Gamma (n) \lambda ^n} e^{-\frac{nw}{\lambda }}~ dw \nonumber \\= & {} \frac{\alpha ^r x^{r(\alpha -1)} n^n }{\Gamma (n) \lambda ^n} \int _{0}^{\infty } w^{n-r-1} e^{-\frac{r x^{\alpha }}{w}} e^{-\frac{nw}{\lambda }} dw \nonumber \\= & {} \frac{ 2 \alpha ^r n^{\frac{n+r}{2}} x^{n \alpha -r} r^{\frac{n-r}{2}} }{ \lambda ^{ \frac{n+r}{2}} \Gamma (n) } K_{n-r} \left( 2 \sqrt{ \frac{r x^{\alpha } n }{\lambda } } \right) \end{aligned}$$
(2.7)

where the last step follows by equation (3.471.9) in [19]. The proof is similar for \(E \left( \widetilde{F}(x)^{r} \right) \). \(\square \)

In the following theorem we obtain the MSE of \(\widetilde{f}(x)\) and \(\widetilde{F}(x)\).

Theorem 2.2

$$\begin{aligned} (A)~~ MSE(\widetilde{f}(x))= & {} \frac{ 2^{\frac{n}{2}} \alpha ^2 n^{\frac{n+2}{2}} x^{n \alpha -2} }{\lambda ^{ \frac{n+2}{2}} \Gamma (n) } K_{n-2} \left( 2 \sqrt{ \frac{2 x^{\alpha } n }{\lambda } } \right) \nonumber \\&- \frac{ 4 f(x) \alpha n^{\frac{n+1}{2}} x^{n \alpha -1}}{\lambda ^{ \frac{n+1}{2}} \Gamma (n) } K_{n-1} \left( 2 \sqrt{ \frac{ x^{\alpha } n }{\lambda } } \right) + f(x)^2 \end{aligned}$$
(2.8)
$$\begin{aligned} (B)~~ MSE(\widetilde{F}(x))= & {} \frac{ 2 n^{\frac{n}{2}} }{ \lambda ^{ \frac{n}{2}} \Gamma (n) } \sum _{j=0}^{2} {2 \atopwithdelims ()j} (-1)^j \Big (j x^{ \alpha } \Big )^{\frac{n}{2}} K_{n} \left( 2 \sqrt{ \frac{n j x^{\alpha } }{\lambda } } \right) \nonumber \\&- \frac{ 2 F(x) n^{\frac{n}{2}} ( x^{ \alpha } )^{\frac{n}{2}} }{ \lambda ^{ \frac{n}{2}} \Gamma (n) } K_{n} \left( 2 \sqrt{ \frac{n x^{\alpha } }{\lambda } } \right) + F(x)^2 \end{aligned}$$
(2.9)

respectively, where \(K_\nu (\cdot )\) denotes the modified Bessel function of the second kind of order \(\nu \).

Proof

Note that \(MSE (\widetilde{f}(x)) = E \left( \widetilde{f}(x) \right) ^2 - 2 f(x) E \left( \widetilde{f}(x) \right) + f^2 (x)\). We have an expression for \(E \left( \widetilde{f}(x) \right) \) and \(E \left( \widetilde{f}(x) \right) ^2\) from Theorem 2.1, yielding the given expression for \(MSE \left( \widetilde{f}(x) \right) \). The proof for \(MSE \left( \widetilde{F}(x) \right) \) is similar.

3 UMVU Estimator of pdf and CDF

In this section, we find the UMVU estimators of pdf and CDF of Weibull distribution. Also we compute the MSEs of these estimators.

Let \(X_{1},\ldots ,X_{n}\) be a random sample of size n from the Weibull distribution given by (1.1). Then \(T=\sum _{i=1}^{n} x_{i}^{\alpha }\) is a complete sufficient statistic for the unknown parameter \(\lambda \) (when \(\alpha \) is known). According to Lehmann Scheffe theorem if \(h(x_{1}|t)=f^{*}(t)\) is the conditional pdf of \(X_{1}\) given T, we have

$$\begin{aligned} E[f^{*}(T)]=\int h(x_{1}|t) h^{*}(t)dt= \int h(x_{1},t) dt= f(x_{1}), \end{aligned}$$

where \(h(x_{1},t)\) is the joint pdf of \(X_{1}\) and T. Therefore \(f^{*}(t)\) is the UMVUE of f(x).

Lemma 3.1

The joint distribution of \(X_{1}\) and T is as follow.

$$\begin{aligned} h(x_{1},t) = \frac{\alpha }{\lambda }x_{1}^{\alpha -1} e^{-\frac{x_{1}^{\alpha }}{\lambda }} \frac{ \left( t - x_{1}^{\alpha } \right) ^{n-2} e^{- \frac{ \left( t - x_{1}^{\alpha } \right) }{ \lambda }} }{ \lambda ^{n-1} \Gamma (n-1)}. \end{aligned}$$
(3.1)

Proof

We have the joint distribution of \((X_{1},X_{2},\ldots ,X_{n})\) as

$$\begin{aligned} f(x_{1},x_{2},\ldots ,x_{n})=\prod _{i=1}^{n} f(x_{i}) = \prod _{i=1}^{n} \left( \frac{\alpha }{\lambda }x_{i}^{\alpha -1} e^{-\frac{x_{i}^{\alpha }}{\lambda }} \right) . \end{aligned}$$
(3.2)

In order to find the joint pdf of \((X_{1},T)\), we set this transformation \(\{ y_{1}=x_{1}^{\alpha },~ y_{2}=x_{2}^{\alpha },\ldots ,~y_{n-1}=x_{n-1}^{\alpha },~ t= \sum _{i=1}^{n} x_{i}^{\alpha } \}\). Then by using some elementary algebra and \((n-2)\) integrations for \(y_{2}, y_{3},\ldots , y_{n-1}\), the proof is done. \(\square \)

Theorem 3.2

If we know \(T = t\), then

  • (A) \(\widehat{f}(x)\) is UMVUE of f(x), where

    $$\begin{aligned} \widehat{f}(x)= \alpha (n-1) x^{\alpha -1} t^{-1} \left( 1-\frac{x^\alpha }{t}\right) ^{n-2}, \quad 0< \frac{x^\alpha }{t} <1. \end{aligned}$$
    (3.3)

  • (B) \(\widehat{F}(x)\) is UMVUE of F(x), where

    $$\begin{aligned} \widehat{F}(x)= 1-\left( 1-\frac{x^\alpha }{t}\right) ^{n-1}, \quad 0< \frac{x^\alpha }{t} < 1. \end{aligned}$$
    (3.4)

Proof

By using Eq. (2.3) and Lemma 3.1, the proof of case (A) is easy. Also by using \(\widehat{F}(x) = \int _{ 0}^{x_{1}} h(x_{1}|~t) dx_{1}\) and some elementary algebra, the proof of case (B) is done.

\(\square \)

Lemma 3.3

The MSEs of \(\widehat{f}(x)\) and \(\widehat{F}(x)\) are given by

$$\begin{aligned} \mathbf (A) ~~ MSE\left( \widehat{f}(x) \right)= & {} \frac{\alpha ^2 (n-1)^2 x^{2\alpha -2}}{\Gamma (n) \lambda ^n} \sum _{j=0}^{2n-4} { 2n-4 \atopwithdelims ()j} (-x^\alpha )^j \Gamma \Big (n-j-2, \frac{x^\alpha }{\lambda } \Big )- f(x)^2.\\ \end{aligned}$$
$$\begin{aligned} \mathbf (B) ~~ MSE\left( \widehat{F}(x) \right)= & {} 1 - \frac{2}{\Gamma (n) \lambda ^n } \sum _{j=0}^{n-1}{n-1 \atopwithdelims ()j} (-x^{\alpha })^j ~ \Gamma \Big (n-j, \frac{x^{\alpha }}{\lambda } \Big ) \\&+\,\frac{1}{\Gamma (n) \lambda ^n } \sum _{j=0}^{2n-2}{2n-2 \atopwithdelims ()j} (-x^{\alpha })^j ~ \Gamma \Big (n-j, \frac{x^{\alpha }}{\lambda } \Big ) - F(x)^2 \end{aligned}$$

respectively, where

$$\begin{aligned} \displaystyle \Gamma (a, x) = \int _x^\infty t^{a - 1} e^{-t} dt \end{aligned}$$

denotes the complementary incomplete gamma function.

Proof (A)

By using Eq. (2.3), we can write

$$\begin{aligned} E(\widehat{f}(x))^2= & {} \int _{}^{} (\widehat{f}(x))^2 h^{*}(t)dt\\= & {} \int _{x^{\alpha }}^{\infty } \left( \alpha (n-1) x^{\alpha -1} t^{-1} \left( 1-\frac{x^\alpha }{t} \right) ^{n-2} \right) ^2 \frac{t^{n-1} e^{-\frac{t}{\lambda }}}{\Gamma (n) \lambda ^n} ~dt\\= & {} \frac{\alpha ^2 (n-1)^2 x^{2\alpha -2}}{\Gamma (n) \lambda ^n} \int _{x^{\alpha }}^{\infty } \left( 1-\frac{x^\alpha }{t} \right) ^{2n-4}~ t^{n-3} e^{-\frac{t}{\lambda }} ~dt \\= & {} \frac{\alpha ^2 (n-1)^2 x^{2\alpha -2}}{\Gamma (n) \lambda ^n} \sum _{j=0}^{2n-4} { 2n-4 \atopwithdelims ()j} (-x^{\alpha })^j \int _{x^{\alpha }}^{\infty } t^{n-j-3} e^{-\frac{t}{\lambda }} dt\\= & {} \frac{\alpha ^2 (n-1)^2 x^{2\alpha -2}}{\Gamma (n) \lambda ^n} \sum _{j=0}^{2n-4} { 2n-4 \atopwithdelims ()j} (-x^{\alpha })^j \Gamma \Big (n-j-2, \frac{x^{\alpha }}{\lambda } \Big ). \end{aligned}$$

where the last step follows by the definition of the complementary incomplete gamma function. The expression for the MSE for \(\widehat{f}(x)\) follows by \(MSE \left( \widehat{f}(x)\right) = E \left( \widehat{f}(x)\right) ^2 - f^2(x)\). The proof for the expression for the MSE for \(\widehat{F}(x)\) is similar. \(\square \)

In the following section we present percentile method of the estimation.

4 Estimators Based on Percentiles

Estimation based on percentiles was originally explored by Kao ([28, 29]), see also [38] and [26]. In fact the nature of percentiles estimators is based on distribution function. In case of a Weibull distribution also it is possible to use the same concept to obtain the estimators of parameters based on the percentiles, because of the structure of its distribution function. If \(p_{i}\) denotes some estimate of \(F(x_{(i)}, \alpha , \lambda )\) then the estimate of \(\lambda \) (when \(\alpha \) is known ) can be obtained by minimizing

$$\begin{aligned} \sum _{i=1}^{n} \left[ \ln (1-p_{i}) - \frac{x_{(i)}^{\alpha }}{\lambda } \right] ^2, \end{aligned}$$
(4.1)

where \(p_{i}=\frac{i}{n+1}\) and \(X_{(i)};~i=1,\ldots , n\) denotes the ordered sample (see [20]). So to obtain the PC estimator of pdf and CDF, we use the same method as for the ML estimator. Therefore

$$\begin{aligned}&\widetilde{f}_{pc}(x)=\frac{\alpha }{\widetilde{\lambda }_{pc}}x^{\alpha -1} e^{-\frac{x^{\alpha }}{\widetilde{\lambda }_{pc}}}, \end{aligned}$$
(4.2)
$$\begin{aligned}&\widetilde{F}_{pc}(x)=1-e^{-\frac{x^{\alpha }}{\widetilde{\lambda }_{pc}}}. \end{aligned}$$
(4.3)

Now we can simulate the expectation and the MSE of these estimators.

5 Least Squares and Weighted Least Squares Estimators

In this section, we derive regression based estimators of the unknown parameter. This method was originally suggested by [49] to estimate the parameters of beta distributions. It can be used for some other distributions also.

Suppose \(X_{1}, X_2, \ldots , X_{n}\) is a random sample of size n from a CDF \(F(\cdot )\) and suppose \(X_{(i)}\), \(i = 1, 2, \ldots , n\) denote the ordered sample in ascending order. The proposed method uses \(F \left( X_{(i)}\right) \). For a sample of size n, we have

$$\begin{aligned} \displaystyle \mathrm{E} \left[ F \left( X_{(j)} \right) \right]= & {} \frac{\displaystyle j}{\displaystyle n+1}, \displaystyle \mathrm{Var} \left[ F \left( X_{(j)} \right) \right] = \frac{\displaystyle j(n-j+1)}{\displaystyle (n+1)^{2}(n+2)},\\ \displaystyle \mathrm{Cov} \left[ F \left( X_{(j)} \right) , F \left( X_{(l)} \right) \right]= & {} \frac{\displaystyle j(n-l+1)}{\displaystyle (n+1)^{2}(n+2)}, \quad \ j<l, \end{aligned}$$

see [26]. Using the expectations and the variances, two variants of the least squares method follow.

5.1 Method 1: Least Squares Estimators

Obtain the estimators by minimizing

$$\begin{aligned} \sum _{j=1}^{n} \left( F(X_{(j)}) - \frac{j}{n+1} \right) ^2 \end{aligned}$$
(5.1)

with respect to the unknown parameters. Therefore in case of Weibull distribution the least squares estimators of \(\lambda \) (when \(\alpha \) is known ), say \(\widetilde{\lambda }_{ls}\), can be obtained by minimizing

$$\begin{aligned} \sum _{j=1}^{n} \left( 1-e^{-\frac{x_{(j)}^{\alpha }}{\widetilde{\lambda }}} - \frac{j}{n+1} \right) ^2. \end{aligned}$$
(5.2)

So to obtain the LS estimator of pdf and CDF, we use the same method as for the ML estimator. Therefore

$$\begin{aligned}&\widetilde{f}_{ls}(x)=\frac{\alpha }{\widetilde{\lambda }_{ls}}x^{\alpha -1} e^{-\frac{x^{\alpha }}{\widetilde{\lambda }_{ls}}}, \end{aligned}$$
(5.3)
$$\begin{aligned}&\widetilde{F}_{ls}(x)=1-e^{-\frac{x^{\alpha }}{\widetilde{\lambda }_{ls}}}. \end{aligned}$$
(5.4)

It is difficult to find the expectation and the MSE of these estimators by mathematical methods. So we calculate them by simulation study.

5.2 Method 2: Weighted Least Squares Estimators

The weighted least squares estimators can be obtained by minimizing

$$\begin{aligned} \sum _{j=1}^{n} w_{j} \left( F(X_{(j)}) - \frac{j}{n+1} \right) ^2 \end{aligned}$$
(5.5)

with respect to the unknown parameters, where \(w_{j}=\frac{1}{Var\left( F(X_{(j)})\right) }=\frac{(n+1)^{2}(n+2)}{j(n-j+1)}.\) Therefore in case of Weibull distribution the wight least squares estimators of \(\lambda \) (when \(\alpha \) is known ), say \(\widetilde{\lambda }_{wls}\), can be obtained by minimizing

$$\begin{aligned} \sum _{j=1}^{n} w_{j} \left( 1-e^{-\frac{x_{(j)}^{\alpha }}{\widetilde{\lambda }}} - \frac{j}{n+1} \right) ^2. \end{aligned}$$
(5.6)

So to obtain the WLS estimator of pdf and CDF, we use the same method as for the ML estimator. Therefore

$$\begin{aligned}&\widetilde{f}_{wls}(x)=\frac{\alpha }{\widetilde{\lambda }_{wls}}x^{\alpha -1} e^{-\frac{x^{\alpha }}{\widetilde{\lambda }_{wls}}}, \end{aligned}$$
(5.7)
$$\begin{aligned}&\widetilde{F}_{wls}(x)=1-e^{-\frac{x^{\alpha }}{\widetilde{\lambda }_{wls}}}. \end{aligned}$$
(5.8)

It is difficult to find the expectation and the MSE of these estimators by mathematical methods. So we calculate them by simulation study.

6 Comparison of UMVU, ML, PC, LS and WLS estimators

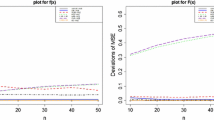
Here, we perform a simulation study to compare the performances of the following estimators: MLE, UMVUE, PCE, LSE and WLSE of the pdf and the CDF. The comparison is based on MSEs. The MSEs were computed by generating one thousand replications of samples of size \(n = 5, 6, \ldots , 35\) from the Weibull distribution with \((\alpha , \lambda )= (1, 0.5)\), (1, 0.75), (1, 1), (2, 1), (2, 2), (1, 2). Figures 1 and 2 plot the the MSEs of the UMVUE, WLSE, LSE and the PCE from the MSE of the MLE versus n.

Fig. 1
figure 1

MSEs of the UMVUE, WLSE, LSE and the PCE from the MSE of the MLE for f (x) and \((\alpha , \lambda )= (1, 0.5)\) (top left), F (x) and \((\alpha , \lambda )= (1, 0.5)\) (top right), f (x) and \((\alpha , \lambda )= (1, 0.75)\) (middle left), F (x) and \((\alpha , \lambda )= (1, 0.75)\) (middle right), f (x) and \((\alpha ,\lambda )= (1, 1)\) (bottom left) and F (x) and \((\alpha , \lambda )= (1, 1)\) (bottom right)

Full size image
Fig. 2
figure 2

MSEs of the UMVUE, WLSE, LSE and the PCE from the MSE of the MLE for f (x) and \((\alpha , \lambda )= (2, 1)\) (top left), F (x) and \((\alpha , \lambda )= (2, 1)\) (top right), f (x) and \((\alpha , \lambda )= (2, 2)\) (middle left), F (x) and \((\alpha , \lambda )= (2, 2)\) (middle right), f (x) and \((\alpha , \lambda )= (1, 2)\) (bottom left) and F (x) and \((\alpha , \lambda )= (1, 2)\) (bottom right)

Full size image

We can see from the figures that the ML estimators of the pdf and the CDF are the most efficient for all n. We can also see that the gain in efficiency by using the MLE over others increases with increasing \(\lambda \).

7 Data Analysis

This paper takes the form of a case study, in which we examine a sample of fibre strength data. The sample are experimental data of the strength of glass fibre of length, 1.5 cm, from the National Physical Laboratory in England. We use a real data set to show that the comparison of MLE, PCE, LSE and WLSE of pdf and CDF. The data is obtained from [50].

0.55, 0.74, 0.77, 0.81, 0.84, 0.93, 1.04, 1.11, 1.13, 1.24, 1.25, 1.27, 1.28, 1.29, 1.30, 1.36, 1.39, 1.42, 1.48, 1.48, 1.49, 1.49, 1.50, 1.50, 1.51, 1.52, 1.53, 1.54, 1.55, 1.55, 1.58, 1.59, 1.60, 1.61, 1.61, 1.61, 1.61, 1.62, 1.62, 1.63, 1.64, 1.66, 1.66, 1.66, 1.67, 1.68, 1.68, 1.69, 1.70, 1.70, 1.73, 1.76, 1.76, 1.77, 1.78, 1.81, 1.82, 1.84, 1.84, 1.89, 2.00, 2.01, 2.24.

Our brief calculations, shows that the Weibull distribution is fitted well to this real data.

It must be note that when we work with real data, in fact all of the parameters, \(\alpha \) and \(\lambda \) are unknown. Therefore we use the following equations for estimating unknown parameters under different methods.

Let \(X_{1},\ldots ,X_{n}\) be a random sample of size n from the Weibull distribution given by (1.1), then the log-likelihood function of the observed sample is

$$\begin{aligned} L(\underline{\theta })= & {} n \log (\alpha )-n\log (\lambda )+(\alpha -1) \sum _{i=1}^{n}\log x_{i}- \frac{\sum _{i=1}^{n}x_{i}^{\alpha }}{\lambda }. \end{aligned}$$
(7.1)

The MLEs of \(\alpha \) and \(\lambda \), say \(\widetilde{\alpha }\) and \(\widetilde{\lambda }\) respectively, can be obtained as the solutions of the equations

$$\begin{aligned}&\frac{\partial L}{\partial \alpha } = \frac{n}{\alpha } + \sum _{i=1}^{n}\log x_{i}- \frac{\sum _{i=1}^{n} x_{i}^{\alpha } \log x_{i}}{\lambda }=0, \end{aligned}$$
(7.2)
$$\begin{aligned}&\frac{\partial L}{\partial \lambda } = -\frac{n}{\lambda } + \frac{\sum _{i=1}^{n} x_{i}^{\alpha }}{\lambda ^2}=0. \end{aligned}$$
(7.3)

The PCEs of \(\alpha \) and \(\lambda \), say \(\widetilde{\alpha }_{pc}\) and \(\widetilde{\lambda }_{pc}\) respectively, can be obtained by minimizing

$$\begin{aligned} \sum _{i=1}^{n} \left[ \ln (1-p_{i}) - \frac{x_{(i)}^{\alpha }}{\lambda } \right] ^2, \end{aligned}$$
(7.4)

where \(p_{i}=\frac{i}{n+1}\) and \(X_{(i)};~i=1,\ldots , n\) denotes the ordered sample.

The LSEs of \(\alpha \) and \(\lambda \), say \(\widetilde{\alpha }_{ls}\) and \(\widetilde{\lambda }_{ls}\) respectively, can be obtained by minimizing

$$\begin{aligned} \sum _{j=1}^{n}\left[ \left( 1-e^{-\frac{x_{(j)}^{\alpha }}{\lambda }} \right) ^{\alpha }-\frac{j}{n+1}\right] ^2. \end{aligned}$$
(7.5)

The weighted least squares estimators of the unknown parameters, \(\alpha \) and \(\lambda \), say \(\widetilde{\alpha }_{wls}\) and \(\widetilde{\lambda }_{wls}\) respectively, can be obtained by minimizing

$$\begin{aligned} \sum _{j=1}^{n} w_{j} \left[ \left( 1-e^{-\frac{x_{(j)}^{\alpha }}{\lambda }} \right) ^{\alpha }-\frac{j}{n+1}\right] ^2, \end{aligned}$$
(7.6)

where \(w_{j}=\frac{1}{Var\left( F(Y_{(j)})\right) }=\frac{(n+1)^{2}(n+2)}{j(n-j+1)}\).

The Weibull distribution was fitted to the strength data by MLE, PCE, LSE and WLSE. Table 1 gives the estimates of \(\alpha \), \(\lambda \) and the corresponding log-likelihood values. The log-likelihood value is the largest for the MLE.

Table 1 Estimates of the parameters and the corresponding log-likelihood
Full size table

We also compared the estimation methods by means of model selection criteria. The ones we considered are:

$$\begin{aligned}&\displaystyle \hbox {`pure' maximum likelihood (ML)} = -2 \ln L(\theta ), \\&\displaystyle \hbox {Akaike information criterion (AIC)} = -2 \ln L(\theta ) + 2k, \\&\displaystyle \hbox {corrected AIC (AICc)} = -2 \ln L(\theta ) + 2k \frac{\displaystyle n}{\displaystyle n - k - 1}, \\&\displaystyle \hbox {Bayes information criterion (BIC, also known as Schwarz criterion)}\\&\quad = -2 \ln L(\theta ) + k \ln n, \\&\displaystyle \hbox {Hannan-Quinn criterion (HQC)} = -2 \ln L(\theta ) + 2 k \ln \ln n, \end{aligned}$$

where \(\ln L(\theta )\) denotes the log-likelihood, n denotes the number of observations (i.e., the length of x) and k denotes the number of parameters of the distribution. The smaller the values of these criteria the better the fit. For more discussion on these criteria, see [10] and [17].

Fig. 3
figure 3

Q–Q plots for the fit for the four different estimation methods

Full size image
Fig. 4
figure 4

Fitted pdf versus the histogram for the four different estimation methods

Full size image

Figures 3, 4 and 5 show the Q–Q plots (observed quantiles versus expected quantiles), the density plots (fitted pdf versus empirical pdf) and the distribution plots (fitted CDF versus empirical CDF) for the four different estimation methods. The figures show that the ML estimators provide the best fit.

Table 2 gives values of the model selection criteria for the four different estimation methods. We can see that the ML estimators give the smallest values for all five model selection criteria.

Hence, evidence based on the MSEs in the simulation study, the log-likelihood values, the Q–Q plots, the density plots, the distribution plots and the model selection criteria show that the ML estimators for the pdf and the CDF are the best.

Fig. 5
figure 5

Fitted CDF versus the empirical CDF for the four different estimation methods

Full size image
Table 2 The values of model selection criteria
Full size table

8 Discussion

We have compared five different estimators (the UMVU estimator, the ML estimator, the LS estimator, the WLS estimator, and the PC estimator) for the pdf and the CDF of the Weibull distribution when the shape parameter is assumed to be known.

We have compared the performances of the five estimators by simulation and a real data application. The results show that the ML estimator performs the best in terms of the MSEs in the simulation study, the log-likelihood values, the Q–Q plots, the density plots, distribution plots, AIC, AICc, BIC and HQC.

Comparisons of the kind performed in Section 6 can be useful to find the best estimators for the pdf and the CDF. The best estimators for the pdf can be used to estimate functionals of the pdf like

  • the differential entropy of f defined by

    $$\begin{aligned} \displaystyle -\int _{-\infty }^\infty f (x) \ln f (x) dx; \end{aligned}$$

  • the negentropy defined by

    $$\begin{aligned} \displaystyle \int _{-\infty }^\infty f (x) \ln f (x) dx - \int _{-\infty }^\infty \phi (x) \ln \phi (x) dx, \end{aligned}$$

    where \(\phi (\cdot )\) denotes the standard normal PDF;

  • the Rényi entropy defined by

    $$\begin{aligned} \displaystyle \frac{\displaystyle 1}{\displaystyle 1-\gamma }\ln \int _0^\infty f^\gamma (x) dx \end{aligned}$$

    for \(\gamma >0\) and \(\gamma \ne 1\);

  • the Kullback-Leibler divergence of f from an arbitrary PDF \(f_0\) defined by

    $$\begin{aligned} \displaystyle \int _{-\infty }^\infty f (x) \ln \left\{ f (x) / f_0 (x) \right\} dx; \end{aligned}$$

  • the Fisher information defined by

    $$\begin{aligned} \displaystyle \int _{-\infty }^\infty \left[ \frac{\displaystyle \partial }{\displaystyle \partial \theta } f(x; \theta ) \right] ^2 f(x; \theta ) d x, \end{aligned}$$

    where \(\theta \) is a parameter specifying the pdf.

Estimation of differential entropy is considered by [42] for data located on embedded manifolds and by [21] for positive random variables. The latter paper illustrates an application in computational neuroscience. Estimation of negentropy is considered by [12] for time series models. This paper illustrates an application to environmental data. Estimation of Rényi entropy is considered by [30] for exponential distributions. UMVU and ML estimators are given. Estimation of Kullback-Leibler divergence is considered by [24] for autoregressive model selection in small samples, by [25] for change detection on SAR images, and by [43] for a class of continuous distributions. Estimation of Fisher information is considered by [37] for model selection, and by [36] for image reconstruction problems based on Poisson data.

The best estimators for the CDF can be used to estimate functionals of the CDF like

  • cumulative residual entropy of F defined by

    $$\begin{aligned} \displaystyle \int _0^\infty \left[ 1 - F(\lambda ) + F (-\lambda ) \right] \ln \left[ 1 - F(\lambda ) + F (-\lambda ) \right] d \lambda ; \end{aligned}$$

  • the quantile function of F defined by \(F^{-1} (\cdot )\);

  • the Bonferroni curve defined by

    $$\begin{aligned} \displaystyle \frac{\displaystyle 1}{\displaystyle p \mu } \int _0^p F^{-1} (t) dt, \end{aligned}$$

    where \(\mu = \mathrm{E} (X)\);

  • the Lorenz curve defined by

    $$\begin{aligned} \displaystyle \frac{\displaystyle 1}{\displaystyle \mu } \int _0^p F^{-1} (t) dt, \end{aligned}$$

    where \(\mu = \mathrm{E} (X)\).

Estimation of cumulative residual entropy is considered by [9] for the Rayleigh distribution. Estimation of quantiles is considered by Ehsanes Saleh et al. (1983) for a location-scale family of distributions including the Pareto, exponential and double exponential distributions, by [15] for the normal distribution, by Rojo (1998) for an increasing failure rate distribution, by [5] for a two-parameter kappa distribution, by [40] for a three-parameter gamma distribution, by [35] for the normal, log-normal and Pareto distributions, by [46] for the generalized Pareto distribution, and by [41] for a three-parameter lognormal distribution. Ehsanes Saleh et al. (1983) use order statistics, [15] use asymptotically best linear unbiased estimators and UMVUEs, [5] use MLEs, [35] uses small sample estimators, and Nagatsuka and Balakrishnan ([40, 41]) use statistics invariant to unknown location. Estimation of the Lorenz curve is considered by [52] for a Pareto distribution. See also [18].

The best estimators for both the pdf and the CDF can be used to estimate functionals of the pdf and the CDF like

  • probability weighted moments defined by

    $$\begin{aligned} \displaystyle \int _{-\infty }^\infty x F^r (x) f (x) dx; \end{aligned}$$

  • the hazard rate function defined by

    $$\begin{aligned} \displaystyle \frac{\displaystyle f (x)}{\displaystyle 1 - F (x)}; \end{aligned}$$

  • the reverse hazard rate function defined by

    $$\begin{aligned} \displaystyle \frac{\displaystyle f(x)}{\displaystyle F (x)}; \end{aligned}$$

  • the mean deviation about the mean defined by

    $$\begin{aligned} \displaystyle 2 \mu F \left( \mu \right) - 2 \mu + 2 \int _{\mu }^\infty x f (x) dx, \end{aligned}$$

    where \(\mu = \mathrm{E} (X)\).

Unbiased estimation of probability weighted moments is considered by [51]. Estimation of hazard rate functions is considered by [47] for two-parameter decreasing hazard rate distributions, by [23] for the inverse Gaussian distribution, by [34] for the linear hazard rate distribution, and by [1] for a mixture distribution with censored lifetimes. [47] use MLEs, [23] uses MLEs and UMVUEs, [34] use MLEs obtained via the EM algorithm, and [1] use MLEs and a Bayesian approach. Estimation of mean deviation is considered by [22] for the normal distribution and by [48] for the Pearson type distribution. The estimators given by the latter are consistent.