1 Introduction

The outcome of a collision is polytomous in nature such as no injury (NI), minimal injury, minor injury, major (incapacitating) injury, and fatal injury. This type of data is mostly modeled using logistic regression models. Most of the models are extensions of the multinomial logit models based on the assumption of independent severity classes [1–11]. Although different modeling methodologies are available from literature to examine collision severity as related to various influencing factors, little is known on the relative merits of these alternatives. The first objective of this research is therefore to compare three most widely used logistic regression models, namely, sequential binary logit models, ordered logit models, and multinomial logit models in a multilevel framework for injury severity analysis.

Some of the issues related to injury severity analysis are within-crash correlation, hierarchical nature of collision data, misclassification, underreporting, endogeneity, sample size, and spatial correlation [5, 11–21]. While a number of recent studies have been devoted to addressing some of these issues, the issue pertaining to the hierarchical nature of collision data has not been addressed adequately. Collision data is hierarchical in nature with possible correlation at the occupant or vehicle level. Ignoring such correlation (intra-class correlation) could lead to false estimation of standard errors and undermine the true significance of parameter estimates [22]. However, little work has been done to account for the multilevel structure of the collision data. Jones and Jørgensen [17] and Lenguerrand et al. [20] were among the first, as identified in Usman et al. [23], to recognize the need to consider the hierarchical crash-car-occupant structure of collision data for crash severity modeling. They discussed the potential issues of ignoring the clustering nature of data and the correlation within the clusters, such as erroneous estimates of model coefficients and understated standard errors and confidence intervals for the effects. They, however, did not discuss the effects of data aggregation. Their conclusions were similar to those from other disciplines such as epidemiology, social research, and political science [24–27]. The second objective of this research is therefore to evaluate the effects of data aggregation through an empirical investigation using three levels of aggregations, i.e., occupant level, vehicle level, and collision level.

This paper contributes to the literature by generating new knowledge about the implications of different modeling alternatives and data aggregation methods for collision severity analysis. The paper first describes the data used in the empirical investigation, including study sites, data sources, and data processing and integration. The three different data aggregation methods are discussed in details. Then, an overview of the three logistic regression models in the construct of the multilevel framework is provided, followed by a discussion on the model calibration process and the results. Finally, the main findings are summarized, focussing particularly on the differences from different approaches.

2 Data description

This research makes use of a collision database prepared in our previous effort [23, 28, 29]. This dataset is unique in several aspects, including reliable observations on traffic and environmental conditions when the collision occurred, and extensive spatial and temporal coverage, as described in the following section.

2.1 Study sites

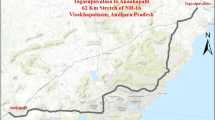
A total of 31 patrol routes, each representing a highway section covered by a single maintenance unit (yard), from different regions of Ontario, Canada, were selected for this analysis as shown in Fig. 1. These sites were selected based on representativeness of different classes of highways, including freeways, four-lane rural highways, and two-lane, two-way highways, and data availability.

Fig. 1
figure 1

Study sites

Full size image

2.2 Data sources

Collision data from six winter seasons (2000–2006) were used for collision severity analysis. Detailed description of each data source can be found in Usman et al. [29] and is also given below.

2.2.1 Traffic volume data

Hourly traffic data were obtained from two sources: Ministry of Transportation, Ontario (MTO) COMPASS system and permanent data count stations (PDCS). Both COMPASS and PDCS use loop detectors for collecting traffic data such as volume, speed, and density. The raw data from the sources were screened for any outliers caused by detector malfunction and then merged into hourly traffic volume data. In cases where multiple readings are available for a segment (e.g., from both sources and/or multiple detectors), average values are used.

2.2.2 Traffic collision data

The Ontario Provincial Police (OPP) maintains a database of all of the collisions that have been reported on Ontario highways. A database including all of the collision records for the study routes was obtained from the MTO. The database includes detailed information on each collision, including collision time, location, collision type, impact type, severity level, vehicle information, driver information, etc. One of the important data fields in these data was related to road surface condition. This variable was converted into a continuous variable—road surface index (RSI) as per the criteria set in Usman et al. [28]. This data is person-based data with an inherent multilevel structure where individuals are nested within vehicles and vehicles within collisions. The data used in this research contains 13,775 collisions involving 39,564 people in 19,635 vehicles for the six winter seasons on the selected routes.

2.2.3 Environment Canada (EC) data

Weather data from Environment Canada includes temperature, precipitation type and intensity, visibility, and wind speed. With exception of the precipitation intensity data, all other data are in hourly format. Most of the EC stations have missing data. For this reason, EC data were obtained from 302 stations for the study routes. These data were processed in three steps: In step 1, a 60 km arbitrary buffer zone was assumed around each route and all stations within this boundary were assigned to the particular route. In the next step using t test, EC stations were identified, which on average are similar to EC stations near the routes. In the last step, data from different EC stations around a route were converted into a single dataset by taking their arithmetic mean. It was found that arithmetic means provide better results than weighted averages.

2.3 Data processing

As described above, collision data are hierarchical with different outcomes possible for a single collision, as shown in Fig. 2. Collisions are categorized into five distinct injury severity levels as follows:

Fig. 2
figure 2

Hierarchical structure of collision data

Full size image
  1. 1.

    NI, where no injuries were sustained;

  2. 2.

    Minimal injury, where the victim suffered minor abrasions and complained of pain but did not go to the hospital;

  3. 3.

    Minor injury, where the victim was treated in the emergency room but not admitted;

  4. 4.

    Major injury, where the victim was admitted to the hospital either for treatment or observation;

  5. 5.

    Fatality, where the victim died within 30 days of collision or on site.

Minimal injury and NI collisions were grouped together into one category because they are similar in terms of consequence. Similarly, major injuries and fatalities were also grouped into a single category. This merging of categories will also take care of the possible correlation that could exist between those closely related outcomes of a collision severity [12, 30]. The hierarchic structure of collision data is shown in Fig. 2, which shows that for a given collision, vehicles are nested within the collision and persons are nested within vehicles and each person could have a given level of severity.

Data from other sources such as weather and traffic were merged with the person-based collision data based on date, time, and location for the 31 patrol routes. A stepwise aggregation process was followed to convert the data from occupant-based records to vehicle-based, and finally to collision-based records. Three datasets were thus formed for this analysis: occupant-based dataset with three levels (occupant—vehicle—collision), vehicle-based dataset with two levels (vehicle—collision), and collision-based dataset with a single level. For the vehicle- and collision-based data, collision severity levels were assigned to the respective vehicles and collisions as per the classification scheme shown in Fig. 3. Note that this classification scheme was not used for occupant-based data as each person has a unique injury severity level.

Fig. 3
figure 3

Data classification scheme (vehicle- and collision-based data)

Full size image

3 Model development

Different approaches can be used for collision severity analysis: (a) incorporating severity into the collision frequency models by modeling collisions classified by severity types [31–34]; and (b) modeling the conditional probability of each severity level for a given collision [14, 15, 17, 35, 36]. In this research, we adopted the second approach for three reasons: (i) different factors could have different effects on collision occurrence and severity (e.g., seat belt use has nothing to do with collision occurrence, but is an important factor in severity analysis); (ii) data that could be used for joint models are limited in nature because most of the data are collected after the collision has happened [12]; and, (iii) consequence outcomes and injury data are at the individual, vehicle, or accident level. Three different model structures were considered for the conditional probability of a collision for each of the three datasets discussed previously.

Multilevel framework is used to account for the correlation between vehicles in a collision or persons in a vehicle. In a multilevel setting, correlation at a sub-level is taken care of by inclusion of random parameters which are constant within the sub-level but are allowed to vary at the upper levels [18, 20, 37].

3.1 Multilevel logistic regression models

The first modeling structure considered is the multilevel multinomial logit model. In this model, a base category is selected out of the different outcomes and other categories are estimated with respect to the base category. Many researchers have used multinomial logit models for accident severity analysis [1–10]. If the three severity levels are represented by 0, 1, and 2 with 0 as the reference or base category then the model structure for a three-level data structure (occupant-based data) is given by Eq. (1). The resulting models are called multilevel multinomial logit models (MML).

$$\left. {\begin{array}{*{20}c} {{ \ln }\left[ {\frac{{P\left( {Y = 1/X} \right)}}{{P\left( {Y = 0/X} \right)}}} \right] = \beta_{10} + \mathop \sum \limits_{n = 1}^{N} \beta_{1n} X_{1ijkn} + U_{jk} + V_{k} }, \\ {{ \ln }\left[ {\frac{{P\left( {Y = 2/X} \right)}}{{P\left( {Y = 0/X} \right)}}} \right] = \beta_{20} + \mathop \sum \limits_{n = 1}^{N} \beta_{2n} X_{2ijkn} + U_{jk} + V_{k} }, \\ \end{array} } \right\}$$
(1)

where P represents the probability of severity level (either 0, 1 or 2); i, j, and k represent occupant, vehicle, and collision levels, respectively; U jk and V k denote the second level (vehicle) and the third level (collision) random effect factors which are assumed to follow a logistic distribution; β is a model coefficient to be estimated; and X ijk represents a set of explanatory variables at the individual level. U jk remains constant for occupants within a vehicle but varies across vehicles and collisions. Similarly, V k is constant for vehicles in a collision but varies across collisions. U jk and V k are obtained by considering the intercept as a random parameter.

The second modeling structure is the sequential binary logistic model. Collision data were divided into two mutually exclusive injury outcomes for a given collision at a given level, and binary logit models were specified at each level such as shown in Fig. 2. Many researchers have used binary logit models for accident severity analysis [5, 11, 13–21].

For multilevel data, the resulting model is called the multilevel sequential binary logit model (MBL). The mathematical form of the model for a three-level data structure (occupant-based data) is shown in Eq. (2):

$${ \ln }\left[ {\frac{{P\left( {Y = 1} \right)}}{{P\left( {Y = 0} \right)}}} \right] = \beta_{0} + \mathop \sum \limits_{n = 1}^{N} \beta_{n} X_{ijkn} + U_{jk} + V_{k},$$
(2)

where P represents the probability of severity level (either 0, or 1).

The third modeling structure considered in this research is multilevel ordered logit model. Ordered logit models are extensions of multinomial logit models to account for the inherent ordering of severity levels in collisions, such as, from no injury to injury and to fatal [10, 38–44]. The mathematical form of a multilevel ordered logit model (MOL) for a three-level data structure (occupant-based data) is shown in Eq. (3):

$${ \log }\left[ {\frac{{S_{ijk}^{\text{s}} }}{{S_{ijk}^{\text{r}} }}} \right] = \beta_{0} + \beta_{1} X_{ijk} + U_{jk} + V_{k},$$
(3)

where severity (represented by “S”) with superscript “r” represents the base severity against which other severity levels, denoted by superscript “s,” are compared at the occupant level. The reference category could be either the least or most severe one. If Y denotes the observed severity level, Y* the unobserved injury severity level from Eq. (3), and µ 1 , µ 2, …, µ j the cut-off points or threshold values for the injury severity levels, then

$$\begin{array}{*{20}l} {Y = {\text{ 1 if}}\,Y^* \, \le \mu_{ 1} ,} \\ {Y = {\text{ 2 if}}\,\mu_{ 1} < Y^* \, \le \mu_{ 2},} \\ \vdots \\ {Y = \;j\;{\text{if}}\,\mu_{{j - 1}} < Y^*.} \\ \end{array}$$
(4)

The probability of a particular injury severity level Y = j can be estimated using Eq. (5) [45]:

$$P(Y = j) = P(\mu_{j - 1} < Y^{*} < \mu_{j} ) = \frac{{\exp (\mu_{j} - \sum {\beta_{k} x_{k} } )}}{{1 + \exp (\mu_{j} - \sum {\beta_{k} x_{k} } )}} - \frac{{{\text{exp(}}\mu_{j - 1} - \sum {\beta_{k} x_{k} } )}}{{1 + {\text{exp(}}\mu_{j - 1} - \sum {\beta_{k} x_{k} } )}},$$
(5)

where β k are model coefficients to be estimated and \(\left\{ {X_{1} , \, X_{2} ,\ldots \, X_{k} } \right\}\) represents a set of explanatory variables. An important aspect of ordered logit models is the proportional odds (or parallel slopes) assumption, where the variables are assumed to have the same slope across all levels of severity/outcome [46–48] with the exception of the intercept [49]. Results of ordered logit models are therefore unidirectional (show either an increase or decrease in severity) and are thus very easy to interpret. This unidirectional effect can sometimes lead to undesirable effects where a variable could cause the probability of high or low severity collision to increase at the cost of the other [38].

The presence of correlation is confirmed by calculating the intra-class correlation (correlation among observations within the same cluster). Intra-class correlation, denoted by ρ, is a coefficient with values ranging from 0 to 1 and is calculated as the ratio of the variance at the sub-level to the total variance [23, 50, 51] as given in Eq. (6):

$$\rho = \frac{{\sigma_{\text{sub - level }}^{2} }}{{\sum \sigma^{2} }}.$$
(6)

The higher the value of ρ, the greater the correlation is and the higher the consequences of ignoring it will be [30]. For details on how ρ can be calculated, readers are referred to e.g., Jones and Jørgenson [18].

3.2 Exploratory data analysis

There are a large number of factors that influence the severity of collisions under winter conditions [52, 53]. The main factors can be grouped into three categories, namely road driving conditions, vehicle characteristics, and driver attributes. Road driving conditions include road geometry, environment, and pavement surface conditions. The latter are affected by weather and maintenance operations. Different sets of variables were considered in analyzing the three datasets as listed in Table 1.

Table 1 List of variables used in the analysis
Full size table

Table 2 provides a summary of collision counts by severity for the different datasets and the changes in the proportions of different types of injury severity levels due to aggregation at each step.

Table 2 Collision count by severity and percent change in collision severity distribution due to data aggregation
Full size table

As shown in Fig. 2, a collision may involve several vehicles and the occupants of an involving vehicle may experience different levels of injury severity. As a result, modeling the collision severity at the collision level will result in a loss of information and misrepresentation of certain severity levels, as show in Table 2. For example, if we aggregate data for a collision with three fatal injuries and two vehicles involved, the fatality count for occupant-, vehicle-, and collision-based datasets will be three (03), two (02), and one (01), respectively.

4 Model calibration and results

MLwinFootnote 1 was used to calibrate the three alternative models discussed in Sect. 3. Tables 3 through 5 provide the calibration results for collision-based data, vehicle-based data, and occupant-based data. MLWin uses Quasi-likelihood for models with discrete dependent variables and thus the reported likelihood estimates are only approximate leading to unreliable likelihood ratio tests [54]. A positive sign is used as an indicator of increase in severity level with respect to the associated variable. Results from all the models are consistent in terms of the direction of their effect on severity; however, effect of the size of coefficient varies across different models and aggregation levels. For evaluating the effect of individual factors, their elasticities are calculated and given in Table 6. For a continuous variable X ki , elasticity for a particular collision severity outcome “i” is computed as

Table 3 Modeling results for collision-based data
Full size table
Table 4 Modeling results for vehicle-based data
Full size table
Table 5 Modeling results for occupant-based data
Full size table
Table 6 Elasticities for the three datasets
Full size table
$$E_{{X_{ki} }}^{P\left( i \right)} = \left[ {1 - P\left( i \right)} \right] \beta_{ki} X_{ki},$$
(7)

where P(i) is the probability of collision severity outcome “i,” and β ki is the coefficient associated with variable X ki . For categorical variables elasticity is calculated as \(E = \left( {{\text{exp }} \beta - 1} \right) / {\text{exp }} \beta\) [3, 7, 8]. Table 7 gives values predicted from the models and the observed severity ratios.

Table 7 Prediction results from models versus observed results
Full size table

4.1 Comparison of quality of fitting

As explained in the previous section, likelihood estimates from MLWin are approximate and the usual goodness of fit criterion such as Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) could not be applied [54]. AIC [55], defined as −2LL + 2p, is a test statistics used to identify the best fit model from a set of models. The term LL is the log likelihood of a fitted model and p the number of parameters, which is included to penalize models with higher number of parameters. A model with smaller AIC value represents a better overall fit. Similarly, Bayesian Information Criterion (BIC) [56], defined as −2LL + pln(n), which is another test statistics and a variation of AIC, is used to identify the best fit model from a set of models. The term “n” represents the number of observations used to calibrate the model. A model with smaller BIC value represents a better overall fit. Alternatively, results from the models were compared to the actual observations and it was found MML models have a better prediction performance compared to MOL models except for collision-based fatalities where MOL has a slightly better prediction. Similarly, MML models have better prediction results compared to MBL models for occupant- and vehicle-based data. For collision-based data, MBL results are slightly better for NI + minimal injury and minor injury collisions, whereas for fatality collisions, MML results are closer to the observed severity ratios. Based on the discussion in this section, MML is found to perform better as a whole than MBL and MOL.

4.2 Effects of data aggregation and correlation

If the collision data are used at a disaggregated level of analysis such as occupant based or vehicle based, then efforts should be made to account for the correlation that exists between occupants in a vehicle or vehicles in a collision such as shown by the variance terms in Tables 4 and 5. Occupant-based results (Table 5) show that around 79 % of the variation (ρ = 0.79) is accounted for at the occupant level, whereas the collision level accounts for 19 % of the variation (ρ = 0.19) and vehicle level for 2 % (ρ = 0.02). Similarly, vehicle-based results (Table 4) show that around 94 % of the variation (ρ = 0.94) is accounted for at the vehicle level, whereas the collision level accounts for 0.06 % of the variation (ρ = 0.06). This flexibility offered by multilevel modeling improves the reliability of the modeling results obtained with such models as compared to single-level models [57–59].

Data used in a collision level severity analysis are, however, aggregated to the level of a collision. This takes care of the correlation within the data but can result in some immediate problems: (i) loss of information by reducing the number of observations, (ii) miss-specification of collision attributes resulting in erroneous share of high severity levels (Table 2), and (iii) the incapability to analyze different variables related to individual persons or vehicles at aggregate level such as seat belt use, position in the vehicle, vehicle age and type, etc. These could result in biased parameter estimates (see e.g., Mensah and Hauer [60] for some of these issues in collision frequency modeling). In this research, we utilized the multilevel framework to account for the correlation between occupants in the same vehicle and vehicles in the same collision. Treating occupant-based data results as the base case we compare modeling results from MML models for the three datasets.

The percent change in parameter estimates for fatality and major injury collisions show a difference ranging from −131 % to 214 % (average = 13 %) between occupant-based (as the base case) and vehicle-based and −9 % to 310 % (average = 62 %) between occupant-based and collision-based data. The difference between vehicle-based data (as the base case) and collision-based data is −52 % to 191 % (average reduction in size of the parameter estimate = 28 %). For minor injuries the difference is from −49 % to 139 % (average = 20 %) between occupant-based and vehicle-based data and from −29 % to 134 % (average = 54 %) between occupant-based and collision-based data, whereas for vehicle-based data (as the base case) and collision-based data this difference is from −3 % to 186 % (average = 64 %). This shows that aggregating the data results in underestimation of the parameters estimates. This could be of grave consequences if the purpose of the analysis is to evaluate the effects of some policies through some variables, in which case precise estimation of the magnitude of the parameter for the variable is of great importance. Besides data aggregation, another reason for this is the model setting (Table 1) where it can be seen that not all the variables used in the occupant-based data model are used for the other two level of aggregation. This will also result in parameter estimates for the remaining variables to be rescaled. This is evident from the results as well where the range is wider for the difference between occupant- and collision-based data than those from occupant- and vehicle-based data.

4.3 Comparison of significant factors

Despite different in quality of fitting and effect sizes of various safety factors from different models and data aggregation methods, there were consistent results in terms of the factors that were found to have statistically significant effect on collision severity. This section discusses the main findings on the contributing factors and the magnitude of their effects (Tables 3 through 6).

4.3.1 Driver characteristics and accident impact type

One percent change in driver age will cause an average increase of 0.297 in the probability of suffering a fatal/major injury and 0.121 increases in the probability of having minor injuries. For male drivers, the probability of suffering minor injuries are 0.46 less compared to female drivers. Alcohol can increase the probability of fatality/major injuries by 0.80. Collisions on bridges increase the probability of fatality/major injuries by 0.58, whereas those occurring at intersections reduce it by 0.21.

4.3.2 Road characteristics

Multilane-divided highways increase the probabilities of fatality/major injuries by 0.26 and minor injuries by 0.09, whereas for freeways these figures are 0.05 and 0.12 compared to undivided two-lane highways. Improvement in road surface condition causes the probability of minor injuries to reduce by 0.20. The presence of curves or hilly terrain increases the probability of minor injuries from 0.12 to 0.17. Increase in number of lanes decreases the probability of fatal/major injuries by 0.96 and minor injuries by 0.43. Increase in speed limit increases the probability of fatality/major injuries by 1.67 and minor injuries by 0.68.

4.3.3 Vehicle and individual

Heavy weight and non-defective vehicles decrease the probability of fatal/major injuries from 0.21 to 0.56 and minor injuries by 0.33–1.43. Increase in the age of a vehicle increases the chances of minor injuries by 0.07. Front position increases the chances of fatal/major injuries by 0.15 and minor injuries by 0.22, whereas the use of safety devices decreases the chances of fatal/major injuries by 1.92 and minor injuries by 0.94.

4.3.4 Weather and environment

Increase in wind speed and visibility decreases the probability of minor injuries by 0.08 and 0.05. The presence of lighting conditions reduces the chances of fatality/major injuries by 0.18.

4.3.5 Traffic volume

Traffic volume is the most influential factor of all and an increase in traffic volume decreases the probability of fatal/major injuries by 3.70 and minor injuries by 1.08. Intuitively, a higher traffic volume will lead to more congestion resulting in lower speeds.

5 Conclusions and future research

Three alternative logistic regression models, namely multinomial logit model, sequential binary logit model, and ordered logit model applied in a multilevel framework, were compared and evaluated for their performance for predicting the conditional probabilities of different severity levels of a given collision. These models were applied to collision data aggregated at three levels—occupant level, vehicle level, and collision level. These three levels were used to evaluate the effects of data aggregation and correlation on collision severity analysis. Collision data from six winter seasons (2,000–2,006) and 31 sites containing 13,775 collisions, involving 39,564 individuals and 19,635 vehicles was used for this analysis. Based on the modeling results, it was found that multilevel multinomial logit (MML) has the best overall fit to the data, and occupant-based data results are more reliable than vehicle- and collision-based data.

Moreover, it was found that data aggregation affects the parameter estimates, on the average, by as much as 13 % for vehicle-based aggregated data and 62 % collision-based aggregated data compared to occupant-based data. Similarly, from correlation perspective, around 79 % of the variation is accounted for when using occupant-based data compared to the 19 % variation accounted for by collision-based data. This could have significant implications for evaluating the effects of different safety-related policies and countermeasures when using, showing the importance of data analysis at a disaggregate level.

Our future efforts will be directed toward the comparison of data compiled from winter seasons and snow storm events using the results from this research. Moreover, other modeling types such as latent class models will also be evaluated and compared to the modeling results from this analysis.