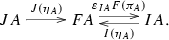Crossed modules and Whitehead sequences

Abstract

We introduce the notion of Whitehead sequence which is defined for a base category together with a system of abstract actions over it. In the classical case of groups and group actions the Whitehead sequences are precisely the crossed modules of groups. For a general setting we give sufficient conditions for the existence of a categorical equivalence between internal groupoids and Whitehead sequences.

1 Introduction

This work may be seen as the continuation of the project initiated in 1982 by Porter [17] in order to generalize the so-called Brown–Spencer result [5] from groups to other structures. The Brown–Spencer result establishes a categorical equivalence between crossed modules of groups and internal groupoids in the category of groups, an important result connecting two types of objects, apparently with a very different nature. As a consequence, this result has significant applications in homotopy theory, homology, cohomology, K-theory and higher dimensional categorical algebra, among others.

Over the last three decades many authors studied this specific problem. The original result, although already known, was first published in 1976 [5] (it was also independently discovered by Lavendhomme and Roisin). In 1982 Loday generalizes it to higher-dimensions [9] by introducing the notion of Cat-n-group. The Brown–Spencer result is the non abelian version of the much more easy, but still important fact that groupoids in abelian groups (or in any abelian category) are the same as morphisms of abelian groups. In the same way, Loday generalization of Brown–Spencer is the truncated non abelian version of Dold–Kan correspondence. During the 80’s much work was done, either as applications of the original result or as generalizations of it, especially in categories of groups with operations, as it can be seen for example in [18]. In the 90’s Brown and his School were still active in this area as one can see in [4] and its references, as well as several other authors. For example internal categories and internal groupoids started to be exhaustively studied, first in the context of Mal’tsev categories and later in the context of semiabelian categories. This work culminated with the notion of internal crossed module by Janelidze, see [8] which also contains some historical notes.

The main motivation for the present work was the possibility of moving from the category of internal actions, defined in the context of a semiabelian category, to a more general context of categories and functors such as the one we introduce in Sect. 2, in which $\mathbf {B}$ is any pointed category while $\mathbf {A}$ can be interpreted as a category of abstract actions on $\mathbf {B}$.

After a close analysis of some of the results obtained during the last three or four decades we concluded that many of the generalizations of the notion of crossed module were obtained by calculating simpler descriptions of internal groupoids. The perspective that we have adopted in this work is somehow different. We study a general system in which a certain sequence of two morphisms without any further assumptions is considered. We call it a Whitehead sequence. Accordingly, we define a crossed module as a Whitehead sequence to which an internal groupoid structure can be associated in a canonical manner, an idea that we will make precise later.

Consider a system of functors and categories displayed as

(1)

and such that $IG=1_{\mathbf {B}}=JG$. A sequence of morphisms in $\mathbf {A}$ of the form

is called a Whitehead sequence whenever

$$\begin{aligned} I(u)=1_{IA},\quad J(v)=1_{JA}, \quad I(v)=J(u). \end{aligned}$$

Our main goal here is to find reasonable conditions under which we have an equivalence of categories

$$\begin{aligned} \mathsf {W}(\mathbf {A}) \sim \mathsf {Gpd}(\mathbf {B}) \end{aligned}$$

(2)

between the category of Whitehead sequences in $\mathbf {A}$ and the category of internal groupoids in $\mathbf {B}$, the guiding example being the case where $\mathbf {B}$ is the category of groups and $\mathbf {A}$ is the category of group actions on groups. The functors I and J are the obvious projections (see Sect. 3) while G gives the action by conjugation [17]. The functor G has a left adjoint, F, which corresponds to the well known construction of the semidirect product in groups (see also [3, 8]). In this case a Whitehead sequence is precisely a crossed module.

A crossed module, as introduced by J.H.C. Whitehead [19], in the category of groups consists of a pair (A, h) in which $A \in \mathbf {A}$ is an action (the group IA acts on the group JA) and $h:JA \longrightarrow IA$ is a group homomorphism such that there is a Whitehead sequence

with $J(u)=h=I(v)$.

This notion of crossed module was already presented in [17]. Here we illustrate the general system of categories and functors (1) and motivate the definition of Whitehead sequence which, in the particular case where $\mathbf {B}$ is the category of groups and $\mathbf {A}$ the category of group actions, gives the classical notion of a crossed module.

First we give additional conditions on the general system of categories and functors (1) in which $\mathbf {B}$ is a pointed category while $\mathbf {A}$ (under some reasonable conditions) is to be understood as a category of actions. More specifically, an object A in $\mathbf {A}$ is considered as an action of the object IA on the object JA in $\mathbf {B}$ and if B is an object in $\mathbf {B}$ then G(B) is considered as an action (by conjugation) of B onto itself.

One of the important aspects of this construction is that we can always define the notion of Whitehead sequence as a triple (A, u, v), in $\mathbf {A}$, of the form

such that

$$\begin{aligned} I(u)=1_{IA},\ J(v)=1_{JA}, \ I(v)=J(u), \end{aligned}$$

and the question is: when does it make sense to call such a sequence a crossed module? One possible answer is: whenever it has an associated groupoid structure.

Next we describe the main ideas that lead us to the notion of category of actions we introduce here.

Concerning the one dimensional case, we assume that I and J are jointly faithful. This restriction means that an action, in general, can be understood as a triple $A=(X,\xi ,B)$ where $\xi$ is some kind of structure defined on B and X, while a morphism $f:A \longrightarrow A'$ is always a pair of morphisms $f_1:JA \longrightarrow JA'$ and $f_2:IA \longrightarrow IA'$ in $\mathbf {B}$ satisfying some compatibility conditions with respect to the structures involved. With this restriction we have that a Whitehead sequence is determined by a pair (A, h) where A is an action, i.e. an object in $\mathbf {A}$, $h:JA \longrightarrow IA$ is a morphism in $\mathbf {B}$, and the existence of u and v as in the definition of Whitehead sequence becomes a property of A and h, giving, in the case of groups [17], the celebrated conditions for a crossed module (Eqs. (13), (14) of Sect.  3). Note that Eq. (13) is equivalent to the existence of u, while the Eq. (14) is equivalent to the existence of v.

In higher dimensions, to assume the above restriction is too much. We will often be interested in considering that the 2-cells are also involved and in that case a morphism between actions can be a triple $f=(f_1,f_2,f_3)$ where $f_1$ and $f_2$ are still morphisms as above but $f_3$ may be a 2-cell linking the two structures. This is what happens in the case of categorical groups [6]. However, also in this case, the 2-cells involved are determined up to equivalence. In the following we are going to consider only the one-dimensional level. Nevertheless, the theory of action-systems presented here is delineated having in mind its application in a two-dimensional setting.

This work is organized as follows. In Sect. 2 we introduce the setting and give the basic definitions. A (right) patch is a jointly epimorphic cospan with the property that there exists a retraction of the right inclusion. If this retraction is the cokernel of the left inclusion then we speak of an exact (right) patch (Definitions 1, 2). A patch is stable if the pullback of its retraction along any morphism exists and is a (right) patch (Definition 3). We briefly recall the well-known concepts of cartesian morphism and fibration. With respect to an ordered pair, (I, J), of functors we define the notion of organic morphism (Definition 4): a morphism $f:{A\longrightarrow E}$ is organic (or (I, J)-organic) if $IE\cong JE$ and the two components I(f) and J(f) give rise to an exact patch.

The notion of a system such as (1) that models a system of actions over the base category $\mathbf {B}$ is given in Definition 7 and it is called an action-system of $\mathbf {A}$ over $\mathbf {B}$. One of the key ingredients of the definition is what we call the L-condition (in honour of Jean Louis Loday [9]). We point out that this condition (see Definition 6) in the context of a semiabelian category is precisely the so-called Smith is Huq condition [15].

In Sect. 3 we present the main examples that have been the guiding lines for this work. If $\mathbf {B}$ is a pointed category with pullbacks along split epimorphisms and binary coproducts then we can always consider the two extreme cases. The first case is displayed as

(3)

while the second one is obtained by taking a system such as the one displayed in (1) with $IG=1_{\mathbf {B}}=JG$, in which $\mathbf {A}$ is a subcategory of $\mathsf {Pt}(\mathbf {B})$ consisting of those split epimorphisms in $\mathbf {B}$

such that the kernel k and the section s are jointly epimorphic. In order to have the functor G well defined with G(B) the canonical split epimorphism

for every object B in $\mathbf {B}$, the pair of morphisms $(\left\langle 0, 1\right\rangle , \left\langle 1, 1\right\rangle )$ must be jointly epimorphic. Concrete examples can be constructed by taking $\mathbf {B}$ equipped with a forgetful (faithful and preserving binary products) functor into the category of algebras with one constant and one binary operation, say (X, 0,  / ), satisfying the conditions

$$\begin{aligned} x/y&=x'/y \implies x=x' \end{aligned}$$

(4)

$$\begin{aligned} x/x&=y/y \end{aligned}$$

(5)

where the homomorphisms are the map**s $f:X \longrightarrow X'$ such that

$$\begin{aligned} f(x/y)&=f(x)/f(y) \end{aligned}$$

(6)

$$\begin{aligned} f(0)&=0. \end{aligned}$$

(7)

In this case, the left adjoint to G, which is comparable to the semidirect product construction in the monadic approach of internal actions, is simply the projection of the middle object of a split extension. Some attempts were done in order to find a categorical notion of semidirect product (see for example [1]). We believe that, in the setting of an action-system (1) as we proposed in this paper, the notion of semidirect product for an object A in $\mathbf {A}$ is the object F(A) in $\mathbf {B}$, with F the left adjoint of the functor G, when it exists (this agrees with the notion of semidirect product introduced in [3]).

Our main result is presented in Sect. 6. It gives sufficient conditions to have the desired categorical equivalence between Whitehead sequences and internal groupoids. This result relies on several other more technical results, such as a simplicial construction (Proposition 2), or an induced functor from certain kind of Whitehead sequences into the category of internal categories (Theorem 1) which are developed on Sects. 4 and 5.

Finally, in Sect. 7, we present the case when the category $\mathbf {B}$ is pointed and protomodular.

2 Basic definitions and properties

Let $\mathbf {B}$ be a pointed category.

Definition 1

A (right) patch in $\mathbf {B}$ is a cospan

in which the pair (k, s) is jointly epimorphic and there exists a (necessarily unique) morphism $p:{Y\longrightarrow B}$ with $ps=1_B$ and $pk=0$. It will be written as a triple (k, s, p) in spite of the fact that the morphism p is uniquely determined.

Similarly we can define a left patch (by requiring the existence of a morphism $q:{Y\longrightarrow X}$ with $qk=1_X$ and $qs=0$) but, since here we are going to deal only with right patches we will call them just patches.

Two examples that illustrate the notion can be obtained as follows. Let $\mathbf {B}$ be a pointed category with kernels and pushouts.

• 1. Every coproduct diagram in $\mathbf {B}$ is a patch

  

• 2. If we denote by $k_0:{B\flat X\longrightarrow X+B}$ the kernel of $[0,1]:{X+B\longrightarrow B}$ and let $\eta _X:{X\longrightarrow B\flat X}$ be such that $k_0\eta _X=\iota _X$, then every morphism $\xi :{B\flat X\longrightarrow X}$ satisfying the condition $\xi \eta _X=1_X$ induces, by taking the pushout of $\xi$ and $k_0$, a patch in $\mathbf {B}$ as illustrated by

  

  The needed morphism p is uniquely determined by $p\iota _2=[0,1]$ and $p\iota _1=0$. Moreover, since $(Q,\iota _1,\iota _2)$ is a pushout diagram, we have that $(\iota _1,\iota _2)$ is a jointly epimorphic pair. In order to prove that the pair $(\iota _1,\iota _2\iota _B)$ is jointly epimorphic we observe that $\iota _1=\iota _2\iota _X$, indeed

  $$\begin{aligned} \iota _1=\iota _1\xi \eta _X=\iota _2k_0\eta _X=\iota _2\iota _X, \end{aligned}$$

  and from here it follows that $(X,Q,B,\iota _1,\iota _2\iota _B,p)$ is a patch.

It will be relevant for us to differentiate the patches that are exact and the patches that are stable under pullback, according to the following definitions:

Definition 2

A patch (X, Y, B, k, s, p) in $\mathbf {B}$ is said to be an exact patch if the morphism $k:{X\longrightarrow Y}$ is the kernel of the morphism $p:{Y\longrightarrow B}$.

The morphisms $\xi :{B\flat X\longrightarrow X}$, in the second example above, that induce an exact patch are precisely the strict actions in the sense of [14], see also [7]. Moreover, in the category of pointed sets and in the category of abelian groups every coproduct diagram is an exact patch. Indeed, in both cases, we have that $\iota _X$ is the kernel of [0, 1].

Definition 3

A patch (X, Y, B, k, s, p) in $\mathbf {B}$ is said to be a stable patch if for every $h:{Z\longrightarrow B}$, the pullback of p along h exists in $\mathbf {B}$, and the induced cospan

is a patch in $\mathbf {B}$.

Clearly, if a patch is exact and stable, then every patch it induces is exact.

In the category of abelian groups every coproduct diagram is a stable patch. This is not true in the category of pointed sets. Indeed any cospan

which is obtained by taking the pullback of the morphism

$$\begin{aligned}{}[0,1]:{X+B\longrightarrow B} \end{aligned}$$

along a given morphism $h:{Y\longrightarrow B}$ is a patch if and only if the kernel of h is trivial.

Let $I:{\mathbf {A}\longrightarrow \mathbf {B}}$ be a functor. We recall that:

• A morphism $\alpha :{E\longrightarrow A}$ in $\mathbf {A}$ is cartesian if for every $g:{W\longrightarrow A}$ in $\mathbf {A}$ and every $h:{I(W)\longrightarrow I(E)}$ in $\mathbf {B}$, with $I(\alpha )h=I(g)$, there exists a unique $u:{W\longrightarrow E}$ in $\mathbf {A}$ such that $\alpha u=g$ and $I(u)=h$. We also say that $\alpha$ is I-cartesian.

• When every morphism in $\mathbf {B}$ can be lifted to an I-cartesian morphism in $\mathbf {A}$ we say that the functor I is a fibration. More specifically, the functor I is a fibration if for every A in $\mathbf {A}$ and $p:{Y\longrightarrow IA}$ in $\mathbf {B}$ there exists a cartesian morphism (called the cartesian lifting of p along A), $\alpha :{E\longrightarrow A}$, with $I(\alpha )=p$.

From now on we consider, other than the functor I another functor J. Let (I, J) be an ordered pair of functors $I,J:{\mathbf {A}\longrightarrow \mathbf {B}}$, which will be displayed as

In this context we consider a special class of morphisms in $\mathbf {A}$ that we call organic (due to the fact that their components under I and under J form an exact patch). Moreover, we observe that the notions of patch and exact patch are stable (in the obvious sense) under isomorphisms $Y \cong Y'$.

Definition 4

A morphism $f:{A\longrightarrow E}$ in $\mathbf {A}$ is said to be a organic morphism (or (I, J)-organic) if $J(E)\cong I(E)$ and the cospan

is an exact (right) patch in $\mathbf {B}$.

Finally, we complete the setting by introducing another ingredient—the Whitehead sequence—and the definition of L-condition and of action-system.

Let (I, G, J) be an ordered triple of functors, displayed as

(8)

and such that $IG=1_{\mathbf {B}}=JG$.

Definition 5

A Whitehead sequence is a triple (A, u, v) where A is an object in $\mathbf {A}$, while u and v are morphisms in $\mathbf {A}$, of the form

(9)

satisfying the following conditions

$$\begin{aligned} I(u)= & {} 1_{IA}\end{aligned}$$

(10)

$$\begin{aligned} J(v)= & {} 1_{JA}\end{aligned}$$

(11)

$$\begin{aligned} I(v)= & {} J(u). \end{aligned}$$

(12)

Definition 6

We say that the L-condition holds for the triple of functors (I, G, J) when for every diagram of solid arrows

with $I(\beta )=I(f)$, $J(\alpha )=J(g)$, $I(\alpha )J(f)=I(g)J(\beta )$ and $\alpha \beta =1_A$, if $\alpha$ is cartesian and f is organic then there exists a unique Whitehead sequence $(f',g')$ such that $\alpha g'=g$ and $f'\beta =f$.

Definition 7

A triple of functors (I, G, J) is called an action-system of $\mathbf {A}$ over $\mathbf {B}$ when:

• 1. The functor I is a fibration and $J(\alpha )$ is an isomorphism whenever $\alpha$ is an I-cartesian morphism;

• 2. For every A in $\mathbf {A}$ there exists an object $Y\in \mathbf {B}$ and a morphism

  $$\begin{aligned} f:{A\longrightarrow G(Y)} \end{aligned}$$

  such that f is organic and, moreover, it is universal from A to G;

• 3. The L-condition holds.

In general, in order to have an action-system, we can always take $\mathbf {A}$ to be the category of all stable and exact patches in $\mathbf {B}$. This example is further developed in the last section.

The three main examples that have motivated these definitions, that is groups, abelian groups and pointed sets, are presented in some detail in the following section.

Some immediate consequences of the definitions are the following.

Proposition 1

Let (I, G, J) be an action-system of $\mathbf {A}$ over $\mathbf {B}$. Then

• (i) The functor G has a left adjoint;

• (ii) There exists a unique natural transformation $\pi :{1_{\mathbf {A}}\longrightarrow GI}$ such that for every object A in $\mathbf {A}$, $I(\pi _A)=1_{IA}$ and $J(\pi _A)=0$;

• (iii) There exists a functor $\mathbf {A}\longrightarrow \mathsf {Pt}(\mathbf {B})$ such that every split epimorphism associated to an object A in $\mathbf {A}$, together with its kernel, is an exact patch;

• (iv) For every Whitehead sequence (A, u, v) there exists, up to isomorphism, a unique diagram in $\mathbf {A}$

  

  in which $\eta _A$ is the universal arrow from A to the functor G, $\alpha$ is a cartesian morphism, $IE\cong FA$, and such that

  $$\begin{aligned} GI(\alpha )\eta _A= & {} u\\ \alpha \beta= & {} 1_A\\ I(\beta )= & {} I(\eta _A)\\ \mu \beta= & {} \eta _A\\ I(\mu )= & {} 1_{FA}; \end{aligned}$$

• (v) Every Whitehead sequence (A, u, v) induces another Whitehead sequence, say $(E,\mu ,\nu )$, with the property that there exists a cartesian split epimorphism

  $$\begin{aligned} \alpha :{E\longrightarrow A} \end{aligned}$$

  (with a section $\beta$) such that $\mu \beta =\eta _A$ and $\alpha \nu =vGJ(\alpha )$;

• (vi) Every Whitehead sequence (A, u, v) induces an infinite sequence of cartesian split epimorphisms

  

  which is uniquely determined by $GI(\alpha _1)\eta _{A}=u$ and if $\beta _i$ is the section of $\alpha _i$, for every $i=1,2,\ldots$, by the equations

  $$\begin{aligned} \alpha _i\beta _i= & {} 1_{A_{i-1}}\\ I(\beta _i)= & {} I(\eta _{A_{i-1}})\\ GI(\alpha _{i+1})\eta _{A_i}\beta _{i}= & {} \eta _{A_{i-1}}\\ I(\alpha _{i+1})I(\eta _{A_i})= & {} 1_{IA_i}. \end{aligned}$$

Proof

• (i) Since, by Definition 7(2), for every object A in $\mathbf {A}$, there exists an object FA in $\mathbf {B}$ and an arrow $\eta _A:{A\longrightarrow GFA}$ which, in particular, is universal from A to the functor G, it follows directly from Theorem 2(ii), on page 83 of [10], that G is (the right) part of an adjuntion $(F,G,\eta ,\varepsilon )$.

• (ii) Using the previous adjunction $(F,G,\eta ,\varepsilon )$, we observe that the existence of a morphism $\pi _A:{A\longrightarrow GIA}$ such that $I(\pi _A)=1_{IA}$ and $J(\pi _A)=0$, is equivalent to the existence of a morphism

  

  such that $\varepsilon _{IA}F(\pi _A)I(\eta _A)=1_{IA}$ and $\varepsilon _{IA}F(\pi _A)J(\eta _A)=0$. The assumption [see Definitions 7(2), 4 and 1] that $\eta _A:{A\longrightarrow GFA}$ is a patch guarantees the existence, as well as the uniqueness, of $\varepsilon _{IA}F(\pi _A)$ and hence of $\pi _A$. The naturality of $\pi$ follows from the naturality of $\eta$ and $\varepsilon$. Further details on this construction can be found in [13].

• (iii) Using again the adjunction $(F,G,\eta ,\varepsilon )$ and the natural transformation

  $$\begin{aligned} \pi :{1_{\mathbf {A}}\longrightarrow GI}, \end{aligned}$$

  from the two items above, we observe that to every A in $\mathbf {A}$ we can associate the split extension

  

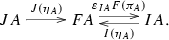
  Recall that the category $\mathsf {Pt}(\mathbf {B})$ is the category whose objects are split epimorphisms (with specified section) and whose morphisms are the squares that preserve the sections. Further details about this construction can be found in [13] (see also Sect. 4 of this paper).

• (iv) Let (A, u, v) be a Whitehead sequence. We will first show how to obtain the morphisms $\alpha$, $\beta$ and $\mu$ and then show that they are uniquely determined by the properties required. The morphism $\alpha :{E\longrightarrow A}$ is the cartesian lifting of the morphism $\varepsilon _{IA}F(u):{FA\longrightarrow IA}$, which exists because the functor I is a fibration, and it is such that $IE=FA$ and $I(\alpha )=\varepsilon _{IA}F(u)$ or equivalently, via the adjunction, $GI(\alpha )\eta _A=u$. The morphism $\beta :{A\longrightarrow E}$ is obtained as the unique morphism such that $\alpha \beta =1_A$ and $I(\beta )=I(\eta _A)$ which exists because $\alpha$ is cartesian and $I(\alpha )I(\eta _A)=1_A$ (this is a consequence of $I(u)=1_{IA}$). The morphism $\mu$ is obtained by applying the L-condition [Definitions 7(3) and 6] to the diagram

  

  which satisfies the needed conditions to guarantee the existence of $\mu$ such that $\mu \beta =\eta _A$ and $I(\mu )=1_{FA}$. It remains to show that $\mu$ is uniquely determined by this two conditions. The morphism $\nu$ is uniquely determined because $\alpha$ is cartesian and hence, by the uniqueness property in the L-condition, we conclude that also $\mu$ is uniquely determined.

• (v) It follows from the Whitehead sequence constructed in the previous item.

• (vi) Having a Whitehead sequence (A, u, v) and using the construction on the previous item we obtain $\alpha _1$ and $\beta _1$ together with a new Whitehead sequence $(A_1,\mu _1,\nu _1)$. This gives us the first element of the infinite sequence. We can continue the sequence by replacing $(A_0,u,v)$ with $(A_1,\mu _1,\nu _1)$ and thus successively iterate in order to obtain $(A_{n},\mu _{n},\nu _{n})$ for an arbitrary n. At each level $i=1,2,\ldots$, the morphism $\beta _i$ is completely determined by $\alpha _i\beta _i=1_{A_{i-1}}$ and $I(\beta _i)=I(\eta _{A_{i-1}})$. In the same way the morphism $\alpha$, being a cartesian morphism, is completely determined by $GI(\alpha _{i+1})\eta _{{A_i}}=\mu _i$. But, since $\mu _i$ itself is determined by $\mu _i\beta _i=\eta _{A_{i-1}}$ and $I(\mu _i)=1_{I(A_i)}$, the two equations

  $$\begin{aligned} GI(\alpha _{i+1})\eta _{A_i}\beta _{i}= & {} \eta _{A_{i-1}}\\ I(\alpha _{i+1})I(\eta _{A_i})= & {} 1_{IA_i} \end{aligned}$$

  uniquely determine $\alpha _i$.

$\square$

We observe that there exists a functor $\mathbf {A}\longrightarrow \mathsf {Pt}(\mathbf {B})$

We are now going to see the main examples of action-systems that motivated the definitions above.

3 Pointed sets, groups and abelian groups

3.1 Pointed sets and abelian groups

Let $\mathbf {B}$ be the category of abelian groups and $\mathbf {A}$ the category $\mathbf {B}\times \mathbf {B}$ with I the second projection, J the first projection and G the diagonal functor. The triple of functors (I, G, J) is an action system of $\mathbf {A}$ over $\mathbf {B}$. As we will see, the same is true for the category of pointed sets and, more generally, in any category $\mathbf {B}$ provided it is pointed, has binary coproducts and such that, for every two objects X and B, the morphism $\iota _X:{X\longrightarrow X+B}$ is the kernel of $[0,1]:{X+B\longrightarrow B}$.

Some simple observations presented next to support our claims are to be compared with the respective items from Definition 7 of an action-system:

• 1. the functor I is a fibration and $J(\alpha )$ is an isomorphism if and only if $\alpha$ is I-cartesian; indeed, $\alpha =(\alpha _1,\alpha _2)$ is I-cartesian if and only if $\alpha _1$ is an isomorphism;

• 2. every $A=(X,B)$ in $\mathbf {A}$ has an object $X+B$ in $\mathbf {B}$ and an arrow

  $$\begin{aligned} (\iota _X,\iota _B):{(X,B)\longrightarrow (X+B,X+B)} \end{aligned}$$

  which is organic and universal;

• 3. to check that the L-condition holds we have to consider a diagram of solid arrows of the form

  

  where we assume that $\alpha$ is cartesian, which means that, up to an isomorphism, we can write it as $\alpha =(1_X,\alpha _2)$, and (k, s) is an exact patch, which means that (k, s) is a jointly epimorphic cospan and there exists $p:{Y\longrightarrow B}$ with $ps=1_B$ and k the kernel of p; the remaining assumptions only give $\alpha _2k=h$ and we easily confirm the existence of a unique Whitehead sequence (dashed arrows) satisfying the desired equations. Note that a Whitehead sequence (A, u, v), in this case, is completely determined by either I(v) or J(u). In other words, it is completely determined by a morphism $h:{X\longrightarrow B}$ and it is of the form

  

3.2 Groups

Another example, in fact the main example since it was the main motivation of this work, is the case where $\mathbf {B}$ is the category of groups and $\mathbf {A}$ is the category of group actions.

Classically, an action of a group B on a set X is a map $\xi :{B \times X \longrightarrow X}$ assigning to every pair (b, x) in $B \times X$ an element $b\cdot x$ in X such that $1\cdot x=x$ and $(bb')\cdot x=b\cdot (b'\cdot x)$. Equivalently it may be presented as a group homomorphism

$$\begin{aligned} \phi :{ B \longrightarrow {{\mathrm{Aut}}}(X)} \end{aligned}$$

from the group B to the automorphism group of X. Another approach consists on considering the group B as a one object groupoid and an action as a functor

$$\begin{aligned} B \longrightarrow \mathsf {Set}\end{aligned}$$

assigning the set X to the (only) object of the groupoid B and an automorphism of X to each morphism in the groupoid B (that is to each element of the group B). A convenient notation that illustrates this situation is the following one.

In this language the conditions above are written as

$$\begin{aligned} X_1=1_{X_{\circ }} \end{aligned}$$

and

$$\begin{aligned} X_{b'} X_{b} =X_{b'b}. \end{aligned}$$

Again, in classical terms, a morphism between actions is a pair (f, g)

in which $g:{B\longrightarrow B'}$ is a group homomorphism while $f:{X\longrightarrow X'}$ is a map, such that

Equivalently, it may be considered as a morphism in a comma-category

where $f:X \longrightarrow X' g$ is a natural transformation.

It is clear that instead of the category $\mathsf {Set}$ we can consider other categories, obtaining there an appropriate notion of group action. In particular, if we consider the category $\mathsf {Grp}$ of groups we obtain the category of group actions on groups.

Let us consider now the case of an action-system where $\mathbf {B}$ is the category of groups and $\mathbf {A}$ is the category of group actions on groups. An object A in $\mathbf {A}$ is a pair (X, B) in which B is a group (considered as a one object groupoid) and $X:{B\longrightarrow \mathsf {Grp}}$ is a functor. The morphisms are the pairs (f, g) with $g:{B\longrightarrow B'}$ a group homomorphism and $f:{X\longrightarrow X'g}$ a natural transformation.

In this case I is the second projection, J is the first projection (in the sense that $J(X,B)=X_{\circ }$) and, for every group B, $G(B)=(\bar{B},B)$ where $\bar{B}:{B\longrightarrow \mathsf {Grp}}$ corresponds to the action by conjugation of B onto itself, that is $\bar{B}_\circ =B$ and $\bar{B}_b(b')=bb'b^{-1}$.

It follows that (I, G, J) is an action-system of $\mathbf {A}$ over $\mathbf {B}$ in which the Whitehead sequences are precisely the crossed modules of groups. Indeed it is not difficult to check that a Whitehead sequence is determined by a pair (A, h) where A is an object in $\mathbf {A}$, $h:JA \longrightarrow IA$ is a morphism in $\mathbf {B}$, and there exist two morphisms u and v

such that

$$\begin{aligned} I(u)=1_{IA},\ J(v)=1_{JA}, \ I(v)=J(u)=h. \end{aligned}$$

In other words a Whitehead sequence becomes a property on the object A and the morphism h which is equivalent to the two well-known conditions for a crossed module, namely

$$\begin{aligned} h(b\cdot x)=bh(x)b^{-1} \end{aligned}$$

(13)

$$\begin{aligned} h(x)\cdot x' =x+x'-x \end{aligned}$$

(14)

in which we write $X=JA$ additively, $B=IA$ multiplicatively and denote by $b\cdot x=X_b(x)$ the result of the action of the element b in B on the element x in X. Condition (13) is equivalent to the existence of u, while condition (14) is equivalent to the existence of v.

The functor I is a fibration: the cartesian lifting of a morphism $g:{B'\longrightarrow B}$ in $\mathbf {B}$ along an action (X, B) in $\mathbf {A}$ is given by

where 1 denotes the identity natural transformation for the functor Xg. If $\alpha$ is a cartesian morphism in $\mathbf {A}$ then $J(\alpha )$ is an isomorphism in $\mathbf {B}$. To each action (X, B) in $\mathbf {A}$ we can associate the semidirect product diagram

in which $F(X,B)=X_{\circ }\rtimes B$ is the set of pairs $(x,b)\in X_{\circ }\times B$ with the operation

$$\begin{aligned} (x,b)+(x',b')=(x+X_b(x'),bb') \end{aligned}$$

and k, s are the canonical injections. This diagram is an exact patch and, moreover, the pair (k, s) can be seen as a universal arrow

$$\begin{aligned} (k,s):{(X,B)\longrightarrow GF(X,B)}. \end{aligned}$$

In order to conclude that the triple (I, G, J) is an action-system of $\mathbf {A}$ over $\mathbf {B}$ it remains to analyse the L-condition. In this case it simplifies to a diagram in $\mathbf {A}$ as the one displayed below

in which $\alpha _2s=1_B$ and $\alpha _2k=h$. This diagram comes from assuming that $\alpha =(1_{X\alpha _2},\alpha _2)$ is a cartesian morphism and that all the conditions in the statement of the L-condition are satisfied. The extra piece of information is the assumption that $f=(k,s)$ is a organic morphism. From this we have to show that (1, k) and (k, 1) are morphisms in $\mathbf {A}$. The fact that (1, h) is a morphism implies that (in fact, it is equivalent to) Xh being equal to the conjugation action on $X_{\circ }$, or in other words $Xh=\bar{X}_{\circ }$. From here we can conclude that (1, k) is a morphism since we have $X\alpha _2k=Xh=\bar{X}_{\circ }$.

The requirement that (k, 1) is a morphism in $\mathbf {A}$ is equivalent to the requirement that

$$\begin{aligned} k(\alpha _2(y)\cdot x')=y+k(x')-y \end{aligned}$$

holds for all $x'\in X_{\circ }$ and all $y\in Y$ (note that we write $X_{\alpha _2(y)}(x')$ as $\alpha _2(y)\cdot x'$ in order to simplify notation). To prove this condition, we now make use of the assumption that the morphism (k, s) is a organic morphism, which means that the cospan

is an exact patch and hence, every element $y\in Y$ can be written in a unique way as $y=(x,b)$ with $x\in X_{\circ }$ and $b\in B$ and, moreover, $\alpha _2(y)=h(x)+b$. It is now an easy calculation to verify the desired condition since we have $h(x)\cdot x'=x+x'-x$ because $Xh=\bar{X}_{\circ }$.

4 A simplicial construction

In this section we introduce a simplicial construction which will be used in the proof of the main result. We construct a simplicial object in a category $\mathbf {B}$ from a sequence of cartesian split epimorphisms in a category $\mathbf {A}$, which is equipped with a realization functor into the category of points in $\mathbf {B}$.

Let $\mathbf {A}$ and $\mathbf {B}$ be two categories and suppose that it is given a functor

$$\begin{aligned} \mathbf {A}\longrightarrow \mathsf {Pt}(\mathbf {B}) \end{aligned}$$

from the category $\mathbf {A}$ into the category of points (i.e. split epimorphisms) in $\mathbf {B}$. We call such functor a realization functor since it allows to consider (or realise) an object in $\mathbf {A}$ as a split epimorphism in $\mathbf {B}$. Giving such a functor is to give an ordered pair of functors

$$\begin{aligned} F,I:\mathbf {A}\longrightarrow \mathbf {B}\end{aligned}$$

(we think of F as the domain functor and of I as the codomain functor) together with two natural transformations

$$\begin{aligned} \pi :F \longrightarrow I \quad \text {and} \quad \iota :I\longrightarrow F \end{aligned}$$

which are related by the following condition

$$\begin{aligned} \pi \iota =1_I. \end{aligned}$$

With this data, $(F,I,\pi ,\iota )$, we are able to associate to every A in $\mathbf {A}$ a split epimorphism in $\mathbf {B}$ of the form

In the proof of the following proposition we explain how to construct a simplicial object in the category $\mathbf {B}$, using the canonical split epimorphisms associated to each object A in $\mathbf {A}$, together with a sequence of cartesian split epimorphisms in $\mathbf {A}$.

Proposition 2

Let $(F,I,\pi ,\iota ):{\mathbf {A}\longrightarrow \mathsf {Pt}(\mathbf {B})}$ be a functor from $\mathbf {A}$ into the category of split epimorphisms in $\mathbf {B}$. Suppose that for every split epimorphism in $\mathbf {A}$,

if $\alpha$ is I-cartesian then the pair $(F\beta ,\iota _E)$ is jointly epimorphic. Then, every sequence of split epimorphisms in $\mathbf {A}$ of the form

(15)

in which $\alpha _n$ is cartesian for all n, and

(16)

induces a simplicial object in $\mathbf {B}$.

Note that we denote $\pi _{A_n}$ and $\iota _{A_n}$ by $\pi _n$ and $\iota _n$ and omit some parenthesis, so that I(A) becomes IA.

Proof

The simplicial object has the following form

in which $F^2(\alpha _1)=F(F(\alpha _1)^*)$ with $F(\alpha _1)^*$ the unique morphism in $\mathbf {A}$ such that $\alpha _1 F(\alpha _1)^*=\alpha _1\alpha _2$ and $I(F(\alpha _1)^*)=F(\alpha _1)$, as illustrated in the following picture

that exists because $\alpha _1$ is I-cartesian and the triangle on the right is commutative (see Eq. (17) below). Similarly, $F^2(\beta _1)=F(F(\beta _1)^*)$ with $F(\beta _1)^*$ the unique morphism in $\mathbf {A}$ such that $\alpha _2 F(\beta _1)^*=1_{A_1}$ and $I(F(\beta _1)^*)=F(\beta _1)$, as displayed in the following picture

In a similar fashion we can obtain $F^i(\alpha _{n-i+1})$ and $F^i(\beta _{n-i+1})$ for all i up to n. The details are omitted since we will not work with n greater than 2.

The necessary equations for the construction of $F^i(\alpha _{n-i+1})$ are satisfied because the pair

$$\begin{aligned} (F(\beta _n), \iota _n) \end{aligned}$$

is jointly epimorphic for all n. Indeed, for example, the construction of $F^2(\alpha _{n-1})$ depends on the equation

$$\begin{aligned} I(\alpha _n)F(\alpha _n)=I(\alpha _n\alpha _{n+1}) \end{aligned}$$

(17)

which is true because we have

$$\begin{aligned} I(\alpha _n)F(\alpha _n)F(\beta _n)=I(\alpha _n)=I(\alpha _n\alpha _{n+1})F(\beta _n) \end{aligned}$$

and (since $\iota$ is natural)

$$\begin{aligned} I(\alpha _n)F(\alpha _n)\iota _n=I(\alpha _n)\iota _{n-1}I(\alpha _n)=I(\alpha _n)=I(\alpha _n\alpha _{n+1})\iota _n. \end{aligned}$$

Using the same technique it is possible to check that all the simplicial equations are satisfied, a routine but demanding task. $\square$

Let us now consider a simple example of this simplicial construction.

Let $\mathbf {B}$ be a pointed category with binary coproducts. Take $\mathbf {A}$ to be the category $\mathbf {B}\times \mathbf {B}$ and, for every pair (X, B) of its objects, define

$$\begin{aligned} I(X,B)=B\\ F(X,B)=X+B\\ \pi _{X,B}=[0,1]:{X+B\longrightarrow B}\\ \iota _{X,B}=\iota _B:{B\longrightarrow X+B}. \end{aligned}$$

In this case the functor I is a fibration and a morphism $\alpha =(\alpha _1,\alpha _2)$ in $\mathbf {A}$ is cartesian if and only if $\alpha _1$ is an isomorphism. Moreover, for any split epimorphism

in $\mathbf {A}$, if $\alpha _1$ is an isomorphism then the cospan

is jointly epimorphic (observe that $(\beta _1+\beta _2)\iota _{A_1}\alpha _1=\iota _{E_1}$).

Now, in the particular case of abelian groups, a sequence such as the one displayed in (15) with $\alpha _n$ cartesian for all n and satisfying Eq. (16) is completely determined, up to isomorphism, by a morphism

$$\begin{aligned} h:{X\longrightarrow B} \end{aligned}$$

and it is of the following form

$$\begin{aligned} A_0= & {} (X,B)\\ A_1= & {} (X,X+B)\\ A_2= & {} (X,X+(X+B))\cong (X,2X+B)\\ A_n= & {} (X,nX+B)\\ \alpha _1= & {} (1_X,[h,1_B])\\ \beta _1= & {} (1_X,\iota _B)\\ \alpha _2= & {} (1_X,[\iota _X,1_{X+B}])\\ \beta _2= & {} (1_X,\iota _{X+B})\\ \alpha _{n+1}= & {} (1_X,[\iota _X,1_{nX+B}])\\ \beta _{n+1}= & {} (1_X,\iota _{nX+B}). \end{aligned}$$

In other words, it is completely determined by the first element of the sequence. This is not true in general but it gives a way to generate examples. Going back again to a category $\mathbf {B}$, pointed with binary coproducts, we can consider a sequence of the form just describd and, by Proposition 2, we are able to construct the following simplicial object

(18)

which, for simplicity, we truncated at level 3.

5 The category of Whitehead sequences

Let (I, G, J) be a triple of functors as displayed in (8) such that

$$\begin{aligned} IG=1_{\mathbf {B}}=JG. \end{aligned}$$

We consider the category $\mathsf {W}(\mathbf {A})$ whose objects are the Whitehead sequences in $\mathbf {A}$ (see Definition 5). A morphism $f:{(A,u,v)\longrightarrow (A',u',v')}$ between two Whitehead sequences is a morphism $f:{A\longrightarrow A'}$ in $\mathbf {A}$ such that the two squares below are commutative

When, moreover, the triple of functors (I, G, J) is an action-system of $\mathbf {A}$ over $\mathbf {B}$ (definition 7) and denoting by $(F,G,\eta ,\varepsilon )$ the adjunction in which F is the left adjoint of G [Proposition 1(i)], then we can define a full subcategory of $\mathsf {W}(\mathbf {A})$, denoted by $\mathsf {W}^{*}(\mathbf {A})$, as follows: a Whitehead sequence (A, u, v) is an object in $\mathsf {W}^{*}(\mathbf {A})$ if every cartesian morphism $\alpha :{E\longrightarrow A}$ in its induced sequence of cartesian morphisms [as in Proposition 1(vi)] has the property that the square

is a pullback square. The morphisms $\pi _E:{E\longrightarrow GIE}$ and $\pi _A:{A\longrightarrow GIA}$ are the components of the natural transformation that is obtained as in the item (ii) of Proposition 1. For example, in the case of the category of groups, together with the action-system of group actions over it (as illustrated in Sect. 3), we have that to each cartesian morphism $\alpha :{E\longrightarrow A}$ its associated square in the sense above is of the form

which is always a pullback square. Indeed, it simply follows from the fact that $\alpha$ is cartesian and hence $J(\alpha )$ is an isomorphism.

We denote by $\mathsf {Simp}(\mathbf {B})$ the category of internal simplicial objects in $\mathbf {B}$ and consider the category of internal categories in $\mathbf {B}$, $\mathsf {Cat}(\mathbf {B})$, as a full subcategory of $\mathsf {Simp}(\mathbf {B})$.

Theorem 1

Let (I, G, J) be an action-system of $\mathbf {A}$ over $\mathbf {B}$. There is a functor from $\mathsf {W}(\mathbf {A})$ into $\mathsf {Simp}(\mathbf {B})$ such that its restriction to $\mathsf {W}^{*}(\mathbf {A})$ factors through $\mathsf {Cat}(\mathbf {B})$

Proof

Following Proposition 1, to every Whitehead sequence (A, u, v) we can associate an infinite sequence of cartesian split epimorphisms $\alpha _i$, with section $\beta _i$,

such that $I(\alpha _1)=\varepsilon _{IA}F(u)$ and for every $i=1,2,\ldots$

$$\begin{aligned} I(\alpha _{i+1})= & {} \varepsilon _{IA_i}F(\mu _i)\\ \alpha _i\beta _i= & {} 1_{A_{i-1}}\\ I(\beta _i)= & {} I(\eta _{A_{i-1}}). \end{aligned}$$

Here, $(F,G,\eta ,\varepsilon )$ is the adjunction as in Proposition 1(i), and $(A_1,\nu _1,\mu _1)$ is the Whitehead sequence obtained (as in item (v) of Proposition 1) from the Whitehead sequence (A, u, v). Similarly we obtain $(A_{i+1},\nu _{i+1},\mu _{i+1})$ from $(A_i,\nu _i,\mu _i)$ for all $i\in \mathbb {N}$.

It follows that

$$\begin{aligned} I(A_i)\cong & {} F(A_{i-1})\\ I(\alpha _i)I(\eta _{A_{i-1}})= & {} I(\alpha _i)I(\beta _{i})=1_{IA_{i-1}}\\ I(\alpha _{i+1})F(\beta _i)= & {} \varepsilon _{A_i}F(\mu _i)F(\beta _i)=\varepsilon _{IA_i}F(\mu _i\beta _i)\\= & {} \varepsilon _{IA_i}F(\eta _{A_{i-1}})=\varepsilon _{FA_{i-1}}F(\eta _{A_{i-1}})\\= & {} 1_{FA_{i-1}}=1_{IA_i}. \end{aligned}$$

In order to make use of Proposition 2 with the sequence of cartesian morphisms as constructed above, the natural transformation $\pi _i=\varepsilon _{IA_i}F(\pi _{A_i})$ (with $\pi _{A_i}$ obtained as in item (ii) of Proposition 1) and with $\iota _i=I(\eta _{A_i})$ we have to verify that the pair $(F(\beta _i),I(\eta _{A_i}))$ is jointly epimorphic. This is a consequence of the fact that, for each $A\in \mathbf {A}$, $\eta _{A}$ is a organic morphism (Definition 4) and hence the cospan $(J(\eta _A),I(\eta _A))$ is jointly epimorphic. In particular, this implies that $(F(\beta _i),I(\eta _{A_i}))$ is jointly epimorphic because each $J(\beta _i)$ is an isomorphism (since $\alpha$ is cartesian then $J(\alpha )$ is an isomorphism and so also $J(\beta )$ is an isomorphism) and we have

$$\begin{aligned} J(\eta _{A_i})=F(\beta _i) J(\eta _{A_i-1})J(\beta _i)^{-1}. \end{aligned}$$

From here we can construct a simplicial object, in the same way as it was done in the proof of Proposition 2, which is displayed up to level 3 (to compare it with the notion of an internal category we will not need to go further) as follows:

Again, checking the simplicial conditions is a routine (although a demanding) task.

This shows that we can assign a simplicial object to every Whitehead sequence and, moreover, that this construction is functorial. Indeed, if

$$\begin{aligned} f:{(A,v,u)\longrightarrow (A',u',v')} \end{aligned}$$

is a morphism between Whitehead sequences then it can be lifted to the level of infinite sequences of cartesian split epimorphisms so that it respects the simplicial equations. This is possible because the morphisms $\alpha _i$ are cartesian and we will have

for all $i\in \mathbb {N}$ with $f_0=f$.

This gives us a functor from $\mathsf {W}(\mathbf {A})$ into $\mathsf {Simp}(\mathbf {B})$. In order to be able to compare the simplicial structure defined above with the one of an internal category, we now give a diagram with the standard notation for an internal category object in $\mathbf {B}$. An internal category in $\mathbf {B}$ is a diagram of the form

(19)

where $C_0$ and $C_1$ are, respectively, the object of objects and the object of morphisms, while d, e, c are, respectively, domain, identity, and codomain; $C_2$ is the object of composable pairs, obtained by the following pullback (with $p_1$, $p_2$ the canonical projections and $e_1$, $e_2$ the induced inclusions)

Similarly, $C_3$ is the object of composable triples, specifically calculated for generalized objects as

$$\begin{aligned} C_3=\{((f,g),(h,k)) {\mid } (f,g),(h,k) \in C_2, g=hk\} \end{aligned}$$

in other words it is the object in the following pullback diagram, of m along $p_2$

Note that $C_3$ can also be given by the following pullback

which is equivalent, being then $C_3$

To the reader not familiar with the above notation for internal categories, and in order to easily compare it with the more standard simplicial one, it may be helpful to consider the particular case where $C_0=1$ and write $m(x,y)=xy$, in this case we have

$$\begin{aligned} p_2(x,y)= & {} y \nonumber \\ p_1(x,y)= & {} x \nonumber \\ e_1(x)= & {} (x,1) \nonumber \\ e_2(y)= & {} (1,y) \nonumber \\ q_2(x,y,z)= & {} (y,z) \nonumber \\ q_1(x,y,z)= & {} (x,y) \nonumber \\ m_1(x,y,z)= & {} (x,yz) \nonumber \\ m_2(x,y,z)= & {} (xy,z) \nonumber \\ i_1(x,y)= & {} (x,y,1) \nonumber \\ i_2(y,z)= & {} (1,y,z) \nonumber \\ i_0(x,z)= & {} (x,1,z). \end{aligned}$$

(20)

Table 1 translates the (relevant) simplicial equations into the definition of internal category. The first column contains the equation in the context of an internal category; the middle column presents the equivalent simplicial equation, obtained by the simplicial construction above; the last column gives the corresponding equation in the context of $\mathbf {A}$ and $\mathsf {W}(\mathbf {A})$ where we can easily see why the equation is true: lines 1 to 6, by definition; lines 7, 10 and 11 by naturality; lines 9 and 12, see Eq. (17); it remains to explain line 8—it follows from the fact that $I(\mu )=1=I(\pi _{A_1})$ and $\pi _0J(\eta _A)=0=J(\pi _{A_1})$, since $\eta _A$ is organic for every A in $\mathbf {A}$. $\square$

Table 1 Translation between equations: from the language of internal categories, to simplicial objects, to Whitehead sequences

We now have the following: if the squares

are pullbacks, then the simplicial object constructed above is, in fact, an internal category object in $\mathbf {B}$. This proves that $\mathsf {W}^{*}(\mathbf {A})$ factors through $\mathsf {Cat}(\mathbf {B})$. Indeed an object of $\mathsf {W}(\mathbf {A})$ is in $\mathsf {W}^{*}(\mathbf {A})$ as soon as every morphism $\alpha$ in its induced infinite sequence of cartesian split epimorphisms has the property that the square

is a pullback.

6 Groupoids and Whitehead sequences

We are now interested in the case when there is an equivalence between the category of Whitehead sequences in $\mathbf {A}$ and the category of internal groupoids in $\mathbf {B}$, as it is the case, for example, for the category of groups and group actions.

Theorem 2

Let (I, G, J) be an action-system of $\mathbf {A}$ over $\mathbf {B}$. If the pair of functors (I, J) is jointly conservative and there is an equivalence of categories

$$\begin{aligned} \mathbf {A}\sim \mathsf {Pt}(\mathbf {B}), \end{aligned}$$

compatible with the system (I, G, J), then there is an equivalence of categories

$$\begin{aligned} \mathsf {W}^{*}(\mathbf {A}) \sim \mathsf {Gpd}(\mathbf {B}). \end{aligned}$$

Proof

Suppose we have an equivalence of categories

$$\begin{aligned} \mathbf {A}\mathop {\longrightarrow }\limits ^{\sim } \mathsf {Pt}(\mathbf {B}) \end{aligned}$$

which is compatible with the action-system, that is, an object A in $\mathbf {A}$ is realized as a point of the form

where F is the left adjoint of G. The equivalence allows us to assume that for any given split extension

we can find an object A in $\mathbf {A}$ such that the following diagram commutes

This fact, together with the assumption that the pair of functors is jointly conservative, proves that $\mathbf {B}$ satisfies the Split Short Five Lemma and hence any internal category object in $\mathbf {B}$ is also a internal groupoid (see [2] and references there). It remains to prove that given a internal groupoid in $\mathbf {B}$ we can find a Whitehead sequence such that, after applying the simplicial construction, the original groupoid is recovered, up to isomorphism.

The procedure is as follows. Given a internal groupoid as in (19), using

we obtain an object A in $\mathbf {A}$ such that

The morphism c gives

$$\begin{aligned} u:A \longrightarrow GIA \end{aligned}$$

with $u=G(c)\eta _A$ which is such that $I(u)=1$ and $J(u)=h=c \circ \ker (d)$.

In order to obtain $v:GJA\longrightarrow A$ with $J(v)=1$ and $I(v)=J(u)=h$, we consider the pair (m, 1) as a morphism of points

and transfer it, via the equivalence, from $\mathsf {Pt}(\mathbf {B})$ to $\mathbf {A}$, in order to obtain, say

It follows that $JE=FA_h$ where $h^*:A_h\longrightarrow A$ is the cartesian lifting of $h:JA \longrightarrow IA$, given by $h=J(u)$ as defined above. This is possible because, on the one hand JE is the kernel of $dp_2$, while on the other hand, $FA_h$ is the pullback of h along d.

In this way we have a morphism

and, via the adjuntion [see Proposition 1(i)], we also have a morphism

such that $I(\rho )=1_{JA}$ and $J(\rho )=1_{JA}$. Now, using the fact that I and J are jointly conservative we conclude that $\rho$ is an isomorphism, and so we obtain the desired $v=h^* \rho ^{-1}$. This gives a Whitehead sequence

such that, applying the simplicial construction to it, we obtain, up to isomorphism, the original groupoid as

and this completes the proof. $\square$

We say that $\mathsf {Pt}(\mathbf {B})$ is an action-system on $\mathbf {B}$ if the triple of functors (I, G, J), with $I(A,B,p,s)=B$ the codomain functor, $J(A,B,p,s)=ker(p)$ the kernel functor and G the right adjoint of the domain functor $F(A,B,p,s)=A$ (for a split epimorphism $p:{A\longrightarrow B}$ with section $s:{B\longrightarrow A}$) is an action system.

Corollary 1

If $\mathsf {Pt}(\mathbf {B})$ is an action system on $\mathbf {B}$, then $W^{*}(\mathsf {Pt}(\mathbf {B}))$ is equivalent to $\mathsf {Gpd}(\mathbf {B})$.

7 Conclusion

We conclude with an application of the previous result in the case where the category $\mathbf {B}$ is pointed and protomodular [2].

In general, in order to have an action-system, we can always take $\mathbf {A}$ to be the category of all stable and exact patches in $\mathbf {B}$. Then, for an object $A=(X,Y,k,s,p)$ as in Definition 2, we define $I(A)=B$, $J(A)=X$ and $F(A)=Y$. Moreover, if for every object B in $\mathbf {B}$ the diagram

is a stable patch (as it is always the case in a pointed protomodular category) then we have a functor G and the system (I, G, J) is an action system of $\mathbf {A}$ over $\mathbf {B}$ provided that the L-condition holds. In the case when $\mathbf {B}$ is a protomodular category, considering the system (I, G, J) as before, if $f:{A\longrightarrow Y'}$ is a organic morphism then we have $Y'\cong FA$, which is an immediate consequence of the Split Short Five Lemma. This means that the L-condition can be simplified and it becomes equivalent, in this context, to the following condition:

Every Peiffer graph is a multiplicative graph.

In the paper [15] it is proved that if $\mathbf {B}$ is a semi-abelian category then this condition is equivalent to the so-called Smith is Huq condition.

As an application of Theorem 2 we can state a similar result to the one presented in [12] concerning the description of internal groupoids in a pointed protomodular category.

Let $\mathbf {B}$ be a pointed and protomodular category in which every Peiffer graph is a multiplicative graph. Then, giving an internal groupoid in $\mathbf {B}$ is to give an exact patch

together with a morphism

$$\begin{aligned} h:{X\longrightarrow B} \end{aligned}$$

such that the two dashed arrows can be inserted in the diagram

in order to make it commutative.

Further details can be found in [12], see also [11, 16].