Smooth projection of mortality improvement rates: a Bayesian two-dimensional spline approach

Abstract

This paper proposes a spline mortality model for generating smooth projections of mortality improvement rates. In particular, we follow the two-dimensional cubic B-spline approach developed by Currie et al. (Stat Model 4(4):279–298, 2004), and adopt the Bayesian estimation and LASSO penalty to overcome the limitations of spline models in forecasting mortality rates. The resulting Bayesian spline model not only provides measures of stochastic and parameter uncertainties, but also allows external opinions on future mortality to be consistently incorporated. The mortality improvement rates projected by the proposed model are smoothly transitioned from the historical values with short-term trends shown in recent observations to the long-term terminal rates suggested by external opinions. Our technical work is complemented by numerical illustrations that use real mortality data and external rates to showcase the features of the proposed model.

1 Introduction

1.1 Background

Due to the steady increases in life expectancy in recent decades, incorporating future mortality improvements in actuarial pricing and valuation has become an increasingly important task for actuaries. For instance, life and pension actuaries often need to use improvement scales to adjust their baseline life table to account for the foreseen deductions in future mortality rates. To facilitate this practical need, the actuarial professions in different countries have been actively exploring new methodologies for generating mortality improvement (MI) scales.

Historically, MI scales are made using simple one-dimensional formulas, for example, the AA scale of the Society of Actuaries (SOA), in which only the effect of age is considered. In 2014, following the conceptual framework developed by the Continuous Mortality Investigation (CMI) of the Institute and Faculty of Actuaries (IFoA) in the UK, the Retirement Plans Experience Committee (RPEC) of the SOA released the RPEC model to address the issues of Scale AA. In particular, the RPEC model exploits expert opinions on long-term mortality improvement rates to produce arrays of two-dimensional (age and time) MI scales. The resulting MI rates converge gradually from recent observations to the long-term externally given values. The RPEC model was updated annually with Scale MP-2020 being the most recent one of the ‘MP’ series. In addition, other actuarial professions have also developed MI scales for their own populations, for example, the MI-2017 scale and the CPM-B scale from the Canadian Institute of Actuaries (CIA).

More recently, the SOA promulgated a new methodology for generating two-dimensional MI scales, called the MIM-2021 model. Compared to its predecessor (the RPEC model), several new features were added. First, the MIM-2021 model uses historical mortality data from not only the Social Security Administration (SSA) of the US, but also the National Center for Health Statistics (NCHS), where the dataset is stratified into socioeconomic categories. Second, the MIM-2021 model allows the user to externally specify an optional set of intermediate-term MI rates, in addition to the long-term ultimate ones, so that a more flexible setting of MI scales can be achieved. Third, using polynomial functions, the resulting MI scales are smoothly transitioned from recently observed values to the intermediate ones and then ultimately to the long-term rates.

Despite being an improved model for generating MI scales, the MIM-2021 model is subject to several limitations. First, the model’s graduation and projection methods are not the same. To have smooth mortality data, the Whittaker–Henderson graduation method is used on the historical mortality rates, whereas the method for projecting future MI rates is based on two polynomial functions that are separately applied to the age and cohort dimensions. Second, the polynomial-based projection method is not flexible. Although the model user can specify intermediate- and long-term values, the rate of transition between different periods cannot be controlled. Third, due to the deterministic projection method, the MIM-2021 model can only produce point estimates for future MI rates, but not provide measures of uncertainty surrounding the projected values. Moreover, the externally given rates are also treated as deterministic inputs with no measure of uncertainty.

The research objective of this paper is to develop a mortality improvement model that carries the features of the MIM-2021 model and also overcomes its limitations. In particular, we aim to build a mortality model that can (1) statistically incorporate external opinions on intermediate- and long-term MI rates, (2) smoothly project MI rates from recent observations to external rates on a two-dimensional surface, and (3) provide measures of uncertainty for the projected MI rates and the externally given rates.

1.2 Literature review

Broadly speaking, there are two types of approaches that can be adopted to achieve our research objective. The first one models MI rates using factor-based mortality models, such as the Lee–Carter model [27] or the Cairns–Blake–Dowd model [3]. For example, Li et al. [30] used the Lee–Carter model to generate MI rates for Canadian insured lives. Haberman and Renshaw [19] considered using the Lee–Carter model to forecast two-dimensional MI rates. Following the work of Hyndman and Ullah [25], Shang [41] proposed to use dynamic principal component regression to forecast MI rates. More recently, to generate two-dimensional MI scales, Li and Liu [31] proposed the heat-wave model, which uses normal distributions to describe the short-term pattern in MI rates. Other examples include those considered by Haberman and Renshaw [20], Hunt and Villegas [24], Renshaw and Haberman [38] and Li and Liu [32].

This first type of approaches is subject to two major issues that are hindering the research objective. First, the MI rates projected by these factor-based models are likely to be jagged across ages and/or cohorts, due to the non-smooth factor estimates. To overcome this problem, studies, such as Renshaw and Haberman [39], Delwarde et al. [10], Currie [7], Pitt et al. [36] and Li et al. [33], have considered using penalization methods or splines to smooth the age-specific factors. Nevertheless, such smoothing methods can hardly be applied simultaneously to both age- and period-specific factors to achieve a smooth two-dimensional MI surface.

Second, the factor-based models often suggest that the high level of mortality improvements observed in recent decades will continue indefinitely into the future. This conjecture is not aligned with the industry’s view that MI rates should gradually converge from recent observations to certain long-term terminal values. More importantly, it is not clear how external opinions on long-term rates can be statistically incorporated in factor-based models. Dowd et al. [14] proposed to deliberately alter the drift values of the period-specific factors. Dodd et al. [13] considered using a weighted average method to blend the external rates and internal results. Moreover, although factor-based models can provide stochastic uncertainty to the projected rates, uncertainty surrounding the external rates cannot be easily measured.

The second type of approaches focuses on using non-parametric methods, such as applying spline functions to directly model and project mortality rates. Under the roof of generalized additive models, Dodd et al. [12] and Hilton et al. [21] considered using one-dimensional P-splines to smooth mortality rates. On two-dimensional modeling, Currie et al. [8] developed a two-dimensional B-spline mortality model. Extending the work of Currie et al. [8], Luoma et al. [34] considered natural Bayesian splines, Camarda et al. [5] used P-splines, while Camarda [4] proposed to use constrained P-splines instead. Other studies that also considered non-parametric methods include Currie et al. [9], Huang and Browne [23], Richards [40] and Tang et al. [43]. Lastly, we remark that the Whittaker–Henderson graduation method used in the MIM-2021 model belongs to this type of approaches.

1.3 Our contributions

In this paper, we focus on the two-dimensional setting of spline mortality modeling. In particular, we follow the seminal work of Currie et al. [8] to construct a Bayesian two-dimensional B-spline model for smoothing and projecting MI rates. To achieve our research objective and also overcome some limitations of spline mortality modeling, we develop our spline MI model with several adaptations, which are outlined as follows.

Firstly, a two-dimensional B-spline can naturally provide a smooth surface of MI rates. However, to reach an appropriate balance between smoothness and goodness-of-fit, a penalty term needs to be added to the likelihood function, which in turn leads to a P-spline. When applied to mortality modeling, a P-spline model is often criticized for its subjective knots, smoothing parameter and limited forecast ability. As discussed in Currie et al. [8], the order of penalty needs to be subjectively determined and has dominant effects on the forecast results. Setting the order of penalty to 1, 2 and 3 is equivalent to assuming no future MI, linear MI and quadratic MI, respectively. To address this problem, we implement LASSO penalty to spline mortality modeling by adopting the method of Park and Casella [35]. Compared to the order-based penalties, the LASSO penalty is able to provide a more robust and flexible setting for projecting MI rates, such as capturing short-term mortality shocks and allowing terminal long-term rates. For autoregressive mortality models, the use of LASSO penalty in parameter estimation has been considered by studies, such as Li and Lu [28], Chang and Shi [6] and Li and Shi [29].

Secondly, to have a joint estimation and projection framework, we adopt the Bayesian method to estimate our model and project MI rates. The idea of applying spline models under the Bayesian method is well explored in the statistical literature (see, e.g.,[11, 26, 42]). Adopting the existing statistical work, the Bayesian method allows us to obtain a joint posterior distribution of the entire MI surface, including both the estimated historical rates and the projected future rates. The resulting predictive distribution will appropriately reflect the extent of stochastic uncertainties in future MI rates. Furthermore, the Bayesian results provide an avenue for us to analyze the different levels of uncertainties, originated from either parameter estimation, external opinions or random noises.

Thirdly, we modify the Bayesian B-spline projection method to develop a straightforward approach of incorporating external opinions on future MI rates. This approach treats any externally given intermediate-term and long-term MI rates as a reliable source of “additional data”. Multiple years of external rates and multiple opinions on the same year-age cell are allowed. This feature is compatible with the industry’s practice, where distinct expert opinions on future MI rates might be collected in a survey. Under the Bayesian method, the uncertainty resulting from different external opinions can be properly reflected by the posterior distribution of the external rates.

Lastly, the technical contributions of this paper are complemented by a numerical illustration that showcases how the proposed model can be used to generate a smooth surface of MI rates using real mortality data and external opinions. The projected MI rates are smoothly transitioned from the short-term patterns shown in recent mortality observations to the externally given intermediate- and long-term rates. The mean forecasts are accompanied by measures of uncertainties generated from different sources. To demonstrate the flexibility of the proposed model on incorporating external opinions, we further consider other scenarios where multiple years or multiple input of external rates are provided.

The rest of this paper is organized as follows. Section 2 provides the setup of our modeling approach, including a brief review of the MIM-2021 model. Section 3 outlines the proposed spline MI model and the technical details. Section 4 discusses the Bayesian estimation and projection methods developed for our model. Section 5 provides a numerical illustration using real data and external rates. Lastly, Sect. 6 concludes the paper with limitations and possible future work.

2 The setup

In this section, we first set up the notation to be used in this paper and provide a brief review of the MIM-2021 model. We then discuss the features and limitations of the MIM-2021 model in detail, and our motivations and objectives for this study.

2.1 Notation

Let $m_{x,t}$ denote the central death rate for age $x \in \{x_1, \ldots , x_{n_a}\}$ in year $t \in \{t_1, \ldots , t_{n_y}\}$, where $n_a$ and $n_y$ are the total number of ages and years in the mortality dataset, respectively. The mortality improvement (MI) rate for age x in year t is defined as

$$\begin{aligned} y_{x,t} = 1- \frac{m_{x,t}}{m_{x,t-1}}. \end{aligned}$$

We can interpret $y_{x,t}$ as the relative change in the central death rates between year t and year $t-1$ for age x. A positive value of $y_{x,t}$ indicates that mortality improved from year $t-1$ and year t (i.e., mortality rate decreased), whereas a negative value of $y_{x,t}$ indicates a year of mortality deterioration.

2.2 The MIM-2021 model

Before applying cubic polynomial functions to project future MI rates, the MIM-2021 model first uses the Whittaker–Henderson method to graduate the historical values of $m_{x,t}$ to obtain the smoothed rates, denoted as $m^s_{x,t}$. In particular, the following objective function is minimized in order to smooth the central death rates:

$$\begin{aligned} \sum _{t=t_1}^{t_{n_y}} \sum _{x = x_1}^{x_{n_a}}(\ln m^s_{x,t}-\ln m_{x,t})^2 + \nu _a \sum _{t=t_1}^{t_{n_y}} \sum _{x = x_1+3}^{x_{n_a}} (\Delta ^3_x(\ln m^s_{x,t}))^2 + \nu _y \sum _{t=t_1+3}^{t_{n_y}} \sum _{x = x_1}^{x_{n_a}} (\Delta ^3_t(\ln m^s_{x,t}))^2. \end{aligned}$$

(1)

The parameters $\nu _a$ and $\nu _y$ are penalty weights that balance the closeness of $m^s_{x,t}$ to $m_{x,t}$ and the smoothness of $m^s_{x,t}$. The functions $\Delta ^3_x(\cdot )$ and $\Delta ^3_t(\cdot )$ are the third-order difference along the age and time dimensions, respectively. The MIM-2021 model uses a value of $\nu _y = 100$ over the time dimension, and a value of $\nu _a = 400$ over the age dimension.

Based on the smoothed values $m^s_{x,t}$, the smooth MI rates are obtained from $y^s_{x,t} = 1- \frac{m^s_{x,t}}{m^s_{x,t-1}}$. To project rates beyond year $t_{n_y}$ (the last year of the dataset), the MIM-2021 model supposes that the MI rates $n_p$ years after year $t_{n_y}$ are externally given; that is, the MI rates for all ages in year $t_{n_y}+n_p$ are externally determined by the model user. The MIM-2021 model then uses two cubic polynomial functions, one along the age dimension and the other one along the cohort dimension, to interpolate MI rates for years between $t_{n_y}$ and $t_{n_y}+n_p$. For each age x, the cubic polynomial over the time dimension is specified as

$$\begin{aligned} y^{\text {age}}_{x,t}&= y^s_{x, t_{n_y}} + l_{x} (t-t_{n_y}) - \left( \frac{2 n_p l_{x} - 3\left( y^s_{x,t_{n_y}+n_p} - y^s_{x,t_{n_y}}\right) }{n_p^2}\right) (t-t_{n_y})^2 \\ &\quad + \left( \frac{n_p l_{x} -2\left( y^s_{x,t_{n_y}+n_p} - y^s_{x,t_{n_y}}\right) }{n_p^3}\right) (t-t_{n_y})^3, \end{aligned}$$

(2)

where $l_{x}$ is an initial slope externally specified by the model user, or set to $y^s_{x,t_{n_y}}-y^s_{x,t_{n_y}-1}$ as the default value. It is further assumed that the ending slope at year $t_{n_y}+n_p$ is zero for all ages. Along the cohort dimension, a similar but more complicated cubic polynomial is used to obtain $y^{\text {cohort}}_{x,t}$. We omit the function here.

The MIM-2021 model is a two-dimensional model in the sense that it separately interpolates MI rates on the age and cohort dimensions. To obtain $y^{\text {age}}$, an age-specific cubic polynomial function over time is used, while a cohort-specific cubic polynomial function over time is used to obtain $y^{\text {cohort}}_{x,t}$. To produce the final MI scales, the interpolated values along the two dimensions are combined using

$$\begin{aligned} y^{MIM}_{x,t} = \omega _{x,t} y^{\text {age}}_{x,t} + (1-\omega _{x,t}) y^{\text {cohort}}_{x,t}, \end{aligned}$$

(3)

where $\omega _{x,t}$ is a weight given again by the model user. The default value in the MIM-2021 model for $\omega _{x,t}$ is $50\%$ for all x and t. Lastly, if the intermediate-term rates are also externally given, then the two cubic polynomials will be applied from year $t_{n_y}$ to the year of the intermediate- rates, and afterwards linear interpolations will be used to connect the intermediate-term and long-term rates.

Fig. 1

An illustration of the interpolation methods used in the MIM-2021 model. The terms ‘SR’, ‘IR’ and ‘LR’ stand for short-term, intermediate-term and long-term rates, respectively

2.3 Our motivations

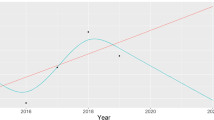
To motivate our study, we now discuss the features and limitations of the MIM-2021 model. An illustration of the interpolation methods used in the MIM-2021 model is provided in Fig. 1. It is assumed in the MIM-2021 model that $t_1 = 1982$ and $t_{n_y} = 2018$. The end of the projection period $t_{n_y}+n_p$ is set by the model user as the long-term terminal point. To project MI rates from $t_{n_y}$ to $t_{n_y}+n_p$, the MIM-2021 model relies on either linear or cubic polynomial functions.

As shown in the left panel of Fig. 1, with only long-term rates externally given, the cubic polynomial function is used to first extend the recently observed and smoothed MI rates to a set of projected short-term rates. These rates highly depend on the recent MI trends formed by the smoothed data. The same function then continues to project MI rates to the externally given long-term rates, which in turn produces a smooth transition between data and external rates. If intermediate-term rates are also given, then the short-term rates will first be connected with the intermediate-term rates, and then further extended to the long-term ones using a linear interpolation, as shown in the right panel of Fig. 1.

Although the MIM-2021 model can produce a smooth projection of future MI rates, it is subject to several limitations. First, as indicated by Eqs. (1) and (2), the graduation method and the projection method used in the MIM-2021 model are not the same method. The data are smoothed by the Whittaker–Henderson method, while the projection is produced by polynomial interpolations. This inconsistent use of two methods may lead to a jagged transition between the last year of data and the first year of projection, known as the “edge effects”.

Second, the MIM-2021 model’s projection of future MI rates is not flexible. The two-dimensional projection is obtained from a weighted average of two independent one-dimensional polynomial functions, as suggested by Eq. (3). The interactions of MI rates across ages and cohorts cannot be captured under this approach. In addition, the projected MI trends will be stagnant, since the projecting function used is either a cubic or linear polynomial.

Third, the MIM-2021 model can only provide point estimates of future MI rates, but not a measure of uncertainty surrounding the point estimates. This shortcoming greatly limits the model’s use in risk management tasks, such as calculating solvency capital requirements. Further, the MIM-2021 model treats external opinions on future MI rates as deterministic ‘true’ values with no uncertainty assumed to these externally given rates.

In the rest of this paper, we aim to develop a mortality improvement model that can produce a smooth projection of two-dimensional future MI rates with external opinions on intermediate- and long-term rates incorporated and appropriate measures of uncertainty for the observed, projected and externally given rates.

3 The proposed model

This section presents the proposed two-dimensional cubic B-spline MI projection model. A brief review of the spline mortality modeling technique developed in Currie et al. [8] is first provided. We then discuss the implementation of LASSO penalty and the incorporation of external opinions under a two-dimensional cubic B-spline. Lastly, the smooth projection method of the final model is provided.

3.1 Spline mortality modeling

3.1.1 One-dimensional smoothing

We first illustrate the idea of spline smoothing on the one-dimensional case. For a particular year t, suppose we want to smooth mortality data along the age dimension from age $x_1$ to $x_{n_a}$. Using a one-dimensional spline function over age, we can obtain smoothed values of $(y_{x_1, t}, \ldots , y_{x_{n_a}, t})$ from

$$\begin{aligned} {y}_{x,t}= \sum _{i=1}^{c_a} \beta _{i} b_{i}(x) + z_{x,t} \end{aligned}$$

(4)

where $c_a$ is the number of basis functions used in the spline, $b_{i}(x)$ is the i-th basis function evaluated at age x, $\beta _{i}$ is the coefficient associated with the i-th basis function, and $\{z_{x,t}\}$ are independent and identically distributed (i.i.d.) normal errors with mean 0 and variance $\sigma ^2$.

Putting the MI rates in a $(n_a \times 1)$ vector form, denoted by ${\varvec{y}}_{t} = (y_{x_1, t}, \ldots , y_{x_{n_a}, t})^T$, Eq. (4) can be expressed in a matrix form as

$$\begin{aligned} {\varvec{y}}_{t}= {\varvec{B}}_{t}\times \varvec{\beta }_{t} + {\varvec{z}}_{t}, \end{aligned}$$

(5)

where ${\varvec{B}}_{t}$ is a $(n_a \times c_a)$ matrix known as the basis matrix, $\varvec{\beta }_{t}$ is a $(c_a \times 1)$ vector consists of the coefficients, and ${\varvec{z}}_{t}$ is a $(n_a \times 1)$ vector of i.i.d. normal errors. The choice of the basis matrix ${\varvec{B}}_{t}$ will be discussed later in this subsection.

3.1.2 Two-dimensional smoothing

For the two-dimensional case, we follow the idea of Currie et al. [8], which uses two one-dimensional marginal splines on each of the age and time dimensions to build a two-dimensional spline for smoothing mortality rates.

Consider the MI rates in a two-dimensional $(n_a \times n_y)$ matrix form, denoted by

$$\begin{aligned} {\varvec{Y}} = ({\varvec{y}}_{t_1}, \ldots , {\varvec{y}}_{t_{n_y}}). \end{aligned}$$

Let ${\varvec{B}}_{a}$ be the $(n_a \times c_a)$ basis matrix of a one-dimensional marginal spline along the age dimension, and ${\varvec{B}}_{y}$ be the corresponding $(n_y \times c_y)$ basis matrix along the time dimension, where $c_y$ is the number of basis functions in ${\varvec{B}}_{y}$. The two-dimensional spline model for ${\varvec{Y}}$ is defined as

$$\begin{aligned} {\varvec{y}} = {\varvec{B}} \times \varvec{\beta } + {\varvec{z}}, \end{aligned}$$

(6)

where

• ${\varvec{y}}=\varvec{vec}({\varvec{Y}})$ is the vectorization of ${\varvec{Y}}$,

• ${\varvec{B}} = {\varvec{B}}_a \otimes {\varvec{B}}_y$ is the basis matrix derived from the Kronecker product of ${\varvec{B}}_{a}$ and ${\varvec{B}}_{y}$,

• $\varvec{\beta }$ is a $(c_a c_y \times 1)$ vector consists of all the coefficients for the basis functions in ${\varvec{B}}$, and

• ${\varvec{z}}$ is a $(n_a n_y \times 1)$ vector of i.i.d. normal errors.

3.1.3 The basis matrix

The basis functions can take various different forms. For our modeling and projecting purposes, we choose to use B-spline. Among numerous choices, B-spline has particular popularity due to its sparse structure. This feature is particularly useful to us, since it greatly enhances the numerical stability of the estimation process when the number of coefficients used is large.

The definition of B-spline is expressed in a recursive form, starting from a B-spline with an order of zero and its i-th basis function being defined as

$$\begin{aligned} b_{i,0}(x) := \left\{ \begin{array}{ll} 1 &{}\quad \text {if }\ k_i \le x < k_{i+1} \\ 0 &{}\quad \text {otherwise} \end{array}, \right. \end{aligned}$$

where $k_{i}$ is called a chosen knot. For the higher orders, $h \ge 1$, the basis function follows

$$\begin{aligned} b_{i,h}(x) := \frac{x-k_i}{k_{i+h} - k_i} b_{i,h-1}(x) + \frac{k_{i+h+1}-x}{t_{i+h+1}-t_{i+1}}b_{i+1, h-1}(x). \end{aligned}$$

Notice that B-spline has only local support, which means the impact of the i-th basis function becomes zero if $x \ge k_{i+h+1}$ or $x \le k_{i}$. This feature makes B-spline particularly suitable for modeling temporary short-term shocks because the effect of shocks will diminish to zero over time.

The common choice of the highest order is $h=3$, which in turn leads to a cubic B-spline. We choose to use $h=3$ for our MI B-spline model as well. If we select $c_a+3$ knots along the age dimension and $c_y+3$ knots along the time dimension, then the total number of basis functions in ${\varvec{B}}$ and coefficients in $\varvec{\beta }$ is $c_a c_y$. We thus need to estimate $c_a c_y$ numbers of coefficients for our cubic B-spline MI model.

3.2 LASSO penalty

The coefficients in a spline model can be estimated via minimizing the following objective function over $\varvec{\beta }$:

$$\begin{aligned} ({\varvec{y}} - {\varvec{B}}\times \varvec{\beta })^T({\varvec{y}} - {\varvec{B}}\times \varvec{\beta }). \end{aligned}$$

However, to achieve an appropriate balance between the smoothness and goodness-of-fit, a penalty term is often added, which results in a P-spline model. In particular, the objective function becomes

$$\begin{aligned} \left( {\varvec{y}} -{\varvec{B}}\times \varvec{\beta }\right) ^T\left( {\varvec{y}} -{\varvec{B}}\times \varvec{\beta }\right) + P(\varvec{\beta }), \end{aligned}$$

(7)

where $P(\varvec{\beta })$ is a penalty function with an order of 1, 2 or 3.

We remark that P-spline is the model originally used in Currie et al. [8]. However, for our objectives of modeling MI rates, P-spline is subject to a number of caveats. First, the number and position of knots are restrictive. On this matter, Currie et al. [8] suggested that “the following simple rule-of-thumb is often sufficient: with equally spaced data, use one knot for every four or five observations up to a maximum of 40 knots ...” We cannot follow this rule-of-thumb, because, when intermediate- and/or long-term external rates are given, the resulting data structure will no longer be equally spaced.

Second, the order of the penalty function in P-spline needs to be subjectively determined, and will greatly affect the projection results. As discussed in Currie et al. [8], setting the penalty order to 1, 2 and 3 is equivalent to assuming no MI, linear MI and quadratic MI in the future, respectively. Thus, a P-spline model may perform well in terms of smoothing historical data, but it cannot achieve our desired feature of smoothly transitioning MI rates from recent observations to external rates.

To address the issues, we choose to adopt the LASSO penalty for our cubic B-spline MI model. The objective function is specified as

$$\begin{aligned} ({\varvec{y}} - {\varvec{B}}\times \varvec{\beta } )^T({\varvec{y}}- {\varvec{B}}\times \varvec{\beta }) + \lambda \left\| \varvec{\beta } \right\| _1 \end{aligned}$$

(8)

where $\lambda$ is the smoothing parameter and $\left\| \varvec{\beta } \right\| _p$ is the p-norm of $\varvec{\beta }$. Under LASSO penalty, the number of basis functions used can dramatically increase, the position of knots no longer needs to be equidistant, and there is no penalty order to determine.

The LASSO penalty will shrink unnecessary coefficients towards zero, especially for those that have no data nearby. This feature is particularly useful to us, because a large number of knots (likely more than the number of data points we have) will need to be placed between the data and external rates achieve a smooth transition. Moreover, our preliminary analysis indicates that a P-spline model may encounter computational errors when the number of knots used is too large, but switching to LASSO penalty will solve the problem. In short, the flexibility and stability of LASSO penalty make it an excellent penalty option for our modeling and projecting objectives.

3.3 External rates

Aside from the observed mortality rates, expert opinions on future mortality rates collected from external sources can be valuable information in modeling and projecting mortality rates. In the literature, many studies have considered incorporating external information in mortality modeling, for example, Billari et al. [1], Billari et al. [2], Dowd et al. [14] and Dodd et al. [13]. In this paper, we propose an alternative approach that is compatible with the cubic B-spline MI model, and also in line with the needs of the insurance industry’s practice.

Suppose we have collected K sets of external opinions on MI rates for p future years, denoted as ${\varvec{y}}^{(k)}_{\tilde{t}} = (y^{(k)}_{x_1, \tilde{t}}, \ldots , y^{(k)}_{x_{n_a}, \tilde{t}})^T$, $\tilde{t} \in \{\tilde{t}_1, \ldots , \tilde{t}_p\}$ and $k=1,\ldots ,K$, where $\tilde{t}_p$ is assumed to be the last year of the projection period. By considering these external rates as an additional source of ‘data’, we combine the observed rates with the external rates to create a synthetic dataset, denoted by

$$\varvec{\tilde{Y}} = \left( {\varvec{Y}}, {\varvec{y}}^{(1)}_{\tilde{t}_1}, \ldots , {\varvec{y}}^{(K)}_{\tilde{t}_1}, \ldots , {\varvec{y}}^{(1)}_{\tilde{t}_p}, \ldots , {\varvec{y}}^{(K)}_{\tilde{t}_p}\right) .$$

The corresponding basis matrix becomes

$$\begin{aligned} \varvec{\tilde{B}} = \begin{pmatrix} {\varvec{B}} \\ J_{K,1} \otimes {\varvec{B}}_{\tilde{t}_1} \\ \vdots \\ J_{K,1} \otimes {\varvec{B}}_{\tilde{t}_p} \\ \end{pmatrix}, \end{aligned}$$

where $J_{K,1}$ is a $(K \times 1)$ vector of ones, and ${\varvec{B}}_{\tilde{t}}$ is the corresponding $(n_a \times c_a c_y)$ basis matrix for the external rates in year $\tilde{t}\in \{\tilde{t}_1,\ldots ,\tilde{t}_p\}$. Since the number of columns in basis matrices $\varvec{\tilde{B}}$ and ${\varvec{B}}$ is the same, the number of coefficients $\varvec{\beta }$ used in the B-spline model is unchanged, and the LASSO penalty of Eq. (8) can be simply adjusted to

$$\begin{aligned} (\varvec{\tilde{y}} - \varvec{\tilde{B}}\times \varvec{\beta } )^T(\varvec{\tilde{y}}- \varvec{\tilde{B}}\times \varvec{\beta }) + \lambda \left\| \varvec{\beta } \right\| _1 \end{aligned}$$

(9)

where $\varvec{\tilde{y}}=\varvec{vec}(\varvec{\tilde{Y}})$.

From a practical point of view, our approach is very sensible because it can simultaneously consider multiple external opinions collected from a single survey. Whether these opinions provides the same or different future MI rates, the proposed approach will consistently incorporate each of them to form an aggregated opinion. More specifically, our Bayesian estimation approach (discussed in Sect. 4) will integrate the similarity and/or difference among the external opinions to form a joint prior belief of future MI rates.

Furthermore, the external opinions collected do not need to include range or volatility estimates, because the point estimates of multiple opinions can naturally reflect a certain level of uncertainty for future rates. In comparison, the MIM-2021 model can be regarded as using only one external opinion (specified by the model user) or using one “consensus” of all external opinions collected. Since the difference among external opinions is not reflected, the uncertainty underlying the external rates will be highly underestimated.

3.4 Smooth projection

We are now ready to present the final smooth projection method of the proposed cubic B-spline model with LASSO penalty and external rates incorporated. Let

$$\begin{aligned} \varvec{\hat{Y}} = (\hat{{\varvec{y}}}_{t_1}, \ldots , \hat{{\varvec{y}}}_{t_{n_y}}, \hat{{\varvec{y}}}_{t_{n_y}+1}, \ldots , \hat{{\varvec{y}}}_{\tilde{t}_p}), \end{aligned}$$

and $\varvec{\hat{y}}=\varvec{vec}(\varvec{\hat{Y}})$ denote the smoothed/estimated values of past MI rates all ages from year $t_1$ to $t_{n_y}$, combined with the projected values of future MI rates for all ages from year $t_{n_y}+1$ and $\tilde{t}_p$ (the last year of the projection period). The proposed two-dimensional cubic B-spline model obtains $\varvec{\hat{y}}$ as

$$\begin{aligned} \varvec{\hat{y}} = \varvec{\hat{B}} \times \varvec{\hat{\beta }}, \end{aligned}$$

where

• $\varvec{\hat{\beta }}$ is a vector consists of all the coefficients estimated from minimizing Eq. (9), and

• $\varvec{\hat{B}} = ({\varvec{B}}^T,{\varvec{B}}_{t_{n_y}+1}^T,\ldots ,{\varvec{B}}_{\tilde{t}_p}^T)^T$, with ${\varvec{B}}$ being the basis matrix defined in Eq. (6) and ${\varvec{B}}_t$ being the corresponding basis matrix for future year $t\in \{t_{n_y}+1,\ldots ,\tilde{t}_p\}$.

4 The Bayesian estimation

As a flexible modeling method, B-spline models can provide accurate in-sample fitting and smooth out-of-sample projections. However, because a large number of parameters/coefficients is used, the parameter uncertainty of a B-spline model should not be ignored in its model estimation and projection process. For instance, the smoothing parameter $\lambda$ of LASSO penalty controls the smoothness and goodness-of-fit of a B-spline model. The frequentist approach often determines the value of $\lambda$ using cross-validation, which provides no straightforward measure of parameter uncertainty for $\lambda$.

Another issue that we encountered in our preliminary analysis is that, when minimizing a penalized objective function (e.g., Eq. (7)), the inversion of a large matrix may become unstable. Since the mortality data used has $n_a$ ages and $n_y$ years, our basis matrix for the sample period already has a large size of $(n_a n_y \times c_a c_y)$. This size will further expand when the projection period and external rates are considered.

The Bayesian estimation approach allows us to overcome the aforementioned issues in a statistically rigorous manner. We thus adopt the Bayesian approach to estimate our proposed model, and present the technical details of our Bayesian estimation procedure in this section.

4.1 Priors

Under the Bayesian approach, all model parameters are considered to be random variables, of which prior distributions must be provided. Our model parameters include the coefficient vector $\varvec{\beta } = (\beta _1, \ldots , \beta _{c_ac_y})^T$, the smoothing parameter $\lambda$ for LASSO penalty, and the variance parameter $\sigma ^2$ of i.i.d. normal errors.

We start with the $\varvec{\beta }$ coefficients. As noted by Tibshirani [44], the LASSO penalty term in Eq. (8) can be interpreted as assuming a Laplace prior to the coefficients. We adopt this result for our model’s LASSO penalty term in Eq. (9). Following the work of Park and Casella [35], the prior of each coefficient in $\varvec{\beta }$ is defined as

$$\begin{aligned} \pi (\beta _i|\sigma ^2,\lambda ) = \frac{\lambda }{2\sqrt{\sigma ^2}}\exp \left( -\frac{\lambda \cdot |\beta _i|}{\sqrt{\sigma ^2}}\right) , \end{aligned}$$

for $i=1,\ldots , c_ac_y$. The reason for including $\sigma ^2$ in the prior of $\beta _i$ is to guarantee a uni-modal posterior for $\beta _i$.

To simplify the implementation of the estimation procedure, an equivalent but hierarchical representation for the prior of $\beta _i$ is adopted:

$$\begin{aligned} \pi (\beta _i|\sigma ^2,\lambda ) = \int _0^{\infty } \left\{ \frac{1}{\sqrt{2\pi \sigma ^2 \tau _i}}\exp \left( -\frac{\beta _i^2}{2\sigma ^2\tau _i}\right) \right\} \times \left\{ \frac{\lambda ^2}{2} \exp \left( -\frac{\lambda ^2\tau _i}{2}\right) \right\} d\tau _i, \end{aligned}$$

where the first term inside the integral indicates a normal distribution, while the second term indicates an exponential distribution. Here a new auxiliary variable $\tau _i$ is introduced for each $\beta _i$. The prior for $\beta _i$ is indeed a normal distribution with mean zero and variance $\sigma ^2\tau _i$, and the hyper-prior for $\tau _i$ follows an exponential distribution with scale parameter $\frac{2}{\lambda ^2}$.

Denote $\varvec{\tau } = (\tau _1, \ldots , \tau _{c_ac_y})^T$ and ${\varvec{D}}_{\varvec{\tau }} = \text {diag}(\varvec{\tau })$. We summarize the prior for $\varvec{\beta }$ in the following vector form:

$$\begin{aligned} \left\{ \begin{aligned} \varvec{\beta }|\sigma ^2,\varvec{\tau }&\sim \text{ MVN}_{c_ac_y}({\varvec{0}}_{c_ac_y}, \sigma ^2{\varvec{D}}_{\varvec{\tau }}),\\ \varvec{\tau }|\lambda&{\mathop {\sim }\limits ^{i.i.d.}} \text{ Exp }\left( \frac{2}{\lambda ^2}\right) . \end{aligned} \right. \end{aligned}$$

For $\lambda ^2$ and $\sigma ^2$, we use a non-informative prior, such that $\sigma ^2 \propto \frac{1}{\sigma ^2}$ and $\lambda ^2 \propto \frac{1}{\lambda ^2}$.

4.2 Full conditionals

Following the priors assumed in the previous subsection, the full conditionals of $\varvec{\beta }$, $\varvec{\tau }$, $\lambda$ and $\sigma ^2$ can be derived as follows.

• The full conditional of $\varvec{\beta }$ is a multivariate normal distribution with a dimension of $c_ac_y$, a mean vector

  $$\begin{aligned} \varvec{\mu _{\beta }} = \left( \varvec{\tilde{B}}^T\varvec{\tilde{B}} + {\varvec{D}}_{\tau }^{-1}\right) ^{-1} \varvec{\tilde{B}}^T \varvec{\tilde{y}}, \end{aligned}$$

  and a covariance matrix of

  $$\begin{aligned} \varvec{\Sigma _{\beta }} = \sigma ^2 \left( \varvec{\tilde{B}}^T\varvec{\tilde{B}} + {\varvec{D}}_{\tau }^{-1}\right) ^{-1}. \end{aligned}$$

• The full conditional of $\sigma ^2$ is an inverse-gamma distribution with shape parameter

  $$\begin{aligned} a_{\sigma ^2} = \frac{n_an_y + c_ac_y + n_a \times K \times p}{2}, \end{aligned}$$

  and scale parameter

  $$\begin{aligned} b_{\sigma ^2} = \frac{(\tilde{{\varvec{y}}}-\tilde{{\varvec{B}}}\varvec{\beta })^T(\tilde{{\varvec{y}}}-\tilde{{\varvec{B}}}\varvec{\beta }) +\varvec{\beta }^T {\varvec{D}}^{-1}_{\tau } \varvec{\beta }}{2}. \end{aligned}$$

• The full conditional of $\tau _i^{-1}$, $i=1,\ldots , c_ac_y$, is an inverse-Gaussian distribution with mean parameter

  $$\begin{aligned} a_{\tau _i} = \sqrt{\frac{\lambda ^2 \sigma ^2}{\beta _i^2}}, \end{aligned}$$

  and shape parameter $b_{\tau _i} = \lambda ^2$.

• The full conditional of $\lambda ^2$ is a gamma distribution with shape parameter $a_{\lambda ^2} = c_a c_y$ and rate parameter

  $$\begin{aligned} b_{\lambda ^2} = \frac{\text{ tr }({\varvec{D}}_{\varvec{\tau }})}{2}. \end{aligned}$$

4.3 Gibbs sampling

Since the full conditionals of all parameters are explicitly derived, Gibbs sampling can be directly applied. The total number of parameters (including the auxiliary ones) is $2c_ac_y+2$. We denote all of the parameters in a single set as

$$\begin{aligned} \Theta = \left\{ \beta _1, \ldots , \beta _{c_ac_y}, \tau _1, \ldots , \tau _{c_ac_y}, \sigma ^2, \lambda \right\} . \end{aligned}$$

In each iteration of Gibbs sampling, a sample of parameter $\theta _j$, for $j=1,\ldots ,2c_ac_y+2$, is drawn from its full conditional, specified in the previous subsection,

$$\pi \left( \theta _j \;\big |\; \varvec{\tilde{y}}, \Theta _{-\theta _j}\right) ,$$

where $\Theta _{-\theta _j}$ is the set $\Theta$ excluding the j-th element $\theta _j$. After a large number of iterations, the drawn samples will converge to the joint posterior distribution of $\pi (\Theta |\varvec{\tilde{y}})$. Finally, denoting $\hat{y}_{x,t}$, $x=x_1,\ldots ,x_{n_a}$ and $t=t_1,\ldots ,t_{n_y}$, as the smoothed MI rate in the sample period, the posterior distribution of $\hat{y}_{x,t}$ given $\varvec{\tilde{y}}$ is obtained from

$$\begin{aligned} f(\hat{y}_{x,t}|\varvec{\tilde{y}}) = \int f(\hat{y}_{x,t}|\Theta ) \pi (\Theta |\varvec{\tilde{y}}) d\Theta . \end{aligned}$$

It is well known that samples drawn from Gibbs sampling exhibit auto-correlation, and hence thinning must be applied to avoid bias in assessing the posterior distribution. We use the method of Effective Sample Size (ESS) to decide the number of effective samples for our final Bayesian analysis. In addition, both the single-chain convergence test Geweke [17] and the multi-chain convergence test Gelman and Rubin [16] are applied to verify the convergence of the effective samples.

4.4 Predictive distribution

The projections of future MI rates and also central death rates are obtained from the posterior predictive distribution. Let ${\bar{y}}_{x,t}$ and ${\bar{m}}_{x,t}$, $x=x_1,\ldots ,x_{n_a}$ and $t=t_{n_y}+1,\ldots ,\tilde{t}_p$, denote the projected future MI rates and central death rates, respectively. Assuming that the past and future rates are independently distributed given $\Theta$, the posterior predictive distribution of ${\bar{y}}_{x,t}$ and ${\bar{m}}_{x,t}$ are obtained from

$$\begin{aligned} f({\bar{y}}_{x,t}|\varvec{\tilde{y}}) = \int f({\bar{y}}_{x,t}|\Theta ) \cdot \pi (\Theta |\varvec{\tilde{y}}) \cdot d\Theta \end{aligned}$$

and

$$\begin{aligned} f({\bar{m}}_{x,t}|\varvec{\tilde{y}}) = \int f({\bar{m}}_{x,t}|\varvec{{\bar{y}}}_{t^-}) \cdot f(\varvec{{\bar{y}}}_{t^-}|\Theta ) \cdot \pi (\Theta |\varvec{\tilde{y}}) \cdot d\Theta d\varvec{{\bar{y}}}_{t^-}, \end{aligned}$$

respectively, where $\varvec{{\bar{y}}}_{t^-} = ({\bar{y}}_{x,t_{n_y}+1}, \ldots , {\bar{y}}_{x,t})^T$.

Empirically, we first draw a realization of $\varvec{\beta }$ and $\sigma ^2$, denoted respectively as $\varvec{\hat{\beta }}$ and $\hat{\sigma }^2$, from their joint posterior distribution $\pi (\varvec{\beta },\sigma ^2|\varvec{\tilde{y}})$. Then, we simulate ${\bar{y}}_{x,t}$ from a normal distribution with mean $\varvec{\hat{b}}(x,t)\varvec{\hat{\beta }}$ and variance $\hat{\sigma }^2$, where $\varvec{\hat{b}}(x,t)$ is the corresponding row from the basis matrix $\varvec{\hat{B}}$ for age x and year t. Lastly, we set

$$\begin{aligned} {\bar{m}}_{x,t} = {m}_{x,t_{n_y}} \left( \prod _{s=t_{n_y}+1}^{t} 1- {\bar{y}}_{x,s} \right) \end{aligned}$$

In our Gibbs sampling procedure, the values of ${\bar{y}}_{x,t}$ and ${\bar{m}}_{x,t}$, $x=x_1,\ldots ,x_{n_a}$ and $t=t_{n_y}+1,\ldots ,\tilde{t}_p$, are obtained at the end of each iteration. Note that the parameters $\varvec{\tau }$ and $\lambda$ do not directly concern the projections.

5 A numerical illustration

In this section, we use real mortality data and external rates to illustrate how the proposed cubic B-spline model can be used to generate smoothed two-dimensional MI rates.

5.1 Data

The mortality data used are obtained from the United States Social Security Administration (SSA). This dataset contains US male and female mortality experience for years 1982 to 2018 and ages 0 to 110. In this illustration, we consider the female population and the entire sample period 1982–2018, but reduce the age range to 35–99 to cover the typical ages of insureds. We further assume that expert opinions on future intermediate-term and long-term MI rates are collected from an external source. For illustrative purposes, we use the intermediate-term and long-term rates adopted from the MIM-2021 model for years 2030 and 2042, respectively.

Fig. 2

The MI rates of the assumed data shown in a surface plot (left) and a heat map (right)

Figure 2 depicts the MI rates of the assumed data in a surface plot (left penal) and a heat map (right panel). We observe that the historical MI rates are not smooth over the age and time dimensions. Both negative and positive values were observed over the sample period. Over the age range, stronger MI rates were observed for old ages in the recent years. Moreover, cohort effect can be detected from the heat map, where regions of ‘hot’ and ‘cold’ colors are formed along the diagonal line. Compared to the historical rates, the external rates are relatively smooth and positive for all ages.

We restate here that the objective of our spline modeling approach is to graduate the historical rates on a two-dimensional scale, and smoothly project the rates from recent observations to the externally given ones with measures of uncertainty.

5.2 Estimation results

The Bayesian estimation results of the model parameters $(\beta _1, \ldots , \beta _{c_ac_y}, \sigma ^2, \lambda )$ are presented in this subsection. From a total of 26,000 iterations of Gibbs sampling, we collected 5000 drawn samples with a burn-in period of 1000 iterations and a thinning frequency of 5 iterations per sample. These 5000 drawn samples form an empirical posterior distribution for all the model parameters.

Figure 3 shows two histograms, depicting the posterior distribution of $\sigma ^2$ (left panel) and $\lambda$ (right panel). For the LASSO penalty parameter $\lambda$, the empirical distribution has a mean of 0.8456, a variance of 0.0405, and is slightly skewed to the right. A higher value of $\lambda$ corresponds to a stronger weight on the penalty term, and consequently a smoother two-dimensional MI surface. For the variance parameter $\sigma ^2$, the empirical distribution is mostly symmetric and stable, with a mean of $2.6424 \times 10^{-4}$ and a variance of $6.1191 \times 10^{-11}$.

Fig. 3

The empirical posterior distribution of $\sigma ^2$ (left) and $\lambda$ (right), generated by 5000 drawn samples

Figure 4 depicts the posterior distribution of three selected $\beta$ parameters. Recall from Eq. (6) that $\beta$ parameters are the coefficients of basis functions. We have used $c_a=16$ basis functions with knots evenly spaced over the age range 35–99, and $c_y=12$ basis functions with knots evenly spaced over the sample period 1982–2018 and also on the external years 2030 and 2042, which in total produces $c_a c_y=192$ numbers of $\beta$ parameters. Since LASSO penalty will shrink certain coefficients to zero, not all of the estimated $\beta$ parameters have non-zero values. Further, because Bayesian estimation is used, the $\beta$ parameters that should have a value of zero will instead have a posterior distribution concentrated around a mean of zero. Other $\beta$ parameters may have a posterior distribution with either a positive or negative mean. The three selected $\beta$ parameters shown in Fig. 4 correspond to these three cases.

Fig. 4

The empirical posterior distribution of three selected $\beta$ parameters with a mean of negative (left), zero (middle) and positive (right) value, generated by 5000 drawn samples

5.3 Projection results

We now examine the projected MI rates, the projected central death rates, and also the smooth transition between the historical values in the dataset and the intermediate-term and long-term rates given by external opinions.

Figure 5 illustrates the estimated and projected two-dimensional MI rates produced by the proposed cubic B-spline model. Compared to Fig. 2 which depicts the raw data, the surface plot (left panel) shows that our model is able to generate a smooth two-dimensional MI surface. From the heat map (right panel), we observe that the smoothed and projected MI rates are not only age- and time-dependent, but also exhibit cohort effects as indicated by the ‘hot’ and ‘cold’ regions formed diagonally. Moreover, one can observe that the short-term MI trends shown in recent observations fade away over time, and the projected MI rates smoothly converge to the intermediate-term and long-term rates.

Fig. 5

The smoothed and projected two-dimensional MI rates shown in a surface plot (left) and a heat map (right)

The smooth transition between recent observations and external rates is further examined in Fig. 6. We use fan charts to show the posterior distribution of the estimated and projected MI rates for ages 45, 55, 65 and 75. The gray fan charts represent the estimated historical rates and the externally given rates, while the green fan charts represent the projected rates. The mean of the posterior predictive distribution is displayed by a solid red line. As shown in Fig. 6, the projected MI rates are smoothly transitioned from recent observations (ended at year 2018) to the intermediate-term rates (in year 2030), and then ultimately converged to the long-term rates (in year 2042). More specifically, the green fan chart shows that the projected MI rates for years 2019–2029 are heavily driven by the MI trends formed before year 2018, but will eventually connect to the intermediate-term rate in year 2030. After year 2030, the projected MI rates are further extended to the long-term rate in year 2042, following the smooth pattern of previous projections.

Fig. 6

Fan charts showing the posterior distribution of the estimated and projected MI rates for ages 45, 55, 65 and 75. The gray fan charts depict the historical rates and the external rates, while the green fan charts represent the projected rates. The solid red line indicates the mean of the posterior predictive distribution

Figure 7 displays the posterior distribution of the projected log central death rates for ages 45, 55, 65 and 75. The mean forecasts are indicated by the darkest region in the center of the fan charts, while the level of uncertainty surrounding the mean forecasts is represented by the width of the fan charts. From Fig. 7, we observe that there is a smooth transition of mortality changes in the projection period. For the first few years after 2018, the projected rates follow the trend indicated by the observed values before year 2018. This period corresponds to the first green fan chart region in Fig. 6 for years 2019–2029. As the projection passes through year 2030, the rate of mortality changes starts to follow the intermediate-term rate, and then ultimately approach to the long-term rate.

Fig. 7

Fan charts showing the posterior distribution of the projected log central death rates for ages 45, 55, 65 and 75. The observed rates in the unsmoothed raw data are indicated by a black solid line

To further examine the composition of the uncertainty surrounding the mean forecasts, we show two sets of predictive intervals at the 90% confidence level for ages 45, 55, 65 and 75 in Fig. 8. The one with solid lines represents the predictive intervals with uncertainty generated from $\beta$ parameters only, while the one with dash lines includes the uncertainty added from random noises. Recall from Eq. (6) that the spline mortality model is subject to random normal noises $z_{x,t}$. From Fig. 8, we observe that the impact of $z_{x,t}$ on predictive intervals is obvious, but not as significant as the uncertainty generated by $\beta$ parameters.

Fig. 8

The 90% predictive intervals of the projected log central death rates for ages 45, 55, 65 and 75, with and without the uncertainty generated from the random noise $z_{x,t}$

We now compare the projected rates between our Bayesian spline model and the MIM-2021 model. Figure 9 shows the log central death rates projected by the MIM-2021 model, and also those projected by our Bayesian spline model with 90% predictive intervals and random noises. First, we observe that, while the projected rates are different between the two models, the ones projected by the MIM-2021 model lie within the 90% predictive intervals of our model. Second, unreasonable projection trends could be produced by the MIM-2021 model. More specially, for age 45, we see that the MIM-2021 model’s projected death rates are increasing for the first few years. Such trend clearly does not align with the historical rates from the SSA dataset. A similar situation can also be observed for age 55, where the decreasing trend is much slower than the one formed by recent historical rates. Third, we remark that the MIM-2021 model is only able to generate the mean forecasts but not the predictive intervals.

Fig. 9

Projected log central death rates for ages 45, 55, 65 and 75, produced by the MIM-2021 model (red dashed line) and our Bayesian spline model with 90% predictive intervals (blue lines)

5.4 The impact of external opinions

In this subsection, we use two different modeling scenarios to showcase the flexibility of the proposed model in incorporating external opinions. In particular, we consider (a) the baseline scenario, which uses the same model settings as in the previous subsections, (b) Scenario I, in which multiple years of external rates are given, and (c) Scenario II, in which multiple external opinions for the same years are given. Figure 10 shows the posterior distribution of the estimated and projected MI rates for age 55 under the baseline scenario and the two alternative scenarios.

Fig. 10

Fan charts showing the posterior distribution of the estimated and projected MI rates for age 55, using single year and single opinion of external rates (Baseline), multiple years of external rates (Scenario I), and multiple opinions of external rates (Scenario II)

Scenario I represents the case that the modeler wants to specify multiple years of intermediate-term and long-term MI rates from external sources. Our model can accommodate this situation by simply adding multiple years of external rates to the synthetic dataset, as discussed in Sect. 3.3. Panel (b) of Fig. 10 shows the Bayesian estimation and projection results for age 55, assuming that the intermediate-term rates for years 2029–2031 and the long-term rates for years 2041–2043 are externally given. Compared to the baseline scenario shown in panel (a), a lower level of uncertainty is observed for years that have external information available in its own or adjacent years. The mean forecast still follows the trend of recent observations, and smoothly connects to the intermediate-term and long-term rates over time.

Scenario II represents the case that the modeler wants to specify multiple external opinions for the same intermediate-term and long-term years. In practice, the modeler may collect multiple opinions about future MI rates. As discussed in Sect. 3.3, by treating these opinions as multiple inputs for the same year in the synthetic dataset, the proposed model is able to simultaneously incorporate all of them. If similar values are provided by multiple opinions, then the model should reflect the fact that we are highly confident about the MI rates of those years. Panel (c) of Fig. 10 shows the results for age 55, assuming that the modeler has collected 10 sets of the same opinions for the intermediate-term year 2030 and the long-term year 2042. It is clear that, when multiple external opinions are used, the level of uncertainty surrounding the mean forecast greatly decreases comparing to the baseline scenario.

5.5 The impact of basis functions

We now examine the impact of basis functions on the projected MI rates. Depending the modeler’s prior beliefs, a different transition rate might be desired between historical values and external rates. For example, assuming that a recent mortality shock was observed in historical values, the modeler may believe that the shock is transitional and will soon fade away while converging to the external rates. Conversely, the modeler may also believe that the shock will last for a while or even further extend to a more extreme shock before connecting back to the external rates. Moreover, as a practical need, the MIM-2021 model also allows the user to specify an external transition rate at the beginning of the projection period. Under the proposed B-spline model, we can change the location of basis functions and knots to achieve this modeling requirement.

Figure 11 shows the posterior distribution of the estimated and projected MI rates for age 55, with basis functions and knots placed in (a) year 2018 (Baseline), (b) year 2015 (Case I), and (c) year 2021 (Case II). The other basis functions used in the sample period and the external years are unchanged. Note that the basis functions and knots are no longer evenly spaced over the sample period under Case I and Case II.

Fig. 11

Fan charts showing the posterior distribution of the estimated and projected MI rates for age 55 when basis functions are used in year 2018 (Baseline), year 2015 (Case I), and year 2021 (Case II)

For Case I, panel (b) of Fig. 11 shows that the rate of convergence from the historical values before year 2018 to the intermediate-term rate in year 2030 is faster than that of the baseline case. The transition during years 2019–2029 is smoother and less volatile, and the erratic MI trend observed during years 2003–2018 has little impact on the projected MI rates. In contrast, the results of Case II shown in panel (c) of Fig. 11 indicate a more pronounced transition from the historical years to the intermediate-term year. The recent erratic MI trend is projected to continue for about 5 more years, and will then converge to the external intermediate-term rate. Lastly, note that the estimated MI rates before year 2013 are largely unchanged among the three cases, because the basis functions used before year 2013 are the same.

5.6 The impact of penalty choice

We now compare the impact of penalty choice for a spline model on the estimation and projection results. Figure 12 shows the posterior distribution of the estimated and projected MI rates for age 55 when the penalty used is (a) LASSO (left penal), (b) P-spline with an order of 2 (middle penal), and (c) no penalty (right penal).

From panel (b), we see that the MI rates projected by a P-spline model with a penalty order of 2 have a linear upward trend that is extrapolated from the estimated rates before year 2018 (within the sample period). This outcome is expected because, as discussed previously in Sect. 3.2 and also in Currie et al. [8], a P-spline model’s penalty order greatly affects the projection results and setting the penalty order to 2 will produce a linear projection trend. Compared to panel (a) where the results from LASSO penalty is shown, we can conclude that our B-spline model with LASSO penalty is able to provide a higher level of flexibility in terms of the smoothness of both estimated and projected MI rates. This conclusion also confirms our objective for develo** a LASSO penalty for the Bayesian two-dimensional B-spline model.

Panel (c) of Fig. 12 shows the estimated and projected MI rates when no penalty is implemented. It is no surprise that the projection results are unreasonable under this case. The magnitude of the projected MI rates is outrageously large as compared to that of the LASSO and P-spline penalties. Thus, we conclude that a penalty function is certainly necessary when using a spline model to project future MI rates.

Fig. 12

Fan charts showing the posterior distribution of the estimated and projected MI rates for age 55 when the penalty used is a LASSO, b P-spline with an order of 2, and c no penalty

6 Conclusion

This paper proposed a two-dimensional cubic B-spline model for generating smooth projections of mortality improvement rates. Our study was motivated by the recently proposed MIM-2021 model, which generates mortality improvement scales for actuarial professions. To build a spline mortality model that addresses the shortcomings of the MIM-2021 model and also maintains its practical features, we adopted the two-dimensional B-spline approach proposed by Currie et al. [8]. To overcome the limitations of spline models in mortality forecasting, we implemented the LASSO penalty and Bayesian estimation for our model. The projected MI rates are smoothly transitioned from historical values with short-term trends to any externally given intermediate- and long-term rates. We numerically demonstrated the features of the proposed model using real mortality data and external opinions.

We acknowledge that the proposed model is subject to several caveats. First, a number of model inputs needs to be subjectively determined. Although we used Bayesian estimation and LASSO penalty to reduce the selection of smoothing parameter and penalty order, as a spline model, one still needs to subjectively specify the position of basis functions (as known as knot selection). We demonstrated that the position of basis functions can bring flexibility to the projected MI rates, but the selection process will require expert knowledge from the model user.

Second, the forecasting performance of our model is contingent on the quality of the external rates incorporated. To fulfill the practical needs of having intermediate- and long-term MI rates, our model projects future MI rates from historical values to any externally given ones. The accuracy of these long-term forecasts is thus highly driven by the quality of the external opinions used. We acknowledge that there are other mortality models that may statistically outperform our model, and do not claim that our model is better than others in term of forecasting performance. Instead, our objective is to provide a modeling approach that satisfies the requirements of actuarial professions for generating future MI rates.

Third, our numerical illustration does not include mortality data from the Covid-19 period. Given that the pandemic data is not fully collected yet, we choose to postpone the study of Covid-19 mortality data for future research. At the time of writing, the MIM-2021 model was updated to the MIM-2021-v2 model by the Society of Actuaries to include data from year 2019 and also adjustments for the pandemic effects. A future study could further analyze the proposed model using a complete Covid-19 mortality dataset along with the MIM-2021-v2 model.

Other future work may focus on addressing some of the other aforementioned limitations. For example, the model’s performance may be improved by considering other penalty options and basis functions, such as ridge regression [22], roughness penalty [15], or elastic net [45]. Further improvement options include applying LASSO regularization to pre-process mortality data [37], or applying elastic net to reduce dimensions in MI modeling [18]. Lastly, to strengthen the cohort effect in mortality dynamics, one may consider applying the proposed B-spline model on the age-cohort dimension instead of the age-period dimension.