SpringerLink
Log in

Free Vibration Frequencies of a Variable Cross-Section Timoshenko-Ehrenfest Beam using Fourier-p Element

  • Research Article-Mechanical Engineering
  • Published:
Arabian Journal for Science and Engineering Aims and scope Submit manuscript

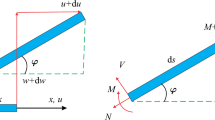
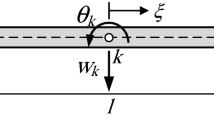
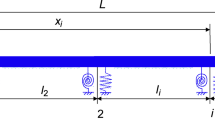
Abstract

An efficient method has been developed to analyze the natural frequencies of a Timoshenko-Ehrenfest beam with variable cross-sections undergoing free flexural vibration. The method uses a single element to discretize the beam and combines polynomial and trigonometric shape functions to represent the displacement fields, with the trigonometric shape functions representing the internal degrees of freedom (DOF) of the beam. By incorporating trigonometric shape functions as enriching functions alongside polynomials, the potential issues related to ill-conditioning associated with higher-order polynomials are avoided. The differential equations of motion for the free vibration are derived using Lagrange’s equation. The generalized eigenvalue problem is then formulated. Non-dimensional natural frequencies are computed considering different parameter variations such as taper ratios, shear deformation, rotary inertia parameters, as well as end conditions. Incorporating rotary inertia and shear deformation in the analysis of Timoshenko-Ehrenfest beam lowers its natural frequencies compared to simpler beam theories like Euler–Bernoulli. It is observed that as taper ratios increase, the beam’s mass decreases toward the tip, causing higher frequency parameter values for the fundamental mode. Increasing rotary inertia parameter leads to a decreasing trend in frequency parameters especially in higher modes. The combined effect of rotary inertia and tapering significantly reduces frequency parameter values for all modes, with the rotary inertia counteracting the tapering influence. The proposed Fourier-p element model accurately predicts Timoshenko-Ehrenfest beam frequencies with high precision compared to other existing models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Germany)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Abbreviations

A :

Cross-sectional area of the beam at an arbitrary location \(x\) (m2)

A 0 :

Cross-sectional area at the root of the beam \(= b_{ \circ } h_{ \circ }\) (m2)

[B]:

Strain displacement matrix

b :

Beam breadth at an arbitrary location \(x\) (m)

b 0 :

Beam breadth at the root of the beam (m)

E :

Modulus of elasticity (N/m2)

G :

Modulus of rigidity (N/m2)

h :

Beam depth at an arbitrary location \(x\) (m)

h 0 :

Beam depth at the root of the beam (m)

I :

Second moment of area of the beam at an arbitrary location \(x\) (m4)

I 0 :

Second moment of area at the root (thick end) of the beam \(= \left( {{1 \mathord{\left/ {\vphantom {1 {12}}} \right. \kern-0pt} {12}}} \right)b_{ \circ } h_{ \circ }^{3}\) (m4)

j :

Number of trigonometric terms used

[K]:

Stiffness matrix \(= \left[ {K_{e} } \right] + \left[ {K_{s} } \right]\) (N/m)

[K e]:

Elastic stiffness matrix (N/m)

[K s]:

Shear stiffness matrix (N/m)

\(\kappa\) :

Shear correction factor

L :

Length of the beam (m)

\(\fancyscript{L}\) :

Lagrangian

[M]:

Mass matrix \(= \left[ {M_{t} } \right] + \left[ {M_{r} } \right]\) (kg)

[M t]:

Translational mass matrix (kg)

[M r]:

Rotary inertia mass matrix (kg)

n :

Number of terms used in the Fourier shape functions

\(\left[ {N_{w} } \right]\) :

Transverse displacement shape functions matrix

\(\left[ {N_{\theta } } \right]\) :

Rotation shape functions matrix

\(r_{g}\) :

Radius of gyration of the cross section \(= \sqrt {{I \mathord{\left/ {\vphantom {I A}} \right. \kern-0pt} A}}\) (m)

\(\overline{r}_{g}\) :

Rotary inertia parameter \(= {{r_{g} } \mathord{\left/ {\vphantom {{r_{g} } L}} \right. \kern-0pt} L}\)

\(\left\{ q \right\}\) :

Vector of nodal coordinates (m)

\(\left\{ {\overline{q}} \right\}\) :

Vector of displacement amplitudes of vibration (m)

T :

Kinetic energy (J)

t :

Time (s)

U :

Strain energy (J)

\(\gamma\) :

Shear strain (rad)

\(\varepsilon\) :

Normal strain

\(u_{x}\), \(u_{z}\) :

Components of the displacement vector in the two coordinate directions \(x\) and \(z\) (m)

\(\theta\) :

Rotation angle due to bending (rad)

\(\nu\) :

Poisson’s ratio

\(\rho\) :

Mass density (Kg/m3)

\(\sigma\) :

Normal stress (N/m2)

\(\tau\) :

Shear stress (N/m2)

\(\tau_{b}\) :

Breadth taper ratio

\(\tau_{h}\) :

Depth taper ratio

\(\omega\) :

Natural frequency (rad/s)

\(\overline{\omega }\) :

Frequency parameter \(= \omega L^{2} \sqrt {{{\rho A_{ \circ } } \mathord{\left/ {\vphantom {{\rho A_{ \circ } } {EI_{ \circ } }}} \right. \kern-0pt} {EI_{ \circ } }}}\)

\(\zeta\) :

Non-dimensional length \(= {x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}\)

\(\left[ {} \right]^{T}\) :

Transpose of []

References

  1. Bazoune, A.: Survey on modal frequencies of centrifugally stiffened beams. Shock Vib. Dig. 37(6), 449–469 (2005). https://doi.org/10.1177/0583102405056752

    Article  Google Scholar 

  2. Downs, B.: Transverse vibrations of cantilever beams having unequal breadth and depth tapers. J. Appl. Mech. 44(4), 737–742 (1977). https://doi.org/10.1115/1.3424165

    Article  ADS  Google Scholar 

  3. Downs, B.: Reference frequencies for the validation of numerical solutions of vibrations of non-uniform Beams. J. Sound Vib. 61(1), 71–78 (1978). https://doi.org/10.1016/0022-460X(78)90042-1

    Article  ADS  Google Scholar 

  4. Leung, A.Y.T.; Zhou, W.E.: Dynamic stiffness analysis of non-uniform Timoshenko beams. J. Sound Vib. 181(3), 447–456 (1995). https://doi.org/10.1006/jsvi.1995.0151

    Article  ADS  Google Scholar 

  5. Eisenberger, M.: Dynamic stiffness matrix for variable cross-section Timoshenko beams. Commun. Numer. Methods Eng. 11, 507–513 (1995). https://doi.org/10.1002/CNM.1640110605

    Article  ADS  Google Scholar 

  6. Banerjee, J.R.; Su, H.; Jackson, D.R.: Free vibration of rotating tapered beams using the dynamic stiffness method. J. Sound Vib. 298, 1034–1054 (2006). https://doi.org/10.1016/j.jsv.2006.06.040

    Article  ADS  Google Scholar 

  7. Yuan, S.; Ye, K.; **ao, C.; Williams, F.W.; Kennedy, D.: Exact dynamic stiffness method for non-uniform Timoshenko beam vibrations and Bernoulli-Euler column buckling. J. Sound Vib. 303, 526–537 (2007). https://doi.org/10.1016/j.jsv.2007.01.036

    Article  ADS  Google Scholar 

  8. Lee, J.W.; Lee, J.Y.: Free vibration analysis using the transfer-matrix method on a tapered beam. Comput. Struct. 164, 75–82 (2016). https://doi.org/10.1016/j.compstruc.2015.11.007

    Article  Google Scholar 

  9. Lee, J.W.: Free vibration analysis of tapered Rayleigh beams using the transfer matrix method. Science 42, 612 (2020). https://doi.org/10.1007/s40430-020-02697-5

    Article  Google Scholar 

  10. Keshmiri, A.; Wu, N.; Wang, Q.: Free vibration analysis of a nonlinearly tapered cone beam by Adomian decomposition method. Int. J. Struct. Stab. Dyn. 18(7), 1850101 (2018). https://doi.org/10.1142/S0219455418501018

    Article  MathSciNet  Google Scholar 

  11. Hsu, J.C.; Lai, H.Y.; Chen, C.K.: An innovative eigenvalue problem solver for free vibration of uniform Timoshenko beams by using the Adomian modified decomposition method. J. Sound Vib. 325, 451–470 (2009). https://doi.org/10.1016/j.jsv.2009.03.015

    Article  ADS  Google Scholar 

  12. Korabathina, R.; Koppanati, M.S.: Linear free vibration analysis of tapered Timoshenko beams using coupled displacement field method. Math. Models Eng. 2(1), 27–33 (2016)

    Google Scholar 

  13. Laura, P.A.A.; Gutierrez, R.H.: Analysis of vibrating Timoshenko beams using the method of differential quadrature. Shock. Vib. 1(1), 89–93 (1993). https://doi.org/10.3233/SAV-1993-1111

    Article  Google Scholar 

  14. Zhou, D.; Cheung, Y.K.: Vibrations of tapered Timoshenko beams in terms of static Timoshenko beam functions. J. Appl. Mech. 68(4), 596–602 (2001). https://doi.org/10.1115/1.1357164

    Article  CAS  ADS  Google Scholar 

  15. Sohani, F.; Eipakchi, H.R.: Analytical solution for modal analysis of Euler-Bernoulli and Timoshenko beam with an arbitrary varying cross-section. Math. Models Eng. 4(3), 164–174 (2018)

    Article  Google Scholar 

  16. Civalek, Ö.; Kiracioglu, O.: Free vibration analysis of Timoshenko beams by DSC method. Int. J. Numer. Methods Biomed. Eng. 26, 1890–1898 (2010). https://doi.org/10.1002/cnm.1279

    Article  Google Scholar 

  17. Ghannadiasl, A.: Natural frequencies of the elastically end restrained non-uniform Timoshenko beam using the power series method. Mech. Based Des. Struct. Mach. 47(8), 1–14 (2018). https://doi.org/10.1080/15397734.2018.1526691

    Article  Google Scholar 

  18. Ruta, P.: The application of Chebyshev polynomials to the solution of the nonprismatic Timoshenko beam vibration problem. J. Sound Vib. 296, 243–263 (2006). https://doi.org/10.1016/j.jsv.2006.02.011

    Article  ADS  Google Scholar 

  19. Attarnejad, R.; Semnani, S.J.; Shahba, A.: Basic displacement functions for free vibration analysis of non-prismatic Timoshenko beams. Finite Elem. Anal. Des. 46, 916–929 (2010). https://doi.org/10.1016/j.finel.2010.06.005

    Article  MathSciNet  Google Scholar 

  20. Lee, J.; Schultz, W.W.: Eigenvalue analysis of Timoshenko beams and axisymmetric Mindlin plates by the pseudospectral method. J. Sound Vib. 269(3–5), 609–621 (2004). https://doi.org/10.1016/S0022-460X(03)00047-6

    Article  ADS  Google Scholar 

  21. Lee, S.J.; Park, K.S.: Vibrations of Timoshenko beams with isogeometric approach. Appl. Math. Model. 37, 9174–9190 (2013). https://doi.org/10.1016/j.apm.2013.04.034

    Article  MathSciNet  Google Scholar 

  22. Lee, B.K.; Oh, S.J.; Lee, T.E.: Free vibration of tapered Timoshenko beams by deformation decomposition. Int. J. Struct. Stab. Dyn. 13(2), 1250057 (2013). https://doi.org/10.1142/S0219455412500575

    Article  MathSciNet  Google Scholar 

  23. Providakis, C.P.; Beskos, D.E.: Dynamic analysis of beams by the boundary element method. Comput. Struct. 22(6), 957–964 (1986). https://doi.org/10.1016/0045-7949(86)90155-0

    Article  Google Scholar 

  24. Thomas, D.L.; Wilson, J.M.; Wilson, R.R.: Timoshenko beam finite elements. J. Sound Vib. 31(3), 315–330 (1973). https://doi.org/10.1016/S0022-460X(73)80276-7

    Article  ADS  Google Scholar 

  25. Thomas, J.; Abbas, B.A.H.: Finite element model for dynamic analysis of Timoshenko beam. J. Sound Vib. 41(3), 291–299 (1975). https://doi.org/10.1016/S0022-460X(75)80176-3

    Article  ADS  Google Scholar 

  26. Dawe, D.J.: A finite element for the vibration analysis of Timoshenko beams. J. Sound Vib. 60(1), 11–20 (1978). https://doi.org/10.1016/0022-460X(78)90397-8

    Article  ADS  Google Scholar 

  27. To, C.W.S.: A linearly tapered beam finite element incorporating shear deformation and rotary inertia for vibration analysis. J. Sound Vib. 78(4), 475–484 (1981). https://doi.org/10.1016/S0022-460X(81)80118-6

    Article  ADS  Google Scholar 

  28. Lees, A.W.; Thomas, D.L.: Unified Timoshenko beam finite element. J. Sound Vib. 80(3), 355–366 (1982). https://doi.org/10.1016/0022-460X(82)90276-0

    Article  ADS  Google Scholar 

  29. Cleghorn, W.L.; Tabarrok, B.: Finite element formulation of a tapered Timoshenko beam for free lateral vibration analysis. J. Sound Vib. 152(3), 461–470 (1992). https://doi.org/10.1016/0022-460X(92)90481-C

    Article  ADS  Google Scholar 

  30. Bazoune, A.; Khulief, Y.A.: A finite beam element for vibration analysis or rotating tapered Timoshenko beam. J. Sound Vib. 156, 141–164 (1992). https://doi.org/10.1016/0022-460X(92)90817-H

    Article  ADS  Google Scholar 

  31. Khulief, Y.A.; Bazoune, A.: Frequencies of rotating tapered Timoshenko beams with different boundary conditions. Comput. Struct. 42(5), 781–795 (1992). https://doi.org/10.1016/0045-7949(92)90189-7

    Article  Google Scholar 

  32. Friedman, Z.; Kosmatka, J.B.: An improved two node Timoshenko beam finite element method. Comput. Struct. 47(3), 473–481 (1993). https://doi.org/10.1016/0045-7949(93)90243-7

    Article  ADS  Google Scholar 

  33. Kosmatka, J.B.: An improved two node finite element method for stability and natural frequencies of axial-loaded Timoshenko beams. Comput. Struct. 51(1), 141–149 (1995). https://doi.org/10.1016/0045-7949(94)00595-T

    Article  Google Scholar 

  34. Reddy, J.N.: On the dynamic behaviour of the Timoshenko beam finite elements. Sadhana 24, 175–198 (1999). https://doi.org/10.1007/BF02745800

    Article  MathSciNet  Google Scholar 

  35. Day, D.: Software for the verification of Timoshenko beam finite elements. Adv. Eng. Softw. 127, 90–95 (2019). https://doi.org/10.1016/j.advengsoft.2018.08.015

    Article  Google Scholar 

  36. Sahin, S.; Karahan, E.; Kilic, B.; Ozdemir, O.: Finite element method for vibration analysis of Timoshenko beams. In: 9th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, pp. 673–679 (2019), https://doi.org/10.1109/RAST.2019.8767827

  37. Sujuan, J.; Jun, L.; Hongxing, H.; Rongying, S.: A spectral finite element model for vibration analysis of a beam based on general higher-order theory. Shock. Vib. 15, 179–192 (2008). https://doi.org/10.1155/2008/953639

    Article  Google Scholar 

  38. Chen, G.; Qian, L.; Yin, Q.: Dynamic analysis of a Timoshenko beam subjected to an accelerating mass using spectral element method. Shock Vib. 2, 12 (2014). https://doi.org/10.1155/2014/768209

    Article  Google Scholar 

  39. Hamioud, S.; Khalfallah, S.: Spectral element analysis of free vibration of Timoshenko beam. Int. J. Eng. Modell. 31(1–2), 61–76 (2018). https://doi.org/10.31534/engmod.2018.1-2.ri.01_vjan

    Article  Google Scholar 

  40. Banerjee, J.R.; Ananthapuvirajah, A.: Free flexural vibration of tapered beams. Comput. Struct. 224, 106106 (2019). https://doi.org/10.1016/j.compstruc.2019.106106

    Article  Google Scholar 

  41. Houmat, A.: Vibrations of Timoshenko beams by variable order finite elements. J. Sound Vib. 187(5), 841–849 (1995). https://doi.org/10.1006/jsvi.1995.0567

    Article  ADS  Google Scholar 

  42. Leung, A.Y.T.; Chan, J.K.W.: Fourier p-element for the analysis of beams and plates. J. Sound Vib. 212(1), 179–185 (1998). https://doi.org/10.1006/jsvi.1997.1423

    Article  ADS  Google Scholar 

  43. Cherif, S.M.H.: Free vibration analysis of rotating flexible beams by using the Fourier p-version of the finite element method. Int. J. Comput. Methods 2(2), 255–269 (2005). https://doi.org/10.1142/S0219876205000466

    Article  Google Scholar 

  44. Gunda, J.B.; Singh, A.P.; Chhabra, P.S.; Ganguli, R.: Free vibration analysis of rotating tapered blades using Fourier-p superelement. Struct. Eng. Mech. 27(2), 243–257 (2007). https://doi.org/10.12989/sem.2007.27.2.243

    Article  Google Scholar 

  45. Khan, M.U.: Vibration analysis of rotating tapered Timoshenko beam using Fourier–\(p\) superelement, Master Thesis, King Fahd University of Petroleum & Minerals, Dhahran, Saudi Arabia (2021).

  46. Banerjee, J.R.; Kennedy, D.; Elishakoff, I.: Further insights into the Timoshenko-Ehrenfest beam theory. ASME. J. Vib. Acoust. 144(6), 061011 (2022). https://doi.org/10.1115/1.4055974

    Article  Google Scholar 

  47. Bazoune, A.; Combined influence of rotary inertia and shear coefficient on flexural frequencies of Timoshenko beam: Numerical experiments. Acta. Mech. (2023) 234, 4997–5013. https://doi.org/10.1007/s00707-023-03648-6

    Article  Google Scholar 

  48. Rossi, R.E.; Laura, P.A.A.: Numerical experiments on vibrating, linearly tapered Timoshenko beams. J. Sound Vib. 168(1), 179–183 (1993). https://doi.org/10.1006/jsvi.1993.1398

    Article  ADS  Google Scholar 

  49. Ozgumus, O.O.; Kaya, M.O.: Flapwise bending vibration analysis of a rotating double-tapered Timoshenko beam. Arch. Appl. Mech. 78, 379–392 (2008). https://doi.org/10.1007/s00419-007-0158-5

    Article  ADS  Google Scholar 

  50. Ghafarian, M.; Ariaei, A.: Free Vibration analysis of a system of elastically interconnecting rotating tapered Timoshenko beams using differential transform method. Int. J. Mech. Sci. 107, 93–109 (2016). https://doi.org/10.1016/j.ijmecsci.2015.12.027

    Article  Google Scholar 

  51. Filipich, C.P.; Rosales, M.B.; Cortinez, V.H.: Natural frequencies of a Timoshenko beam: exact values by means of a generalized solution. Mecánica Computacional 14(1), 134–143 (1994)

    Google Scholar 

  52. Bhashyam, G.R.; Prathap, G.: The second frequency spectrum of Timoshenko beams. J. Sound Vib. 76(3), 407–420 (1981). https://doi.org/10.1016/0022-460X(81)90520-4

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The support of King Fahd University of Petroleum & Minerals is greatly appreciated.

Author information

Authors and Affiliations

  1. Mechanical Engineering Department, King Fahd University of Petroleum and Minerals, KFUPM BOX 579, 31261, Dhahran, Saudi Arabia

    Abdelaziz Bazoune

Authors
  1. Abdelaziz Bazoune
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Abdelaziz Bazoune.

Appendix

Appendix

The non-zeros entries of the beam enriched Fourier-\(p\) element shape functions are given by

$$\begin{aligned} & N_{w1} = N_{\theta 2} = \frac{1}{24}\left( {24 - 274\xi + 1125\xi^{2} - 2125\xi^{3} + 1875\xi^{4} - 625\xi^{5} } \right) \\ & N_{w3} = N_{\theta 4} = \frac{1}{24}\left( {600\xi - 3850\xi^{2} + 8875\xi^{3} - 8750\xi^{4} + 3125\xi^{5} } \right) \\ & N_{w5} = N_{\theta 6} = \frac{1}{12}\left( { - 300\xi + 2675\xi^{2} - 7375\xi^{3} - 8125\xi^{4} - 3125\xi^{5} } \right) \\ & N_{w7} = N_{\theta 8} = \frac{1}{12}\left( {200\xi + 1950\xi^{2} + 6125\xi^{3} - 7500\xi^{4} + 3125\xi^{5} } \right) \\ & N_{wj1} = N_{\theta j2} = \sin \left( {j\pi \xi } \right) \\ & N_{w9} = N_{\theta 10} = \frac{1}{24}\left( { - 150\xi + 1525\xi^{2} - 5125\xi^{3} + 6875\xi^{4} - 3125\xi^{5} } \right) \\ & N_{w11} = N_{\theta 12} = \frac{1}{24}\left( {24\xi - 250\xi^{2} + 875\xi^{3} - 1250\xi^{4} + 625\xi^{5} } \right) \\ \end{aligned}$$

where \(\xi = {x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L};\;\left( {0 \le \xi \le 1} \right)\) is the non-dimensional length.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bazoune, A. Free Vibration Frequencies of a Variable Cross-Section Timoshenko-Ehrenfest Beam using Fourier-p Element. Arab J Sci Eng 49, 2831–2851 (2024). https://doi.org/10.1007/s13369-023-08289-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13369-023-08289-4

Keywords

Search

Navigation