Optimization of integrated production scheduling and vehicle routing problem with batch delivery to multiple customers in supply chain

Abstract

In supply chain literature, production coordination and vehicle routing have received a lot of attention. Even though all functions in the supply chain are interrelated, they are normally handled independently. This disconnected approach might lead to less-than-ideal outcomes. Increasing total efficiency by integrating manufacturing and delivery scheduling processes is popular. This study focuses on synchronic production–distribution scheduling difficulties, particularly permutation flow shop scheduling in production and sequence-dependent setup time (SDST) and vehicle routing alternatives in distribution. To create a cost-effective distribution among the placement of geographically separated clients and hence to minimize delivery costs, batch delivery to customers employing a succession of homogenized capacity limitation vehicles is examined here. However, this might result in the failure to complete multiple client orders before their deadlines, raising the cost of lateness. As a result, the goal of this study is to lower the overall cost of tardiness and batch distribution in the supply chain. To accomplish so, a mixed-integer nonlinear programming model is developed, and the model is solved using a suggested genetic algorithm (GA). Because there is no established benchmark for this issue, a set of genuine problem scenarios is created in order to assess the proposed GA in a viable and difficult environment. Ruiz's benchmark data, which is derived from Taillard's benchmark cases of permutation flow shops, was supplemented with SDSTs in the production of test examples. In comparison to an exact method, the results show that the proposed GA can rapidly seek solutions to optimality for most small-sized instances. Furthermore, for medium and large-scale cases, the proposed GA continues to work well and produces solutions in a fair amount of time in comparison to GA without the local search.

1 Introduction

The majority of supply and operations management research has divided production processes into two categories: make-to-order (MTO) and make-to-stock (MTS) production systems [19]. An MTO production environment is more tailored to the consumer's needs and often produces high-priced products. Order acceptance or rejection assessments and configuration of production capacity, order arrival timeline, and distribution time or due dates are all part of the production planning in MTO [21]. On the other hand, MTS manufacturing processes tend to focus on lower-cost, lower-selection goods. A traditional MTS system's production preparation considers forecasting demands, how to satisfy those demands, the size of each component's batch, and the production cycle duration. The most important aspect of MTO is the efficient and productive utilization of available capacity to meet consumer demands. To improve the consumer experience in such manufacturing processes, goods are advised to be shipped once they are finished in an assembly line to meet the consumers' timetable or schedule, resulting in high delivery costs. A cost–benefit analysis of the cost of lateness and the cost of delivery was intended for the necessity of combining output and distribution in MTO industries; when making tactical decisions, a trade-off between lateness and delivery costs should be considered [34].

Extensive collaboration through the supply chain's various stages is essential to maintain a high-performing overall structure and meet consumer expectations and demands. According to Ulrich (2013), a mean improvement between 5 and 20% may result in integration at the tactical judgment stage compared to an uncoordinated strategy. Traditional VRP must be included in production planning for organizational level manufacturing and distribution concerns, notably schedule preparation issues. Orders must be conveyed using a vehicle's fleet to a group of geographically dispersed clients at one or more depots, using a network to construct routes that meet all the customer's standards in conventional VRP. Even though development and vehicle route scheduling difficulties have been well-studied in the literature, integrating the two has gotten less attention.

The permutation flow shop scheduling problem (PFSP) has received a lot of attention in the last few decades [35]. The PFSP has been investigated utilizing several conditions to reduce the make span [31]. Any set of customer orders to be shipped in a single trip is referred to as a "batch," and after the production of any sequence of customer orders in a batch is completed, they are allocated to different customers in the same order. Batch delivery to multiple customers becomes substantially more complex because PFSP is proven to be powerfully NP-complete with two or more machines by mixing production and delivery decisions in a PFSP with batch supply to multiple clients (Kai [33]. In the study of Qin et al. [18], products are firstly produced in a number of distributed hybrid flow shops (HFS) and then delivered to a customer in batches. Setup times, on the other hand, are normally negligible. It is important to consider the impact of sequence-dependent setup operations when deciding on a schedule. As a result, integrating it into models might be a promising research direction. Any configuration operations dependent on the ordering of these two customer orders should be conducted between the processes of two consecutive customer orders on similar devices. Setup activities, such as cleaning or replacing appliances, do not seem to be expected except between orders in a variety of practical situations, such as printing, chemical, automobile manufacturing, and pharmaceutical, but rather heavily reliant on the immediately preceding procedure on the same system. Given the above, we incorporate sequence-dependent setup time (SDST) into our problem to bridge the distance between the proposal and the following.

Since integrated output scheduling-vehicle routing issues are complex, solving vast instances of those problems with real solutions is incredibly difficult. Exact techniques are mostly applicable for small-sized problems [14]. To solve large scheduling vehicle routing problems, most studies use metaheuristics such as simulated annealing, genetic algorithm (GA), particle swarm optimization, ant colony optimization, tabu search, differential evolution, and so on [26]. Compared with the other algorithms, GAs are more widely used as a solution approach [14]. Because it is difficult to solve and impossible to obtain optimal solutions, particularly for large-scale instances, a hybridized version of GA, i.e., GA with local search, is proposed here.

The hybrid GA is also known as memetic algorithm (MA), which is simple to design and implement and effectively solve complex optimization problems [19]. In GA, using a population of solutions allows seeking in several directions. However, a lack of sufficient intensification prompts researchers to consider a different approach with more powerful search operators. MAs combines the advantages of GAs with the inclusion of a local search engine to boost intensification. MAs have recently gotten a lot of attention from the evolutionary computation community (ECC). They've been proved to be promising and successful at addressing challenging optimization issues in various application areas [3]. Since its birth in the late 1980s, MA and, in general, methodologies underpinning the broader Memetic Computing (MC) paradigm have been at the center of a frenetic research effort. MAs have evolved rapidly to produce techniques with sophisticated cooperative mechanisms, combining modern population-based metaheuristics (such as evolutionary algorithms, swarm methods, and others) with trajectory-based techniques (such as variable neighborhood search, simulated annealing, tabu search), and other constructive algorithms (such as GRASP, branch and bound, backtracking, etc.). Furthermore, even though they were established some decades ago, the MC study fields continue to attract a lot of interest from the scientific community [16]. As a result, the memetic algorithm has become a common method for solving various engineering optimization problems, which has been considered accordingly in this work. To the authors’ knowledge, there has been no investigation of the issue of reducing the overall cost of tardiness and batch distribution to multiple customers, considering production scheduling and vehicle routing problems simultaneously. More specifically, the contributions of this study can be summarized as follows:

• A new integrated scheduling system in a PFSP considering SDST and vehicle routing issues is proposed to reduce lateness and batch distribution costs to various supply chain customers.

• A novel mixed-integer nonlinear programming model (MINLP) is developed to determine the best solution to the problem at hand.

• To solve the model, a hybrid GA (i.e., memetic algorithm) is proposed to solve a realistic problem–instances to achieve efficient or near-optimal solutions.

To determine the effectiveness of the proposed approach, numerical experiments are conducted to analyses the efficacy of the proposed approach. The remainder of the work is organized as follows. The study on joined production and distribution planning and routing decisions is reviewed in the following section. Section three demonstrates the formal definition and conclusions of an interconnected problem and explains the proposed MINLP formulation for the problem at hand, along with an illustrative illustration. The suggested algorithm's key points are revealed in section four. Section five discusses the findings and interpretation of scientific trials, including the comparative results of algorithms. Conclusions and possible directions are presented in section six.

2 Relevant literature

Production and delivery are two interconnected functions of the supply chain, with the latter beginning as soon as the final order of the production function is accomplished. These two issues of scheduling have traditionally been resolved sequentially and discretely. Integration can solve the problem of suboptimality by combining the two problems into one. Several scholars including explain the whys and wherefores of companies choosing an uncoordinated solution over an integrated one. These decisions are initially made by various departments or several businesses, like third-party logistic service providers. Second, a VRP for distribution planning architecture, for example, is impossible to overcome on its own and is a different issue. Third, inventory buffers between certain roles are normally separated to minimize the need to combine the supply chain's production scheduling and functions of distribution.

However, to further exploit resources and compete in the globalized economy, there is a growing need to lessen these intermediate buffer inventories. As a result, companies are increasingly moving toward a just-in-time (JIT) strategy in which delivery delays will cause major glitches at the customer's site. Still, there is no point in preventing this situation at the expense of high transportation costs. Integration of production and distribution into a single problem would be desirable. An integrated approach would be appreciated, particularly for perishable or time-sensitive products [30]. Newspapers, diet, ready-mixed concrete, pharmacy, and commercial adhesive materials are examples of products for which an optimized method is used. This paper integrates experiments focusing on batch processing and initialization time in various machine environments. These two manufacturing characteristics requirements were chosen because they substantially affect the method of manufacturing orders instead of other aspects, such as production costs and periods.

2.1 Production scheduling and delivery under single machine environments

A single machine arrangement is used in the large command studies to fulfil customer orders, and several of those papers' customer orders are mixed into a batch. Setup operations are often ignored in single-machine reviews of production scheduling and vehicle routing problems (PS-VRPs), and they are not included in batch studies. Chang and Lee [5] investigated a condition of two consumer areas and a single unit environment in their analysis. Furthermore, Li et al. [11] investigated the overall situation for an extra two customers with a drag version of two customers. Chen and Vairaktarakis [7] investigated dual variants with several customers for a single machine environment. The problems vary depending on the output metric, such as mean or limited delivery time. Orders are generated one after the other in these three trials and then transmitted by a related vehicle driver. In the literature of Li et al. [11], it was assumed that a customer order could be shipped in one trip but that separate orders from the same client will be distributed in several trips. Wherever the aim is to lessen the overall time required to finish all the vehicle's deliveries and return to the depot and to reduce the sum of order delivery times at clients, respectively. Chen and Vairaktarakis [7] looked for ways to maximize the trade-off between delivery costs and the quality of consumer experience determined by distribution times.

The experiments described earlier with a machine environment of a single setting may not account for setting up operations. Park and Hong [17] investigated an optimized PS-VRP for inventory items that are only available for a single time, taking sequence-dependent configuration activities into account in a single manufacturing system that needs to process entirely separate iterations of a component. Since each version is produced only once, consumer orders for similar products are managed in a batch process. Customers are given a date on both soft and rough deliveries. A breach of the flexible deadline would result in a delay fee, while a hard deadline would result in a penalty. Split distributions with a single order do not seem appropriate, although where consumers order several items, it is possible to distribute each commodity by a different car. The MILP's goal is to reduce manufacturing, transportation, and delivery costs. Even though they considered SDST and batch processing of materials, the system environment was not advanced.

2.2 Production scheduling and delivery under a parallel machine environment

A parallel machine environment is used in around a third of the experiments on combined PS-VRPs. Such experiments are based on the use of similar parallel machines. Synchronal problems of standardized parallel machines are studied by Belo-Filho et al. [4]s. Chang et al. [6] are the first to examine unrelated parallel machines. Most studies process customer orders in batches, like those conducted in a single system environment, and set up operations are largely unnoticed. Any customer order, according to Ullrich, must be performed on one of the identical parallel machines, where time frames are thought of as rigid edges at the customer's geographical positions, as orders must be processed as quickly as possible [30]. Delay deliveries are permitted; however, the MILP's goal is to reduce overall order lateness to the absolute minimum. Batch loading and startup time was not taken into consideration in this research. Chen and Vairaktarakis [7] explore a parallel machine background in addition to a machine environment considering a single setting. For an analogous parallel machine configuration, two versions like those for the single machine setting that differ within the output metric, such as mean or most delivery time, are investigated. The balance of delivery costs and customer service level is considered a parameter of the objective, much as it is within the single system setup. Different orders from various consumers can be served on unrelated parallel machines, according to Chang et al.[6]. Both consumer orders delivered by a common vehicle are serialized, and batch produced. The developed nonlinear mathematical model's goal function is like that of Chen and Vairaktarakis [7], reducing the weighted combination of ship** times and net delivery costs.

Compared to prior research using an environment of the parallel machine, Farahani et al. [10] explored a combined PS-VRP for unpreserved food goods where a supplier produces many combinations of items that must be processed at completely various temperature ranges in one of the identical ovens. Many customer orders can be processed in real-time. In this analysis, the MILP is used to account for SDSTs and costs. The intention is to achieve a balance between ship** and setup costs while maintaining the quality of unpreserved food items.

2.3 Production scheduling and delivery under flow shop environment

Previous research, in general, investigated a relatively basic machine design where each customer order consists of a single and parallel machine production process, according to a careful study of the characteristics of the considered production environment. Since most experiments use a machine configuration of a single setting or a parallel resource configuration in parallel machine environments, where largely similar parallel machines are conceived of. Since several layers of a manufacturing environment, like job and flow shops, are frequently used for production operation, combining those with a distribution option like VRP would be an important forthcoming research path. Nonetheless, the interconnected problem can become more complicated to overcome because of these advanced machine settings. Metaheuristics are the most successful algorithms used to solve flow shop scheduling. In general, the metaheuristic algorithms are categorized into local search-based methods such as: Iterated greedy algorithm [23],tabu search and population-based algorithms such as artificial immune system and artificial bee colony. Recently, many heuristic techniques have been proposed to solve flow shops scheduling problems, such as the insertion of local search and constructive heuristics.

2.4 Vehicle routing problem in distribution in supply chain

Most research considers an undiversified fleet of vehicles when it comes to the transmission aspect of the interconnected issue. In recent years, analysts have assumed that the fleet is made up of a variety of vehicles of varying capabilities and/or prices. For example, Toptal et al.[29] investigated cost structure variability and time convenience. Nonetheless, since it is impossible to consolidate the different orders, vehicle routing is not considered in their analysis. Transportation times must be factored in to ensure a consistent on-time distribution. Moreover, most of the papers account for delivery costs, including multiple transportation costs depending on factors such as distance or time travelled and fixed transportation costs for renting a vehicle. Many of the surveys that do not include transit expenses have a service target. We prefer to research a simple variant of the vehicle routing called the Capacitated Vehicle Routing Problem (CVRP) during this work, like the recently published study of L. Liu and Liu [12]. For the first time, the cost of batch ship** to multiple customers with multiple orders is determined by the vehicle's unutilized capacity costs, which are dependent on the travel time involved.

The complexity of the problem system grows as each supply chain task, such as output and delivery, is solved simultaneously. An applied planning problem typically involves many variables and constraints to devise a model. Exact techniques are only used for experiments with a comparatively simplistic single machine setup for this involution of integrated PS-VRPs [14]. Heuristics and metaheuristics are proposed as solution strategies in a single machine setting of batch processing. All experiments involving parallel system configurations are resolved using a heuristic or meta(heuristic), like tabu search, adaptive massive neighborhood search (A)LNS, GA, and ACO. Apart from Amorim et al.[2], this was the only analysis that used professional optimization tools as a solution technique. Belo-Filho et al. [4] suggested a rebuild heuristic and an ALNS algorithm to resolve the issue suggested by Amorim et al.[2]. Within experiments of various machine configurations, as a solution methodology for determining the solution to the problem, either an optimization program or a heuristic is used [14].

To calculate the efficiency of the built (meta)heuristics, examples of at most one hundred customer orders are typically used. Cases with up to 200 orders were used in a small number of trials. Furthermore, to balance the outcomes of each solution method, the issue is normally resolved with commercial optimization tools like CPLEX and LINGO. Except for Park et al. [17], who address cases of up to twenty-one customers, commercial optimization tools will find the right options for up to seven customers. Furthermore, using a branch and cut algorithm solved instances of up to fifty customers in an extremely basic single-machine setup with batching. Metaheuristic-based solution methods, such as TS, and GA, are commonly used to locate high-quality solutions in a short period.

2.5 Summary

To summarize, previous studies have rigid expectations that make it difficult to coordinate output and delivery schedules within the supply chain. The following assumptions are made: (1) While configuration activities influence the resiliency of the development schedule, they are often overlooked in the manufacturing process. (2) In the manufacturing stage, most studies assume a relatively basic system environment, such as a single or a parallel machine configuration (3) The majority of researchers use a simple VRP with undiversified vehicles to one customer within the delivery aspect of the integrated issue. (4) Each batch contains some or all orders of a particular customer. (5) Distribution time constraints, such as delivery due dates and time frames, are needed in nearly half portion of the research. (6) The most common target measures are service quality maximization and cost reduction. Where real-life manufacturing and delivery chains are considered, only combined PS-VRP models can be useful to decision-makers. The limiting assumptions of previous studies prevent the experiments from accurately reflecting the true existence of the issue at hand. Considering the gaps in the previous research, this paper aims to integrate SDST in a PFSP within the MINLP to lower the overall cost of tardiness and batch distribution to multiple supply chain customers.

3 Problem description and assumptions

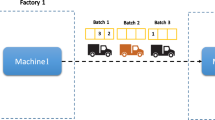
The following is a formal description of the problem: a permutation flow shop-based factory owned by a single manufacturer, where a set of machines m = $\{\mathrm{1,2},\dots ., M\}$ in series. The production process runs in an MTO production system. A set of customers f $=\left\{\mathrm{1,2},..,\right\}$ F, reside at F different locations. Every pair of locations (f,g), where f, g ∈ F, and f ≠ g, is associated with a travel time ${t}_{fg}$ which is assumed to be constant. At the initial stages of the production, a set of customer orders $i=\mathrm{1,2},..,n$ arrive at the plant. Since the customer orders are processed by an SDST flow shop where λ is a permutation or sequence of n orders and the order in position i of the sequence is denoted as λ_i, each order must be processed through all of the machines within the same order. The processing time of customer order $i=\{\mathrm{1,2},..,n\}$ on machine m= $\left\{\mathrm{1,2},\dots .,M\right\}$ is symbolized by${PT}_{{\lambda }_{i} , m}$. Meanwhile, ${ST}_{{\lambda }_{i}, { \lambda }_{j}}^{m}$ denotes SDST when order j follows an order i on the M^th machine in the PFSP. Per order is linked to a specific customer. Two operating choices must be combined to solve SDST PFSP for batch distribution to various customers: sequencing orders for production in a permutation flow shop considering SDST and separating items into enough batches where b= $\left\{\mathrm{1,2},..,\right\}$ B for distribution. It is also thought that every customer order i is non-splitable, ready at time 0 and that as soon as it is started on the Mth machine, it cannot be stopped till it is done (i.e., anticipation is not allowed). Once all customer orders in a batch have been processed, v = 1,2,…., V is a set of multiple homogeneous vehicles with equal capacities, where the capacity of every vehicle v is defined by Q, which delivers the customer orders to the related customers based on the due date of each order i. (denoted as ddi). Customer orders from various customers can be fulfilled by the same vehicle in a single delivery. Furthermore, customer orders from the same customer may be delivered by separate vehicles. Each vehicle may carry one or more customer orders in a single delivery (allowing the capacity constraint), either for the same or different customers. After serving a customer, a vehicle essentially leaves that customer and either (1) serves another customer in a different location (in case it carries order(s) for that customer) or (2) returns to the depot. Due to the vehicle's capacity limit, certain batches must be kept at the plant before the next visit. The routing portion of the problem is represented graphically by nodes 0 through F, where F is the set of nodes within which 0 represents the plant and the location of the customer order is represented by the remaining nodes. The aim is to figure out the sequence of customer orders on all the M machines and the order of customers' order visits and distribution times to those customers. Figure 1 depicts the combined output and delivery scheduling process based on our problem set.

Fig. 1

The integrated production scheduling and delivery planning procedure

The following assumptions are taken to formulate SDST PFSP for batch distribution to multiple customers.

In the production stage:

• All customer orders are sent to the permutation flow shop promptly.(Kai [33]

• Only one customer order can be processed at a time by a single machine, and preemption is not allowed.

• The customer order processing sequence is the same for all machines.(Kai [33]

• The time taken to set up two machines in a sequence is considered.

In the delivery stage:

• For each batch delivery, there is no quantity or distance limitation.(Kai [33]

• Every batch contains several customer orders.

• Any order cannot be split and shipped in one tour/vehicle, but separate orders from a similar customer can be distributed through several tours/vehicles.

• There are an infinite number of vehicles available to ensure that each batch is shipped as soon as it is available.

3.1 Illustrative example

The problem of m-machine flow shop scheduling with SDSTs, multi-customers and homogeneous vehicles with capacity constraints is regarded in this section as a basic example of an integrated production and delivery problem. Table 1 shows the customers’ co-ordinate value for the illustrative example. Here, the first column represents the customers’ id denoted by f where f is {0,1…,3}. The plant in the center of the two-dimensional plane is denoted by the number 0. The customer's coordinates are listed in the second and third columns. Table 2 displays the dataset produced for a scenario with five machines, three customers, and fifteen customer orders. The first two columns in Table 2 show the customer and order id, respectively. ${\mu }_{i}$ denotes the size of the demand for customer order i, ${PT}_{{\lambda }_{i}, 1}$, ${PT}_{{\lambda }_{i}, 2}$, ${PT}_{{\lambda }_{i}, 3},$ ${PT}_{{\lambda }_{i}, 4} and {PT}_{{\lambda }_{i}, 5}$ represent the processing times of the customer order on machines 1, 2, 3, 4, and 5, respectively. The last two columns reflect different customer order due dates and unit tardiness costs per order, with the values in the last column created at random using a uniform distribution.

Table 1 Customers co-ordinate for the illustrative example

Table 2 Randomly generated sample dataset of illustrative example

Let us assume that each vehicle's capacity Q is set to 150 kg. The freight time between customers f and j is symbolized by t_fg and assumed that t_fg = t_gf, i.e., the distances are symmetric. Here t_0f represents the distance between the production plant and customer F. For this problem matter, initial setup times on the machines are presented in Table 11 (Appendix A). The data is generated randomly using a uniform distribution with a range (1, 10). Table 12 represents the ship** times, and Table 13, 14, 15, 16, and 17 (Appendix A) represent the data for the SDSTs on machines 1, 2, 3, 4, and 5, respectively. The unit cost of the unutilized vehicle per delivery $\alpha$ is randomly generated between (1, 10).

In five (M = 5) machines within the production stage, the arrangement of customer orders is {9–15-6–3-1–4-2–14-12–5-7–11-8–10-13}, and for both production and delivery, each batch contains the same orders according to Fig. 2. The load capacity of the vehicles is not surpassed for a specific trip. As seen in Fig. 2, the completed customer order series includes orders from three customers, namely customers 1, 2, and 3. Customer orders {1,2,3,4,5}, {6,7,8,9,10}, and {11,12,13,14,15} belong to customers 1, 2 and 3 respectively.

Fig. 2

Example of a 5 × 15 SDST Permutation flow shop

Figure 3 represents the delivery stage where several homogeneous vehicles of the same capacity complete their tours. The below are the four tours offered by the distribution service: 0–2-3–1–0 (tour 1), 0–1–0 (tour 2), 0–3-1–2–0 (tour 3) and 0–2-3–0 (tour 4). At the time, t = 0, we undertake that all vehicles are available in the plant or depot. Therefore, we assume that vehicle ID, v = 1 makes the first tour, ID v = 2 makes the second tour, ID v = 3 makes the third tour, and finally, vehicle v = 4 makes the fourth tour.

Fig. 3

Feasible solutions for the illustrative example at the distribution stage

When we look at Figs. 2 and 3, although the production of orders 9, 15, and 6 complete at times 207, 262, and 340, respectively, the production completion time is 369 after completing customer order 3, which is also included in the first batch. Therefore, the batch arrival time of the first batch carrying a total load (20 + 50 + 67 + 10 = 147 < 150 kg) by vehicle v = 1 containing the customer orders to the associated customer. So, customer order 9 is received by its customer f = 2 at time 369 + t_0,2 = 440 as the due date of customer order 9 is 605, so this order is not tardy. Customer order 15 is received by its customer f = 3 at time 369 + t_{0,2 +} t_2,3 = 478. As the due date of the customer order, 15 is 429, so the order is tardy, and the amount of tardiness is (478–429) = 49. Customer order 6 is received by its customer f = 2 at time 440 as this order belongs to customer 2 and will be served with customer order 9, because if a vehicle carries orders of the same customer, they will be served at the arrival time of the first order to that customer. The due date of order 6 is 702 so the order is not tardy. Finally, customer order 3 is received by its customer f = 1 at time 369 + t_{0,2 +} t_2,3 + t_{2,1 =} 470 as it is due date is 146, so this order becomes tardy, and the amount of tardiness is 324 and the total delivery time of batch 1 by 1^st vehicle is (470–369) = 101.

So, for batch 1, the cost of tardiness is (2.90 × 49 + 0.56 × 324) = 323.54 and cost of delivery is {1.02 × (150–147) × 101} = 309.06 and the net cost of lateness and distribution is (323.54 + 309.06) = 632.6. For this illustrative case, we will measure the overall cost of delay and distribution for the remaining batches and then add the total costs of each batch to achieve our objective value, which will reduce the entire cost of lateness and batch distribution to multiple customers.

3.2 A mathematical formulation

The following notations are applied to formulate the mathematical model and proposed algorithm:

Parameters:
f	Index of customer, f $=\mathrm{1,2},..,F$
i	Index of customer order, $i=\mathrm{1,2},..,n.$
m	Index of machine in SDST PFSP, m = $\mathrm{1,2},\dots .,M.$
b	Index of batch, $b=\mathrm{1,2},\dots .,B$
v	Index of vehicle, v $=\mathrm{1,2},\dots ., V$
F	The number of customers in the system
n	The number of customer orders arriving in the system
M	The number of machines in the PFSP environment
B	The number of batches
V	The number of vehicles
${\lambda }_{i}$	ith customer order in the customer order sequence λ = {λ1, ……λn $\}$, $i=\mathrm{1,2},..,n.$
${PT}_{{\lambda }_{i}, m}$	Processing time of customer order sequence ${\lambda }_{i}$ on machine m, $i=\mathrm{1,2},..,n;$ m = $\mathrm{1,2},\dots .,M$
${ST}_{{\lambda }_{i}, { \lambda }_{j}}^{m}$	Sequence dependent set-up time of changing over from order ${\lambda }_{i}$ to order ${\lambda }_{j}$ on machine m, $i,j=\mathrm{1,2},..,n;$ m = $\mathrm{1,2},\dots .,$ M
Q	The maximum carrying capacity of the vehicle
µi	The demand size of order i, we assume that µi ≤ Q (∀$i=\mathrm{1,2},..,n)$; Suppose there are B delivery batches with one vehicle for each batch
${t}_{fg}={t}_{gf}$	Travel time between customers f and g (f, g = 1,……, F; i ≠ g; index 0 indicates depot)
ddi	Due date of customer order i
${A}_{ib}$	The arrival time of batch b with customer order i to the associated customer
$\alpha$	The unit cost of unutilized vehicle capacity per delivery
${\beta }_{i}$	Per unit tardiness cost of customer order i
Continuous variable:
${CT}_{{\lambda }_{i}, m}$	Time of completing the customer order ${\lambda }_{i}$ on machine m, $i=\mathrm{1,2},..,n;$ m = $\mathrm{1,2},\dots .,M$
Decision Variable:
${X}_{fg}$	1, if vehicle drives straight from node f to node g (f, g = 0, 1,…., F; f ≠ g)
	0 otherwise
${Y}_{ifb}$	1, if customer order i belongs to customer f in batch b
	0 otherwise
${Z}_{{\lambda }_{i} b}$	1, if ${\lambda }_{i}$ is allocated to batch b, and
	0 otherwise

A mixed-integer nonlinear programming model (MINLP) for synchronization of production scheduling and distribution in permutation flow shop-based supply chain considering SDST and an infinite number of vehicles to distribute the orders to the customer is given as:

$$ \begin{aligned} & Minimize \sum\limits_{{b = 1}}^{B} \left[\left( \sum\limits_{{i = 1}}^{n} {\beta _{i} } \times \max \{ 0,Z_{{\lambda _{i} b}} \times A_{{ib}} - dd_{i} \} \right)\right.\\ &\qquad \qquad \left. + \alpha \times \left( Q - \sum\limits_{{i = 1}}^{n} {Z_{{\lambda _{i} b}} } \mu _{i} \right) \times \sum\limits_{{i = 1}}^{n} {\sum\limits_{{f = 0}}^{F} {\sum\limits_{{g = 0}}^{F} {Y_{{ifb}} } } } t_{{fg}} X_{{fg}}\right]\end{aligned}$$

(1)

Subject to-

$${CT}_{{\lambda }_{1},1}\ge {PT}_{{\lambda }_{1},1}+{ST}_{0, {\lambda }_{1}}^{1}$$

(2)

$${CT}_{{\lambda }_{i}, 1}\ge {CT}_{{\lambda }_{i}-1 ,1}+ {ST}_{{\lambda }_{i}-1 , {\lambda }_{i}}^{1}+{PT}_{{\lambda }_{i},1}\,\,\,i=\mathrm{2,3},\dots \dots .,n$$

(3)

$${CT}_{{\lambda }_{1} ,m}\ge {max\{CT}_{{\lambda }_{1} ,m-1} ,{ST}_{0, {\lambda }_{1}}^{m}\}+{PT}_{{\lambda }_{1} , m}\,\,\,m=\mathrm{2,3},\dots \dots .,M$$

(4)

$${CT}_{{\lambda }_{i} , m}\ge \mathit{max}\left\{ {CT}_{{\lambda }_{i}-1 , m} + {ST}_{{\lambda }_{i}-1 , { \lambda }_{i}}^{m} , {CT}_{{\lambda }_{i} ,m-1} \right\} +{PT}_{{\lambda }_{i} , m}\,\,\,i=\mathrm{2,3},\dots \dots .,n ;\,\,\,\,m=\mathrm{2,3},\dots \dots .,M$$

(5)

$$\sum _{\mathrm{i}=1}^{\mathrm{n}}{X}_{fg}\ge 1\dots \dots \dots\,\,\,g=\mathrm{1,2},\dots .,F$$

(6)

$$\sum_{b=1}^{B}{Z}_{{\lambda }_{i} b}=1 ,\,\,\,\forall i=\mathrm{1,2},\dots .,n$$

(7)

$$\sum_{i=1}^{n}{Z}_{{\lambda }_{i} b}{\mu }_{i} \le Q\,\,\,\,\forall b=\mathrm{1,2},\dots .,B$$

(8)

$${\sum }_{i=1}^{n}{Y}_{ifb}\ge 1 \,\,\,\forall f=\mathrm{1,2},\dots .,F \,\,\,\forall b=\mathrm{1,2},\dots .,B \dots \dots \dots $$

(9)

$${\sum }_{f=1}^{F}{Y}_{ifb}=1 \,\,\,\forall i=\mathrm{1,2},\dots .,n \,\,\,\forall b=\mathrm{1,2},\dots .,B \dots \dots .$$

(10)

$${A}_{ib}\ge {\mathit{max}}_{i=\mathrm{1,2},\dots ,n}\left\{ {Z}_{{\lambda }_{i} b} \times {CT}_{{\lambda }_{i} M} \right\} +{t}_{fg}{X}_{fg}{Y}_{ifb}\,\,\,\,b=\mathrm{1,2},\dots .,B \,\,\,\forall i=\mathrm{1,2},..,n \,\,\,\forall f=\mathrm{1,2},\dots .,F$$

(11)

$${\mu }_{i }{, C}_{{\lambda }_{i} , m} , {A}_{ib}, \ge 0 \,\,\,\forall i=\mathrm{1,2},..,n;\,\,\,b=\mathrm{1,2},\dots .,B;\,\,\,\,m=\mathrm{1,2},\dots .,M$$

(12)

$${Z}_{{\lambda }_{i} b} , {X}_{fg ,}{Y}_{ifb}\upepsilon \{\mathrm{0,1}\}$$

(13)

$$B=\frac{{\sum }_{i=1}^{n}{\upmu }_{i}}{Q}.$$

(14)

The objective function (1) minimizes the total cost of tardiness and delivery. Constraints (2) and (3) provide the completion times of the first customer order and the remaining (n–1) customer orders on the first machine, respectively. Similarly, for each of the other (M–1) machines, constraints (4) and (5) determine the completion times of the first customer order and the remaining (n–1) job customer orders, respectively. Constraint (6) ensures that each node is visited at least once. According to constraint (7), each completed customer order can only be assigned to a single batch. Constraint (8) states that the cumulative size of all customer orders within a batch cannot be greater than Q, which is the capacity constraint of each vehicle. Constraint (9) ensures that each customer has at least one order or more, while constraint (10) ensures that each order has exactly one customer. Constraint (11) gives the batch arrival time to the associative customer. Constraint (12) preserves the non-negativity of the variables. Constraint (13) indicates that ${Z}_{{\lambda }_{i} b}$, ${Y}_{ifb},$ and ${X}_{fg}$ are binary variables. For ease of computation, an obvious lower bound is defined on the minimum number of vehicles/batches needed to service the customers provided by Eqs. 14.

4 Proposed algorithm

It is worth noting how important heuristic and metaheuristic algorithms are for diverse decision problems in many disciplines. Online learning, terminal operations scheduling, multi-objective optimization, medicine, data categorization, other fields, and the vehicle routing problem are only a few examples. In the study of Zhao and Zhang [36], a learning-based algorithm is proposed which aimed to enhance the generalization ability. Learning automation (LA) is included in the algorithm based on a decomposition many-objective optimization framework.

Evolutionary many-objective optimization has been gaining increasing attention from the evolutionary computation research community. Much effort has been devoted to addressing this issue by improving the scalability of multi objective evolutionary algorithms. Abu Doush et al. [1] proposes a new algorithm that applies heuristic techniques in harmony search algorithm (HSA) to minimize the total flow time. Z. Liu et al. [13] designed an Evolutionary Algorithm to effectively combine vector angle with shift-based density estimation for solving multi-objective problems using complementary properties. For truck scheduling optimization at a cold-chain cross-docking terminal with product perishability considerations, Theophilus et al. [28] developed an Evolutionary Algorithm, which is found to be the most promising metaheuristic, considering both solution quality and CPU time perspectives. A Hybrid Evolutionary Algorithm, which deploys a set of local search heuristics, is developed to solve the problem of minimizing carbon dioxide emissions due to container handling at marine container terminals in the study of Dulebenets et al. [9], where the proposed solution algorithm can be adopted as effective planning tools by the marine container terminal operators and improve the environmental sustainability of the terminal operations..

4.1 Genetic algorithm

A GA, which is an evolutionary algorithm, has been developed in this article. It was first proposed by Holland in 1992, who was influenced by human evolution. The GA's theory is to prevent inbreeding replication by renewing the population (set of solutions) based on a natural selection rule and the best survival mechanism (local optimum). The renewal cycle repeats itself from generation to generation before a predetermined stop** point is reached. GA has been successfully used to solve a wide range of difficult optimization problems in recent years. Its popularity stems from its convenience, ease of use, and versatility are the primary reasons for using GA as an optimization method in this study.

The key components of the GA for the problem at hand, such as solution encoding, population initialization, genetic operators, assessment of fitness, and generation renewal, are represented in the following section. The genetic algorithm depicted in Fig. 4 is a flow map, with every chromosome representing a solution determined by a representation mechanism.

Fig. 4

The flowchart of the proposed genetic algorithm

4.1.1 Encoding schemes and evaluation

The encoding of a candidate of the SDST PFSP with batch supply to multiple customers for the issue at hand synchronizes two operating choices, assessing the order management sequencing and sorting consumer orders into batches while taking capacity constraints into account for delivery to the associated customer. As a result, a matrix of three rows and n columns can be used to represent the chromosome. The second row reflects the truck supply batches used to assign the customer order to an appropriate number of batches. The batch distribution assumes that the same batch can ship orders from separate customers in a single delivery, and orders from the same customer can be delivered by different batches in multiple deliveries. The first row of the matrix is a permutation of n customer orders which represents the customer order processing sequence on the machines in an SDST PFSP and the customer visit sequence in each delivery batch as described by Ruiz et al. [25]. For the illustrative example presented in Sect. 3.1, the chromosome of its partial solution is illustrated in Fig. 5. In the second row ‘1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4’ signifies that 4 vehicle delivery tours are being used to deliver all the customer orders. The vehicles take the delivery tours immediately after all the customer orders contained in that tour are completed in the production stage. According to the first row, customers {4, 13, 5, 2}, {6, 1,9}, {14,10,3,7,15} and {12, 8, 11} are successively delivered by the first, second, third and four homogeneous vehicle tours of identical capacity, respectively. The third row represents the customer numbers. As shown in Fig. 2, the completed customer order sequence contains orders from three customers, i.e., customers 1, 2 and 3, where customer orders {1,2,3,4,5}, {6,7,8,9,10} and {11,12,13,14,15} belongs to customer 1, 2 and 3, respectively.

Fig. 5

Example of encoding representation

4.1.2 Population initialization

It is recommended to use a quick and easy heuristic to find a good solution for the first generation to speed up algorithmic convergence. This method will drastically minimize the amount of time it takes GA to reach a reasonable local minimum. In GA, the initial population is traditionally generated at random. Nevertheless, random initialization could not achieve a great solution in a fair amount of time [20]. We suggest that such non–random individuals be Population _size included in the initial population for this reason. The following describes how individuals with Population _size are constructed: In population initialization, the first individual is generated by using the NEH_RMB heuristic [25] to handle set up time in the production phase of permutation flow shop scheduling to give a satisfactory result. The second individual is generated by the modified NEH_RMB heuristic considering EDD. The orders are first grouped by their EDD, and then the technique is the same as the NEH_RMB heuristic. The Earliest Due Date (EDD) is a widely used scheduling guideline to achieve successful outcomes for tardiness-related metrics. As a result, NEH_RMB with EDD is considered for population initialization when dealing with PFSP with batch distribution to several customers. Finally, the random insertion procedure is used for the initial population to find (Population _size–2) individuals.

4.1.3 Selection and crossover operation

An elitist approach dependent on the fitness feature is used to select chosen individuals (parents) from the children's generation population. When genetic operators (mutation and crossover) are used, it is possible to lose the best chromosomes. Elitism is a way of maintaining a clone of the best chromosomes in future generations. The process outlined above allows the genetic algorithm to retain some of the best solutions in each generation. Previous research has shown that this process improves the performance of genetic algorithms and reduces coverage time [22].

Two crucial genetic activities, exploitation and exploration, are used to advance the genetic search [8]. In certain cases, the crossover operator takes advantage of a superior approach. For replication, the proposed algorithm uses a modified two-point crossover. As seen in Fig. 6, the total number of customer orders, batch, and customer is 15, 4, and 3, respectively, in the illustrative illustration given in Sect. 3.1. In every iteration, a real value between 0 and 1 is produced randomly for the two parents until the crossover probability (Pc) is less than the given value. If the random number is ≤ P_c (crossover probability), the modified two-point crossover operator splits each parent into three sections by selecting two columns (C_c1 and C_c2) at random. The genes in one parent's middle section are then replicated from one father or mother to a child. The rest of the genes are eventually inserted in the child's unfilled positions according to their order of appearance in the other parent, from left to left right.

Fig. 6

Two-point crossover for Generating two children from two-parent

4.1.4 Mutation

There are some methods for avoiding local optima. One of them is a mutation (K. [32], one of the operators frequently used to fix the local optimality of intelligent optimization algorithms when they are being used built. The likelihood that a crossover operator's offspring will undergo mutation during a mutation phase is known as the probability of mutation. To diversify, a pairwise interchange mutation is applied to every child with a mutation probability, Pm. Every iteration generates a random real number between 0 and 1 that is lower than the mutation probability (Pm), then two pair genes with positions Cm1 and Cm2 are randomly selected and exchanged to form a new child. Figure 7 depicts an example of the pairwise interchange mutation procedure for the illustrative example, discussed in Sect. 3.1, where the total number of customer orders, batch, and customers is 15, 4, and 3.

Fig. 7

Generating a solution according to interchange mutation

4.1.5 Repair process

A newly generated chromosome may violate the vehicle's capacity. As a consequence of that, the corresponding solution becomes infeasible. In such a case, a repairing operator is implemented in the GA. The repairing operator consists of a nonstop accumulation of the loads demand of customer orders in a vehicle route until the overall weight of the load exceeds the vehicle's carrying capacity Q. If the total weight of the vehicle exceeds the vehicle's carrying capacity at the i^th column, then the batch index ‘b’ where $b=\mathrm{1,2},\dots .,n$ at the (i-1)^th column allocated for a particular batch index in row two is changed to ‘n + 1’. Furthermore, to indicate the end of the deliveries, the last genetic element in row two must be certain to be ‘n + 1'. An example is illustrated in Fig. 7. According to Table 2, customer orders 9, 15, 6, 3, 1, 4, 2, 14, 12,5,7,11,8,10 and 13 have demands 20, 50, 67, 10, 59, 30, 30, 45, 30,10,20,30,40,20 and 50, respectively. The vehicle capacity is Q = 150. We can observe in Fig. 8 that the cumulative load of the first six customer orders 14, 12,5,7,11, and 8 in the third vehicle route is equal to 175, which violates the vehicle’s capacity, the vehicle route is infeasible because the last item of the third vehicle in row 2 is finished by ‘b = 3’. To repair it, the last batch index of the third vehicle in row 2 is changed to ‘3 + 1 = 4’. In addition, we observe that it does not violate the capacity constraint of the fourth vehicle so, the batch index of customer orders 8,10, and 13 will be b = 4. The pseudo-code of the Repair procedure is presented in Fig. 12 (Appendix A).

Fig. 8

An example of a repairing operator

4.1.6 Local search

Local search searches simply explore the solution's environment to find the algorithm in an improved neighborhood than the current solution. In this analysis, the best solution for each generation is subjected to local search. The new chromosome swaps the existing chromosome if it produces a better objective function. The proposed local search is aimed at lowering overall costs.

The neighborhood structure is the insertion neighborhood search, which searches for the best fit based on the EDD for consumer orders in a similar batch. Customer order i is moved and tested in all possible positions inside batch b before being put in the best position. The process is repeated before all customer requests from all batches have been considered.

5 Results and experimental analysis

The literature does not include any scheduling algorithms to deal with PFSP considering SDST under practical circumstances. It is a truly new combinatorial optimization problem, enabling orders from numerous customers to be grouped and transported by vehicles of limited capacity to multiple customers. As a result, an explicit approach is used rather than comparing the proposed GA to any known algorithms. This section is divided into four subsections: random check instances generation, experimental design, parameter standardizations, and experimental results and discussions.

5.1 Generation of random test instances

The requirement for creating test examples significantly affects evaluating the heuristic's success over MINLP. Sine there is no standard benchmark available for the problem under study, we extended the standard benchmark data for the flow shop scheduling problem [25] in the following way.

Ruiz’s benchmark [25] is extended from Taillard's benchmark instances [27]. In this paper, four problem sets from Ruiz’s benchmark [25] were considered by considering the processing time of each job in machine and their SDST as the input data for the experiment. Each of the four sets considered four different processing times to sequence-dependent setup time ratios. For example, the SSD-10 instance set includes 120 instances with processing times that fit Taillard's benchmark data and SDSTs that are 10% of the processing times. The instance set SSD-50 has a setup time of 50% of the processing time, while the instance sets SSD-100 and SSD-125 have setup times of 100% and 125% of the processing time, respectively. For the suggested solution, we usually choose the first two instances from the sets {20 × 5, 20 × 10, 20 × 20, 50 × 5, 50 × 10, 50 × 20, 100 × 5, 100 × 10, 100 × 20, 200 × 10, 20 × 20}, where the cumulative 88 is made up of {11 sets × 2 instances × 4 SSD} problem sets. We selected to address only the eighty-eight instances (up to two hundred jobs and twenty machines). Apart from job-machine processing times and SDSTs for each instance, other input data for each problem instance is generated as follows. The number of customers is randomly generated within 30% to 60% of the total number of orders for every instance set. Below are the time and cost-related parameters: We usually set a general value before generating the demand size, and this value can be used as a basis for generating all different parameters. It is assumed that the demand size µi of customer order i, is distributed uniformly randomly and is expressed by U (β/2, β). We usually believe it cannot be smaller than the maximum demand size when it comes to vehicle capacity. U (max µ_i,$\frac{\sum \mu i}{2}$) is the upper bound for availability, which is set at $\frac{1}{2}$ the total size of demand of all customer orders. It is known that the distances are symmetric (i.e., ${t}_{fg}={t}_{gf}$ where f and j represent customer (f, g = 1…., N; f ≠ g). Travel time between customers f and g (${t}_{fg}={t}_{gf}$) is mounted to U (1, 100). To successfully handle each production and distribution activity, it is important to strike a balance between processing and travel times. Since machine scheduling problems are negligible, the combined problem comes down to a VRP if process times are much longer than travel times. We prefer to use (m + n-1) as the multiplier factor in the production stage of the integrated problem, but (n + 1) in the distribution stage, where m and n denote the number of machines and orders, respectively. The per-unit cost of tardiness β_i for a customer order i belonged to customer f and therefore the unit cost of the unutilized vehicle per delivery, α is fixed to U (1, 10). Generations of due dates are determined in the last row using similar expressions. All these datasets can be obtained from this link for future use: https://research.unsw.edu.au/projects/cross-disciplinary-optimisation-under-capability-context.

5.2 Experimental design

The proposed algorithm was coded in Python 3.7 and run on an Intel(R) Core (TM) i5-10210U CPU running at 1.60 GHz with an 8-GB RAM processor. The relative proportion deviation (RPD) is a common performance parameter that is used to assess an algorithm's performance as follows:

$$\mathrm{RPD }=|\frac{{ObjVal}_{i}-{ObjVal}_{best}}{{ObjVal}_{best}}| \times 100$$

(15)

${ObjVal}_{i}$ denotes the objective value of a solution made by a particular algorithm i while ${ObjVal}_{best}$ denotes the objective value of the best solution generated by all the algorithms considered. Meta heuristics can yield entirely different outcomes in multiple runs due to their inherent randomness. Rather than using RPD as a performance measure directly, the metaheuristic runs a test problem ten times and then uses the best RPD (BRPD) and average RPD (ARPD) from those ten runs to show its efficiency. A meta-heuristic with lower BRPD and ARPD, as seen in Eqs. 16 and 17, could provide more practical solutions for integrating the output of the problem at hand.

$$\mathrm{BRPD }=|\frac{{BObjVal}_{i} - {ObjVal}_{best}}{{ObjVal}_{best}}| \times 100$$

(16)

$$\mathrm{ARPD }=\frac{1}{10 }\sum_{r=1}^{10}|\frac{{ObjVal}_{i}^{r} - {ObjVal}_{best}}{{ObjVal}_{best}} | \times 100$$

(17)

The value of the objective function of the best solution produced by algorithm i over ten runs is represented by Eq. 16, and the value of the objective function of the solution obtained by algorithm i in the r^th run is represented by Eq. 17.

Since the PFSP where SDST is considered for batch distribution to numerous customers can be an innovative combinatorial problem, as in the literature, there are no benchmark data sets. As seen in Sect. 6 of Table 3, completely different sets of test problems were created at random from the extension of the benchmark data information during this paper to demonstrate the efficacy of the suggested algorithms (Fig. 8).

Table 3 Time-related and cost-related parameters for test problem

5.3 Parameter standardization

Subsequently, the efficiency of a meta(heuristic) is dependent on its parameters (K. [32], tuning the main parameters of GA, like the Tournament size, populations number (Pop), generations number (Gen), probability of crossover (Pc), and probability of mutation (Pm) is essential. As compared to the classic full factorial experimental design, Taguchi's design experiment method [15] significantly decreases the number of experiments expected and is thus used to standardize the parameters of the proposed GA (Table 4).

Table 4 Parameters and their Levels in the proposed GA algorithm

Since there are five parameters, each of which has four stages, a total of 45 = 1024 experiments must be required to be performed within the maximum factorial experimental framework. On the other hand, the Taguchi technique solely examines 16 variations of factor levels based on the orthogonal array L₁₆(4⁵) seen in Table 5. Each combination algorithm is run ten times independently to ensure correct parameters to evaluate an appropriate GA parameter configuration. GA runs ten times with a specific parameter configuration for this set of samples, and the stop** criteria for each run are close to the maximum number of fitness evaluations. After that, ARPD is collected as an efficiency indicator. The Taguchi experimental findings show the inclination of every parameter is shown in Fig. 9 by the Taguchi experimental findings. The x-axis in this diagram represents the primary GA parameters that need to be adjusted, while the y-axis represents the average objective value for every parameter level. The subsequent parameter of GA could offer satisfactory results: Tournament size = 25, Pop = 150, Gen = 400, Pc = 0.3 and Pm = 0.10.

Table 5 Orthogonal Array L₁₆ (4⁵)

Fig. 9

The value of ARPD for each parameter level of GA

Table 6 shows the value of response and rank of every parameter for every stage based on ARPD values. This table also displays each parameter's delta values, which is the gap between the highest and lowest average values of response for every element. Tournament size, for example, has a delta value of 1.9148 (= 2.1115–0.1968) in Table 6. It is critical to recognize that a parameter with a higher delta value is more significant than another. The Tournament size is the most critical parameter for the proposed genetic algorithm, according to the delta value in Table 6, while the Pm is the least important parameter. To check the parameters, all eighty-eight instances were chosen that were generated by extending Taillard’s benchmark data information from [24] of permutation flow shops with SDST. Wherever the stop** criteria of every run are set to the generation (Gen number; it will stop once the number of recent generations reaches the maximum generation (Gen) number.

Table 6 The value of response and significance rank for GA

5.4 Experimental results and discussions

Even with moderately sized customer orders, the MINLP model is unable to have optimum solutions due to the difficulty of the problem. To inspect the effectiveness of the proposed GA, LINGO 18.0 was employed. A comparative analysis has been done between the obtained result from the genetic algorithm and the outputs of lingo 18.0. The indicator considered in the comparison is the RPD value. A comparison of the outcomes is also given in Table 7 to determine the success of the proposed MINLP model.

Table 7 Comparison of the proposed GA and Exact approach for small-sized example

In terms of calculation, Table 7 indicates the results of GA and an exact solution. The first column indicates the size of the instance, and the second, third, and fourth columns indicate the customer order (i), machine number (m), and several customers (f), respectively. The fifth and sixth column shows the objective value of the exact approach solved in LINGO18.0 and the proposed algorithm, and in the last three columns, the relative proportion deviation (RPD) of the exact approach and best and average RPD value for metaheuristic is provided.

The relative percentage deviation (RPD) shows that the exact method (LINGO) generates the same solutions as GA, which indicates the validation of the proposed GA. But for such a complex problem at hand, the commercial software LINGO could not give any feasible solution with the increased number of variables, even for a moderate size of instances. On the other hand, the proposed GA finds high-quality solutions for medium and large-scale problems in a short amount of time.

In terms of calculation, Table 8 indicates the results of GA (GA without local search and repair process).and proposed GA (where a genetic algorithm is hybridized with local search and a repair process is also implemented here to avoid constraint violation). The first column indicates the size of the instance, and the second column indicates the machine number (m). The third and fourth column shows the objective value of the GA and the proposed genetic algorithm, the fifth and sixth column represents the CPU time in seconds for GA and Proposed GA, respectively, and in the last four columns, the best and average RPD value for metaheuristics (GA and Proposed GA) is provided respectively.

Table 8 Comparison of GA and the proposed GA for different-sized example

The average relative percentage deviation (ARPD) shows that the proposed GA, finds high-quality solutions for different sized problems in a short amount of time.

5.4.1 Impact on variations in the number of customer orders and machines of the proposed algorithm's efficiency

This section is designed to interpret the overall success of the proposed Genetic algorithm for a variety of customer orders and machine numbers. Table 9 shows the experimental results of the proposed algorithms for different sized {20 × 5, 20 × 10, 20 × 20, 50 × 5, 50 × 10, 50 × 20, 100 × 5, 100 × 10, 100 × 20, 200 × 10, 20 × 20} instances. Where the first column represents instance type, the number of machines is represented by the second column, the column numbers third, fourth, fifth, and sixth represent the order size, respectively, and the last column represents the average CPU time in the second.

Table 9 Experimental results of the proposed algorithms for small and large-sized instances

Table 9 groups all 88 instances into four order size categories, and a statistical study of the average value of all four categories reveals that the ARPD value of GA steadily declines as the number of customer orders grows. As a result, the proposed algorithm's solution efficiency vastly outperforms for large-sized instances. We have also divided the findings into a certain number of orders and various machines. As can be seen from the solution, the number of machines does not affect the efficiency of the proposed algorithm, but the total CPU time of orders of different instance types increases as the number of machines increases.

5.4.2 Impact of variation of setup time in the proposed algorithm’s efficiency

This section is designed for viewing the proposed Genetic algorithm's overall output in terms of setup time variability. The proposed algorithms' experimental findings for four types of Taillard benchmark data are shown in Table 9: SSD-10, SSD-50, SSD-100, and SSD-125. The setup times in the SSD-10 instance set are evenly distributed in the range [1; 9] if the processing times in Taillard instances are obtained from a uniform distribution in the range [1; 99], and in the instance sets SSD-50, SSD-100, and SSD-125, [1; 49], [1; 99], and [1; 124], respectively, The first column in Table 10 represents order size, the number of machines is represented by the second column, the third, fourth, fifth, seventh, and ninth columns designate the instance type, and the fourth, sixth, eighth, and last columns represent the CPU time of the specific instance type in seconds, respectively.

Table 10 Experimental results of the proposed algorithm for small and large-sized instances

The ARPD value and the computing time of GA steadily increase as the percentage of setup time with the uniform distribution of processing time in the range [1; 99] increases, according to a comparative study of the average value of all four-instance types with differing setup time. As a result, the proposed algorithm's solution efficiency improves as the percentage of setup time decreases. Figure 10 depicts the overall percentage rise as the setup time varies with the processing time.

Fig. 10

Effects of the variability of setup time

5.4.3 Generation wise solution improvement

The success of any algorithm is often measured by its speedy convergence. This sub-section represents the convergence speed of the proposed metaheuristic. Figure 11 reveals convergence behaviour for a large (200 × 20), medium (100 × 10, 50 × 5), and small-sized (20 × 5) instances pictured by a graph (a), (b), (c), and (d), respectively. Wherever the number of generations is 400. The graph plots the total values of the objective function of all genes (in the y-axis) against every generation number (in the x-axis). It is reasonable to expect the evolved metaheuristic to converge at around 250 generations for large and medium-sized instances and around 50 generations for small-sized instances.

Fig. 11

Convergence of GA for a different size and typed instances

6 Conclusions and future directions

In this paper, we have addressed synchronous production scheduling and distribution planning where permutation flow shop scheduling and VRPs are addressed practically. This study differs from others in that-

• Several previous studies have neglected to consider the SDST for PFSP to combine it with the distribution scheme.

• To reduce production costs, SDST is combined with PFSP, which makes this issue more realistic.

• To reduce ship** costs, batching is performed to distribute each batch to several consumers by a different homogeneous capacity-constrained vehicle.

• To identify optimal solutions with our proposed MINLP, we have suggested a genetic algorithm to generate a close-to-optimal solution.

• To validate the solution exact method (LINGO) was applied to small instances, generating the same solutions as the proposed GA.

• To compare the performance of proposed GA, especially for medium and large-sized problem instances, we have implemented GA (GA without local search) where the average relative percentage deviation (ARPD) shows that the proposed GA finds high-quality solutions for different sized problems in a short amount of time.

• To assess the success of the proposed solution, we created a series of trials where numerical studies show that the recommended solution improves the problem's efficiency by lowering the average cost of lateness and distribution.

Obtaining the optimal or best solutions within realistic computational times for PFSP considering SDST with batch distribution to multiple customers is difficult, particularly for large-scale problems. Our proposed GA yields near-optimum solutions for integrating production and distribution decisions in a PFSP. The only shortcoming is we assumed an infinite number of vehicles rather than considering a finite number to avoid more complexity.

This research would be expanded in many areas to shed light on upcoming studies. A sensitivity analysis will be performed to see how different vehicle capacities affect the problem and, as a result, the effect of a finite number of multiple vehicles with homogeneous/heterogeneous capacities. In addition, alternative metaheuristics can be combined with efficient local search methods to provide even better outcomes.

7 Appendix

See Fig. 12 and Tables 11, 12, 13, 14, 15, 16 and 17.

Fig. 12

The pseudo-code of the Repair process

Table 11 Data for initial setup times on the machines

Table 12 The required travel time between the customers

Table 13 Random data for the SDSTs on the machine 1

Table 14 Random data for the SDSTs on the machine 2

Table 15 Random data for the SDSTs on the machine 3

Table 16 Random data for the SDSTs on the machine 4

Table 17 Random data for the SDSTs on the machine 5