The Equilibrium α (Al-Li Solid Solution) and Metastable δ′ (Al₃Li) Phase Boundaries in Aluminum–Lithium Alloys

Abstract

Data on the equilibrium solubilities of the α Al-Li solid solution phase and the ordered metastable δ′ Al₃Li (L1₂ crystal structure) precipitate phase are critically reviewed, and a new binary alloy phase diagram is proposed. The δ′ solvus, describing the equilibrium solubility of Li in the α phase, X_αe, in atom fraction Li, is given by the equation $X_{\alpha e} \, = \,0.{6}00{\text{86 exp}}\left\{ {{-}{8669}.{55}/{\text{R}}T} \right\},$ where R is the gas constant, and the temperature T is in K. The α solvus, i.e. the equilibrium solubility of Li in the δ′ phase, X_δ′e, is given by the equation $X_{\delta \prime e} \, = \,0.{18}0{9}\, + \,{6}.{413}\, \times \,{1}0^{{{-}{4}}} {{T}}{-}{1}.{861}\, \times \,{1}0^{{{-}{6}}} T^{{2}} \, + \,{1}.{4684}\, \times \,{1}0^{{{-}{9}}} T^{{3}} ,$ which represents a compromise between previously published theoretical curves that predict retrograde behavior. It is emphasized that that all the data cited and re-analyzed exclusively involve binary Al-Li alloys. The new phase diagram eliminates data that were previously mis-attributed. Most importantly, it is informed by considerable re-analysis of previously published data, supplemented by the inclusion of data that were not previously considered, and eschews data on both X_αe and X_δ′e that are indubitably non-equilibrium in nature.

1 Introduction

One would think that after many decades of research^[1,2,3,4] undertaken with the intent of commercializing aluminum–lithium base alloys owing to their lower density and higher stiffness with lithium in solid solution, not to mention the increased strength concomitant with precipitation of the metastable ordered δ′ (Al₃Li) phase, we would have by now secure knowledge of the Al-rich region of the underlying binary Al-Li phase diagram. After all, this phase diagram serves as the basis for exploring the effects of assorted alloying additions. Despite its importance, it is fair to state that the locations of the phase boundaries separating the 2-phase α + δ′ region of the metastable phase diagram are imprecise. This is evident on viewing the α + δ′ regions of two phase diagrams shown in Fig. 1, one being the most recent thermodynamic assessment of the entire Al-Li alloy system by Hallstedt and Kim^[5], and the other by Neibecker et al.^[6] who investigated the early stages of precipitation in a ternary Al-Li-Cu alloy. The scatter in the locations of the phase boundaries in Fig. 1 is quite palpable.

Fig. 1

Two versions of the Al-Li phase diagram, illustrating the equilibrium compositions of the α (Al-Li) solid solution matrix and the metastable δ′ (Al₃Li) precipitates: (a) Thermodynamic assessment of Hallstedt and Kim^[5]; (b) Compilation of data by Neibecker et al.^[6]. The figure in (a) has been compressed to equalize the ordinate scales in both figures. The regions within the 2-phase field in (b) represent the calculated results of the BMG model of Khachaturyan et al.^[14]. The original attributions associated with the plotting symbols have been removed for clarity, but several remain identified^{[7,8,9,10,11,13]}

It is obvious on comparing the 2 phase diagrams in Fig. 1 that they do not both include identical sets of data. The extensive data set published by Noble and Bray^[7] was not included in Fig. 1(a) and the data of Livet and Bloch^[8] and Mergia et al.,^[9] which are both represented by the same plotting symbol in Fig. 1(b), were also excluded in Fig. 1(a). On the other hand, the data of Tsao et al.^[10] shown in Fig. 1(a) are not present in Fig. 1(b). Additionally, solubility limits attributed to Papazian et al.^[11] are presented in Fig. 1(a); Papazian et al. themselves point out that the data in their Fig. 1 were taken from the literature, which is easily confirmed in a nearly identical figure published previously by Sigli and Sanchez^[12]. There is one additional set of data in Fig. 1(b) by Pitcher et al.^[13] on a ternary Al-Li-Cu alloy; the solubility limits disagree significantly at low temperatures. The intent herein is not to heap criticisms on the work of Hallstedt and Kim^[5] and Neibecker et al.^[6], but instead to point out that the attempt to acquire data on the equilibrium solute concentrations of the α and δ′ phases is fraught with shortcomings. It is fully appreciated that the compilation of Neibecker et al.^[6] was not intended as a critical review of the literature but instead a straightforward reporting of results published by the authors of the various investigations. Hallstedt and Kim^[5], on the other hand, certainly had access to all the data ignored in Fig. 1(a), so the reason for their exclusion is not clear. Most importantly, it is evident on examining the data in Fig. 1 that the equilibrium concentrations between the α and δ′ phases are either incomplete or inaccurate, thereby justifying a new and critical evaluation.

Imagine now the conundrum in attempting to calculate the equilibrium volume fraction, f_e, of δ′ precipitates in an alloy of given initial composition X₀ at a specific temperature, T, using the lever rule. Ignoring the small differences between the mass densities of the α and δ′ phases, f_e is given by the equation

$$ f_{e} = \frac{{X_{0} - X_{\alpha e} }}{{X_{{\delta^{\prime}e}} - X_{\alpha e} }} $$

(1)

where X_αe and X_δ′e are the equilibrium compositions of the α and δ′ phases, respectively. The magnitude of f_e plays a crucial role in the precipitation strengthening of Al-Li alloys by δ′ precipitates^[15], as well as in the coarsening behavior of δ′ precipitates in these alloys^[16,17]. The uncertainty in calculating f_e is illustrated in Fig. 1 using a hypothetical alloy containing 10 at.% Li aged at 425 K (all Li concentrations in this paper will be expressed as at.% or atom fraction). The green horizontal lines and shaded thick lines in Fig. 1(a) and (b) represent the minimum and maximum possible values of ∆X_e = X_δ′e−X_αe, respectively. The disparities are quite large, varying from ~ 0.23 to ~ 0.29 in Fig. 1(a) and from ~ 0.24 to ~ 0.28 in Fig. 1(b). The new evaluation of the phase boundaries resulting from this work provides, among other things, guidance for calculating f_e confidently and reproducibly.

2 Re-evaluation of Published Data on Solubility Limits

2.1 Data Handling and Processing

Much of the data re-analyzed herein were originally presented in graphical form, necessitating extraction from published figures. In most cases the axes in the original figures were truly orthogonal and parallel to the edges of the computer screen. However, there were exceptions where the axes were rotated, and in some cases non-orthogonal. In these circumstances the rotations and non-orthogonality were easily rectified using Adobe Photoshop. Data were then extracted from the processed images using the software WebPlotDigitizer, which does a respectable, though imperfect, job of reproducing the data. Final processing was done by superimposing a transparent copy of the image used for data extraction onto a plot generated by Microsoft Excel, scaled so that the axes of the plots overlapped to the maximum extent possible. The numerical values in the individual cells in Excel were then adjusted so that the data points in the Excel plot overlapped those in the transparent figure. Perfect reproduction was nearly impossible due to irregularities in the scales, unusual plotting symbols in the original figures and small errors in the authors’ original locations of the symbols. Despite these minor shortcomings the results were reasonably accurate, with accuracy that was relatively easy to assess (for example by comparing the slopes and intercepts of extracted data on kinetics with those reported by the authors).

Numerous methods were used by a plethora of researchers and groups to obtain data on the equilibrium concentrations of the α and δ′ phases. In some instances the results of the research were accepted herein without additional data processing, but in many cases it was necessary to re-evaluate the original analyses to obtain more meaningful results. As noted earlier, only data on binary Al-Li alloys were considered.

This paper is organized as follows. The new phase diagram is presented at the outset, with the sources of data identified. Each contribution is discussed later so that the reader can appreciate the decisions taken to evaluate the data. Numerical descriptions of the phase boundaries (the δ′ and α solvus curves describing the equilibrium solubility of Li in the α phase and the δ′ phase, respectively) are also provided to enable input for the best possible estimates of f_e as a function of initial alloy composition and aging temperature. After closing comments and conclusions, all the data are presented in tabular form in the Appendix.

2.2 The α- δ′ Phase Diagram

The main product of this research effort is presented in Fig. 2. The data shown are the results of 20 investigations^{[7,8,9,10,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]}. The acceptable data on the δ′ solvus were fitted to an Arrhenius-type equation, yielding the result

$$ X_{ae} = \, 0.{6}00{\text{86 exp}}\left\{ {\hbox{-}\hbox{8},{669}.{55}/{\text{R}}T} \right\}, $$

(2)

where R is the gas constant. Equation 2 specifies a heat of solution of ~ 8.67 kJ/mol, which is about 5.5% smaller than the value 9.18 kJ/mol reported by Noble and Bray^[7]. It is important to point out that not all the data were included in the fit. In particular, the data indicated by the small symbols (which are color-coordinated with the corresponding larger ones) were excluded, primarily because they deviate substantially from the clusters of data points near the ultimate solubility curve favored in this investigation (the black curve). Additionally, the data of Ceresara et al.^[20], Cocco et al.^[21] and Khushaim et al.^[32] were excluded for reasons discussed later.

Fig. 2

The Al-rich region of the Al-Al₃Li phase diagram resulting from this work. The Legend identifies the authors of the data in chronological order: Tamura et al.^[18], Williams and Edington^[19], Ceresara et al.^[20], Cocco et al.^[21], Nozato and Nakai^[22], Jensrud and Ryum^[23], Livet and Bloch^[8], Baumann and Williams^[33], Fujikawa et al.^[24], Sung et al.^[25], Liu and Williams^[26], Liu and Williams^[27], Shaiu et al.^[28], Jo^[29], Abis et al.^[30], Del Rio^[31], Noble and Bray^[7], Mergia et al.^[9], Tsao et al.^[10] and Khushaim et al.^[32]. In addition, the theoretically predicted δ′ and α solvus curves due to Khachaturyan^[14] and Hallstedt and Kim^[5] are also included, as well as the empirical curves from this investigation. The data identified using the small symbols were excluded from the fit to the δ′ solvus curve, Eq 2, and deviate significantly from most of the data on the temperature dependence of the α solvus

It is plainly evident in Fig. 2 that the δ′ solvus curve calculated by Khachaturian et al. (red)^[14] is in quite good overall agreement with the experimental data, especially in the important mid-temperature region from 400 to 600 K; their heat of solution is ~ 9.07 kJ/mol. The δ′ solvus curve of Hallstedt and Kim (green)^[5] also agrees reasonably well with the data and heat of solution, ~ 8.88 kJ/mol, though the predicted solubility of δ′ is slightly larger in the mid-temperature region. There are two other theoretical δ′ solvus curves reported in the literature, one by Chen et al.^[34] and the other by Mao et al.^[35]. Both agree reasonably well in the mid-temperature region in Fig. 2, but they are excluded to reduce clutter in the figure. Most recently, Liu et al.^[36] and Shao et al.^[37] have published papers on first-principles predictions of the Al-Li phase diagram, but their comparisons with experimental data in the Al-rich α-δ′ region are superficial, both papers citing early phase boundaries reported by Gayle and Vander Sande^[38].

As is apparent in Fig. 2, when it comes to the α solvus there is unfortunately far too much scatter in the data to fit a meaningful curve. Though one would be hard pressed to find an example in previously published literature, there are even concentrations of δ′ that exceed 25% Li. There is no a priori reason why excess Li should be forbidden in the δ′ phase, but it has not appeared in prior work, as is evident in Fig. 1. The reasons why this has happened in this study will be exposed when the relevant data are discussed. Despite the large scatter, the α solvus curves from the models of Khachaturyan et al.^[14] and Hallstedt and Kim^[5] are in quite reasonable agreement with the middle range of data. There does not appear to be a preference enabling a choice between the two theoretical curves, and it is evident that only one should be used for the purpose of calculating f_e. To this end it seems best to compromise by computing the average of the two theoretical curves. The equation describing this average is

$$ _{\delta^{\prime} e} = \, 0.{18}0{9 } + { 6}.{413} \times {1}0^{{{-}{4}}} T{-}{ 1}.{861} \times {1}0^{{{-}{6}}} T^{{2}} + { 1}.{4684} \times {1}0^{{{-}{9}}} T^{{3}} , $$

(3)

which is represented by the solid black curve in Fig. 2. For the sake of completeness the equations describing the solves curves of Hallstedt and Kim^[5] and Khachaturyan et al.^[14] are presented in Table 1.

Table 1 The empirical δ′ and α solvus curves extracted from the published figures of Hallstedt and Kim^[5] and Khachaturyan et al.^[14]

2.3 Comments on the Contributions to the Phase Diagram

The methods used to measure the equilibrium concentrations of the α and δ′ phases were quite varied. Five employed small-angle x-ray scattering (SAXS)^{[8,10,20,21,28]} and two used small-angle neutron scattering (SANS)^[9,30]. Electrical resistivity was measured as a function of aging time in three experiments^[7,24,29], two experiments used calorimetric measurements^[7,22], x-ray diffraction (XRD)^[18,26], electron energy-loss spectroscopy (EELS)^[25,27] or conventional transmission electron microscopy (TEM)^[19,23] and single experiments involving quantitative metallography (QM)^[26], positron annihilation spectroscopy (PAS)^[31] or atom probe tomography (APT)^[32] were reported. As we shall see, the results of quite a few experiments were based on measurements of the instantaneous volume fraction, f, not necessarily f_e, from which either X_αe or X_δ′e was nevertheless estimated, assuming that the other was already known. It should be obvious that the most accurate temperature-dependency possible of X_αe is needed if meaningful values of X_δ′e are to be extracted from measurements of f_e, and vice versa. The results of several of those experiments necessitated re-analysis of the original data.

2.3.1 Electrical Resistivity Measurements

Fujikawa et al.^[24], Jo^[29] and Noble and Bray^[7] monitored the temporal dependence of the electrical resistivity, ρ, of the Al-Li solid solution during coarsening to obtain a value of X_αe. The method exploits the typical linear relationship between ρ and X_α as a calibration curve and utilizes the temporal dependence of X_α during diffusion-controlled coarsening, i.e.

$$ X_{a} = X_{ae} + \, (kt)^{{{-}{1}/{3}}} $$

(4)

where κ is a rate constant that depends on the thermo-physical parameters of the alloy system. Measurements of ρ are converted to X_α, plotted versus t^–1/3 and extrapolated to t^–1/3 = 0 to obtain a value of X_αe for a given initial alloy concentration and aging temperature. It is apparent immediately on viewing Fig. 2 that the values of X_αe measured by Fujikawa et al.^[24] and Jo^[29] are much smaller than the other data in the temperature range 400 to 550 K. Factors that could affect the accuracy of the measurements are differences in the calibration curves used by the various authors, but the differences were relatively small, as noted by Noble and Bray. More likely, as also noted by Noble and Bray, was the failure of Fujikawa et al.^[24] and Jo^[29] to take into account the contribution to ρ from the precipitates and the possible appearance of stable δ phase¹ particles in the microstructures, which were not examined by those authors. The relatively high aging temperatures and longer aging times used in the experiments of Fujikawa et al. and Jo would have exacerbated the problems by promoting the transformation of δ′ to δ.

2.3.2 Calorimetric Measurements

Nozato and Nakai^[22] and Noble and Bray^[7] used somewhat different calorimetric procedures to obtain data on X_αe, the former measuring specific heats during heating of all specimens at the same rate and the latter using differential scanning calorimetry involving heating at different rates. Both investigations monitored the temperatures at which peaks in the heating curves disappeared to zero as the solubility limits for an alloy of given composition were approached. The data from the two investigations are quite consistent, the two exceptions being rather low equilibrium concentrations measured by Nozato and Nakai^[22] corresponding to 505 and 510 K; these data are excluded from the fit in Fig. 2.

2.3.3 TEM Observations of δ′ Precipitation in Aged Specimens

Williams and Edington^[19] and Jensrud and Ryum^[23] conducted aging experiments on binary alloys to explore, among other things, the temperatures at which δ′ precipitates were or were not observed. If coherent spherical δ′ precipitates were present in the microstructure the aging temperature was deemed below the δ′ solvus for a particular overall alloy composition. If not, the aging temperature was above the δ′ solvus. Using aging temperatures in intervals of 10 K in both studies, the δ′ solvus was bracketed to within ± 5 K of uncertainty.

2.3.4 XRD Experiments

The magnitude of the intensity ratios of superlattice and fundamental x-ray reflections in aged 2-phase α + δ′ alloys provides a direct measurement of f. Tamura et al.^[18] and Liu and Williams^[26] used somewhat nearly identical approaches to measure f using XRD in several binary Al-Li alloys, but only Liu and Williams reported values of f_e for their combinations of initial alloy concentration and aging temperatures.

Tamura et al.^[18] measured the kinetics of volume fraction augmentation in a 10.73% Li alloy aged at 473 K. They measured the intensity ratios of the (300) superlattice and (400) fundamental reflections to obtain f as a function of aging time. They did not report values of either X_αe or X_δ′e and were not aware that they could obtain a value of f_e at this temperature by analyzing the kinetics of volume fraction augmentation. The data of Tamura et al. are analyzed herein in precisely that way to obtain f_e for their alloy. The kinetics of volume fraction augmentation follow the equation^[39,40]

$$ f = f_{e} - \frac{{\left( {\kappa t} \right)^{ - 1/3} }}{{\Delta X_{e} }}, $$

(5)

where ∆X_e = X_δ′e−X_αe. According to Eq 5 a plot of f versus t^–1/3 should be linear in the late stages of coarsening and extrapolate to f_e at t^–1/3 = 0 (t = ∞). The data of Tamura et al. are plotted in this manner in Fig. 3, resulting in f_e = 0.2539; it is evident that linearity expected for the late-stage kinetics is quite good, with a correlation coefficient R² = 0.9826. Application of Eq 1, with X_αe calculated using Eq 2, produces the result X_δ′e = 0.2314. This value of X_δ′e is a new addition to the data on the Al-Li phase diagram.²

Fig. 3

The data of Tamura et al.^[18] plotted as volume fraction, f, versus aging time, t, raised to the –1/3 power, for consistency with Eq 5. The late-stage coarsening data show that f is linearly related to t^–1/3. The shorter-time data are shown in black symbols. The equilibrium volume fraction, f_e, is obtained by extrapolation to t^–1/3 = 0, as shown.

Liu and Williams^[26] relied upon suitably long aging times at two temperatures for their XRD experiments, 428 K for 4 months and 498 K for 4 days. The assumption that f = f_e is implicit in these aging treatments. Similar to the procedure used by Tamura et al., Liu and Williams measured the intensity ratios of the (300) and (400) reflections to obtain values of f_e, which they reported as 0.370 and 0.346 at 428 and 498 K, respectively. Using these values of f_e in conjunction with Eqs 1 and 2, the resulting values of X_δ′e at 428 and 498 K are 0.2537 and 0.2271, respectively. These results differ significantly from those reported by Liu and Williams (0.241 and 0.233) undoubtedly because the values of X_αe used in their calculations differ significantly from those calculated using Eq 2. The fact that X_δ′e = 0.2537 at 428 K exceeds 0.25 might raise some eyebrows, but there is nothing in principle to prevent the concentration of the δ′ phase from exceeding 25 at.% Li.

Liu and Williams^[26] also presented a datum on a measurement of X_δ′e made using a value of f_e determined from TEM-based QM on a specimen containing 7.9% Li aged at 493 K. Their reported value of f_e is 0.072, which yields X_δ′e = 0.1628 using Eq 1 and 2. This concentration, the smallest of any evaluated for the δ′ phase, is due entirely to the fact that X_αe calculated using Eq 2, 0.0725, is slightly larger than the value of X_αe, 0.070, used by Liu and Williams. The upshot of this discrepancy illustrates the perils of calculating an equilibrium concentration from a measured volume fraction when the difference between the overall alloy solute concentration and the equilibrium matrix solute concentration is small; i.e. X₀−X_αe = 0.079−0.070 = 0.009 (Liu and Williams^[26]), cf. X₀ −X_αe = 0.079 –0.0725 = 0.0065 (this investigation). The calculation of X_δ′e is particularly perilous when X_αe is not known with sufficient accuracy.

2.3.5 Experiments Using EELS

In principle EELS measures the chemistry of phases in the TEM. In Al-Li alloys this specialized technique is difficult to implement for a variety of reasons discussed by Liu and Williams^[27], but it has several advantages for the quantitative analysis of phases containing light elements. The method is most accurate when it can be assured that the phase in question occupies the entire thickness of the thin foil specimen, which means that the δ′ precipitates must be through-thickness. EELS contributed five data points to the Al-Li phase diagram, four by Liu and Williams and one by Sung et al.^[25]

Sung et al. reported the ratio of Al to Li in their through-thickness δ′ particle as 3.6 to 1, resulting in an approximate concentration of 22% Li. Since the reported error in their measurement was ± 20% this approximate concentration was deemed acceptable. It seems here that there is no harm done in reporting the more accurate concentration of 21.74% Li, so X_δ′e = 0.2174 is the concentration that appears in Fig. 2. The δ′ compositions measured by Liu and Williams^[27] were reported in the text of their paper as X_δ′e = 0.236, 0.218 and 0.205 at T = 428, 498 and 563 K, respectively. To check the influence of their specimen preparation procedures on X_α, Liu and Williams also used EELS to measure the Li concentration in the matrix of a specimen containing 12.7% Li aged for 4 h at 563 K. The result was 8.8% Li. Perhaps 4 h of aging at 563 K is not quite long enough to attain thermodynamic equilibrium, but X_α should be close enough to X_αe to add this value to the δ′ solvus. Therefore, the datum X_αe = 0.088 at 563 K is included in Fig. 2; it is a new entry to the phase diagram.

2.3.6 Small-Angle x-ray Scattering (SAXS) Experiments

The very first measurements of the δ′ solvus curve were the products of SAXS experiments conducted by Ceresara et al.^[20] The integrated intensity, Q₀, of SAXS scattering curves from a specimen containing small precipitates provides data on the volume fraction and sizes of the precipitates^[41]. Q₀ can be predicted theoretically as a function of f or its constituent components, X₀, X_α and X_δ′. If both X_α and X_δ′ are unknown to begin with, the value of one of them must be assumed to ascertain the value of the other. This was the task undertaken by Ceresara et al. They acquired the SAXS spectra from an alloy containing 6.72% Li aged under five conditions: 200 h at 293 K (room temperature); 24 h at 398 K; 24 and 112 h at 423 K; 24 h at 473 K. Q₀ is related to the concentrations of the phases in the alloy by an equation due to Gerold^[42], namely

$$ Q_{0} = \, (X_{\delta \prime } {-}X_{0} )(X_{0} {-}X_{a} )\left( {Z_{Al} {-}Z_{Li} } \right)^{{2}} /V_{ave} , $$

(6)

where Z_Al and Z_Li are the atomic numbers of Al and Li and V_ave is the average volume per atom in the alloy.

With no better option available to them, Ceresara et al.^[20] assumed X_δ′ = X_δ′e = 0.25 to estimate X_α from their measured values of Q₀. They reported their results in tabular form. They are shown in Fig. 2 but are not included in the fit to the data on the δ′ solvus because the aging times were short and the concentrations far from thermodynamic equilibrium, especially at the lower aging temperatures. This shortcoming was also noted by Tsao et al.^[10]

Following the work of Ceresara et al.^[20], Cocco et al.^[21] realized that when alloys of two different compositions, X₀₁ and X₀₂, are aged at the same temperature Eq 6 becomes 2 equations with 2 unknowns, X_α and X_δ′, which must be identical and equal to X_αe and X_δ′e at the single aging temperature of the experiment. The same method was used by Gerold^[42] to determine the solubility limits at room temperature in Al-Zn alloys. The benefits of the approach of Cocco et al. are manifest because values of X_δ′ are also included in the results. Since the aging temperatures and times used by Cocco et al. were identical to those used by Ceresara et al.^[20] the compositions, especially X_α, at the lower aging temperatures are far from equilibrium. This is not the case for X_δ′, since the compositions of precipitate phases after short aging times are close to their equilibrium values^[43]. The data of Cocco et al. on X_α were not included in the δ′ solvus fit, for this reason, though the values are shown in Fig. 2. It is evident in Fig. 2 (see also Table 7) that the values of X_α reported by Cocco et al. differ only slightly from those of Ceresara et al.

Livet and Bloch^[8] investigated the kinetics of precipitation by SAXS in 3 binary Al-Li alloys containing 7.5, 9.0 and 10.5% Li aged at 423 and 453 K. They reported the composition of the 10.5% Li alloy as 11% Li, but subsequent publications by Bley et al.^[44,45] clearly indicate that the composition was in fact 10.5%, which is the composition used in the subsequent analysis in this section. Livet and Bloch simplified and re-defined Eq 6 by dividing it by (Z_Al−Z_Li)²/V_ave. Livet and Bloch analyzed their data assuming the temporal dependencies of X_α and Q₀ to be identical, linearly dependent on t^–1/3 as in Eq 4, with a time-independent X_δ′. Extrapolating Q₀(t) to t^–1/3 = 0 yields an “equilibrium” value of Q₀(∞) from which values of X_αe can be obtained at each aging temperature, assuming X_δ′e is known. Livet and Bloch report 2 values of X_δ′e = 0.242 at 423 K and 0.219 at 453 K, and cite two sources, but did not specify the references in their paper. Their reported values of X_αe are 0.044 at 423 K and 0.053 at 453 K.

It is possible to obtain more reliable values of X_αe and X_δ′e from the data of Livet and Bloch by re-analyzing their data more realistically, as done by Cocco et al.^[21] The expectation is that using the tabulated values of Q₀(∞) reported by Livet and Bloch, we should find the equilibrium compositions of both the α and δ′ phases independently. The easiest way to proceed is to process the necessary data graphically. At any given temperature the analysis from data on kinetics from an alloy of initial composition X_0j will produce, from a plot of Q_0j vs t^–1/3, a value of Q_0j(∞). On solving Eq 6, sans the factor (Z_Al −Z_Li)²/V_ave, for X_α, we can write

$$ X_{\alpha } = \frac{{Q_{0j} \left( \infty \right) + X_{0j}^{2} - X_{0j} X_{{\delta^{\prime}}} }}{{X_{0j} - X_{{\delta^{\prime}}} }}. $$

(7)

If data on two alloys are available (j = 1,2) curves of X_α versus X_δ′ will intersect at a point representing X_αe and X_δ′e. If data on three alloys are available (j = 1,2,3) all three curves of X_α versus X_δ′ will intersect at the same point, with the same significance.

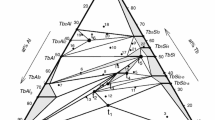
The procedure is illustrated in Fig. 4, using the original data of Livet and Bloch on Q₀(∞) presented in Table 2. We see in Fig. 4(a) that the curves of X_α versus X_δ′ generated by Eq 7 (T = 423 K) do not intersect at the same point when Q₀(∞) = 0.00520. Instead, there are 3 intersections, all at concentrations of X_δ′ exceeding 25% Li. Since the data on Q₀ versus t^–1/3 for the 7.5% Li alloy aged at 423 K are clearly non-linear, as opposed to the data on the other 2 alloys (see Fig. 5, Livet and Bloch). Nevertheless, it can be inferred^[8] that the values of Q₀(∞) for the 7.5% Li alloy were obtained from plots of Q₀ versus t^–1/3 for the data taken at both temperatures. Only a small adjustment of Q₀(∞) from 0.00520 to 0.00543 (Table 1) is needed to rectify this situation, as seen in Fig. 4(b), which shows the curves for all 3 alloys intersecting at a concentration of X_δ′e = 0.2514. The value of X_αe at 423 K turns out to be only slightly larger than that reported by Livet and Bloch. Applying the same approach to the data on aging at 453 K yields significant differences in the values of X_αe and X_δ′e, as shown in Table 2. All the equilibrium concentrations from this investigation are presented in Fig. 2.

Fig. 4

Illustrating the graphical procedure based on Eq 7 for determining X_αe and X_δ′e from data on integrated intensity, Q₀(∞), measured at the same temperature for 2 or more alloys of different compositions, X₀. The data on 3 alloys with X₀ = 0.075, 0.090 and 0.105 are shown in (a) and (b) respectively. A slight adjustment of Q₀(∞), from 5.2 × 10^–3 to 5.43 × 10^–3 enabled the intersection of the 3 curves in (b), leading to the results on the equilibrium solubilities at 423 K reported in Table 1

Table 2 The data of Livet and Bloch^[8] re-evaluated using the method of Cocco et al.^[21] embodied in Eq 7. The adjusted value of Q₀(∞) was chosen to bring the 3 curves in Fig. 4(b) into coincidence, leading to the values of X_αe and X_δ′e shown in the 5 and 7th rows of the table

Fig. 5

The data of Tsao et al.^[10] on the kinetics of volume fraction augmentation plotted as f versus t^–1/3, as in Fig. 3, prescribed by Eq (5). The equilibrium volume fractions, f_e, are determined by the extrapolating the curves to t^–1/3 = 0. The datum encircled was published in an earlier paper by Tsao et al.,^[47] but was not included in the fit. The results are reported in Table 3

The final contribution in the SAXS category stems from the work of Tsao et al.^[10] They analyzed data on the kinetics of average particle growth and volume fraction augmentation to obtain values of X_αe and X_δ′e in an alloy containing 7.9% Li aged at 423, 433 and 443 K. Their analysis utilizes an equation describing the kinetics of particle evanescence, i.e. the decrease in the number density, N_v, with aging time^[46], that requires several necessary assumptions in order to extract the equilibrium solubilities. A far more satisfactory approach to acquire the data on X_αe is to use their data on volume fraction augmentation, in conjunction with Eqs 3 and 1. This procedure produces revised values of X_αe, adding to the δ′ solvus, but eliminates their data on the α solvus.

The data of Tsao et al. on the kinetics of volume fraction augmentation are shown in Fig. 5, plotted as f versus t^–1/3 in accordance with Eq 5, exactly like the treatment of the data of Tamura et al.^[18] The values of f_e at the 3 different aging temperatures are the intercepts of the plots, from which the decision was taken to calculate X_αe, using Eq 3 to calculate X_δ′e, then Eq 1 to calculate X_αe. The results are summarized in Table 3.

Table 3 Results of the re-examination of the data of Tsao et al.^[10] The data in the rows labelled This Work stem from the volume fractions, f_e, obtained by extrapolation of the plots in Fig. 5

It is evident in Table 3 that the equilibrium volume fractions obtained from the plots in Fig. 5 are in very good agreement with those reported by Tsao et al., but the derived values of X_αe and calculated values of X_δ′e differ, though in a few cases the difference is quite small. Two of the three values of X_αe (423 and 433 K) are in excellent agreement with the data on the δ′ solvus curve (Fig. 2). Unfortunately, the much larger value of the volume fraction at 443 K is clearly erroneous, given that f_e must decrease with increasing temperature. In this context it should be noted that the linear fits to the plots of f versus t^–1/3 are all fairly poor, none more so than the 3-point fit to the 443 K data. Additionally, Tsao et al. chose to ignore one data point from their measurements at 433 K^[47] (see Fig. 5) without explanation. Their result^[10] is nevertheless accepted here, giving them the benefit of the doubt.

2.3.7 Small Angle Neutron Scattering (SANS) Experiments

There are two contributions in this category, the first by Abis et al.^[30] and a later one by Mergia et al.^[9]. Abis et al. investigated the kinetics of δ′ precipitation in a binary Al-10.73% Li alloy aged at 463 K. They reported tabulated data on several variables, including the volume fraction as a function of aging time from 1 to 90 h. The dependence of f on t is essentially constant, independent of t^–1/3, with an average value of 0.2413 and a very small standard deviation of ± 0.0063. Accordingly, it is assumed here that X_αe can be computed using Eq 1 after having calculated X_δ′e = 0.2246 from Eq 3; the result is X_αe = 0.070.

The second of the two papers by Mergia et al.^[9] provides the source of data on the δ′ solvus. They measured the kinetics of volume fraction augmentation in an alloy containing 8.9% Li aged at 363, 393, 423, 458 and 483 K for aging times up to 600 h. The data on f were converted to X_α using Eq 1, assuming X_δ′e = 0.25, independent of aging time and aging temperature. The data on X_α versus t were then subjected to a least-squares fit of Eq 5 (not a plot of X_α versus t^–1/3) to obtain X_αe; the values were reported in tabular form. The main drawback of the analysis of Mergia et al. is the assumption that X_δ′e = 0.25. It is possible to do better, as described below.

Mergia et al. reported their data on X_α versus t in graphical form at 4 aging temperatures: 393, 423, 458 and 483 K; these data are representative at long aging times, in the coarsening regime. They also reported data on f versus t at 363 K in graphical form over the entire range of aging times, beginning at the nucleation stage. To update the results, the data on X_α versus t were extracted from the published figures and converted to values of f using Eq 1, with X_δ′e = 0.25. The assumption here is that these values of f were the original ones transformed by Mergia et al. to values of X_α for analysis using Eq 1. This being the case, it is then a simple matter to re-convert the original data on f to data on X_α again using Eq 1 but calculating X_δ′e for the 4 different aging temperatures using Eq 3. Two choices then remain to obtain the proper values of X_αe: 1. Plot f versus t^–1/3 and extrapolate the results to t^–1/3 = 0 to obtain proper values of f_e and then use Eq 1 to calculate X_αe; 2. Plot the corrected values of X_α vs t^–1/3 and extrapolate the data to t^–1/3 = 0 to obtain X_αe directly. Both methods produce the same result. The choice here was the former since the data on f versus t at 363 K were already available. The plots are shown in Fig. 6 and the results are summarized in Table 4. The values of f_e (with one exception) and X_αe are slightly larger than those reported by Mergia et al. and all the values of X_αe except for the datum on 363 K are included in the fit to the δ′ solvus in Fig. 2.

Fig. 6

The data of Mergia et al. on the kinetics of volume fraction augmentation plotted as f versus t^–1/3, as in Fig. 3, prescribed by Eq 5. The equilibrium volume fractions, f_e, are determined by the extrapolating the curves to t^–1/3 = 0. The results are reported in Table 4. The data indicated by the black symbols were excluded from the fitting

Table 4 The results of the re-analyses of the data of Mergia et al.^[9] The values of f_e were obtained by extrapolating the data in Fig. 6 to t^–1/3 = 0, after which X_αe was calculated using Eq 1. The original data of Mergia et al. are also shown

2.3.8 Dissolution Experiments

The idea behind dissolution experiments is straightforward. Alloys aged below the δ′ solvus will contain a typical coarsened δ′ microstructure. If specimens of the alloy are re-aged at successively higher temperatures for short times the precipitates will normally grow, though their numbers will decrease. Finally, if the specimens are aged above the solvus temperature the δ′ precipitates will disappear from the microstructure. These types of experiments were undertaken by Baumann and Williams^[33], Shaiu et al.^[28], Del Río et al.^[31] and Khushaim et al.^[32] using a variety of techniques.

Baumann and Williams^[33] used TEM to investigate the roles of capillarity and coherency strains on the reversion of δ′ precipitates, copious quantities of which were produced in an alloy containing 7.9% Li aged initially for 2 h at 453 and 463 K. The precipitates persisted on re-aging the alloy for 3 h at 526 K, but completely dissolved after aging for 3 h at 531 K. This places the solubility limit for X_αe = 0.079 at T ≈ 528 K, which is the entry in Fig. 2.

Shaiu et al.^[28] used SAXS and TEM to study the early stages of aging and dissolution in three alloys containing 5.2, 7.0 and 12.0% Li aged at temperatures between 300 and 600 K. The main objective was to explore the ordering reaction and aging kinetics from the beginning of precipitation. Dissolution experiments were used to determine the δ′ solvus, which is why their results are included here rather than in Sec. 2.3.6. The results reported in the text of their paper show that the δ′ solvus temperature is 468 K for X_αe = 0.070 and 578 K for X_αe = 0.120, both temperatures having an uncertainty of ± 2.5 K; these data are reported in Fig. 2. Curiously, Shaiu et al. did not observe δ′ precipitation in the alloy containing 5.2% Li, which is clearly supersaturated at temperatures below ~ 420 K according to Fig. 2. The reason for this finding is unclear.

Del Río et al.^[31] investigated δ′ precipitation and dissolution in an alloy containing 9.9% Li using positron annihilation spectroscopy (PAS). They solution-treated this alloy at 843, water-quenched it to room temperature and used TEM to detect the presence of ordered δ′ precipitates from L1₂ superlattice reflections in electron diffraction patterns. Subsequent annealing experiments on the as-quenched specimens using PAS lifetime measurements revealed dissolution of the δ′ precipitates at around 423 K (as indicated by decreasing lifetimes), but growth of the δ′ precipitates up to a temperature of 550 K (increasing lifetimes), followed by decreasing lifetimes at T > 550. They interpreted their data to mean that the δ′ solvus temperature of the 9.9% Li alloy had been placed at 550 K. Thus X_αe = 0.099 at 550 K is taken as the δ′ solvus point for this alloy.

The final entry in this section, and paper, involves the investigation of Khushaim et al.^[32] They used atom probe tomography (APT) in conjunction with pulsed laser heating to study the redistribution of the δ′ precipitate microstructures and concomitant solute concentrations in the α matrix and δ′ precipitate phases. Their alloy contained 7.8% Li and was aged initially at 463 K for 3 h, after which APT tips were prepared for subsequent regulated and well-characterized in-situ pulsed laser heating to known energies ranging from 10 to 100 pJ. After each application of laser heating the authors measured the average diameter, <d>, N_v, X_α and X_δ′. The temperature of the APT specimen tips could not be measured directly, so the authors used data on the diffusion of Li as well as assumptions about the diffusion distance, and a diffusion time of t = 1 s, to obtain an estimate of the diffusion coefficient for Li in the solid solution, D, corresponding to the energy applied to the APT tip. The diffusion distance, L, as a function of energy was taken as the difference between the average size before and after application of the laser pulses. Having assigned t = 1 s and estimated L, D was calculated using the relationship D = L²/4t, after which T was calculated by making use of the Arrhenius relationship D = D₀exp(-Q_d/RT), with the activation energy for diffusion, Q_d = 119 kJ/mol, and an unreported value of D₀. Using the values of D reported in Table 2 of Khushaim et al. it is easy to show that the average value of D₀ used by the authors must have been 1.458 × 10^–5 m²/s.

Khushaim et al.^[32] reported the main results of their work, specifically their data on X_α and X_δ′ as equilibrium solubilities, X_αe and X_δ′e for their calculated temperatures. It has already been noted that the concentrations reported as equilibrium solubilities are not regarded as such in this work. The reasons why are severalfold. Perhaps the most important reason has to do with thermodynamic and kinetics imperatives when specimens containing precipitates are doubly aged. Recall that all the specimens subjected to pulsed laser heating were first aged for 3 h at 463 K. According to the authors the δ′ precipitate dispersion was characterized initially by the parameters <d> = 14.2 nm, X_α = 0.054 and X_δ′ = 0.226. Taking T = 463 K as a reference temperature, T₁, and denoting the re-aging temperature as T₂, consider the consequences of the sign of ∆T = T₁−T₂. If ∆T > 0 the δ′ precipitates must initially dissolve, concomitantly enrich the matrix locally and find their own concentrations depleted. On the other hand, if ∆T < 0 the precipitates must initially grow as solute flows towards them as demanded by the phase diagram, hence the matrix must become locally depleted in solute and the precipitates must become enriched. This mandatory behavior is completely belied by the results of Khushaim et al. They report that <d> and X_δ′ both decrease, while X_α increases, monotonically as the laser energy and T increase. This behavior is reproduced in Table 5, which shows that ∆T < 0 for two of their calculated temperatures, with the associated and non-physical increase in <d> instead of the expected decrease.

Table 5 Partial summary of the data of Khushaim et al.^[32] reported in Tables 1 and 2 of their paper

There are also shortcomings associated with the diffusivities calculated by Khushaim et al.^[32] The diffusion of Li in Al-Li solution has been measured in an 8.1% Li alloy by Pérez-Landazábal et al.^[48] using an internal friction method; their diffusivities are denoted here as D_PL. The temperature range of the internal friction measurements encompasses that of δ′ precipitation, thereby obviating the need for large extrapolations of conventional diffusion data to low temperatures. The temperature dependence of D_PL is represented by an Arrhenius equation with D_0PL = 3 × 10^–7 m²/s and Q_PL = 115.79 kJ/mol^[48]; the calculated values of D_PL are shown in Table 5. Comparison of the diffusion coefficients calculated by Khusheim et al. with those measured by Pérez-Landazábal et al. (see the last 2 columns of Table 5) shows that the former are about 23 to 24 times faster. This means that the diffusion distances, L, estimated from D_PL are a factor of roughly 4.8 smaller than those estimated by Khusheim et al.^[32] Referring to their Table 2, their values of L vary between 0.8 and 5 nm over the temperature range of their calculations. The diffusion distances calculated using D_PL therefore imply that a Li atom will random-walk a distance of only ~ 1 nm even at the highest temperature measured by Khushaim et al. The main implication of these much smaller calculated values of L is that the temperatures accompanying pulsed laser heating must have been significantly higher than those estimated by Khushaim et al. Higher temperatures are entirely consistent with the reported monotonic decrease of <d> with increasing laser pulse energy.

Having noted all the deficiencies in the work of Khushaim et al.^[32], it is nevertheless quite obvious on viewing Fig. 2 that their reported values of X_α agree exceptionally well with the data on the δ′ solvus. After full consideration of their methods of analysis, it can only be concluded that the agreement is fortuitous.

3 Summary

The primary objective of this critical review of the literature on the Al-Al₃Li (δ′) phase diagram was to establish beyond a reasonable doubt the phase boundaries that define equilibrium between the α and δ′ phases, i.e. the δ′ and α solvus curves. A total of 64 data points were considered in connection with the δ′ solvus, 22 of which were rejected, either has having concentrations too far removed from the mainstream data or because the concentrations could not be accepted as equilibrium values. The latter category includes the data of Ceresara et al.^[20], Cocco et al.^[21] and Khushaim et al.^[32], even though it is apparent in Fig. 2 that most of the rejected data agree quite well with the bulk of the data on the δ′ solvus. The data on X_α of Ceresara et al. and Cocco et al., which are nearly overlap** in Fig. 2, are very likely close to X_αe at the higher temperatures of their investigations and might well have been included in the fit without having much influence on the outcome. The same is true for the data of Khushaim et al. However, knowing that the exclusion of non-equilibrium data is the appropriate path towards establishing the δ′ solvus, provides additional confidence in Eq 2 moving forward.

The data on the α solvus consist of 11 data points that agree remarkably well with the retrograde theoretical curves of Khachaturyan et al.^[14] and Hallstedt and Kim.^[5], and the compromise offered by Eq 3 provides a solid foundation for future work involving the calculation of equilibrium volume fractions using the lever rule, Eq 1.

In closing, the phase diagram in Fig. 2 has not only been informed by considerable re-analysis of previously published data, but also by the inclusion of data that have not been previously considered^[18,30,33]. Additionally, the data of Papazian et al.^[11], which were mis-attributed through no fault of their own, have been removed. It is reiterated that only data on binary alloys have been considered in this work.

Appendix

See (Tables 6 and 7).

Table 6 Data used in evaluating the δ′ solvus curve, presented as (X_αe, T) coordinates specifying the equilibrium atom fraction Li and the solvus temperature in K

Table 7 Data used in evaluating the α solvus curve, presented as (X_δ′e, T) coordinates specifying the equilibrium atom fraction Li and the solvus temperature in K