Optical Susceptibility of Hybrid Semiconductor Quantum Dot-Metallic Nano Ellipsoid System Under the Effect of the Exciton-Plasmon Coupling Field Interaction

Abstract

We examine the optical susceptibility of the semiconductor quantum dot-metallic nano ellipsoid system under the effect of the exciton-plasmon coupling field. Also, we determine the optical susceptibility for the semiconductor quantum dot and the three metallic nano ellipsoids under the responses to the total effect of the three applied electromagnetic fields. The phenomena of Fano-resonance with amplification and Autler-Town doublet peaks are obtained and discussed. The phenomena of Fano-resonances and Autler-Town doublet peaks can be controlled by varying the depolarization factor of nano ellipsoid, semi-axes, and other parameters in a hybrid system.

Introduction

Nano-scale semiconductor quantum dot (SQD) and metallic nanoparticle (MNP) have been extensively studied in modern nanoscience and nanotechnology, allowing for the construction of hybrid nanostructures for their application in optoelectronics and photonics [1,2,3,4,5], such as nano-sensor [6, 7]. In the opinion of quantum physics, quantum dots (QDs) are different from metallic nanoparticles despite their identical spatial confinement size [8,9,10], where the metallic nanoparticles can change the optical properties of semiconductor nanostructures via the localized surface plasmon or their collective resonances [11,12,13]. The advantage of the spectrally widely separated localized plasmon resonance of the gold nanorods and silver nanoparticles is shown and demonstrated in [14, 15]. These reviews summarize the importance and applications of plasmonic metallic nanoparticles in photodynamic therapy (PDT). The future prospects of these plasmonic nanoengineering strategies have a significant impact on improving the therapeutic efficacy of cancer PDT. The plasmonic and the dipole-dipole interaction between semiconductor quantum dots (SQD) and metallic nanoparticles (MNP) are studied, where the interaction between optical excitation in a quantum dot and localized surface plasmons in metallic nanoparticle occur when MNP and a QD are nearby from each other and the optical excitation frequencies of the two constituents are resonant with one another [16, 17]. Due to these interactions, several attractive phenomena are shown, such as electromagnetically induced transparency (EIT) [18, 19], local field enhancement [20], and the Fano effect [21,22,23,24,25,26,27]. These phenomena depend on demonstrating novel properties and the coupling between the components of the hybrid nanostructure [28]. The plasmon-exciton dipole interaction between three electromagnetic fields and a hybrid nanosystem, which consist of three spherical metallic nanoparticles-semiconductor quantum dot, and split the Rabi frequencies into three parts according to the quantitative multipoles of the plasmonic fields have been studied [29, 30]. The excitons-plasmon coupling effects, for modification of the nonlinear susceptibilities of QD placed near MNP, were investigated [31,32,33]. Energy levels and the third-order nonlinear optical susceptibility in an ellipsoidal core-shell quantum dot embedded with three different dielectric surrounding matrices were studied [34, 35]. It is interesting to study the optical properties of hybrid spherical nanoclusters, which contain quantum emitters and metallic nanoparticles in [36], and the coherent nonlinear optics of quantum emitters in nanophotonic waveguides [37]. A novel emitter resonant system consisting of a double-nanohole-assisted slot cavity to improve its emission performance was demonstrated [38].

The goal of this paper is to study the optical susceptibility of the semiconductor quantum dot-metallic nano ellipsoid system under the effect of the exciton-plasmon coupling alone, which considers the indirect contribution of the semiconductor quantum dot and the dipole-dipole interaction with the plasmons (i.e., the coherent term of the effective plasmonic fields). We take a hybrid system composed of the semiconductor quantum dot with a four-level two Lambda-type and three distinct metallic nanoparticles. The three metallic nanoparticles are considered an oblate, spherical, and prolate ellipsoid. The three electromagnetic fields are applied to the transitions between the levels to induce dipole moments in the semiconductor quantum dot and consequent the multi-pole interaction between the components of the hybrid system. Specifically, we solve the relevant density matrix equations for the hybrid system at a steady state, study the effective Rabi frequency of the three fields, and calculate the susceptibilities for semiconductor quantum dots, the combination of the three metallic nano ellipsoid, and the coherent term of effective plasmons fields. This paper is organized as follows: in the "Description Model and Methods", we describe the model and methods of the SQD-MNE hybrid nanosystem. In "Numerical Results", we discuss our numerical results. Finally, we present our conclusion in "Conclusion" section.

Description Model and Methods

Fig. 1

A schematic diagram of the SQD with four levels of two quasi lambda-type and three different MNEs hybrid nanosystem. The SQD is coupling with three electromagnetic fields

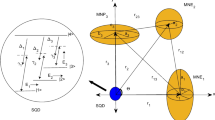
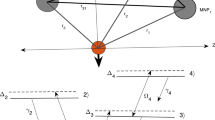
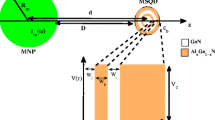
A schematic of a hybrid system is shown in Fig. 1, where a single semiconductor quantum-dot (SQD) has a quasi-two-lambda type coupled to three distinct metallic nanoparticles. These components are situated in two dimensions (2-D), plane (xoy). The SQD is situated at the origin (o), which has a four-level atomic structure $\left| 1\right\rangle ,$ $\left| 2\right\rangle ,$ $\left| 3\right\rangle$, and $\left| 4\right\rangle$ whose energy levels $\hbar \omega _{1}$, $\hbar \omega _{2}$, $\hbar \omega _{3}$, and $\hbar \omega _{4}$, respectively. The dielectric constant for the SQD is $\varepsilon _{s}$. The resonance frequencies for the interband transition from level $\left| 4\right\rangle$ to levels $\left| n\right\rangle$ are $\omega _{4n}=\omega _{4}-\omega _{n}$ ($n=1,2,3$). The components of the hybrid system interact with the three electromagnetic fields ($\textbf{E}_{\kappa }$) with frequency $\nu _{\kappa }$ ($\kappa =1,2,3$). The probe, control, and pump electromagnetic field excited the transition between level $\left| 4\right\rangle \leftrightarrow \left| \kappa \right\rangle$, respectively, and applied in the y-direction. The Rabi frequencies for the three electromagnetic fields are as follows: $\Omega _{\kappa }=\frac{\mathbf {\mu }_{4\kappa }\cdot \ \textbf{E}_{\kappa }}{\hbar }$, where $\mu _{4\kappa }$ is the electric-dipole moment of exciton between the transition levels $\left| 4\right\rangle \leftrightarrow \left| \kappa \right\rangle$, respectively. We consider each particle of the three metallic nanoparticles to be a special case of ellipsoid shape, called metallic-nano ellipsoid (MNE$_{i}$, $i=1,2,3$). The first particle is a prolate ellipsoid (MNE$_{1}$), which has two equal minor axes ($b_{1}=c_{1}$), and $a_{1}$ is the major axis. The distance from the center of SQD to the midpoint of the major axis of MNE$_{1}$ is $d_{1}$, which is parallel to the x-axis. The second particle is spherical (MNE$_{2}$) with three equal axes, whose radius $a_{2}$, and the center-to-center distance between SQD and MNE$_{2}$ is $d_{2}$, which inclined by angle $\theta$ to an x-axis. The third particle is an oblate ellipsoid (MNE$_{3}$) with two equal major axes ($a_{3}=b_{3}$), the minor axis is $c_{3}$, and the distance from the center of SQD to the midpoint of the minor axis of MNE$_{3}$ is $d_{3}$ which is parallel to the y-axis. Each one of the three MNE$_{i}$ is treated as a classical ellipsoid with dielectric function which was determined from the Drude model [39]: $\varepsilon _{i}\left( \omega \right) =1-\omega _{p_{i}}^{2}/\left( \omega ^{2}+i\gamma _{p_{i}}\omega \right)$, where $\omega _{p_{i}}$ and $\gamma _{p_{i}}$ represent the plasmon frequency and dam** constant for MNE$_{i}$. This system is characterized by multi-pole interactions and surrounded by dielectric background constant $\varepsilon _{b}$. The total Hamiltonian of the hybrid system is written as follows:

$$\begin{aligned} H=\underset{n=1}{\overset{4}{\sum }}\hbar \omega _{n}\sigma _{nn}-\sum _{\kappa =1}^{3}\mu _{4\kappa } \, E_{Q}^{\kappa } \ \sigma _{4\kappa }+h.c. \end{aligned}$$

(1)

where the first part describes the Hamiltonian of the SQD with dipole transition operator $\sigma _{nn}=\left| n\right\rangle \left\langle n\right|$, and the second term is the Hamiltonian which describes the interaction between the SQD with each MNE$_{i}$, where $\textbf{E}_{Q}^{\kappa }$ represent the total electric fields inside the SQD due to the contributions of the system components induced with the three electromagnetic fields $\textbf{E}_{\kappa }$, and given by the following:

$$\begin{aligned} \textbf{E}_{Q}^{\kappa }=\frac{1}{\varepsilon _{effs}}(\textbf{E}_{\kappa }\mathbf {+}\sum _{i=1}^{3}\textbf{E}_{Q}^{\kappa i}) \end{aligned}$$

(2)

Since the screen factor of SQD is $\varepsilon _{effs}=\left( 2\varepsilon _{b}+\varepsilon _{s}\right) /3\varepsilon _{b}$, $\textbf{E}_{Q}^{\kappa 1}$, $\textbf{E}_{Q}^{\kappa 2}$, and $\textbf{E}_{Q}^{\kappa 3}$ are the electric field induced on the SQD due to dipole induced on MNE$_{1}$, MNE$_{2}$, and MNE$_{3}$, where $\textbf{E}_{Q}^{\kappa i}$ are calculated from the relation [40]:

$$\begin{aligned} \textbf{E}_{Q}^{\kappa i}=\frac{3\left( \textbf{p}_{\kappa i}\mathbf {\cdot \hat{d}}_{i}\right) \mathbf {\hat{d}}_{i}\mathbf {-p}_{\kappa i}}{4\pi \varepsilon _{\circ }\varepsilon _{b}d_{i}^{3}} \end{aligned}$$

(3)

where $\left( \kappa ,i=1,2,3\right)$ and $\mathbf {\hat{d}}_{i}$ is the unit vector along the vector $\textbf{d}_{i}$. The vector dipole moment $\textbf{p}_{\kappa i}$ comes from the charge induced on the surface of each MNE$_{i}$ and is given by the following:

$$\begin{aligned} \textbf{p}_{\kappa i}=\alpha _{i}\textbf{E}_{\kappa i} \end{aligned}$$

(4)

We consider the dipole direction of MNE$_{1}$ ($\textbf{p}_{\kappa 1}$) and MNE$_{2}$ ($\textbf{p}_{\kappa 2}$) lie in the x-direction, and the dipole direction of MNE$_{3}$ ($\textbf{p}_{\kappa 3}$) lies in the y-direction. $\alpha _{i}$ ($i=1,2,3$) represents the polarizability of MNE$_{i}$. The ploraziability for the Ellipsoid is given by the following [41]:

$$\begin{aligned} \alpha _{i}=4\pi a_{i}b_{i}c_{i}\varepsilon _{0}\varepsilon _{b}\frac{\left( \varepsilon _{i}\left( \omega \right) -\varepsilon _{b}\right) }{3\varepsilon _{b}+3L_{i}\left( \varepsilon _{i}\left( \omega \right) -\varepsilon _{b}\right) } \end{aligned}$$

(5)

The depolarization factor for the prolate Ellipsoid MNE$_{1}$:

$$\begin{aligned} L_{1}=\frac{1-e_{1}^{2}}{e_{1}^{2}}\left( -1+\frac{1}{2e_{1}}\ln \frac{1+e_{1}}{1-e_{1}}\right) \end{aligned}$$

(6)

where $e_{1}^{2}=1-\frac{b_{1}^{2}}{a_{1}^{2}}$, and for the spherical particle MNE$_{2}$:

$$\begin{aligned} L_{2}=1/3 \end{aligned}$$

(7)

and the depolarization factor for the oblate Ellipsoid MNE$_{3}$:

$$\begin{aligned} L_{3}=\frac{g\left( e_{3}\right) }{2e_{3}^{2}}\left( \frac{\pi }{2}-\tan ^{-1}g\left( e_{3}\right) \right) -\frac{g^{2}\left( e_{3}\right) }{2} \end{aligned}$$

(8)

where $g\left( e_{3}\right) =\left( \left( 1-e_{3}^{2}\right) /e_{3}^{2}\right) ^{1/2}$, $e_{3}^{2}=1-c_{3}^{2}/a_{3}^{2}$.

The electric field $\textbf{E}_{\kappa i}$ acting on each MNE$_{i}$, is due to the applied field $\textbf{E}_{\kappa }$, the dipole field of SQD $\textbf{E}_{\kappa i}^{Q}$, and the dipole field $\textbf{E}_{\kappa i}^{\kappa g}$ ($\textbf{E}_{\kappa i}^{\kappa l}$) is due to the dipole-dipole interaction between the metallic nano ellipsoid MNE$_{g}$ (MNE$_{l}$) and MNE$_{i}$, which is given by the following:

$$\begin{aligned} \textbf{E}_{\kappa i}=\frac{1}{\varepsilon _{effi}}\left( \textbf{E}_{\kappa }\mathbf {+E}_{\kappa i}^{Q}\mathbf {+E}_{\kappa i}^{\kappa g}+\textbf{E}_{\kappa i}^{\kappa l}\right) \end{aligned}$$

(9)

the screen factor for MNE$_{i}$ is $\varepsilon _{effi}=\left( 2\varepsilon _{b}+\varepsilon _{i}\left( \omega \right) \right) /3\varepsilon _{b}$. The field from the SQD on MNE$_{i}$ is given by the relationship:

$$\begin{aligned} \textbf{E}_{\kappa i}^{Q}=\frac{3\left( \textbf{p}_{\kappa }^{Q}\mathbf {\cdot \hat{d}}_{i}\right) \mathbf {\hat{d}}_{i}\mathbf {-p}_{\kappa }^{Q}}{4\pi \varepsilon _{\circ }\varepsilon _{b}d_{i}^{3}} \end{aligned}$$

(10)

With the dipole of SQD ($p_{\kappa }^{Q}=\mu _{4\kappa }\rho _{4\kappa }+h.c., \ \kappa =1,2,3$), where $\rho _{4\kappa }$ is the coherent element. Also, the fields $\textbf{E}_{\kappa i}^{\kappa g}$ and $\textbf{E}_{\kappa i}^{\kappa l}$ are resulted from the interaction between the dipole of every two of MNE, ( i, g, l $=1,2,3$ and $i\ne g\ne l,\kappa =1,2,3)$ and given by:

$$\begin{aligned} \textbf{E}_{\kappa i}^{\kappa g}=\frac{3\left( \textbf{p}_{\kappa i}\mathbf {\cdot \hat{d}}_{ig}\right) \mathbf {\hat{d}}_{ig}\mathbf {-p}_{\kappa i}}{4\pi \varepsilon _{\circ }\varepsilon _{b}d_{ig}^{3}} \end{aligned}$$

(11)

where the expression for $\textbf{E}_{\kappa i}^{\kappa l}$ is obtained from above equation by replacing g with l. $d_{ig}\left( d_{il}\right)$ is the distance between the MNE$_{i}$ and MNE$_{g}$ (or MNE$_{i}$ and MNE$_{l}$). Then, the total field experienced by the SQD $E_{Q}^{\kappa }$ ($\kappa =1,2,3$) takes the form:

$$\begin{aligned} E_{Q}^{\kappa }=\frac{1}{K_{1}\varepsilon _{effs}\varepsilon _{eff3}}\left( E_{\kappa }\eta _{1}\mathbf {+}\mu _{4\kappa }\rho _{4\kappa }\eta _{2}\right) \end{aligned}$$

(12)

The effective Rabi frequency $\Omega _{\kappa }^{eff}$ is associated with the electric field $E_{Q}^{\kappa }$ by the equation:

$$\begin{aligned} \Omega _{\kappa }^{eff}=\frac{\mu _{4\kappa }E_{Q}^{\kappa }}{\hbar } \end{aligned}$$

(13)

where the value of $\eta _{1}$ and distance $\eta _{2}$ are found as follows:

$$\begin{aligned} \eta _{1}&= 1/\left( 4\pi \varepsilon _{\circ }\varepsilon _{b}\right)^{2} \Big[ \Gamma _{1}\Big( \left( 4\pi \varepsilon _{\circ }\varepsilon _{b}\right) ^{2}\varepsilon _{eff3}+8\pi \varepsilon _{\circ }\varepsilon _{b}\alpha _{3}/d_{3}^{3}\\ &\quad -6d_{1}d_{3}\beta _{1}\alpha _{1}\alpha _{3}/d_{3}^{3}d_{13}^{5}\Big) {} +2\Gamma _{2}\alpha _{2}\Big( 6\pi \varepsilon _{\circ }\varepsilon _{b}\cos \theta \sin \theta \varepsilon _{eff3}/d_{2}^{3}\\&\quad-3d_{1}d_{3}\beta _{2}\alpha _{1}\alpha _{3}/d_{3}^{3}d_{13}^{5}+4\pi \varepsilon _{\circ }\varepsilon _{b}C_{23}\alpha _{3}/d_{3}^{3}\Big) \Big]\end{aligned}$$

$$\begin{aligned} \eta _{2}=& 1/\left( 4\pi \varepsilon _{\circ }\varepsilon _{b}\right) ^{2} \left[ 2\alpha _{3}\Gamma _{1}\left( 2/d_{3}^{6}-3d_{1}d_{3}\beta _{3}\alpha _{1}/d_{3}^{3}d_{13}^{5}\right) \right. \\{} & +\left. 2\Gamma _{3}\alpha _{2}\left( 6\pi \varepsilon _{\circ }\varepsilon _{b}\cos \theta \sin \theta \varepsilon _{eff3}/d_{2}^{3}\right.\right. \\ & \left.\left.-3d_{1}d_{3}\beta _{2}\alpha _{1}\alpha _{3}/d_{3}^{3}d_{13}^{5}+4\pi \varepsilon _{\circ }\varepsilon _{b}C_{23}\alpha _{3}/d_{3}^{3}\right) \right] \end{aligned}$$

With the constant:

$$\begin{aligned} \beta _{1}=\left( 4\pi \varepsilon _{\circ }\varepsilon _{b}\varepsilon _{eff3}+\left( 3d_{3}^{2}-d_{13}^{2}\right) \alpha _{3}/d_{13}^{5}\right) /4\pi \varepsilon _{\circ }\varepsilon _{b}\beta _{4} \end{aligned}$$

(14)

$$\begin{aligned} \beta _{2}=\left( 4\pi \varepsilon _{\circ }\varepsilon _{b}C_{12}\varepsilon _{eff3}+\left( 3d_{3}^{2}-d_{13}^{2}\right) C_{23}\alpha _{3}/d_{13}^{5}\right) /4\pi \varepsilon _{\circ }\varepsilon _{b}\beta _{4} \end{aligned}$$

(15)

$$\begin{aligned} \beta _{3}=\left( -4\pi \varepsilon _{\circ }\varepsilon _{b}\varepsilon _{eff3}/d_{1}^{3}+2\left( 3d_{3}^{2}-d_{13}^{2}\right) \alpha _{3}/d_{13}^{5}d_{3}^{3}\right) /(4\pi \varepsilon _{\circ }\varepsilon _{b})^{2}\beta _{4} \end{aligned}$$

(16)

$$\begin{aligned} \beta _{4}=\left( \left( 4\pi \varepsilon _{\circ }\varepsilon _{b}\right) ^{2}\varepsilon _{eff1}\varepsilon _{eff3}+3d_{1}d_{3}\left( 3d_{3}^{2}-d_{13}^{2}\right) \alpha _{3}\alpha _{1}/d_{13}^{10}\right) /(4\pi \varepsilon _{\circ }\varepsilon _{b})^{2} \end{aligned}$$

(17)

$$\begin{aligned} \begin{aligned} \Gamma _{1}&=\left[ \left( \varepsilon _{eff2}\varepsilon _{eff3}-C_{23}A_{23}\alpha _{3}\alpha _{2}\right) -\right. \\&\quad \ \left. \alpha _{1}\alpha _{2}\beta _{2}\left( 4\pi \varepsilon _{\circ }\varepsilon _{b}d_{13}^{5}C_{12}\varepsilon _{eff3}-3d_{1}d_{3}A_{23}\alpha _{3}\right) /4\pi \varepsilon _{\circ }\varepsilon _{b}d_{13}^{5}\right] \end{aligned} \end{aligned}$$

(18)

$$\begin{aligned} \begin{aligned} \Gamma _{2}&=\left[ \left( \varepsilon _{eff3}+A_{23}\alpha _{3}\right) +\right. \\&\quad \ \left. \beta _{1}\alpha _{1}\left( 4\pi \varepsilon _{\circ }\varepsilon _{b}d_{13}^{5}C_{12}\varepsilon _{eff3}-3d_{1}d_{3}A_{23}\alpha _{3}\right) /4\pi \varepsilon _{\circ }\varepsilon _{b}d_{13}^{5}\right] \end{aligned} \end{aligned}$$

(19)

$$\begin{aligned} \Gamma _{3}&=\left[ \left( \left( 3\sin ^{2}\theta -1\right) d_{3}^{3}\varepsilon _{eff3}+2d_{2}^{3}A_{23}\alpha _{3}\right) /4\pi \varepsilon _{\circ }\varepsilon _{b}d_{2}^{3}d_{3}^{3}\right. \\&\quad \ \left. +\beta _{3}\alpha _{1}\left( 4\pi \varepsilon _{\circ }\varepsilon _{b}d_{13}^{5}C_{12}\varepsilon _{eff3}-3d_{1}d_{3}A_{23}\alpha _{3}\right) /4\pi \varepsilon _{\circ }\varepsilon _{b}d_{13}^{5}\right] \end{aligned}$$

(20)

$$\begin{aligned} \begin{aligned} A_{23}&=(3\left( d_{3}-d_{2}\sin \theta \right) ^{2}-d_{23}^{2})/4\pi \varepsilon _{\circ }\varepsilon _{b}d_{23}^{5} \\ C_{23}&=3\left( -d_{2}\cos \theta \right) \left( d_{3}-d_{2}\sin \theta \right) /4\pi \varepsilon _{\circ }\varepsilon _{b}d_{23}^{5} \\ C_{12}&= {} 3\left( d_{2}\sin \theta \right) \left( d_{2}\cos \theta -d_{1}\right) /4\pi \varepsilon _{\circ }\varepsilon _{b}d_{12}^{5} \end{aligned} \end{aligned}$$

(21)

We derive the equations of motion for the density matrix elements of SQD-MNE hybrid nanostructure by using the rotating wave approximation (RWA) and the electric-dipole approximation, that can be written as follows [42]:

$$\begin{aligned} \dot{\rho }_{22}\left( t\right) =i\Omega _{2}^{eff}\rho _{24}-i\Omega _{2}^{eff^{*}}\rho _{42}+2\gamma _{2}\rho _{44}+2\gamma _{00}\rho _{11}-2\gamma _{0}\rho _{22} \end{aligned}$$

(22)

$$\begin{aligned} \dot{\rho }_{33}\left( t\right) =i\Omega _{3}^{eff}\rho _{34}-i\Omega _{3}^{eff^{*}}\rho _{43}+2\gamma _{3}\rho _{44} \end{aligned}$$

(23)

$$\begin{aligned} \dot{\rho }_{44}\left( t\right)= & {} -i\Omega _{1}^{eff}\rho _{14}+i\Omega _{1}^{eff^{*}}\rho _{41}-i\Omega _{2}^{eff}\rho _{24}+i\Omega _{2}^{eff^{*}}\rho _{42} \\{} & {} -i\Omega _{3}^{eff}\rho _{34}+i\Omega _{3}^{eff^{*}}\rho _{43}-2\left( \gamma _{1}+\gamma _{2}+\gamma _{3}\right) \rho _{44} \end{aligned}$$

$$\begin{aligned} \dot{\rho }_{12}\left( t\right) =-\delta _{1}\rho _{12}-i\Omega _{1}^{eff^{*}}\rho _{42}+i\Omega _{2}^{eff}\rho _{14} \end{aligned}$$

(24)

$$\begin{aligned} \dot{\rho }_{13}\left( t\right) =-\delta _{2}\rho _{13}-i\Omega _{1}^{eff^{*}}\rho _{43}+i\Omega _{3}^{eff}\rho _{14} \end{aligned}$$

(25)

$$\begin{aligned} \dot{\rho }_{14}\left( t\right) =-\delta _{3}\rho _{14}-i\Omega _{1}^{eff^{*}}\left( \rho _{44}-\rho _{11}\right) +i\Omega _{2}^{eff^{*}}\rho _{12}+i\Omega _{3}^{eff^{*}}\rho _{14} \end{aligned}$$

(26)

$$\begin{aligned} \dot{\rho }_{23}\left( t\right) =-\delta _{4}\rho _{23}-i\Omega _{2}^{eff^{*}}\rho _{43}\ +i\Omega _{3}^{eff}\rho _{24} \end{aligned}$$

(27)

$$\begin{aligned} \dot{\rho }_{24}\left( t\right) =-\delta _{5}\rho _{24}+i\Omega _{1}^{eff^{*}}\rho _{21}-i\Omega _{2}^{eff^{*}}\left( \rho _{44}-\rho _{22}\right) +i\Omega _{3}^{eff^{*}}\rho _{23} \end{aligned}$$

(28)

$$\begin{aligned} \dot{\rho }_{34}\left( t\right) =-\delta _{6}\rho _{34}+i\Omega _{1}^{eff^{*}}\rho _{31}+i\Omega _{2}^{eff^{*}}\rho _{32}-i\Omega _{3}^{eff^{*}}\left( \rho _{44}-\rho _{33}\right) \end{aligned}$$

(29)

The density matrix equations have the identity property: $\sum _{n=1}^{4}\rho _{ii}=1$, $\rho _{\kappa i}=\rho _{i\kappa }^{*}$. Where:

$$\begin{aligned} \begin{aligned} \delta _{1}&=\gamma _{0}+\gamma _{00}+i\left( \Delta _{2}-\Delta _{1}\right) , \\ \delta _{2}&=i\left( \Delta _{3}-\Delta _{1}\right) +\gamma _{00}, \\ \delta _{3}&=\gamma _{00}+\gamma _{1}+\gamma _{2}+\gamma _{3}-i\Delta _{1} \\ \delta _{4}&=\left( \gamma _{0}+i\left( \Delta _{3}-\Delta _{2}\right) \right) , \\ \delta _{5}&=\gamma _{0}+\gamma _{1}+\gamma _{2}+\gamma _{3}-i\Delta _{2},\\ \delta _{6}&=\gamma _{1}+\gamma _{2}+\gamma _{3}-i\Delta _{3} \end{aligned} \end{aligned}$$

(30)

where $\Delta _{\kappa }$ is the detuning of the applied fields: $\Delta _{\kappa }=\omega _{4\kappa }-\nu _{\kappa }$, ($\kappa =1,2,3$), and $\gamma _{1},\gamma _{2}$ and $\gamma _{3}$ represent the radiative decay rates from the transition $\left| 4\right\rangle$ to $\left| 1\right\rangle$, $\left| 4\right\rangle$ to $\left| 2\right\rangle$, and $\left| 4\right\rangle$ to $\left| 3\right\rangle$ due to spontaneous emission, respectively. $\gamma _{0}$ and $\gamma _{00}$ are the nonradioactive decay from the transition $\left| 1\right\rangle$ to $\left| 2\right\rangle$ and from the transition $\left| 2\right\rangle$ to $\left| 1\right\rangle$, respectively [43].

We get an analytical expression for the optical susceptibility $\chi _{Q}^{eff}$ for SQD, and $\chi _{E}^{eff}$ for the sum of three metallic-nano ellipisoids. The optical susceptibility of SQD can be expressed by the following equation:

$$\begin{aligned} \chi _{Q}^{eff}=\frac{N}{\varepsilon _{0}}\sum _{\kappa =1}^{3}\frac{\mu _{4\kappa }\rho _{4\kappa }}{\text E_{\kappa }} \end{aligned}$$

(31)

where N is the number of atoms per unit volume. The susceptibility of each MNE$_{i}$ which is related to dipole moment by equation:

$$\begin{aligned} \chi _{E_{i}}^{eff}=\frac{N}{\varepsilon _{0}}\sum _{\kappa =1}^{3}\frac{p_{\kappa i}}{E_{\kappa }} \end{aligned}$$

(32)

The value of $p_{\kappa i}$ is calculated by using Eqs. (4), (9), (10), and (11), then we get the following:

$$\begin{aligned} p_{\kappa 1}=\frac{\alpha _{1}}{\Gamma _{1}}\left\{ \left( \Gamma _{1}\beta _{1}+\alpha _{2}\Gamma _{2}\beta _{2}\right) E_{\kappa}+\left( \Gamma _{1}\beta _{3}\mathbf {+}\alpha _{2}\Gamma _{3}\beta _{2}\right) \mu _{4\kappa }\rho _{4\kappa }\right\} \end{aligned}$$

(33)

$$\begin{aligned} p_{\kappa 2}=\frac{\alpha _{2}}{\Gamma _{1}}\left( \Gamma _{2}E_{\kappa}+\Gamma _{3}\mu _{4\kappa }\rho _{4\kappa }\right) \end{aligned}$$

(34)

$$\begin{aligned} \begin{aligned} p_{\kappa 3}&=\frac{\alpha _{3}}{\Gamma _{1}\varepsilon _{eff3}}\left\{ \left( \Gamma _{1}+\alpha _{2}\Gamma _{2}C_{23}-\frac{3d_{1}d_{3}\alpha _{1}\left( \Gamma _{1}\beta _{1}+\alpha _{2}\Gamma _{2}\beta _{2}\right) }{4\pi \varepsilon _{\circ }\varepsilon _{b}d_{13}^{5}}\right) E_{\kappa}\right. \\&\quad +\left. \left( \frac{2\Gamma _{1}}{4\pi \varepsilon _{\circ }\varepsilon _{b}d_{3}^{3}}+\alpha _{2}\Gamma _{3}C_{23}-\frac{3d_{1}d_{3}\alpha _{1}\left( \Gamma _{1}\beta _{3}\mathbf {+}\alpha _{2}\Gamma _{3}\beta _{2}\right) }{4\pi \varepsilon _{\circ }\varepsilon _{b}d_{13}^{5}}\right) \mu _{4\kappa }\rho _{4\kappa }\right\} \end{aligned} \end{aligned}$$

(35)

Then, the optical susceptibility expression for the total metallic-nano ellipsoid:

$$\begin{aligned} \chi _{E}^{eff}=\sum _{i=1}^{3}\chi _{E_{i}}^{eff} \end{aligned}$$

(36)

We can obtain the susceptibility of the SQD-MNE hybrid system under the effect of the plasmon–exciton coupling field interaction ($\chi _{I}^{eff}$), where

$$\begin{aligned} \chi _{Ii}^{eff}=\frac{N}{\varepsilon _{0}}\sum _{\kappa =1}^{3} \ \frac{p_{I\kappa i}}{E_{\kappa }} \end{aligned}$$

(37)

where $P_{I\kappa i}$ is the indirect contribution dipole moment, which represents the indirect contribution of the SQD via the dipole-dipole interaction with the plasmons only (i.e., the coherent term of the effective plasmon fields), and obtain from the second term in Eqs. (33), (34), and (35):

$$\begin{aligned} p_{I\kappa 1}=\frac{\alpha _{1}}{\Gamma _{1}}\left( \Gamma _{1}\beta _{3}\mathbf {+}\alpha _{2}\Gamma _{3}\beta _{2}\right) \mu _{4\kappa }\rho _{4\kappa } \end{aligned}$$

(38)

$$\begin{aligned} p_{I\kappa 2}=\frac{\alpha _{2}}{\Gamma _{1}}\Gamma _{3}\mu _{4\kappa }\rho _{4\kappa } \end{aligned}$$

(39)

$$\begin{aligned} p_{I\kappa 3}=&\frac{\alpha _{3}}{\Gamma _{1}\varepsilon _{eff3}}\left( \frac{2\Gamma _{1}}{4\pi \varepsilon _{\circ }\varepsilon _{b}d_{3}^{3}}+\alpha _{2}\Gamma _{3}C_{23}\right. \\ & \left.-\frac{3d_{1}d_{3}\alpha _{1}\left( \Gamma _{1}\beta _{3}\mathbf {+}\alpha _{2}\Gamma _{3}\beta _{2}\right) }{4\pi \varepsilon _{\circ }\varepsilon _{b}d_{13}^{5}}\right) \mu _{4\kappa }\rho _{4\kappa } \end{aligned}$$

(40)

Then, the optical susceptibility expression for the total metallic-nano ellipsoid is as follows:

$$\begin{aligned} \chi _{I}^{eff}=\sum _{i=1}^{3}\chi _{Ii}^{eff} \end{aligned}$$

(41)

Numerical Results

In this section, we discuss the results concerning the optical properties of the imaginary part of susceptibility of the hybrid system under the effect of the plasmon–exciton coupling field interaction $\mathop{\text{Im}}$ ($\chi _{I}^{eff}$), and we also discuss the imaginary part of the susceptibility of the SQD $\mathop{\text{Im}}$($\chi _{Q}^{eff}$) and MNE $\mathop{\text{Im}}$($\chi _{E}^{eff}$) individually and show its influence when the multi-pole interaction occur between the three MNE in the hybrid system. The imaginary part of the susceptibilities $\mathop{\text{Im}}$($\chi _{I}^{eff}$), $\mathop{\text{Im}}$($\chi _{Q}^{eff}$), and $\mathop{\text{Im}}$($\chi _{E}^{eff}$), which represent the absorption spectra, shows the phenomena of Fano-resonance and Autler-Town doublet peaks that are discussed in these numerical results. We take the parameters of SQD-MNE as follows: the three MNEs are gold with $\omega _{p_{i}}=9.02ev$, and $\gamma _{p_{i}}=0.026ev$ [44], $\Delta _{2}=\Delta _{3}=0$, $a_{1}=20nm$, $b_{1}=4nm$, $a_{2}=9nm$, $a_{3}=10nm$, $c_{3}=3nm$, $\gamma _{0}=\gamma _{00}=0.001ns^{-1}$, $\gamma _{2}=1ns^{-1}$, $\gamma _{1}=\gamma _{3}=0.02ns^{-1}$, $\mu _{41}=\mu _{42}=\mu _{43}=0.7e$ nm, and ($\Omega _{1}$,$\Omega _{2}$, $\Omega _{3}$) $=$ ($0.01ns^{-1}$, $2ns^{-1}$, $8ns^{-1}$). ($d_{1}$, $d_{2}$, $d_{3}$) $=$ (20nm, 40nm, 30nm), $\varepsilon _{s}=6$, $\varepsilon _{b}=12$, $\theta =\pi /4$. We take the angular frequency of plasmon surface $\omega =1.5$ for SQD, and $\omega =25$ for MNE. The coherence terms $\rho _{nm}$ and $\rho _{mn}$ are calculated by solving the density matrix equations at a steady state. Other parameters are indicated in figure captions and further described in what follows.

Fig. 2

$\mathop{\text{Im}}(\chi _{1}^{eff})$ versus $\left( \Delta _{1}\right)$. a, c and b, d for $\omega =1.5$ and $\omega =25$ respectively. $\left( a_{1}\right)$ are as follows: 14 nm (blue curve), 22 nm (red curve), and 32 nm (black curve) in a and b. $\left( a_{3}\right)$ are as follows: 9 nm (blue curve), 15 nm (red curve), and 21 nm (black curve) in c and d

Figure 2 displays the spectra of the imaginary part of the susceptibility of the hybrid system for the plasmon–exciton coupling field interaction ($\mathop{\text{Im}}$($\chi _{I}^{eff}$)) as a function of the probe detuning $\Delta _{1}$. Calculations have been performed with various of the major axis for MNE$_{1}$: $a_{1}=14$ (blue curve), 22 (red curve), 32 (black curve) in Fig. 2a and b, and obtained for the value of the major axis for MNE$_{3}$: $a_{3}=9$ (blue curve), 15 (red curve), 21 (black curve) in Fig. 2c and d. Figure 2(a, c) and (b, d) are taken for $\omega =1.5$ and $\omega =25$, respectively. The spectra of $\mathop{\text{Im}}$($\chi _{I}^{eff}$) have negative and positive values when $\omega =1.5$ and $\omega =25$, respectively. It is notable that the forming of Fano-resonance with a sharp peak occurs when the frequency of the incident probe field is near-resonant with the transition frequency between the level $\left| 1\right\rangle$ and $\left| 4\right\rangle$) of SQD (i.e., $\upsilon _{1}\approx \omega _{41}$). The broad peak of Fano-resonance has appeared in the negative detuning. In Fig. 2a, the spectra of $\mathop{\text{Im}}$($\chi _{I}^{eff}$) have a weak influence by changing the major axis $a_{1}$ at $\omega =1.5$, where it is almost identical. The spectra of $\mathop{\text{Im}}$($\chi _{I}^{eff}$) show that the height of the broaden and sharpen peaks decrease by increasing the value of the major axis $a_{1}$, that is in Fig. 2b when $\omega =25$. Figure 2c and d shows the height of the spectra of $\mathop{\text{Im}}$($\chi _{I}^{eff}$) increase with increasing $a_{3}$, in Fig. 2c the broaden peak is shifted far from zero $\Delta _{1}$ with increasing $a_{3}$, and in Fig. 2d, the broad peak is wider when increasing $a_{3}$. We conclude that the $\mathop{\text{Im}}$($\chi _{I}^{eff}$) is affected in different ways by the major axes $a_{1}$and $a_{3}$ for MNE$_{1}$ and MNE$_{3}$, respectively.

Fig. 3

$\mathop{\text{Im}}(\chi _{E}^{eff})$ versus $\left( \Delta _{1}\right)$. a, c and b, d for $\theta = (\frac{\pi }{4}$, $\frac{3\pi }{2})$ respectively. $L_{1}$ are as follows: 0.0897 (blue curve), 0.0489 (red curve), (0.0284) black curve in a, b. $L_{3}$ are as follows: 0.1853 (blue curve), 0.1265 (red curve), 0.0955 (black curve) in b and d

In Fig. 3, we study the spectra of the imaginary part of susceptibilities of MNE ($\mathop{\text{Im}}(\chi _{E}^{eff})$) as a function of the probe detuning $\Delta _{1}$. Figure 3a and b describes the role for the three different values of the depolarization factor of MNE$_{1}$:$L_{1}=$(0.0897 (blue curve), 0.0489 (red curve), 0.0284 (black curve)) on the spectra $\mathop{\text{Im}}(\chi _{E}^{eff})$. Figure 3c and d examines the influence of the three various values of the depolarization factor of MNE$_{3}$: $L_{3}=$(0.1853 (blue curve), 0.1265 (red curve), 0.0955 (black curve)) on the spectra $\mathop{\text{Im}}(\chi _{E}^{eff})$. Figure 3(a, c) and (b, d) are taken for $\theta =\frac{\pi }{4}$ and $\theta =\frac{3\pi }{2}$, respectively. We note that the spectra for $\mathop{\text{Im}}(\chi _{E}^{eff})$ exhibit a Fano-resonance with a sharp peak occurring near-resonance detuning and broaden symmetric peak occurring in the negative detuning, where this is due to the interaction and interference between two different types of waves in SQD-MNE. Figure 3a illustrates for $\theta =\frac{\pi }{4}$ at large value of $L_{1}$ (0.0897) of MNE$_{1}$, and the spectra have positive value of $\mathop{\text{Im}}(\chi _{E}^{eff})$. At $L_{1}=0.0489$ (red curve) and 0.0284 (black curve), the spectra have negative value of $\mathop{\text{Im}}(\chi _{E}^{eff})$. In Fig. 3b, we notice for large value of $L_{1}$ of MNE$_{1}$ (blue curve) the spectra $\mathop{\text{Im}}(\chi _{E}^{eff})$ become at large value, but for small value of $L_{1}$ of MNE$_{1}$ (black curve), the spectra show negative $\mathop{\text{Im}}(\chi _{E}^{eff})$ when $\theta =\frac{3\pi }{2}$. We notice the behavior of Fig. 3 a and c are opposite because of the different effects of the depolarization factor of MNE$_{1}$ and MNE$_{3}$. In Fig. 3d, the spectra show positive values of $\mathop{\text{Im}}(\chi _{E}^{eff})$ for the three various values of $L_{3}$ of MNE$_{3}$, where the spectra increase in height when the value of $L_{3}$ decreases. The phenomenon of Fano-resonance is affected by the depolarization factor of MNE$_{1}$ ($L_{1}$), MNE$_{3}$ ($L_{3}$), and the angle ($\theta$).

Fig. 4

$\mathop{\text{Im}}(\chi _{Q}^{eff})$ versus $\left( \Delta _{1}\right)$. a, c and b, d for $\theta = (\frac{\pi }{4}, \ \frac{2\pi }{5})$ respectively. $\left( b_{1}\right)$ are as follows: 9 nm (blue curve), 14 nm (red curve), 15 nm (black curve) in a, b. $\left( c_{3}\right)$ are as follows: 3 nm (blue curve), 5 nm (red curve), 7 nm (black curve) in c, d. Black curve for ($\mathop{\text{Im}}(\chi _{Q}^{eff})\times 10$) in d

Figure 4 shows the optical properties for the spectra of imaginary part $\mathop{\text{Im}}(\chi _{Q}^{eff})$ as a function of probe detuning $\Delta _{1}$. Figure 4(a, c) and (b, d) are taken for $\theta =\frac{\pi }{4}$ and $\theta =\frac{2\pi }{5}$, respectively. Figure 4(a, b) and (c, d) examine the optical spectra for various values of the minor-axis $b_{1}$ for MNE$_{1}$:$b_{1}$ $=$(9 (blue curve), 14 (red curve), 15 (black curve)), and the minor-axis $c_{3}$ of MNE$_{3}$: $c_{3}$ = (3 (blue curve), 5 (red curve), 7 (black curve)), respectively. In Fig. 4a, the broaden peak is shifted towards zero $\Delta _{1}$ with increasing $b_{1}$. At $b_{1}=15$, we notice the optical dispersion spectra with two sharp lines around zero $\Delta _{1}$. In Fig. 4c, the spectra have negative $\mathop{\text{Im}}(\chi _{Q}^{eff})$, and the broad peak makes a displacement with unsymmetrical distribution at changing $c_{3}$. When $\theta =\frac{2\pi }{5}$, as in Fig. 4b and d, the spectra of $\mathop{\text{Im}}(\chi _{Q}^{eff})$ show the phenomenon of Fano-resonance in behavior different, where the broad peak appears in a positive detuning $\Delta _{1}$ at a certain value of the minor-axis $b_{1}$: ($b_{1}$ $=9,15$) for MNE$_{1}$ as in Fig. 4b, but at $b_{1}$ $=14$, the broad peak appears in a negative detuning $\Delta _{1}$. In Fig. 4d, the broad peak shows positive region of detuning $\Delta _{1}$ and $\mathop{\text{Im}}(\chi _{Q}^{eff})$ at $c_{3}=3$, but at $c_{3}=5$, negative region of detuning $\Delta _{1}$ and $\mathop{\text{Im}}(\chi _{Q}^{eff})$. The phenomenon of Fano-resonance appears at $c_{3}=7$, in the negative and positive region of detuning $\Delta _{1}$ and $\mathop{\text{Im}}(\chi _{Q}^{eff})$, and have amplification, so we can call this phenomenon: the phenomenon of Fano-resonance with amplification. This behavior of the optical spectra, under the effect of the minor axes $b_{1}$, $c_{3}$, and $\theta$, reflects the formation of the hybrid exciton-plasmon coupling.

Fig. 5

$\mathop{\text{Im}}(\chi _{1}^{eff})$ versus $\left( \Delta _{1}\right)$. a, c and b, d for $\theta = (\frac{\pi }{4}$, $\frac{2\pi }{5}$) respectively. In a, b, $\left( L_{1}\right)$ are as follows: 0.1546, (blue curve), 0.2441 (red curve), 0.2603 (black curve). In c, d, $\left( L_{3}\right)$ are as follows: 0.1725 (blue curve), 0.2146 (red curve), $-0.0947$ (black curve). Blue curves for ($\mathop{\text{Im}}(\chi _{1}^{eff})\times 10$) in (b), and black curve for ($\mathop{\text{Im}}(\chi _{1}^{eff})\times 10$) in d

In Fig. 5, we investigate the influence of the depolarization factor $L_{1}$ and $L_{3}$ on $\mathop{\text{Im}}$($\chi _{I}^{eff}$) spectra as a function of the probe detuning $\Delta _{1}$. Figure 5(a, c) and (b, d) are presented for $\theta =\frac{\pi }{4}$ and $\theta =\frac{2\pi }{5}$, respectively. Figure 5(a, b) and (c, d) illustrate the optical spectra for the three various values of the depolarization factor $L_{1}$ and $L_{3}$, respectively. The blue, red, and black curves correspond to $L_{1}=$ (0.1546, 0.2441, and 0.2603) in Fig. 5a and b and $L_{3}=$(0.1725, 0.2146, and $-0.0947$) in Fig. 5c and d, respectively. Figure 5a exhibits the optical spectra of Fano-resonance which are shifted towards zero $\Delta _{1}$ at increasing $L_{1}$ at ($L_{1}=0.2603$), the optical spectra of Fano-resonance become very narrow and height. In Fig. 5c, the optical spectra behavior is unsymmetrical when increasing the depolarization factor $L_{3}$. At $\theta =\frac{2\pi }{5}$, the optical spectra of Fano-resonance with amplification occur at a positive region of detuning $\Delta _{1}$ at the values of $L_{1}=$(0.1546, and 0.2603), and at $L_{3}=0.1725$ in Fig. 5b and d, respectively. The Fano-resonance with amplification occurs at a positive region of $\mathop{\text{Im}}$($\chi _{I}^{eff}$) at $L_{1}=$(0.2603) and at $L_{3}=$($-0.0947$) in Fig. 5b and d, respectively. We consider the phenomenon of Fano-resonance with amplification to be interesting, which appears at the positive region of detuning $\Delta _{1}$ in the optical spectra of Fig. 5b and d when $\theta =\frac{2\pi }{5}$.

Fig. 6

a, b for $\mathop{\text{Im}}(\chi _{1}^{eff})$, and c, d for $\mathop{\text{Im}}(\chi _{Q}^{eff})$ versus $\left( \Delta _{1}\right)$. a, c and b, d for $\theta = (\frac{\pi }{4}, \, \frac{2\pi }{5})$ respectively. $\left( a_{2}\right)$ are as follows: 6nm (blue curve), 9nm (red curve), and 12nm (black curve), blue and red cuvres for $(5\times \mathop{\text{Im}}(\chi _{1}^{eff}))$ in b

Figure 6 illustrates the $\mathop{\text{Im}}$($\chi _{I}^{eff}$) and $\mathop{\text{Im}}(\chi _{Q}^{eff})$ spectra as a function of the probe detuning $\Delta _{1}$ with diverse values of the radius of MNE$_{2}$: $a_{2}=6$ nm (blue curve), 9 nm (red curve), 12 nm (black curve). Figure 6(a, b) and (c, d) describe the spectra of $\mathop{\text{Im}}$($\chi _{I}^{eff}$) and $\mathop{\text{Im}}(\chi _{Q}^{eff})$, and Fig. 6(a, c) and (b, d) are taken for $\theta =\frac{\pi }{4}$ and $\theta =\frac{2\pi }{5}$. In Fig. 6a and c, the negative optical spectra of the Fano-resonance are shifted towards zero detuning $\Delta _{1}$ when increasing the radius of MNE$_{2}$ ($a_{2}$), and in Fig. 6c, the spectra decrease in height when increasing the radius of $a_{2}$ for the $\mathop{\text{Im}}(\chi _{Q}^{eff})$. When $\theta =\frac{2\pi }{5}$, the optical spectra of the Fano-resonance with amplification occur at changing the radius of MNE$_{2}$ ($a_{2}$). At $a_{2}=9$, the optical spectra of Fano-resonance with amplification have negative $\mathop{\text{Im}}$($\chi _{I}^{eff}$) and positive $\mathop{\text{Im}}(\chi _{Q}^{eff})$ and occur at the positive region of detuning $\Delta _{1}$, are shown in Fig. 6b and d respectively. At a small value of ($a_{2}=6$), the spectrum is near the region of zero detuning $\Delta _{1}$, and unlike at a large value of ($a_{2}=12$), the spectrum is far from the region of zero detuning $\Delta _{1}$ (Fig. 6b, d). Then, we notice that the optical spectra of the Fano-resonance with amplification for $\mathop{\text{Im}}$($\chi _{I}^{eff}$) and $\mathop{\text{Im}}(\chi _{Q}^{eff})$ are affected by the radius and angle ($\theta$) of MNE$_{2}$.

Fig. 7

$\mathop{\text{Im}}(\chi _{E}^{eff})$ versus $\left( \Delta _{1}\right)$. a–d for $d_{1}$, $d_{2}$, $d_{3}$, and d, respectively. 20 nm (blue curve), 24 nm (red curve), and 30 nm (black curve) in every plot. $\theta =\frac{\pi }{4}$

In Fig. 7, we study the dependence of the imaginary part of susceptibility $\mathop{\text{Im}}(\chi _{E}^{eff})$) on the distance from the center of SQD to the center of the midpoint of semi-axes of MNE, and we take the parameters $d_{1}$, $d_{2}$, $d_{3}$, and d in Fig. 7a–d, respectively, which have the same values in every plot: 20 nm (blue curve), 24 nm (red curve), 30 nm (black curve) where $d=d_{1}=d_{2}=d_{3}$. Figure 7a corresponds to $d_{1}$, and the optical spectra of the Fano-resonance increase in height when increasing $d_{1}$ where at small $d_{1}$($=20$), the spectra have negative $\mathop{\text{Im}}(\chi _{E}^{eff})$. Figure 7c, which corresponds to $d_{3}$, is unlike Fig. 7a where the spectra of the Fano-resonance decrease in height when increasing $d_{3}$, where at large $d_{3}=30$, the spectra have negative $\mathop{\text{Im}}(\chi _{E}^{eff})$. Figure 7b and d show the positive optical spectra of the Fano-resonance, which decrease in height when increasing $d_{2}$ and d in Fig. 7b and d respectively. This figure proves the benefit of taking the three metallic-nano ellipsoids together, where the optical spectra of the Fano-resonance have a different behavior depending on the distance from SQD.

Fig. 8

a, c and b, d for $\mathop{\text{Im}}(\ \chi _{Q}^{eff})$, and $\mathop{\text{Im}}(\ \chi _{E}^{eff})$ versus $\left( \Delta _{1}\right)$, respectively. $\Omega _{2}=16$ ns$^{-1}$. $\left( L_{1}\right)$ are as follows: 0.0954 (blue curve), 0.1546 (red curve), 0.1920 (black curve), and 0.2273 (pink curve) in a, b. $\left( L_{3}\right)$ are as follows: 0.1265 (blue curve), 0.1725 (red curve), 0.2059 (black curve), and 0.1594 (pink curve) in c, d

Figure 8 illustrates the imaginary part of susceptibilities for SQD, and MNE at $\Omega _{2}=16$ $ns^{-1}$ for various values of the depolarization factor of MNE$_{1}$ ($L_{1}$) and MNE$_{3}$ ($L_{3}$) in Fig. 8(a, b) and (c, d) respectively. The various value of the depolarization factor of MNE$_{1}$ ($L_{1}$) are as follows: 0.0954 (blue curve), 0.1546 (red curve), 0.1920 (black curve), and 0.2273 (pink curve). The various values of the depolarization factor of MNE$_{3}$ ($L_{3}$) are as follows: 0.1265 (blue curve), 0.1725 (red curve), 0.2059 (black curve), and 0.1594 (pink curve). Figure 8(a, c) and (b, d) show the spectra of $\mathop{\text{Im}}(\chi _{Q}^{eff})$ and $\mathop{\text{Im}}\left( \ \chi _{E}^{eff}\right)$ respectively. We observe the spectra of $\mathop{\text{Im}}(\chi _{Q}^{eff})$ and $\mathop{\text{Im}}\left( \ \chi _{E}^{eff}\right)$ are special cases of electromagnetically induced transparency (EIT), which are called Autler-Townes doublet peaks (AT) when taking the Rabi frequency $\Omega _{2}$ is large. The behavior of the spectra of $\mathop{\text{Im}}(\chi _{Q}^{eff})$ and $\mathop{\text{Im}}\left( \ \chi _{E}^{eff}\right)$ is different with changing the value of the depolarization factor of MNE$_{1}$ and MNE$_{3}$. It is noteworthy that in Fig. 8a and c, two separate peaks of spectra $\mathop{\text{Im}}(\chi _{Q}^{eff})$ approach each other according to the increase of $L_{1}$ as in Fig. 8a or decrease of $L_{3}$ as in Fig. 8c. In Fig. 8b, as the depolarization factor $L_{1}$ increase, the width and height of the Autler-Townes doublet peaks increase gradually in the negative $\mathop{\text{Im}}\left( \ \chi _{E}^{eff}\right)$. In Fig. 8d, the spectra of $\mathop{\text{Im}}(\chi _{E}^{eff})$ have positive absorption at $L_{3}=$(0.2059, 0.1594) and negative value at $L_{3}=$(0.1265, 0.1725). We conclude that the phenomenon of Autler-Townes doublet peaks (AT) occurs when the Rabi frequency $\Omega _{2}$ is large. Also, the phenomenon of Autler-Townes doublet peaks (AT) in the spectra $\mathop{\text{Im}}(\chi _{Q}^{eff})$ and $\mathop{\text{Im}}(\chi _{E}^{eff})$ is affected by the depolarization factor of MNE$_{1}$ ($L_{1}$) and MNE$_{3}$ ($L_{3}$).

Conclusion

In this paper, we have calculated the susceptibility of a hybrid system that contains a spherical semiconductor quantum dot and three distinct metallic nano ellipsoids. This work explains the importance of the following:

• When we take the three distinct metallic nano ellipsoids, the hybrid system will have many variables, so the properties and the susceptibility of a hybrid system can be controlled by these variables.

• The dipole-dipole interactions between the three metallic nano ellipsoids and SQD, in this case, become strong.

• The imaginary part of susceptibility under the effect of the plasmon-exciton coupling term only ($\mathop{\text{Im}}\chi _{I}^{eff}$), which consider a new idea in this area, gives distinctive and different results.

• The susceptibility of a spherical semiconductor quantum dot and the three distinct metallic nano ellipsoids are calculated.

• The susceptibility is affected by the angular frequency of the incident field, the distance between the semiconductor quantum dot and metallic nano ellipsoid, the depolarization factor of the ellipsoid, the Rabi frequencies of the fields, the angle ($\theta$), and semi-axes of the ellipsoid, which these variables play an outstanding role in our results.

• From our results, the Fano-resonance with amplification and Autler-Town doublet phenomena are formed.