A strategic analysis of incorporating corporate environmental responsibility into managerial incentive design: a differential game approach

Abstract

As corporations’ environmental impacts come under greater scrutiny from global financial, regulatory, and societal stakeholders, management scholars have increasingly focused on the role corporate governance plays in undertaking corporate environmental responsibility (CER). This paper combines managerial incentives and CER in a dynamic environment to formulate a differential game model of managerial incentive design in a duopolistic market, investigating whether companies with profit-maximizing interests are motivated to provide their professional managers with incentives related to CER and the impact of such incentives on corporate profitability, social welfare and emissions reduction. The results demonstrate the following: (1) Employing professional managers increases the emissions reduction efforts of firms and giving incentives to professional managers further increases the emissions reduction level of firms. (2) When a firm employs a professional manager and pays him or her a fixed salary, it generates slightly less income than it does when a manager is not employed; however, if the professional manager is given CER-related incentives, the firm’s income is greatly increased. (3) As long as professional managers are employed, social welfare increases regardless of whether professional managers are given incentive pay. (4) The emissions reduction of a firm increases with an increase in the income distribution coefficient π₁. This paper extends the existing CER decision-making model by considering different managerial incentive designs, providing new insights into CER and enterprise organizational strategy and offering useful policy recommendations and a scientific basis for environmental governance, which is expected to be useful for finding ways to balance economic development and environmental protection.

Graphical abstract

Appendices

Appendix 1. Neither firm employs a professional manager

The objective functions of the decisions of firm 1 and firm 2 are simplified as:

$$\underset{E_1}{\max }{J}_1={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_1w(t)-\frac{1}{2}{\eta}_1{\left({E}_1\right)}^2\right] dt$$

(33)

$$\underset{E_2}{\max }{J}_2={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_2w(t)-\frac{1}{2}{\eta}_2{\left({E}_2\right)}^2\right] dt$$

(34)

To obtain the Markov-refined Nash equilibrium of the noncooperative game, we construct a continuous and bounded differential function, V₃(G), V₆(G), which satisfies the Hamilton-Jacobi-Bellman (HJB) equation for all G ≥ 0.

$$\rho V_1(G)=\displaystyle\max_{E_1}\left\{\begin{array}{l}\pi_1\left.\left[w_0+\mu_1E_1(t)+\mu_2E_2(t)+\theta G(t)\right]\right)\\-\frac{\eta_1}2\left(E_1(t)\right)^2+V_1^{'}(G)\left[\lambda_1E_1(t)+\lambda_2E_2(t)-\delta G(t)\right]\end{array}\right\}$$

(35)

$$\rho V_2(G)=\displaystyle\max_{E_2}\left\{\begin{array}{l}\pi_2\left.\left[w_0+\mu_1E_1(t)+\mu_2E_2(t)+\theta G(t)\right]\right)-\frac{\eta_2}2\left(E_2(t)\right)^2\\+V_2^{'}(G)\left[\lambda_1E_1(t)+\lambda_2E_2(t)-\delta G(t)\right]\end{array}\right\}$$

(36)

We solve the first-order partial derivative of E₁ and E₂ on the right side of the HJB equation, set the first-order partial derivative equal to zero, and obtain the maximization condition.

$${\displaystyle \begin{array}{cc}{E}_1=\frac{\pi_1{\mu}_1+{V}_1^{\prime }{\lambda}_1}{\eta_1}& {E}_2=\frac{\pi_2{\mu}_2+{V}_2^{\prime}\lambda }{\eta_2}\end{array}}$$

(37)

By substituting Formula (37) into HJB Equation (35), we can obtain (36):

$$\rho {V}_1(G)={\pi}_1{W}_0+\left({\pi}_1\theta -\delta {V}_1^{\prime}\right)G+\frac{{\left({\pi}_1{\mu}_1+{V}_1^{\prime }{\lambda}_1\right)}^2}{2{\eta}_1}+\frac{\left({\pi}_2{\mu}_2+{V}_2^{\prime }{\lambda}_2\right)\left({\pi}_1{\mu}_2+{V}_1^{\prime }{\lambda}_2\right)}{\eta_2}$$

(38)

$$\rho {V}_2(G)={\pi}_2{W}_0+\left({\pi}_2\theta -\delta {V}_2^{\prime}\right)G+\frac{{\left({\pi}_2{\mu}_2+{V}_2^{\prime }{\lambda}_2\right)}^2}{2{\eta}_2}+\frac{\left({\pi}_1{\mu}_1+{V}_1^{\prime }{\lambda}_1\right)\left({\pi}_2{\mu}_1+{V}_2^{\prime }{\lambda}_1\right)}{\eta_1}$$

(39)

We assume that the expression of function V₁(G), V₂(G) is in linear form.

$${\displaystyle \begin{array}{cc}{V}_1(G)={a}_1G+{b}_1& {V}_2(G)={a}_2G+{b}_2\end{array}}$$

(40)

where a₁, b₁, a₂, and b₂ are constants.

$${\displaystyle \begin{array}{cc}{V}_1^{\prime }(G)={a}_1& {V}_2^{\prime }(G)={a}_2\end{array}}$$

(41)

By substituting Formula (40) and Formula (41) into Formula (38), we can obtain Formula (41):

$$\rho \left({a}_1G+{b}_1\right)={\pi}_1{W}_0+\left({\pi}_1\theta -\delta {a}_1\right)G+\frac{{\left({\pi}_1{\mu}_1+{a}_1{\lambda}_1\right)}^2}{2{\eta}_1}+\frac{\left({\pi}_2{\mu}_2+{a}_2{\lambda}_2\right)\left({\pi}_1{\mu}_2+{a}_1{\lambda}_2\right)}{\eta_2}$$

(42)

$$\rho \left({a}_2G+{b}_2\right)={\pi}_2{W}_0+\left({\pi}_2\theta -\delta {a}_2\right)G+\frac{{\left({\pi}_2{\mu}_2+{a}_2{\lambda}_2\right)}^2}{2{\eta}_2}+\frac{\left({\pi}_1{\mu}_1+{a}_1{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_2{\lambda}_1\right)}{\eta_1}$$

(43)

The linear equations about a₁, b₁, a₂, b₂ can be obtained, and the coefficients of the same terms at both ends of the equation can be obtained:

$${a}_1=\frac{\pi_1\theta }{\rho +\delta }$$

(44)

$${b}_1=\frac{\pi_1{W}_0}{\rho }+\frac{{\left({\pi}_1{\mu}_1+{a}_1{\lambda}_1\right)}^2}{2{\eta}_1\rho }+\frac{\left({\pi}_2{\mu}_2+{a}_2{\lambda}_2\right)\left({\pi}_1{\mu}_2+{a}_1{\lambda}_2\right)}{\rho {\eta}_2}$$

(45)

$${a}_2=\frac{\pi_2\theta }{\rho +\delta }$$

(46)

$${b}_2=\frac{\pi_2{W}_0}{\rho }+\frac{{\left({\pi}_2{\mu}_2+{a}_2{\lambda}_2\right)}^2}{2{\eta}_2\rho }+\frac{\left({\pi}_1{\mu}_1+{a}_1{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_2{\lambda}_1\right)}{\rho {\eta}_1}$$

(47)

By substituting Formulas (44)~(45) into Formulas (37) and (40), respectively, we can obtain proposition 1.

Proposition 1

If professional managers are not employed, the Nash equilibrium solutions of the decentralized and independent decision-making of firm 1 and firm 2 are as follows:

$${E}_1^{\ast }=\frac{\pi_1\left({\mu}_1\rho +{\pi}_1\delta +\theta {\lambda}_1\right)}{\left(\rho +\delta \right){\eta}_1}$$

(48)

$${E}_2^{\ast }=\frac{\pi_2\left({\mu}_2\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\left(\rho +\delta \right){\eta}_2}$$

(49)

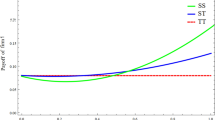
The steady-state emissions reductions are:

$${G}_{\infty}^{\ast }=\frac{\lambda_1{\pi}_1\left({\mu}_1\rho +{\mu}_1\delta +\theta {\lambda}_1\right)}{\delta {\eta}_1\left(\rho +\delta \right)}+\frac{\lambda_2{\pi}_2\left({\mu}_2\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\delta {\eta}_2\left(\rho +\delta \right)}$$

(50)

Under this game equilibrium, the optimal income expression of high-pollution firm 1 and firm 2 are as follows:

$${V}_1^{\ast }(G)=\frac{\pi_1\theta }{\rho +\delta }G+\frac{\pi_1{W}_0}{\rho }+\frac{{\left({\pi}_1{\mu}_1+{a}_1{\lambda}_1\right)}^2}{2{\eta}_1\rho }+\frac{\left({\pi}_2{\mu}_2+{a}_2{\lambda}_2\right)\left({\pi}_1{\mu}_1+{a}_1{\lambda}_2\right)}{\rho {\eta}_2}$$

(51)

$${V}_2^{\ast }(G)=\frac{\pi_2\theta }{\rho +\delta }G+\frac{\pi_2{W}_0}{\rho }+\frac{{\left({\pi}_2{\mu}_2+{a}_2{\lambda}_2\right)}^2}{2{\eta}_1\rho }+\frac{\left({\pi}_1{\mu}_1+{a}_1{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_2{\lambda}_2\right)}{\rho {\eta}_1}$$

(52)

Appendix 2. One firm pays a fixed salary to employ a professional manager, and the other firm does not employ a professional manager

The objective functions of the decisions of firm 1 and firm 2 are simplified as:

$$\underset{E_2}{\max }{J}_1={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_1w(t)-\frac{1}{2}{\eta}_1{\left({E}_1\right)}^2-{\gamma}_1\left({\pi}_1{W}_0-\frac{1}{2}{\eta}_1{\left({E}_1\right)}^2\right)\right] dt$$

(53)

$$\underset{E_2}{\max }{J}_2={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_2w(t)-\frac{1}{2}{\eta}_2{\left({E}_2\right)}^2\right] dt$$

(54)

To obtain the Markov-refined Nash equilibrium of the noncooperative game, we construct a continuous and bounded differential function, V₃(G), V₄(G), which satisfies the Hamilton-Jacobi-Bellman (HJB) equation for all G ≥ 0.

$$\rho {V}_3(G)=\underset{E_1}{\max}\left\{\begin{array}{l}{\pi}_2\left.\left[{w}_0+{\mu}_1{E}_1(t)+{\mu}_2{E}_2(t)+\theta G(t)\right]\right)-{\gamma}_1{\pi}_1{W}_0\\ {}-\left(1-{\gamma}_1\right)\frac{\eta_1}{2}{\left({E}_1(t)\right)}^2+{V}_3^{\prime }(G)\left[{\lambda}_1{E}_1(t)+{\lambda}_2{E}_2(t)-\delta G(t)\right]\end{array}\right\}$$

(55)

$$\rho {V}_4(G)=\underset{E_2}{\max}\left\{\begin{array}{l}{\pi}_2\left.\left[{w}_0+{\mu}_1{E}_1(t)+{\mu}_2{E}_2(t)+\theta G(t)\right]\right)\\ {}-\frac{\eta_2}{2}{\left({E}_2(t)\right)}^2+{V}_4^{\prime }(G)\left[{\lambda}_1{E}_1(t)+{\lambda}_2{E}_2(t)-\delta G(t)\right]\end{array}\right\}$$

(56)

We solve the first-order partial derivative about E₁ and E₂ on the right side of the HJB equation, set the first-order partial derivative equal to zero, and obtain the maximization condition.

$${\displaystyle \begin{array}{cc}{E}_1=\frac{\pi_1{\mu}_1+{V}_3^{\prime }{\lambda}_1}{\eta_1\left(1-{\gamma}_1\right)}& {E}_2=\frac{\pi_2{\mu}_2+{V}_4^{\prime }{\lambda}_2}{\eta_2}\end{array}}$$

(57)

By substituting Formula (57) into HJB Equation (55), we can obtain (56):

$$\rho {V}_3(G)={\pi}_1{W}_0\left(1-{\gamma}_1\right)+\left({\pi}_1\theta -\delta {V}_3^{\prime}\right)G+\frac{{\left({\pi}_1{\mu}_1+{V}_3^{\prime }{\lambda}_1\right)}^2}{2{\eta}_1\left(1-{\gamma}_1\right)}+\frac{{\left({\pi}_2{\mu}_2+{V}_4^{\prime }{\lambda}_2\right)}^2\left({\pi}_1{\mu}_2+{V}_3^{\prime }{\lambda}_2\right)}{\eta_2}$$

(58)

$$\rho {V}_4(G)={\pi}_2{W}_0+\left({\pi}_2\theta -\delta {V}_3^{\prime}\right)G+\frac{{\left({\pi}_2{\mu}_2+{V}_4^{\prime }{\lambda}_2\right)}^2}{2{\eta}_2}+\frac{{\left({\pi}_1{\mu}_1+{V}_3^{\prime }{\lambda}_1\right)}^2\left({\pi}_2{\mu}_1+{V}_4^{\prime }{\lambda}_1\right)}{\eta_1}$$

(59)

We assume that the expression of function V₃(G), V₄(G) is in linear form:

$$\begin{array}{cc}V_1(G)=a_1G+b_1&V_2(G)=a_2G+b_2\end{array}$$

(60)

where a₃, b₃, a₄, and b₄ are constants.

$$\begin{array}{cc}V_1^{'}(G)=a_1&V_2^{'}(G)=a_2\end{array}$$

(61)

By substituting Formula (60) and Formula (61) into Formula (58), we can obtain Formula (59):

$$\rho \left({a}_3G+{b}_3\right)={\pi}_1{W}_0\left(1-{\gamma}_1\right)+\left({\pi}_1\theta -\delta {a}_3\right)G+\frac{{\left({\pi}_1{\mu}_1+{a}_3{\lambda}_1\right)}^2}{2{\eta}_1\left(1-{\gamma}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{a}_4{\lambda}_2\right)\left({\pi}_1{\mu}_2+{a}_3{\lambda}_2\right)}{\eta_2}$$

(62)

$$\rho \left({a}_4G+{b}_4\right)={\pi}_2{W}_0+\left({\pi}_2\theta -\delta {a}_4\right)G+\frac{{\left({\pi}_2{\mu}_2+{a}_4{\lambda}_2\right)}^2}{2{\eta}_2}+\frac{\left({\pi}_1{\mu}_1+{a}_3{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_4{\lambda}_1\right)}{\eta_1}$$

(63)

The linear equations about a₃, b₃, a₄, b₄ can be obtained, and the coefficients of the same terms at both ends of the equation can be obtained:

$${a}_3=\frac{\pi_1\theta }{\rho +\delta }$$

(64)

$${b}_3=\frac{\left(1-{\gamma}_1\right){\pi}_1{W}_0}{\rho }+\frac{{\left({\pi}_1{\mu}_1+{a}_3{\lambda}_1\right)}^2}{2{\eta}_1\rho \left(1-{\gamma}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{a}_4{\lambda}_2\right)\left({\pi}_1{\mu}_2+{a}_3{\lambda}_2\right)}{\rho {\eta}_2}$$

(65)

$${a}_4=\frac{\pi_2\theta }{\rho +\delta }$$

(66)

$${b}_4=\frac{\pi_1{W}_0}{\rho }+\frac{{\left({\pi}_2{\mu}_2+{a}_4{\lambda}_2\right)}^2}{2{\eta}_2\rho }+\frac{\left({\pi}_1{\mu}_1+{a}_3{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_4{\lambda}_1\right)}{\rho {\eta}_1}$$

(67)

By substituting Formulas (64)~(67) into Formulas (57) and (60), respectively, we can obtain proposition 2.

Proposition 2

When high-pollution firm 1 employs a professional manager and provides incentives and firm 2 does not employ a professional manager, the independent and decentralized Nash equilibrium solution when each owner makes production decisions is as follows:

$${E}_1^{\ast \ast }=\frac{\pi_1\left({\mu}_1\rho +{\mu}_1\delta +\theta {\lambda}_1\right)}{\left(\rho +\delta \right){\eta}_1\left(1-{\gamma}_1\right)}$$

(68)

$${E}_2^{\ast \ast }=\frac{\pi_2\left({\mu}_2\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\left(\rho +\delta \right){\eta}_2}$$

(69)

The steady-state emissions reductions are:

$${G}_{\infty}^{\ast }=\frac{\lambda_1{\pi}_1\left({\mu}_1\rho +{\mu}_1\delta +\theta {\lambda}_1\right)}{\delta {\eta}_1\left(\rho +\delta \right)\left(1-{\gamma}_1\right)}+\frac{\lambda_2{\pi}_2\left({\mu}_2\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\delta {\eta}_2\left(\rho +\delta \right)}$$

(70)

Under this game equilibrium, the optimal income expression of high-pollution firms 1 and 2 are as follows:

$${V}_3^{\ast }(G)=\frac{\pi_1\theta }{\rho +\delta }G+\frac{\left(1-{\gamma}_1\right){\pi}_1{W}_0}{\rho }+\frac{{\left({\pi}_1{\mu}_1+{a}_3{\lambda}_1\right)}^2}{2{\eta}_1\rho \left(1-{\gamma}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{a}_4{\lambda}_2\right)\left({\pi}_1{\mu}_2+{a}_3{\lambda}_2\right)}{\rho {\eta}_2}$$

(71)

$${V}_4^{\ast }(G)=\frac{\pi_2\theta }{\rho +\delta }G+\frac{\pi_2{W}_0}{\rho }+\frac{{\left({\pi}_2{\mu}_2+{a}_4{\lambda}_2\right)}^2}{2{\eta}_2\rho }+\frac{\left({\pi}_1{\mu}_1+{a}_3{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_4{\lambda}_1\right)}{\rho {\eta}_1}$$

(72)

Appendix 3. One firm pays additional incentive compensation to an employed professional manager, and the other firm does not employ a professional manager

The objective functions of the decisions of firm 1 and firm 2 are simplified as:

$$\underset{E_1}{\max }{J}_1={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_1w(t)-\frac{1}{2}{\eta}_1{\left({E}_2\right)}^2-{\gamma}_1\left({\pi}_1{W}_0-\frac{1}{2}{\eta}_1{\left({E}_1\right)}^2\right)-{\beta}_1\left({\pi}_1w(t)-\frac{1}{2}{\eta}_1{\left({E}_1\right)}^2\right)\right] dt$$

(73)

$$\underset{E_1}{\max }{J}_2={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_2w(t)-\frac{1}{2}{\eta}_1{\left({E}_2\right)}^2\right] dt$$

(74)

To obtain the Markov-refined Nash equilibrium of the noncooperative game, we construct a continuous and bounded differential function, V₅(G), V₆(G), which satisfies the Hamilton-Jacobi-Bellman (HJB) equation for all G ≥ 0.

$$\rho {V}_5(G)=\underset{E_1}{\max}\left\{\begin{array}{l}\left(1-{\beta}_1\right){\pi}_1\left.\left[{w}_0+{\mu}_1{E}_1(t)+{\mu}_2{E}_2(t)+\theta G(t)\right]\right)\\ {}-\left(1-{\gamma}_1-{\beta}_1\right)\frac{\eta_1}{2}{\left({E}_1(t)\right)}^2{\gamma}_1{\pi}_1{W}_0+{V}_5^{\prime }(G)\left[{\lambda}_1{E}_1(t)+{\lambda}_2{E}_2(t)-\delta G(t)\right]\end{array}\right\}$$

(75)

$$\rho {V}_6(G)=\underset{E_2}{\max}\left\{\begin{array}{l}{\pi}_2\left.\left[{w}_0+{\mu}_1{E}_1(t)+{\mu}_2{E}_2(t)+\theta G(t)\right]\right)-\frac{\eta_2}{2}{\left({E}_2(t)\right)}^2\\ {}{V}_6^{\prime }(G)\left[{\lambda}_1{E}_1(t)+{\lambda}_2{E}_2(t)-\delta G(t)\right]\end{array}\right\}$$

(76)

We solve the first-order partial derivative about E₁ and E₂ on the right side of the HJB equation, set the first-order partial derivative equal to zero, and obtain the maximization condition.

$${\displaystyle \begin{array}{cc}{E}_1=\frac{\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{V}_5^{\prime }{\lambda}_1}{\eta_1\left(1-{\gamma}_1-{\beta}_1\right)}& {E}_2=\frac{\pi_2{\mu}_2+{V}_6^{\prime}\lambda }{\eta_2}\end{array}}$$

(77)

By substituting Formula (77) into HJB Equation (75), we can obtain (75):

$${\displaystyle \begin{array}{l}\rho {V}_5(G)=\left(1-{\gamma}_1-{\beta}_1\right){\pi}_1{W}_0+\left(\left(1-{\beta}_1\right){\pi}_1\theta -\delta {V}_5^{\prime}\right)G\\ {}+\frac{{\left(\left(1-{\gamma}_1-{\beta}_1\right){\pi}_1{\mu}_1+{V}_5^{\prime }{\lambda}_1\right)}^2}{2{\eta}_1\left(1-{\gamma}_1-{\beta}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{V}_6^{\prime }{\lambda}_2\right)\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{V}_5^{\prime }{\lambda}_2\right)}{\eta_2}\end{array}}$$

(78)

$$\rho {V}_6(G)={\pi}_2{W}_0+\left({\pi}_2\theta -\delta {V}_5^{\prime}\right)G+\frac{{\left({\pi}_2{\mu}_2+{V}_6^{\prime }{\lambda}_2\right)}^2}{2{\eta}_2}+\frac{\left({\pi}_1{\mu}_1+{V}_5^{\prime }{\lambda}_1\right)\left({\pi}_2{\mu}_1+{V}_6^{\prime }{\lambda}_2\right)}{\eta_1}$$

(79)

We assume that the expression of function V₅(G),   V₆(G) is in linear form:

$${\displaystyle \begin{array}{cc}{V}_5(G)={a}_5G+{b}_5& {V}_6(G)={a}_6G+{b}_6\end{array}}$$

(80)

where a₅ b₅, a₆, and b₆ are constants.

$${\displaystyle \begin{array}{cc}{V}_5^{\prime }(G)={a}_5& {V}_6^{\prime }(G)={a}_6\end{array}}$$

(81)

By substituting Formula (80) and Formula (81) into Formula (78), we can obtain Formula (79):

$${\displaystyle \begin{array}{c}\rho \Big({a}_5G+{b}_5=\left(1-{\beta}_1-{\gamma}_1\right){\pi}_1{W}_0+\left(\left(1-{\beta}_1\right){\pi}_1\theta -\delta {a}_5\right)G+\frac{{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_5{\lambda}_1\right)}^2}{2{\eta}_1\left(1-{\gamma}_1-{\beta}_1\right)}\\ {}+\frac{\left({\pi}_2{\mu}_2+{a}_6{\lambda}_2\right)\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{a}_5{\lambda}_2\right)}{\eta_2}\end{array}}$$

(82)

$$\rho \Big({a}_6G+{b}_6={\pi}_2{W}_0+\left({\pi}_2\theta -\delta {a}_6\right)G+\frac{{\left({\pi}_2{\mu}_2+{a}_6{\lambda}_2\right)}^2}{2{\eta}_2}+\frac{\left({\pi}_1{\mu}_1+{a}_5{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_6{\lambda}_1\right)}{\eta_1}$$

(83)

The linear equations about a₅, b₅, a₆, b₆ can be obtained, and the coefficients of the same terms at both ends of the equation can be obtained:

$${a}_5=\frac{\left(1-{\beta}_1\right){\pi}_1\theta }{\rho +\delta }$$

(84)

$${b}_5=\frac{\left(1-{\gamma}_1-{\beta}_1\right){\pi}_1{W}_0}{\rho }+\frac{{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_5{\lambda}_1\right)}^2}{2{\eta}_1\rho \left(1-{\gamma}_1-{\beta}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{a}_6{\lambda}_2\right)\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{a}_5{\lambda}_2\right)}{\rho {\eta}_2}$$

(85)

$${a}_6=\frac{\pi_2\theta }{\rho +\delta }$$

(86)

$${b}_6=\frac{\pi_2{W}_0}{\rho }+\frac{{\left({\pi}_2{\mu}_2+{a}_6{\lambda}_2\right)}^2}{2{\eta}_2\rho }$$

(87)

Substituting Formulas (84)~(87) into Formulas (77) and (80), respectively, yields proposition 3.

Proposition 3

High-pollution firm 1 employs a professional manager and pays incentives. When firm 2 does not employ a professional manager, the Nash equilibrium of firm 1 and firm 2 is solved as:

$${E}_1^{\ast \ast \ast }=\frac{\left(1-{\beta}_1\right){\pi}_1\left({\mu}_1\rho +{\mu}_1\delta +\theta {\lambda}_1\right)}{\left(\rho +\delta \right){\eta}_1\left(1-{\gamma}_1-{\beta}_1\right)}$$

(88)

$${E}_2^{\ast \ast \ast }=\frac{\pi_2\left({\mu}_1\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\left(\rho +\delta \right){\eta}_2}$$

(89)

The steady-state emissions reductions are:

$${G}_{\infty}^{\ast \ast \ast }=\frac{\lambda_1{\pi}_1\left(1-{\beta}_1\right)\left({\mu}_1\rho +{\mu}_1\delta +\theta {\lambda}_1\right)}{\delta {\eta}_1\left(\rho +\delta \right)\left(1-{\gamma}_1-{\beta}_1\right)}+\frac{\lambda_2{\pi}_2\left({\mu}_2\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\delta {\eta}_2\left(\rho +\delta \right)}$$

(90)

Under this game equilibrium, the optimal income expressions of high-pollution firms 1 and 2 are as follows:

$${\displaystyle \begin{array}{l}{V}_5^{\ast }(G)=\frac{\left(1-{\beta}_1\right){\pi}_1\theta }{\rho +\delta }G+\frac{\left(1-{\gamma}_1-{\beta}_1\right){\pi}_1{W}_0}{\rho }+\frac{{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_5{\lambda}_1\right)}^2}{2{\eta}_1\rho \left(1-{\gamma}_1-{\beta}_1\right)}\\ {}+\frac{\left({\pi}_2{\mu}_2+{a}_6{\lambda}_2\right)\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{a}_5{\lambda}_2\right)}{\rho {\eta}_2}\end{array}}$$

(91)

$${V}_6^{\ast }(G)=\frac{\pi_2\theta }{\rho +\delta }G+\frac{\pi_2{W}_0}{\rho }+\frac{{\left({\pi}_2{\mu}_2+{a}_6{\lambda}_2\right)}^2}{2{\eta}_2\rho }+\frac{\left({\pi}_1{\mu}_1+{a}_5{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_6{\lambda}_1\right)}{\rho {\eta}_1}$$

(92)

Appendix 4. Both firms pay a fixed salary to employ a professional manager

The objective functions of the decisions of firm 1 and firm 2 are simplified as:

$$\underset{E_1}{\max }{J}_2={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_1w(t)-\frac{1}{2}{\eta}_1{\left({E}_2\right)}^2-{\gamma}_1\left({\pi}_1{W}_0-\frac{1}{2}{\eta}_1{\left({E}_1\right)}^2\right)\right] dt$$

(93)

$$\underset{E_1}{\max }{J}_2={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_2w(t)-\frac{1}{2}{\eta}_2{\left({E}_2\right)}^2-{\gamma}_2\left({\pi}_1{W}_0-\frac{1}{2}{\eta}_2{\left({E}_2\right)}^2\right)\right] dt$$

(94)

To obtain the Markov-refined Nash equilibrium of the noncooperative game, we construct a continuous and bounded differential function, V₇(G)V₈(G), which satisfies the Hamilton-Jacobi-Bellman (HJB) equation for all G ≥ 0.

$$\rho {V}_5(G)=\underset{E_1}{\max}\left\{\begin{array}{l}{\pi}_1\left.\left[{w}_0+{\mu}_1{E}_1(t)+{\mu}_2{E}_2(t)+\theta G(t)\right]\right)-\left(1-{\gamma}_1\right)\frac{\eta_1}{2}{\left({E}_1(t)\right)}^2\\ {}{\gamma}_1{\pi}_1{W}_0+{V}_7^{\prime }(G)\left[{\lambda}_1{E}_1(t)+{\lambda}_2{E}_2(t)-\delta G(t)\right]\end{array}\right\}$$

(95)

$$\rho {V}_8(G)=\underset{E_2}{\max}\left\{\begin{array}{l}{\pi}_2\left.\left[{w}_0+{\mu}_1{E}_1(t)+{\mu}_2{E}_2(t)+\theta G(t)\right]\right)-\left(1-{\gamma}_1\right)\frac{\eta_2}{2}{\left({E}_2(t)\right)}^2\\ {}{\gamma}_2{\pi}_2{W}_0+{V}_8^{\prime }(G)\left[{\lambda}_1{E}_1(t)+{\lambda}_2{E}_2(t)-\delta G(t)\right]\end{array}\right\}$$

(96)

We solve the first-order partial derivative about E₁ and E₂ on the right side of the HJB equation, set the first-order partial derivative equal to zero, and obtain the maximization condition.

$${\displaystyle \begin{array}{cc}{E}_1=\frac{\pi_1{\mu}_1+{V}_7^{\prime }{\lambda}_1}{\eta_1\left(1-{\gamma}_1\right)}& {E}_8=\frac{\pi_2{\mu}_2+{V}_8^{\prime }{\lambda}_2}{\eta_2\left(1-{\gamma}_2\right)}\end{array}}$$

(97)

By substituting Formula (97) into HJB Equation (95), we can obtain (96):

$$\rho {V}_7(G)=\left(1-{\gamma}_1\right){\pi}_1{W}_0+\left({\pi}_1\theta -\delta {V}_7^{\prime}\right)G+\frac{{\left({\pi}_1{\mu}_1+{V}_7^{\prime }{\lambda}_1\right)}^2}{2{\eta}_1\left(1-{\gamma}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{V}_8^{\prime }{\lambda}_2\right)\left({\pi}_1{\mu}_2+{V}_7^{\prime }{\lambda}_2\right)}{\eta_2\left(1-{\gamma}_2\right)}$$

(98)

$$\rho {V}_8(G)=\left(1-{\gamma}_2\right){\pi}_2{W}_0+\left({\pi}_2\theta -\delta {V}_8^{\prime}\right)G+\frac{{\left({\pi}_2{\mu}_2+{V}_8^{\prime }{\lambda}_2\right)}^2}{2{\eta}_2\left(1-{\gamma}_2\right)}+\frac{\left({\pi}_1{\mu}_1+{V}_7^{\prime }{\lambda}_1\right)\left({\pi}_2{\mu}_1+{V}_8^{\prime }{\lambda}_1\right)}{\eta_1\left(1-{\gamma}_1\right)}$$

(99)

We assume that the expression of function V₇(G), V₈(G) is in linear form:

$${\displaystyle \begin{array}{cc}{V}_7(G)={a}_7G+{b}_7& {V}_8(G)={a}_8G+{b}_8\end{array}}$$

(100)

where a₇, b₇, a₈, and b₈ are constants.

$${\displaystyle \begin{array}{cc}{V}_7^{\prime }(G)={a}_7& {V}_8^{\prime }(G)={a}_8\end{array}}$$

(101)

By substituting Formula (100) and Formula (101) into Formula (98), Formula (99) can be obtained:

$$\rho \left({a}_7G+{b}_7\right)=\left(1-{\gamma}_1\right){\pi}_1{W}_0+\left({\pi}_1\theta -\delta {a}_7\right)G+\frac{{\left({\pi}_1{\mu}_1+{a}_7{\lambda}_1\right)}^2}{2{\eta}_1\left(1-{\gamma}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{a}_8{\lambda}_2\right)\left({\pi}_1{\mu}_2+{a}_7{\lambda}_2\right)}{\eta_2\left(1-{\gamma}_2\right)}$$

(102)

$$\rho \left({a}_8G+{b}_8\right)=\left(1-{\gamma}_2\right){\pi}_2{W}_0+\left({\pi}_2\theta -\delta {a}_8\right)G+\frac{{\left({\pi}_2{\mu}_2+{a}_8{\lambda}_2\right)}^2}{2{\eta}_2\left(1-{\gamma}_2\right)}+\frac{\left({\pi}_1{\mu}_1+{a}_7{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_8{\lambda}_1\right)}{\eta_1\left(1-{\gamma}_1\right)}$$

(103)

The linear equations about a₇, b₇, a₈, b₈ can be obtained, and the coefficients of the same terms at both ends of the equation can be obtained:

$${a}_7=\frac{\pi_1\theta }{\rho +\delta }$$

(104)

$${b}_7=\frac{\left(1-{\gamma}_1\right){\pi}_1{W}_0}{\rho }+\frac{{\left({\pi}_1{\mu}_1+{a}_7{\lambda}_1\right)}^2}{2{\eta}_1\rho \left(1-{\gamma}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{a}_8{\lambda}_2\right)\left({\pi}_1{\mu}_2+{a}_7{\lambda}_2\right)}{\rho {\eta}_2\left(1-{\gamma}_2\right)}$$

(105)

$${a}_8=\frac{\pi_2\theta }{\rho +\delta }$$

(106)

$${b}_8=\frac{\left(1-{\gamma}_2\right){\pi}_2{W}_0}{\rho }+\frac{{\left({\pi}_2{\mu}_2+{a}_8{\lambda}_2\right)}^2}{2{\eta}_2\rho \left(1-{\gamma}_2\right)}+\frac{\left({\pi}_1{\mu}_1+{a}_7{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_8{\lambda}_1\right)}{\rho {\eta}_1\left(1-{\gamma}_1\right)}$$

(107)

By substituting formulas (104)~(107) into Formulas (97) and (100), respectively, we can obtain proposition 4.

Proposition 4

The Nash equilibrium solution when high-pollution firms 1 and 2 both employ professional managers and pay fixed salaries is as follows:

$${E}_1^{\ast \ast \ast \ast }=\frac{\pi_1\left({\mu}_1\rho +{\mu}_1\delta +\theta {\lambda}_1\right)}{\left(\rho +\delta \right){\eta}_1\left(1-{\gamma}_1\right)}$$

(108)

$${E}_2^{\ast \ast \ast \ast }=\frac{\pi_2\left({\mu}_2\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\left(\rho +\delta \right){\eta}_2\left(1-{\gamma}_2\right)}$$

(109)

The steady-state emissions reductions are:

$${G}_{\infty}^{\ast \ast \ast \ast }=\frac{\lambda_1{\pi}_1\left({\mu}_1\rho +{\mu}_1\delta +\theta {\lambda}_1\right)}{\delta {\eta}_1\left(\rho +\delta \right)\left(1-{\gamma}_1\right)}+\frac{\lambda_2{\pi}_2\left({\mu}_2\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\delta {\eta}_2\left(\rho +\delta \right)\left(1-{\gamma}_2\right)}$$

(110)

Under this game equilibrium, the optimal income expressions of high-pollution firms 1 and 2 are as follows:

$${V}_7^{\ast }(G)=\frac{\pi_1\theta }{\rho +\delta }G+\frac{\left(1-{\gamma}_1\right){\pi}_1{W}_0}{\rho }+\frac{{\left({\pi}_1{\mu}_1+{a}_7{\lambda}_1\right)}^2}{2{\eta}_1\rho \left(1-{\gamma}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{a}_8{\lambda}_2\right)\left({\pi}_1{\mu}_2+{a}_7{\lambda}_2\right)}{\left(1-{\gamma}_2\right)\rho {\eta}_2}$$

(111)

$${V}_8^{\ast }(G)=\frac{\pi_2\theta }{\rho +\delta }G+\frac{\left(1-{\gamma}_2\right){\pi}_2{W}_0}{\rho }+\frac{{\left({\pi}_2{\mu}_2+{a}_8{\lambda}_2\right)}^2}{2{\eta}_2\rho \left(1-{\gamma}_2\right)}+\frac{\left({\pi}_1{\mu}_1+{a}_7{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_8{\lambda}_1\right)}{\rho {\eta}_1\left(1-{\gamma}_1\right)}$$

(112)

Appendix 5. One firm pays a fixed salary to employ a professional manager, and the other firm pays additional incentive compensation an employed professional manager

The objective functions of the decisions of firm 1 and firm 2 are simplified as:

$$\underset{E_1}{\max }\ {J}_1={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_1w(t)-\frac{1}{2}{\eta}_1{\left({E}_1\right)}^2-{\gamma}_1\left({\pi}_1{W}_0-\frac{1}{2}{\eta}_2{\left({E}_2\right)}^2\right)-{\beta}_1\left({\pi}_1w(t)-\frac{1}{2}{\eta}_1{\left({E}_1\right)}^2\right)\right] dt$$

(113)

$$\underset{E_2}{\max }\ {J}_2={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_2w(t)-\frac{1}{2}{\eta}_2{\left({E}_2\right)}^2-{\gamma}_2\left({\pi}_2{W}_0-\frac{1}{2}{\eta}_2{\left({E}_2\right)}^2\right)\right] dt$$

(114)

To obtain the Markov-refined Nash equilibrium of the noncooperative game, we construct a continuous and bounded differential function, V₉(G), V₁₀(G), which satisfies the Hamilton-Jacobi-Bellman (HJB) equation for all G ≥ 0.

$$\rho {V}_9(G)=\underset{E_1}{\max}\left\{\begin{array}{l}\left(1-{\beta}_1\right){\pi}_1\left.\left[{w}_0+{\mu}_1{E}_1(t)+{\mu}_2{E}_2(t)+\theta G(t)\right]\right)-\left(1-{\gamma}_1\right)\frac{\eta_1}{2}{\left({E}_1(t)\right)}^2\\ {}-{\gamma}_2{\pi}_1{W}_0+{V}_9^{\prime }(G)\left[{\lambda}_1{E}_1(t)+{\lambda}_2{E}_2(t)-\delta G(t)\right]\end{array}\right\}$$

(115)

$$\rho {V}_{10}(G)=\underset{E_2}{\max}\left\{\begin{array}{l}{\pi}_2\left.\left[{w}_0+{\mu}_1{E}_1(t)+{\mu}_2{E}_2(t)+\theta G(t)\right]\right)-\left(1-{\gamma}_2\right)\frac{\eta_2}{2}{\left({E}_2(t)\right)}^2\\ {}-{\gamma}_2{\pi}_2{W}_0+{V}_{10}^{\prime }(G)\left[{\lambda}_1{E}_1(t)+{\lambda}_2{E}_2(t)-\delta G(t)\right]\end{array}\right\}$$

(116)

We solve the first-order partial derivative about E₁, E₂, respectively, on the right side of the HJB equation, set the first-order partial derivative equal to zero, and obtain the maximization condition:

$${\displaystyle \begin{array}{cc}{E}_1=\frac{\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{V}_9^{\prime }{\lambda}_1}{\eta_1\left(1-{\gamma}_1-{\beta}_1\right)}& {E}_2=\frac{\pi_2{\mu}_2+{V}_{10}^{\prime }{\lambda}_2}{\eta_2\left(1-{\gamma}_2\right)}\end{array}}$$

(117)

Substituting formula (118) into HJB equations (116) and (117) yields:

$${\displaystyle \begin{array}{l}\rho {V}_9(G)=\left(1-{\gamma}_1-{\beta}_1\right){\pi}_1{W}_0+\left(\left(1-{\beta}_1\right){\pi}_1\theta -\delta {V}_9^{\prime}\right)G\\ {}+\frac{{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{V}_9^{\prime }{\lambda}_1\right)}^2}{2{\eta}_1\left(1-{\gamma}_1-{\beta}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{V}_{10}^{\prime }{\lambda}_2\right)\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{V}_9^{\prime }{\lambda}_2\right)}{\left(1-{\gamma}_2\right){\eta}_2}\end{array}}$$

(118)

$${\displaystyle \begin{array}{c}\rho {V}_{10}(G)=\left(1-{\gamma}_2\right){\pi}_2{W}_0+\left({\pi}_2\theta -\delta {V}_{10}^{\prime}\right)G+\frac{{\left({\pi}_2{\mu}_2+{V}_{10}^{\prime }{\lambda}_2\right)}^2}{2{\eta}_2\left(1-{\gamma}_2\right)}\\ {}+\frac{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{V}_9^{\prime }{\lambda}_1\right)\left({\pi}_2{\mu}_1+{V}_{10}^{\prime }{\lambda}_1\right)}{\eta_1\left(1-{\gamma}_1-{\beta}_1\right)}\end{array}}$$

(119)

We assume that the expression of function V₉(G), V₁₀(G) is in linear form:

$${\displaystyle \begin{array}{cc}{V}_9(G)={a}_9G+{b}_9& {V}_{10}(G)={a}_{10}G+{b}_{10}\end{array}}$$

(120)

where a₉ b₉, a₁₀, and b₁₀ are constants.

$${\displaystyle \begin{array}{cc}{V}_9^{\prime }(G)={a}_9& {V}_{10}^{\prime }(G)={a}_{10}\end{array}}$$

(121)

By substituting formula (120) and formula (121) into formula (119), we can obtain formula (118):

$${\displaystyle \begin{array}{l}\rho \left({a}_9G+{b}_9\right)=\left(1-{\gamma}_1-{\beta}_1\right){\pi}_1{W}_0+\left(\left(1-{\beta}_1\right){\pi}_1\theta -\delta {a}_9\right)G\\ {}+\frac{{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_9{\lambda}_1\right)}^2}{2{\eta}_1\left(1-{\gamma}_1-{\beta}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{a}_{10}{\lambda}_2\right)\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{a}_9{\lambda}_2\right)}{\left(1-{\gamma}_2\right){\eta}_2}\end{array}}$$

(122)

$${\displaystyle \begin{array}{c}\rho \left({a}_{10}G+{b}_{10}\right)=\left(1-{\gamma}_2\right){\pi}_2{W}_0+\left({\pi}_2\theta -\delta {a}_{10}\right)G\\ {}+\frac{{\left({\pi}_2{\mu}_2+{a}_{10}{\lambda}_2\right)}^2}{2{\eta}_2\left(1-{\gamma}_2\right)}+\frac{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_9{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_{10}{\lambda}_1\right)}{\eta_1\left(1-{\gamma}_1-{\beta}_1\right)}\end{array}}$$

(123)

The linear equations about a₉, b₉, a₁₀, b₁₀ can be obtained, and the coefficients of the same terms at both ends of the equation can be obtained:

$${a}_9=\frac{\left(1-{\beta}_1\right){\pi}_1\theta }{\rho +\delta }$$

(124)

$${b}_9=\frac{\left(1-{\gamma}_1-{\beta}_1\right){\pi}_1{W}_0}{\rho }+\frac{{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_9{\lambda}_1\right)}^2}{2{\eta}_1\rho \left(1-{\gamma}_1-{\beta}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{a}_{10}{\lambda}_2\right)\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{a}_9{\lambda}_2\right)}{\rho {\eta}_2\left(1-{\gamma}_2\right)}$$

(125)

$${a}_{10}=\frac{\pi_2\theta }{\rho +\delta }$$

(126)

$${b}_{10}=\frac{\left(1-{\gamma}_2\right){\pi}_2{W}_0}{\rho }+\frac{{\left({\pi}_2{\mu}_2+{a}_{10}{\lambda}_2\right)}^2}{2{\eta}_2\rho \left(1-{\gamma}_2\right)}+\frac{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_9{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_{10}{\lambda}_1\right)}{\rho {\eta}_1\left(1-{\gamma}_1-{\beta}_1\right)}$$

(127)

By substituting formulas (124)~(41) into formulas (118) and (119), respectively, we can obtain proposition 5.

Proposition 5

The Nash equilibrium solution when high-pollution firms 1 and 2 both employ professional managers and pay a fixed salary is:

$${E}_1^{\ast \ast \ast \ast \ast }=\frac{\left(1-{\beta}_1\right){\pi}_1\left({\mu}_1\rho +{\mu}_1\delta +\theta {\lambda}_1\right)}{\left(\rho +\delta \right){\eta}_2\left(1-{\gamma}_1-{\beta}_1\right)}$$

(128)

$${E}_1^{\ast \ast \ast \ast \ast }=\frac{\pi_2\left({\mu}_2\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\left(\rho +\delta \right){\eta}_2\left(1-{\gamma}_2\right)}$$

(129)

The steady-state emissions reductions are:

$${G}_{\infty}^{\ast \ast \ast \ast \ast }=\frac{\lambda_1{\pi}_1\left(1-{\beta}_1\right)\left({\mu}_1\rho +{\mu}_1\delta +\theta {\lambda}_1\right)}{\delta {\eta}_1\left(\rho +\delta \right)\left(1-{\gamma}_1-{\beta}_1\right)}+\frac{\lambda_2{\pi}_2\left({\mu}_2\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\delta {\eta}_2\left(\rho +\delta \right)}$$

(130)

Under this game equilibrium, the optimal income expression of high-pollution firms 1 and 2 are as follows:

$${\displaystyle \begin{array}{l}{V}_9^{\ast }(G)=\frac{\left(1-{\beta}_1\right){\pi}_1\theta }{\rho +\delta }G+\frac{\left(1-{\beta}_1-{\gamma}_1\right){\pi}_1{W}_0}{\rho }+\frac{{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_9{\lambda}_2\right)}^2}{2{\eta}_1\rho \left(1-{\gamma}_1-{\beta}_1\right)}\\ {}+\frac{\left({\pi}_2{\mu}_2+{a}_{10}{\lambda}_2\right)\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{a}_9{\lambda}_2\right)}{\rho {\eta}_2\left(1-{\gamma}_2\right)}\end{array}}$$

(131)

$${V}_{10}^{\ast }(G)=\frac{\pi_2\theta }{\rho +\delta }G+\frac{\left(1-{\gamma}_2\right){\pi}_2{W}_0}{\rho }+\frac{{\left({\pi}_2{\mu}_2+{a}_{10}{\lambda}_2\right)}^2}{2{\eta}_2\rho \left(1-{\gamma}_2\right)}+\frac{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_9{\lambda}_1\right)\left({\pi}_2{\mu}_1+{a}_{10}{\lambda}_1\right)}{\rho {\eta}_1\left(1-{\gamma}_1-{\beta}_1\right)}$$

(132)

Appendix 6. Both firms pay additional incentive compensation to employed professional managers

The objective functions of the decisions of firm 1 and firm 2 are simplified as:

$$\underset{E_1}{\max }\ {J}_1={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_1w(t)-\frac{1}{2}{\eta}_1{\left({E}_1\right)}^2-{\gamma}_1\left({\pi}_1{W}_0-\frac{1}{2}{\eta}_1{\left({E}_2\right)}^2\right)-{\beta}_1\left({\pi}_1w(t)-\frac{1}{2}{\eta}_1{\left({E}_1\right)}^2\right)\right] dt$$

(133)

$$\underset{E_2}{\max }\ {J}_2={\int}_0^{\infty }{e}^{-\rho t}\left[{\pi}_2w(t)-\frac{1}{2}{\eta}_2{\left({E}_2\right)}^2-{\gamma}_2\left({\pi}_2{W}_0-\frac{1}{2}{\eta}_2{\left({E}_2\right)}^2\right)-{\beta}_2\left({\pi}_2w(t)-\frac{1}{2}{\eta}_2{\left({E}_2\right)}^2\right)\right] dt$$

(134)

To obtain the Markov-refined Nash equilibrium of the noncooperative game, we construct a continuous and bounded differential function, V₁₁(G), V₁₂(G), which satisfies the Hamilton-Jacobi-Bellman (HJB) equation for all G ≥ 0.

$$\rho V_{11}(G)=\displaystyle\max_{E_1}\left\{\begin{array}{l}\left(1-\beta_1\right)\pi_1\left.\left[w_0+\mu_1E_{11}(t)+\mu_2E_2(t)+\theta G(t)\right]\right)-\left(1-\gamma_1-\beta_1\right)\frac{\eta_1}2\left(E_1(t)\right)^2\\-\gamma_2\pi_1+W_0+V_{11}^{'}(G)\left[\lambda_1E_1(t)+\lambda_2E_2(t)-\delta G(t)\right]\end{array}\right\}$$

(135)

$$\rho V_{12}(G)=\displaystyle\max_{E_2}\left\{\begin{array}{l}\left(1-\beta_2\right)\pi_2\left.\left[w_0+\mu_1E_1(t)+\mu_2E_2(t)+\theta G(t)\right]\right)-\left(1-\gamma_2-\beta_2\right)\frac{\eta_2}2\left(E_2(t)\right)^2\\-\gamma_2\pi_2+W_0+V_{12}^{'}(G)\left[\lambda_1E_1(t)+\lambda_2E_2(t)-\delta G(t)\right]\end{array}\right\}$$

(136)

We solve the first-order partial derivative about E₁, E₂, respectively, on the right side of the HJB equation, set the first-order partial derivative equal to zero, and obtain the maximization condition:

$${\displaystyle \begin{array}{cc}{E}_1=\frac{\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{V}_{11}^{\prime }{\lambda}_1}{\eta_1\left(1-{\gamma}_1-{\beta}_1\right)}& {E}_2=\frac{\left(1-{\beta}_2\right){\pi}_2{\mu}_2+{V}_{12}^{\prime }{\lambda}_2}{\eta_2\left(1-{\gamma}_2-{\beta}_2\right)}\end{array}}$$

(137)

By substituting formula (138) into HJB equation (136), we can obtain (137):

$${\displaystyle \begin{array}{l}\rho {V}_{11}(G)=\left(1-{\gamma}_1-{\beta}_1\right){\pi}_1{W}_0+\left(\left(1-{\beta}_1\right){\pi}_1\theta -\delta {V}_{11}^{\prime}\right)G\\ {}+\frac{{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{V}_{11}^{\prime }{\lambda}_1\right)}^2}{2{\eta}_1\left(1-{\gamma}_1-{\beta}_1\right)}+\frac{{\left({\pi}_2{\mu}_2+{V}_{12}^{\prime }{\lambda}_2\right)}^2\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{V}_{11}^{\prime }{\lambda}_2\right)}{\eta_2}\end{array}}$$

(138)

$${\displaystyle \begin{array}{l}\rho {V}_{12}(G)=\left(1-{\gamma}_2-{\beta}_2\right){\pi}_2{W}_0+\left(\left(1-{\beta}_2\right){\pi}_2\theta -\delta {V}_{12}^{\prime}\right)G\\ {}+\frac{{\left(\left(1-{\beta}_2\right){\pi}_2{\mu}_2+{V}_{12}^{\prime }{\lambda}_2\right)}^2}{2{\eta}_2\left(1-{\gamma}_2-{\beta}_2\right)}+\frac{{\left({\pi}_1{\mu}_1+{V}_{11}^{\prime }{\lambda}_1\right)}^2\left(\left(1-{\beta}_1\right){\pi}_2{\mu}_1+{V}_{12}^{\prime }{\lambda}_1\right)}{\eta_1}\end{array}}$$

(139)

We assume that the expression of function V₁₁(G), V₁₂(G) is in linear form:

$${\displaystyle \begin{array}{cc}{V}_{11}(G)={a}_{11}G+{b}_{11}& {V}_{12}(G)={a}_{12}G+{b}_{12}\end{array}}$$

(140)

where a₁₁ b₁₁, a₁₂, and b₁₂ are constants.

$${\displaystyle \begin{array}{cc}{V}_{11}^{\prime }(G)={a}_{11}& {V}_{12}^{\prime }(G)={a}_{12}\end{array}}$$

(141)

By substituting formula (140) and formula (141) into formula (138), we can obtain formula (139):

$${\displaystyle \begin{array}{l}\rho \left({a}_{11}G+{b}_{11}\right)=\left(1-{\gamma}_1-{\beta}_1\right){\pi}_1{W}_0+\left(\left(1-{\beta}_1\right){\pi}_1\theta -\delta {a}_{11}\right)G\\ {}+\frac{{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_{11}{\lambda}_1\right)}^2}{2{\eta}_1\left(1-{\gamma}_1-{\beta}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{a}_{12}{\lambda}_2\right)\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{a}_{11}{\lambda}_2\right)}{\eta_2}\end{array}}$$

(142)

$${\displaystyle \begin{array}{l}\rho \left({a}_{12}G+{b}_{12}\right)=\left(1-{\gamma}_2-{\beta}_2\right){\pi}_2{W}_0+\left(\left(1-{\beta}_2\right){\pi}_2\theta -\delta {a}_{12}\right)G\\ {}+\frac{{\left(\left(1-{\beta}_2\right){\pi}_2{\mu}_2+{a}_{12}{\lambda}_2\right)}^2}{2{\eta}_2\left(1-{\gamma}_2-{\beta}_2\right)}+\frac{\left({\pi}_1{\mu}_1+{a}_{11}{\lambda}_1\right)\left(\left(1-{\beta}_2\right){\pi}_2{\mu}_1+{a}_{12}{\lambda}_1\right)}{\eta_1}\end{array}}$$

(143)

The linear equations about a₁₁, b₁₁, a₁₂, b₁₂ can be obtained, and the coefficients of the same terms at both ends of the equation can be obtained:

$${a}_{11}=\frac{\left(1-{\beta}_1\right){\pi}_1\theta }{\rho +\delta }$$

(144)

$${b}_{11}=\frac{\left(1-{\gamma}_1-{\beta}_1\right){\pi}_1{W}_0}{\rho }+\frac{{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_{11}{\lambda}_1\right)}^2}{2{\eta}_2\rho \left(1-{\gamma}_1-{\beta}_1\right)}+\frac{\left({\pi}_2{\mu}_2+{a}_{12}{\lambda}_2\right)\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{a}_{11}{\lambda}_2\right)}{\rho {\eta}_2}$$

(145)

$${a}_{12}=\frac{\left(1-{\beta}_2\right){\pi}_2\theta }{\rho +\delta }$$

(146)

$${b}_{12}=\frac{\left(1-{\gamma}_2-{\beta}_2\right){\pi}_2{W}_0}{\rho }+\frac{{\left(\left(1-{\beta}_2\right){\pi}_2{\mu}_2+{a}_{12}{\lambda}_2\right)}^2}{2{\eta}_2\rho \left(1-{\gamma}_2-{\beta}_2\right)}+\frac{\left({\pi}_1{\mu}_1+{a}_{11}{\lambda}_1\right)\left(\left(1-{\beta}_2\right){\pi}_2{\mu}_1+{a}_{12}{\lambda}_1\right)}{\rho {\eta}_1}$$

(147)

By substituting formulas (144)~(147) into formulas (137) and (140), respectively, we can obtain proposition 6.

Proposition 6

The Nash equilibrium solution when high-pollution firms 1 and 2 both employ professional managers and pay incentives is:

$${E}_1^{\ast \ast \ast \ast }=\frac{\left(1-{\beta}_1\right){\pi}_1\left({\mu}_1\rho +{\mu}_1\delta +\theta {\lambda}_1\right)}{\left(\rho +\delta \right){\eta}_1\left(1-{\gamma}_1-{\beta}_1\right)}$$

(148)

$${E}_2^{\ast \ast \ast \ast }=\frac{\left(1-{\beta}_1\right){\pi}_2\left({\mu}_2\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\left(\rho +\delta \right){\eta}_2\left(1-{\gamma}_2-{\beta}_2\right)}$$

(149)

The steady-state emissions reductions are:

$${G}_{\infty}^{\ast \ast \ast \ast \ast \ast }=\frac{\lambda_1{\pi}_1\left(1-{\beta}_1\right)\left({\mu}_1\rho +{\mu}_1\delta +\theta {\lambda}_1\right)}{\delta {\eta}_1\left(\rho +\delta \right)\left(1-{\gamma}_1-{\beta}_1\right)}+\frac{\lambda_2{\pi}_2\left(1-{\beta}_2\right)\left({\mu}_2\rho +{\mu}_2\delta +\theta {\lambda}_2\right)}{\delta {\eta}_2\left(\rho +\delta \right)\left(1-{\gamma}_2-{\beta}_2\right)}$$

(150)

Under this game equilibrium, the optimal income expressions of high-pollution firms 1 and 2 are as follows:

$${\displaystyle \begin{array}{l}{V}_{11}^{\ast }(G)=\frac{\left(1-{\beta}_1\right){\pi}_1\theta }{\rho +\delta }G+\frac{\left(1-{\beta}_1-{\gamma}_1\right){\pi}_1{W}_0}{\rho }+\frac{{\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_1+{a}_{11}{\lambda}_1\right)}^2}{2{\eta}_1\rho \left(1-{\gamma}_1-{\beta}_1\right)}\\ {}+\frac{\left({\pi}_2{\mu}_2+{a}_{12}{\lambda}_2\right)\left(\left(1-{\beta}_1\right){\pi}_1{\mu}_2+{a}_{11}{\lambda}_2\right)}{\rho {\eta}_2}\end{array}}$$

(151)

$${\displaystyle \begin{array}{l}{V}_{12}^{\ast }(G)=\frac{\left(1-{\beta}_2\right){\pi}_2\theta }{\rho +\delta }G+\frac{\left(1-{\beta}_2-{\gamma}_2\right){\pi}_2{W}_0}{\rho }+\frac{{\left(\left(1-{\beta}_2\right){\pi}_2{\mu}_2+{a}_{12}{\lambda}_2\right)}^2}{2{\eta}_1\rho \left(1-{\gamma}_2-{\beta}_2\right)}\\ {}+\frac{\left({\pi}_1{\mu}_1+{a}_{11}{\lambda}_1\right)\left(1-{\beta}_2\right)\left({\pi}_2{\mu}_1+{a}_{12}{\lambda}_1\right)}{\rho {\eta}_1}\end{array}}$$

(152)