SpringerLink
Log in

Determination of Stress Intensity Factor KIII for Three-Dimensional Crack by Using Caustic Method in Combination with Stress-Freezing and Stress-Releasing Technique

  • Published:
Experimental Mechanics Aims and scope Submit manuscript

Abstract

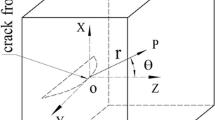
In this paper, an experimental technique to determine the stress intensity factor KIII for three-dimensional cracks using the method of reflected caustics in combination with the photoelastic stress-freezing and stress-releasing techniques is presented. The experimental model is a cylindrical bar with a three-dimensional surface crack under a load of pure torsion. To obtain the caustic pattern, a slice cut from the frozen model is annealed to release the frozen-stress. The results of this experimental method coincide favorably with the theoretical analysis results of Tweed and Rooke. Moreover, the mixed-mode stress intensity factors KII and KIII of the three-dimensional crack are separately determined using the photoelastic and caustic methods. By using the present experimental technique, the mixed-mode stress intensity factors KII and KIII for a three-dimensional crack are found to be easily separated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

References

  1. Manogg P (1964) Schattenoptische Messung der spezifischen Bruchenergie während des Bruchvorgangs bei Plexiglas. Proocedings of the International Conference on the Physics of Non-Crystalline Solids. Delft, The Netherlands, pp 481–490

  2. Theocaris PS, Joakimides N (1971) Some properties of generalized epicycloids applied to fracture mechanics. Z Angew Math Phys 22(5):876–890

    Article  MATH  Google Scholar 

  3. Theocaris PS, Gdoutos E (1972) An optical method for determining of opening-mode and edge sliding-mode stress intensity factors. J Appl Mech 39(1):91–97

    Article  Google Scholar 

  4. Theocaris PS (1981) Elastic stress intensity factors evaluated by caustics. Mech Fract 7:189–252

    Google Scholar 

  5. Beinert J, Kalthoff JF (1981) Experimental determination of dynamic stress intensity factors by shadow patterns. Mech Fract 7:281–330

    Google Scholar 

  6. Rosakis AJ, Ma CC, Freund LB (1983) Analysis of the optical shadow spot method for a tensile crack in a power-law hardening material. J Appl Mech 50(4a):777–782

    Article  Google Scholar 

  7. Theocaris PS, Razem C (1977) Deformed boundaries determined by the method of caustics. J Stain Anal Eng Des 12(3):223–232

    Article  Google Scholar 

  8. Theocaris PS, Papadopoulos GA (1981) Stress intensity factors from reflected caustics in birefringent plates with cracks. J Stain Anal Eng Des 16(1):29–36

    Article  Google Scholar 

  9. Baik MC, Choi SH, Hawong JS, Kwon JD (1995) Determination of stress-intensity factors by the method of caustics in anisotropic materials. Exp Mech 35(2):137–143

    Article  Google Scholar 

  10. Semenski D (1997) Method of caustics in fracture mechanics of mechanically anisotropic materials. Eng Fract Mech 58(1-2):1–10

    Article  Google Scholar 

  11. Rosakis AJ, Freund LB (1982) Optical measurement of the plastic strain concentration at a crack tip in a ductile steel plate. J Eng Mater Technol 104(2):115–120

    Article  Google Scholar 

  12. Meyn DA (1989) Hydrogen-assisted cracking studies of 4340 steel by using the optical method of caustics. Eng Fract Mech 33(6):913–925

    Article  MathSciNet  Google Scholar 

  13. Theocaris PS (1971) Reflected shadow method for the study of constrained zones in cracked plates. Appl Opt 10(10):2240–2247

    Article  Google Scholar 

  14. Rossmanith HP (1979) Determination of stress intensity factors by the dynamic method of caustics for optically isotropic materials. Ing Arch 48(6):363–381

    Article  MATH  Google Scholar 

  15. Badalouka BG, Papadopoulos GA (2012) Experimental evaluation of the plastic zone at crack tip by caustics. Open Mech Eng J 6:83–89

    Article  Google Scholar 

  16. Can T (2014) Experimental investigation of the fiber bundle shielding effect on the dynamic matrix crack using optical caustic method. Polym Test 40:46–53

    Article  Google Scholar 

  17. Yang RS (2009) Dynamic fracture behavior of rock under impact load using the caustics method. Min Sci Technol 19(1):79–83

    Google Scholar 

  18. Theocaris PS (1981) The reflected caustics method for the evaluation of mode III stress intensity factor. Int J Mech Sci 23(2):105–117

    Article  MATH  Google Scholar 

  19. Taudou C, Ravi-Chandar K (1992) Experimental determination of the dynamic stress intensity factor using caustics and photoelasticity. Exp Mech 32(3):203–210

    Article  Google Scholar 

  20. Yazdanmehr A, Soltani N (2014) Evaluation of stress intensity factors of rounded V and U notches under mixed mode loading, using the experimental method of caustics. Theor Appl Fract Mech 74:79–85

    Article  Google Scholar 

  21. Raftopoulos DD, Farahmand B (1982) An investigation of stress intensity factors for plates with equal and unequal parallel edge cracks. Int J Fract 20(3):223–239

    Article  Google Scholar 

  22. Rosakis AJ, Ravi-Chandar K (1986) On crack-tip stress state: an experimental evaluation of three-dimensional effects. Int J Solids Struct 22(2):121–134

    Article  Google Scholar 

  23. Yao Jianchu, Chu Kunliang (1988) A study of three-dimensional cracked-body problems by caustics. Proceedings of the international conference on advanced experimental mechanics, pp 153–158

  24. Lai ZM, Sun P (1983) Photoelastic determination of mixed mode stress intensity factor KI KII and KIII. Exp Mech 23(2):228–235

    Article  Google Scholar 

  25. Theocaris PS, Georgiadis HG (1984) Mode III stress-intensity factors in cracked orthotropic plates—an analogy with propagating cracks in isotropic media. Exp Mech 24(3):177–183

    Article  Google Scholar 

  26. Kalthoff JF (1987) The shadow optical method of caustics. In: Static and dynamic photoelasticity and caustics, pp 407–522

  27. Tweed J, Rooke DP (1972) The torsion of a circular cylinder containing a symmetric array of edge cracks. Int J Eng Sci 10(9):801–812

    Article  MATH  Google Scholar 

  28. Rooke DP, Cartwright DJ (1976) Compendium of stress intensity factors. Her Majesty’s Stationery Office, London

    Google Scholar 

  29. Sih GC (1981) Mechanics of fracture. Martinus Nijhoff Publishers, The Hague/ Boston/ London

  30. Katsuhiko W, Toshiaki H, Yasuo H, Hideo K (1978) Photoelastic analyses of three-dimensional crack problems by newly-developed method presenting accurate solution. Trans Jpn Soc Mech Eng 44(388):4040–4051

    Article  Google Scholar 

  31. Sih GC (1973) Methods of analysis and solutions of crack problem. Noordhoff International Publishing, Leyden

    Book  Google Scholar 

  32. Ramesh K, Gupta S, Akelkar A (1997) Evaluation of stress field parameters in fracture mechanics by photoelasticity-revisited. Eng Fract Mech 56(1):25–45

    Article  Google Scholar 

Download references

Acknowledgments

The authors thank the National Natural Science Foundation of China (No. 11427802 and No. 11172026) and the Specialized Research Fund for the Doctoral Program of Higher Education (No. 20131102110014) for their supports.

Author information

Authors and Affiliations

  1. School of Aeronautic Science and Engineering, Bei**g University of Aeronautics and Astronautics, Bei**g, 100191, China

    D. F. Wu, L. Shang, Y. Pu & H. T. Wang

Authors
  1. D. F. Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L. Shang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Y. Pu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. H. T. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. F. Wu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, D.F., Shang, L., Pu, Y. et al. Determination of Stress Intensity Factor KIII for Three-Dimensional Crack by Using Caustic Method in Combination with Stress-Freezing and Stress-Releasing Technique. Exp Mech 56, 463–474 (2016). https://doi.org/10.1007/s11340-015-0113-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11340-015-0113-2

Keyword

Search

Navigation