Improvement of SWIPT Relaying System Performance Under the Interference Environment

Abstract

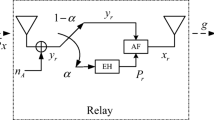
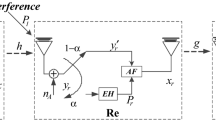
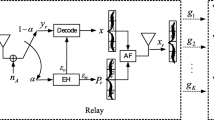
Based on the simultaneous wireless information and power transfer, this paper investigates an amplify-and-forward relaying system. It is assumed that the system works in an environment with the interference, and the system cannot implement the normal information transmission (IT) when the interference reaches a certain level. We analyze the system rate in this environment, and propose the scheme to improve the system rate. First, we divide the communication process of the system into two periods: the interference period (IP) and the communication period (CP). In the IP, the energy-constrained relay harvests the energy of the radio frequency signals received during this period and stores the energy into its energy storage till the interference ends. Then, in the CP, the relay allocates the energy of its energy storage to the blocks of the communication process, and the system performs the normal communication process. According to the principle of power splitting, the blocks that are allocated energy can reduce the signal stream proportion of the energy harvesting mode and increase the signal stream proportion of the IT mode. Thus the system rate is improved. We discuss two kinds of energy allocation scheme of the relay. Through strict formula derivation, we prove that the proposed average-energy-allocation (AEA) scheme can maximize the system rate. In addition, through numerical simulation, we observe the influence of the AEA scheme on the system rate, and compare the effect of with/without the AEA scheme on the system rate when changing two system parameters. The results show that the proposed AEA scheme can effectively improve the relaying system rate under the interference channel.

Appendix

Notation$f^{1} (x)\left| {_{x} } \right.$ represents the first-order derivative of $f(x)$ with respect to $x$; $f^{2} (x)\left| {_{x} } \right.$ denotes the second-order derivative of $f(x)$ with respect to $x$. It is important to point out that $\rho \in [0,1)$, $\rho_{1}^{*} \in [0,1)$, $\rho_{2}^{*} \in (0,1)$, and $\rho_{3}^{*} \in [0,1)$ hold in the following discussion.

For (21), $R^{ *}$ can be regarded as a function of $\beta$, $R^{ *} (\beta )$. We can observe that $R^{ *} (\beta \to 1^{ + } ) =$$R^{*} (\beta \to 1^{ - } )$ ,i.e., the left limit of $R^{*} (\beta )$ at $\beta { = }1$ is equal to the right limit, namely, $R^{*} (\beta )$ is continuous at $\beta = 1$. Therefore, if we can prove that, when $0 < \beta < 1$, $R^{*} (\beta )$ increases monotonically as $\beta$ increases; when $\beta \ge 1$, $R^{*} (\beta )$ decreases monotonically as $\beta$ increases, $\beta = 1$ is the optimal solution of $R^{*} (\beta )$. The two cases are shown separately as follows.

a. Case of $0 < \beta < 1$

$$R_{0 < \beta < 1} { = }\frac{1}{1 + \xi }\left( \begin{aligned} & \beta \log_{2} \left( {1 + \frac{{\left( {1 - \rho_{1}^{*} } \right)hgP}}{{\left( {1 - \rho_{1}^{*} } \right)g\sigma_{A}^{2} + g\sigma_{P}^{2} + \frac{{\left( {\left( {1 - \rho_{1}^{*} } \right)\left( {hP + \sigma_{A}^{2} } \right) + \sigma_{P}^{2} } \right)\sigma_{R}^{2} }}{{\eta \left( {h\rho_{1}^{*} P + \lambda } \right)}}}}} \right) \\ & \quad + \left( {1 - \beta } \right)\log_{2} \left( {1 + \frac{{\left( {1 - \rho_{2}^{*} } \right)hgP}}{{\left( {1 - \rho_{2}^{*} } \right)g\sigma_{A}^{2} + g\sigma_{P}^{2} + \frac{{\left( {\left( {1 - \rho_{2}^{*} } \right)\left( {hP + \sigma_{A}^{2} } \right) + \sigma_{P}^{2} } \right)\sigma_{R}^{2} }}{{\eta h\rho_{2}^{*} P}}}}} \right) \\ \end{aligned} \right)$$

(22)

$$r^{1} (\rho ,\lambda )\left| {_{\lambda } } \right. = \frac{ac\eta }{\ln 2} \cdot \frac{1}{{\left( {(a + b)d + c + (a + b)\eta \lambda } \right)\left( {bd + c + b\eta \lambda } \right)}}$$

(23)

$$r^{2} (\rho ,\lambda )\left| {_{\lambda } } \right. = \frac{ac\eta }{\ln 2} \cdot \left( {\frac{{ - \left( {\left( {a + b} \right)\eta \cdot \left( {bd + c + b\eta \lambda } \right) + b\eta \cdot \left( {\left( {a + b} \right)d + c + \left( {a + b} \right)\eta \lambda } \right)} \right)}}{{\left( {\left( {\left( {a + b} \right)d + c + \left( {a + b} \right)\eta \lambda } \right)\left( {bd + c + b\eta \lambda } \right)} \right)^{2} }}} \right)$$

(24)

When $0 < \beta < 1$, $R^{*} (\beta )$ is expressed as (19). An auxiliary variable $\lambda = {{\xi P_{I} } \mathord{\left/ {\vphantom {{\xi P_{I} } \beta }} \right. \kern-0pt} \beta }$ is introduced so that $R_{0 < \beta < 1}^{*}$ can be rewritten as (22), shown at the bottom of this page.

An auxiliary function $r(\rho ,\lambda )$ is defined as

$$r(\rho ,\lambda ) = log_{2} \left( {1 + \frac{a}{{b + \frac{c}{d + \eta \lambda }}}} \right)$$

(25)

where $a,b,c,d$ is the function of $\rho$, and $a = (1 - \rho )hgP > 0$, $b = (1 - \rho )g\sigma_{A}^{2} + g\sigma_{P}^{2} > 0$, $c = \left( {(1 - \rho )(hP + \sigma_{A}^{2} ) + \sigma_{P}^{2} } \right)\sigma_{R}^{2} > 0$, $d = \eta h\rho P > 0$.

Taking the first-order and second-order derivatives of $r(\rho ,\lambda )$ with respect to $\lambda$, we obtain (23) and (24), shown at the bottom of this page. We can observe that,for any $\lambda > 0$ , $r^{1} (\rho ,\lambda )\left| {_{\lambda } } \right. > 0$ and $r^{2} (\rho ,\lambda )\left| {_{\lambda } } \right. < 0$.

According to the auxiliary function, $R_{0 < \beta < 1}^{*}$ can be rewritten as

$$R_{0 < \beta < 1}^{*} = \frac{1}{1 + \xi }\left( {\beta \cdot r(\rho_{1}^{*} ,\lambda ){ + }(1 - \beta ) \cdot r(\rho_{2}^{*} ,0)} \right)$$

(26)

Taking the first-order derivative of $R_{0 < \beta < 1}^{*}$ with respect to $\beta$, we have

$$R_{{_{0 < \beta < 1} }}^{ * ,\, 1} \left| {_{\beta } } \right.{ = }\frac{1}{1 + \xi }\left( {r(\rho_{1}^{*} ,\lambda ) - \lambda \cdot r^{1} (\rho_{1}^{*} ,\lambda )\left| {_{\lambda } } \right. - r(\rho_{2}^{*} ,0)} \right)$$

(27)

We introduce the auxiliary function defined as

$$s(\lambda ) = r(\rho_{1}^{*} ,\lambda ) - \lambda \cdot r^{1} (\rho_{1}^{*} ,\lambda )\left| {_{\lambda } } \right. - r(\rho_{2}^{*} ,0)$$

(28)

The derivation of (28) is

$$s^{1} (\lambda )\left| {_{\lambda } } \right. = - \lambda \cdot r^{2} (\rho_{1}^{*} ,\lambda )\left| {_{\lambda } } \right.$$

(29)

For any $\lambda > 0$, $r^{2} (\rho ,\lambda )\left| {_{\lambda } } \right. < 0$, so $s^{1} (\lambda )\left| {_{\lambda } } \right. > 0$ and $s(\lambda )$ monotonically increasing. In mathematics, when $\lambda = 0$, we have $R_{1}^{*} = R_{2}^{*}$, $\rho_{1}^{*} = \rho_{2}^{*}$, and, from (28),

$$s(0) = r(\rho_{1}^{*} ,0) - r(\rho_{2}^{*} ,0) = 0$$

(30)

Consequently, for any $\lambda > 0$, $s(\lambda ) > 0$ and $R_{0 < \beta < 1}^{*, \, 1} \left| {_{\beta } } \right. > 0$, and then $R_{0 < \beta < 1}^{*}$ is monotonically increasing for any $\beta \in \left( {0,1} \right)$.

b. Case of $\beta \ge 1$

When $\beta \ge 1$, $R^{*} (\beta )$ is expressed as (20). Similarly, we can obtain

$$R_{\beta \ge 1}^{*} = \frac{{r(\rho_{3}^{*} ,\lambda )}}{1 + \xi }$$

(31)

Taking the first-order derivative of $R_{\beta \ge 1}^{*}$ with respect to $\beta$, we have

$$R_{{_{\beta \ge 1} }}^{ * ,\, 1} \left| {_{\beta } } \right. = - \frac{\lambda }{\beta (1 + \xi )}r^{1} (\rho_{3}^{*} ,\lambda )\left| {_{\lambda } } \right.$$

(32)

For any $\lambda > 0$, $r^{1} (\rho_{3}^{ *} ,\lambda )\left| {_{\lambda } } \right. > 0$, so we have $R_{{_{\beta \ge 1} }}^{ * ,\, 1} \left| {_{\beta } } \right. < 0$. As a result, $R_{\beta \ge 1}^{*}$ decreases monotonically for any $\beta \ge 1$.

To sum up, $R^{*} (\beta )$ is monotonically increasing for any $\beta \in \left( {0,1} \right)$, and monotonically decreasing for any $\beta \ge 1$, and $R^{*} (\beta )$ is continuous at the point $\beta { = }1$, so $\beta { = }1$ is the optimal solution of $R^{*} (\beta )$.