Learned Anomaly Detection with Terahertz Radiation in Inline Process Monitoring

Abstract

Terahertz tomographic imaging as well as machine learning tasks represent two emerging fields in the area of nondestructive testing. Detecting outliers in measurements that are caused by defects is the main challenge in inline process monitoring. An efficient inline control enables to intervene directly during the manufacturing process and, consequently, to reduce product discard. We focus on plastics and ceramics, for which terahertz radiation is perfectly suited because of its characteristics, and propose a density based technique to automatically detect anomalies in the measured radiation data. The algorithm relies on a classification method based on machine learning. For a verification, supervised data are generated by a measuring system that approximates an inline process. The experimental results show that the use of terahertz radiation, combined with the classification algorithm, has great potential for a real inline manufacturing process. In a further investigation additional data are simulated to enlarge the data set, especially the variety of defects. We model the propagation of terahertz radiation by means of the Eikonal equation.

1 Introduction

Terahertz (THz) radiation is a part of the electromagnetic spectrum with wavelengths between 30 µm to $3\;\mathrm {mm}$. The corresponding frequencies from 0.1 to $10\;\mathrm {THz}$ are located between microwaves and infrared radiation. Due to the special position in the electromagnetic spectrum, THz radiation is characterized by ray and wave character. It is possible to obtain information about the amplitude from measurements of the absorption of the radiation whereas the phase can be identified using time-of-flight measurements. The radiation is non-ionizing and therefore not dangerous to health. It can penetrate many materials, especially non-conductive ones such as many ceramics, does not require a medium to couple with [7] and is thus used as a non-contact technique. Furthermore, the radiation achieves a better resolution compared to microwaves because of its shorter wavelength [21]. In spite of this wide range of advantages the so called ’THz gap’, referring to a lack of effective transducer and detectors [29, 30], prevented an extensive application. This gap has only recently been closed. Until a few years ago the costs were not yet competitive, but during the last three decades the technique has improved and the high costs have been reduced [5]. The field of THz inspection has expanded rapidly and has nowadays the chance to compete with X-ray, ultrasonic and microwaves. Consequently, THz radiation has become an interesting and powerful tool for many applications. The radiation is utilized, for example, in body scanners for security purposes [27], car painting control, composite materials and for the pharmaceutical industry [29]. In particular, the radiation receives increasing attention in the field of nondestructive testings (NDT), where many techniques have been adopted and adapted from competing technologies like computerized tomography (CT) or ultrasound [12, 25, 28, 30]. While we observe a fast progress in the offline control of NDT, THz systems are currently too slow for inline inspection, and hence only a few selected applications were demonstrated in the past. Recommendations indicate that the systems have to treble their acquisition speed [5]. This is especially relevant for the surveillance of the inline manufacturing, where defects such as cracks, voids and inclusions are mostly produced in the course of the process [29]. To avoid short-cycle products and to be able to intervene directly, a fast and reliable method to evaluate THz radiation data is necessary. First investigations of a contactless and nondestructive inline control with THz radiation, for instance, were shown in [16]. An overview of THz tomography techniques is presented by Guillet et al. [10].

A second emerging field in the last years, driven by increasing computer power, are machine learning (ML) techniques. ML is a subsection of artificial intelligence (AI) and includes many algorithms and techniques like regression, classification, and prediction, or deep learning (DL) [9, 13]. Generally speaking, an ML algorithm is trained by observing large data sets, which refers to the learning process, in order to be able to make predictions from unobserved data. One usually distinguishes between supervised and unsupervised learning. In the supervised context, algorithms learn from pairs of labeled input and output data [11], whereas unsupervised learning is able to cope with unlabeled data. Such trained algorithms are thus able to interpret structure or statistical properties of data sets, and they have become the most powerful tool for data analysis. Applications can in particular be found in almost all sectors of industry and economy (see [22] or [17]).

In our work, we evaluate measurements of THz radiation scans from an inline process with an ML technique called anomaly detection (AD) in order to test its applicability in inline monitoring, and, more precisely, the detection of defects in the product. An example is the extrusion of plastics, which are particularly suited for THz radiation-based testing techniques [7]. The algorithm is based on learning a multivariate Gaussian distribution that reflects the properties of measurement data. Considering the definition of an anomaly as a significant variation from typical values [19], the detection of such outliers is perfectly suited for our targeted application: We aim to detect defects and deviations in an inline manufacturing process of plastics from their impact on the measured data. In a first study we use training data from a real-time measurement generated by a measuring system that approximates an inline process. We obtain a large set of data encoding intensity, refraction and reflection and temporal information. These supervised data are used for learning whether an inline measurement lies inside a certain norm and, subsequently, for detecting deviations from this norm. To complete our investigation, we test our AD algorithm on an unknown object. In a second step, we restrict ourselves to a single feature that encompasses temporal information. Importantly, we include simulated data from a suitable mathematical model in order to enlarge our set of data for this feature without conducting further time-consuming measurements, and to simulate the diversity of defects. For this purpose, we introduce the Eikonal equation to calculate time-of-flight data. Finally, we compare the AD trained on the hybrid data set with the AD just based on non-simulated data.

The article is structured as follows: In Sect. 2 we introduce the basics for AD as well as the resulting algorithm. The THz measuring system as well as the measured data are discussed in Sect. 3. In Sect. 4, we present our numerical results for purely measured data sets. Our model-based data set augmentation strategy is explained and evaluated in Sect. 5, and our findings are summarized and discussed in Sect. 6. This article is further development of the research done in [20].

2 A Classification Algorithm for Inline Monitoring

The idea of AD to trigger alarm if a measurement is inconsistent with the expected behavior is a typical ML task. Applications can be found in fields like fraud detection, insurance, health care and cyber security [2], or, as in our case, in the monitoring of an inline manufacturing process. The starting point of the algorithm is a set of training data $\{x^{(1)},x^{(2)},\ldots ,x^{(m)} \}\subset \mathbb {R}^n$. We assume that the training set contains only measurements from an intact object. Each single data point consists of n attributes, called features, which are represented by real numbers. Assuming that the data $x^{(i)}$ are realizations of a real-valued random variable with probability density function p(x), it is appropriate to identify typical data from intact objects with large values $p(x^{(i)})$, whereas anomalies can be characterized by small values $p(x^{(i)})$. For a given training data set, we first estimate a probability density function $p: \mathbb {R}^n\rightarrow \mathbb {R}$. Subsequently, we decide, depending on a threshold parameter $\epsilon ^*$, whether a new data point $x_{\mathrm {test}}$ is an anomaly or not. The threshold parameter is also learned. For this purpose, we use a cross validation set and a decision function. The algorithm is inspired by [18, 26].

In order to estimate the probability density function p, we assume that the data and, more precisely, its features follow a Gaussian distribution, which is on the one hand motivated by our own measured data, see Fig. 4, on the other hand it is a common procedure to describe the scattering of measurements as normally distributed, see [6].

By using a univariate set of data ($n=1$) with $x^{(i)}\in \mathbb {R}$ as a realization of an $\mathcal {N}(\mu , \sigma ^2)$-distributed random variable X with mean $\mu \in \mathbb {R}$ and variance $\sigma ^2\in \mathbb {R}$, we receive the probability density function of the univariate Gaussian distribution

$$\begin{aligned} p(x;\mu ,\sigma ^2) = \frac{1}{\sqrt{2\pi }\sigma }e^{-\frac{(x-\mu )^2}{2\sigma ^2}}. \end{aligned}$$

(2.1)

The parameters $\mu$ and $\sigma ^2$ are estimated by the training data using the formulas

$$\begin{aligned} \mu = \frac{1}{m}\sum _{i=1}^m x^{(i)} \;\;\; \text {and} \;\;\; \sigma ^2 = \frac{1}{m}\sum _{i=1}^m (x^{(i)}-\mu )^2. \end{aligned}$$

In case of a multivariate set of data $x^{(i)}\in \mathbb {R}^n$ ($n>1$) as a realization of an $\mathcal {N}(\mu , \Sigma )$-distributed random variable X we compute the expected value $\mu \in \mathbb {R}^n$ and the covariance matrix $\Sigma \in \mathbb {R}^{n\times n}$, obtaining the probability density function of the multivariate Gaussian distribution

$$\begin{aligned} p(x;\mu ,\Sigma ) = \frac{1}{(2\pi )^{\frac{n}{2}}|\Sigma |^{\frac{1}{2}}}e^{-\frac{1}{2}(x-\mu )^T\Sigma ^{-1}(x-\mu )} \end{aligned}$$

(2.2)

with

$$\begin{aligned} \mu = \frac{1}{m}\sum _{i=1}^m x^{(i)} \;\;\; \text {and} \;\;\; \Sigma = \frac{1}{m}\sum _{i=1}^m (x^{(i)}-\mu )(x^{(i)}-\mu )^T, \end{aligned}$$

(2.3)

where $|\Sigma |$ represents the determinant of $\Sigma$. The inverse of a matrix A is indicated by $A^{-1}$, its transpose by $A^T$.

In a second step, we learn the threshold parameter $\epsilon ^*$. To this end we need a labeled cross validation set

$$\begin{aligned} \left\{ (x_{\mathrm {CV}}^{(1)},y_{\mathrm {CV}}^{(1)}),(x_{\mathrm {CV}}^{(2)},y_{\mathrm {CV}}^{(2)}),\ldots ,(x_{\mathrm {CV}}^{(l)},y_{\mathrm {CV}}^{(l)})\right\} \subset \mathbb {R}^n\times \{0,1\}, \quad l \in \mathbb {N}, \end{aligned}$$

with labels $y_{\mathrm {CV}}^{(i)}\in \{0,1\}$, where $y_{\mathrm {CV}}^{(i)}=1$ means that $x_{\mathrm {CV}}^{(i)}$ is anomalous, whereas $y_{\mathrm {CV}}^{(i)}=0$ indicates a defect-free measurement $x_{\mathrm {CV}}^{(i)}$. For any $\epsilon \ge 0$ we compute the decision function f by

$$\begin{aligned} f\big (x_{CV}^{(i)},\epsilon \big ) = {\left\{ \begin{array}{ll} 1,\;\; \text {if}\;\;p\big (x_{CV}^{(i)};\mu ,\Sigma \big ) < \epsilon \\ 0,\;\; \text {otherwise}, \end{array}\right. } \qquad i=1,\ldots ,l. \end{aligned}$$

(2.4)

By means of f we compute the confusion matrix

$$\begin{aligned} \mathbf {C} = \left( \begin{array}{cc} TP &{} FP \\ FN &{} TN \end{array} \right) \in \mathbb {N}^{2\times 2} \end{aligned}$$

for a fixed threshold parameter $\epsilon$, where the entries represent the number of data points correctly labeled as positive (true positives, TP), data points falsely labeled as positive (false positives, FP), data points correctly labeled as negative (true negatives, TN), and data points incorrectly labeled as negative (false negatives, FN) (cf. [4]). The confusion matrix $\mathbf {C}$ characterizes the quality of the classification given $\epsilon$ and ideally resembles a diagonal matrix. From its entries we deduce the two values $\mathrm {prec}=\mathrm {prec}(\epsilon )$ (precision) and $\mathrm {rec}=\mathrm {rec}(\epsilon )$ (recall), which both depend on the threshold $\epsilon$, by

$$\begin{aligned} \mathrm {prec} = \frac{TP}{TP+FP}\;\;\; \text {and}\;\;\; \mathrm {rec} = \frac{TP}{TP+FN}. \end{aligned}$$

If the classifier works accurately, we have $\mathrm {prec} = \mathrm {rec} = 1$, and it performs poorly if both values are close to zero. Finally we compute the $F_1$-score $F_1 (\epsilon )$ as the harmonic mean of $\mathrm {prec}$ and $\mathrm {rec}$,

$$\begin{aligned} F_1 (\epsilon ) = 2\,\frac{\mathrm {prec} \cdot \mathrm {rec}}{\mathrm {prec} + \mathrm {rec}}. \end{aligned}$$

(2.5)

The threshold $\epsilon ^*$ is then determined as the value maximizing the $F_1$-Score,

$$\begin{aligned} \epsilon ^* := \arg \max _{\epsilon \in [0,p_{\max }]} F_1 (\epsilon ). \end{aligned}$$

(2.6)

Here, the parameter $p_{\max }$ represents the maximum value of the probability density function p. We iterate through the interval $[0,p_{\max }]$ with a given step size and take the value of $\epsilon$ resulting in the highest $F_1$-score as the maximizer. We choose the number of grid points depending on $p_{\max }$.

Finally we evaluate the algorithm by means of a test set

$$\begin{aligned} \left\{ (x_{\mathrm {test}}^{(1)},y_{\mathrm {test}}^{(1)}),(x_{\mathrm {test}}^{(2)},y_{\mathrm {test}}^{(2)}),\ldots ,(x_{\mathrm {test}}^{(l)},y_{\mathrm {test}}^{(l)})\right\} \subset \mathbb {R}^n\times \{0,1\}. \end{aligned}$$

The test set usually consists of measured and, if it is possible, of simulated data, and contains as many normal and anomalous data as the cross validation set. If the evaluation fails, then the set of training data should be enhanced by acquiring more measurement data or adding simulated data. After the parameters have been learned, a classification can be used to indicate whether an irregularity exists for an unknown data set: If the value of the probability density function falls below the optimal threshold parameter $\epsilon ^*$, then the inline process should be intervened. A summary of the density-based AD and classification algorithm is given by Algorithm 1.

3 The THz Measuring System and the Data Set

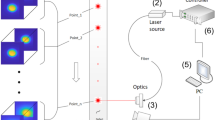
The THz measuring system that simulates the procedure of an inline monitoring process for our studies has been set up at the Plastics Center (SKZ) in Würzburg, Germany. All real measured data used for our AD algorithm have been recorded at the SKZ, the system is displayed in Fig. 2. The emitter and the receivers are placed on a turntable which rotates around the object under investigation. It is possible to shift the turntable vertically, while at the same time the observed object is fixed. The emitter sends electromagnetic radiation of a frequency between 0.12 and 0.17 THz and, simultaneously, measures reflection data. One receiver is located opposite the emitter to register deviations in the transmission process. A second one is placed close to the first one to collect information on the refraction of the radiation. Figure 1 illustrates this setup of the actual THz tomograph from Fig. 2. We receive data $x^{(i[k,z])}$, $k=1,\ldots ,K$, $z=1,\ldots ,Z$, for the two-dimensional slice of the object in step k, in which a complete $360^\circ$ rotation in Z steps of the measuring system is performed; the entire three-dimensional object is then scanned by shifting the measuring system in K steps, such that we obtain K scans of slices of the object.

During an inline process, however, the emitter—and accordingly the receivers—describe a slightly different trajectory. For example, in an extrusion process, the material moves through a horizontally and vertically fixed measuring system that rotates around the object. Since the investigated object continuously moves through the measuring system instead of step-wise, the measuring system moves on a helical trajectory relative to the object. In this case, we thus acquire 3D data, but since the object is not shifted but moved along, there are only few data points per slice.

Fig. 1

Schematic THz tomograph

Fig. 2

THz tomography system at the Plastics Center (SKZ) in Würzburg

For our investigations we used solid pipes made of polyethylene with a diameter of 10 cm and various lengths. The material has a refractive index of about $n=1.53$ and an absorption coefficient of about $\alpha =0.06\;\mathrm {cm}^{-1}$. After scanning the pipes without defects, we manufactured horizontal and vertical holes in some pipes to generate defects. Furthermore, we filled some holes with materials like oil and metal. This way we obtain a data set consisting of 220400 measurements from intact samples and 105965 anomalous data points from defect samples. We split it into three subsets: a training set, a cross validation set and a test set. The cross validation set and the test set each are composed of $50\%$ of the anomalous data and $20\%$ of the typical data, while the training set just includes $60\%$ of the unaffected elements. One single data point $x^{(i)} = x^{(i[k,z])}$ is composed of five features: In each position [k, z], where $k=1,\ldots ,K$ refers to the shift and $z=1,\ldots ,Z$ to the angle position, the receivers $R_1$ and $R_3$ measure absorption and phase information, while receiver $R_2$ only registers the absorption information since no reference signal is available that is required for the phase information. Figure 3 illustrates a measured horizontal shift (i.e., the phase shift) and a vertical shift (i.e., the absorption loss) of the amplitude (red) compared to the reference signal (blue).

Fig. 3

Horizontal and vertical shift of the amplitude [24]

Figure 4 shows the distribution of a normal set of data measured by the receiver $R_1$ opposite the emitter. We see that, indeed, the measurements resemble a Gaussian distribution concerning both the absorption data as well as the phase shifts. We find similar results for receiver $R_3$ and receiver $R_2$, whereas the latter only provides useful data about the amplitude due to the lacking reference signal from the calibration measurement, where refraction does not occur.

Fig. 4

Distribution of the measured data in transmission

We work with the $K\times Z$-matrices represented in Fig. 5. The angle position is illustrated on the x-axis, while the vertical shift is shown on the y-axis. In the case shown, $Z=380$ measurements are made per rotation and the system is shifted in $K=120$ steps of $1\;\mathrm {mm}$. We see a time-of-flight measurement of the receiver opposite the emitter illustrated by the path difference on the left side and its amplitude ratio an the right side.

Fig. 5

Data points of a normal solid pipe in transmission

4 Numerical Results

In this section, we present the computational results of our investigations. By using the data set described in Sect. 3, we evaluate the algorithm and, more generally, determine whether the application of terahertz radiation for the inline monitoring of plastics is suitable. Based on this, we investigate an unknown pipe with the learned algorithm to resolve the locations of the defects. We use the software MATLAB for the implementation.

By including the measured values of receivers $R_1$, $R_2$ and $R_3$, we integrate information about transmission, reflection and refraction, respectively, of the terahertz radiation in our setting. The multivariate Gaussian distribution is estimated as

$$\begin{aligned} p(x;\mu ,\Sigma ) = \frac{1}{(2\pi )^{\frac{5}{2}} |\Sigma |^{\frac{1}{2}}}\mathrm {e}^{-\frac{1}{2}(x-\mu )^T\Sigma ^{-1}(x-\mu )} \end{aligned}$$

with

$$\begin{aligned} \mu = \left( \begin{array}{c} 53.601002 \\ \ 1.015691 \\ \ 0.139608 \\ \ 0.010417 \\ \ 83.159275 \end{array}\right) ,\;\Sigma = \left( \begin{array}{rrrrr} 0.258068 &{} -0.012679 &{} 0.003472 &{} 0.000218 &{} -0.355831 \\ -0.012679 &{} 0.001625 &{} -0.000057 &{} -0.000001 &{} -0.012545 \\ 0.003472 &{} -0.000057 &{} 0.002129 &{} -0.000013 &{} -0.034956 \\ 0.000218 &{} -0.000001 &{} -0.000013 &{} 0.000016 &{} -0.000867 \\ -0.355831 &{} -0.012545 &{} -0.034956 &{} -0.000867 &{} 3.299866 \\ \end{array}\right) . \end{aligned}$$

We obtain the learned threshold parameter $\epsilon ^*=2.260130$ and the corresponding confusion matrix

$$\begin{aligned} \mathbf {C} = \left( \begin{array}{cc} 52982 &{} 434 \\ 0 &{} 43266 \end{array} \right) . \end{aligned}$$

The respective $F_1$-score is given by $F_1 (\epsilon ^*)=0.995921$, which is an impressive result. Only 434 out of 96682 data points are predicted positive though being negative and all anomalous data points are found.

We finally apply the AD process to investigate an unknown solid pipe that potentially contains defects. We use scanning data with the above mentioned five features to calculate values of the probability density function with estimated expected values and covariance matrix. Figure 6 visualizes the results $Y = \big (y^{(i[k,z])}\big )_{k,z}$ according to Algorithm 1: The anomalous data with $y^{(i[k,z])}=1$ are marked yellow. Two defects are detected by our algorithm, which both appear twice in the plot since they are scanned in intervals of $180^{\circ }$ when the system is rotated. The plot is read from top to bottom: The first horizontal yellow lines represent the transition between air and pipe. They are followed by an area of about $40\;\mathrm {mm}$ which includes a defect. After a small section with no defects, a second damage of about $10\;\mathrm {mm}$ follows. The last measurements are unaffected.

Fig. 6

Anomaly detection of an unknown pipe

By comparing our results with the exact dimension of the pipe, we note that again promising results are achieved: The solid pipe was built with two damaged areas, a vertical hole of $4\;\mathrm {cm}$ from above and a lateral hole with a diameter of $8\;\mathrm {mm}$. Note that the aim of our investigation was not to determine the exact dimensions of the defects and to characterize them, but to localize the approximate anomalous areas which was completely achieved.

Considering the computational time of Algorithm 1, the second step is the most expensive one, since an optimization problem is solved. The total time depends on the amount of data and, in our case (Intel Core i7-8565U processor), it amounts to about three seconds. Furthermore, the performance of the algorithm increases by the number of correct measurements that are used for the training process. Additionally, we found that using less anomalous data worsens the performance. We used the maximal amount of the available data. The partition of the correct data into the training set, the cross validation set and the test set does not influence the generalizability significantly, e.g., we tested a split of 80/10/10 for the correct data and obtained a comparable result.

5 Learned Anomaly Detection Based on Partly Simulated Data Sets

In a further investigation we include simulated data into our data set. For this purpose, we model the propagation of terahertz radiation, more precisely the space-dependent travel time T and propagation velocity v, by the Eikonal equation

$$\begin{aligned} |\nabla T(x,y)|^2 = \frac{1}{v^2(x,y)} \;\;\text { for all }\;(x,y)\in \Omega \subset \mathbb {R}^2 \end{aligned}$$

with a suitable constraint

$$\begin{aligned} T(x_0,y_0)=0 \end{aligned}$$

for an initial value $(x_0,y_0)\in \partial \Omega$ on the boundary $\partial \Omega$ of the domain $\Omega$. The Eikonal equation can be regarded as a high frequency approximation of the Helmholtz equation and, more generally, of the wave equation taking into account time harmonic waves [3, 8, 15]. The solution of this nonlinear partial differential equation is the (travel) time T(x, y) the terahertz wave needs to reach the point (x, y) in the domain $\Omega$ and depending on the propagation velocity v. The latter is directly related to the refractive index n of the object via

$$\begin{aligned} n(x,y) = \frac{c}{v(x,y)}, \end{aligned}$$

where c is the speed of light in vacuum. The point $(x_0,y_0)$ on the boundary represents the position of the emitter and therefore the source of the radiation.

By solving the Eikonal equation for known refractive indices n resp. propagation times v, we enlarge the data set and, more precisely, the feature ’travel time’ of receiver $R_1$. The Eikonal equation is solved by the Fast Marching Method [1, 14], which had been introduced by Sethian in [23]. We implement the algorithm in MATLAB paying attention to the usual geometry of a terahertz beam, encompassing in particular a Gaussian intensity profile and a Rayleigh zone whose length depends on the lenses in our measuring system (see also [25, 28]). A simulation of the travel time of the THz radiation emitted from a point source is presented in Fig. 7.

Fig. 7

Numerical calculation of the travel time for a Gaussian terahertz beam

We validate the physical model by comparing the simulated data with real measurements for a solid pipe with a diameter of $10\;\mathrm {cm}$ and refractive index $n=1.53$. Figure 8 shows the path differences on the y-axis as a function of the angle position for one rotation. The simulated data are plotted in blue while the measured ones are illustrated by the red line. We added a uniform noise of $3\%$ to the simulated data. Since the scanned object is a rotationally symmetric solid pipe with homogeneous refractive index and the beam is directed at the rotation axis, we expect to obtain the same travel time for all angular positions of the measurement setup. Indeed, both simulated and real measurement series yield comparable results. Due to the specific setup of this experiment, the mean value of the travel time is a good benchmark to compare the simulation with the experiment: The mean value of the simulated travel time is computed as $s_{\mathrm {sim}} = 53.119081\;\mathrm {mm}$ and the one of the measured travel time as $s_{\mathrm {real}}= 53.602705\;\mathrm {mm}$. In addition, we determine the relative deviation $\Delta _{\mathrm {rel}}$ of the mean values via

$$\begin{aligned} \Delta _{\mathrm {rel}} = \frac{s_{\mathrm {real}}-s_{\mathrm {sim}}}{s_{\mathrm {real}}}\cdot 100\;\%, \end{aligned}$$

which yields $\Delta _{\mathrm {rel}} = 0.9022\;\%$, indicating a good consistency of simulation and experiment.

Fig. 8

Path difference of the simultated (blue) and real (red) data in comparison

The main advantage of the simulation is that we can easily extend the set of investigated objects by varying the number and types of defects. The manufacturing of representative objects and materials - such as the pipes from our first experiments - can thus be limited or entirely omitted in order to create suitable data sets for the learning process. As a consequence, such a virtual object design and the respective generation of simulated data can provide a basis for a more economic application of AD algorithms in practice. In particular, by combining simulated data and real measurements, not every single defect has to be created and included in the real material. For complex inline products, such as window frames for instance, this would have huge advantages. In our case, we purely augment our training data by means of simulations for the Eikonal equation, so that we only simulate one of the five measured features, which defines a one-dimensional setting.

We now illustrate the performance of our hybrid data sets in practice: We use the feature travel time of our simulated and the real data from receiver $R_1$ and perform a one-dimensional AD. For this, we supplement the data set of Sect. 3 with simulated data calculated from the solution of the Eikonal equation. According to the previous investigations, we learn the parameters of a one-dimensional Gaussian distribution and the threshold parameter $\epsilon ^*$. We then perform the respective trained AD method for the unknown pipe. The calculated Gaussian distribution $p(x;\mu ,\sigma ^2)$ (see also (2.1)) is given by the learned parameters $\mu = 53.546907$ and $\sigma ^2 = 0.282028$.

As described in Sect. 2, we calculate the confusion matrix $\mathbf {C}$ for a varying threshold $\epsilon$ and compute a maximal $F_1$-score of 0.489209 for the optimal threshold parameter $\epsilon ^*$. Here, as expected, the $F_1$-score is significantly lower than in our first experiment due to the reduced number of available features. The resulting plot of the output of our algorithm, which indicates whether a defect has been detected (value 1) or not (value 0), is shown in Fig. 9 on the left-hand side.

In order to show an added value of the simulated data, we also learn the one-dimensional parameters only with the real measured data and neglect the simulated data. Figure 9 illustrates the result: It is obvious that by using both simulated and measured data, the defect areas can be resolved and detected more reliably than without simulated data.

Fig. 9

One-dimensional anomaly detection of the unknown pipe. Left-hand side: using a hybrid data set comprising simulated and real measured data; right-hand side: using only measured data

Relating the results shown in Fig. 9 to the one from Fig. 6, we conclude that the best results were achieved by the multidimensional setting. However, a tendency to over-sensitivity can be seen at this point, which would result from a further increase in features. For a multi-dimensional approach with simulated data, other models need to be investigated for the simulation of refraction and absorption data. However, the increased accuracy gained by using simulated data from the Eikonal equation indicates the potential of simulated data in ML applications.

6 Discussion and Conclusion

In this article we evaluated THz tomographic measurements with an AD algorithm to investigate its use in the inline process monitoring of plastics and ceramics. We introduced the algorithm and tested it on a real data set measured at the Plastics Center (SKZ) in Würzburg, Germany. The computational results show that our presented technique has great potential for the inline monitoring and for applying it in a real time system. A good detection of defects and anomalous data was demonstrated.

In a further experiment we restricted ourselves to using data with only a single feature, i.e., travel time data, which reduced our investigation to a one-dimensional setting. We simulated the propagation of the THz radiation by using the Eikonal equation as a physical model, taking into account the beam profile of THz radiation. We combined simulated data with real measured data and performed a one-dimensional AD. For the considered case, again, promising results were demonstrated. In this setting the simulation of data by the Eikonal equation improves the detection of anomalies.

It is a future challenge to transfer the results to further materials and production processes. This includes finding physical models that are able to serve as a basis for simulations of the remaining features of the measuring system, in particular the reflection and the absorption data. A possibility for simulating the intensity is given by Tepe et al. [25], where a modified Algebraic Reconstruction Technique has been developed and used to identify the refractive index and the absorption coefficient. Regarding the use of our technique in industry, our methods shall be extended in such a way that, in addition to defect detection, a defect classification is possible to enable a more detailed diagnostic of the production process and to simplify a targeted intervention. To this end, we aim at extending the AD algorithm towards a deep learning based technique that is trained to classify defects and their properties (shape, size, material properties in the case of impurities). For the generation of simulated data, it will be vital to investigate the nature of typical defects in practical applications.