SpringerLink
Log in

Nonlinear dynamic analysis of spur gear pair for varying crack depth scenario

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

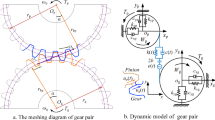
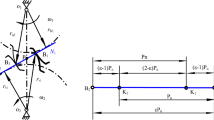
This paper presents an eight degree-of-freedom dynamic model of a spur gear system under varying crack depth scenarios for nonlinear analysis. Unlike previously reported reduced order models, which fail to capture realistic system behavior, such as chaos in healthy gears observed experimentally, this realistic model offers a more accurate representation. The proposed model is validated against experimental data and used to analyze the effect of varying tooth root crack depth as a bifurcation parameter, a novel investigation in this field. The proposed model incorporates major nonlinearities such as analytically improved time-varying mesh stiffness (AI-TVMS), backlash, static transmission error, and bearing clearances. The AI-TVMS model under healthy and varying crack depth scenarios is incorporated to analyze the nonlinear characteristics of the system. The analysis is presented via different tools such as bifurcation diagrams, phase portraits, Poincare maps, power spectral density, cepstrum analysis, envelope analysis, multifractal spectral analysis, Lyapunov exponents, and approximate entropy. The results demonstrate the chaotic nature of both healthy and defective gear systems. Additionally, the transient nature of the system at fault locations increased with the severity of % the crack depth, due to which the transient chaos phenomenon appeared for defective gear systems. Finally, the evaluation of tools attempts to distinguish between inherent nonlinearity and crack-induced nonlinearity. The findings of this study will aid in more precise gear system failure diagnosis in the future.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Data avaliliability

Data available on request from the authors.

References

  1. Liu, Y., Qin, Z., Chu, F.: Nonlinear forced vibrations of FGM sandwich cylindrical shells with porosities on an elastic substrate. Nonlinear Dyn. 104, 1007–1021 (2021)

    Article  Google Scholar 

  2. Liu, Y., Qin, Z., Chu, F.: Nonlinear forced vibrations of rotating cylindrical shells under multi-harmonic excitations in thermal environment. Nonlinear Dyn. 108(4), 2977–2991 (2022)

    Article  Google Scholar 

  3. Liu, Y., Qin, Z., Chu, F.: Nonlinear forced vibrations of functionally graded piezoelectric cylindrical shells under electric-thermo-mechanical loads. Int. J. Mech. Sci. 201, 106474 (2021)

    Article  Google Scholar 

  4. Zhao, Wu., Liu, J., Zhao, Wh., Wang, H., Yang, N.: Modeling and vibration feature analysis of a spur gear-bearing system with a misaligned shaft angle. Nonlinear Dyn. 112(1), 151–174 (2024)

    Article  Google Scholar 

  5. Geng, Z., Chen, M., Wang, J., **a, Y., Kong, Y., **ao, K.: Nonlinear dynamic analysis of a spur gear pair system with wear considering the meshing position. Lubricants 12(1), 25 (2024)

    Article  Google Scholar 

  6. Ma, H., Zeng, J., Feng, R., Pang, X., Wang, Q., Wen, B.: Review on dynamics of cracked gear systems. Eng. Fail. Anal. 55, 224–245 (2015)

    Article  Google Scholar 

  7. **e, C., Shu, X.: A new mesh stiffness model for modified spur gears with coupling tooth and body flexibility effects. Appl. Math. Model. 91, 1194–1210 (2021)

    Article  MathSciNet  Google Scholar 

  8. Ma, H., Song, R., Pang, X., Wen, B.: Time-varying mesh stiffness calculation of cracked spur gears. Eng. Fail. Anal. 44, 179–194 (2014)

    Article  Google Scholar 

  9. Ma, H., Pang, X., Feng, R., Song, R., Wen, B.: Fault features analysis of cracked gear considering the effects of the extended tooth contact. Eng. Fail. Anal. 48, 105–120 (2015)

    Article  Google Scholar 

  10. **e, C., Hua, L., Lan, J., Han, X., Wan, X., **ong, X.: Improved analytical models for mesh stiffness and load sharing ratio of spur gears considering structure coupling effect. Mech. Syst. Signal Process. 111, 331–347 (2018)

    Article  Google Scholar 

  11. Chen, Z., Shao, Y.: Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth. Eng. Fail. Anal. 18(8), 2149–2164 (2011)

    Article  Google Scholar 

  12. **e, C., Hua, L., Han, X., Lan, J., Wan, X., **ong, X.: Analytical formulas for gear body-induced tooth deflections of spur gears considering structure coupling effect. Int. J. Mech. Sci. 148, 174–190 (2018)

    Article  Google Scholar 

  13. Shi, H., Chen, W., Li, J., Wang, Z., Jiang, L.: Vibration stability and bifurcation analysis of spur gear systems based on time-varying backlash and random load. Int. J. Non-Linear Mech. 160, 104648 (2024)

    Article  Google Scholar 

  14. Hu, Y.H., Du, Q.G., **e, S.H.: Nonlinear dynamic modeling and analysis of spur gears considering uncertain interval shaft misalignment with multiple degrees of freedom. Mech. Syst. Signal Process. 193, 110261 (2023)

    Article  Google Scholar 

  15. Kahraman, A., Singh, R.: Non-linear dynamics of a spur gear pair. J. Sound Vib. 142(1), 49–75 (1990)

    Article  Google Scholar 

  16. Litak, G., Friswell, M.I.: Vibration in gear systems. Chaos Solitons Fractals 16(5), 795–800 (2003)

    Article  Google Scholar 

  17. Yang, Y., Cao, L., Li, H., Dai, Y.: Nonlinear dynamic response of a spur gear pair based on the modeling of periodic mesh stiffness and static transmission error. Appl. Math. Model. 72, 444–469 (2019)

    Article  Google Scholar 

  18. Kahraman, A., Singh, R.: Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system. J. Sound Vib. 146(1), 135–156 (1991)

    Article  Google Scholar 

  19. Huang, K., Cheng, Z., **ong, Y., Han, G., Li, L.: Bifurcation and chaos analysis of a spur gear pair system with fractal gear backlash. Chaos Solitons Fractals 142, 110387 (2021)

    Article  MathSciNet  Google Scholar 

  20. Kahraman, A., Singh, R.: Non-linear dynamics of a geared rotor-bearing system with multiple clearances. J. Sound Vib. 144(3), 469–506 (1991)

    Article  Google Scholar 

  21. Yang, Y., **a, W., Han, J., Song, Y., Wang, J., Dai, Y.: Vibration analysis for tooth crack detection in a spur gear system with clearance nonlinearity. Int. J. Mech. Sci. 157, 648–661 (2019)

    Article  Google Scholar 

  22. Zhou, S., Song, G., Ren, Z., Wen, B.: Nonlinear dynamic analysis of coupled gear-rotor-bearing system with the effect of internal and external excitations. Chin. J. Mech. Eng. 29(2), 281–292 (2016)

    Article  Google Scholar 

  23. Wang, J., Zhang, J., Yao, Z., Yang, X., Sun, R., Zhao, Y.: Nonlinear characteristics of a multi-degree-of-freedom spur gear system with bending-torsional coupling vibration. Mech. Syst. Signal Process. 121, 810–827 (2019)

    Article  Google Scholar 

  24. **ang, L., Jia, Y., Hu, A.: Bifurcation and chaos analysis for multi-freedom gear-bearing system with time-varying stiffness. Appl. Math. Model. 40(23–24), 10506–10520 (2016)

  25. Lu, J.W., Chen, H., Zeng, F.L., Vakakis, A.F., Bergman, L.A.: Influence of system parameters on dynamic behavior of gear pair with stochastic backlash. Meccanica 49, 429–440 (2014)

  26. Huang, K., Yi, Y., **ong, Y., Cheng, Z., Chen, H.: Nonlinear dynamics analysis of high contact ratio gears system with multiple clearances. J. Braz. Soc. Mech. Sci. Eng. 42(2), 98 (2020)

    Article  Google Scholar 

  27. Molaie, M., Samani, F.S., Zippo, A., Iarriccio, G., Pellicano, F.: Spiral bevel gears: Bifurcation and chaos analyses of pure torsional system. Chaos Solitons Fractals 177, 114179 (2023)

    Article  MathSciNet  Google Scholar 

  28. Kumar, V., Mukherjee, S., Sarangi, S.: Nonlinear distribution of the gearbox dynamic model including tooth cracks. In: Recent Advances in Machines and Mechanisms: Select Proceedings of the iNaCoMM 2021, pp. 257–269. Springer (2022)

  29. Kumar, V., Kumar, A., Kumar, S., Sarangi, S.: TVMS calculation and dynamic analysis of carburized spur gear pair. Mech. Syst. Signal Process. 166, 108436 (2022)

    Article  Google Scholar 

  30. Soleimani, A., Khadem, S.: Early fault detection of rotating machinery through chaotic vibration feature extraction of experimental data sets. Chaos Solitons Fractals 78, 61–75 (2015)

    Article  Google Scholar 

  31. Liu, Y., Zhang, Y., Wu, Z.: Stochastic dynamic analysis of the rotor-bearing system considering the randomness of the radial clearance. J. Braz. Soc. Mech. Sci. Eng. 41(11), 1–13 (2019)

    Article  Google Scholar 

  32. Raghothama, A., Narayanan, S.: Bifurcation and chaos in geared rotor bearing system by incremental harmonic balance method. J. Sound Vib. 226(3), 469–492 (1999)

    Article  Google Scholar 

  33. While, M.: Rolling element bearing vibration transfer characteristics: effect of stiffness. J. Appl. Mech. 46(3), 677–684 (1979)

    Article  Google Scholar 

  34. El-Saeidy, F.M.: Finite element modeling of a rotor shaft rolling bearings system with consideration of bearing nonlinearities. J. Vib. Control 4(5), 541–602 (1998)

    Article  Google Scholar 

  35. Gou, X., Zhu, L., Qi, C.: Nonlinear dynamic model of a gear-rotor-bearing system considering the flash temperature. J. Sound Vib. 410, 187–208 (2017)

    Article  Google Scholar 

  36. Li, Z., Peng, Z.: Nonlinear dynamic response of a multi-degree of freedom gear system dynamic model coupled with tooth surface characters: a case study on coal cutters. Nonlinear Dyn. 84(1), 271–286 (2016)

    Article  Google Scholar 

  37. Kumar, V., Rai, A., Mukherjee, S., Sarangi, S.: A Lagrangian approach for the electromechanical model of single-stage spur gear with tooth root cracks. Eng. Fail. Anal. 129, 105662 (2021)

    Article  Google Scholar 

  38. Kumar, V., Mukherjee, S., Kumar, S., Sarangi, S.: A comprehensive assessment of gearbox tooth faults based on dynamic modelling and machine learning. In: ASME 2022 International Mechanical Engineering Congress and Exposition. Volume 5: Dynamics, Vibration, and Control. American Society of Mechanical Engineers Digital Collection. V005T07A060 (2022)

  39. Chang-Jian, C.W.: Strong nonlinearity analysis for gear-bearing system under nonlinear suspension-bifurcation and chaos. Nonlinear Anal. Real World Appl. 11(3), 1760–1774 (2010)

    Article  MathSciNet  Google Scholar 

  40. Rosenstein, M.T., Collins, J.J., De Luca, C.J.: A practical method for calculating largest Lyapunov exponents from small data sets. Physica D 65(1–2), 117–134 (1993)

    Article  MathSciNet  Google Scholar 

  41. Pavlov, A.N., Anishchenko, V.S.: Multifractal analysis of complex signals. Phys. Usp. 50(8), 819 (2007)

    Article  Google Scholar 

  42. Wendt, H., Abry, P., Jaffard, S.: Bootstrap for empirical multifractal analysis. IEEE Signal Process. Mag. 24(4), 38–48 (2007)

    Article  Google Scholar 

  43. Jaffard, S., Lashermes, B., Abry, P.: Wavelet leaders in multifractal analysis. In: Wavelet Analysis and Applications, pp. 201–246. Springer (2007)

  44. Li, Y., Wang, X., Liu, Z., Liang, X., Si, S.: The entropy algorithm and its variants in the fault diagnosis of rotating machinery: a review. IEEE Access 6, 66723–66741 (2018)

Download references

Acknowledgements

This research was supported by Dynamics of Machines Laboratory, Indian Institute of Technology Patna.

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Indian Institute of Technology Patna, Patna, Bihar, 801103, India

    Vikash Kumar, Shubham Wasnik & Somnath Sarangi

Authors
  1. Vikash Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shubham Wasnik
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Somnath Sarangi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vikash Kumar.

Ethics declarations

Conflict of interest

All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, V., Wasnik, S. & Sarangi, S. Nonlinear dynamic analysis of spur gear pair for varying crack depth scenario. Nonlinear Dyn (2024). https://doi.org/10.1007/s11071-024-09859-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11071-024-09859-3

Keywords

Search

Navigation