SpringerLink
Log in

An improved physics-informed neural network with adaptive weighting and mixed differentiation for solving the incompressible Navier–Stokes equations

  • Research
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

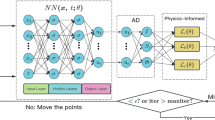
Physics-informed neural networks (PINNs) have been an effective tool for approximating the map** between points in the spatio-temporal domain and solutions of partial differential equations (PDEs). However, there are still some challenges in dealing with the nonlinear characteristics and complexity of the Navier–Stokes (N–S) equations. In this paper, the improved adaptive weighting PINNs based on the Gaussian likelihood estimation are applied to solve the N–S equations. The weights of the different loss items are allocated adaptively by the maximum likelihood estimation. The improved network structure has been designed with considering both the global and local information, making it easier to capture the part of PDEs solution with drastic changes. A combinational method of the numerical differentiation (ND) and the automatic differentiation (AD) is proposed to compute the differential operators, with the improved computational efficiency. The derivative operation of the convection and pressure-gradient terms was carried out using the combined method in solving the incompressible N–S equations. The results show that the effectiveness and training efficiency of this method are better than PINNs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

Data availability

The code can be found at https://github.com/upwaj/aw-in-md-PINNs.

References

  1. Girault, V., Raviart, P.-A.: Finite element methods for Navier–Stokes equations: theory and algorithms, vol. 5. Springer Science & Business Media, Cham (2012)

    Google Scholar 

  2. Coelho, P.J., Pereira, J.C.F.: Finite volume computation of the turbulent flow over a hill employing 2D or 3D non-orthogonal collocated grid systems. Int. J. Numer. Methods Fluids 14(4), 423–441 (1992)

    Article  Google Scholar 

  3. Weinan, E., Liu, J.-G.: Finite difference methods for 3D viscous incompressible flows in the vorticity-vector potential formulation on nonstaggered grids. J. Comput. Phys. 138(1), 57–82 (1997)

    Article  MathSciNet  Google Scholar 

  4. Ranade, R., Hill, C., Pathak, J.: DiscretizationNet: a machine-learning based solver for Navier–Stokes equations using finite volume discretization. Comput. Methods Appl. Mech. Eng. 378, 113722 (2021)

    Article  MathSciNet  Google Scholar 

  5. Wang, Y., Lai, C.-Y.: Multi-stage neural networks: function approximator of machine precision. J. Comput. Phys. 504, 112865 (2024)

    Article  MathSciNet  Google Scholar 

  6. Li, X., Liu, Y., Liu, Z.: Physics-informed neural network based on a new adaptive gradient descent algorithm for solving partial differential equations of flow problems. Phys. Fluids 35(6), 063608 (2023)

    Article  Google Scholar 

  7. Eivazi, H., Tahani, M., Schlatter, P., Vinuesa, R.: Physics-informed neural networks for solving Reynolds-averaged Navier–Stokes equations. Phys. Fluids 34(7), 075117 (2022)

    Article  Google Scholar 

  8. **ao, M.-J., Teng-Chao, Y., Zhang, Y.-S., Yong, H.: Physics-informed neural networks for the Reynolds-averaged Navier–Stokes modeling of Rayleigh–Taylor turbulent mixing. Comput. Fluids 266, 106025 (2023)

    Article  MathSciNet  Google Scholar 

  9. Azizzadenesheli, K., Kovachki, N., Li, Z., Liu-Schiaffini, M., Kossaifi, J., Anandkumar, A.: Neural operators for accelerating scientific simulations and design. Nat. Rev. Phys. 6, 1–9 (2024)

    Article  Google Scholar 

  10. Lee, H., Kang, I.S.: Neural algorithm for solving differential equations. J. Comput. Phys. 91(1), 110–131 (1990)

    Article  MathSciNet  Google Scholar 

  11. Lagaris, I.E., Likas, A., Fotiadis, D.I.: Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 9(5), 987–1000 (1998)

    Article  Google Scholar 

  12. Weinan, E., Bing, Y.: The deep Ritz method: a deep learning-based numerical algorithm for solving variational problems. Commun. Math. Stat. 6, 1–12 (2018)

    Article  MathSciNet  Google Scholar 

  13. Chen, M., Niu, R., Zheng, W.: Adaptive multi-scale neural network with resnet blocks for solving partial differential equations. Nonlinear Dyn. 111, 6499–6518 (2022)

    Article  Google Scholar 

  14. Gao, R., Wei, H., Fei, J., Hongyu, W.: Boussinesq equation solved by the physics-informed neural networks. Nonlinear Dyn. 111, 15279–15291 (2023)

    Article  Google Scholar 

  15. Zhang, T., Hui, X., Guo, L., Feng, X.: A non-intrusive neural network model order reduction algorithm for parameterized parabolic PDEs. Comput. Math. Appl. 119, 59–67 (2022)

    Article  MathSciNet  Google Scholar 

  16. Hou, J., Li, Y., Ying, S.: Enhancing PINNs for solving PDEs via adaptive collocation point movement and adaptive loss weighting. Nonlinear Dyn. 111, 15233–15261 (2023)

    Article  Google Scholar 

  17. Wang, H., Zou, B., Jian, S., Wang, D.: Variational methods and deep Ritz method for active elastic solids. Soft Matter 18(7), 6015–6031 (2022)

    Article  Google Scholar 

  18. Gao, Z., Yan, L., Zhou, T.: Failure-informed adaptive sampling for PINNs. SIAM J. Sci. Comput. 45, A1971–A1994 (2023)

    Article  MathSciNet  Google Scholar 

  19. Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019)

    Article  MathSciNet  Google Scholar 

  20. Karniadakis, G.E., Kevrekidis, I.G., Lu, L., Perdikaris, P., Wang, S., Yang, L.: Physics-informed machine learning. Nat. Rev. Phys. 3(6), 422–440 (2021)

    Article  Google Scholar 

  21. Lu, L., Meng, X., Mao, Z., Karniadakis, G.E.: DeepXDE: a deep learning library for solving differential equations. SIAM Rev. 63(1), 208–228 (2021)

    Article  MathSciNet  Google Scholar 

  22. Chiu, P.-H., Wong, J.C., Ooi, C., Dao, M.H., Ong, Y.-S.: CAN-PINN: a fast physics-informed neural network based on coupled-automatic-numerical differentiation method. Comput. Methods Appl. Mech. Eng. 395, 114909 (2022)

    Article  MathSciNet  Google Scholar 

  23. Patel, R.G., Manickam, I., Trask, N.A., Wood, M.A., Lee, M., Tomas, Ignacio, Cyr, Eric C.: Thermodynamically consistent physics-informed neural networks for hyperbolic systems. J. Comput. Phys. 449, 110754 (2022)

    Article  MathSciNet  Google Scholar 

  24. Jagtap, A.D., Kharazmi, E., Karniadakis, G.E.: Conservative physics-informed neural networks on discrete domains for conservation laws: applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 365, 113028 (2020)

    Article  MathSciNet  Google Scholar 

  25. Jagtap, A.D., Karniadakis, G.E.: Extended physics-informed neural networks (XPINNs): a generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations. Commun. Comput. Phys. 28, 2002–2041 (2020)

    Article  MathSciNet  Google Scholar 

  26. Wei, W., Feng, X., Hui, X.: Improved deep neural networks with domain decomposition in solving partial differential equations. J. Sci. Comput. 93, 1–34 (2022)

    MathSciNet  Google Scholar 

  27. Wang, S., Sankaran, S., Wang, H., Perdikaris, P.: An expert’s guide to training physics-informed neural networks (2023). ar**v preprint: ar**v: 2308.08468

  28. McClenny, L.D., Braga-Neto, U.M.: Self-adaptive physics-informed neural networks. J. Comput. Phys. 474, 111722 (2023)

    Article  MathSciNet  Google Scholar 

  29. Tang, S., Feng, X., Wei, W., Hui, X.: Physics-informed neural networks combined with polynomial interpolation to solve nonlinear partial differential equations. Comput. Math. Appl. 132, 48–62 (2023)

    Article  MathSciNet  Google Scholar 

  30. Peng, P., Pan, J., Hui, X., Feng, X.: RPINNs: rectified-physics informed neural networks for solving stationary partial differential equations. Comput. Fluids 245, 105583 (2022)

    Article  MathSciNet  Google Scholar 

  31. Chenxi, W., Zhu, M., Tan, Q., Kartha, Y., Lu, L.: A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 403, 115671 (2023)

    Article  MathSciNet  Google Scholar 

  32. Bai, Y., Chaolu, T., Bilige, S.: Solving Huxley equation using an improved PINN method. Nonlinear Dyn. 105, 3439–3450 (2021)

    Article  Google Scholar 

  33. **, X., Cai, S., Li, H., Karniadakis, G.E.: NSFnets (Navier–Stokes flow nets): physics-informed neural networks for the incompressible Navier–Stokes equations. J. Comput. Phys (2021). https://doi.org/10.1016/j.jcp.2020.109951

    Article  MathSciNet  Google Scholar 

  34. Rao, C., Sun, H., Liu, Y.: Physics-informed deep learning for incompressible laminar flows. Theor. Appl. Mech. Lett. 10(3), 207–212 (2020)

    Article  Google Scholar 

  35. Dwivedi, B.S.V., Parashar, N.: Distributed learning machines for solving forward and inverse problems in partial differential equations. Neurocomputing 420, 299–316 (2021)

    Article  Google Scholar 

  36. Gao, H., Sun, L., Wang, J.-X.: PhyGeoNet: physics-informed geometry-adaptive convolutional neural networks for solving parameterized steady-state PDEs on irregular domain. J. Comput. Phys. 428, 110079 (2021)

    Article  MathSciNet  Google Scholar 

  37. Sitzmann, V., Martel, J., Bergman, A., Lindell, D., Wetzstein, G.: Implicit neural representations with periodic activation functions. Adv. Neural Inf. Process. Syst. 33, 7462–7473 (2020)

    Google Scholar 

  38. Mattey, R., Ghosh, S.: A novel sequential method to train physics informed neural networks for Allen–Cahn and Cahn–Hilliard equations. Comput. Methods Appl. Mech. Eng. 390, 114474 (2022)

    Article  MathSciNet  Google Scholar 

  39. Stein, M.: Large sample properties of simulations using Latin hypercube sampling. Technometrics 29(2), 143–151 (1987)

    Article  MathSciNet  Google Scholar 

  40. Liu, D.C., Nocedal, J.: On the limited memory BFGS method for large scale optimization. Math. Program. 45(1–3), 503–528 (1989)

  41. Kendall, A., Gal, Y., Cipolla, R.: Multi-task learning using uncertainty to weigh losses for scene geometry and semantics. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 7482–7491 (2018)

  42. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, Ł, Polosukhin, I.: Attention is all you need. Adv. Neural Inf. Process. Syst. 30, 1 (2017)

    Google Scholar 

  43. Cho, K., Merrienboer, B., Gulcehre, C., Bougares, F., Schwenk, H., Bengio, Y.: Learning phrase representations using RNN encoder-decoder for statistical machine translation. In: Conference on Empirical Methods in Natural Language Processing (EMNLP 2014) (2014)

  44. Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., Devin, M., Ghemawat, S., Irving, G., Isard, M.: Tensorflow: a system for large-scale machine learning on heterogeneous distributed systems (2016). ar**v: 1603.04467

  45. **ao, F., Akoh, R., Ii, S.: Unified formulation for compressible and incompressible flows by using multi-integrated moments ii: multi-dimensional version for compressible and incompressible flows. J. Comput. Phys. 213(1), 31–56 (2006)

    Article  MathSciNet  Google Scholar 

  46. Sheu, T.W.H., Chiu, P.H.: A divergence-free-condition compensated method for incompressible Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 196(45–48), 4479–4494 (2007)

    Article  MathSciNet  Google Scholar 

  47. Ethier, C.R., Steinman, D.A.: Exact fully 3D Navier–Stokes solutions for benchmarking. Int. J. Numer. Methods Fluids 19(5), 369–375 (1994)

    Article  Google Scholar 

  48. Ghia, U.K.N.G., Ghia, K.N., Shin, C.T.: High-Re solutions for incompressible flow using the Navier–Stokes equations and a multigrid method. J. Comput. Phys. 48(3), 387–411 (1982)

    Article  Google Scholar 

  49. Williamson, C.H.K.: Vortex dynamics in the cylinder wake. Ann. Rev. Fluid Mech. 28(1), 477–539 (1996)

    Article  MathSciNet  Google Scholar 

Download references

Funding

This work is supported by the National Natural Science Foundation of China (Nos. 12361090, 12071406 and 12271465), the Natural Science Foundation of **njiang Province (Nos. 2023D01C164, 6142A05230203, 2022D01D32), and the Tianshan Talent Training Program (No. 2023TSYCQNTJ0015 and No. 2022TSYCTD0019).

Author information

Authors and Affiliations

  1. College of Mathematics and System Science, **njiang University, Urumqi, 830046, People’s Republic of China

    Jie Wang, Xufeng **ao, **nlong Feng & Hui Xu

  2. School of Aeronautics and Astronautics, Shanghai Jiao Tong University, Shanghai, 200240, People’s Republic of China

    Hui Xu

Authors
  1. Jie Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xufeng **ao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. **nlong Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hui Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Jie Wang: investigation, software, validation, writing—original draft. Xufeng **ao: conceptualization, methodology, formal analysis, software, writing—review and editing. **nlong Feng: formal analysis, writing—review and editing. Hui Xu: formal analysis, writing—review and editing.

Corresponding author

Correspondence to Xufeng **ao.

Ethics declarations

Conflict of interest

No conflict of interest exists in the submission of this manuscript, and the manuscript is approved by all authors for publication.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, J., **ao, X., Feng, X. et al. An improved physics-informed neural network with adaptive weighting and mixed differentiation for solving the incompressible Navier–Stokes equations. Nonlinear Dyn (2024). https://doi.org/10.1007/s11071-024-09856-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11071-024-09856-6

Keywords

Search

Navigation