1 Introduction

Partial differential equations are widely employed to describe the evolution of complex systems in various fields, including physics, engineering and finance. However, obtaining analytical solutions for PDEs is often impractical, especially in the case of strongly nonlinear and high-dimensional systems. Due to their robust fitting capability and adaptability to complex data relationships, artificial neural networks (ANNs) have been employed as a universal method to solve PDEs [1,2,3]. This leads to physics informed neural networks commonly known as PINN. ANNs transform the PDE solution process into optimization problems, whose objective is to minimize a suitably defined loss function, such that the neural networks output approximates the solution to a high level of accuracy. The loss function of PINN usually consists of residuals of the PDE, boundary conditions and possibly other constraints and therefore requires the computation of high order derivatives of the equation. The computation of derivatives in the loss function in the repeated trainings of the neural networks can substantially increase the CPU time and sacrifice the accuracy of the solution. Furthermore, this approach may also face challenges such as vanishing gradient or exploding gradient problems, which can impede the convergence and overall effectiveness [4]. A Monte Carlo method was proposed to compute second derivatives, which proves to be time-consuming [5]. The simplicity and flexibility of the PINN approach render it suitable for a wide range of PDEs. Some literature on solving the FPK equation using the PINN approach includes [6,7,8,9].

The Feynman–Kac formula gives a connection between a semilinear parabolic PDE and a stochastic process with the martingale property [10, 11]. The solution to the parabolic PDE is proven to be the expectation of the martingale process driven by a Brownian motion. The theory of backward stochastic differential equations (BSDEs) extends the application of the Feynman–Kac method from semilinear parabolic PDEs to fully nonlinear PDEs [12, 13]. Xu further applied the concepts of the Feynman–Kac formula and BSDE to the complex PDEs [14]. The Feynman–Kac formula provides a route to solve PDEs with the help of simulated random paths without the need for derivative calculations.

The Feynman–Kac formula can be used to relate stochastic differential equation (SDE) to a corresponding PDE. An algorithm of variational quantum imaginary time evolution has been developed to solve the PDE in order to obtain the expectations of the SDEs [15]. The primary application of the Feynman–Kac formula remains providing a method for solving PDEs by simulating stochastic processes, thereby circumventing the need for derivative calculations. Monte Carlo simulations (MCS) can be employed to directly generate random trajectories in order to obtain the expectation of the stochastic process, which represents the solution to the PDE. However, direct simulations would require significant computational efforts [16,17,18]. To enhance the computational efficiency, the h-conditioned Green’s function, which enables the representation of the integral along random paths as a volume integral, is employed instead of directly simulating random trajectories to obtain the expectation of the stochastic process [19]. Dalang et al. established a probabilistic representation for PDEs that is different from the Feynman–Kac formula. The advantage of their method lies in deriving an analytical expression for the moments of the response process without the need for numerical simulations [20]. Computation of the expectation of the martingale process with direct simulations can be even more intensive for high dimensional systems [16, 17]. Deep learning methods based on variational formulations for the associated stochastic differential equations are investigated extensively in [21]. The Feynman–Kac formula is also used in the study, leading to a very efficient computational algorithm.

The authors of [22] have developed a derivative-free method to solve a series of elliptical PDEs. Furthermore, this derivative-free deep neural network method has been extended to solve viscous incompressible fluid flow problems [23]. Weinan et al. solve a class of parabolic PDEs by reformulating them as BSDEs using deep neural networks [2].

Although the calculation of derivatives can be circumvented by the Feynman–Kac formula, the traditional neural network methods still require numerical simulations to compute the expectation of random paths of the martingale stochastic process, which remains time-consuming and inconvenient. This paper develops an effective way to compute the expectation of the martingale process by making use of the short-time Gaussian approximation of the response process. We also utilize the RBFNN to accurately approximate the PDF of the response process. RBFNN is an example of PINN and has been successfully applied to obtain transient and stationary PDFs of the FPK equation of nonlinear systems [24,25,26] and the reliability function of the first-passage problem [27]. Since the output of the RBFNN is a weighted sum of Gaussian activation functions, by applying the short-time Gaussian approximation (STGA) technique, we have derived the analytical expression for the expectation of the Feynman–Kac formula. This approach obviates the need for numerical simulations. Compared to directly solving PDEs using RBFNN, the method proposed in this paper additionally eliminates the need for derivative calculations, thereby reducing computational time. Three numerical examples, including a strongly nonlinear system, a non-smooth system, and a high-dimensional system, are employed to demonstrate the feasibility and effectiveness of our approach. Furthermore, the comparison between the Feynman–Kac formula-based solution and the solution from directly solving PDE is discussed. The FPK equation is the primary example in this paper, while the method is also applicable to other PDEs, such as the Hamilton–Jacobi–Bellman (HJB) equation and heat equation.

The remainder of the paper is outlined as follows. Section 2 provides a brief description of the Feynman–Kac formula and the FPK equation. In Sect. 3, we elaborate on the implementation of the Feynman–Kac formula utilizing the RBFNN approach. We apply the STGA technique to derive the analytical expression for the expectation of the stochastic process, thereby circumventing both derivative calculations and numerical simulations. In Sect. 4, we briefly review a RBFNN approach of directly solving the FPK equation. In Sect. 5, three examples are presented, including a strongly nonlinear system, a non-smooth tri-stable system, and a high-dimensional system, to validate the feasibility and effectiveness of the proposed method. The computational time of the proposed method is compared with that of the equation-based RBFNN method in Sect. 6. Section 7 concludes the paper.

2 Feynman–Kac formula

In this section, we present an overview of the Feynman–Kac formula, which provides a connection between a second-order parabolic PDE and a stochastic process with the martingale property. However, we shall not show how to derive the FPK equation from the Feynman–Kac formula. The interested reader should refer to the reference [15].

Consider the following n-dimensional parabolic PDE,

$$\begin{aligned} \frac{\partial p(\textbf{x},t)}{\partial t}+\mathcal {L}_t [p(\textbf{x},t)]-c(\textbf{x},t)p(\textbf{x},t) = 0, \end{aligned}$$
(1)

where the differential operator \(\mathcal {L}_t [ p ]\) is defined as,

$$\begin{aligned} \mathcal {L}_t [ p ]{} & {} \equiv \sum _{i=1}^{n} a_{i}(\textbf{x},t) \frac{\partial p}{\partial x_i} +\frac{1}{2} \sum _{i=1}^{n} \sum _{j=1}^{n} b_{ij}(\textbf{x},t) \nonumber \\{} & {} \quad \frac{\partial ^2 p}{\partial x_i \partial x_j}. \end{aligned}$$
(2)

The coefficients \(a_i(\textbf{x},t)\), \(b_{ik}(\textbf{x},t)\) and \(c(\textbf{x},t)\) are known functions \(\mathbb {R}^n \times [0, T] \rightarrow \mathbb {R}\), \(\textbf{a}=[a_i] \in \mathbb {R}^{n\times 1}\) and \(\textbf{b}=[b_{ik}] \in \mathbb {R}^{n\times m}\). As discussed in the introduction [15], the Feynman–Kac formula can be used to derive PDE (1) governing the PDF of the n dimensional stochastic process \(\textbf{X}(t)=[X_j (t)] \in \mathbb {R}^n\) satisfying the following Itô differential equation,

$$\begin{aligned} dX_j=a_j(\textbf{X},t)dt+ \sum _{k=1}^{m} \sigma _{jk}(\textbf{X},t) dB_k(t), \end{aligned}$$
(3)

where \(b_{ij} (\textbf{x},t) = \sum _{k=1}^{m} \sigma _{ik} \sigma _{jk}(\textbf{x},t)\) and \(B_j(t)\) \((j=1,2, \ldots , m)\) are independent unit Brownian motions. Hence, the FPK equation for the stochastic process \(\textbf{X}(t)\) satisfying Eq. (3) must be a special case of Eq. (1).

Consider the n-dimensional FPK equation with the initial condition.

$$\begin{aligned} \frac{\partial p(\textbf{x},t)}{\partial t}&= \mathcal {L}_{FPK}[p(\textbf{x},t)] \end{aligned}$$
(4)
$$\begin{aligned}&\equiv -\sum \limits _{i=1}^{n}\frac{\partial [m_{i}(\textbf{x})p(\textbf{x},t)]}{\partial x_{i}}\nonumber \\&\quad +\frac{1}{2}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n} \frac{\partial ^{2}[ b_{ij}(\textbf{x})p(\textbf{x},t)] }{\partial x_{i}\partial x_{j}},\nonumber \\ p( \textbf{x},0)&=p_0(\textbf{x}), \end{aligned}$$
(5)

where the deterministic functions \(m_{i}(\textbf{x})\) and \(b_{ij}(\textbf{x})\) are the drift and diffusion terms. The FPK operator can be expressed in the form of a linear parabolic equation as,

$$\begin{aligned} \mathcal {L}_{FPK}[p(\textbf{x},t)]=\mathcal {L}_t[{p(\textbf{x},t)}]-c(\textbf{x}) p(\textbf{x},t), \end{aligned}$$
(6)

where \(\mathcal {L}_t [ p ]\) is defined in Eq. (2), and

$$\begin{aligned} c(\textbf{x})&= \sum _{i=1}^{n} \frac{\partial m_i (\textbf{x})}{\partial x_i} -\frac{1}{2}\sum _{i=1}^{n}\sum _{j=1}^{n} \frac{\partial ^2 b_{ij}(\textbf{x})}{\partial x_i \partial x_j }, \nonumber \\ a_i(\textbf{x})&=-m_i(\textbf{x})+\sum _{j=1}^{n} \frac{\partial b_{ij}(\textbf{x})}{\partial x_j}. \end{aligned}$$
(7)

Note that this is a special case when \(a_i(\textbf{x})\), \(b_{ij}(\textbf{x})\) and \(c(\textbf{x})\) are not explicit functions of time.

We are now back to the parabolic PDE (1) and the stochastic process \(\textbf{X}(t)\), and define another stochastic process \(\mathcal {M}(t)\) as,

$$\begin{aligned} \mathcal {M}(t)= e^{-\int _{0}^{t}c(\textbf{X}(s),s)ds} p(\textbf{X},t), \ \ 0 < t \le T, \end{aligned}$$
(8)

where \(p: \mathbb {R}^n \times [0, T] \rightarrow \mathbb {R}\) is an arbitrary function at this point. The differentiation of \(\mathcal {M}(t)\) can be obtained by Itô’s lemma as,

$$\begin{aligned} d\mathcal {M}(t)&= e^{-\int _{0}^{t}c(\textbf{X}(s),s)ds}dp(\textbf{X}, t) \nonumber \\&\quad -e^{-\int _{0}^{t}c(\textbf{X}(s),s)ds}p(\textbf{X},t) c(\textbf{X},t)dt \nonumber \\&= e^{-\int _{0}^{t}c(\textbf{X}(s),s)ds} \left( \frac{\partial p}{\partial t}+\mathcal {L}_t [p]-cp \right) dt \nonumber \\&\quad + \sum _{ j=1}^{n} \sum _{k=1}^{m} \sigma _{jk} \frac{\partial p}{ \partial x_j}dB_k(t). \end{aligned}$$
(9)

When \(p(\textbf{x}, t)\) is the solution of PDE (1), we take the expectation of Eq. (9) and obtain

$$\begin{aligned} d \mathbb {E}[\mathcal {M}(t)]=0. \end{aligned}$$
(10)

Hence, \(\mathcal {M}(t)\) is a martingale process. Integrating this equation over [0, T] gives \(\mathbb {E}[\mathcal {M}(0)]=\mathbb {E}[\mathcal {M}(T)]\) where \(T>0\) is arbitrary. We have

$$\begin{aligned} p(\textbf{x},0)=\mathbb {E} \left[ e^{-\int _{0}^{T}c(\textbf{X}(s),s)ds} p(\textbf{X}(T),T)|\textbf{X}(0)=\textbf{x} \right] . \nonumber \\ \end{aligned}$$
(11)

The equation relates the initial distribution \(p(\textbf{x},0)\) to the PDF \(p(\textbf{x}, T)\) at an arbitrary time \(T>0\). This is an implicit integral equation for determining the PDF of the stochastic process \(\textbf{X}(t)\) without the differential operations of PDE (1). Therefore, the derivative calculations, which are typically time-consuming in computations for solving PDEs, are not required when \(p(\textbf{x},T)\) is obtained from the equation.

Equation (11) needs samples of the stochastic process \(\textbf{X}(t)\) over the time interval [0, T] to evaluate the expectation. For nonlinear systems, Monte Carlo simulations have been the only effective method to compute the expectation. In the following, we present a novel neural networks method to obtain the PDF solution from Eq. (11) subject to the constraint of normalization.

$$\begin{aligned} \int \limits _{\mathbb {R}^{n}}p(\textbf{x})d\textbf{x}=1. \end{aligned}$$
(12)

3 The proposed method

3.1 Outline of the method

The proposed method making use of the Feynman–Kac formula consists of a few steps. In the first step, we divide the time interval [0, T] into a collection of small time intervals \([k\Delta t, (k+1) \Delta t]\) (\(k=0, 1, \ldots \)). In each sub-interval, the martingale property of the stochastic process \(\mathcal {M}(t)\) holds

$$\begin{aligned} p(\textbf{x}, k\Delta t)= & {} \mathbb {E} \left[ e^{-\int _{k\Delta t}^{(k+1)\Delta t}c(\textbf{X}(s),s)ds} p( \textbf{X}((k+1)\Delta t),\right. \nonumber \\{} & {} \left. (k+1)\Delta t)|\textbf{X}(k\Delta t)=\textbf{x} \right] . \end{aligned}$$
(13)

In the second step, we develop a way to compute the conditional expectation on the right hand side of Eq. (13). \(p( \textbf{x}, (k+1)\Delta t)\) is a short-time response starting from the deterministic initial condition \(p(\textbf{x}, k\Delta t)\). Because the stochastic process \(\textbf{X}(t)\) satisfies Eq. (3), the STGA of the PDF of the response \(\textbf{X}((k+1)\Delta t)\) is valid. The details of the STGA strategy can be found in [28]. The mathematical expression of the STGA approximation of the PDF will be presented later.

With the PDF of the response \(\textbf{X}((k+1)\Delta t)\), we can analytically evaluate the conditional expectation of the nonlinear and unknown function of \(\textbf{X}(t)\) in Eq. (13).

In the third step, we propose a neural networks representation of the unknown function \(p(\textbf{x}, (k+1)\Delta t)\), which is a probability density function. From our previous experience [24,25,26,27], we find that the radial basis function neural networks (RBFNN) with Gaussian activation functions can be an excellent choice for modeling \(p( \textbf{x}, (k+1)\Delta t)\).

3.2 RBFNN

Let \(\bar{p}(\textbf{x}, \textbf{w}(k))\) be the function approximating \(p( \textbf{x}, k\Delta t)\) at the k th time step where \(\textbf{w}(k)\) denotes all the trainable coefficients of the neural networks. The trial solution \(\bar{p}(\textbf{x}, \textbf{w}(k))\) is written as the RBFNN with Gaussian activation functions

$$\begin{aligned} \bar{p}(\textbf{x},\textbf{w}(k))=\sum _{j=1}^{N_{G}}w_{j}(k) G_j(\textbf{x}), \end{aligned}$$
(14)

where \(N_{G}\) represents the total number of neurons. \(G_j(\textbf{x})\equiv G(\textbf{x},\varvec{\mu }_j, \varvec{\Sigma }_j)\) is a n-variate Gaussian radial basis function with the mean \(\varvec{\mu }_{j}\) and covariance matrix \(\varvec{\Sigma }_{j}=\textrm{diag}[\varvec{\sigma }^2_{j}]\). The n-variate Gaussian radial basis function is separable and can be expressed as a product of multiple uni-variate Gaussian functions as,

$$\begin{aligned} G(\textbf{x},\varvec{\mu }_{j},\varvec{\Sigma }_{j})&=\prod _{k=1}^{n}g(x_{k},\mu _{j k},\sigma _{j k}), \nonumber \\ g(x_{k},\mu _{j k},\sigma _{j k})&{=} \frac{1}{\sqrt{2\pi \sigma ^2_{j k}}}\exp \left[ {-}\frac{1}{2\sigma ^2_{j k}}(x_k{-}\mu _{j k})^2\right] , \end{aligned}$$
(15)

where \(\mu _{j k}\) is the k th component of the mean \(\varvec{\mu }_{j}\) and \(\sigma _{j, k}\) is the k th component of the standard deviation \(\varvec{\Sigma }_{j}\). In this paper, the means \(\varvec{\mu }_j\) and standard deviations \(\varvec{\sigma }_j\) are taken as constants.

The RBFNN solution (14) is a neural network with a single hidden layer using the Gaussian activation function. The diagram of the RBFNN for \(n=4\) is shown in Fig. 1.

Fig. 1
figure 1

An example of the diagram of the RBFNN for a 4D state space

Full size image

This shallow neural network has been proven to possess universal approximation capabilities [29]. Furthermore, the normalization condition (12) now reads,

$$\begin{aligned} \sum _{j=1}^{N_G} w_{j}(k) = 1,\ \ k\ge 0. \end{aligned}$$
(16)

Let \(D_G\) denote the domain where the system stays with probability not less than 99%. We discretize the domain into uniform grids, which represent the means of Gaussian neurons. The standard deviations for all the Gaussian function are set equal to the grid size.

3.3 Loss function

Let us consider the time-invariant case again. Assume that the duration of each sub-interval \(\Delta t\) is sufficiently small. Let \(\int _{(k-1)\Delta t}^{k\Delta t}c(\textbf{X}(s))ds = \bar{c}\Delta t\) where \(\bar{c}\) is determined from the trapezoidal rule. Before presenting the loss function, let us introduce a shorthand for the expectation with the help of Eq. (14)

$$\begin{aligned}&\mathbb {E} \left[ e^{-\bar{c} \Delta t} \bar{p}(\textbf{X}(k\Delta t),\textbf{w}(k) )|\textbf{X}((k-1)\Delta t) =\textbf{x}_i \right] \nonumber \\&\quad = \mathbb {E} \left[ e^{-\bar{c} \Delta t} \sum _{j=1}^{N_{G}}w_{j}(k) G_j(\textbf{X}(k\Delta t)) | \textbf{X}((k-1)\Delta t)=\textbf{x}_i \right] , \end{aligned}$$
(17)
$$\begin{aligned}&e_j(\textbf{x}_i) = \mathbb {E} \left[ e^{-\bar{c} \Delta t} G_j(\textbf{X}(k\Delta t)) | \textbf{X}((k-1)\Delta t)=\textbf{x}_i \right] . \end{aligned}$$
(18)

\(e_j(\textbf{x}_i)\) is the expectation of the Gaussian activation function \(G_j(\textbf{x})\).

Define a loss function and make use of Eq. (18). We have

$$\begin{aligned} J(\textbf{w}(k), k)&=\sum _{i=1}^{N_s} \left[ p(\textbf{x}_i, (k-1)\Delta t)-w_{j}(k)e_j(\textbf{x}_i) \right] ^2 \nonumber \\&=\sum _{i=1}^{N_s} r^2(\textbf{x}_i), \end{aligned}$$
(19)

where \(r(\textbf{x}_i)\) measures the degree to which the trial solution satisfies the martingale property at the the sampling point \(x_i\),

$$\begin{aligned} r(\textbf{x}_i) =p(\textbf{x}_i, (k-1)\Delta t)-\sum _{j=1}^{N_{G}} w_{j}(k)e_j(\textbf{x}_i). \end{aligned}$$
(20)

3.4 STGA technique for the expectation

The short-time probability density solution of the stochastic process, as defined in Eq. (3), starting from the initial condition \(\textbf{X}(k\Delta t)=\textbf{x}_i\), is approximately a Gaussian PDF with the mean \(\textbf{A}_i=\textbf{x}_i+ \textbf{a}(\textbf{x}_i)\Delta t\) and covariance \(\textbf{B}_i=\varvec{\sigma }\varvec{\sigma }^T(\textbf{x}_i)\Delta t\), as follows [30],

$$\begin{aligned}&p(\textbf{x}, (k+1)\Delta t|\textbf{x}_i, k\Delta t) =\frac{1}{\sqrt{(2\pi )^{2n}\det (\textbf{B}_{i})}}\nonumber \\&\qquad \exp \left[ -\frac{1}{2}(\textbf{x}-\textbf{A}_{i})^{T}\textbf{B}_{i}^{-1} (\textbf{x}-\textbf{A}_{i})\right] \nonumber \\&\quad \equiv G(\textbf{x}, \textbf{A}_{i}, \textbf{B}_{i}). \end{aligned}$$
(21)

With this Gaussian PDF, the expectation \(\mathbb {E}\) \([G_j(\textbf{X}(k\Delta t)) | \textbf{X}((k-1)\Delta t)=\textbf{x}_i]\) can be calculated analytically. The calculation is detailed as follows:

$$\begin{aligned}&\mathbb {E}[ G_j(\textbf{X}((k+1)\Delta t))|\textbf{X}(k\Delta t)=\textbf{x}_i] \nonumber \\&\quad = \int _{\mathbb {R}^n} G(\textbf{x},\varvec{\mu }_{j},\varvec{\Sigma }_{j}) p(\textbf{x}, (k+1)\Delta t|\textbf{x}_i, k\Delta t) d\textbf{x} \nonumber \\&\quad = \int _{\mathbb {R}^n} G(\textbf{x},\varvec{\mu }_{j},\varvec{\Sigma }_{j}) G(\textbf{x}, \textbf{A}_{i}, \textbf{B}_{i}) d\textbf{x} \nonumber \\&\quad =\frac{1}{\sqrt{(2\pi )^{2n}\det (\varvec{\Sigma }_{j}+\textbf{B}_{j})}}\nonumber \\&\qquad \exp \left[ -\frac{1}{2}(\textbf{A}_{i}-\varvec{\mu }_{j})^{T}(\varvec{\Sigma }_{j}+\textbf{B}_{i})^{-1} (\textbf{A}_{i}-\varvec{\mu }_{j})\right] \nonumber \\&\quad =G(\textbf{x}_i, \varvec{\mu }_{j}-\textbf{a}(\textbf{x}_i) \Delta t, \varvec{\Sigma }_{j}+\varvec{\sigma }\varvec{\sigma }^T(\textbf{x}_i)\Delta t). \end{aligned}$$
(22)

The analytical expression for the function \(e_j(\textbf{x}_i)\) is obtained as,

$$\begin{aligned} e_j(\textbf{x}_i)= & {} e^{-\bar{c} \Delta t}G(\textbf{x}_i, \varvec{\mu }_{j}-\textbf{a}(\textbf{x}_i) \Delta t, \varvec{\Sigma }_{j}\nonumber \\{} & {} +\varvec{\sigma }\varvec{\sigma }^T(\textbf{x}_i)\Delta t). \end{aligned}$$
(23)

Therefore, there is no longer a need for simulations to compute the expectation in the loss function (19) from the Feynman–Kac formula.

3.5 Transient response

Let \(\textbf{w}(k)=[w_j(k)] \in \mathbb {R}^{N_G \times 1}\), \(\textbf{p}(k)=[p(\textbf{x}_i, k\Delta t)] \in \mathbb {R}^{N_s \times 1}\), \(\textbf{G}=[G_{ij}]=[G_i(\textbf{x}_j)] \in \mathbb {R}^{N_G \times N_s}\) and \(\textbf{E}=[e_{ij}]=[e_i(\textbf{x}_j)] \in \mathbb {R}^{N_G \times N_s}\), we can rewrite the loss function (19) together with the normalization condition (16) in the matrix form as,

$$\begin{aligned} J(\textbf{w}(k), \lambda (k))&=\frac{1}{2}(\textbf{p}(k-1)-\textbf{E}^T \textbf{w}(k))^T(\textbf{p}(k-1)\nonumber \\&\quad -\textbf{E}^T \textbf{w}(k)) \nonumber \\&\quad +\lambda (k) \left( \sum _{j=1}^{N_G} w_j (k)-1 \right) \nonumber \\&= \frac{1}{2}\left[ \textbf{w}^T(k)\textbf{E}\textbf{E}^T\textbf{w}(k)-2\textbf{w}^T(k)\right. \nonumber \\&\quad \left. \textbf{E}\textbf{p}(k-1)+\textbf{p}^T(k-1)\textbf{p}(k-1)\right] \nonumber \\&\quad +\lambda (k) \left( \sum _{j=1}^{N_G} w_j (k)-1 \right) ,\ \ k\ge 1. \end{aligned}$$
(24)

The optimal weight coefficients are determined to satisfy the necessary conditions for minimization of the loss:

$$\begin{aligned} \frac{\partial J(\textbf{w}(k), \lambda (k))}{\partial \textbf{w}(k)}&= \textbf{E}\textbf{E}^T\textbf{w}(k)-\textbf{E}\textbf{p}(k-1)\nonumber \\&\quad +\lambda (k) \textbf{e}_w=0, \nonumber \\ \frac{\partial J(\textbf{w}(k), \lambda (k))}{\partial \lambda (k)}&= \sum _{j=1}^{N_G} w_j (k)-1 = 0, \end{aligned}$$
(25)

where \(\textbf{e}_w \in \mathbb {R}^{N_G \times 1}\) is a column vector of ones with the same size as \(\textbf{w}\).

We should note that the optimal weight coefficients can also be obtained by making the gradient search algorithms in machine learning. This will be conducted in another paper.

Remark 1

To extend the the Feynman–Kac formula to the steady-state, we assume that \(T\rightarrow \infty \) and \(k\rightarrow \infty \) while \(\Delta t\) is kept finite. We further assume that the stationary solution of the PDF exists. Let \(p_{ss}(\textbf{x})\) denote the stationary PDF. Then, Eq. (13) reads,

$$\begin{aligned} p_{ss}(\textbf{x})=\mathbb {E}\left[ e^{-\int _{0}^{\Delta t}c(\textbf{X}(s))ds} p_{ss}( \textbf{X})\right] . \end{aligned}$$
(26)

Remark 2

Another way to reach the steady-state for autonomous or periodic systems is to consider the solution over consecutive finite time intervals \([k\Delta t, (k+1)\Delta t]\) (\(k=0,1,2,\ldots \)). This approach would lead to map**s of \(p(\textbf{x},k\Delta t) \rightarrow p(\textbf{x},(k+1)\Delta t)\). Such a map** described in the discretized state space has been known as the generalized cell map** (GCM) for stochastic systems [31]. In the framework of cell map**, the stationary response can be obtained with the help of one step transient probability matrix, which we shall discuss later.

3.6 Computation of optimal weights

Let \(D_G\) denote the domain where the system stays with probability not less than 99%. We discretize the domain into uniform grids, which represent the means of Gaussian neurons. The standard deviations for all the Gaussian functions are set equal to the grid size.

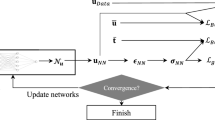
The optimal weight coefficients \(\textbf{w}(k)\) can be computed in Algorithm 1.

Algorithm 1
figure a

The RBFNN method based on the Feynman–Kac formula for the FPK equation.

Full size image

4 Review of the equation-based RBFNN method

Before presenting the computational examples, we briefly review the method of directly solving the FPK equation using RBFNN, referred to as the equation-based RBFNN method. Let the RBFNN in Eq. (14) be the trial solution of the FPK equation at the \(k^{th}\) time step. Consider a finite difference scheme to approximate the time derivative as follows,

$$\begin{aligned} \frac{\partial \bar{p}}{\partial t}=\frac{1}{\Delta t}[\bar{p}(\textbf{x}, \textbf{w}(k))-p(\textbf{x}, (k-1) \Delta t)]. \end{aligned}$$
(27)

By substituting the RBFNN trial solution shown in Eq. (14) and the time derivative shown in Eq. (27) into the FPK Eq. (4), we obtain a local residual \(r(\textbf{x}, \textbf{w}(k))\) as a function of the weight parameters \(\textbf{w}(k)\),

$$\begin{aligned}&r(\textbf{x}, \textbf{w}(k)) = p((k-1)\Delta t, \textbf{x})-\sum _{j=1}^{N_G} w_j(k) s_j(\textbf{x}) , \end{aligned}$$
(28)
$$\begin{aligned}&s_j(\textbf{x}) = -\mathcal {L}_{FPK}[G( \textbf{x}, \varvec{\mu }_j,\! \varvec{\Sigma }_j)]\Delta t + G(\textbf{x}, \varvec{\mu }_j, \! \varvec{\Sigma }_j). \end{aligned}$$
(29)

We define the loss function as

$$\begin{aligned} J(\textbf{w}(k), \lambda (k))&=\frac{1}{2} \sum _{j=1}^{N_s} r^2(\textbf{x}_j, \textbf{w}(k)) +\lambda (k)\nonumber \\&\quad \left( \sum _{i=1}^{N_G} w_i(k)-1 \right) \nonumber \\&= \frac{1}{2}\left[ \textbf{w}^T(k)\textbf{S}\textbf{S}^T\textbf{w}(k)-2\textbf{w}^T(k)\right. \nonumber \\&\quad \left. \textbf{S}\textbf{p}(k-1)+\textbf{p}^T(k-1)\textbf{p}(k-1)\right] \nonumber \\&\quad +\lambda (k) \left( \sum _{j=1}^{N_G} w_j (k)-1 \right) ,\ \ k\ge 1 , \end{aligned}$$
(30)

where \(\textbf{S}=[s_{ij}]=[s_i(\textbf{x}_j)] \in \mathbb {R}^{N_G \times N_s}\). Although both the methods employ the same RBFNN, they represent fundamentally distinct computational paradigms.

The effectiveness and accuracy of the equation-based RBFNN method have been well-documented in previous studies [24,25,26,27]. Therefore, the equation-based RBFNN method will serve as a substitute for MCS to evaluate the proposed RBFNN method based on the Feynman–Kac formula.

5 Examples

We apply the proposed method to obtain steady-state and transient solutions of the FPK equation for three distinct systems without directly using the FPK equation. These systems include a strongly nonlinear system, a vibro-impact non-smooth system and a high-dimensional system.

To evaluate the accuracy of the proposed method, we define two errors. The first is the root mean square (RMS) error of the FPK equation,

$$\begin{aligned} J_{FPK}{=}\sqrt{\int _{\mathbb {R}^n} \left| \frac{\partial \bar{p}_{\Delta t}( \textbf{x},t)}{\partial t} {-} \mathcal {L}_{FPK}\big (\bar{p}_{\Delta t}( \textbf{x},t) \big ) \right| ^2 d\textbf{x}}, \nonumber \\ \end{aligned}$$
(31)

where \(\bar{p}_{\Delta t}( \textbf{x},t)\) represents the PDF derived from the proposed method with the time step size \(\Delta t\).

The second error metric, denoted as \(J_{PDF}\), represents the discrepancy between the PDFs derived from the Feynman–Kac formula and those obtained by the equation-based RBFNN method.

$$\begin{aligned} J_{PDF}=\sqrt{\int _{\mathbb {R}^n} \left| \bar{p}(\textbf{x},t) -p^*(\textbf{x},t) \right| ^2 d\textbf{x}}, \end{aligned}$$
(32)

where \(p^*(\textbf{x},t)\) denotes the PDF derived via the equation-based RBFNN method. These errors are also valid for steady-state cases when \(t\rightarrow \infty \) and \(\frac{\partial \bar{p}_{\Delta t}( \textbf{x},t)}{\partial t} =0\).

Fig. 2
figure 2

The PDFs obtained by the proposed method and the differences to the equation-based RBFNN result for the Van der Pol system in Eq. (33). a–d correspond to time steps \(\Delta t= [10^{-1}, 10^{-2}, 10^{-3}, 10^{-4}]\). e, f show the differences between the results obtained by proposed method and the equation-based RBFNN result

Full size image

5.1 Van der Pol system

We first consider a strongly nonlinear Van der Pol system subject to both additive and multiplicative Gaussian noises.

$$\begin{aligned} \frac{d{X_1}}{d{t}}&=X_2, \nonumber \\ \frac{d{X_2}}{d{t}}&=-\beta (X_1^{2}-1) X_2 - X_1 \nonumber \\&\quad + X_1W_{1}(t) + X_2W_{2}(t) + W_{3}(t), \end{aligned}$$
(33)

where \(W_i(t)\) represent independent Gaussian white noises with intensities \(2D_i\). The drift and diffusion terms of the FPK equation of the Van der Pol system are shown as follows,

$$\begin{aligned} m_{1}&=x_2, \nonumber \\ m_{2}&=-\beta ( x_1^{2}-1) x_2 -x_1+D_2x_2, \nonumber \\ b_{22}&=2D_1x_1^2+2D_2x_2^2+2D_3. \end{aligned}$$
(34)

The parameters are set as \(\beta =1\) and \(2D_i=0.2\). The domain for Gaussian neurons is \(D_G=[-3.2, 3.2]\times [-6.4, 6.4]\) divided into \(N_G=61\times 61\) grids, where \(N_G\) represents the total number of Gaussian neurons. The domain for sampling points is \(D_S=[-4, 4]\times [-8, 8]\) with \(N_s=81\times 81\) points uniformly distributed in the domain. For the sake of fair comparison, the equation-based RBFNN method uses the same parameters and settings.

The computation of expectation of the Feynman–Kac formula is over a time step \(\Delta t\). The integration of the function \(c(\textbf{X}(t))\) and short-time Gaussian approximation both introduce an error of order \(\Delta t\). A proper choice of \(\Delta t\) should balance the solution accuracy and computational cost. We shall examine the effect of \(\Delta t\) in the numerical studies.

5.1.1 Stationary response

We first report the stationary response of the Van der Pol system. Figure 2 presents the PDFs obtained using the proposed RBFNN method based on the Feynman–Kac formula for various time steps \(\Delta t = [10^{-1}, 10^{-2}, 10^{-3}, 10^{-4}]\), along with their discrepancies to the PDFs derived from the equation-based RBFNN method. It is noticeable that the difference decreases with the reduction in time step. Moreover, when \(\Delta t \le 10^{-3}\), the results of the proposed method exhibit good agreement with the equation-based RBFNN result.

Figure 3 shows the effect of the time step \(\Delta t\) on the errors defined earlier. It appears that \(\Delta t=10^{-3}\) is a turning point of \(J_{FPK}\) and can be considered as optimal in terms of the balance of accuracy and efficiency. This is also confirmed by the results in Fig. 2.

Fig. 3
figure 3

Variation of errors with time step \(\Delta t\). Red and blue curves denote the errors defined in Eqs. (31) and (32). Black dashed line represents the FPK error of the solution obtained by the equation-based RBFNN method

Full size image

The total computational times for calculating the stationary responses with the proposed method and the equation-based RBFNN method are 1.7687 s and 2.3383 s, respectively.

5.1.2 Transient response analysis

Next, the RBFNN method based on the Feynman–Kac formula is applied to study the transient responses of the Van der Pol system. The time interval is set to [0, 10]. The time step is \(\Delta t=10^{-3}\). We take a Gaussian PDF with the mean \(\varvec{\mu }_0=[0, 0]\) and the standard deviation \(\varvec{\sigma }_0=[0.1, 0.1]\) as the initial condition.

Figures 4 and 5 show the evolution of the transient response through 3D surface plots and color contours, respectively. Figure 6 shows the marginal PDFs of the transient response of the Van der Pol system.

These results clearly demonstrate that the proposed method with a time step \(10^{-3}\) yields results that are in close agreement with those obtained from the equation-based RBFNN method. The total computational times for calculating the transient responses with the proposed method and the equation-based RBFNN method are 2393 s and 2386 s, respectively.

Fig. 4
figure 4

3D surface plots of PDFs and differences to the equation-based RBFNN result of the Van der Pol system. a–d are the transient PDFs at \(t=1.5\) s, 3 s, 5 s and the stationary PDF, respectively, obtained by the proposed method. e–h show the differences between the results obtained by proposed method and the equation-based RBFNN results. The peaks of the error are of order \(10^{-4}\)

Full size image
Fig. 5
figure 5

Color contours of PDFs and differences to the equation-based RBFNN result of the Van der Pol system. a–d are the transient PDFs at \(t=1.5\) s, 3 s, 5 s and the stationary PDF, respectively, obtained by the proposed method. e–h show the differences between the results obtained by proposed method and the equation-based RBFNN results

Full size image
Fig. 6
figure 6

The \(x_1\) and \(x_2\) marginal PDFs of the Van der Pol system at different times. a \(p_{x_1}(\textbf{x}_1)\). b \(p_{x_2}(\textbf{x}_2)\). Lines: by the proposed method. Circles: by the equation-based RBFNN method

Full size image

5.2 Nonlinear vibro-impact system

Next, we consider a tri-stable vibro-impact system subject to both additive and multiplicative Gaussian noises.

$$\begin{aligned} \frac{d{X_1}}{d{t}}&=X_2, \nonumber \\ \frac{d{X_2}}{d{t}}&=-\beta _1X_2-f(X_1)-\alpha _1 X_1-\alpha _3 X_1^3 \nonumber \\&\quad -\alpha _5X_1^5 + X_1W_{1}(t) + X_2W_{2}(t) + W_{3}(t), \end{aligned}$$
(35)

where \(W_i(t)\) represent independent Gaussian white noises with intensities \(2D_i\), and \(f(x_1)\) denotes the impact force. This force is described by the Hertz contact law when the mass collides with the barrier.

$$\begin{aligned} f(x_1) = \left\{ \begin{array}{cr} B_r (x_1-\delta _r)^{1.5}, &{} x_1 \ge \delta _r \\ 0, &{} \ \ \delta _l \le x_1 \le \delta _r \\ -B_l (\delta _l-x_1)^{1.5}, &{} x_1 \le \delta _l \end{array} \right. \end{aligned}$$
(36)

where \(\delta _r\) and \(\delta _l\) denote the distances from the equilibrium point of the impact oscillator to the right and left impact barriers, respectively. The constants \(B_r\) and \(B_l\) correspond to properties determined by the material composition and geometric characteristics of these impact barriers.

The drift and diffusion terms of the vibro-impact system are shown as follows,

$$\begin{aligned} m_{1}&=x_2,\nonumber \\ m_{2}&{=}{-}\beta _1x_2-f(x_1){-}\alpha _1 x_1{-}\alpha _3 x_1^3-\alpha _5x_1^5 +D_2x_2,\nonumber \\ b_{22}&=2D_1x_1^2+2D_2x_2^2+2D_3. \end{aligned}$$
(37)

The parameters are set as \(\beta _1=0.2\), \(\alpha _1=1\), \(\alpha _3=-4\), \(\alpha _5=1\) and \(2D_i=0.2\). The domain \(D_G=[-3.2, 3.2]\times [-6.4, 6.4]\) is divided into \(N_G=61\times 61\) grids. The domain of sampling points is \(D_S=[-4, 4]\times [-8, 8]\). \(N_s=81\times 81\) points are uniformly sampled in \(D_s\).

5.2.1 Stationary response analysis

Figure 7 presents the PDFs obtained using the proposed RBFNN method based on the Feynman–Kac formula for various time steps \(\Delta t = [10^{-1}, 10^{-2}, 10^{-3}, 10^{-4}]\). These results clearly demonstrate that for systems with multiple equilibrium states, the errors introduced by a larger \(\Delta t\) can lead to incorrect predictions, causing the steady-state response to erroneously converge to incorrect equilibrium states. This highlights the importance of selecting an appropriate \(\Delta t\) for accurate prediction in such complex systems.

Fig. 7
figure 7

The stationary PDF solutions of the vibro-impact system using the proposed method for various time steps \(\Delta t=[10^{-1}, 10^{-2}, 10^{-3}, 10^{-4}]\). a–d are color contours. e, f are 3D surface plots

Full size image

The variation of errors with \(\Delta t\) is illustrated in Fig. 8. The result indicates again that \(\Delta \le 10^{-3}\) is optimal with a good balance of accuracy and efficiency.

Fig. 8
figure 8

Variation of the error with time step \(\Delta t\) for the Vibro-impact system. Red and blue curves denote the errors defined in Eqs. (31) and (32). Black dashed line represents the FPK error of the accurate solution derived by the equation-based RBFNN method

Full size image

For the proposed method and the equation-based RBFNN method, the total computational times for calculating the stationary responses are 1.3746 s and 5.2292 s, respectively.

5.2.2 Transient response analysis

Next, we study the transient responses of the vibro-impact system. The time interval is set as [0, 10] and the time step is chosen as \(\Delta t=10^{-3}\). We consider a Gaussian PDF with the mean \(\varvec{\mu }_0=[0, 0]\) and the standard deviation \(\varvec{\sigma }_0=[0.1, 0.1]\) as the initial condition.

Figures 9 and 10 illustrate the transient response evolution using the 3D surface plots and color contours, in comparison with the equation-based RBFNN result. Figure 11 shows the evolution of the marginal PDFs of the transient response of the vibro-impact system. These results clearly demonstrate that the proposed method, when employed with a time step size of \(10^{-3}\) yields results that are in close agreement with those obtained from the equation-based RBFNN method.

For the proposed method and the equation-based RBFNN method, the total computational times for calculating the transient responses are 2561 s and 2570 s, respectively.

Fig. 9
figure 9

3D surface plots of PDFs and differences to the equation-based RBFNN result for the vibro-impact system. a–d are the transient PDFs at \(t=3\) s, 6 s, 8 s and the stationary PDF, respectively, obtained by the proposed method. e–h show the differences between the results obtained by proposed method and the equation-based RBFNN results. The peaks of the error are of order \(10^{-3}\)

Full size image
Fig. 10
figure 10

Color contours of PDFs and differences to the equation-based RBFNN result for the vibro-impact system. a–d are the transient PDFs at \(t=3\) s, 6 s, 8 s and the stationary PDF, respectively, obtained by the proposed method. e–h show the differences between the results obtained by proposed method and the equation-based RBFNN results

Full size image
Fig. 11
figure 11

The marginal PDFs of the vibro-impact system for \(x_1\) and \(x_2\) at different instants. a The marginal PDF \(p_{x_1}(\textbf{x}_1)\). b The marginal PDF \(p_{x_2}(\textbf{x}_2)\). Lines: solutions obtained by the proposed method. Circles: solutions obtained by the equation-based RBFNN method

Full size image

5.3 System of two coupled duffing oscillators

As the last example, we consider a 4D coupled-Duffing system to demonstrate the effectiveness of the proposed method in high-dimensional systems. The governing equations are given by,

$$\begin{aligned} \frac{d{X_1}}{d{t}}&=X_2, \nonumber \\ \frac{d{X_2}}{d{t}}&=-\omega _1^2X_1-k_1X_1^3-k_3X_3-k_4X_1^2X_3 \nonumber \\&\quad -\mu _1X_2+ X_1W_{1}(t) + X_2W_{2}(t) + W_{3}(t), \nonumber \\ \frac{d{X_3}}{d{t}}&=X_4, \nonumber \\ \frac{d{X_4}}{d{t}}&=-\omega _2^2X_3-k_2X_3^3-k_3X_1-k_4X_1^3/3 \nonumber \\&\quad -\mu _2X_4+ X_3W_{4}(t) + X_4W_{5}(t) + W_{6}(t), \end{aligned}$$
(38)

where \(W_i(t)\) are independent and zero-mean Gaussian white noises with intensities \(2D_i\). The drift and diffusion terms are given by

$$\begin{aligned} m_{1}&=x_2,\nonumber \\ m_{2}&{=}{-}\omega _1^2x_1-k_1x_1^3{-}k_3x_3-k_4x_1^2x_3{-}\mu _1x_2+D_2x_2,\nonumber \\ m_{3}&=x_4, \nonumber \\ m_{4}&{=}{-}\omega _2^2x_3{-}k_2x_3^3-k_3x_1{-}k_4x_1^3/3-\mu _2x_4{+}D_2x_2, \nonumber \\ b_{22}&=2D_1x_1^2+2D_2x_2^2+2D_3 \nonumber \\ b_{44}&=2D_4x_3^2+2D_5x_4^2+2D_6. \end{aligned}$$
(39)

The parameters are \(k_1=0.3\), \(k_2=0.5\), \(k_3=0.3\), \(k_4=0.12\), \(\mu _1=0.2\), \(\mu _2=0.2\), \(\omega _1=0.2\), \(\omega _2=0.4\) and \(2D_i=0.04\). The domain \(D_G=[-2, 2]^4\) is divided into \(N_G=16^4\) grids. The sampling domain is \(D_S=[-2.5, 2.5]^4\). \(N_s=21^4\) points are uniformly sampled in \(D_s\). The equation-based RBFNN method with the same settings is utilized for comparison.

5.3.1 Stationary response analysis

The variation of the errors with \(\Delta t\) is illustrated in Fig. 12. It can be observed that \(J_{FPK}\) converges towards the RMS error of the solution directly obtained from the FPK equation with \(\Delta \le 10^{-3}\).

Fig. 12
figure 12

Variation of errors with \(\Delta t\) for the 4D coupled Duffing system. Red and blue curves denote the errors defined in Eqs. (31) to (32). Black dashed line represents the FPK error of the accurate solution by the equation-based RBFNN method

Full size image

We select the time step size \(\Delta t=10^{-3}\). The color contours of the stationary joint PDFs projected to different sub-spaces are shown in Fig. 13. The agreement between the proposed method and the equation-based RBFNN results is very good. The total computational times for calculating the stationary responses with the proposed method and the equation-based RBFNN method are 2671 s and 3592 s, respectively.

We skip the transient responses of this example for the sake of length of the paper.

6 Comparison of computational time

Finally, we analyze the computational time for both the proposed method and the equation-based RBFNN method. We focus on the results for stationary response PDFs. It can be observed that the main time-consuming steps of both the methods can be divided into three parts:

  1. 1.

    Compute the matrix \(\textbf{G}\).

  2. 2.

    Compute the matrix \(\textbf{E}\).

  3. 3.

    Search for the optimal coefficients.

The computational times required for the stationary responses of three examples are listed in Tables 1 to 3.

Fig. 13
figure 13

Color contours of the stationary joint PDFs projected to \(x_1-x_2\), \(x_1-x_3\), \(x_2-x_3\) and \(x_2-x_4\) subspaces. a–d display the joint PDFs by the proposed method. e–h display the joint PDFs by the equation-based RBFNN method

Full size image
Table 1 The computational time for stationary response PDF of the Van der Pol system
Full size table
Table 2 The computational time for stationary response PDF of the vibro-impact system
Full size table
Table 3 The computational time for stationary response PDF of the 4D coupled Duffing system
Full size table

Since both the methods make use of RBFNN, the times for the first and third steps are similar. However, it is observable that the proposed method significantly reduces computational time in the second step compared to the equation-based RBFNN method. This reduction is attributed to the fact that the proposed method does not involve derivative calculations in computing the expected function shown in Eq. (18). These examples offer compelling evidence of efficiency of the proposed method.

7 Conclusion

We have developed a numerical method based on the Feynman–Kac formula, capable of solving parabolic PDEs without directly dealing with the equation. The proposed method employs a RBFNN to approximate the PDF of the stochastic process. The STGA technique is used to derive an analytical expression for the expectation of the stochastic martingale process \(\mathcal {M}(t)\), thus eliminating the need for numerical simulations. The martingale property of the process \(\mathcal {M}(t)\) provides an implicit integral equation describing the evolution of the PDF starting from a given initial condition. The integral equation has been shown to be equivalent to the FPK equation. Hence, the solution of the FPK equation is obtained without using the FPK equation. Three challenging examples of nonlinear stochastic systems are studied with the proposed method. The results are compared with the equation-based RBFNN solution in terms of accuracy and efficiency. It is found that the proposed method is quite competitive and promising for analyzing high-dimensional nonlinear stochastic systems. However, in this preliminary study of applying the Feynman–Kac formula to obtain the solution of the FPK equation, many theoretical issues of the method are not addressed including stability and convergence of the proposed method.