1 Introduction

In December 2019, a novel enveloped RNA beta-coronavirus that causes coronavirus disease, COVID-19, emerged in Wuhan, China, and the disease has quickly turned into a global crisis. The effects of the spread of the disease and the factors affecting its spread have been investigated [1, 2]. In the COVID-19 outbreak, presymptomatic, asymptomatic, and symptomatic cases are known to have separate roles on the transmission chains [3,4,5,6] due to the considerable length of the incubation periods [7]. The COVID-19 outbreak has lower latency periods than the incubation periods, which explains the existence of the presymptomatic transmission [3]. Additionally, the role of presymptomatic and asymptomatic transmissions was shown to be around %50 of total cases [5].

The existence of the presymptomatic, asymptomatic, and symptomatic infectors led the mathematical modelers to derive suitable compartmental models [5, 8,9,10] for the COVID-19 outbreak. These models are represented by the ordinary differential equations (ODEs) system and have the exponential distribution assumption of the sojourn times. However, statistical analyses of the latency, presymptomatic, asymptomatic, and symptomatic periods of the COVID-19 outbreak with clinical data suggest that the necessity of the Erlang, lognormal, or Weibull-like probability distributions functions (pdf) to represent the sojourn times [11,12,13,14]. In this context, the exponentially distributed ODE models fail to represent the true dynamics by approximating the realistic pdf of sojourn times.

Non-exponentially distributed compartmental models such as the SIR [15, 16], the SEIR [17, 18] or the SEQIHR models [19,20,21] were extensively studied in the literature to represent the existing sojourn time distributions realistically. The idea behind such models consisted of using survival functions in the model equations. The resulting non-exponentially distributed models have been generally represented by the Volterra integral equations [19]. These models were derived from understanding the effect of the sojourn time distributions on non-pharmacological interventions such as quarantine and isolation [19,20,21]. Additionally, how and when exponential distribution assumptions may fail were investigated through these studies.

The basic reproduction number \(\left( R_0\right) \) of an outbreak denotes the mean number of secondary infections during which the whole population is susceptible, and the non-pharmacological interventions have not yet been implemented. As realized from the definition, one needs two critical parameters for the estimation of \(R_0\): the transmission rate and infectiousness period of an outbreak such as COVID-19 [8, 22]. For early dynamics of an outbreak, it is common to relate \(R_0\) with the intrinsic growth rate (r) of the stage functions [23,24,25,26]. In this context, various studies have been carried out to find more realistic \(r-R_0\) relations in the presence of an arbitrary distribution of the sojourn times. For example, widely considered formulations \(R_0=1+rT_P\) and \(R_0=\left( 1+rT_E\right) \left( 1+rT_P\right) \) (\(T_E\) and \(T_P\) are the mean latency and infectious periods) were shown to belong to the exponentially distributed SIR and SEIR models, respectively [25]. Generalizations of these formulae were done by using the well-known Euler–Lotka equations [27]. Thence, derivation of such a generalized relation \(r-R_0\) for the early dynamics of the COVID-19 outbreak is one of the primary aims of this study.

Fig. 1
figure 1

Graphical illustration for branching process of the SEPADC model. \(P_E\left( s\right) ,\ P_P\left( s\right) ,\ P_A\left( s\right) \) and \(P_D\left( s\right) \) denote the survival functions for exposed, presymptomatic, asymptomatic and symptomatic stages

Full size image
Fig. 2
figure 2

Illustration of the various survival functions for latency and infectious periods with mean \(\mu =4\)

Full size image

In this study, we have derived an S (Susceptible)-E (Exposed)-P (Presymptomatic)-A (Asymptomatic)-D (Symptomatic)-C (Reported) model by taking into account the arbitrary distribution of latency, presymptomatic, asymptomatic and symptomatic periods. Derivation of the SEPADC model is inspired by two facts: the existence of the separate roles of presymptomatic, asymptomatic, and symptomatic infectors [4] and the reality of the arbitrary distributions of the sojourn times [19]. Here we have shown that the exponential and delta-distributed models can be reduced from the general SEPADC model by converting the Volterra integral equations into the system of ODEs. Using the well-known Euler–Lotka equation, we have formulated \(r-R_0\) relation of the SEPADC model through the Laplace transforms of the pdf of sojourn time distributions. We have also shown that some existing \(r-R_0\) relations are exceptional cases of our \(r-R_0\) formula by considering the widely used exponential, delta, and Erlang distributions. \(R_0\) values of COVID-19 outbreak for 152 countries around the world are estimated through our novel \(r-R_0\) formulation. We have shown the global convergence, \(R_0=4.58\), through the Erlang distribution of the sojourn times. We have also studied how the sojourn time distributions affected the morphologies of the epidemic curves.

2 SEPADC model with arbitrary sojourn time distributions

2.1 Derivation of the SEPADC model

We assume that the whole population is divided into six categories with \(S\left( t\right) \) (susceptible), E(t) (exposed), P(t) (presymptomatic), A(t) (asymptomatic), D(t) (symptomatic) and C(t) (reported). The existence of the separate roles of the presymptomatic, asymptomatic, and symptomatic infectors for the dynamics of COVID-19 can be seen in various studies such as [4, 5]. Graphical illustration of our SEPADC model can be seen in Fig. 1. Let us denote the survival functions \(P_E,\ P_P,\ P_A,\ P_D:\left[ 0,\ \infty \right) \rightarrow [0,1]\) having the probability density functions \(p_{E},p_{P},p_{A},p_{D}:\left[ 0,\ \infty \right) \rightarrow \left[ 0,1\right] \) with the relation

$$\begin{aligned} P_X\left( s\right) =\int ^{\infty }_s{p_X\left( x\right) \textrm{d}x} \end{aligned}$$
(1)

where \(X=E,\ P,\ A,\ D.\) The survival function \(P_X\left( s\right) \) has the following properties [19].

$$\begin{aligned} P_X\left( 0\right) =1,\ \dot{P}_X(s)\le 0 \quad \text {and} \quad \int ^{\infty }_0{P_X\left( s\right) \textrm{d}s<\infty .} \end{aligned}$$
(2)

The derivative of survival function is denoted by \(\dot{P}_X(s)\) and \(-\dot{P}_X(s)=p_X\left( s\right) \) yields the rate of removal from the state i at state age s. In mathematical epidemiology, exponential, delta, and gamma-distributed sojourn times are standard in practice [25], and some of the survival functions generated by these distributions are illustrated in Fig. 2.

In our modeling framework, susceptible persons become exposed if they encounter presymptomatic, asymptomatic, or symptomatic persons by considering bilinear incidence term \(\theta \left( t\right) \frac{S(t)}{N}\) with

$$\begin{aligned} \theta \left( t\right) =\beta \left[ P\left( t\right) +{\mu }_aA\left( t\right) +{\mu }_dD(t)\right] \end{aligned}$$
(3)

where N is the total population, \(\beta \) is the constant transmission rate, \({\mu }_a\) is the reduction/extension factor of asymptomatic transmission, and \({\mu }_d\) is the reduction/extension factor of symptomatic transmission. The baseline transmission rate \(\beta \) is then varying according to the person’s stage since presymptomatic, asymptomatic, and symptomatic transmission rates may not be equivalent [4]. Thus, assuming S(0) as the initial number of susceptible persons, the following equation

$$\begin{aligned} S\left( t\right) =S\left( 0\right) -\int ^t_0{\theta \left( s\right) \frac{S\left( s\right) }{N}\textrm{d}s} \end{aligned}$$
(4)

is considered. Since \(\dot{S}\left( t\right) =-\theta \left( t\right) \frac{S\left( t\right) }{N}\), the number of exposed persons must satisfy the following equation by considering arbitrary survival function, \(P_E\left( s\right) \),

$$\begin{aligned} E\left( t\right) =\tilde{E}\left( t\right) +\int ^t_0{\theta \left( s\right) \frac{S\left( s\right) }{N}P_E\left( t-s\right) \textrm{d}s} \end{aligned}$$
(5)

where \(\tilde{E}\left( t\right) \) represents the number of initially exposed and still exposed persons as

$$\begin{aligned} \tilde{E}\left( t\right) =E(0)P_E\left( t\right) . \end{aligned}$$
(6)

We assume that exposed persons continue their way by either becoming presymptomatic with probability \(\alpha \) or asymptomatic with probability \((1-\alpha ).\) Thus, since \(-\dot{P}_E(s)\) denotes the removal rate from the exposed stage, \(P\left( t\right) \) and \(A\left( t\right) \) should satisfy the following equations

$$\begin{aligned} P\left( t\right)= & {} \tilde{P}(t){+}\alpha \int ^t_0 \int ^{\tau }_0\theta \left( s\right) \frac{S\left( s\right) }{N}\left[ {-}\dot{P_E}\left( \tau {-}s\right) \right] \nonumber \\{} & {} \times P_P(t{-}\tau )\textrm{d}s\textrm{d}\tau ,\end{aligned}$$
(7)
$$\begin{aligned} A\left( t\right)= & {} \tilde{A}(t){+}(1{-}\alpha )\int ^t_0 \int ^{\tau }_0 \theta \left( s\right) \frac{S\left( s\right) }{N}\nonumber \\{} & {} \times \left[ {-}\dot{P_E}\left( \tau {-}s\right) \right] P_A(t{-}\tau )\textrm{d}s\textrm{d}\tau \nonumber \\ \end{aligned}$$
(8)

where \(\tilde{P}(t)\) and \(\tilde{A}(t)\) represent the number of presymptomatic and asymptomatic persons who were either exposed or pre/asymptomatic at \(t=0\) defined by

$$\begin{aligned} \tilde{P}(t)= & {} P\left( 0\right) P_P(t)+\alpha E(0)\int ^t_0{\left[ {-}\dot{P}_E\left( s\right) \right] P_P(t{-}s)}\nonumber \\{} & {} \times \textrm{d}s, \end{aligned}$$
(9)
$$\begin{aligned} \tilde{A}(t)= & {} A\left( 0\right) P_A(t)\nonumber \\{} & {} +(1{-}\alpha )E(0)\int ^t_0 {\left[ {-}\dot{P}_E\left( s\right) \right] P_A(t-s)}\textrm{d}s.\nonumber \\ \end{aligned}$$
(10)

Since asymptomatically recovered persons have no impact on reported cases, we omit the future of the asymptomatic persons after they are removed. Presymptomatic persons will be removed with the rate \(-\dot{P}_P(s)\) to become symptomatically infected and the equation of D(t) can be expressed as follows

$$\begin{aligned}{} & {} D\left( t\right) {=}\tilde{D}(t){+}\alpha \int ^t_0{\int ^u_0{\int ^{\tau }_0{\theta \left( s\right) \frac{S\left( s\right) }{N}\left[ {-}{\dot{P}}_E\left( \tau {-}s\right) \right] }}}\nonumber \\{} & {} \qquad \quad \left[ {-}{\dot{P}}_P\left( u{-}\tau \right) \right] P_D(t{-}u)\textrm{d}s\textrm{d}\tau \textrm{d}u. \end{aligned}$$
(11)

where \(\tilde{D}(t)\) denotes the contributions of \(E\left( 0\right) ,\ P\left( 0\right) \) and \(D\left( 0\right) \) as follows

$$\begin{aligned} \tilde{D}\left( t\right)= & {} D\left( 0\right) D_P\left( t\right) {+}I\left( 0\right) \int ^t_0{\left[ {-}\dot{P_I}\left( s\right) \right] }\nonumber \\{} & {} {\times P_D\left( t{-}s\right) }\textrm{d}s {+}\alpha E\left( 0\right) \int ^t_0\int ^{\tau }_0\left[ {-}{\dot{P}}_E\left( \tau \right) \right] \nonumber \\{} & {} \times \left[ {-}{\dot{P}}_P\left( t{-}\tau \right) \right] P_D\left( t-u\right) \textrm{d}\tau \textrm{d}u. \end{aligned}$$
(12)

In our modeling framework, symptomatic persons become the reported ones after they complete their symptomatic periods with survival function \(P_D\left( s\right) \). Function \(P_D\left( s\right) \) can be realized as the probability of going to the hospital of a symptomatic person with age s. Thence, C(t) should satisfy the following equation

$$\begin{aligned} C\left( t\right)= & {} \tilde{C}(t)+\alpha \int ^t_0\int ^v_0\int ^u_0\int ^{\tau }_0\theta \left( s\right) \frac{S\left( s\right) }{N}\nonumber \\{} & {} \times \left[ -{\dot{P}}_E\left( \tau -s\right) \right] \left[ -{\dot{P}}_P\left( u-\tau \right) \right] \nonumber \\{} & {} \times \left[ -{\dot{P}}_D\left( v-u\right) \right] \textrm{d}s\textrm{d}\tau \textrm{d}u\textrm{d}v. \end{aligned}$$
(13)

where \(\tilde{C}(t)\) represents the contributions of \(E\left( 0\right) ,\!\!\ P\left( 0\right) ,\) \(D\left( 0\right) \) and \(C\left( 0\right) \) as follows

$$\begin{aligned} \tilde{C}\left( t\right)= & {} C\left( 0\right) +D\left( 0\right) \int ^t_0{\left[ {-\dot{P}}_D\left( s\right) \right] }\textrm{d}s\nonumber \\{} & {} +I\left( 0\right) \int ^t_0{\int ^{\tau }_0{\left[ -{\dot{P}}_I\left( u\right) \right] \left[ -{\dot{P}}_D\left( v-u\right) \right] }}\textrm{d}u\textrm{d}v\nonumber \\{} & {} +\alpha E\left( 0\right) \int ^t_0{\int ^u_0\int ^\tau }_0\left[ -{\dot{P}}_E\left( \tau \right) \right] \nonumber \\{} & {} \times \left[ -\!{\dot{P}}_P\left( u\!-\!\tau \right) \right] \left[ -{\dot{P}}_D\left( v\!-\!u\right) \right] \textrm{d}\tau \textrm{d}u\textrm{d}v. \end{aligned}$$
(14)

Combining all these equations, we reach the following system of the Volterra integral equations representing our SEPADC model

$$\begin{aligned}{} & {} S\left( t\right) =S\left( 0\right) -\int ^t_0{\theta \left( s\right) \frac{S\left( s\right) }{N}\textrm{d}s,}\nonumber \\{} & {} E\left( t\right) =\tilde{E}\left( t\right) +\int ^t_0{\theta \left( s\right) \frac{S\left( s\right) }{N}P_E\left( t-s\right) \textrm{d}s},\nonumber \\{} & {} P\left( t\right) =\tilde{P}(t)+\alpha \int ^t_0\int ^{\tau }_0\theta \left( s\right) \frac{S\left( s\right) }{N}\nonumber \\{} & {} \quad \left[ -\dot{P_E}\left( \tau -s\right) \right] P_P(t-\tau )\textrm{d}s\textrm{d}\tau ,\\{} & {} A\left( t\right) =\tilde{A}(t)+(1-\alpha )\nonumber \\{} & {} \quad \int ^t_0{\int ^{\tau }_0{\theta \left( s\right) \frac{S\left( s\right) }{N}\left[ -\dot{P_E}\left( \tau -s\right) \right] P_A(t-\tau )}\textrm{d}s\textrm{d}\tau ,}\nonumber \\{} & {} D\left( t\right) {=}\tilde{D}(t){+}\alpha \nonumber \\{} & {} \quad \int ^t_0\int ^u_0\int ^{\tau }_0\theta \left( s\right) \frac{S\left( s\right) }{N}\left[ {-}{\dot{P}}_E\left( \tau {-}s\right) \right] \left[ {-}{\dot{P}}_P\left( u{-}\tau \right) \right] \nonumber \\{} & {} \quad P_D(t-u)\textrm{d}s\textrm{d}\tau \textrm{d}u,\nonumber \\{} & {} C\left( t\right) =\tilde{C}(t)+\alpha \nonumber \\{} & {} \quad \int ^t_0\int ^v_0\int ^u_0\int ^{\tau }_0\theta \left( s\right) \frac{S\left( s\right) }{N}\left[ -{\dot{P}}_E\left( \tau -s\right) \right] \nonumber \\{} & {} \left[ -{\dot{P}}_P\left( u-\tau \right) \right] \nonumber \\{} & {} \left[ -{\dot{P}}_D\left( v-u\right) \right] \textrm{d}s\textrm{d}\tau \textrm{d}u\textrm{d}v,\nonumber \end{aligned}$$
(15)

where \(S\left( 0\right) ,\ E\left( 0\right) ,\ P\left( 0\right) ,\ A\left( 0\right) ,\ D\left( 0\right) ,C\left( 0\right) \le N\) are the given initial conditions of the model. The following subsection shows that the SEPADC model can be simplified with ordinary differential equations (ODEs) by considering exponential or delta distributions for sojourn times.

2.2 Special cases: exponential and delta distributions (SEPADC-e, SEPADC-d)

2.2.1 Exponentially distributed sojourn times, the SEPADC-e model

Here we reduce the Volterra integral equation system (15) into the system of ODEs by using \(P_i\left( s\right) =e^{-\frac{1}{T_i}s}\). Exponentially distributed sojourn times (EDST) with mean \(\frac{1}{T_i}\) and survival function \(P_i\left( s\right) =e^{-\frac{1}{T_i}s}\) for \(i=E,P,A,D\). The EDST assumption is the most common assumption for modeling COVID-19 [8, 10, 28]. The EDST assumption reduces system (15) into the following system of ODEs

$$\begin{aligned}{} & {} \frac{\textrm{d}s}{\textrm{d}t}=-\theta \left( t\right) \left( \frac{S\left( t\right) }{N}\right) , \\{} & {} \frac{\textrm{d}E}{\textrm{d}t}=\theta \left( t\right) \left( \frac{S\left( t\right) }{N}\right) -\frac{1}{T_E}E\left( t\right) , \end{aligned}$$
$$\begin{aligned} \frac{\textrm{d}P}{\textrm{d}t}=\alpha \frac{E\left( t\right) }{T_E}-\frac{P\left( t\right) }{T_P}, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} \frac{\textrm{d}A}{\textrm{d}t}=\left( 1-\alpha \right) \frac{E\left( t\right) }{T_E}-\frac{A\left( t\right) }{T_A}, \\{} & {} \frac{\textrm{d}D}{\textrm{d}t}=\frac{P\left( t\right) }{T_P}-\frac{D\left( t\right) }{T_D}, \\{} & {} \frac{\textrm{d}C}{\textrm{d}t}=\frac{D\left( t\right) }{T_D}, \end{aligned}$$

where \(T_E,\ T_P,\ T_A\), and \(T_D\) stand for mean sojourn times of exposed, presymptomatic, asymptomatic, and symptomatic persons, respectively. Derivation of model (16) can be found in “Appendix A”. We call this model as the SEPADC-e model having the EDST assumption.

2.2.2 Delta-distributed sojourn times, the SEPADC-d model

The EDST assumptions fail when the sojourn times are distributed around their means. In such scenarios, a limit case with non-random or delta-distributed sojourn times (DDST) play a vital role by selecting the survival functions as [25]

$$\begin{aligned} P_i\left( s\right) =\left\{ \begin{array}{ll} 1, &{}\quad s\le T_i \\ 0,&{} \quad s>T_i \end{array} \right. \end{aligned}$$
(17)

where \(i=E,\ P,\ A,\ D\) and \(T_i\) are corresponding fixed sojourn times. The DDST assumption with survival functions (17) yields the following system of delay ODEs

$$\begin{aligned}{} & {} \frac{\textrm{d}S}{\textrm{d}t}=-\theta \left( t\right) \left( \frac{S\left( t\right) }{N}\right) , \\{} & {} \frac{\textrm{d}E}{\textrm{d}t}=\theta \left( t\right) \left( \frac{S\left( t\right) }{N}\right) -\theta \left( t-T_E\right) \left( \frac{S\left( t-T_E\right) }{N}\right) , \end{aligned}$$
$$\begin{aligned}{} & {} \frac{\textrm{d}P}{\textrm{d}t}=\alpha \theta \left( t-T_E\right) \left( \frac{S\left( t-T_E\right) }{N}\right) \nonumber \\{} & {} \quad -\alpha \theta \left( t-T_E-T_P\right) \left( \frac{S\left( t-T_E-T_P\right) }{N}\right) , \end{aligned}$$
(18)
$$\begin{aligned}{} & {} \frac{\textrm{d}A}{\textrm{d}t}=\left( 1-\alpha \right) \theta \left( t-T_E\right) \left( \frac{S\left( t-T_E\right) }{N}\right) \\{} & {} -\left( 1-\alpha \right) \theta \left( t-T_E-T_A\right) \left( \frac{S\left( t-T_E-T_A\right) }{N}\right) , \\{} & {} \frac{\textrm{d}D}{\textrm{d}t}=\alpha \theta \left( t-T_E-T_P\right) \left( \frac{S\left( t-T_E-T_P\right) }{N}\right) \\{} & {} -\alpha \theta \left( t-T_E-T_P{-T}_D\right) \left( \frac{S\left( t-T_E-T_P{-T}_D\right) }{N}\right) , \\{} & {} \frac{\textrm{d}C}{\textrm{d}t}=\alpha \theta \left( t-T_E-T_P{-T}_D\right) \\{} & {} \qquad \times \left( \frac{S\left( t-T_E-T_P{-T}_D\right) }{N}\right) , \end{aligned}$$

where \(T_E,\ T_P,\ T_A\) and \(T_D\) are the fixed sojourn times of the corresponding states. The history of the number of infected persons is assumed to be zero, i.e., \(E\left( t\right) ,\ P\left( t\right) ,\ A\left( t\right) ,\ D\left( t\right) =0\) for \(t<0\) for simplicity. We call model (18) as SEPADC-d. The detailed derivation of the model (18) from the generalized model (15) can be found in “Appendix B”. Note that it is also possible to consider the Erlang distributed sojourn times and reduce the system (15) into \(4\left( k+1\right) +2\) dimensional ODEs where k is the shape parameter of the Erlang distribution [19]. For the sake of simplicity, we only derive the relations \(r-R_0\) in the presence of the Erlang distributions in the next section.

3 \(\varvec{r}\varvec{-}{\varvec{R}}_{\varvec{0}}\) relation for the SEPADC model

Early dynamics of the SEPADC model (15) with \(S\cong N\) provides a branching process as illustrated in Fig. 1 by considering separate roles of presymptomatic, asymptomatic, and symptomatic infectors. Thus, the SEPADC model (15) is compatible with earlier versions of branching models such as the SIR and SEIR [25]. In this context, it is inevitable to benefit from existing generalized formulae given in the literature [25, 27]

$$\begin{aligned}{} & {} \int ^{\infty }_0{\beta (\tau )\overline{A}}(\tau )\textrm{d}\tau =R_0 \end{aligned}$$
(19)
$$\begin{aligned}{} & {} \int ^{\infty }_0{e^{-r\tau }\beta (\tau )\overline{A}}(\tau )\textrm{d}\tau =1 \end{aligned}$$
(20)

where r is the intrinsic growth rate of branching process, \(\beta (\tau )\) is the instantaneous function for infectivity at time \(\tau \), and \(\overline{A}(\tau )\) is the age of infection function. Equation (20) is also known as the Euler–Lotka equation [25, 27] and provides valuable insight over various types of renewal equations of compartmental models such as the SIR or SEIR models [27]. r denotes the intrinsic growth rate of a branching process and is equal to the growth rate of the system around the disease-free equilibrium (dfe), i.e., the largest eigenvalue of the linearized model around the dfe. Our SEPADC model (15) assumes constant infectivity rate \(\beta (\tau )=\beta \) and \(\overline{A}(\tau )\) have three contributions from \(P(t),\ A(t)\) and D(t) as follows

$$\begin{aligned} \overline{A}(\tau )=\alpha {\overline{A}}_P(\tau )+\left( 1-\alpha \right) {\mu }_a{\overline{A}}_A(\tau )+\alpha {\mu }_d{\overline{A}}_D(\tau ) \end{aligned}$$
(21)

where \({\overline{A}}_X(\tau )\) denotes the age of infection function of the individual belonging to the stage X for \(X=P,A,D.\) Let us first formulate \({\overline{A}}_P(\tau )\) for general survival functions \(P_X\left( \tau \right) \) as follows

$$\begin{aligned} {\overline{A}}_P(\tau )=\int ^{\tau }_0{P_P\left( \tau -x\right) p_E\left( x\right) \textrm{d}x} \end{aligned}$$
(22)

where \(p_E\left( x\right) \) denotes the probability density function (pdf) of the exposed stage. By using the relation given in Eq. (1), Eq. (22) can be written as

$$\begin{aligned} {\overline{A}}_P(\tau )= & {} \int ^{\infty }_{\tau }{\int ^y_0{p_P\left( y-x\right) p_E\left( x\right) \textrm{d}x\textrm{d}y}}\nonumber \\{} & {} -\int ^{\infty }_{\tau }p_E\left( x\right) \textrm{d}x\nonumber \\= & {} p_{E+P}(\tau )-P_E(\tau ). \end{aligned}$$
(23)

In a similar way, \({\overline{A}}_A(\tau )\) and \({\overline{A}}_D(\tau )\) can be stated as follows

$$\begin{aligned} {\overline{A}}_A(\tau )= & {} \int ^{\infty }_{\tau }{\int ^y_0{p_A\left( y-x\right) p_E\left( x\right) \textrm{d}x\textrm{d}y}}\nonumber \\{} & {} -\int ^{\infty }_{\tau }p_E\left( x\right) \textrm{d}x\nonumber \\= & {} p_{E+A}(\tau )-P_E(\tau ), \end{aligned}$$
(24)
$$\begin{aligned} {\overline{A}}_D(\tau )= & {} \int ^{\infty }_{\tau }\int ^z_0\int ^y_0 p_D\left( z-y\right) \nonumber \\{} & {} \times p_P\left( y-x\right) p_E\left( x\right) \textrm{d}x\textrm{d}y\textrm{d}z \nonumber \\{} & {} -\int ^{\infty }_{\tau }\int ^y_0 p_P\left( y-x\right) p_E\left( x\right) \textrm{d}x\textrm{d}y\nonumber \\= & {} p_{E+P+D}(\tau )-p_{E+P}(\tau ) \end{aligned}$$
(25)

Inserting Eqs. (23)–(25) into Eq. (20) and using \(\beta (\tau )=\beta \) lead to

$$\begin{aligned}{} & {} \beta \int ^{\infty }_0 e^{-r\tau } [\alpha \left( p_{E+P}\left( \tau \right) -P_E\left( \tau \right) \right) \nonumber \\{} & {} \quad +\left( 1-\alpha \right) {\mu }_a\left( p_{E+A}\left( \tau \right) -P_E\left( \tau \right) \right) \nonumber \\{} & {} \quad +\alpha {\mu }_d\left( p_{E+P+D}(\tau )-p_{E+P}(\tau )\right) ]\textrm{d}\tau =1. \end{aligned}$$
(26)

Now, we should recall the Laplace transform of a function and the convolution integral as follows

$$\begin{aligned}{} & {} L\left\{ f(t)\right\} =\int ^{\infty }_0{e^{-st}f\left( t\right) \textrm{d}t}, \end{aligned}$$
(27)
$$\begin{aligned}{} & {} L\left\{ f\left( t\right) *g\left( t\right) \right\} =L\left\{ f(t)\right\} L\left\{ g(t)\right\} \nonumber \\{} & {} \quad =\int ^{\infty }_0{\int ^t_0{e^{-st}f\left( t-x\right) g\left( x\right) \textrm{d}x\textrm{d}t.}} \end{aligned}$$
(28)

Let us introduce the notation \(L\left\{ p_X(r)\right\} =L_X\left( r\right) \) and \(L\left\{ P_X(r)\right\} =L^X\left( r\right) .\) In the following proposition, we prove that \(L_{E+P+D}\left( r\right) \) can be expressed in terms of \(L_E\left( r\right) ,\) \(L_P\left( r\right) \) and \(L_D\left( r\right) \) to simplify Eq. (26).

Proposition 1

Prove that \(L_{E{+}P{+}D}\left( r\right) {=}\) \(\frac{1{-}L_E\left( r\right) L_P\left( r\right) L_D\left( r\right) }{r},\ L_{E{+}P}\left( r\right) {=}\frac{1-L_E\left( r\right) L_P\left( r\right) }{r}\) and \(L_{E+A}\left( r\right) =\frac{1-L_E\left( r\right) L_A\left( r\right) }{r}.\)

Proof

For simplicity, we only prove the first equality, and the remaining ones are special cases of the first one. According to the definition of \(p_{E+P+D}\left( r \right) ,\) Laplace transform of \(p_{E+P+D}\left( r \right) \) takes the following form

$$\begin{aligned}{} & {} L_{E+P+D}\left( r\right) =L\left\{ p_{E+P+D}(r)\right\} \nonumber \\{} & {} \quad =\int ^{\infty }_0\int ^{\infty }_{\tau }\int ^z_0 \int ^y_0 {e^{-r\tau }p}_D\left( z-y\right) \nonumber \\{} & {} \quad p_P\left( y-x\right) p_E\left( x\right) \textrm{d}x\textrm{d}y\textrm{d}z\textrm{d}\tau . \end{aligned}$$
(29)

Let us define the following functions

$$\begin{aligned}{} & {} Q\left( y\right) =\int ^y_0{p_P\left( y-x\right) p_E\left( x\right) \textrm{d}x}\quad \text {and} \quad \nonumber \\{} & {} H\left( z\right) =\int ^z_0{p_D\left( z-y\right) Q\left( y\right) \textrm{d}y.} \end{aligned}$$
(30)

Equation (29) can then be rewritten as

$$\begin{aligned} L_{E+P+D}\left( r\right) =\int ^{\infty }_0{e^{-r\tau }\left\{ \int ^{\infty }_{\tau }{H\left( z\right) \textrm{d}z}\right\} }\textrm{d}\tau . \end{aligned}$$
(31)

Since \(p_{E+P+D}\left( 0\right) =\int ^{\infty }_0{H\left( z\right) \textrm{d}z}=1,\) Eq. (31) becomes

$$\begin{aligned} L_{E+P+D}\left( r\right) =\int ^{\infty }_0{e^{-r\tau }\left\{ 1-\int ^{\tau }_0{H\left( z\right) \textrm{d}z}\right\} }\textrm{d}\tau \end{aligned}$$
(32)

or

$$\begin{aligned} L_{E+P+D}\left( r\right)= & {} \frac{1-L\left\{ H(\tau )\right\} }{r}\nonumber \\= & {} \frac{1-L\left\{ p_D(\tau )\right\} L\left\{ Q(\tau )\right\} }{r}\nonumber \\= & {} \frac{1-L_E\left( r\right) L_P\left( r\right) L_D\left( r\right) }{r}. \end{aligned}$$
(33)

We also need to see that \(L^E\left( r\right) =\frac{\left( 1-L_E\left( r\right) \right) }{r}\) by using the simple relation between \(p_E(r)\) and \(P_E(r)\) as follows

$$\begin{aligned}{} & {} L^E\left( r\right) =\mathrm {\ }L\left\{ P_E(\tau )\right\} =\int ^{\infty }_0{e^{-r\tau }}P_E\left( \tau \right) \textrm{d}\tau \nonumber \\{} & {} \quad =\int ^{\infty }_0{e^{-r\tau }}\left[ 1-\int ^{\tau }_0{p_E\left( t\right) \textrm{d}t}\right] \textrm{d}\tau \nonumber \\{} & {} \quad =\frac{\left( 1-L_E\left( r\right) \right) }{r}. \end{aligned}$$
(34)

\(\square \)

By using Proposition 1 and Eq. (34) in Eq. (26), we reach the following general \(r-\beta \) relation

$$\begin{aligned} \beta =\frac{r}{F_1+F_2+F_3} \end{aligned}$$
(35)

where

$$\begin{aligned}{} & {} F_1={\mu }_a\left[ -1+L_E\left( r\right) L_A\left( r\right) +rL_E\left( r\right) \right] ,\nonumber \\{} & {} F_2=\alpha \left[ -1+{\mu }_a+L_E\left( r\right) \left( r-{\mu }_ar\right) \right] ,\nonumber \\{} & {} F_3=\alpha L_E\left( r\right) [L_P\left( r\right) -{\mu }_aL_A\left( r\right) \nonumber \\{} & {} \qquad +{\mu }_d\left( L_D\left( r\right) -1\right) L_P\left( r\right) ]. \end{aligned}$$
(36)

Let us denote the mean sojourn times at presymptomatic, asymptomatic, and symptomatic stages by \(T_P,\ T_A\), and \(T_D\), respectively. These values are given by

$$\begin{aligned}{} & {} T_P=\int ^{\infty }_0{{\overline{A}}_P(\tau )\textrm{d}\tau },\quad T_A=\int ^{\infty }_0{{\overline{A}}_A(\tau )\textrm{d}\tau }\nonumber \\{} & {} T_D=\int ^{\infty }_0{{\overline{A}}_D(\tau )\textrm{d}\tau }. \end{aligned}$$
(37)

Thus, with the use of Eqs. (19) and (35), the general relation \(r-R_0\) of the SEPADC model (15) can be expressed as follows

$$\begin{aligned} {\left( R_0\right) }_{\text {SEPADC}}=\frac{r\left[ \alpha T_P+\left( 1-\alpha \right) {\mu }_aT_A+\alpha {\mu }_dT_D\right] }{F_1+F_2+F_3}. \end{aligned}$$
(38)

Note that \({\left( R_0\right) }_{\text {SEPADC}}\) formula (38) generalizes many existing relations \(r-R_0\) proposed in the literature [25, 29]. For the sake of simplicity, let us denote again \({\left( R_0\right) }_{\text {SEPADC-e}}\,\ \ {\left( R_0\right) }_{\text {SEPADC-d}}\) and \({\left( R_0\right) }_{\text {SEPADC-er}}\) as the basic reproduction number formula in the presence of the exponential, delta, and Erlang distributed sojourn times, respectively. In “Appendix C”, we present some special formulae of \({\left( R_0\right) }_{\text {SEPADC-e}}\,\ {\left( R_0\right) }_{\text {SEPADC-d}}\) and \({\left( R_0\right) }_{\text {SEPADC-er}}\) derived from the general formula (38). The relation \(r-R_0\) given by (38) also permits different probability distributions for different stages. In the next section, we provide the most reliable pdf of sojourn times to estimate \(R_0\) values of 152 countries around the world.

Table 1 Symbols, descriptions, and values of the model parameters
Full size table

4 Results

This section provides some estimates of local and global \(R_0\) values of the COVID-19 pandemic through our generalized formulation given in Eq. (38). Our theoretical results apply to the mathematical modeling of various infectious diseases; here, the hot topic is numerically addressed: \(R_0\) values of the COVID-19 pandemic. Note that the involvement of asymptomatic, presymptomatic, or symptomatic carriers in the dynamics does not affect our overall theoretical observations. As illustrated in “Appendix C”, various simplified models can be generated from the SEPADC model (15) and general relation \(r-R_0\) (38).

Finding \(R_0\) value of a country with Eq. (38) needs the following: using more reliable model parameters and sojourn time distributions, use of a reliable algorithm to find the growth rate of a country and the reported data of the country. The most reliable parameter values have been investigated and most have been taken from the study of [4], as presented in Table 1. Based on some clinical data and observations, we also consider the sojourn time distributions as the Erlang distributions with shape parameter \(k=4\) (see Table 1 and [4]). Additionally, we assume that the presymptomatic carriers are as infectious as the symptomatic carriers and the asymptomatic carriers are 50% less infectious with respect to the presymptomatic and symptomatic ones, i.e., \({\mu }_1=0.5,\ {\mu }_2=1\) [4]. According to a very detailed meta-analysis of [30], the presymptomatic ratio is taken as \(\alpha =0.75.\)

As realized from our theoretical analysis, observations of \(R_0\) values strictly depend on the growth rate \(\left( r\right) \) of the corresponding country. There exist various studies on the observation of r values of the COVID-19 pandemic [31,32,33]. Since declining from the exponential phases with non-pharmacological interventions occurs rapidly for most countries, finding the most reliable exponential phase of the given data is critical. In this study, we consider the following steps to obtain r values

  1. 1.

    Consider the data pair \(\left( t,X\right) \) where \(t=[0,\ 1, \)\(\ldots ,N]\) is time vector (in day) and \(X=[x_0,\ x_1,\ldots \) , \(x_N]\) is cumulative cases of the country.

  2. 2.

    Find all possible subvectors \(X_{ij}=[x_i,\ x_{i+1},\ldots , \) \( x_j]\) satisfying \(\left| j-i\right| \ge 9\) and \(x_j<10000.\)

  3. 3.

    Obtain the slope of the linear fit of data \(\left( [i,\ i+1,\right. \) \(\left. \ldots ,j],ln\left( X_{ij}\right) \mathrm {\ }\right) \) as \(r_{ij}\) with corresponding \(R^2\) value denoted by \({RS}_{ij}.\)

  4. 4.

    Determine r from the maximum possible \(r_{ij}\) satisfying \({RS}_{ij}>0.95.\)

This algorithm searches the possible series subvectors with at least ten elements less than or equal to 10000 and calculates the growth rate with the exponential fitting. Maximum of all possible growth rates satisfying \(R^2\mathrm {>0.95}\) is assigned as the desired growth rate. Taking the maximum is in line with the formal definition of the natural exponential phase: the natural exponential phase occurs when non-pharmacological or pharmacological interventions have not yet been implemented.

Daily confirmed cases of 214 countries had been obtained from the European Center for Disease Prevention and Control (ECDPC) [22]. Data from 152 out of 214 countries have given us representative intrinsic growth rates \(\left( r>0.05\right) \). The intrinsic growth rates of 34 out of 152 countries are presented in Table 2. As discussed earlier here, \({\left( R_0\right) }_{\text {SEPADC-er}}\) are calculated with the formula given in “Appendix C” and the parameter values given in Table 1. To observe the effect of the realistic sojourn time distributions, we also illustrate the values \({\left( R_0\right) }_{\text {SEPADC-e}}\) (exponential distribution of sojourn times) and \({\left( R_0\right) }_{\text {SEPADC-d}}\) (delta distribution of sojourn times) with the formulae in “Appendix C” and the mean parameter values in Table 1. \(r-{\left( R_0\right) }_{\text {SEPADC-er}},\) \(r-{\left( R_0\right) }_{\text {SEPADC-e}} \text { and } {r} {\left( R_0\right) }_{\text {SEPADC-d}}\mathrm {\ }\) curves are illustrated for 152 countries in Fig. 3. For these 34 out of 152 countries, \(r,\ {\beta }_{er},{\beta }_e,\ {\beta }_d,\) \({\left( R_0\right) }_{\text {SEPADC-er},\ \ }{\left( R_0\right) }_{\text {SEPADC-e}}\ \)and\(\ \ {\left( R_0\right) }_{\text {SEPADC-d}}\) values are presented in Table 2. \({\beta }_{er},\ {\beta }_e\ \)and\(\ {\beta }_d\) values refer to the naive transmission rates by considering the Erlang, exponential and delta distributions for sojourn times in Table 2.

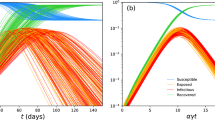
According to Fig. 3 and Table 2, \({\left( R_0\right) }_{\text {SEPADC-e}}\ \)and \({\left( R_0\right) }_{\text {SEPADC-d}}\) provide optimistic and pessimistic \(R_0\) estimates for the COVID-19 outbreak depending on the growth rate of the given country. For relatively higher values of growth rates (\(r>0.158\), 89 out of 152 countries), \({\left( R_0\right) }_{\text {SEPADC-e}}\) underestimates \({\left( R_0\right) }_{\text {SEPADC-er}}\) and \({\left( R_0\right) }_{\text {SEPADC-d}}\ \) overestimates \({\left( R_0\right) }_{\text {SEPADC-er}}\)\(\left( {\left( R_0\right) }_{\text {SEPADC-e}}<{\left( R_0\right) }_{\text {SEPADC-er}}<{\left( R_0\right) }_{\text {SEPADC-d}}\right) \). On the other hand, for relatively low values of the growth rates \(\left( r<0.158\right) ,\) we observe the inequality \({\left( R_0\right) }_{\text {SEPADC-e}}>{\left( R_0\right) }_{\text {SEPADC-er}}>{\left( R_0\right) }_{\text {SEPADC-d}}\) and no considerable difference between any of the estimates. The threshold value \(r\cong 0.158\) depends on the existing parameters rather than the shape parameters (k) of the Erlang distributions. Since \(k=1\) yields the exponential distribution and \(k\rightarrow \infty \) yields the delta distribution, the more realistic Erlang estimate with \(k>1\) \({\left( R_0\right) }_{\text {SEPADC-er}}\) should always be between \({\left( R_0\right) }_{\text {SEPADC-e}}\ \)and\(\ {\left( R_0\right) }_{\text {SEPADC-d}}.\) Note that, if r is high enough, \({\left( R_0\right) }_{\text {SEPADC-d}}\) yields an upper bound among all possible \(R_0\) values and \({\left( R_0\right) }_{\text {SEPADC-e}}\) underestimates the actual \(R_0\) value.

Table 2 Our growth rate algorithm evaluates intrinsic growth rates for 35 out of 214 countries reported in the ECDPC dataset
Full size table

According to Fig. 3, the sojourn time distributions play a significant role for the majority of the countries with higher r values. The benefit of our innovative formula is dependent on the early growth of the reported cases. Overall, we notice that the role of the pdf of sojourn times should be considered in the COVID-19 pandemic. On the other hand, if the early increase in reported cases is not significant (for a country or another pandemic), then the choice in pdf of sojourn times is negligible, and the SEPADC-e model (16) offers a computational advantage over the SEPADC model (15).

Fig. 3
figure 3

The basic reproduction numbers \({\left( R_0\right) }_{\text {SEPADC-er}}\), \({\left( R_0\right) }_{\text {SEPADC-d}}\) and \({\left( R_0\right) }_{\text {SEPADC-e}}\) are calculated for 152 countries around the world with \(r-R_0\) formulae given in “Appendix C”. The curves represent \(r-{\left( R_0\right) }_{\text {SEPADC-er}}\), \(r-{\left( R_0\right) }_{\text {SEPADC-e}}\) and \(r-{\left( R_0\right) }_{\text {SEPADC-d}}\) relations and the circles on the curves represent \(R_0\) values of a country having the corresponding growth rate

Full size image
Fig. 4
figure 4

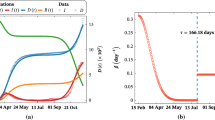
Smoothed (by taking 7-day moving means) data of cumulative cases (C(t)) versus daily patients \((\textrm{d}C(t)/\textrm{d}t)\) are obtained for 55 European countries (ECDPC dataset). The dashed lines denote the smoothed and normalized (by dividing the population of each country) \(\overline{C}\left( t\right) \) versus \(d\overline{C}\left( t\right) /\textrm{d}t\) relation. The global exponential phase must obey the relation \({\textrm{log} \left( \frac{\textrm{d}\overline{C}\left( t\right) }{\textrm{d}t}\right) \ }={\textrm{log} \left( \overline{C}\left( t\right) \right) \ }+\textrm{log}\mathrm {}(r)\) where r is the intrinsic growth rate. r value is calculated by fitting the sub-data (\(\overline{C}\left( t\right) \) versus \(d\overline{C}\left( t\right) /\textrm{d}t\)) of 55 countries that are obtained with our growth rate algorithm. The intercept of the black line gives us our global estimate \(r=0.254\)

Full size image

We aim to estimate a global basic reproduction number using the parameter values given in Table 1. Determining a global intrinsic growth rate is vital for this process [22]. We follow the methodology provided by [22] by considering C(t) versus \(\textrm{d}C(t)/\textrm{d}t\) relation in the same phase space. First of all, to increase the reliability of the data, we have also smoothed C(t) and \(\textrm{d}C(t)/\textrm{d}t\) values by taking 7-day moving means \((C^S\left( t\right) =movmean\left( C\left( t\right) ,7\right) \) and \(\textrm{d}C^S(t)/\textrm{d}t=movmean(\textrm{d}C(t)/\textrm{d}t,7))\). To create a global perspective, the data is also normalized with the population of the countries, i.e., \(\overline{C}\left( t\right) =C^S\left( t\right) /N\) and \(\frac{\textrm{d}\overline{C}\left( t\right) }{\textrm{d}t}=\frac{1}{N}\frac{\textrm{d}C^S\left( t\right) }{\textrm{d}t}\). Since the exponential phase of an outbreak should obey the relation \(\frac{\textrm{d}\overline{C}\left( t\right) }{\textrm{d}t}=r\overline{C}\left( t\right) ,\) we get the line equation \({\textrm{log} \left( \frac{\textrm{d}\overline{C}\left( t\right) }{\textrm{d}t}\right) \ }={\textrm{log} \left( \overline{C}\left( t\right) \right) \ }+{\textrm{log} \left( r\right) \ }.\) In Fig. 4, \({\textrm{log} \left( \overline{C}\left( t\right) \right) \ }\) versus \({\textrm{log} \left( \frac{\textrm{d}\overline{C}\left( t\right) }{\textrm{d}t}\right) \ }\) corresponding to the first 100 days of the pandemic are illustrated through the dashed lines for 55 European countries [22]. Linear regions obey the exponential phase, and the remaining areas show a decline from the exponential phase. The global black dashed line is obtained using the only data in the exponential phases according to our growth rate algorithm. Thus, we find the global intrinsic growth rate as \(r=0.254.\) By considering the parameter values given in Table 1 (Erlang distributions of the sojourn times), we estimate the global convergence \({\left( R_0\right) }_{\text {SEPADC-er}}=R_0=4.58.\) Additionally, according to the exponential and delta distributions, we estimate \({\left( R_0\right) }_{\text {SEPADC-e}}=4.21\) and \({\left( R_0\right) }_{\text {SEPADC-d}}=4.88.\) Our global estimate \(R_0=4.58\) is in line with previous estimates such as \(R_0=4.5\) [22], \(R_0=4.1\) [34] and \(R_0=4.9\) [35].

Fig. 5
figure 5

Effects of the model parameters \(T_E\), \(T_P\), \(T_A\), \(T_D\), \(k_E\), \(k_P\), \(k_A\), \(k_D\), \(\alpha \), \(\mu _a\) and \(\mu _d\) on the \(R_0\) predictions by considering the \(\text {SEPADC-e}\), \(\text {SEPADC-er}\) and \(\text {SEPADC-d}\) models with \(r=0.254\)

Full size image

Here we have shown how our theoretical formulations work with real data under some prior assumptions. The assumed parameter values such \(\alpha = 0.75\), \(\mu _a=0.5\), and \(\mu _d=1\) can vary between countries. To make more rigorous predictions, local estimations of such parameter values should be considered for each country. Nevertheless, we can see how the changing values of such parameter values affect the \(R_0\) predictions. By using the parameter values given in Table 1 and \(r=0.254\), we have illustrated the effect of changing values of each parameter \(T_E\), \(T_P\), \(T_A\), \(T_D\), \(k_E\), \(k_P\), \(k_A\), \(k_D\), \(\alpha \), \(\mu _a\) and \(\mu _d\) on the \(R_0\) predictions in Fig. 5. The results are calculated through \((R_0)_{\text {SEPADC}}\) formula (38) for the \(\text {SEPADC-e}\), \(\text {SEPADC-er}\) and \(\text {SEPADC-d}\) models. Increasing most of the parameters (by fixing intrinsic growth rate \(r=0.254\)), except the fraction of presymptomatic infections (\(\alpha \)), increases \(R_0\) values. \(R_0\) estimations of the \(\text {SEPADC-e}\) model is more sensitive the asymptomatic infections than both \(\text {SEPADC-er}\) and \(\text {SEPADC-d}\) models. Additionally, increasing the values of Erlang distributions’ shape parameters \(k_E\), \(k_P\), \(k_A\), \(k_D\) (from exponential distribution to delta distribution) yields asymptotically increasing pattern in \(R_0\) curve. The \(k-R_0\) curve shows how the \(\text {SEPADC-d}\) and \(\text {SEPADC-e}\) models overestimate and underestimate the \(R_0\) values, respectively. Additionally, Fig. 5 implies that the same exponential phase (\(r=0.254\)) can be approximated with different scenarios in model assumptions. Thus, increasing the reliability of \(R_0\) predictions highly depends on the prior information on such model parameters. Some prior clinical data can help in determining most of the parameters of our SEPADC model.

We observe how different sojourn time distributions affect the behavior of stage functions throughout the pandemic progress in Fig. 6 when the same intrinsic growth rate is assumed for all models. We have shown that the \(\text {SEPADC-e}\), \(\text {SEPADC-er}\), and \(\text {SEPADC-d}\) models require different \(\beta \) and \(R_0\) values to catch the same intrinsic growth rate. Figure 6 shows that different sojourn time distributions yield diverse epidemic curves even if they yield the same r values in the exponential phase. The \(\text {SEPADC-e}\) model leads to wider epidemic curves with less peak value than both the \(\text {SEPADC-er}\) and \(\text {SEPADC-d}\) models. On the other hand, \(\text {SEPADC-d}\) model yields narrower epidemic curves with higher peak values. In line with the skewness of the epidemic curves, the earliest peak time is observed for the \(\text {SEPADC-e}\) model. The SEPADC model can yield less skewed to highly skewed epidemic curves by considering various sojourn time distributions having the same expectations. Observing the epidemic curves of the countries may thus provide some insight into the selection of the sojourn time pdfs.

Fig. 6
figure 6

Epidemic curves of the \({\text {SEPADC-e}}\), \({\text {SEPADC-er}}\) and \({\text {SEPADC-d}}\) models by considering the parameter values given in Table 1 and \(r=0.399\) (the intrinsic growth rate estimated for Turkey)

Full size image

5 Discussions and conclusions

In this study, the SEPADC model has been derived with arbitrary sojourn time distributions represented by the system of the Volterra integral equations. It has been proven that the SEPADC model generalizes the well-known exponential and delta-distributed compartmental models by taking into account the corresponding survival functions in the model. The SEPADC model consists of three infectious stages: presymptomatic, asymptomatic, and symptomatic. This assumption is in line with the existence of the separate roles of these stages for the COVID-19 pandemic [4]. Separate roles of these stages are due to the two known facts: they may have different survival functions and infectivity potentials. The SEPADC model includes both effects, and it is more likely to represent the expected dynamics than the existing SEIR [36] or SIR [22] models. Additionally, the SPC, SEPC, and SEPAC models are reduced from the SEPADC model depending on the corresponding infectious diseases and the importance of the separate roles of the exposed, presymptomatic, asymptomatic, and symptomatic stages. We have extensively reduced the SEPADC model (15) into the system of ODEs by considering the widely used exponential and delta distributions for sojourn times.

\(r-R_0\) relation of an outbreak determines the future dynamics and has great importance in mathematical epidemiology [23,24,25]. With the help of the well-known Euler–Lotka equation (20), we have derived a generalized relation \(r-R_0\) (38) for the SEPADC model by taking arbitrary sojourn time distributions into account. It has been here shown that by taking the Laplace transforms of the probability distribution functions of each stage, one can easily express \(R_0\) in terms of r. Note that in the absence of analytic expressions for the Laplace transforms, it is more suitable to use some quadrature formulas for the corresponding improper integrals. We have shown that some of the existing formulas in the literature [25] can be reduced from our formula (38). Since the extensive acceptance of the exponential, delta, and Erlang distributions for sojourn times, we have formulated \(r-R_0\) according to the distributions and model assumptions.

In the last part of this study, we have used our theoretical observations to evaluate the \({R}_0\) values of 152 countries around the world. A growth rate algorithm has been proposed to calculate the intrinsic growth rates from given data. We have shown that exponential and delta distributions yield optimistic and pessimistic estimates with respect to the most reliable Erlang distribution assumption [4]. According to our observations, higher values of intrinsic growth rates yield optimistic \({R}_0\) estimations of the exponentially distributed compartmental models. Additionally, the global convergence \({R}_0 =4.58 \), which is in line with previous estimates [22, 34, 35], has been obtained through our assumptions on the SEPADC model and global intrinsic growth rate estimate \(r=0.254.\)

To capture both early and entire dynamics, separate roles for presymptomatic, asymptomatic, and symptomatic infections yield more model parameters than the simple SIR model. Using clinical data to predict some parameters such as \(\alpha \), \(\mu _a\) or \(\mu _d\) as well as the shape of sojourn time pdfs, can reduce parameter uncertainty and increase the biological relevance of the \(\beta \) and \(R_0\) estimations. To increase the biological relevance of the parameters, we recommend using this strategy before fitting time series data from a certain country. If the individual roles of different infection phases are uncertain, the SEPADC model can be reduced to more simple models like the SIR or SEIR models. Furthermore, if epidemic curves follow less skewed patterns and there is no clinical data on the sojourn time pdfs, a simpler ODE model (16) rather than the general Volterra integral equation model (38) may be assumed to reduce computing complexity.