SpringerLink
Log in

On the Darboux transformation of a generalized inhomogeneous higher-order nonlinear Schrödinger equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

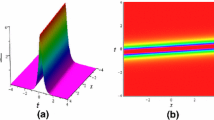
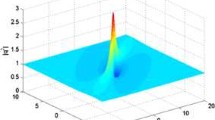
Abstract

Recently, a paper about the Nth-order rogue waves for an inhomogeneous higher-order nonlinear Schrödinger equation using the generalized Darboux transformation is published. Song et al. (Nonlinear Dyn 82(1):489–500. doi:10.1007/s11071-015-2170-6, 2015). However, the inhomogeneous equation which admits a nonisospectral linear eigenvalue problem is mistaken for having a constant spectral parameter by the authors. This basic error causes the results to be wrong, especially regarding the Darboux transformation (DT) in Sect. 2 when the inhomogeneous terms are dependent of spatial variable x. In fact, the DT for inhomogeneous equation has an essential difference from the isospectral case, and their results are correct only in the absence of inhomogeneity which was already discussed in detail before. Consequently, we firstly modify the DT based on corresponding nonisospectral linear eigenvalue problem. Then, the nonautonomous solitons are obtained from zero seed solutions. Properties of these solutions in the inhomogeneous media are discussed graphically to illustrate the influences of the variable coefficients. Finally, the failure of finding breather and rogue wave solutions from this modified DT is also discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Zabusky, N.J., Kruskal, M.D.: Interaction of “solitons” in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 15(6), 240–243 (1965)

    Article  MATH  Google Scholar 

  2. Enns, R.H., Jones, B.L., Miura, R.M., Rangnekar, S.S.: Nonlinear Phenomena in Physics and Biology. Springer, New York (1981)

    Book  MATH  Google Scholar 

  3. Hasegawa, A., Kodama, Y.: Solitons in Optical Communications. Oxford University Press, Oxford (1995)

    MATH  Google Scholar 

  4. Ablowitz, M.J., Clarkson, P.A.: Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1991)

    Book  MATH  Google Scholar 

  5. Akhmediev, N.N., Ankiewicz, A.: Dissipative Solitons: From Optics to Biology and Medicine. Springer, Berlin (2008)

    MATH  Google Scholar 

  6. Chen, H.H., Liu, C.S.: Solitons in nonuniform media. Phys. Rev. Lett. 37(11), 693–697 (1976)

    Article  MathSciNet  Google Scholar 

  7. Calogero, F., Degasperis, A.: Coupled nonlinear evolution equations solvable via the inverse spectral transform, and solitons that come back: the boomeron. Lettere al Nuovo Cimento 16(14), 425–433 (1976)

    Article  MathSciNet  Google Scholar 

  8. Serkin, V.N., Hasegawa, A., Belyaeva, T.L.: Nonautonomous solitons in external potentials. Phys. Rev. Lett. 98(7), 074102 (2007)

    Article  Google Scholar 

  9. Serkin, V.N., Hasegawa, A., Belyaeva, T.L.: Nonautonomous matter-wave solitons near the Feshbach resonance. Phys. Rev. A. 81(2), 023610 (2010)

    Article  Google Scholar 

  10. Serkin, V.N., Hasegawa, A., Belyaeva, T.L.: Solitary waves in nonautonomous nonlinear and dispersive systems: nonautonomous solitons. J. Mod. Opt. 57(14–15), 1456–1472 (2010)

    Article  MATH  Google Scholar 

  11. Bhrawy, A.H., Alzaidy, J.F., Abdelkawy, M.A., Biswas, A.: Jacobi spectral collocation approximation for multi-dimensional time-fractional schrödinger’s equation. Nonlinear Dyn. 84(3), 1553–1567 (2016)

    Article  MathSciNet  Google Scholar 

  12. Abdelkawy, M.A., Bhrawy, A.H., Zerrad, E., Biswas, A.: Application of tanh method to complex coupled nonlinear evolution equations. Acta Phys. Pol. A 129(3), 278–283 (2016)

    Article  Google Scholar 

  13. Kumar, S., Zhou, Q., Bhrawy, A.H., Zerrad, E., Biswas, A., Belic, M.: Optical solitons in birefringent fibers by Lie symmetry analysis. Rom. Rep. Phys. 68(1), 341–352 (2016)

    Google Scholar 

  14. Masemola, P., Kara, A.H., Bhrawy, A.H., Biswas, A.: Conservation laws for coupled wave equations. Rom. J. Phys. 61(3–4), 367–377 (2016)

    Google Scholar 

  15. Biswas, A., Mirzazadeh, M., Eslami, M., Zhou, Q., Bhrawy, A.H., Belic, M.: Optical solitons in nano-fibers with spatio-temporal dispersion by trial solution method. Optik 127(18), 7250–7257 (2016)

    Article  Google Scholar 

  16. Xu, Y.N., Zhou, Q., Bhrawy, A.H., Khan, K.R., Mahmood, M.F.: Bright solitons in optical metamaterials by traveling wave hypothesis. Optoelectron. Adv. Mat. 9(3–4), 384–387 (2015)

    Google Scholar 

  17. Vega-Guzman, J.M., Zhou, Q., Alshaery, A.A., Hilal, E.M., Bhrawy, A.H., Biswas, A.: Optical solitons in cascaded system with spatio-temporal dispersion by ansatz approach. J. Optoelectron. Adv. Mat. 17(1–2), 165–171 (2015)

    Google Scholar 

  18. Zhou, Q., Zhu, Q.P., Savescu, M., Bhrawy, A.H., Biswas, A.: Optical solitons with nonlinear dispersion in parabolic law medium. Proc. Rom. Acad. A 16(2), 152–159 (2015)

    MathSciNet  Google Scholar 

  19. Vega-Guzman, J.M., Hilal, E.M., Alshaery, A.A., Bhrawy, A.H., Mahmood, M.F., Moraru, L., Biswas, A.: Thirring optical solitons with spatio-temporal dispersion. Proc. Rom. Acad. A 16(1), 41–46 (2015)

    MathSciNet  Google Scholar 

  20. Zhou, Q., Zhu, Q.P., Yu, H., Liu, Y.X., Wei, C., Yao, P., Bhrawy, A.H., Biswas, A.: Bright, dark and singular optical solitons in a cascaded system. Laser Phys. 25(2), 025402 (2015)

    Article  Google Scholar 

  21. Estabrook, F.B., Wahlquist, H.D.: Prolongation structures of nonlinear evolution equations II. J. Math. Phys. 16(1), 1–7 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  22. Zhao, W.Z., Bai, Y.Q., Wu, K.: Generalized inhomogeneous Heisenberg ferromagnet model and generalized nonlinear Schrödinger equation. Phys. Lett. A 352, 64–68 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  23. Radha, R., Kumar, V.R.: Explode-Decay Solitons in the Generalized Inhomogeneous Higher-Order Nonlinear Schrödinger Equations. Z. Naturforsch. A 62(7–8), 381–386 (2014)

    MATH  Google Scholar 

  24. Song, N., Zhang, W., Yao, M.H.: Complex nonlinearities of rogue waves in generalized inhomogeneous higher-order nonlinear Schrödinger equation. Nonlinear Dyn. 82(1), 489–500 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  25. Wang, L.H., Porsezian, K., He, J.S.: Breather and rogue wave solutions of a generalized nonlinear schrödinger equation. Phys. Rev. E 87(5), 1558–1561 (2013)

    Google Scholar 

  26. Gu, C.H., Hu, H.S., Zhou, Z.X.: Darboux Transformations in Integrable Systems. Springer, New York (2005)

    Book  MATH  Google Scholar 

  27. Matveev, V.B., Salle, M.A.: Darboux transformations and solitons. Springer, Berlin (1991)

    Book  MATH  Google Scholar 

  28. Chen, D.Y.: Introduction to Soliton Theory. Science Press, Bei**g (2006)

    Google Scholar 

  29. Shin, H.J.: Darboux invariants of integrable equations with variable spectral parameters. J. Phys. A: Math. Theor. 41, 285201 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  30. Zeng, Y.B., Ma, W.X., Shao, Y.J.: Two binary Darboux transformations for the KdV hierarchy with self-consistent sources. J. Math. Phys. 42, 2113–2128 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  31. Ma, W.X.: Darboux transformations for a Lax integrable system in 2n-dimensions. Lett. Math. Phys. 39, 33–49 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  32. Zhao, D., Zhang, Y.J., Lou, W.W., Luo, H.G.: AKNS hierarchy, Darboux transformation and conservation laws of the 1D nonautonomous nonlinear Schrödinger equations. J. Math. Phys. 52, 043502 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  33. Zhou, L.J.: Darboux transformation for the nonisospectral AKNS system. Phys. Lett. A 345, 314–322 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  34. Zhou, L.J.: Darboux transformation for the nonisospectral AKNS hierarchy and its asymptotic property. Phys. Lett. A 372, 5523–5528 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  35. Rajan, M.S.M., Mahalingam, A.: Nonautonomous solitons in modified inhomogeneous Hirota equation: soliton control and soliton interaction. Nonlinear Dyn. 79(4), 2469–2484 (2015)

    Article  MathSciNet  Google Scholar 

  36. Jiang, H.J., **ang, J.J., Dai, C.Q., Wang, Y.Y.: Nonautonomous bright soliton solutions on continuous wave and cnoidal wave backgrounds in blood vessels. Nonlinear Dyn. 75(1–2), 201–207 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  37. Liu, X.T., Yong, X.L., Huang, Y.H., Yu, R., Gao, J.W.: Deformed soliton, breather and rogue wave solutions of an inhomogeneous nonlinear Hirota equation. Commun. Nonlinear Sci. Numer. Simulat. 29, 257–266 (2015)

    Article  MathSciNet  Google Scholar 

  38. Li, J.T., Han, J.Z., Du, Y.D., Dai, C.Q.: Controllable behaviors of Peregrine soliton with two peaks in a birefringent fiber with higher-order effects. Nonlinear Dyn. 82(3), 1393–1398 (2015)

    Article  MathSciNet  Google Scholar 

  39. Liu, W.J., Pang, L.H., Yan, H., Lei, M.: Optical soliton sha** in dispersion decreasing fibers. Nonlinear Dyn. 84(4), 2205–2209 (2016)

    Article  MathSciNet  Google Scholar 

  40. Yu, F.J.: Nonautonomous soliton, controllable interaction and numerical simulation for generalized coupled cubic-quintic nonlinear Schrödinger equations. Nonlinear Dyn. 85(2), 1203–1216 (2016)

    Article  MATH  MathSciNet  Google Scholar 

  41. Li, M., Tian, B., Liu, W.J., Zhang, H.Q., Meng, X.H., Xu, T.: Soliton-like solutions of a derivative nonlinear Schrödinger equation with variable coefficients in inhomogeneous optical fibers. Nonlinear Dyn. 62, 919–929 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  42. Zuo, D.W., Gao, Y.T., Meng, G.Q., Shen, Y.J., Yu, X.: Multi-soliton solutions for the three-coupled KdV equations engendered by the Neumann system. Nonlinear Dyn. 75(4), 1–8 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  43. Yang, J., Zhang, D.J., Chen, D.Y.: Localized solitary waves of non-isospectral general coupled nonlinear Schrödinger equation. Commun. Appl. Math. Comput. 26(2), 239–247 (2012)

    MathSciNet  MATH  Google Scholar 

  44. Sun, Z.Y., Gao, Y.T., Yu, X., Liu, Y.: Dynamics of bound vector solitons induced by stochastic perturbations: soliton breakup and soliton switching. Phys. Lett. A 377, 3283–3290 (2013)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This work is supported by the 13th Five-Year National Key Research and Development Program of China with Grant No. 2016YFC0401401, the NSF of China with Grant Nos.71271083, 11301179, the SSF of Bei**g with Grant No.15ZDA19, the Co-construction Project and Young Talents Plan of Bei**g Municipal Commission of Education. The authors also acknowledge the support by the Fundamental Research Funds of the Central Universities with the Grant Nos.2014ZZD08, 2014ZZD10, 2015MS56, 2016MS63. Xuelin Yong is partially supported by the State Scholarship Fund of China.

Author information

Authors and Affiliations

  1. School of Mathematical Sciences and Physics, North China Electric Power University, Bei**g, 102206, China

    Xuelin Yong, Guo Wang, Wei Li & Yehui Huang

  2. School of Economics and Managements, North China Electric Power University, Bei**g, 102206, China

    Jianwei Gao

Authors
  1. Xuelin Yong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guo Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yehui Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jianwei Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jianwei Gao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yong, X., Wang, G., Li, W. et al. On the Darboux transformation of a generalized inhomogeneous higher-order nonlinear Schrödinger equation. Nonlinear Dyn 87, 75–82 (2017). https://doi.org/10.1007/s11071-016-3026-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-3026-4

Keywords

Search

Navigation