SpringerLink
Log in

Vibration control of a pipe conveying fluid under external periodic excitation using a nonlinear energy sink

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

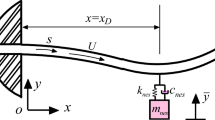
This paper investigates the effects of a smooth nonlinear energy sink (NES) on the vibration suppression of a fixed-fixed pipe conveying fluid under excitation of an external harmonic load. Pipe is modeled using the Euler–Bernoulli beam theory, and the NES has an essentially nonlinear stiffness and a linear dam**. The required conditions that allow for saddle-node bifurcation, Hopf bifurcation and strongly modulated responses (SMRs) in the system are studied. The SMR phenomenon in the system response is considered as the most efficient regime of response for vibration mitigation. In addition, the effects of dam** value of the NES, location of the NES on the pipe, magnitude of the external force and the fluid velocity on the dynamical behavior of the system are investigated. The Runge–Kutta and complexification-averaging methods are employed for numerical and analytical solutions, respectively. Finally, the efficiency of an optimal NES in the energy reduction of the primary system is compared to that of an optimal linear absorber. It can be seen that reducing the distance between the NES and the pipe supports decreases the probability of occurrence of the SMR and weak modulated response; moreover, it provides suitable conditions for occurrence of the saddle-node bifurcation. Furthermore, increasing the fluid velocity decreases the amplitude of steady-state response of the system and extends the unstable region of the response. The results show that the middle of the pipe is the best position for connecting the NES to a fixed-fixed pipe conveying fluid under the external periodic excitation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (United Kingdom)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32

Similar content being viewed by others

References

  1. Paidoussis, M.P.: Fluid-Structure Interactions: Slender Structures and Axial Flow, vol. 1. Academic Press, London (1998)

    Google Scholar 

  2. Semler, C., Li, G., Paıdoussis, M.: The non-linear equations of motion of pipes conveying fluid. J. Sound Vib. 169(5), 577–599 (1994)

    Article  MATH  Google Scholar 

  3. Paıdoussis, M., Li, G.: Pipes conveying fluid: a model dynamical problem. J. Fluids Struct. 7(2), 137–204 (1993)

    Article  Google Scholar 

  4. Benjamin, T.B.: Dynamics of a system of articulated pipes conveying fluid. I. Theory. In: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 1961, vol. 1307, pp. 457–486. The Royal Society

  5. Jensen, J.S.: Fluid transport due to nonlinear fluid-structure interaction. J. Fluids Struct. 11(3), 327–344 (1997)

    Article  Google Scholar 

  6. Zhai, H.-B., Wu, Z.-Y., Liu, Y.-S., Yue, Z-f: Dynamic response of pipeline conveying fluid to random excitation. Nucl. Eng. Des. 241(8), 2744–2749 (2011)

    Article  Google Scholar 

  7. Liang, F., Wen, B.: Forced vibrations with internal resonance of a pipe conveying fluid under external periodic excitation. Acta Mech. Solida Sin. 24(6), 477–483 (2011)

    Article  Google Scholar 

  8. Doki, H., Hiramoto, K., Skelton, R.: Active control of cantilevered pipes conveying fluid with constraints on input energy. J. Fluids Struct. 12(5), 615–628 (1998)

    Article  Google Scholar 

  9. Yau, C.-H., Bajaj, A., Nwokah, O.: Active control of chaotic vibration in a constrained flexible pipe conveying fluid. J. Fluids Struct. 9(1), 99–122 (1995)

    Article  Google Scholar 

  10. Rinaldi, S., Païdoussis, M.: Dynamics of a cantilevered pipe discharging fluid, fitted with a stabilizing end-piece. J. Fluids Struct. 26(3), 517–525 (2010)

    Article  Google Scholar 

  11. Yu, D., Wen, J., Zhao, H., Liu, Y., Wen, X.: Vibration reduction by using the idea of phononic crystals in a pipe-conveying fluid. J. Sound Vib. 318(1), 193–205 (2008)

    Article  Google Scholar 

  12. Sigalov, G., Gendelman, O., Al-Shudeifat, M., Manevitch, L., Vakakis, A., Bergman, L.: Resonance captures and targeted energy transfers in an inertially-coupled rotational nonlinear energy sink. Nonlinear Dyn. 69(4), 1693–1704 (2012)

    Article  MathSciNet  Google Scholar 

  13. Grinberg, I., Lanton, V., Gendelman, O.: Response regimes in linear oscillator with 2DOF nonlinear energy sink under periodic forcing. Nonlinear Dyn. 69(4), 1889–1902 (2012)

    Article  MathSciNet  Google Scholar 

  14. Colvin, M.: Energy sinks with nonlinear stiffness and nonlinear dam** (2010)

  15. Nili Ahmadabadi, Z., Khadem, S.E.: Self-excited oscillations attenuation of drill-string system using nonlinear energy sink. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 227, 230–245 (2012)

  16. **ong, H., Kong, X., Yang, Z., Liu, Y.: Response regimes of narrow-band stochastic excited linear oscillator coupled to nonlinear energy sink. Chin. J. Aeronaut. 28(2), 457–468 (2015)

    Article  Google Scholar 

  17. Kani, M., Khadem, S.E., Pashaei, M.H., Dardel, M.: Design and performance analysis of a nonlinear energy sink attached to a beam with different support conditions. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 230, 527–542 (2015)

  18. Starosvetsky, Y., Gendelman, O.: Dynamics of a strongly nonlinear vibration absorber coupled to a harmonically excited two-degree-of-freedom system. J. Sound Vib. 312(1), 234–256 (2008)

    Article  Google Scholar 

  19. Ahmadabadi, Z., Khadem, S.: Annihilation of high-amplitude periodic responses of a forced two degrees-of-freedom oscillatory system using nonlinear energy sink. J. Vib. Control 19, 2401–2412 (2012)

  20. Kani, M., Khadem, S., Pashaei, M., Dardel, M.: Vibration control of a nonlinear beam with a nonlinear energy sink. Nonlinear Dyn. 83, 1–22 (2015)

  21. Bab, S., Khadem, S., Shahgholi, M.: Vibration attenuation of a rotor supported by journal bearings with nonlinear suspensions under mass eccentricity force using nonlinear energy sink. Meccanica 50, 2441–2460 (2015)

  22. Nili Ahmadabadi, Z., Khadem, S.: Nonlinear vibration control and energy harvesting of a beam using a nonlinear energy sink and a piezoelectric device. J. Sound Vib. 333, 4444–4457 (2014)

  23. Zulli, D., Luongo, A.: Control of primary and subharmonic resonances of a Duffing oscillator via non-linear energy sink. Int. J. Non-Linear Mech. 80, 170–182 (2016)

  24. Yang, T.-Z., Yang, X.-D., Li, Y., Fang, B.: Passive and adaptive vibration suppression of pipes conveying fluid with variable velocity. J. Vib. Control 20(9), 1293–1300 (2014)

    Article  MathSciNet  Google Scholar 

  25. Bab, S., Khadem, S.E., Shahgholi, M.: Lateral vibration attenuation of a rotor under mass eccentricity force using non-linear energy sink. Int. J. Non-Linear Mech. 67, 251–266 (2014)

    Article  Google Scholar 

  26. Ahmadabadi, Z.N., Khadem, S.: Nonlinear vibration control of a cantilever beam by a nonlinear energy sink. Mech. Mach. Theory 50, 134–149 (2012)

    Article  Google Scholar 

  27. Gendelman, O.V.: Targeted energy transfer in systems with non-polynomial nonlinearity. J. Sound Vib. 315(3), 732–745 (2008)

    Article  Google Scholar 

  28. Bab, S., Khadem, S.E., Mahdiabadi, M.K., Shahgholi, M.: Vibration mitigation of a rotating beam under external periodic force using a nonlinear energy sink (NES). J. Vib. Control 125 (2015)

  29. Meirovitch, L.: Analytical Methods in Vibration, vol. 16. Macmillan, New York (1967)

    MATH  Google Scholar 

  30. Manevitch, L.: The description of localized normal modes in a chain of nonlinear coupled oscillators using complex variables. Nonlinear Dyn. 25(1–3), 95–109 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  31. Abbasi, A., Khadem, S., Bab, S.: Vibration control of a continuous rotating shaft employing high-static low-dynamic stiffness isolators. J. Vib. Control (2016). doi:10.1177/1077546315587611

  32. Nayfeh, A.H., Balachandran, B.: Applied Nonlinear Dynamics: Analytical, Computational and Experimental Methods. Wiley, London (2008)

    MATH  Google Scholar 

  33. Vakakis, A.F., Gendelman, O.V., Bergman, L.A., McFarland, D.M., Kerschen, G., Lee, Y.S.: Nonlinear Targeted Energy Transfer in Mechanical and Structural Systems, vol. 156. Springer, Berlin (2008)

    MATH  Google Scholar 

  34. Gourc, E., Michon, G., Seguy, S.b., Berlioz, A.: Experimental investigation and theoretical analysis of a nonlinear energy sink under harmonic forcing. In: ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference 2011, pp. 391–397. American Society of Mechanical Engineers

  35. Lee, Y., Vakakis, A., Bergman, L., McFarland, D.M., Kerschen, G.: Suppression aeroelastic instability using broadband passive targeted energy transfers, part 1: theory. AIAA J. 45(3), 693–711 (2007)

    Article  Google Scholar 

  36. Gendelman, O.V.: Bifurcations of nonlinear normal modes of linear oscillator with strongly nonlinear damped attachment. Nonlinear Dyn. 37(2), 115–128 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  37. Fenichel, N.: Geometric singular perturbation theory for ordinary differential equations. J. Differ. Equ. 31(1), 53–98 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  38. Savadkoohi, A.T., Lamarque, C.-H., Dimitrijevic, Z.: Vibratory energy exchange between a linear and a nonsmooth system in the presence of the gravity. Nonlinear Dyn. 70(2), 1473–1483 (2012)

    Article  MathSciNet  Google Scholar 

  39. Lamarque, C.-H., Gendelman, O.V., Savadkoohi, A.T., Etcheverria, E.: Targeted energy transfer in mechanical systems by means of non-smooth nonlinear energy sink. Acta Mech. 221(1–2), 175–200 (2011)

  40. Gendelman, O., Starosvetsky, Y., Feldman, M.: Attractors of harmonically forced linear oscillator with attached nonlinear energy sink I: description of response regimes. Nonlinear Dyn. 51(1–2), 31–46 (2008)

    MATH  Google Scholar 

  41. Parseh, M., Dardel, M., Ghasemi, M.H., Pashaei, M.H.: Steady state dynamics of a non-linear beam coupled to a non-linear energy sink. Int. J. Non-Linear Mech. 79, 48–65 (2016)

    Article  Google Scholar 

  42. Den Hartog, J.P.: Mechanical Vibrations. McGraw-Hill, New York (1956)

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Tarbiat Modares University, P.O. Box 14115-177, Tehran, Iran

    Ali Ebrahimi Mamaghani, S. E. Khadem & Saeed Bab

Authors
  1. Ali Ebrahimi Mamaghani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. E. Khadem
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Saeed Bab
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. E. Khadem.

Appendices

Appendix 1

$$\begin{aligned} m_{11}= & {} \int _0^1 {\phi _1^2 (\bar{{x}})\hbox {d}\bar{{x}},\mu =\int _0^1 \bar{{U}}_f ^{2}\phi _1 (\bar{{x}})\left[ \frac{\hbox {d}^{2}\phi _1 (\bar{{x}})}{\hbox {d}\bar{{x}}^{2}}\right] \hbox {d}\bar{{x}}} ,k_{11}\\= & {} \int _0^1 {\phi _1 (\bar{{x}})\left[ \frac{\hbox {d}^{4}\phi _1 (\bar{{x}})}{\hbox {d}\bar{{x}}^{4}}\right] } \hbox {d}\bar{{x}}, \xi =\int _0^1 {\bar{{c}}_p \phi _1 ^{2}(\bar{{x}})} \hbox {d}\bar{{x}},\bar{{F}}\\= & {} \int _0^1 {\bar{{F}}\phi _1 (\bar{{x}})\hbox {d}\bar{{x}}} \end{aligned}$$

Appendix 2

$$\begin{aligned} \alpha _1= & {} 16\Omega ^{6}\left( {\begin{array}{l} \phi _{1d}^4 \alpha ^{2}\Omega ^{4}+2\phi _{1d}^3 \alpha \xi \Omega ^{4}-2\phi _{1d}^3 \alpha ^{2}\mu \Omega ^{2}\\ \quad +\phi _{1d}^2 \alpha ^{2}\xi ^{2}\Omega ^{2}+\phi _{1d}^2 \xi ^{2}\Omega ^{4}+\alpha ^{2}\sigma ^{2} \\ -2\phi _{1d}^2 \alpha ^{2}\sigma \Omega ^{2}+\phi _{1d}^2 \alpha ^{2}\mu ^{2} +\phi _{1d}^2 \mu ^{2}\Omega ^{2}\\ \quad +2\phi _{1d} \alpha ^{2}\mu \sigma +2\phi _{1d} \mu \sigma \Omega ^{2}+\sigma ^{2}\Omega ^{2} \\ \end{array}} \right) \\ \alpha _2= & {} 24\beta \Omega ^{4}\left( \phi _{1d}^3 \mu \Omega ^{2}-\phi _{1d}^2 \xi ^{2}\Omega ^{2}+\phi _{1d}^2 \sigma \Omega ^{2}\right. \\&\quad \left. -\,\phi _{1d}^2 \mu ^{2}-2\phi _{1d} \mu \sigma -\sigma ^{2} \right) \\ \alpha _3= & {} 9\beta ^{2}\left( \phi _{1d}^4 \Omega ^{4}-2\phi _{1d}^3 \mu \Omega ^{2}+\phi _{1d}^2 \xi ^{2}\Omega ^{2}\right. \\&\quad \left. -\,2\phi _{1d}^2 \sigma \Omega ^{2}+\phi _{1d}^2 \mu ^{2}+2\phi _{1d} \mu \sigma +\sigma ^{2} \right) \\ \alpha _4= & {} -16\phi _{1d}^2 F^{2}\Omega ^{10} \end{aligned}$$

Appendix 3

$$\begin{aligned} \eta _1= & {} \phi _{1d}^2 \alpha \varepsilon +\phi _{1d} \varepsilon \xi +\alpha \\ \eta _2= & {} \frac{1}{64\Omega ^{6}}(16\phi _{1d}^4 \alpha ^{2}\varepsilon ^{2}\Omega ^{6}+32\phi _{1d}^3 \alpha \varepsilon ^{2}\xi \Omega ^{6}\\&+\,27\phi _{1d}^4 \beta ^{2}\varepsilon ^{2}\phi _{2f}{}^{4}+16\phi _{1d}^2 \varepsilon ^{2}\xi ^{2}\Omega ^{6}\\&+\,48\phi _{1d}^3 \beta \varepsilon ^{2}\mu \Omega \phi _{2f}{}^{2} +32\phi _{1d}^2 \alpha ^{2}\varepsilon \Omega ^{6}\\&+\,48\phi _{1d}^2 \beta \varepsilon ^{2}\sigma \Omega ^{2}\phi _{2f}{} ^{2}+16\phi _{1d}^2 \varepsilon ^{2}\mu ^{2}\Omega ^{4}\\&+\,64\phi _{1d} \alpha \varepsilon \xi \Omega ^{6}+54\phi _{1d}^2 \beta ^{2}\varepsilon \phi _{2f}{} ^{4} \\&+\,32\phi _{1d} \varepsilon ^{2}\mu \sigma \Omega ^{4}+16\alpha ^{2}\Omega ^{6}+16\varepsilon ^{2}\sigma ^{2}\Omega ^{4}\\&+\,16\Omega ^{8}-48\beta \Omega ^{4}\phi _{2f}{} ^{2}+27\beta ^{2}\phi _{2f}{} ^{4}) \\ \eta _3= & {} \frac{\varepsilon }{64\Omega ^{6}}(16\phi _{1d}^3 \alpha ^{2}\varepsilon \xi \Omega ^{6}+16\phi _{1d}^2 \alpha \varepsilon \xi ^{2}\Omega ^{6}\\&+\,27\phi _{1d}^3 \beta ^{2}\varepsilon \xi \phi _{2f}{} ^{4}+16\phi _{1d}^2 \alpha \Omega ^{8}\\&+\,16\phi _{1d}^2 \alpha \varepsilon \mu ^{2}\Omega ^{4} +16\phi _{1d} \alpha ^{2}\xi \Omega ^{6}+16\phi _{1d} \xi \Omega ^{8}\\&+\,32\phi _{1d} \alpha \varepsilon \mu \sigma \Omega ^{4}-48\phi _{1d} \beta \xi \Omega ^{4}\phi _{2f}{} ^{2}\\&+27\phi _{1d} \beta ^{2}\xi \phi _{2f}{} ^{4}+16\alpha \varepsilon \sigma ^{2}\Omega ^{4}) \\ \eta _4= & {} \frac{\varepsilon ^{2}}{256\Omega ^{8}}(16\phi _{1d}^4 \alpha ^{2}\Omega ^{10}+32\phi _{1d}^3 \alpha \xi \Omega ^{10}\\&+\,27\phi _{1d}^4 \beta ^{2}\Omega ^{4}\phi _{2f}{} ^{4}-32\phi _{1d}^3 \alpha ^{2}\mu \Omega ^{8}\\&-\,48\beta \sigma ^{2}\Omega ^{4}\phi _{2f}{} ^{2} +16\phi _{1d}^2 \alpha ^{2}\xi ^{2}\Omega ^{8}\\&+\,16\phi _{1d}^2 \xi ^{2}\Omega ^{10}+48\phi _{1d}^3 \beta \mu \Omega ^{6}\phi _{2f}{} ^{2}\\&-\,32\phi _{1d}^2 \alpha ^{2}\sigma \Omega ^{8}-48\phi _{1d}^2 \beta \xi ^{2}\Omega ^{6}\phi _{2f}{} ^{2} \\&-\,54\phi _{1d}^3 \beta ^{2}\mu \Omega ^{2}\phi _{2f}{} ^{4}+16\phi _{1d}^2 \alpha ^{2}\mu ^{2}\Omega ^{6}\\&+\,27\phi _{1d}^2 \beta ^{2}\xi ^{2}\Omega ^{2}\phi _{2f}{} ^{4}+48\phi _{1d}^2 \beta \sigma \Omega ^{6}\phi _{2f}{} ^{2}\\&+\,27\beta ^{2}\sigma ^{2}\phi _{2f}{} ^{4} +16\phi _{1d}^2 \mu ^{2}\Omega ^{8}\\&-54\phi _{1d}^2 \beta ^{2}\sigma \Omega ^{2}\phi _{2f}{} ^{4}-48\phi _{1d}^2 \beta \mu ^{2}\Omega ^{4}\phi _{2f}{} ^{2}\\&+\,32\phi _{1d} \alpha ^{2}\mu \sigma \Omega ^{6}+32\phi _{1d}^ \mu \sigma \Omega ^{8} \\&+\,27\phi _{1d}^2 \beta ^{2}\mu ^{2}\phi _{2f}{} ^{4}-96\phi _{1d} \beta \mu \sigma \Omega ^{4}\phi _{2f}{} ^{2}\\&+\,16\alpha ^{2}\sigma ^{2}\Omega ^{6}+16\sigma ^{2}\Omega ^{8}+54\phi _{1d} \beta ^{2}\mu \sigma \phi _{2f}{} ^{4}) \end{aligned}$$

Appendix 4

$$\begin{aligned} v_1= & {} -\frac{729}{4096}\frac{\varepsilon \phi _{1d} \beta ^{4}\xi \left( {\phi _{1d}^2 \varepsilon +1} \right) ^{2}\left( {\phi _{1d}^4 \alpha \varepsilon ^{2}+\phi _{1d}^3 \varepsilon ^{2}\xi +2\phi _{1d}^2 \alpha \varepsilon +\alpha } \right) }{\Omega ^{12}}\\ v_2= & {} -\frac{81\varepsilon \phi _{1d} \beta ^{3}\xi \left( {\phi _{1d}^2 \varepsilon +1} \right) }{256\Omega ^{10}}\\&(\phi _{1d}^5 \alpha \varepsilon ^{3}\mu +\phi _{1d}^4 \alpha \varepsilon ^{3}\sigma -\phi _{1d}^4 \alpha \varepsilon ^{2}\Omega ^{2}\\&+\,\phi _{1d}^4 \varepsilon ^{3}\mu \xi +\phi _{1d}^3 \varepsilon ^{3}\sigma \xi \\&-\,\phi _{1d}^3 \varepsilon ^{2}\xi \Omega ^{2}+\phi _{1d}^3 \alpha \varepsilon ^{2}\mu +\phi _{1d}^2 \alpha \varepsilon ^{2}\sigma \\&-\,3\phi _{1d}^2 \alpha \varepsilon \Omega ^{2}-2\alpha \Omega ^{2}) \\ v_3= & {} -\frac{9\varepsilon \phi _{1d} \beta ^{2}}{256\Omega ^{8}}\{6\phi _{1d} ^{8}\alpha ^{3}\varepsilon ^{4}\xi \Omega ^{2}+15\phi _{1d} ^{7}\alpha ^{2}\varepsilon ^{4}\xi ^{2}\Omega ^{2}\\&+\,12\phi _{1d} ^{6}\alpha \varepsilon ^{4}\xi ^{3}\Omega ^{2}+22\alpha \xi \Omega ^{4}+3\phi _{1d} ^{7}\alpha ^{2}\varepsilon ^{4}\mu ^{2}\\&+\,24\phi _{1d} ^{6}\alpha ^{3}\varepsilon ^{3}\xi \Omega ^{2} +3\phi _{1d} ^{5}\varepsilon ^{4}\xi ^{4}\Omega ^{2}+6\phi _{1d} ^{6}\alpha ^{2}\varepsilon ^{4}\mu \sigma \\&+\,6\phi _{1d} ^{6}\alpha ^{2}\varepsilon ^{3}\mu \Omega ^{2}+6\phi _{1d} ^{6}\alpha \varepsilon ^{4}\mu ^{2}\xi \\&+\,6\alpha ^{3}\xi \Omega ^{2}-12\phi _{1d} \alpha \varepsilon ^{2}\mu \sigma \xi +3\phi _{1d} \alpha ^{2}\Omega ^{4} \\&+\,42\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{3}\xi ^{2}\Omega ^{2}+3\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{4}\sigma ^{2}\\&+\,6\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{3}\sigma \Omega ^{2}+3\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{2}\Omega ^{4}\\&+\,18\phi _{1d} ^{4}\alpha \varepsilon ^{3}\xi ^{3}\Omega ^{2}+6\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{3}\mu ^{2}\\&-\,6\alpha \varepsilon ^{2}\sigma ^{2}\xi +12\phi _{1d} ^{5}\alpha \varepsilon ^{4}\mu \sigma \xi -4\phi _{1d} ^{5}\alpha \varepsilon ^{3}\mu \xi \Omega ^{2}\\&+\,3\phi _{1d} ^{5}\varepsilon ^{4}\mu ^{2}\xi ^{2}-4\phi _{1d} ^{4}\alpha \varepsilon ^{3}\sigma \xi \Omega ^{2}\\&+\,6\phi _{1d} ^{4}\alpha \varepsilon ^{2}\xi \Omega ^{4}+6\phi _{1d} ^{4}\varepsilon ^{4}\mu \sigma \xi ^{2} \\&+\,36\phi _{1d} ^{4}\alpha ^{3}\varepsilon ^{2}\xi \Omega ^{2}+6\phi _{1d} ^{4}\alpha \varepsilon ^{4}\sigma ^{2}\xi \\&-\,10\phi _{1d}^4 \varepsilon ^{3}\mu \xi ^{2}\Omega ^{2}+12\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{3}\mu \sigma \\&+\,12\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{2}\mu \Omega ^{2}+39\phi _{1d} ^{3}\alpha ^{2}\varepsilon ^{2}\xi ^{2}\Omega ^{2} \\&+\,3\phi _{1d}^3 \varepsilon ^{4}\sigma ^{2}\xi ^{2}10\phi _{1d} ^{3}\varepsilon ^{3}\sigma \xi ^{2}\Omega ^{2}\\&+\,3\phi _{1d} ^{3}\varepsilon ^{2}\xi ^{2}\Omega ^{4}+6\phi _{1d} ^{3}\alpha ^{2}\varepsilon ^{3}\sigma ^{2}\\&+\,12\phi _{1d} ^{3}\alpha ^{2}\varepsilon ^{2}\sigma \Omega ^{2}+6\phi _{1d} ^{3}\alpha ^{2}\varepsilon \Omega ^{4}\\&+\,3\phi _{1d} \alpha ^{2}\varepsilon ^{2}\sigma ^{2} \\&-\,4\phi _{1d} ^{3}\alpha \varepsilon ^{2}\mu \xi \Omega ^{2}+6\phi _{1d} ^{2}\alpha \varepsilon ^{2}\xi ^{3}\Omega ^{2}\\&+\,3\phi _{1d} ^{3}\alpha ^{2}\varepsilon ^{2}\mu ^{2}+24\phi _{1d} ^{2}\alpha ^{3}\varepsilon \xi \Omega ^{2} -4\phi _{1d} ^{2}\alpha \varepsilon ^{2}\sigma \xi \Omega ^{2}\\&+\,28\phi _{1d} ^{2}\alpha \varepsilon \xi \Omega ^{4} +6\phi _{1d} ^{2}\alpha ^{2}\varepsilon \mu \Omega ^{2}-6\phi _{1d} ^{2}\alpha \varepsilon ^{2}\mu ^{2}\xi \\&+\,12\phi _{1d} \alpha ^{2}\varepsilon \xi ^{2}\Omega ^{2}+6\phi _{1d} \alpha ^{2}\varepsilon \sigma \Omega ^{2} +6\phi _{1d} ^{2}\alpha ^{2}\varepsilon ^{2}\mu \sigma \} \\ \end{aligned}$$
$$\begin{aligned} v_4= & {} -\frac{3\varepsilon \phi _{1d} \alpha \beta }{16\Omega ^{6}}\{\phi _{1d} ^{7}\alpha ^{2}\varepsilon ^{4}\mu \xi \Omega ^{2}\\&+\,\phi _{1d} ^{6}\alpha ^{2}\varepsilon ^{4}\sigma \xi \Omega ^{2}-\phi _{1d} ^{6}\alpha ^{2}\varepsilon ^{3}\xi \Omega ^{4}\\&+\,2\phi _{1d} ^{6}\alpha \varepsilon ^{4}\mu \xi ^{2}\Omega ^{2}+2\varepsilon ^{2}\sigma ^{2}\xi \Omega ^{2} \\&-\,2\phi _{1d} ^{5}\alpha \varepsilon ^{3}\xi ^{2}\Omega ^{4}+\phi _{1d} ^{5}\varepsilon ^{4}\mu \xi ^{3}\Omega ^{2}\\&+\,\phi _{1d} ^{6}\alpha \varepsilon ^{4}\mu ^{3}+2\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{3}\mu \xi \Omega ^{2}\\&+\,\phi _{1d} ^{4}\varepsilon ^{4}\sigma \xi ^{3}\Omega ^{2}-\phi _{1d} ^{4}\varepsilon ^{3}\xi ^{3}\Omega ^{4} \\&+\,3\phi _{1d} ^{5}\alpha \varepsilon ^{4}\mu ^{2}\sigma +\phi _{1d} ^{5}\alpha \varepsilon \mu \Omega ^{2}\\&+\,\phi _{1d} ^{5}\varepsilon ^{4}\mu ^{3}\xi +2\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{3}\sigma \xi \Omega ^{2}\\&-\,4\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{2}\xi \Omega ^{4}+2\phi _{1d} ^{4}\alpha \varepsilon ^{3}\mu \xi ^{2}\Omega ^{2} \\&+\,3\phi _{1d} ^{4}\alpha \varepsilon ^{4}\mu \sigma ^{2}+2\phi _{1d} ^{4}\alpha \varepsilon ^{3}\mu \sigma \Omega ^{2}\\&-\,\phi _{1d} ^{4}\alpha \varepsilon ^{2}\mu \Omega ^{4}+3\phi _{1d} ^{4}\varepsilon \epsilon ^{4}\mu ^{2}\sigma \xi \\&+\,\phi _{1d} ^{4}\varepsilon ^{3}\mu ^{2}\xi \Omega ^{2}+2\phi _{1d} ^{3}\alpha \varepsilon ^{3}\sigma \xi ^{2}\Omega ^{2} \\&-\,6\phi _{1d} ^{3}\alpha \varepsilon ^{2}\xi ^{2}\Omega ^{4}+\phi _{1d} ^{4}\alpha \varepsilon ^{3}\mu ^{3}\\&+\,\phi _{1d} ^{3}\alpha ^{2}\varepsilon ^{2}\mu \xi \Omega ^{2}+\phi _{1d} ^{3}\alpha \varepsilon ^{4}\sigma ^{3}\\&+\,\phi _{1d} ^{3}\alpha \varepsilon ^{3}\sigma ^{2}\Omega ^{2}-\phi _{1d} ^{3}\alpha \varepsilon ^{2}\sigma \Omega ^{4}-2\xi \Omega ^{6} \\&-\,\phi _{1d} ^{3}\alpha \varepsilon \Omega ^{6}+3\phi _{1d} ^{3}\varepsilon ^{4}\mu \sigma ^{2}\xi +2\phi _{1d} ^{3}\varepsilon ^{3}\mu \sigma \xi \Omega ^{2}\\&-\,\phi _{1d} ^{3}\varepsilon ^{2}\mu \xi \Omega ^{4}-2\phi _{1d} ^{2}\varepsilon ^{2}\xi ^{3}\Omega ^{4}+3\phi _{1d} ^{3}\alpha \varepsilon ^{3}\mu ^{2}\sigma \\&+\,\phi _{1d} ^{3}\alpha \varepsilon ^{2}\mu ^{2}\Omega ^{2}+\phi _{1d} ^{2}\alpha ^{2}\varepsilon ^{2}\sigma \xi \Omega ^{2}-5\phi _{1d} ^{2}\alpha ^{2}\varepsilon \xi \Omega ^{4}\\&+\,\phi _{1d} ^{2}\varepsilon ^{4}\sigma ^{3}\xi +\phi _{1d} ^{2}\varepsilon ^{3}\sigma ^{2}\xi \Omega ^{2}-\phi _{1d} ^{2}\varepsilon ^{2}\sigma \xi \Omega ^{4} \\&-\,\phi _{1d} ^{2}\varepsilon \xi \Omega ^{6}+3\phi _{1d} ^{2}\alpha \varepsilon ^{3}\mu \sigma ^{2}+2\phi _{1d} ^{2}\alpha \varepsilon ^{2}\mu \sigma \Omega ^{2}\\&-\,\phi _{1d} ^{2}\alpha \varepsilon \mu \Omega ^{4}+2\phi _{1d} ^{2}\varepsilon ^{2}\mu ^{2}\xi \Omega ^{2}-4\phi _{1d} \alpha \varepsilon \xi ^{2}\Omega ^{4} \\&+\,\phi _{1d} \alpha \varepsilon ^{3}\sigma ^{3}+\phi _{1d} \alpha \varepsilon ^{2}\sigma ^{2}\Omega ^{2}-\phi _{1d} \alpha \varepsilon \sigma \Omega ^{4}\\&-\,\phi _{1d} \alpha \Omega ^{6}+4\phi _{1d} \varepsilon ^{2}\mu \sigma \xi \Omega ^{2}-2\alpha ^{2}\xi \Omega ^{4}\\&+\,2\phi _{1d}^5 \alpha \varepsilon ^{4}\sigma \xi ^{2}\Omega ^{2}\} \\ v_5= & {} -\frac{\varepsilon \phi _{1d} \alpha }{16\Omega ^{4}}\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{2}\xi \Omega ^{2}+2\phi _{1d} ^{3}\alpha \varepsilon ^{2}\xi ^{2}\Omega ^{2}\\&+\,\phi _{1d}^2 \varepsilon ^{2}\xi ^{3}\Omega ^{2}+\phi _{1d} ^{3}\alpha \varepsilon ^{2}\mu ^{2}+2\phi _{1d}^2 \alpha ^{2}\varepsilon \xi \Omega ^{2} \\&+\,2\phi _{1d}^2 \alpha \varepsilon ^{2}\mu \sigma +2\phi _{1d} ^{2}\alpha \varepsilon \mu \Omega ^{2}+\phi _{1d} ^{2}\varepsilon ^{2}\mu ^{2}\xi \\&+\,2\phi _{1d} \alpha \varepsilon \xi ^{2}\Omega ^{2}+\phi _{1d} \alpha \varepsilon ^{2}\sigma ^{2}\\&+\,2\phi _{1d} \alpha \varepsilon \sigma \Omega ^{2}+\phi _{1d} \alpha \Omega ^{4}+2\phi _{1d} \varepsilon ^{2}\mu \sigma \xi \\&+\,\alpha ^{2}\xi \Omega ^{2}+\varepsilon ^{2}\sigma ^{2}\xi +2\varepsilon \sigma \xi \Omega ^{2}\\&+\,2\phi _{1d} \varepsilon \mu \xi \Omega ^{2}\}\times \{\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{2}\Omega ^{2}+2\phi _{1d} ^{3}\alpha \varepsilon ^{2}\xi \Omega ^{2} \\&+\,\phi _{1d} ^{2}\varepsilon ^{2}\xi ^{2}\Omega ^{2}+\varepsilon ^{2}\sigma ^{2}+\phi _{1d} ^{2}\varepsilon ^{2}\mu ^{2}+2\phi _{1d} \alpha \varepsilon \xi \Omega ^{2}a \\&+\,2\phi _{1d} \varepsilon ^{2}\mu \sigma +2\phi _{1d} ^{2}\alpha ^{2}\varepsilon \Omega ^{2}-2\phi _{1d} \varepsilon \mu \Omega ^{2}+\alpha ^{2}\Omega ^{2}\\&-\,2\varepsilon \sigma \Omega ^{2}+\xi \Omega ^{4}+\Omega ^{4}\} \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mamaghani, A.E., Khadem, S.E. & Bab, S. Vibration control of a pipe conveying fluid under external periodic excitation using a nonlinear energy sink. Nonlinear Dyn 86, 1761–1795 (2016). https://doi.org/10.1007/s11071-016-2992-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-2992-x

Keywords

Search

Navigation