Nonlinear dynamics of coupled oscillators in 1:2 internal resonance: effects of the non-resonant quadratic terms and recovery of the saturation effect

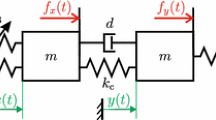
Abstract

This article considers the nonlinear dynamics of coupled oscillators featuring strong coupling in 1:2 internal resonance. In forced oscillations, this particular interaction is the source of energy exchange, leading to a particular shape of the response curves, as well as quasi-periodic responses and a saturation phenomenon. These main features are embedded in the simplest system which considers only the two resonant quadratic monomials conveying the 1:2 internal resonance, since they are the proeminent source allowing one to explain these phenomena. However, it has been shown recently that those features can be substantially modified by the presence of non-resonant quadratic terms. The aim of the present study is thus to explain the effect of the non-resonant quadratic terms on the dynamics. To that purpose, the normal form up to the third order is used, since the effect of the non-resonant quadratic terms will be transferred into the resonant cubic terms. Analytical solutions are detailed using a second-order mutliple scale expansion. A thorough investigation of the backbone curves, their stability and bifurcation, and the link to the forced–damped solutions, is detailed, showing in particular interesting features that had not been addressed in earlier studies. Finally, the saturation effect is investigated, and it is shown how to correct the detuning effect of the cubic terms thanks to a specific tuning of non-resonant quadratic terms and resonant cubic terms. This choice, derived analytically, is shown to extend the validity of the saturation effect to larger amplitudes, which can thus be used in all applications where this effect is needed e.g. for control.

Appendices

A Relationships between nonlinear coefficients

This appendix details the known relationships existing between the coefficients of the monomials given in Eq. (1) when the internal force is assumed to derive from a potential. In such case, the potential energy is a quartic function whose general expression reads:

$$\begin{aligned} \mathcal {V}&=\frac{1}{2}(\omega _1^2X_1^2 +\omega _2^2X_2^2) + \frac{1}{3}(g_{11}^1X_1^3 + g_{22}^2X_2^3)+g_{11}^2X_1^2X_2\\& +g_{22}^1X_1X_2^2 + \frac{1}{4}(h_{111}^1X_1^4 + h_{222}^2X_2^4)+\frac{1}{2}h_{112}^2X_1^2X_2^2 \\& +h_{111}^2X_1X_2^3+h_{222}^1X_1^3X_2. \end{aligned}$$

(35)

The internal forces are found by deriving this expression with respect to $X_1$ and $X_2$, which leads to the following relationships between the coefficients:

$$\begin{aligned} g_{12}^1&=2g_{11}^2, \end{aligned}$$

(36a)

$$\begin{aligned} g_{12}^2&=2g_{22}^1,\end{aligned}$$

(36b)

$$\begin{aligned} h_{122}^1&=h_{112}^2,\end{aligned}$$

(36c)

$$\begin{aligned} h_{122}^2&=3h_{222}^1,\end{aligned}$$

(36d)

$$\begin{aligned} h_{112}^1&=3h_{111}^2. \end{aligned}$$

(36e)

B Detailed calculation of the normal form

This appendix is devoted to the complete presentation of the calculations needed to arrive at the normal form given in Eq. (2), starting from the original set of two coupled nonlinear oscillators, Eq. (1). The calculation follows the general guidelines given in [11, 38], and is adapted here to take into account the additional condition given by the presence of a 1:2 internal resonance between the two eigenfrequencies of the system. This resonance condition being on the second-order terms will have consequences on the calculation of the cubic terms, which needs to be properly tracked. Since the normal form calculation is sequential in nature, the first step consists in processing the quadratic terms. To that purpose, let us truncate Eq. (1) at the second-order of the nonlinearity, and rewrite them as a first-order problem in time, in order to make clearly appear the contributions due to the two independent variables displacement and velocity:

$$\begin{aligned} \dot{X}_1&=Y_1, \end{aligned}$$

(37a)

$$\begin{aligned} \dot{Y}_1&= -\omega _1^2X_1 - g_{11}^1X_1^2 -g_{12}^1X_1X_2-g_{22}^1X_2^2, \end{aligned}$$

(37b)

$$\begin{aligned} \dot{X}_2&=Y_2, \end{aligned}$$

(37c)

$$\begin{aligned} \dot{Y}_2&= -\omega _2^2X_2 - g_{11}^2X_1^2 -g_{12}^2X_1X_2-g_{22}^2X_2^2. \end{aligned}$$

(37d)

A quadratic, indentity-tangent, nonlinear change of coordinates, is first introduced in order to cancel as much as possible the nonlinear terms in Eq. (37). New variables ($U_i$, $V_i$) are introduced as:

$$\begin{aligned} X_1&=U_1+a_{11}^1U_1^2+a_{12}^1U_1U_2+a_{22}^1U_2^2+b_{11}^1V_1^2+b_{12}^1V_1V_2+b_{22}^1V_2^2, \end{aligned}$$

(38a)

$$\begin{aligned} Y_1&= V_1+\gamma _{11}^1U_1V_1+\gamma _{12}^1U_1V_2+\gamma _{21}^1U_2V_1+\gamma _{22}^1U_2V_2,\end{aligned}$$

(38b)

$$\begin{aligned} X_2&=U_2+a_{11}^2U_1^2+a_{12}^2U_1U_2+a_{22}^2U_2^2+b_{11}^2V_1^2+b_{12}^2V_1V_2+b_{22}^2V_2^2,\end{aligned}$$

(38c)

$$\begin{aligned} Y_2&= V_2+\gamma _{11}^2U_1V_1+\gamma _{12}^2U_1V_2+\gamma _{21}^2U_2V_1+\gamma _{22}^2U_2V_2. \end{aligned}$$

(38d)

In these equations, the introduced coefficients $a_{ij}^p$, $b_{ij}^p$, and $\gamma _{ij}^p$, for i, j, p=1, 2; are unknowns and will be set according to the idea of canceling non-resonant monomials in the equations of motion. To that purpose, Eq. (38) are differentiated with respect to time and introduced in (37). Identification of the same monomials leads to the values of the coefficients that can be used. Let us first recall the general solution reported in [11, 38] for the case where no internal resonance exists between $\omega _1$ and $\omega _2$. One obtains:

$$\begin{aligned} a_{11}^1&=\frac{-g_{11}^1}{3\omega _1^2}, \qquad b_{11}^1=\frac{-2g_{11}^1}{3\omega _1^4}, \qquad \gamma ^1_{11}=\frac{2g^1_{11}}{3\omega _1^2}, \qquad \gamma _{21}^1= \frac{g_{12}^1}{4\omega _1^2-\omega _2^2},\nonumber \\ a_{12}^1&= \frac{g^1_{12}}{\omega _2^2-4\omega _1^2}, \qquad b_{12}^1=\frac{2g_{12}^2}{\omega _2^2(\omega _2^2-4\omega _1^2)},\qquad \gamma ^1_{12}=\frac{g^1_{12}(2\omega _1^2-\omega _2^2)}{\omega _2^2(4\omega _1^2-\omega _2^2)}, \qquad \gamma _{21}^2=\frac{g_{12}^2(\omega _1^2-2\omega _2^2)}{\omega _1^2(\omega _1^2-4\omega _2^2)},\nonumber \\ a_{22}^1&=\frac{g_{22}^1(2\omega _2^2-\omega _1^2)}{\omega _1^2(\omega _1^2-4\omega _2^2)}, \qquad b_{22}^1=\frac{2g_{22}^1}{\omega _1^2(\omega _1^2-4\omega _2^2)}, \qquad \gamma _{22}^1=\frac{2g_{22}^1}{4\omega _2^2-\omega _1^2}, \nonumber \\ a_{11}^2&= \frac{g_{11}^2(\omega _2^2-2\omega _1^2)}{\omega _2^2(4\omega _1^2-\omega _2^2)}, \qquad b_{11}^2=\frac{2g_{11}^2}{\omega _2^2(\omega _2^2-4\omega _1^2)}, \qquad \gamma _{11}^2=\frac{2g_{11}^2}{4\omega _1^2-\omega _2^2}, \nonumber \\ a_{12}^2&=\frac{g_{12}^2}{\omega _1^2-4\omega _2^2}, \qquad b_{12}^2=\frac{2g_{12}^2}{\omega _1^2(\omega _1^2-4\omega _2^2)}, \qquad \gamma _{12}^2=\frac{g_{12}^2}{4\omega _2^2-\omega _1^2}, \nonumber \\ a_{22}^2&=\frac{-g_{22}^2}{3\omega _2^2}, \qquad b_{22}^2=\frac{-2g_{22}^2}{3\omega _2^4}, \qquad \gamma _{22}^2=\frac{2g_{22}^2}{3\omega _2^2}. \end{aligned}$$

(39)

In the case of the 1:2 internal resonance condition (i.e., $\omega _2 \approx 2\omega _1$), it appears that the coefficients $a_{12}^1$, $b_{12}^1$, $\gamma _{12}^1$, $\gamma _{21}^1$, $a_{11}^2$, $b_{11}^2$, and $\gamma _{11}^2$ are singular since their denominators contains the term $(\omega _2-2\omega _1)$. In such case, the remedy is to set all these coefficients to zero. The coefficients used in Eq. (3) in the main text are thus those given in Eq. (39), except for the singular ones that are replaced by:

$$\begin{aligned} a_{12}^1 = b_{12}^1 = \gamma _{12}^1 = \gamma _{21}^1 = a_{11}^2 = b_{11}^2 = \gamma _{11}^2 = 0. \end{aligned}$$

(40)

As a consequence, the associated resonant second-order monomials, which are here $g_{12}^1 X_1X_2$ and $g_{11}^2X_1^2$, cannot be eliminated from the normal form, in contrary to the other four quadratic terms. After this first step, one is thus able to write the normal form of the problem with 1:2 resonance, up to the quadratic terms, as:

$$\begin{aligned} \dot{U}_1&=V_1 +O(U_i^3,V_i^3), \end{aligned}$$

(41a)

$$\begin{aligned} \dot{V}_1&= -\omega _1^2U_1-g_{12}^1 U_1U_2 +O(U_i^3,V_i^3),\end{aligned}$$

(41b)

$$\begin{aligned} \dot{U}_2&=V_2+O(U_i^3,V_i^3),\end{aligned}$$

(41c)

$$\begin{aligned} \dot{V}_2&= -\omega _2^2U_2 -g_{11}^2U_1^2+O(U_i^3,V_i^3). \end{aligned}$$

(41d)

The next step of the calculation is to rewrite Eq (41) up to the cubic terms. Besides the original cubic terms with coefficients $h^p_{ijk}$, present in Eq (1), new cubic terms will appear due to the nonlinear nature of the change of coordinates, where products involving linear and quadratic terms will produce new cubic terms. Let us first focus on the processing of these new terms. In the calculation, the derivatives of Eq. (38) with respect to time need to be computed. The derivative of quadratic terms (e.g. $V_1^2$) makes appear products involving the time derivative ($2V_1 \dot{V}_1$ in this case). To eliminate time, one can simply use Eq. (41), such that, up to order four, one can write for the monomial considered as an example: $V_1\dot{V}_1 = -\omega _1^2 U_1 V_1 - g^1_{12}U_1 U_2 V_1 + O(U_i^4,V_i^4)$, hence making appear the new expected cubic terms. Repeating this procedure for the four equations, and using Eq. (40) to simplify the expressions, one easily arrives at:

$$\begin{aligned} \dot{U}_1&=V_1{+2b_{11}^1g_{12}^1U_1U_2V_1+2b_{22}^1g_{11}^2U_1^2V_2}, \end{aligned}$$

(42a)

$$\begin{aligned} \dot{V}_1&= -\omega _1^2U_1 -g_{12}^1U_1U_2{+\gamma _{11}^1g_{12}^1U_1^2U_2+\gamma _{22}^1g_{11}^2U_1^2U_2},\end{aligned}$$

(42b)

$$\begin{aligned} \dot{U}_2&=V_2{+b_{12}^2g_{12}^1U_1U_2V_2+b_{12}^2g_{11}^2V_1U_1^2+2b_{22}^2g_{11}^2U_1^2V_2},\end{aligned}$$

(42c)

$$\begin{aligned} \dot{V}_2&= -\omega _2^2U_2 - g_{11}^2U_1^2{+\gamma _{12}^2g_{11}^2U_1^3+\gamma _{21}^2g_{12}^1U_1U_2^2+\gamma _{22}^2g_{11}^2U_1^2U_2}. \end{aligned}$$

(42d)

Note that the obtained cubic terms in (42) are solely due to the presence of the 1:2 internal resonance condition. Importantly, those terms were not present in the previous calculations shown in [11, 38], led under the specific assumption of no internal resonance. This means that the general guidelines provided in [11, 38] to derive the normal form can be followed, provided the changes underlined here to take correctly into account a 1:2 resonance.

At this stage, one can observe that the first and third lines, Eqs. (42a)–(42c), are not as simple as they were at the starting point, see e.g. Eq. (37), underlining a simple link between displacement and velocity. To recover this and obtain a more convenient expression of (42a)-(42c), one can define $W_1$ and $W_2$ as:

$$\begin{aligned} W_1&=V_1+2b_{11}^1g_{12}^1U_1U_2V_1+2b_{22}^1g_{11}^2U_1^2V_2, \end{aligned}$$

(43a)

$$\begin{aligned} W_2&=V_2+b_{12}^2g_{12}^1U_1U_2V_2+b_{12}^2g_{11}^2V_1U_1^2+2b_{22}^2g_{11}^2U_1^2V_2, \end{aligned}$$

(43b)

such that the system (42) can be rewritten as:

$$\begin{aligned} \dot{U}_1&=W_1, \end{aligned}$$

(44a)

$$\begin{aligned} \dot{W}_1&= -\omega _1^2U_1 -g_{12}^1U_1U_2+\gamma _{11}^1g_{12}^1U_1^2U_2\nonumber \\&\quad +\gamma _{22}^1g_{11}^2U_1^2U_2+2b_{11}^1g_{12}^1(W_1^2U_2\nonumber \\&\quad +U_1W_2W_1-U_1^2U_2\omega _1^2)+2b_{22}^1g_{11}^2(2U_1W_1W_2-U_1^2U_2\omega _2^2)\nonumber \\&\quad +O(U_i^4,W_i^4), \end{aligned}$$

(44b)

$$\begin{aligned} \dot{U}_2&=W_2,\end{aligned}$$

(44c)

$$\begin{aligned} \dot{W}_2&=-\omega _2^2U_2 - g_{11}^2U_1^2+\gamma _{12}^2g_{11}^2U_1^3\nonumber \\&\quad +\gamma _{21}^2g_{12}^1U_1U_2^2+\gamma _{22}^2g_{11}^2U_1^2U_2 \nonumber \\&\quad +b_{12}^2g_{12}^1(W_1U_2W_2+U_1W_2^2-U_1U_2^2\omega _2^2)\nonumber \\&\quad +b_{12}^2g_{11}^2(-\omega _1^2U_1^3+2U_1W_1^2)\nonumber \\&\quad +2b_{22}^2g_{11}^2(2U_1W_1W_2-U_1^2U_2\omega _2^2)+O(U_i^4,W_i^4). \end{aligned}$$

(44d)

As mentioned earlier, Eq. (44) refer to the problem up to cubic nonlinearity where only the terms added by the presence of the 1:2 resonance have been tracked. We are now in the position of rewriting the complete system up to the third order, on which the next step of the normal transform could be applied by vanishing the non-resonant cubic monomials thanks to a third-order nonlinear change of coordinates. To that purpose, one simply needs to track the cubic terms coming from the original system with $h^p_{ijk}$ coefficients, and those created by the quadratic nonlinear change of coordinate and appearing without the second-order internal resonance. This leads to the following equations:

$$\begin{aligned} \dot{U}_1&=W_1, \end{aligned}$$

(45a)

$$\begin{aligned} \dot{W}_1&=-\omega _1^2U_1-g_{12}^1{U_1U_2}-(h_{111}^1+A_{111}^1)U_1^3 \\& -(h_{112}^1+A_{112}^1-{D_{112}^1})U_1^2U_2 -(h_{122}^1+A_{122}^1)U_1U_2^2 \\& -(h_{222}^1+A_{222}^1)U_2^3-B_{111}^1U_1W_1^2-B_{122}^1U_1W_2^2 \\& -(B_{112}^1-{E_{112}^1)}U_1W_1W_2-(B_{211}^1-{E_{211}^1})U_2W_1^2 \\& -B_{212}^1U_2W_1W_2 -B_{222}^1U_2W_2^2 +O(U_i^4,W_i^4) , \end{aligned}$$

(45b)

$$\begin{aligned} \dot{U}_2&=W_2, \end{aligned}$$

(45c)

$$\begin{aligned} \dot{W}_2&= -\omega _2^2U_2-g_{11}^2{U_1^2}-(h_{111}^2+A_{111}^2-{D_{111}^2})U_1^3 \\& -(h_{112}^2+A_{112}^2-{D_{112}^2})U_1^2U_2 -(h_{122}^2+A_{122}^2-{D_{122}^2})U_1U_2^2 \\& -(h_{222}^2+A_{222}^2)U_2^3-(B_{111}^2-{E_{111}^2})U_1W_1^2 \\& -(B_{122}^2-{E_{122}^2})U_1W_2^2-(B_{112}^2-{E_{112}^2})U_1W_1W_2 \\& -B_{211}^2U_2W_1^2 -(B_{212}^2-{E_{212}^2})U_2W_1W_2 \\& -B_{222}^2U_2W_2^2 +O(U_i^4,W_i^4). \end{aligned}$$

(45d)

In these equations, the coefficients $A_{ijk}^p$ and $B_{ijk}^p$, with $i,j,k,p=1,2$; are the same as those already reported in [11, 38], meaning that they arise from the computation of the non internally resonant case. Their general expressions are the same as reported in [11, 38] and read:

$$\begin{aligned} A^p_{ijk}&=\sum ^N_{l \ge i} g_{il}^p a_{jk}^l+\sum _{l \le i}^N g_{li}^p a_{jk} ^l, \end{aligned}$$

(46a)

$$\begin{aligned} B^p_{ijk}&=\sum ^N_{l \ge i} g_{il}^p b_{jk}^l+\sum _{l \le i}^N g_{li}^p b_{jk} ^l. \end{aligned}$$

(46b)

As compared to the case without internal resonance, one can note that the general expression is exactly similar, but one has just to take care that due to the 1:2 resonance, some of the $a^p_{ij}$, $b^p_{ij}$, $\gamma ^p_{ij}$ coefficients vanish following Eq. (40).

On the other hand, the coefficients $D_{ijk}^p$ and $E_{ijk}^p$, with $i,j,k,p=1,2$, comes from Eq. (45), and are only due to the presence of the 1:2 internal resonance. They read:

$$\begin{aligned} \begin{aligned} D_{112}^1&=\gamma _{11}^1g_{12}^1+\gamma _{22}^1g_{11}^2-2b_{11}^1g_{12}^1\omega _1^2-2b_{22}^1g_{11}^2\omega _2^2, \\ D_{111}^2&=\gamma _{12}^2g_{11}^2-b_{12}^2g_{11}^2\omega _1^2,\\ D_{112}^2&=\gamma _{22}^2g_{11}^2-2b_{22}^2g_{11}^2\omega _2^2,\\ D_{122}^2&=\gamma _{21}^2g_{12}^1-b_{12}^2g_{12}^1\omega _2^2,\\ E_{112}^1&=2b_{11}^1g_{12}^1+4b_{22}^1g_{11}^2,\\ E_{211}^1&=2b_{11}^1g_{12}^1,\\ E_{111}^2&=2b_{12}^2g_{11}^2,\\ E_{122}^2&=b_{12}^2g_{12}^1,\\ E_{112}^2&=4b_{22}^2g_{11}^2,\\ E_{212}^2&=b_{12}^2g_{12}^1. \end{aligned} \end{aligned}$$

(47)

The last step of the computation of the real normal form up to cubic terms consists of applying a third-order nonlinear change of coordinates in order to cancel all non-resonant cubic monomials in (45). As already noted, for example, in [11, 12, 38], the main difference with second-order is the presence of trivial resonances at the cubic order. Due to the fact that the eigenspectrum is composed of pairs of purely imaginary complex conjugate numbers, trivial resonances are always fulfilled at third order so that numerous monomials cannot be cancelled whatever the values of the eigenvalues. This is in contrast to quadratic terms where, in case of no second-order internal resonance, all the terms can be cancelled by the change of coordinate. Here the procedure simply follows the general guidelines given in [11, 12, 38]. The nonlinear change of coordinates is introduced as:

$$\begin{aligned} U_p&=R_p + \sum ^N_{i=1}\sum ^N_{j\ge i} \sum _{k \ge j}^N r_{ijk}^p R_iR_jR_k + \sum ^N_{i=1}\sum ^N_{j=1} \sum _{k \ge j}^N u_{ijk}^p R_iS_jS_k, \end{aligned}$$

(48a)

$$\begin{aligned} W_p&=\dot{U}_p=S_p +\sum _{i=1}^N \sum _{j \ge i}^N \sum ^N _{k\ge j} \mu _{ijk}^pS_iS_jS_k +\sum ^N_{i=1} \sum ^N_{j=1}\sum ^N_{k \ge j} v_{ijk}^p S_iR_jR_k. \end{aligned}$$

(48b)

To derive the expressions of the unknown coefficients $r_{ijk}^p$, $u_{ijk}^p$, $\mu _{ijk}^p$, and $\nu _{ijk}^p$, with $i,j,k,p=1,\ldots ,2$; introduced in Eq. (48), one has to differentiate (48) with respect to time and report in the equations of motion, Eq.  (45). Identifying the monomials term-by-term leads to explicit expressions for the unknowns, some of them being set directly to zero because of the trivial resonances. Interestingly, this step of the calculation exactly follows the guidelines already provided in [11, 12, 38]. Hence the general formula can be simply used without changes.

After this calculation, most of the cubic monomials present in Eq. (45) can be cancelled by the nonlinear change of coordinates, the only remaining being linked to trivial resonances. Finally, the normal form, up to the third order, and with the 1:2 internal resonance taken into account, reads:

$$\begin{aligned} \dot{R_1}=&S_1, \end{aligned}$$

(49a)

$$\begin{aligned} \dot{S_1}=&-\omega _1^2R_1-{g_{12}^1R_1R_2}-(h_{111}^1+A_{111}^1)R_1^3-(h_{122}^1+A_{122}^1)R_1R_2^2\nonumber \\&-B_{111}^1R_1S_1^2-B_{122}^1R_1S_2^2-B_{212}^1R_2S_1S_2, \end{aligned}$$

(49b)

$$\begin{aligned} \dot{R_2}=&S_2, \end{aligned}$$

(49c)

$$\begin{aligned} \dot{S_2}=&-\omega _2^2R_2-g_{11}^2R_1^2-(h_{112}^2+A_{112}^2-{D_{112}^2})R_1^2R_2\\& -(h_{222}^2+A_{222}^2)R_2^3 -(B_{112}^2-{E_{112}^2})R_1S_1S_2 \\& -B_{211}^2R_2S_1^2-B_{222}^2R_2S_2^2. \end{aligned}$$

(49d)

One can note that the normal form is equivalent to that obtained in [11], except for the additional terms $E_{112}^2$ and $D_{112}^2$, which comes as a direct consequence of kee** the resonant quadratic terms due to the 1:2 internal resonance.

C Detailed calculation of the Multiple scales solution

In this section, we develop the application of the second-order MSM to Eq. (2). The starting point is the system given by Eq. (6), that makes appear the scaled following coefficients:

$$\begin{aligned} g_{12}^1&=\varepsilon \beta _1, \quad g_{11}^2=\varepsilon \beta _2, \end{aligned}$$

(50a)

$$\begin{aligned} h_{111}^1 + A_{111}^1&=\varepsilon ^2 \alpha _1, \quad h^1_{122} + A^1_{122}=\varepsilon ^2 \alpha _2, \nonumber \\ B^1_{111}&=\varepsilon ^2 \alpha _3, \quad B^1_{122}=\varepsilon ^2 \alpha _4, \quad B^1_{212}=\varepsilon ^2 \alpha _5, \end{aligned}$$

(50b)

$$\begin{aligned} h^2_{112}&+A^2_{112}-D^2_{112}=\varepsilon ^2 \alpha _6, \quad h^2_{222}+A^2_{222}=\varepsilon ^2 \alpha _7, \\& B^2_{112}-E^2_{112}=\varepsilon ^2 \alpha _8, \end{aligned}$$

(50c)

$$\begin{aligned} B^2_{211}&=\varepsilon ^2 \alpha _9, \quad B^2_{222}=\varepsilon ^2 \alpha _{10}. \end{aligned}$$

(50d)

The unknowns $R_1(t)$ and $R_2(t)$ of Eq. (6) are expanded in powers of $\varepsilon$ as:

$$\begin{aligned} R_1(t;\varepsilon )&= r_{10}(T_0,T_1,T_2)+\varepsilon r_{11}(T_0,T_1,T_2) \\& +\varepsilon ^2 r_{12}(T_0,T_1,T_2) +O(\varepsilon ^3), \end{aligned}$$

(51a)

$$\begin{aligned} R_2(t;\varepsilon )&= r_{20}(T_0,T_1,T_2)+\varepsilon r_{21}(T_0,T_1,T_2) \\& +\varepsilon ^2 r_{22}(T_0,T_1,T_2)+O(\varepsilon ^3). \end{aligned}$$

(51b)

In addition, the first and second derivatives with respect to the initial time t are expressed as:

$$\begin{aligned} \frac{d}{d t}&=D_0+\varepsilon D_1 + \varepsilon ^2 D_2 +O(\varepsilon ^3), \end{aligned}$$

(52a)

$$\begin{aligned} \frac{d^2}{d t^2}&=D_0^2+2\varepsilon D_0 D_1 + \varepsilon ^2( D_1^2+2D_0D_2)+ O(\varepsilon ^3), \end{aligned}$$

(52b)

where $D_n \equiv {\partial }/{\partial T_n}$. Substituting Eq. (51) in (6), using (52) and equating the coefficients of like powers of $\varepsilon$ yields:

• At order $\varepsilon ^0$:

  $$\begin{aligned} D_0^2 r_{10} +\omega _1^2 r_{10}&=0, \end{aligned}$$

  (53a)
  $$\begin{aligned} D_0^2 r_{20}+\omega _2^2 r_{20}&=0. \end{aligned}$$

  (53b)

• At order $\varepsilon$:

  $$\begin{aligned} D_0^2 r_{11} +\omega _1^2 r_{11}&=-2D_0D_1r_{10}-\beta _1 r_{10}r_{20}, \end{aligned}$$

  (54a)
  $$\begin{aligned} D_0^2 r_{21}+\omega _2^2 r_{21}&=-2D_0D_1r_{20}-\beta _2 r_{10}^2. \end{aligned}$$

  (54b)

• At order $\varepsilon ^2$:

  $$\begin{aligned} D_0^2 r_{12} +\omega _1^2 r_{12}&=-2D_0D_1r_{11}-2D_0D_2r_{10}-D_1^2r_{10}\\& - \beta _1 r_{10}r_{21} -\beta _2 r_{11} r_{20}-\alpha _1 r_{10}^3 -\alpha _2 r_{10}r_{20}^2 \\& -\alpha _3 r_{10}(D_0r_{10})^2 -\alpha _4 r_{10}(D_0r_{20})^2 \\& -\alpha _5 r_{20} D_0r_{10}D_0 r_{20}, \end{aligned}$$

  (55a)
  $$\begin{aligned} D_0^2 r_{22}+\omega _2^2 r_{22}&= -2D_0D_1 r_{21} -2 D_0 D_2 r_{20} -D_1^2 r_{20} \\& -2\beta _2 r_{10}r_{11} -\alpha _6 r_{10}^2r_{20} -\alpha _7 r_{20}^3 \\& -\alpha _8 r_{10} D_0 r_{10} D_0 r_{20} -\alpha _9 r_{20} (D_0 r_{10})^2 \\& -\alpha _{10} r_{20} (D_0 r_{20})^2. \end{aligned}$$

  (55b)

The solutions of (53a, 53b) are expressed as:

$$\begin{aligned} r_{10}&=A_1(T_1,T_2) e^{i\omega _1 T_0} +cc, \end{aligned}$$

(56a)

$$\begin{aligned} r_{20}&=A_2(T_1,T_2) e^{i\omega _2 T_0} +cc, \end{aligned}$$

(56b)

where cc stands for the complex conjugate. Upon substituting (56) in (54), the elimination of the resonant terms yield the following solvability condition:

$$\begin{aligned} D_1A_1&= \frac{i\beta _1 \bar{A}_1A_2}{2\omega _1} e^{-i\sigma T_1}, \end{aligned}$$

(57a)

$$\begin{aligned} D_1 A_2&= \frac{i\beta _2 A_1^2}{2\omega _2} e^{i\sigma T_1}, \end{aligned}$$

(57b)

where the internal detuning is $\varepsilon \sigma =2\omega _1-\omega _2$, already introduced by Eq. (8) in the main text to quantify the nearness of $\omega _2$ to $2\omega _1$. With the elimination of the resonant terms, Eq. (54) are rewritten as:

$$\begin{aligned} D_0^2 r_{11} +\omega _1^2 r_{11}&=-\beta _1 A_1 A_2 e^{i(\omega _1+\omega _2)T_0}+cc, \end{aligned}$$

(58a)

$$\begin{aligned} D_0^2 r_{21}+\omega _2^2 r_{21}&=-2 \beta _2 A_1 \bar{A}_1. \end{aligned}$$

(58b)

The solutions of Eq. (58) can be expressed as:

$$\begin{aligned} r_{11}&=B_1 e^{i\omega _1 T_0} +\frac{\beta _1 A_1 A_2}{\omega _2(2\omega _1+\omega _2)}e^{i(\omega _1+\omega _2)t}+cc, \end{aligned}$$

(59a)

$$\begin{aligned} r_{21}&=B_2 e^{i\omega _2 T_0} -\frac{\beta _2 A_1 \bar{A}_1}{\omega _2^2}+cc. \end{aligned}$$

(59b)

Note that in the latter equations, both homogeneous and particular solutions have been taken into account, hence explaining that two terms are present. Indeed, homogeneous solutions to (58) leads to the first terms with coefficients $B_i(T_1,T_2)$, $i=1,2$; while the particular solutions give rise to the other two terms.

The modulation equations at order $\varepsilon ^2$ can now be constructed by substituting Eqs. (59), (57) and (56) in (55). By canceling the resonant terms, one obtains the solvability condition at this order as:

$$\begin{aligned} 2i\omega _1 D_2 A_1&= \Lambda _1 A_1 A_2 \bar{A}_2 +\Lambda _2 A_1^2 \bar{A}_1 -\sigma \frac{\beta _1 \bar{A}_1A_2}{2\omega _1} e^{-i\sigma T_1} \\& -\Big [2i\omega _1D_1B_1 +(\beta _1 \bar{A}_1B_2 +\beta _2A_2 \bar{B}_1 )e^{-i\sigma T_1}\Big ], \end{aligned}$$

(60a)

$$\begin{aligned} 2i\omega _2 D_2 A_2&= \Lambda _3A_1 A_2 \bar{A}_1 +\Lambda _4 A_2^2 \bar{A}_2 +\sigma \frac{\beta _2 A_1^2}{2\omega _2} e^{i\sigma T_1} \\& -\Big [2i\omega _1D_1B_2+2\beta _2A_1B_1e^{i\sigma T_1}\Big ], \end{aligned}$$

(60b)

with the coefficients $\Lambda _k$ defined in the main text by Eq. (12a–12d).

The present second-order MSM has the peculiarity of the treatment of the homogeneous solution introduced at order $\varepsilon$ (terms of coefficients $B_i$ in Eq. (59)). To derive a solution, one has to find the complex amplitudes $(A_1, A_2, B_1, B_2)$, requiring eight real numbers, whereas the system has two DOFs and thus only four initial conditions. As a consequence, one has to find four real additional relationships to close the problem. In [54, §4.1] and [1, §2.3.1], considering a free Duffing equation, it is shown with a straightforward expansion that it is equivalent to: (i) consider the homogeneous solution of the order $\varepsilon$ system and compute its redundant complex amplitude at the end of the process by considering the initial conditions; and (ii) simply discard the homogeneous solution. In [55, §6.2.1], the MSM, up to second-order, is applied to a Duffing equation using method (ii), since much less algebra is involved. This issue is precisely the subject of [39], in which second-order MSM is applied to several forced one DOFs examples and the free vibration of the 2-DOFs system considered here, Eq. (6), but without cubic terms. It is shown that better solutions, as compared to those obtained by other perturbation methods, are obtained by considering a non-zero homogeneous solution and by computing it using conditions based on physical considerations. In particular, the system (6) is assumed to derive from a potential energy (with the relations on quadratic and cubic coefficients given in "Appendix A") and the $B_i$ complex amplitudes are selected as functions of $A_i$, such that the modulation equations (60) also derives from a potential. This method is tested in "Appendix E" for our system. However, it seems to us that this approach is not consistent in our case since our initial system (6) does not necessarily derive from a potential. Consequently, as done for the free Duffing equation in [55, §6.2.1], we propose here to simply cancel the homogeneous solution ($B_1=B_2=0$). It is shown in "Appendix E" that the obtained solution is more accurate at large amplitude, compared to a numerical reference simulation. It must also be noted that in [39], a solution with $B_1=B_2=0$ and $D_1^2A_i=0$ (which leads to cancel also the terms in the second members of Eq. (60) proportional to $\sigma$) is proposed, as well as in [8, 56, 57] for the same system in forced vibrations. Our solution is slightly different as we only enforce $B_1=B_2=0$ and we compute $D_1^2A_i$ with Eq. (57).

Another issue is the treatment of the two time scales $T_1$ and $T_2$ since our initial ordinary differential equations (ODEs) (6) have been replaced by partial differential equations (57),(60) as functions of the two time scales $(T_1,T_2)$. For simple systems like a free Duffing oscillator, it is possible to exactly integrate them (see [55, §6.2.1]). However, we prefer here recombining them in a single ODE using the chain rule (52a) (also called the reconstitution method [39, 41]), as given by Eq. (9).

The complex-valued amplitudes $A_1 (T_1, T_2)$, $A_2 (T_1, T_2)$ are expressed in polar form as follows:

$$\begin{aligned} A_k(T_1,T_2)=\frac{1}{2} a_k(T_1,T_2) e^{i\theta _k(T_1,T_2)},\quad k=1,2. \end{aligned}$$

(61)

Then, by substituting those equations in Eqs. (57), (60) and by using Eq. (9), the separation of the real and imaginary parts yields to:

$$\begin{aligned} \dot{a}_1&= \frac{\varepsilon \beta _1 a_1 a_2}{4\omega _1}\left[ 1+ \frac{\varepsilon \sigma }{2\omega _1}\right] \sin {(2\theta _1-\theta _2+\sigma T_1)}, \end{aligned}$$

(62a)

$$\begin{aligned} \dot{a}_2&= - \frac{\varepsilon \beta _2a_1^2}{4\omega _2}\left[ 1 - \frac{\varepsilon \sigma }{2\omega _2} \right] \sin {(2\theta _1-\theta _2+\sigma T_1)}, \end{aligned}$$

(62b)

$$\begin{aligned} a_1 \dot{\theta }_1&=\frac{\varepsilon \beta _1a_1a_2}{4\omega _1}\left[ 1 + \frac{\varepsilon \sigma }{2\omega _1} \right] \cos {(2\theta _1-\theta _2+\sigma T_1)} \\& - \varepsilon ^2 \frac{\Lambda _1 a_1a_2^2+\Lambda _2 a_1^3}{8\omega _1} , \end{aligned}$$

(62c)

$$\begin{aligned} a_2 \dot{\theta }_2&= \frac{\varepsilon \beta _2a_1^2}{4\omega _2}\left[ 1 - \frac{\varepsilon \sigma }{2\omega _2} \right] \cos {(2\theta _1-\theta _2+\sigma T_1)} \\& - \varepsilon ^2 \frac{\Lambda _3 a_1^2a_2+\Lambda _4 a_2^3}{8\omega _2} . \end{aligned}$$

(62d)

It is convenient to rewrite the above equations as:

$$\begin{aligned} \dot{a}_1&= \Gamma _1 a_1 a_2 \sin \gamma _p, \end{aligned}$$

(63a)

$$\begin{aligned} \dot{a}_2&= - \Gamma _4 a_1^2 \sin \gamma _p,\end{aligned}$$

(63b)

$$\begin{aligned} a_1 \dot{\theta }_1&= \Gamma _1 a_1a_2\cos \gamma _p + \Gamma _2 a_1^3 + \Gamma _3 a_1a_2^2,\end{aligned}$$

(63c)

$$\begin{aligned} a_2 \dot{\theta }_2&= \Gamma _4 a_1^2 \cos \gamma _p + \Gamma _5 a_1^2a_2 + \Gamma _6 a_2^3. \end{aligned}$$

(63d)

where

$$\begin{aligned} \gamma _p=2\theta _1-\theta _2+\sigma T_1, \end{aligned}$$

(64)

and

$$\begin{aligned} \Gamma _1= & {} \frac{\varepsilon \beta _1 }{4\omega _1}\left[ 1+ \frac{\varepsilon \sigma }{2\omega _1}\right] ,\quad \Gamma _4=\frac{\varepsilon \beta _2}{4\omega _2}\left[ 1 - \frac{\varepsilon \sigma }{2\omega _2} \right] , \end{aligned}$$

(65)

$$\begin{aligned} \Gamma _2= & {} -\frac{\varepsilon ^2 \Lambda _2}{8\omega _1},\quad \Gamma _3=-\frac{\varepsilon ^2 \Lambda _1}{8\omega _1},\quad \Gamma _5=-\frac{\varepsilon ^2 \Lambda _3}{8\omega _2}, \quad \Gamma _6=-\frac{\varepsilon ^2 \Lambda _4}{8\omega _2}. \end{aligned}$$

(66)

Those coefficients can be rewritten as function of the initial parameters of the system as

$$\begin{aligned} \Gamma _1&= \frac{g^1_{12}(4\omega _1-\omega _2)}{8\omega _1^2}, \end{aligned}$$

(67a)

$$\begin{aligned} \Gamma _2&=\frac{1}{8\omega _1}\Bigg [3h_{111}^1-\Bigg (\frac{2}{\omega _2^2}+\frac{1}{4\omega _1\omega _2}\Bigg )g^1_{12}g^2_{11}-\frac{10\big (g^1_{11}\big )^2}{3\omega _1^2}\Bigg ] ,\end{aligned}$$

(67b)

$$\begin{aligned} \Gamma _3&= \frac{1}{8\omega _1}\Bigg [2 h^1_{122}+\frac{16 \omega _2^2-4\omega _1^2}{\omega _1^2(\omega _1^2-4\omega _2^2)} g^1_{11}g^1_{22} -\frac{2g^1_{12}g^2_{22}}{\omega _2^2} \\& +\Bigg ( \frac{1}{4\omega _1^2} + \frac{1}{\omega _2(2\omega _1+\omega _2)} \Bigg )\big ( g_{12}^1 \big ) ^2 +\frac{4 g^1_{22} g^2_{12}}{\omega _1^2-4\omega _2^2} \Bigg ],\end{aligned}$$

(67c)

$$\begin{aligned} \Gamma _4&= \frac{g^2_{11}(3\omega _2-2\omega _1)}{8\omega _2^2},\end{aligned}$$

(67d)

$$\begin{aligned} \Gamma _5&=\frac{1}{8\omega _2}\Bigg [ 2h_{112}^2 + \frac{2}{\omega _1^2-4\omega _2^2}\big (g_{12}^2\big )^2 -\frac{4g^2_{11}g^2_{22}}{3\omega _2^2}\nonumber \\&\quad +\Bigg ( \frac{2}{\omega _2(2\omega _1+\omega _2)}-\frac{1}{2\omega _1\omega _2} \Bigg ) g_{12}^1g_{11}^2-\frac{2g_{11}^{1}g_{12}^2}{\omega _1^2} \Bigg ],\end{aligned}$$

(67e)

$$\begin{aligned} \Gamma _6&=\frac{1}{8\omega _2}\Bigg [3h_{222}^2+ \frac{8 \omega _2^2-3\omega _1^2}{\omega _1^2(\omega _1^2-4\omega _2^2)} g_{22}^1g_{12}^2 -\frac{10\big (g_{22}^2\big )^2}{3\omega _2^2} \Bigg ] , \end{aligned}$$

(67f)

Using Eq. (64) with (63c,d) to eliminate $\theta _1$ or $\theta _2$, one has:

$$\begin{aligned} \dot{\gamma }_p=2\omega _1-\omega _2+\left( 2\Gamma _1a_2-\Gamma _4 \frac{a_1^2}{a_2}\right) \cos \gamma _p+(2\Gamma _2-\Gamma _5)a_1^2+(2\Gamma _3-\Gamma _6)a_2^2 \end{aligned}$$

(68)

D Stability details

The Jacobian of the modulation equations in polar coordinates (63a, 63b),(68) reads:

$$\begin{aligned} {\varvec{J}}=\begin{pmatrix} \Gamma _1 a_2\sin \gamma _p &{} \Gamma _1a_1\sin \gamma _p &{} \Gamma _1a_1a_2\cos \gamma _p \\ -2\Gamma _4 a_1\sin \gamma _p &{} 0 &{} -\Gamma _4a_1^2\cos \gamma _p \\ J_{31} &{} J_{32} &{} J_{33} \end{pmatrix} \end{aligned}$$

(69)

with

$$\begin{aligned} J_{31}&=-2\Gamma _4\frac{a_1}{a_2}\cos \gamma _p+2(2\Gamma _2-\Gamma _5)a_1, \end{aligned}$$

(70)

$$\begin{aligned} J_{32}&=\left( 2\Gamma _1+\frac{\Gamma _4 a_1^2}{a_2^2}\right) \cos \gamma _p+2(2\Gamma _3-\Gamma _6)a_2,\end{aligned}$$

(71)

$$\begin{aligned} J_{33}&= -\left( 2\Gamma _1a_2-\frac{\Gamma _4 a_1^2}{a_2}\right) \sin \gamma _p. \end{aligned}$$

(72)

For the coupled solutions C+ or C−, $\sin \gamma _p=0$ and $\cos \gamma _p=p$, which leads to:

$$\begin{aligned} {\varvec{J}}=\begin{pmatrix} 0 &{} 0 &{} J_{13} \\ 0 &{} 0 &{} J_{23} \\ J_{31} &{} J_{32} &{} 0 \end{pmatrix} \end{aligned}$$

(73)

with

$$\begin{aligned} & J_{13} = \Gamma _1 p a_1a_2, \quad \\& J_{23} = -\Gamma _4 p a_1^2,\\& J_{31}=-2\Gamma _4 p \frac{a_1}{a_2}+2(2\Gamma _2-\Gamma _5)a_1, \\& J_{32} = 2\Gamma _1 p +\frac{\Gamma _4 a_1^2}{a_2^2} p +2(2\Gamma _3-\Gamma _6)a_2. \end{aligned}$$

(74)

To assess the stability of the uncoupled U2 solution, the modulation equations must be rewritten under a Cartesian form. To do so, according to [4, 31], we define:

$$\begin{aligned} p_1=a_1 \cos \left( \gamma _p/2\right) , \quad \quad q_1=a_1 \sin \left( \gamma _p/2\right) , \quad \quad p_2= a_2. \end{aligned}$$

(75)

Differentiating $p_1$, $q_1$ and $p_2$ with respect to t, one obtains:

$$\begin{aligned} \dot{p}_1=\dot{a}_1\cos (\gamma _p/2)-a_1\dot{\gamma }_p/2\sin (\gamma _p/2),\quad \dot{q}_1=\dot{a}_1\sin (\gamma _p/2)+a_1\dot{\gamma }_p/2\cos (\gamma _p/2),\quad \dot{p_2}=\dot{a_2}. \end{aligned}$$

(76)

Then, replacing in the above equations $\dot{a}_1$, $\dot{a}_2$ and $\dot{\gamma }_p$ by their values in the polar modulation equations (63) and (68), using basic trigonometric identities and the definitions (75) of $p_1$, $q_1$ and $p_2$, one replaces the modulation equations (63) and (68) by:

$$\begin{aligned} \dot{p}_1&=\Gamma _1 p_2 q_1 +\frac{\Gamma _4}{2} \frac{q_1}{p_2} \left( p_1^2-q_1^2\right) - \left( \Gamma _3 -\frac{\Gamma _6}{2}\right) p_2^2 q_1 \\& - \left( \Gamma _2 -\frac{\Gamma _5}{2}\right) q_1 \left( p_1^2+q_1^2\right) -\frac{1}{2}(2\omega _1-\omega _2) q_1, \end{aligned}$$

(77a)

$$\begin{aligned} \dot{q}_1&=\Gamma _1 p_1 p_2 - \frac{\Gamma _4 }{2} \frac{p_1}{p_2} (p_1^2-q_1^2) +\left( \Gamma _3 -\frac{\Gamma _6}{2}\right) p_1 p_2^2 \\& + \left( \Gamma _2 -\frac{\Gamma _5}{2}\right) p_1 (p_1^2+q_1^2) +\frac{1}{2}(2\omega _1-\omega _2) p_1, \end{aligned}$$

(77b)

$$\begin{aligned} \dot{p}_2&=-2\Gamma _4 p_1 q_1 . \end{aligned}$$

(77c)

Computing the Jacobian ${{\varvec{J}}}$ of the above modulation equations and imposing $a_1=0\;\Rightarrow \;p_1=q_1=0$ for the uncoupled U2 solution, one obtains:

$$\begin{aligned} {\varvec{J}}=\begin{pmatrix} 0 &{} J_{12} &{} 0 \\ J_{21} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix} \end{aligned}$$

(78)

with

$$\begin{aligned} J_{12}=-(2\omega _1-\omega _2)/2+\Gamma _1 a_2 - (\Gamma _3-\Gamma _6/2) a_2^2,\quad J_{21}=(2\omega _1-\omega _2)/2+\Gamma _1 a_2 + (\Gamma _3-\Gamma _6/2) a_2^2, \end{aligned}$$

(79)

where $a_2=p_2$ by definition. Its eigenvalues are thus:

$$\begin{aligned} \lambda _1=0,\quad \lambda _{2,3}=\pm \sqrt{J_{12}J_{21}} \end{aligned}$$

(80)

E MSM with homogeneous solution and enforced Lagrangian

We consider here the approach of [39] that considers the homogeneous solutions in Eq. (59) and enforces the modulation Eq. (60) to derive from a potential. This is obtained by enforcing:

$$\begin{aligned} 2i\omega _1D_1B_1+ D_1^2 A_1=0,\quad 2i\omega _1D_1B_2+ D_1^2 A_2=0, \end{aligned}$$

(81)

or

$$\begin{aligned} B_1&=\frac{-\beta _1}{4\omega _1^2}A_2 \bar{A}_1 e^{-i \sigma T_1}+cc, \end{aligned}$$

(82a)

$$\begin{aligned} B_2&=\frac{-\beta _2}{4\omega _2^2}A_1^2 e^{i \sigma T_1}+cc. \end{aligned}$$

(82b)

One can note that upon substituting (82) in (60), all the terms related to $B_1$ and $B_2$ in addition to the terms multiplied by $\sigma$ will be eliminated. We arrive at the following modulation equations:

$$\begin{aligned} 2i\omega _1 D_2 A_1&= \Lambda _1' A_1 A_2 \bar{A}_2 +\Lambda _2' A_1^2 \bar{A}_1, \end{aligned}$$

(83a)

$$\begin{aligned} 2i\omega _2 D_2 A_2&= \Lambda _3'A_1 A_2 \bar{A}_1 +\Lambda _4' A_2^2 \bar{A}_2, \end{aligned}$$

(83b)

with

$$\begin{aligned} \Lambda _1'&=\beta _1^2 \Bigg [ \frac{1}{4\omega _1^2} - \frac{1}{\omega _2(2\omega _1+\omega _2)}\Bigg ]-2 \alpha _4 \omega _2^2 -2 \alpha _2, \end{aligned}$$

(84a)

$$\begin{aligned} \Lambda _2'&=\frac{9\beta _1 \beta _2}{4\omega _2^2} -\alpha _3 \omega _1^2-3\alpha _1, \end{aligned}$$

(84b)

$$\begin{aligned} \Lambda _3'&=2\beta _1 \beta _2 \Bigg [\frac{1}{4 \omega _1^2}- \frac{1}{\omega _2(2\omega _1+\omega _2)}\Bigg ]-2 \alpha _6 -2\alpha _9 \omega _1^2, \end{aligned}$$

(84c)

$$\begin{aligned} \Lambda _4'&=-3 \alpha _7 -\alpha _{10} \omega _2^2. \end{aligned}$$

(84d)

Note that coefficients $\Lambda _k'$ are different than the $\Lambda _k$ in Eq. (60). In addition, one can note that the modulation equations in (83a, b) don’t derive from a potential since $\Lambda _1' \ne \Lambda _3'$ even if it is the case for the initial system (i.e., by setting $g_{12}^1=2g_{11}^2$, $g_{12}^2=2g_{22}^1$, $h_{122}^1=h_{112}^2$, $h_{122}^2=3h_{222}^1$ and $h_{112}^1=3h_{111}^2$). This can be analyzed by realizing that if one considers the initial system (1a, 1b) to derivee from a potential, it is not necessarily the case for the normal form system (2a, 2b) which relies on a truncation from an asymptotic development. In particular, if one neglects all the cubic terms from ((2a, 2b), one obtains the same results as in [39] where the Lagrangian is enforced.

Following the same procedure in Sect. 2.2, the modulation equations are expressed in the polar form as:

$$\begin{aligned} \frac{\text {d}a_1}{\text {d}t}=&\frac{\varepsilon \beta _1 a_1 a_2}{4\omega _1}\sin {\gamma _p}, \end{aligned}$$

(85a)

$$\begin{aligned} \frac{\text {d}a_2}{\text {d}t}=&- \frac{\varepsilon \beta _2a_1^2}{4\omega _2} \sin {\gamma _p}, \end{aligned}$$

(85b)

$$\begin{aligned} \frac{\text {d}\theta _1}{\text {d}t}=&\frac{\varepsilon \beta _1a_2}{4\omega _1} \cos {\gamma _p} - \varepsilon ^2 \frac{\Lambda _1' a_2^2+\Lambda _2' a_1^2}{8\omega _1}, \end{aligned}$$

(85c)

$$\begin{aligned} \frac{\text {d}\theta _2}{\text {d}t}=&\frac{\varepsilon \beta _2a_1^2}{4\omega _2a_2} \cos {\gamma _p} - \varepsilon ^2 \frac{\Lambda _3' a_1^2+\Lambda _4' a_2^2}{8\omega _2}, \end{aligned}$$

(85d)

and the autonomous version is obtained by combining (85c, 85d) with Eq. (11), yielding:

$$\begin{aligned} \frac{\text {d}\gamma _p}{\text {d}t}=&\varepsilon \sigma + \varepsilon \left( \frac{\beta _1a_2}{2\omega _1} - \frac{\beta _2 a_1^2}{4 a_2\omega _2}\right) \cos \gamma _p \nonumber \\&\quad +\varepsilon ^2\left( \frac{\Lambda _3' a_1^2 +\Lambda _4' a_2^2}{8\omega _2} - \frac{\Lambda _1' a_2^2+\Lambda _2' a_1^2}{4\omega _1}\right) . \end{aligned}$$

(86)

Using the same procedure in Sect. 2.2, we can find the expressions governing the relation between $a_1$ and $a_2$ in addition to the expressions of the nonlinear modes $\omega _{\text {nl}1}$ and $\omega _{\text {nl}2}$, as:

$$\begin{aligned} a_1^2&=\frac{(2\omega _1-\omega _2)a_2+2\Gamma _1'a_2^2+(2\Gamma _3'-\Gamma _6')a_2^3}{\Gamma _4'+(\Gamma _5'-2\Gamma _2') a_2}, \end{aligned}$$

(87a)

$$\begin{aligned} \omega _{\text {nl}1}&= \omega _1+\Gamma _1' a_2 + \Gamma _2' a_1^2 +\Gamma _3' a_2^2, \end{aligned}$$

(87b)

$$\begin{aligned} \omega _{\text {nl}2}&= \omega _2+\Gamma _4' \frac{a_1^2}{a_2} + \Gamma _5' a_1^2 +\Gamma _6' a_2^2, \end{aligned}$$

(87c)

where

$$\begin{aligned} \Gamma _1'&= p\,\frac{g^1_{12}}{4\omega _1}, \end{aligned}$$

(88a)

$$\begin{aligned} \Gamma _2'&=\frac{1}{8\omega _1}\Bigg [3h_{111}^1-\frac{9}{4\omega _2^2} g_{12}^1 g_{11}^2 -\frac{10}{3\omega _1^2}\big (g_{11}^1\big )^2\Bigg ] ,\end{aligned}$$

(88b)

$$\begin{aligned} \Gamma _3'&= \frac{1}{8\omega _1}\Bigg [2 h^1_{122}+\Bigg (\frac{16 \omega _2^2-4\omega _1^2}{\omega _1^2(\omega _1^2-4\omega _2^2)} \Bigg )g^1_{11}g^1_{22} -\frac{2g^1_{12}g^2_{22}}{\omega _2^2}\nonumber \\&\quad +\Bigg (\frac{1}{\omega _2(2\omega _1+\omega _2)}- \frac{1}{4\omega _1^2} \Bigg )\big ( g_{12}^1 \big ) ^2 +\frac{4 g^1_{22} g^2_{12}}{\omega _1^2-4\omega _2^2} \Bigg ],\end{aligned}$$

(88c)

$$\begin{aligned} \Gamma _4'&= p\,\frac{g^2_{11}}{4\omega _2},\end{aligned}$$

(88d)

$$\begin{aligned} \Gamma _5'&=\frac{1}{8\omega _2}\Bigg [ 2h_{112}^2 + \Bigg ( \frac{2}{\omega _1^2-4\omega _2^2}\Bigg )\big (g_{12}^2\big )^2 -\frac{4g^2_{11}g^2_{22}}{3\omega _2^2}\nonumber \\&\quad +\Bigg ( \frac{2}{\omega _2(2\omega _1-\omega _2)}-\frac{1}{4\omega _1^2} \Bigg ) g_{12}^1g_{11}^2-\frac{2g_{11}^{1}g_{12}^2}{\omega _1^2} \Bigg ],\end{aligned}$$

(88e)

$$\begin{aligned} \Gamma _6'&=\frac{1}{8\omega _2}\Bigg [3h_{222}^2+ \Bigg ( \frac{8 \omega _2^2-3\omega _1^2}{\omega _1^2(\omega _1^2-4\omega _2^2)}\Bigg ) g_{22}^1g_{12}^2 -\frac{10\big (g_{22}^2\big )^2}{3\omega _2^2} \Bigg ] , \end{aligned}$$

(88f)

Note that the relation $\omega _{\text {nl}2}=2\omega _{\text {nl}1}$ is still satisfied. In addition, the solution of $R_1(t)$ and $R_2(t)$ illustrates the same locking properties in the amplitudes and phase angles illustrated in Section 2.2.

A comparison is shown in Fig. 11 between the analytical results governing the backbone curves of both approaches presented in (18a, 18b) and (87b, 87c), with the numerical solution computed with the continuation method implemented in Manlab, which is considered as our reference solution. The plots are done for positive, negative, and zero values of $\sigma$ to underline the effect of the additional term appearing in (60a, 60b). Both results match with the numerical solution at low amplitudes. However, at higher amplitudes, the first approach used in Sect. 2.2 suggests more accurate results as compared to the numerical ones, especially for the C+ mode. Namely, the second approach that leads to the results in (87b, 87c) shows a kind of softening behavior associated with the response of the C+ mode at high amplitudes.

Fig. 11

Comparison between the analytical results of the two approaches presented in (18a, b) and (87a, b) with the numerical results computed with Manlab. Only the quadratic resonant terms are considered such that $g_{12}^1=g_{11}^2=1$ with the other nonlinear coefficients are set to zero. The backbones are plotted in the planes ($a_1$, $\omega _{\text {nl}2}$) and ($a_2$, $\omega _{\text {nl}2}$) in the first and second row, respectively. The first, second, and third column are the results for $\sigma =-0.07$, $\sigma =0$, $\sigma =0.07$, respectively. The analytical results for the C+ and C− modes are plotted in blue and red, respectively. The dotted and solid lines are results of (87) and (18), respectively. The Manlab results are shown in black for the C+ and C− modes. (Color figure online)