SpringerLink
Log in

On the Distribution of the Number of Success Runs in a Continuous Time Markov Chain

  • Published:
Methodology and Computing in Applied Probability Aims and scope Submit manuscript

Abstract

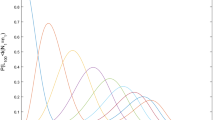
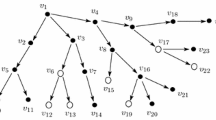
We propose a continuous-time adaptation of the well-known concept of success runs by considering a marked point process with two types of marks (success-failure) that appear according to an appropriate continuous-time Markov chain. By constructing a bivariate imbedded process (consisting of a run-counting and a phase process), we offer recursive formulas and generating functions for the distribution of the number of runs and the waiting time until the appearance of the n-th success run. We investigate the three most popular counting schemes: (i) overlap** runs of length k, (ii) non-overlap** runs of length k and (iii) runs of length at least k. We also present examples of applications regarding: the total penalty cost in a maintenance reliability system, the number of risky situations in a non-life insurance portfolio and the number of runs of increasing (or decreasing) asset price movements in high-frequency financial data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Balakrishnan N, Koutras MV (2002) Runs and scans with applications. Wiley, New York

    MATH  Google Scholar 

  • Binswanger K, Embrechts P (1994) Longest runs in coin tossing. Insur: Math Econ 15:139–149

    MathSciNet  MATH  Google Scholar 

  • Boutsikas MV, Koutras MV (2002) Modeling claim exceedances over thresholds. Insurance: Mathematics and Economics 30:67–83

    MathSciNet  MATH  Google Scholar 

  • Embrechts P, Kluppelberg C, Mikosch T (2013) Modelling extremal events for insurance and finance. Springer, Berlin

    MATH  Google Scholar 

  • Eryilmaz S (2018) Stochastic ordering among success runs statistics in a sequence of exchangeable binary trials. Methodol Comput Appl Probab 20:563–573

    Article  MathSciNet  Google Scholar 

  • Eryilmaz S, Demir S (2007) Success runs in a sequence of exchangeable binary trials. J Stat Plan Infer 137:2954–2963

    Article  MathSciNet  Google Scholar 

  • Fu JC, Koutras MV (1994) Distribution theory of runs: a Markov chain approach. J Am Stat Assoc 89:1050–1058

    Article  MathSciNet  Google Scholar 

  • Fu JC, Lou WYW (2003) Distribution theory of runs and patterns and its applications: a finite Markov chain imbedding approach. World Scientific

  • Fu JC, Wu TL, Lou WYW (2012) Continuous, discrete, and conditional scan statistics. J Appl Prob 49:199–209

    Article  MathSciNet  Google Scholar 

  • Glaz J, Naus J, Wallenstein S (2001) Scan statistics. Springer

  • Koutras MV (2003) Applications of Markov chains to the distribution theory of runs and patterns. Handbook of statistics. Elsevier 21:431–472

    MATH  Google Scholar 

  • Koutras MV, Alexandrou VA (1995) Runs, scans and URN model distributions: A unified Markov chain approach. Ann Inst Stat Math 47:743–766

    Article  MathSciNet  Google Scholar 

  • Makri FS, Psillakis ZM (2011) On success runs of length exceeded a threshold. Methodol Comput Appl Probab 13:269–305

    Article  MathSciNet  Google Scholar 

  • Makri FS, Psillakis ZM (2016) On runs of ones defined on a q-sequence of binary trials. Metrika 79:579– 602

    Article  MathSciNet  Google Scholar 

  • Makri FS, Philippou AN, Psillakis ZM (2007) Success run statistics defined on an urn model. Adv Appl Probab 39:991–1019

    Article  MathSciNet  Google Scholar 

  • Mytalas GC, Zazanis MA (2013) Central limit theorem approximations for the number of runs in Markov-dependent binary sequences. J Statist Plann Inference 143:321–333

    Article  MathSciNet  Google Scholar 

  • Talbot A (1979) The accurate numerical inversion of laplace transforms. IMA J Appl Math 23:97–120

    Article  MathSciNet  Google Scholar 

  • Weideman JAC, Trefethen LN (2007) Parabolic and hyberbolic contours for computing the Bromwich integral. Math Comput 76:1341–1356

    Article  Google Scholar 

  • Wu T-L, Glaz J (2015) A new adaptive procedure for multiple window scan statistics. Comput Stat Data Anal 82:164–172

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Statistics & Insurance Science, University of Piraeus, Piraeus, Greece

    Boutsikas V. Michael

  2. Department of Mathematics, National and Kapodistrian University of Athens, Athens, Greece

    Vaggelatou Eutichia

Authors
  1. Boutsikas V. Michael
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vaggelatou Eutichia
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Boutsikas V. Michael.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Michael, B.V., Eutichia, V. On the Distribution of the Number of Success Runs in a Continuous Time Markov Chain. Methodol Comput Appl Probab 22, 969–993 (2020). https://doi.org/10.1007/s11009-019-09743-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11009-019-09743-3

Keywords

Mathematics Subject Classification (2010)

Search

Navigation