Abstract
This paper establishes the algorithmic principle of alternating projections onto incoherent low-rank subspaces (APIS) as a unifying principle for designing robust regression algorithms that offer consistent model recovery even when a significant fraction of training points are corrupted by an adaptive adversary. APIS offers the first algorithm for robust non-parametric (kernel) regression with an explicit breakdown point that works for general PSD kernels under minimal assumptions. APIS also offers, as straightforward corollaries, robust algorithms for a much wider variety of well-studied settings, including robust linear regression, robust sparse recovery, and robust Fourier transforms. Algorithms offered by APIS enjoy formal guarantees that are frequently sharper than (especially in non-parametric settings) or competitive to existing results in these settings. They are also straightforward to implement and outperform existing algorithms in several experimental settings.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and problem statement
We have a regression problem with n training points with regression values (aka responses or signal) denoted by the vector \({\mathbf{a}}^*\in {\mathbb{R}}^n\) (see below for examples). An adversary introduces additive corruptions \({\mathbf{b}}^*\in {\mathbb{R}}^n\) so that the responses we actually observe are given by
Can, under some conditions on \({\mathbf{a}}^* \text{ and } {\mathbf{b}}^*\), we recover \({\mathbf{a}}^*\) (as well as parameters in its generative model) despite the corruptions? This paper develops the APIS framework to answer this question in the affirmative.
Key idea: If \({\mathbf{a}}^*\in \mathscr {A}\) and \({\mathbf{b}}^*\in \mathscr {B}\), where \(\mathscr {A} \text{ and } \mathscr {B}\) are unions of low-rank subspaces that are incoherent with respect to each other (see Sect. 1.1 for an introduction to incoherence and Sect. 6.1 for details), then this paper shows that such recovery is indeed possible. Specifically, let \({\mathbf{a}}^*\in \mathscr {A} \text{ and } {\mathbf{b}}^*\in \mathscr {B}\), where \(\mathscr {A}= \bigcup _{i=1}^P A_i\) and \(\mathscr {B}= \bigcup _{j=1}^Q B_j\) are the unions of subspaces, with \({{\,\mathrm{rank}\,}}(A_i) \le s\) for all \(i \in [P]\) and \({{\,\mathrm{rank}\,}}(B_j) \le k\) for all \(j \in [Q]\) for some integers \(s, k > 0\). Then, this paper shows that it is possible to recover \({\mathbf{a}}^*\) consistently using a simple strategy that involves alternating projections onto these unions using projection operators \(\varPi _\mathscr {A}(\cdot ) \text{ and } \varPi _\mathscr {B}(\cdot )\) (see Algorithm 1). As we shall see, such incoherent unions of subspaces implicitly arise in several learning settings, e.g., if \({\mathbf{a}}^* \text{ and } {\mathbf{b}}^*\) are known to have s- and k-sparse representations in two bases that are incoherent to each other. We denote the privileged subspaces within these unions to which \({\mathbf{a}}^*\) and \({\mathbf{b}}^*\) belong as \({A}^*\ni {\mathbf{a}}^* \text{ and } {B}^*\ni {\mathbf{b}}^*\).

What all is known to APIS: APIS requires the projection operators \(\varPi _\mathscr {A}(\cdot ), \varPi _\mathscr {B}(\cdot )\) to be executable efficiently at runtime as its alternating strategy may invoke these operators multiple times. Thus, it needs the unions \(\mathscr {A} \text{ and } \mathscr {B}\) to be (implicitly) known. The discussions in Sects. 2 and 5.1, 5.2 assure that these conditions are indeed satisfied in several interesting learning applications. However, APIS does not require the vectors \({\mathbf{a}}^* \text{ and } {\mathbf{b}}^*\) to be known, nor does it assume that the subspaces \({A}^* \text{ and } {B}^*\) to which they belong are known, nor does it require \({A}^* \text{ and } {B}^*\) to be unique either.
1.1 A key to the manuscript
The reader may be curious about several questions that need solutions for the above strategy to make sense. We summarize APIS’s solutions to these questions below but provide more details in subsequent discussions (that are underlined in italics for easy identification).
-
1.
How are \(\mathscr {A} \text{ and } \mathscr {B}\) known to the algorithm? Sect. 2 shows how in the case of robust linear regression, the union \(\mathscr {A}\) is implicitly known the moment training data is made available. Section 5.1 shows that the same is true in several other important learning applications. Section 5.2 on the other hand, shows how the union \(\mathscr {B}\) is defined for several interesting corruption models.
-
2.
How are the projection operators for these unions constructed and efficiently executed? Projection onto unions of spaces can be intractable in general. Nevertheless, Sect. 5 shows how for several interesting learning applications, the projection operators \(\varPi _\mathscr {A}(\cdot ) \text{ and } \varPi _\mathscr {B}(\cdot )\) can be executed efficiently. Moreover, Table 1 gives explicit time complexity for these projection operations in a variety of applications.
-
3.
What if \(\mathscr {A} \text{ and } \mathscr {B}\) are not incoherent to each other? As discussed in Sects. 3 and 6.4, APIS can exploit local incoherence properties to guarantee recovery even when strict notions of incoherence fail to hold. See Sect. 2 for an introduction to incoherence.
-
4.
Does the adversary know \(\mathscr {A}\) (or, perhaps even \({\mathbf{a}}^*\)) before deciding \({\mathbf{b}}^*\)? As discussed in Sect. 4, APIS allows a fully adaptive adversary that is permitted to decide the corruption vector \({\mathbf{b}}^*\) with complete knowledge of \({\mathbf{a}}^*, {A}^*\) as well as \(\mathscr {A} \text{ and } \mathscr {B}\).
-
5.
Is the model in Eq. (1) general enough to capture interesting applications and can the unions \(\mathscr {A} \text{ and } \mathscr {B}\) be data-dependent? The discussion in Sect. 5 shows that the model does indeed capture several statistical estimation and signal processing problems such as low-rank kernel regression, sparse signal transforms, robust sparse recovery, and robust linear regression. In most of these settings, the union \(\mathscr {A}\) is indeed data-dependent.
-
6.
What if \({\mathbf{a}}^* \text{ and } {\mathbf{b}}^*\) are only approximate members of these unions? As discussed in Sect. 6.4, APIS can readily accommodate compressible signals, where the clean signal \({\mathbf{a}}^*\) does not belong to \(\mathscr {A}\) but is well-approximated by vectors in \(\mathscr {A}\), as well as handle unmodelled errors such as simultaneous sparse corruptions and dense Gaussian noise.
-
7.
How low-rank must the subspaces in the unions be, i.e., how large can s and k be? The key result in this paper Theorem 1 guarantees recovery the moment a certain incoherence requirement is satisfied. The pursuit of satisfying this requirement results in bounds on s and k to emerge for various applications. Table 1 summarizes the signal-corruption pairings for which APIS guarantees perfect recovery and bounds how large s and k can be. Detailed derivations of these results are presented in the appendices and summarized in Sect. 6.
2 A gentle introduction to the intuition behind APIS
We recall our model from Sect. 1. We have \(\mathbf{y}= {\mathbf{a}}^*+ {\mathbf{b}}^*\) with \({\mathbf{a}}^*\in \mathscr {A} \text{ and } {\mathbf{b}}^*\in \mathscr {B}\), where \(\mathscr {A}= \bigcup _{i=1}^P A_i\) and \(\mathscr {B}= \bigcup _{j=1}^Q B_j\) are the unions of subspaces, with \({{\,\mathrm{rank}\,}}(A_i) \le s\) for all \(i \in [P]\) and \({{\,\mathrm{rank}\,}}(B_j) \le k\) for all \(j \in [Q]\) for some integers \(s, k > 0\). To present the core ideas behind APIS , we consider a simplified scenario where \(P = 1 = Q\), i.e., the unions consist of a single subspace each \(\mathscr {A}= \left\{ A\right\} , \mathscr {B}= \left\{ B\right\}\). As Definition 1 shows, we say two subspaces \(A, B \subseteq {\mathbb{R}}^n\) (of possibly different ranks) are \(\mu\)-incoherent for some \(\mu > 0\), if \(\forall ~\mathbf{u}\in A\), \(\left\| \varPi _B(\mathbf{u}) \right\| _2^2 \le \mu \cdot \left\| \mathbf{u} \right\| _2^2\) and \(\forall ~\mathbf{v}\in B\), \(\left\| \varPi _A(\mathbf{v}) \right\| _2^2 \le \mu \cdot \left\| \mathbf{v} \right\| _2^2\). As the discussion after Definition 1 shows, an alternate interpretion of this property is that for any two unit vectors \(\mathbf{a}\in A, \mathbf{b}\in B\), we must always have \((\mathbf{a}^\top \mathbf{b})^2 \le \mu\). This means that if \(\mu\) is small, then no two vectors from these two subspaces can be very aligned to each other and thus, the vectors must be near-orthonormal. Definition 2 extends the concept of incoherence to unions of subspaces.
Figure 1 illustrates this concept using a toy example where A is a rank-2 subspace of \({\mathbb{R}}^3\) and B is a rank-1 subspace of \(\mathbb{R}^3\) , i.e., \(s = 2, k = 1\). Notice that in Fig. 1a, the subspaces A, B are highly incoherent indicating a value of \(\mu \rightarrow 0\). It is not possible for two vectors, one each from A, B, to be very aligned to each other. On the other hand, Fig. 1b illustrates an example of a pair of subspaces that are quite coherent and have a high value of \(\mu \rightarrow 1\). Also, shown in Fig. 1b are examples of two vectors \({\mathbf{a}}^*\in A, {\mathbf{b}}^*\in B\) that are extremely aligned to each other since the subspaces A, B are not incoherent and allow vectors to get very aligned.
Why incoherence helps robust recovery? To appreciate the benefits of incoherence, consider an extreme example where A, B are perfectly incoherent with \(\mu = 0\) as illustrated in Fig. 2. For example, take \(A = \left\{ (x,y,z) \in {\mathbb{R}}^3, x + y + z = 0\right\}\) to be a rank-2 subspace of \({\mathbb{R}}^3\) and \(B = \left\{ (t,t,t) \in {\mathbb{R}}^3, t \in {\mathbb{R}}\right\}\) to be a rank-1 subspace of \({\mathbb{R}}^3\). Clearly, for any \((x,y,z) \in A, (t,t,t) \in B\), we have \(\left\langle (x,y,z),(t,t,t) \right\rangle = t(x + y + z) = 0\). Now suppose the signal and corruption vectors are chosen as \({\mathbf{a}}^*\in A, {\mathbf{b}}^*\in B\) and we are presented with \(\mathbf{y}= {\mathbf{a}}^*+ {\mathbf{b}}^*\). Separating these two components is extremely simple in this case. To extract \({\mathbf{b}}^*\) from \(\mathbf{y}\), we simply project \(\mathbf{y}\) onto the subspace B to get \(\varPi _B(\mathbf{y}) = \varPi _B({\mathbf{a}}^*+ {\mathbf{b}}^*) = \varPi _B({\mathbf{a}}^*) + \varPi _B({\mathbf{b}}^*) = \mathbf{0}+ {\mathbf{b}}^*= {\mathbf{b}}^*\), where we have \(\varPi _B({\mathbf{b}}^*) = {\mathbf{b}}^*\) due to the idempotence of orthonormal projections and \(\varPi _B({\mathbf{a}}^*) = \mathbf{0}\) due to perfect incoherence between the two subspaces. Having done this, we can recover \({\mathbf{a}}^*\) by simply shaving off the contribution of \({\mathbf{b}}^*\) in \(\mathbf{y}\) and projecting onto A to get \(\varPi _A(\mathbf{y}- {\mathbf{b}}^*) = \varPi _A({\mathbf{a}}^*) = {\mathbf{a}}^*\). It is easy to see that the above two steps are simply a single iteration of Algorithm 1. Thus, perfect incoherence allows straightforward recovery. Theorem 1 shows that APIS assures recovery even when the subspaces are reasonably incoherent but not perfectly incoherent. Section 6.4 extends this further to show how APIS offers recovery even in cases where only local incoherence is present in the task structure.
An extreme example illustrating how perfect incoherence (\(\mu = 0\)) allows APIS to perform recovery in a single iteration of Algorithm 1. However APIS does not require perfect incoherence and guarantees recovery even if we only have \(\mu < \frac{1}{9}\) (see Theorem 1) and even if only local incoherence is assured (see Sect. 6.4)
Why lack of incoherence can make recovery impossible: To see why some form of incoherence is essential in general, consider a case similar to the one in Fig. 1b but taken to the extreme, i.e., where \(\mu = 1\). To present a general case, let us take A, B to be higher rank spaces. For example, let \(A = \left\{ (a,b,c,d) \in {\mathbb{R}}^4, a + b = 0\right\}\) and \(B = \left\{ (p,q,0,s) \in {\mathbb{R}}^4, p + q = 0\right\}\) be the two subspaces of \({\mathbb{R}}^4\) with ranks 3 and 2 respectively. Since the unit vector \(\left( \frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}, 0, 0\right)\) lies in both A and B, the subspaces are coherent with \(\mu = 1\). Suppose we are unlucky to have chosen the signal as \({\mathbf{a}}^*= (u, -u, 0, v) \in A\) for some \(u, v \in {\mathbb{R}}\). Note that \({\mathbf{a}}^*\in A \cap B\). Then the adversary can readily choose \({\mathbf{b}}^*= (x, -x, 0, y) \in B\) for some secret values of \(x, y \in {\mathbb{R}}\) that the adversary does not reveal to anybody. Recall that the adversary is allowed to choose \({\mathbf{b}}^*\) having seen the value of \({\mathbf{a}}^*\). Thus, we are presented with \(\mathbf{y}= {\mathbf{a}}^*+ {\mathbf{b}}^*= ((u+x), -(u+x), 0, (v+y))\). However, depending on x, y, this can be an arbitrary vector in the space B. Thus, recovering \({\mathbf{a}}^*\) becomes equivalent to recovering the secret values x, y which makes recovery impossible.
A real-life example: To make the above intuitions concrete, let us take the example of robust linear regression where we have \({\mathbf{a}}^*= X^\top {\mathbf{w}}^*\in {\mathbb{R}}^n\), where \(X = [\mathbf{x}^1,\ldots ,\mathbf{x}^n] \in {\mathbb{R}}^{d \times n}\) is the covariate matrix of the n data points and \({\mathbf{w}}^*\in {\mathbb{R}}^d\) is the linear model. In this case we always have \({\mathbf{a}}^*\in \text {span}(\mathbf{x}^1,\ldots ,\mathbf{x}^n)\), i.e. \(P = 1\) and \(\mathscr {A}= \left\{ A\right\} = \text {span}(\mathbf{x}^1,\ldots ,\mathbf{x}^n)\). Suppose \(\mathscr {B}= \left\{ B\right\}\) with \(B = A\) i.e., a completely coherent system with \(\mu = 1\). In this case, the adversary can choose an adversarial model \(\tilde{\mathbf{w}} \in {\mathbb{R}}^d\) and set \({\mathbf{b}}^*= X^\top (\tilde{\mathbf{w}} - {\mathbf{w}}^*) \in B\) so that we are presented with \(\mathbf{y}= {\mathbf{a}}^*+ {\mathbf{b}}^*= X^\top \tilde{\mathbf{w}}\). Since \(\tilde{\mathbf{w}}\) is kept secret by the adversary, recovery yet again becomes impossible. On the other hand, as Table 1 and calculations in Sect. B in appendix show, if the adversary is restricted to impose only sparse corruptions, specifically \(\mathscr {B}= \left\{ \mathbf{b}\in {\mathbb{R}}^n, \left\| \mathbf{b} \right\| _0 \le k\right\}\) for \(k \le \frac{n}{154}\), then \(\mathscr {A}\) is sufficiently incoherent from \(\mathscr {B}\) and APIS guarantees recovery.
3 Related works and our contributions in context
3.1 Summary of contributions
APIS presents a unified framework for designing robust (non-parametric) regression algorithms based on the principle of successive projections onto incoherent sub-spaces and applies it to various settings (see Sect. 5). APIS also offers explicit breakdown points and offers some of the fastest recoveries in experiments. Below, we give a survey of past works in these settings and offer comparisons with our contributions.
3.2 Robust non-parametric regression
Classical results in this are mostly relying on robust estimators such as Huber, \(L_1\) and median (Cizek and Sadikoglu 2020; Fan et al. 1994), some of which (e.g., those based on Tukey’s depth) are computationally intractable (Du et al. 2018). Please refer to recent reviews in Cizek and Sadikoglu (2020) and Du et al. (2018) for details. More recent work includes the LBM method (Du et al. 2018) that uses binning and median-based techniques.
Comparison: We compare experimentally to all these methods in Sect. 7. Classical techniques mostly do not offer explicit breakdown points; instead, they analyze the influence function of their estimators (Cizek and Sadikoglu 2020). Classical works and LBM also consider only Huber contamination models where the adversary is essentially stochastic. In contrast, APIS offers explicit breakdown points against a fully adaptive adversary (see Sect. 4). LBM does not scale well with dimension d. Unless it receives \(n = (\varOmega \left( 1\right) )^d\) training points, it has to settle for coarse bins that increase the bias or face a situation where most bins are unpopulated, affecting the recovery. In contrast, APIS requires kernel ridge regression problems to be solved, for which efficient routines exist even for large d.
3.3 Robust linear regression
Past works adopt various strategies such as robust gradient methods e.g., SEVER (Diakonikolas et al. 2019), RGD (Prasad et al. 2018), hard thresholding techniques TORRENT (Bhatia et al. 2015), and reweighing techniques STIR (Mukhoty et al. 2019), apart from classical techniques based on robust loss functions such as Tukey’s Bisquare and constrained L1-minimization based morphological component analysis (MCA) (McCoy and Tropp 2014).
Comparison: We compare experimentally to all these methods in Sect. 7. On the theoretical side, APIS offers more attractive guarantees. SEVER requires \(n > d^5\) samples, whereas APIS requires \(n > \varOmega \left( d\log (d)\right)\) samples. RGD offers theoretical guarantees only for Huber and heavy-tailed contamination models where the adversary is essentially stochastic, whereas APIS can tolerate a fully adaptive adversary (see Sect. 4). APIS offers much sharper guarantees (see Sect. 6.4) than TORRENT and STIR in the hybrid corruption case where apart from sparse corruptions, all points face Gaussian noise. However, TORRENT and STIR offer better breakdown points than APIS .
3.4 Robust Fourier and other signal transforms
Several works offer recovery of Fourier-sparse functions under sparse outliers, with the discrete cube or torus being candidate domains, and propose algorithms based on linear programming (Chen and De 2020; Guruswami and Zuckerman 2016). These offer good theoretical guarantees but are expensive (\(\text {poly}(n)\) runtime) to implement (the authors themselves offer no experimental work). On the other hand, APIS only requires “fast” transforms such as FFT to be carried out several times (and consequently, APIS offers an \(\mathscr {O}\left( n\log n\right)\) runtime in these settings). Under sparse corruptions, APIS guarantees robust versions of several other transforms such as robust Hadamard transforms (see Table 1). APIS is additionally able to handle dense corruptions in special cases as well (see Sect. 6). The work of Bafna et al. (2018) uses an algorithm proposed by Baraniuk et al. (2010), in the context of performing robust Fourier transforms in the presence of sparse corruptions. However, their RIP-based analysis is restrictive and only applies to transforms such as Fourier, for which every entry of the design matrix is \(\mathscr {O}\left( 1/{\sqrt{n}}\right)\) (see Bafna et al. 2018, Theorem 2.2). This is not true of transforms, e.g., Haar wavelet, where design matrix entries can be \(\varOmega \left( 1\right)\). APIS continues to give recovery guarantees even in such cases, and it can handle certain cases where corruptions are dense, i.e., \(\left\| {\mathbf{b}}^* \right\| _0 = \varOmega \left( n\right)\) which Bafna et al. (2018) do not consider.
3.5 Use of (local) incoherence in literature
The general principle of alternating projections and the notion of incoherence has been used in prior work. For example, Hegde and Baraniuk (2012) apply this principle to the problem of signal recovery on incoherent manifolds. However, our application of the alternating projection principle to robust non-parametric regression is novel and not addressed by prior work. Notions of incoherence and incoherent bases are also well-established in compressive sensing (Candes and Wakin 2008) and matrix completion (Chen 2015). However, to the best of our knowledge, APIS offers the first application of these notions to robust non-parametric recovery. It is well-known (Krahmer and Ward 2014; Zhou et al. 2016) that (global) incoherence may be unavailable in practical situations (e.g., Fourier and wavelet bases are not incoherent). Nevertheless, several results in compressive sensing (Krahmer and Ward 2014), matrix completion (Chen et al. 2014) and robust PCA (Zhang et al. 2015) assert that local notions of incoherence can still guarantee recovery. Section 6.4shows that APIS can as well exploit local incoherence properties to guarantee recovery in settings where strict notions of incoherence fail to hold.
3.6 Learning incoherent spaces
An interesting line of work has pursued the goal of learning incoherent dictionaries for the task of classification (Schnass and Vandergheynst 2010; Barchiesi and Plumbley 2013, 2015). Specifically, a set of discriminative subspaces (sub-dictionaries) are learnt, one per class so as to offer discriminative advantage in supervised classification tasks. However, in the problem setting for APIS, as described after Eq. (1), the subspaces \(\mathscr {A}, \mathscr {B}\) are well defined once once training data has been obtained and the corruption model has been fixed and thus, do not need to be learnt. For this reason, these works do not directly relate to the work in the current paper.
4 APIS: alternating projections onto incoherent subspaces
Adversary model: APIS allows a fully adaptive adversary that is permitted to decide the corruption vector \({\mathbf{\underline{b}}}^*\) with complete knowledge of \(\underline{{\mathbf{a}}^*, {A}^*}\) as well as \(\underline {\mathscr {A} \text{ and } \mathscr {B}}\).
We note that this is the most potent adversary model considered in the literature. Specifically, given a pair of incoherent unions \(\mathscr {A} \text{ and } \mathscr {B}\), first a subspace \({A}^*\) and \({\mathbf{a}}^*\in {A}^*\) are chosen arbitrarily. The adversary is now told \({A}^*, {\mathbf{a}}^*\) and is then free to choose a subspace \({B}^*\) in the union \(\mathscr {B}\) and \({\mathbf{b}}^*\in B^*\) using its knowledge in any way.
APIS is described in Algorithm 1 and involves alternately projecting onto unions of subspaces \(\mathscr {A}, \mathscr {B}\). For specific applications, the projection steps take on various forms, e.g., solving a (kernel) least-squares problem, a Fourier transform, or hard-thresholding. These are discussed in Sect. 5.
Notation: For \(\mathbf{v}\in {\mathbb{R}}^d\) and set \(F \subseteq [d]\), let \(\mathbf{v}_F \in {\mathbb{R}}^d\) denote a vector with coordinates in the set F identical to those in \(\mathbf{v}\) and others set to zero. For any matrix \(X \in {\mathbb{R}}^{d \times n}\) and any sets \(S \subseteq [n], F \subseteq [d]\), we let \(X^F_S = [\tilde{x}_{ij}] \in {\mathbb{R}}^{d \times n}\) be a matrix such that \(\tilde{x}_{ij} = x_{ij}\) if \(i \in F, j \in S\) and \(\tilde{x}_{ij} = 0\) otherwise. We similarly let \(X^F = [z_{ij}]\) denote the matrix with entries in the rows in F identical to those in X and other entries zeroed out i.e. \(z_{ij} = x_{ij}\) if \(i \in F\) and \(z_{ij} = 0\) otherwise. \(X_S\) is similarly defined as a matrix with entries in the columns in S identical to those in X and other entries zeroed out.
Projections: For any subspace \(S \subseteq {\mathbb{R}}^n\), \(\varPi _S\) denotes orthonormal projection onto S and \(\varPi _S^\perp\) denotes the orthonormal projection onto the ortho-complement of S so that for any \(\mathbf{v}\in {\mathbb{R}}^n\) and any subspace S, we always have \(\mathbf{v}= \varPi _S(\mathbf{v}) + \varPi _S^\perp (\mathbf{v})\). We abuse notation to extend the projection operator \(\varPi _\cdot (\cdot )\) to unions of low-rank subspaces. Let \(\mathscr {A}= \bigcup _{i=1}^P A_i \subseteq {\mathbb{R}}^n\) be a union of P subspaces, then for any \(\mathbf{v}\in {\mathbb{R}}^n\) we define \(\varPi _{\mathscr {A}}(\mathbf{v}) = \arg \min _{\mathbf{z}= \varPi _{A_i}(\mathbf{v}), i \in [P]}\left\| \mathbf{v}- \mathbf{z} \right\| _2^2\). Projection onto a union of subspaces is expensive in general (requiring time linear in P, the number of subspaces in the union) but will be efficient in all cases we consider (see Table 1).
Hard thresholding: The hard-thresholding operator will be instrumental in allowing efficient projections in APIS. For any \(n, k < n\), let \(\mathscr {S}^n_k = \left\{ \mathbf{z}\in {\mathbb{R}}^n: \left\| \mathbf{z} \right\| _0 \le k\right\}\) be the set of all k-sparse vectors. For any \(\mathbf{z}\in {\mathbb{R}}^n, k < n\), let \(\text {HT} _k(\mathbf{z}) {:}{=} \varPi _{\mathscr {S}^n_k}(\mathbf{z})\) denote the projection of \(\mathbf{z}\) onto \(\mathscr {S}^n_k\). Note that this operation is possible in \(\mathscr {O}\left( n\log n\right)\) time by sorting all the coordinates by magnitude, retaining the top k coordinates (in magnitude) and setting rest to 0.
5 Applications and projection details
The signal and corruption model in Eq. ( 1) does indeed capture several statistical estimation and signal processing problems. In most of these settings, the union \(\underline{\mathscr {A}}\) is indeed data-dependent. The discussion below shows that in each case, the union of subspaces \(\mathscr {A}\) is well-defined once training data is available. On the other hand, the union of subspaces \(\mathscr {B}\) is well-defined once the corruption model has been identified. The projection operators \(\varPi _\mathscr {A}(\cdot) \text{ and } \varPi _\mathscr {B}(\cdot)\) can be executed in polynomial time (see Table 1 for time complexity details).
5.1 Examples of signal models supported by APIS
Linear regression: Here we have \({\mathbf{a}}^*= X^\top {\mathbf{w}}^*\), where \(X = [\mathbf{x}^1,\ldots ,\mathbf{x}^n] \in {\mathbb{R}}^{d \times n}\) is the covariate matrix of the n data points and \({\mathbf{w}}^*\in {\mathbb{R}}^d\) is the linear model. It is easy to see that Eq. (1) recovers robust linear regression as a special case with \(P = 1\) and \(\mathscr {A}= A\), where \(A = \text {span}(\mathbf{x}^1,\ldots ,\mathbf{x}^n)\). Using the SVD \(X = U\varSigma V^\top\), we can project onto \(\mathscr {A}\) simply by solving a least squares problem i.e. we have \(\varPi _\mathscr {A}(\mathbf{z}) = VV^\top \mathbf{z}= (X^\top X^\dagger) \mathbf{z}\).
Low-rank kernel regression: Consider a Mercer kernel \(K: {\mathbb{R}}^d \times {\mathbb{R}}^d \rightarrow {\mathbb{R}}\) such as the RBF kernel and let \(G \in {\mathbb{R}}^{n \times n}\) be the Gram matrix with \(G_{ij} = K(\mathbf{x}^i,\mathbf{x}^j)\). Low-rank kernel regression corresponds to the case when the uncorrupted signal satisfies \({\mathbf{a}}^*= G{{\boldsymbol{\alpha }}}^*\) where \({{\boldsymbol{\alpha }}}^*\in {\mathbb{R}}^n\) belongs to the span of the some s eigenvectors of G. Specifically, consider the eigendecomposition \(G = V\varSigma V^\top\), \(V = [\mathbf{v}^1,\ldots ,\mathbf{v}^r] \in {\mathbb{R}}^{n \times r}\) is the matrix of eigenvectors (r is the rank of the Gram matrix) and \(\varSigma = {{\,\mathrm{diag}\,}}(s_1,\ldots ,s_r) \in {\mathbb{R}}^{r \times r}\) is the diagonal matrix of strictly positive eigenvalues (assume \(s_1 \ge s_2 \ge \ldots \ge s_r > 0\)). APIS offers the strongest guarantees in the case when \({{\boldsymbol{\alpha }}}^*\in \text {span}(\mathbf{v}^1,\ldots ,\mathbf{v}^s)\), i.e., when \({{\boldsymbol{\alpha }}}^*\) lies in the span of the the top eigenvectors. Note that in this case, \({\mathbf{a}}^*\) too is spanned by the top s eigenvectors of G since \({\mathbf{a}}^*= G{{\boldsymbol{\alpha }}}^*\). We stress that the guarantees continue to hold (see Sect. C in appendix) but deteriorate if \({{\boldsymbol{\alpha }}}^*, {\mathbf{a}}^*\) are spanned by s eigenvectors that include the lower ones as well. This is because Gram matrices corresponding to popular kernels such as the RBF kernel are often very ill-conditioned. Then, we can see that Eq. (1) recovers the robust low-rank kernel regression problem as a special case with \(P = 1\) and \(\mathscr {A}= A\), where \(A = \text {span}(\mathbf{v}^1,\ldots ,\mathbf{v}^s)\). Projection onto \(\mathscr {A}= A\) is given by \(\varPi _\mathscr {A}(\mathbf{z}) = \varPi _A(\mathbf{z}) = V_sV_s^\top \mathbf{z}\), where \(V_s = [\mathbf{v}^1,\ldots ,\mathbf{v}^s] \in {\mathbb{R}}^{n \times s}\). Section 6.5 shows how this restriction of the signal to the span of the top-s eigenvectors does not affect the universality of popular kernels such as the RBF kernel.
Sparse signal transforms: Consider signal transforms such as Fourier, Hadamard, wavelet, etc. Sparse signal transforms correspond to the case when \({\mathbf{a}}^*= M^\top {{\boldsymbol{\alpha }}}^*\), where \(M \in {\mathbb{R}}^{n \times n}\) is the design matrix of the transform (for sake of simplicity, assume M to be orthonormal as is often the case) and \({{\boldsymbol{\alpha }}}^*\in {\mathbb{R}}^n\) is an s-sparse vector, i.e., \(\left\| {{\boldsymbol{\alpha }}}^* \right\| _0 \le s\). It is easy to see that Eq. (1) recovers the robust sparse signal transform problem with \(P = \left( {\begin{array}{c}n\\ s\end{array}}\right)\) and \(\mathscr {A}= \bigcup _{F \subset [n], \left| {F} \right| = s}A_F\) with \(A_F = \text {span}(\left\{ \mathbf{m}^i\right\} _{i \in F})\), where \(\mathbf{m}^i\) is the \(i^\mathrm{th}\) column of the design matrix M. Given that M is orthonormal, projection onto a given subspace \(A_F\) is given by \(\varPi _{A_F}(\mathbf{z}) = M_FM_F^\top \mathbf{z}\). The orthonormality of \(M\) can be further exploited to carry out projection onto the union \(\mathscr {A}\) in \(\mathscr {O}\left( n\log n\right)\) time by using “fast” versions of these transforms followed by a hard-thresholding operation. Specifically, we have \(\varPi _\mathscr {A}(\mathbf{z}) = M\mathbf{v}\), where \(\mathbf{v}= \text {HT} _s(M^\top \mathbf{z})\).
Sparse recovery: In the sparse recovery signal model, the uncorrupted signal satisfies \({\mathbf{a}}^*= X^\top {\mathbf{w}}^*\) where \({\mathbf{w}}^*\in {\mathbb{R}}^d\) is an \({s}^*\)-sparse linear model, i.e., \(\left\| {\mathbf{w}}^* \right\| _0 \le {s}^*\) for some \({s}^*< d\). Equation (1) recovers the robust sparse recovery problem as a special case with \(P = \left( {\begin{array}{c}d\\ {s}^*\end{array}}\right)\) and \(\mathscr {A}= \bigcup _{F \subset [d], \left| {F} \right| = {s}}^*A_F\) , where the subspace \(A_F\) is given by \(A_F = \text {span}(\mathbf{x}^1_F,\ldots ,\mathbf{x}^n_F)\). Projection onto a given subspace \(A_F\) can be easily seen to be \(\varPi _{A_F}(\mathbf{z}) = ((X^F)^\top (X^F)^\dagger) \mathbf{z}\). Projection onto the union \(\mathscr {A}\) can then be shown to be simply the classical sparse recovery problem that can be solved efficiently if X satisfies properties such as RIP or RSC (see Agarwal et al. (2012)). Specifically, we have \(\varPi _\mathscr {A}(\mathbf{z}) = X^\top {\hat{\mathbf{w}}}\) , where \({\hat{\mathbf{w}}}= \arg \min _{\left\| \mathbf{w} \right\| _0 \le {s}}^*\left\| X^\top \mathbf{w}- \mathbf{z} \right\| _2^2\). The projection step \(\varPi _\mathscr {A}(\cdot )\) can be carried out in \(\mathscr {O}\left( nd\right)\) time here as well by employing projected gradient and iterative hard-thresholding methods (see Agarwal et al. (2012)).
5.2 Examples of corruption models supported by APIS
Sparse fully adaptive adversarial corruptions This is most widely studied case in literature and assumes a sparse corruption vector i.e. \(\left\| {\mathbf{b}}^* \right\| _0 \le k\) for some \(k < n\). The model in Eq. (1) recovers this case with \(Q = \left( {\begin{array}{c}n\\ k\end{array}}\right)\) and \(\mathscr {B}= \bigcup _{T \subset [n], \left| {T} \right| = k}B_T\) with \(B_T\) as the subspace of all vectors with support within the set T. Note that the convergence guarantees for APIS do not impose any restrictions on the magnitude of corruptions. Instead, the number of iterations required for recovery merely scale logarithmically with the \(L_2\) norm of the corruption vector i.e. the runtime scales as \(\log (\left\| {\mathbf{b}}^* \right\| _2)\) (see Theorem 1). It can be easily seen that the hard-thresholding operator \(\text {HT} _k(\cdot )\) (Sect. 4) offers projection onto the union \(\mathscr {B}\).
Dense fully adaptive adversarial corruptions Unlike several previous works, APIS also allows corruption vectors that are dense \(\left\| {\mathbf{b}}^* \right\| _0 = \varOmega \left( n\right)\), i.e., most points suffer corruption. This is because APIS only requires the unions \(\mathscr {A}, \mathscr {B}\) to be incoherent and does not care if \(\mathscr {B}\) contains dense vectors. We will see such examples in Sect. 6, with noiselet corruptions, and in Sect. 6.4 where we will exploit local incoherence results to guarantee recovery when the signal is Fourier-sparse, and the corruptions are Wavelet-sparse. In Sect. 7, we will establish that APIS offers recovery in such dense corruption settings, experimentally as well.
As noted earlier, in both the corruption models, the adversary has full knowledge of \({\mathbf{a}}^*, {A}^*\) before choosing \({\mathbf{b}}^*, {B}^*\) in any manner, i.e., the adversary is fully adaptive.
5.3 Do the subspaces really need to be low-rank? What if this is too strict and \({\mathbf{a}}^*\notin \mathscr {A}\)?
For exact recovery guarantees (which APIS does offer), some low-rank restriction seems to be necessary, especially when working with universal models such as the Gaussian kernel whose Gram matrix is often full-rank (and ill-conditioned), or the Fourier transform whose design matrix is also full-rank (but well-conditioned). Given such full-rank designs, unless additional restrictions are put (e.g., low-rank), recovery remains an ill-posed problem. However, in Sect. 6.4, we will see that APIS offers non-trivial recovery even if the clean signal \(\underline{{\mathbf{a}}^*}\) does not belong to \(\underline{\mathscr {A}}\) but is well-approximated by vectors in \(\underline{\mathscr {A}}\). Specifically, these are cases when \({\mathbf{a}}^*\notin \mathscr {A}\) but rather \({\mathbf{a}}^*+ {\mathbf{e}}^*\in \mathscr {A}\) and \(\left\| {\mathbf{e}}^* \right\| _2\) is small. It is common in signal processing tasks to consider signals (images, etc.) that are well-approximated by a sparse wavelet/Fourier representation but not exactly sparse themselves.
6 Recovery, breakdown points, misspecified models and universality
All detailed proofs and derivations are provided in the appendices.
6.1 Incoherence
A key requirement for robust recovery in model presented in Eq. (1) is for the unions \(\mathscr {A} \text{ and } \mathscr {B}\) to be incoherent with respect to each other. We present below a notion of subspace incoherence suitable to our technique. We note that the notion presented below is similar to notions of subspace incoherence prevalent in literature but suited for our setting.
Definition 1
(Subspace incoherence) For any \(\mu > 0\), we say two subspaces \(A, B \subseteq {\mathbb{R}}^n\) (of possibly different ranks) are \(\mu\)-incoherent if for all \(\mathbf{u}\in A\), \(\left\| \varPi _B(\mathbf{u}) \right\| _2^2 \le \mu \cdot \left\| \mathbf{u} \right\| _2^2\) and for all \(\mathbf{v}\in B\), \(\left\| \varPi _A(\mathbf{v}) \right\| _2^2 \le \mu \cdot \left\| \mathbf{v} \right\| _2^2\).
Note that the above definition uses the same incoherence constant \(\mu\) for projections both ways. This is justified since \(\max _{\mathbf{u}\in A} \frac{\left\| \varPi _B(\mathbf{u}) \right\| _2^2}{\left\| \mathbf{u} \right\| _2^2} = \max _{\mathbf{v}\in B} \frac{\left\| \varPi _A(\mathbf{v}) \right\| _2^2}{\left\| \mathbf{v} \right\| _2^2}\). To see why, let U and V be orthonormal matrices whose columns span A and B resp. and notice that \(\mu = \left\| V^\top U \right\| _{\text {op}}^2 = \left\| U^\top V \right\| _{\text {op}}^2\) where \(\left\| \cdot \right\| _{\text {op}}\) is the operator norm. Since orthonormal projections are non-expansive, we always have \(\mu \le 1\). However, our results demand stronger contractions which we will establish for our application settings discussed in Sect. 5. However, first we extend the notion of incoherence to unions of subspaces.
Definition 2
(Subspace union (SU) incoherence) For any \(\mu > 0\), we say that a pair of unions of subspaces \(\mathscr {A}= \bigcup _{i=1}^P A_i\) and \(\mathscr {B}= \bigcup _{j=1}^Q B_j\) is \(\mu\)-SU incoherent if for all \(i \in [P] \text{ and all } j \in [Q]\), the subspaces \(A_i \text{ and } B_j\) are \(\mu\)-incoherent.
Theorem 1 states the main claim of this paper. Restrictions on s, k and breakdown points emerge when trying to satisfy the incoherence criterion demanded by Theorem 1.
Theorem 1
Suppose we obtain data as described in Eq. (1) where the two unions \(\mathscr {A} \text{ and } \mathscr {B}\) are \(\mu\)-incoherent with \(\mu < \frac{1}{9}\). Then, for any \(\epsilon > 0\) within \(T = \mathscr {O}\left( \log \frac{\left\| {\mathbf{a}}^* \right\| _2 + \left\| {\mathbf{b}}^* \right\| _2}{\epsilon }\right)\) iterations, APIS offers \(\left\| \mathbf{a}^T - {\mathbf{a}}^* \right\| _2 \le \epsilon\). Moreover, in the known signal support case when \(P = 1\) (see below), the requirement is further relaxed to \(\mu < \frac{1}{3}\).
Proof
(Sketch) We present the main steps in deriving the result for the known signal support case when \(P = 1\). We recall the notation from Algorithm 1 where \(A^{t+1} \ni \mathbf{a}^{t+1}, B^{t+1} \ni \mathbf{b}^{t+1}\), and let \(\mathbf{p}^t = \varPi _A({\mathbf{b}}^*- \mathbf{b}^t)\) and \(\mathbf{p}^{t+1} = \varPi _A({\mathbf{b}}^*- \mathbf{b}^{t+1})\). Thus, we have \(\mathbf{a}^{t+1} = \varPi _A(\mathbf{y}- \mathbf{b}^{t+1}) = {\mathbf{a}}^*+ \varPi _A({\mathbf{b}}^*- \mathbf{b}^{t+1})\) (since \({\mathbf{a}}^*\in A\) and orthonormal projections are idempotent) which gives us \(\left\| \mathbf{a}^{t+1} - {\mathbf{a}}^* \right\| _2 = \left\| \varPi _A({\mathbf{b}}^*- \mathbf{b}^{t+1}) \right\| _2 = \left\| \mathbf{p}^{t+1} \right\| _2\). Let \(\mathfrak {Q}{:}{=} B^{t+1} \cap {B}^*\) denote the meet of the two subspaces, as well as denote the symmetric difference subspaces \(\mathfrak {P}{:}{=} B^{t+1} \cap ({B^*})^\perp\) and \(\mathfrak {R}= {B}^*\cap (B^{t+1})^\perp\) (recall that \(A \ni {\mathbf{a}}^* \text{ and } {B}^*\ni {\mathbf{b}}^*\)).
Below we show that \(\left\| \mathbf{p}^{t+1} \right\| _2 \le 3\mu \cdot \left\| \mathbf{p}^t \right\| _2\) that establishes a linear rate of convergence if \(\mu < \frac{1}{3}\) as it grants \(\left\| \mathbf{a}^{t+1} - {\mathbf{a}}^* \right\| _2 = \left\| \mathbf{p}^{t+1} \right\| _2 \le 3\mu \cdot \left\| \mathbf{p}^t \right\| _2 = 3\mu \cdot \left\| \mathbf{a}^t - {\mathbf{a}}^* \right\| _2\). To show that \(\left\| \mathbf{p}^{t+1} \right\| _2 \le 3\mu \cdot \left\| \mathbf{p}^t \right\| _2\), we note that
and thus \({\mathbf{b}}^*- \mathbf{b}^{t+1} = {\mathbf{b}}^*- \varPi _{B^{t+1}}({\mathbf{b}}^*- \mathbf{p}^t) = \varPi _\mathfrak {R}({\mathbf{b}}^*) + \varPi _{B^{t+1}}(\mathbf{p}^t)\). This gives us, by an application of the triangle inequality, \(\left\| \mathbf{p}^{t+1} \right\| _2 = \left\| \varPi _A({\mathbf{b}}^*- \mathbf{b}^{t+1}) \right\| _2 \le \left\| \varPi _A(\varPi _\mathfrak {R}({\mathbf{b}}^*)) \right\| _2 + \left\| \varPi _A(\varPi _{B^{t+1}}(\mathbf{p}^t)) \right\| _2\). Applying incoherence now tells us that, since \(\mathbf{p}^t \in \mathscr {A}\) by projection, we have
Using other arguments given in the full proof, it can be shown that \(\left\| \varPi _A(\varPi _\mathfrak {R}({\mathbf{b}}^*)) \right\| _2 \le 2\mu \cdot \left\| \mathbf{p}^t \right\| _2\) which gives us \(\left\| \mathbf{p}^{t+1} \right\| _2 \le 3\mu \cdot \left\| \mathbf{p}^t \right\| _2\) concluding the proof sketch.
Section A in the appendix gives the complete proof this result. APIS offers a stronger guarantee, requiring \(\mu < \frac{1}{3}\), in the known signal support case (Chen and De 2020). These are cases when the union \(\mathscr {A}\) consists of a single subspace, i.e., \(P = 1\). Note that this is indeed the case (see Sect. 5) for linear regression and low-rank kernel regression. We now derive breakdown points, as well as restrictions on s, k for various applications that arise when we attempt to satisfy the incoherence requirements of Theorem 1. Table 1summarizes the signal-corruption pairings for which APIS guarantees perfect recovery and their corresponding breakdown points essentially bounding how large s, k can be. Detailed derivations of these results are presented in the appendix and summarized below.
6.2 Cases with sparse corruptions
In this case \(\mathscr {B}= \mathscr {S}^n_k\), the set of all k-sparse vectors. Calculating the incoherence constants then reduces to application-specific derivations which we sketch below.
Linear regression If the covariate matrix is X, then we get \(\mu \le \max _{\begin{array}{c} S \subset [n]\\ |S| = k \end{array}}\frac{\left\| X_S \right\| _{\text {op}}^2}{\lambda _{\min }(XX^\top )}\), where \(\left\| \cdot \right\| _{\text {op}}\) is the operator norm (see Appendix B for proofs). It turns out that this is satisfied in several natural settings. For example, if the covariates are Gaussian i.e. \(\mathbf{x}^i \sim \mathscr {N}(\mathbf{0}, I_d)\) then \(\mu < \frac{1}{3}\) (as required by Theorem 1) with high probability whenever \(k < \frac{n}{154}\). We stress that our results do not require data points to be sampled from a standard Gaussian per se. The requirement \(\mu < \frac{1}{3}\) is satisfied by other data distributions as well (see Appendix B).
Kernel regression For a Gram matrix G (calculated on covariates \(\mathbf{x}^i, i \in [n]\) using a PSD kernel), we get \(\mu \le \frac{\Lambda ^{\text {unif}}_k(G)}{\lambda _s(G)}\) where \(\lambda _s\) is the \(s^\mathrm{th}\) largest eigenvalue of G and \(\Lambda ^{\text {unif}}_k\) is the largest eigenvalue of any principal \(k \times k\) submatrix of G. For the special case of RBF kernel, further calculations show that \(\mu < \frac{1}{9}\) is satisfied, for instance, when covariates are sampled uniformly over the unit sphere and we have \(s < {\tilde{\boldsymbol{\varOmega }}}\left( \log n\right) , k \le \mathscr {O}\left( \sqrt{n}\right)\). Yet again, these settings (RBF kernel, unit sphere etc) are not essential, but merely sufficient conditions where APIS is guaranteed to succeed.
Signal transforms For a variety of signal transforms including Fourier, Hadamard, noiselet, we are assured \(\mu < \frac{1}{9}\), as desired by Theorem 1, whenever \(sk < \frac{n}{9}\). This can be realized in several ways, e.g., \(s = \mathscr {O}\left( 1\right) , k = \mathscr {O}\left( n\right)\) or \(s, k = \mathscr {O}\left( \sqrt{n}\right)\), etc. See Table 1 for a summary.
6.3 Cases with dense corruptions
Notably, APIS offers exact recovery even in certain cases where the corruption vector is completely dense, i.e., \(\left\| {\mathbf{b}}^* \right\| _0 = n\). Note that the adversary is still allowed to be completely adaptive. One such case is when the signal is s-sparse in the Fourier or wavelet (Haar or Daubechies D4/D8) bases, and the corruptions are k-sparse in noiselet basis (Coifman et al. 2001). Since wavelets are known to represent natural signals well, this is a practically useful setting. Note that a vector \({\mathbf{b}}^*\) with a k-sparse noiselet representation even for \(k = 1\) can be completely dense, i.e., \(\left\| {\mathbf{b}}^* \right\| _0 = n\). APIS also supports dense Gaussian noise the responses as is discussed below.
6.4 Handing model misspecifications
In certain practical situations, the model outlined in Eq. (1) may not be satisfied. For instance, we could have \({\mathbf{a}}^*\notin \mathscr {A}\) if we have an image that is not entirely (but only approximately) sparse in the wavelet basis. Similarly, the unions \(\mathscr {A} \text{ and } \mathscr {B}\) could fail to be incoherent (as is the case in the Fourier-Wavelet pair). In this section, we show how APIS can still offer non-trivial recovery in these settings.
Unmodelled error In this case we modify Eq. (1) to include an unmodelled error term.
where \({\tilde{\mathbf{a}}}\in \mathscr {A}, {\mathbf{b}}^*\in \mathscr {B}\) and \({\mathbf{a}}^*= {\tilde{\mathbf{a}}}+ {\mathbf{e}}^*\notin \mathscr {A}\). We make no assumptions on \({\mathbf{e}}^*\) belonging to any union of subspaces etc and allow it to be completely arbitrary. Section E in the appendix shows that if \(\mu < \frac{1}{9}\) is satisfied, then for any \(\epsilon > 0\), within \(T \le \mathscr {O}\left( \log ((\left\| {\mathbf{a}}^*_2 \right\| + \left\| {\mathbf{b}}^*_2 \right\| )/\epsilon )\right)\) iterations, APIS guarantees a recovery error of
We now look at two applications of this result.
Simultaneous sparse corruptions and dense Gaussian noise. Consider linear regression where, apart from k adversarially corrupted points, all n points get Gaussian noise i.e. \(\mathbf{y}= X^\top {\mathbf{w}}^*+ {\mathbf{b}}^*+ {\mathbf{e}}^*\), where \({\mathbf{e}}^*\sim \mathscr {N}(\mathbf{0}, \sigma ^2\cdot I_n)\). The above result shows that within \(T = \mathscr {O}\left( \log n\right)\) iterations, APIS guarantees \(\left\| \mathbf{w}^T - {\mathbf{w}}^* \right\| _2^2 \le \mathscr {O}\left( \sigma ^2\left( \frac{(d+k)\ln n}{n}\right) \right)\). As \(n \rightarrow \infty\), the model error behaves as \(\left\| \mathbf{w}- {\mathbf{w}}^* \right\| _2^2 \le \mathscr {O}\left( k\log n/n\right)\). This guarantees consistent recovery if \(k\log n/n \rightarrow 0\) as \(n \rightarrow \infty\). This is a sharper result than previous works (Bhatia et al. 2015; Mukhoty et al. 2019) that do not offer consistent estimation even if \(k\log n/n \rightarrow 0\).
Compressible signals. Given an image \({\mathbf{a}}^*\) that is not itself wavelet-sparse, but still \((s,\epsilon )\)-approximately wavelet sparse i.e. there exists an image \({\tilde{\mathbf{a}}}\) that is s wavelet-sparse, and \(\left\| {\mathbf{a}}^*- {\tilde{\mathbf{a}}} \right\| _2 \le \epsilon \cdot \left\| {\mathbf{a}}^* \right\| _2\). In particular, \({\tilde{\mathbf{a}}}\) can be taken to be the best s wavelet-sparse approximation of \({\mathbf{a}}^*\). The above shows that even if \({\mathbf{a}}^*\) is subjected to adversarial corruptions, APIS offers a recovery of \({\tilde{\mathbf{a}}}\) to within \(\mathscr {O}\left( \epsilon \cdot \left\| {\mathbf{a}}^* \right\| _2\right)\) error within \(\mathscr {O}\left( \log (1/\epsilon )\right)\) iterations.
Handling lack of incoherence: Pairs of bases that are not incoherent are well-known (Krahmer and Ward 2014; Zhou et al. 2016), the most famous example being the Fourier-Wavelet pair which can only assure \(\mu \approx 1\) no matter how small s, k are. Thus, Theorem 1, if applied directly, would fail to offer a non-trivial recovery result if the signal is wavelet-sparse and corruptions are Fourier-sparse. However, in Sect. F in the appendix, we show that using local incoherence properties of these two bases [which are also well-studied e.g. Krahmer and Ward (2014)], APIS can be shown to continue to offer exact recovery if the signal is not just sparse in the wavelet domain, but also anti-concentrated as well i.e. it spreads its mass over its wavelet support elements (please see Sect. F in the appendix for details). For this setting, we show that the incoherence constant satisfies \(\mu \le \frac{k^4}{s} + \frac{sk^2}{n}\). Now \(\mu < \frac{1}{9}\) can be ensured if, for example, \(sk^2 \le n/18\) (i.e. s, k are small compared to n which controls the second term) and \(k^4 < s/18\) (i.e. \(s \gg k\) which controls the first term). We note that some form of signal restriction, for example, signal anti-concentration, seems to be necessary since a spike signal having support over a single wavelet-basis element, can be irrevocably corrupted by an adaptive Fourier-sparse signal, given that the bases are not incoherent. Also, notice that this is yet another instance of APIS guaranteeing recovery when the corruptions are dense since a Fourier-sparse vector \({\mathbf{b}}^*\) can still have \(\left\| {\mathbf{b}}^* \right\| _0 = \varOmega \left( n\right)\).
6.5 Does APIS retain universality?
Kernel (ridge) regression with the RBF kernel is known to be a universal estimator (Micchelli et al. 2006). However, APIS requires the signal \({\mathbf{a}}^*\) to have a low-rank representation in terms of the top-s eigenvectors of the Gram matrix. As Table 1 indicates, for the RBF kernel, Theorem 1 allows \(s\) to be as large as \(\mathscr {O}\left( \log n/\log \log n\right)\) for n points. Does this model retain universality despite this restriction? What sort of functions can \({\mathbf{a}}^*\) still approximate? We sketch an argument below that indicates an answer in the affirmative, along with a qualitative outline of functions that can be still described by this low-rank model.
Several results on random matrix approximation guarantee that if data covariates are chosen from nice distributions then, as the number of covariates \(n \rightarrow \infty\), not only do the eigenvalues of the Gram matrix closely approximate those of the integral operator induced the PSD kernel (Minh et al. 2006; Rosasco et al. 2010), but the empirical operator also approaches the integral operator in the Hilbert-Schmidt norm. This assures us that eigenvectors of the Gram matrix closely approximate the eigenfunctions of the integral operator. For instance, Rosasco et al. (2010) offer an explicit two-way relation between the eigenvectors and the eigenfunctions. Now, in the uni-dimensional case (\(d = 1\)), for any \(i \le n\), the \(i^\mathrm{th}\) largest eigenfunction of the integral operator for the RBF kernel is represented in terms of the \(i^\mathrm{th}\)-order Hermite polynomial (Rasmussen and Williams 2006). The \(i^\mathrm{th}\) Hermite polynomial is of degree i and Hermite polynomials form a universal basis (as they constitute an orthogonal polynomial sequence). In particular, the first s Hermite polynomials span all degree-s polynomial functions. Thus, even with the restriction on \(s\), APIS does allow signals \({\mathbf{a}}^*\) that are (upto vanishing approximation errors) spanned by Hermite polynomials of order upto \(s\). Now, APIS allows \(s \le \mathscr {O}\left( \log n/\log \log n\right)\) and as \(n \rightarrow \infty\), \(s \rightarrow \infty\) as well (albeit slowly). Thus, \({\mathbf{a}}^*\) can represent functions that are (upto approximation errors) arbitrarily high degree polynomials.
A similar argument holds for multi-dimensional spaces and product kernels e.g. RBF since, for such kernels, the eigenfunctions and eigenvalues in the multi-dimensional case are products of their uni-dimensional counterparts (Fasshauer 2011). Although it would be interesting to make the above arguments rigorous, they nevertheless indicate that APIS offers robust recovery for a model that is still universal in the limit. In Sect. 7, we will see that APIS offers excellent reconstruction for sinusoids, polynomials as well as their combinations over multi-dimensional spaces, even under adversarial corruptions.
7 Experiments
Extensive experiments were carried out comparing APIS to state-of-the-art competitor algorithms on three key robust regression tasks
-
1.
Robust non-parametric regression to learn (multi-dimensional) sinusoidal and polynomial functions (see Figs. 3, 8, and Table 2) and robust Fourier transform (see Fig. 8)
-
2.
Robust linear regression (see Fig. 4)
-
3.
Image denoising on the benchmark Set12 images (see Fig. 5) with sparse adversarial salt-and-pepper corruption, as well as dense-checkerboard pattern corruptions (see Figs. 6, 7, and Table 3).
7.1 System configuration
Experiments for which runtimes for various algorithms were recorded were carried out on a 64-bit machine with Intel® Core™ i7-6500U CPU @ 2.50 GHz, 4 cores, 16 GB RAM and Ubuntu 16.04 OS, except for the Deep CNN model from (Zhang et al. 2017) which was trained on NVidia K80 GPUs (made available by the Kaggle platform for which the authors are grateful). All methods were implemented in Python, except those from (Gu et al. 2014; Cizek and Sadikoglu 2020), for which codes were made available by the authors themselves, in R and MATLAB, respectively. All figures e.g. Figs. 3, 4, 6 and 7 show actual predictions by various algorithms, and all results are reported over a single run of the algorithms.
7.2 Baselines and competitor algorithms
Below are described the state-of-the-art competitor algorithms chosen alongside APIS in various experiments.
Robust non-parametric kernel regression: Based on recommendations of the recent survey by Cizek and Sadikoglu (2020), the widely studied Huber and median estimators were chosen as baselines. The Nadaraya-Watson (kernel regression) and kernel ridge regression estimators were also chosen as baselines. In addition, the recently proposed LBM method (Du et al. \(\mathscr {N}(0,0.1^2)\) was added to all points (even clean ones). In the figures, corrupted points are depicted using a red cross and clean points using an empty gray circle. Hyperparameter tuning was done for all methods as described in the main text. 1000 test points were sampled from \(\mathscr {N}(0,1.5^2)\) for estimating the RMSE for various algorithms. No corruption or Gaussian noise was added to test responses. In all cases, APIS offers the best test RMSE that is 2 to \(5\times\) smaller than the next best method
Linear regression. The figures demonstrate convergence of the algorithms with respect to time (top) and sensitivity with respect to hyper-parameter k (bottom). The headings of the panels show the number of training points, the fraction of corrupted training points, and the variance of the dense Gaussian noise (if present). For the top row, 10000 training points were generated as \(\mathbf{x}^i \sim \mathscr {N}(\mathbf{0}, I_d)\) for \(d = 100\). A true model and an adversarial model were both chosen as \({\mathbf{w}}^*, {\mathbf{w}^\text {a}}\sim \mathscr {N}(\mathbf{0}, I_d)\). For clean points, \(y = \mathbf{x}^\top {\mathbf{w}}^*\), for 20% corrupted points \(y = \mathbf{x}^\top {\mathbf{w}^\text {a}}\). The left column has no Gaussian noise, while the plots on the right column have Gaussian noise \(\mathscr {N}(0,0.1^2)\), added to all points (even clean ones). The timed convergence plots show that in absence of Gaussian noise, most methods offer recovery of \({\mathbf{w}}^*\) to machine precision level although APIS offers fastest recovery (RGD, SEVER offer slow recovery). The bottom row shows APIS offer stable recovery in a wide range of settings
Image denoising with sparse adversarial corruptions. For each image, sparse adversarial salt-and-pepper corruptions were added to 20% of the pixels. Corruptions were added to these pixels by setting lighter pixels i.e. those with grayscale value \(> 127\) to completely black i.e., the grayscale value of 0, and setting darker pixels i.e. those with grayscale value \(< 127\) to completely white i.e., the grayscale value of 255. The first column shows the image obtained as a result of these corruptions. The subsequent columns show the image recovered by various algorithms. Below each image is shown the PSNR and SSIM values for that image. APIS not only offers visually better recovery, but also the best PSNR and SSIM values, often significantly better than the next best method. In particular, APISis able to preserve the minute checkerboard pattern on the tablecloth and the fine stripes on the scarf in the Barbara image (second row), and the fine details of the flowers and the extremely thin antennae of the butterfly in the Monarch image (third row), whereas all the other methods lose these fine details.
Image denoising with dense corruptions. For each image, dense corruptions were introduced by superimposing a dense checkerboard pattern on the entire image, thus corrupting all pixels. The first column shows the image obtained as a result of these corruptions. The subsequent columns show the image recovered by various algorithms. Below each image is shown the PSNR and SSIM values for that image. Similar to the observation made in the caption for Fig. 6, APIS offers superior recovery and preserves fine details in both images. In contrast, TV-Bregman, BM3D, and WNNM fail to offer any reasonable recovery in either of the examples, while DnCNN-Block retains much of the block corruption
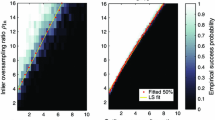
Phase transition. This figure demonstrates the phase transition behavior of APIS on robust non-parametric regression with RBF kernel (left) and robust Fourier transform (right) tasks, by considering various sparsity and corruption levels. For each combination of \((s,k) \in [n] \times [n]\), a synthetic dataset \(({\mathbf{a}}^*, {\mathbf{b}}^*)\) was created randomly and APIS was executed to obtain its estimate \(\hat{\mathbf{a}}\) of the signal. An approximation error of \(\left\| {\mathbf{a}}^*- \hat{\mathbf{a}} \right\| _2 < 10^{-4}\cdot \left\| {\mathbf{a}}^* \right\| _2\) was considered a “success”. The experiment was repeated 50 times for each (s, k) pair giving us a success likelihood \(p_{(s,k)} \in [0,1]\) for each pair (s, k). The figures plot these success likelihood values with a white pixel indicating \(p_{(s,k)} = 1\) i.e. all 50 experiments succeeded for that value of (s, k), a black pixel indicating \(p_{(s,k)} = 0\) i.e. none of the 50 experiments succeeded for that value of (s, k) and shades of gray indicating intermediate likelihood values in the range (0, 1). For robust non-parametric regression with RBF kernel, a Gram matrix was first generated by sampling 100 data points, from the surface of the unit sphere in 10 dimensions, i.e. \(S^9\). Next, the signal was generated as a random vector in the span of the top s eigen-vectors of the Gram matrix. For robust Fourier transform, first a random s-sparse vector \({{\boldsymbol{\alpha }}}^*\) was generated and then the signal was created as \({\mathbf{a}}^*= F{{\boldsymbol{\alpha }}}^*\) where F is the matrix corresponding to the Fourier transform. In both cases, adversarial corruption was introduced to \({\mathbf{a}}^*\) as done in Fig.3. In both figures, the recovery limit guaranteed by Theorem 1 is outlined in magenta whereas the empirical 100% success region is outlined in green. Additionally, the figure on the left for robust non-parametric regression with RBF kernel is zoomed in for easy viewing