Construction of cospectral graphs

Abstract

Construction of non-isomorphic cospectral graphs is a nontrivial problem in spectral graph theory especially for large graphs. In this paper, we establish that graph theoretical partial transpose of a graph is a potential tool to create non-isomorphic cospectral graphs by considering a graph as a partitioned graph.

1 Introduction

In this work, we propose methods to construct cospectral graphs by utilizing the framework of partitioned graphs. Here, a graph $G=(V, E)$ with labeled vertices is called partitioned if the vertex set is partitioned as $V=\sqcup _{j=1}^n C_j$ where each $C_j$, along with the edge set induced by the vertices in it, is called a partition of the graph. Throughout the paper, we denote $C_j$ for both as a set of vertices, and the subgraph induced by the vertices in $C_j$. The meaning will be clarified from the context. For example, a multipartite graph can be considered as a partitioned graph under specific labelings of vertices.

The adjacency matrix $\mathbf{A }(G)=[a_{ij}]$ associated with a graph G is defined by $a_{ij}=1$ if the vertices i, j are adjacent and $a_{ij}=0$ otherwise. The spectrum of G is the multiset of eigenvalues of $\mathbf{A }(G)$. Two isomorphic graphs have the equal spectrum since the corresponding adjacency matrices are permutation similar, but the converse need not be true [2, Chapter 6]. Characterization of graphs that are determined by their spectra is an open problem in algebraic graph theory [17, 25]. Indeed, in the quest of finding graphs that are determined by their spectra, it is equally important to determine graphs which are not determined by their spectra. Besides, new constructions of cospectral non-isomorphic graphs can have implications on the complexity of the graph isomorphism problem. This calls for develo** methods for detection and/or generation of cospectral non-isomorphic graphs. Well-known methods for construction of cospectral graphs include Seidel switching, Godsil–McKay (GM) switching etc., and many more [9, 10, 13, 24, 25]. In this paper, we show that partial transpose of a graph developed in [4, 14, 26] can become a handy tool to construct cospectral partitioned graphs, in particular large cospectral graphs.

First we recall the following definition from [4].

Definition 1

Let G be a partitioned graph on mn vertices with partitions $C_i=\{v_{i,1}, v_{i,2}, \dots v_{i,m}\}, i=1,\ldots , n$. Then, the graph theoretical partial transpose (GTPT) of G is the graph $G^{\tau }$ obtained from G by removing the edges $(v_{i,k}, v_{j,l}),$ for all $k \ne l, i \ne j$ in G and correspondingly adding the edges $(v_{i,l},v_{j,k}).$

Note that GTPT is defined for partitioned graphs when its partitions contain the same number of vertices. Also, the number of edges in G and $G^\tau$ is equal. The adjacency matrix of such a partitioned graph G (as defined in Definition 1) can be represented by the block matrix

$$\begin{aligned} \mathbf{A }(G) = \begin{bmatrix} A_{1,1}&\quad A_{1,2}&\quad \cdots&\quad A_{1,n} \\ A_{2,1}&\quad A_{2,2}&\quad \cdots&\quad A_{2,n} \\ \vdots&\quad \vdots&\quad \vdots&\quad \vdots \\ A_{n,1}&\quad A_{n,2}&\quad \cdots&\quad A_{n,n} \end{bmatrix}_{mn \times mn}, \end{aligned}$$

(1)

where $A_{ii}$ is the adjacency matrix of the partition $C_i$ and the block matrix $A_{i,j}$ represents the adjacency relations between the vertices of $C_i$ and $C_j, i\ne j; i,j=1,\ldots , n.$ It is easy to ascertain that the adjacency matrix associated with $G^{\tau }$ is given by $\mathbf{A }(G^{\tau })=\mathbf{A }(G)^{\tau } = [A_{i,j}^t]_{mn \times mn}$, where $^t$ denotes the transpose of a matrix. The matrix $\mathbf{A }^{\tau }$ is called the partial transpose of $\mathbf{A }.$ The concept of partial transpose has found many applications in quantum information theory, in particular in the detection of quantum entanglement [16, 19]. If G is isomorphic to $G^\tau$ where the identity map acts as the isomorphism, G is called a partially symmetric graph which is shown to be useful in quantum information theory [4].

The graphs G and $G^\tau$ are called GTPT equivalent. Two pertinent questions about GTPT equivalent graphs are as follows. Are GTPT equivalent graphs isomorphic and/or cospectral? Are the graphs $G^\tau$ and $H^\tau$ isomorphic if G and H are isomorphic?

The following examples depict that GTPT operation can produce isomorphic graphs, non-isomorphic and non-cospectral graphs, and non-isomorphic but cospectral graphs. For instance, the graphs $G_1$ and $G_1^\tau$ given by

are GTPT equivalent and isomorphic, hence cospectral. The graphs $G_2$ and $G_2^\tau$ given by

are GTPT equivalent but neither isomorphic nor cospectral. Indeed GTPT equivalent graphs $G_3$ and $G_3^\tau$ given by

are non-isomorphic but cospectral. The following example shows that two isomorphic graphs G and H need not imply the isomorphism of $G^\tau$ and $H^\tau .$

Example 1

Consider the graphs G and H as follows:

Then,

are not isomorphic. Computing the eigenvalues of $G^\tau$ and $H^\tau$, it can be easily verified that they are not cospectral.

Several approaches are introduced in the literature for the construction of cospectral graphs. For example, see [3, 7, 9, 12, 18, 20] and the references therein. Schwenk et al. investigated the problem of construction of cospectral graphs for a few structured graphs using the concept of bigraphs and the characteristic polynomial of a graph, for example see [22, 23]. Indeed, observe that these techniques are proposed for graphs with a very specific structure, and hence, the applicability of these techniques is limited. In this paper, we show that the GTPT approach generates a pair of cospectral graphs from any given bipartite graph, and for a graph on a composite number of vertices, it opens up a possibility of generation of a cospectral mate of the given graph. Note that given a graph on n vertices, where n is a composite number, multiple partitioned graphs can be obtained by multiple factorizations of n. Hence, multiple GTPT equivalent graphs can be obtained for the same graph. Besides, since the GTPT approach acts like a matrix function on the algebra of (weighted) adjacency matrices, the matrix theoretic results can be used to determine specific properties of an adjacency matrix to ensure cospectrality. Here, we mention that Willem H. Haemers attempted to investigate Seidel switching operation as a matrix operation in [10, 11].

The main contributions of this paper are as follows. We determine classes of graphs for which GTPT approach guarantees to produce cospectral graphs, for example bipartite graphs and pseudo-bipartite graphs defined in Sect. 2. By using matrix theoretic arguments, we prove that if the blocks of the adjacency matrix of a partitioned graph form a set of normal commuting matrices, then its GTPT equivalent graph is cospectral. Further, using the recently developed graph structure corresponding to such adjacency matrices, we demonstrate the class of graphs which ascertain cospectrality with its GTPT. In Sect. 3, we propose procedures to create new GTPT equivalent cospectral graphs by utilizing GTPT equivalent cospectral graphs. These procedures can be used to generate large cospectral graphs. Finally in Sect. 4, we produce several GTPT equivalent non-isomorphic cospectral graphs by employing the procedures introduced in Sect. 3. Thus, we establish that GTPT approach can act as potential method for generation of non-isomorphic cospectral graphs. Then, we conclude this article with some future research problems in this direction.

2 Constructing cospectral graphs

In this section, we determine classes of GTPT equivalent graphs that are cospectral. Before that we recall GM-switching as an operation on certain type of matrices as described in [11]. We also show that partial transpose of the adjacency matrix of a partitioned graph bears a partial resemblance of GM-switching.

First, we recall the following theorem which explains GM-switching as a matrix operation. Let $\mathbf{1 }$ denote the all-one vector.

Theorem 1

[11] Let N be a (0, 1)-matrix of size $b \times c$ (say) whose column sums are 0, b or b / 2. Define ${\widetilde{N}}$ to be the matrix obtained from N by replacing each column v with b / 2 ones by its complement $\mathbf{1 }-v$. Let B be a symmetric $b\times b$ matrix with constant row (and column) sums, and let C be a symmetric $c \times c$ matrix. Put

$$\begin{aligned} M = \begin{bmatrix} B&\quad N\\ N^t&\quad C \end{bmatrix} \,\, \text{ and } \,\, {\widetilde{M}} = \begin{bmatrix} B&\quad {\tilde{N}}\\ {\tilde{N}}^t&\quad C \end{bmatrix}. \end{aligned}$$

Then, M and ${\widetilde{M}}$ are cospectral.

Observe from Theorem 1 that considering a graph G as a partitioned graph with 2 partitions and M as its adjacency matrix, the matrices B and C represent the adjacency matrices of the partitions and N captures the adjacency relations between vertices in B and C. The switching of G is produced by removing and adding some edges which connect the vertices in B with the vertices in C. Whereas, in contrast to GM-switching, a graph G can have any number of partitions depending on the number of vertices in G for GTPT and each partition should have same number of vertices. Alike GM-switching, the only removal/addition of edges are done in GTPT only for the edges which link the vertices between any two partitions.

2.1 Bipartite and pseudo-bipartite graphs

Recall that a bipartite graph is a partitioned graph with 2 partitions. Now, we define pseudo-bipartite graphs as follows.

Definition 2

(Pseudo-bipartite graph) Let $G = (V(G), E(G))$ be a partitioned graph on 2m vertices having two partitions say $C_i=\{v_{i,j} : j=1,\dots , m\}, i=1,2$ each of which contains m vertices. Then, G is said to be a pseudo-bipartite graph if $C_1$ and $C_2$ are isomorphic and the ‘identity’ map $Id:V(C_1)\rightarrow V(C_2)$ defined as $Id(v_{1,j})=v_{2,j}$ acts as the isomorphism.

Then, we have the following theorem.

Theorem 2

GTPT equivalent pseudo-bipartite graphs are isomorphic and hence cospectral. In particular, GTPT equivalent bipartite graphs are isomorphic when the partitions in the bipartition contain the same number of vertices.

Proof

Let G be a pseudo-bipartite graph on 2m vertices where the partitions $C_1$ and $C_2$ of G are isomorphic and $Id: V(C_1)\rightarrow V(C_2)$ is the isomorphism. Let $C_1=\{v_{1,i}: i=1,\ldots ,m\}$ and label the vertices of $C_2$ by $v_{2,i}=Id(v_{1,i}), i=1,\ldots ,m.$ Observe that any edge of the type $(v_{i,j}, v_{i,k}), i=1,2$ and $j\ne k$ does not get affected in the formation of $G^\tau .$ Now, consider the function $f: V(G)\rightarrow V(G^\tau )$ as defined by

$$\begin{aligned} f(v_{i,j}) = {\left\{ \begin{array}{ll} v_{2,j} &{}~\text{ for }~ i = 1, \\ v_{1,j} &{}~\text{ for }~ i = 2. \end{array}\right. } \end{aligned}$$

(2)

Then, $(v_{1,i}, v_{1,j})\in E(G)$ implies $(f(v_{1,i}), f(v_{1,j}))=(v_{2,i}, v_{2,j})=(Id(v_{1,i}), Id(v_{1,j}))\in E(G^\tau )$ since Id is an isomorphism. Similarly, $(v_{2,i}, v_{2,j})\in E(G)$ means $(f(v_{2,i}), f(v_{2,j})) = (v_{1,i}, v_{1,j})\in E(G^\tau )$ since $(v_{2,i}, v_{2,j}) = (Id(v_{1,i}), Id(v_{1,j})) \in E(G)$ and $\psi$ is isomorphism. For other edges of the form $(v_{1,i}, v_{2,j})$, the result follows as in the case of bipartite graphs. Hence the proof. $\square$

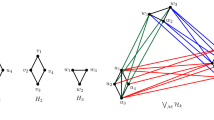
We mention that Theorem 2 is no longer true when the pseudo-bipartite graph is replaced by a graph with 2 isomorphic partitions say $C_1, C_2$ and the isomorphism is not the identity map. For instance, consider GTPT equivalent graphs in Fig. 1 in which spectrum of G is $\{\pm \, 2, \pm \,1.618, \pm \,0.618, 0, 0\}$ and spectrum of $G^\tau$ is $\{\pm \, 2.149, \pm \,1.5434, 0, 0, 0, 0\}$.

Fig. 1

The graph G has two isomorphic partitions and G,  $G^\tau$ are not cospectral mates

Now, we have the following result for bipartite graphs.

Theorem 3

Let G be a bipartite graph such that the vertex set is partitioned as $V(G)=C_1\sqcup C_2$ where $|C_1|=m_1\ne m_2=|C_2|.$ Then, G and $G^\tau$ are isomorphic.

Proof

Without loss of generality assume that $m_1 < m_2$. Then add $(m_2 - m_1)$ adhoc isolated vertices into the set $C_1$ such that the resultant graph becomes a bipartite graph with equal partition. For brevity, we use the same notation for the modified graph as G. Then, by using Theorem 2, G and $G^\tau$ are isomorphic and the isomorphism must correspond the isolated vertices in G to isolated vertices in $G^\tau .$ Hence, by removing the isolated vertices from G and $G^\tau$, the desired result follows. $\square$

2.2 Construction of cospectral GTPT equivalent graphs

As mentioned in the introduction recall that two GTPT equivalent graphs need not be cospectral. In this subsection, we provide a sufficient condition on the structural properties of a partitioned graph G so that the graph $G^\tau$ becomes cospectral with G. First we prove the following theorem.

Theorem 4

Let $\{A_i, i=1,\ldots , k\}$ be a commuting family of normal real matrices of order m. Then, there exists a nonsingular matrix X such that $A_i^t = X^{-1}A_iX$ for $i=1,\ldots , k.$

Proof

Note that the problem of finding a nonsingular matrix X for which $A_i^t = X^{-1}A_iX$ is equivalent to solving a system of Lyapunov equations $XA_i^T=A_iX, i=1,\ldots , k.$ This implies that it is enough to find a nontrivial solution for the set of linear systems of the form

$$\begin{aligned} (I_m\otimes A_i -A_i^t\otimes I_m)x=0, \quad i=1,\ldots , k \end{aligned}$$

(3)

such that $x={{\,\mathrm{vec}\,}}(X)=[X_1^t \, X_2^t \, \ldots , X_m^t]^t,$ the vectorization of some nonsingular matrix X whose jth column is $X_j, j=1,\ldots , m$, and $I_m$ is the identity matrix of order m.

Recall that a commuting family of normal matrices is simultaneously unitarily diagonalizable [15, Theorem 2.5.5], that is, there exists a unitary matrix U such that

$$\begin{aligned} A_i=U^*D_iU \end{aligned}$$

where $D_i$ is a diagonal matrix (not necessarily real) and $U^*$ denotes the conjugate transpose of U. Hence, $A_i^t=U^tD_i{\overline{U}}, i=1,\ldots , k.$ Let $S(A_i)=I_m \otimes A_i - A_i^t \otimes I_m.$ Then,

$$\begin{aligned} S(A_i)= & {} I_m \otimes U^* D_i U - U^t D_i {\overline{U}} \otimes I_m \nonumber \\= & {} (U^t I_m {\overline{U}})\otimes (U^* D_i U) - (U^t D_i {\overline{U}}) \otimes (U^* I_m U) \nonumber \\= & {} (U^t \otimes U^*) (I \otimes D_i - D_i \otimes I) ({\overline{U}} \otimes U) \nonumber \\= & {} ({\overline{U}} \otimes U)^* (I \otimes D_i - D_i \otimes I) ({\overline{U}} \otimes U) \end{aligned}$$

(4)

where ${\overline{U}}=[{\overline{u}}_{ij}]$ if $U=[u_{ij}].$

Let ${\mathcal {U}} = ({\overline{U}} \otimes U)$. Then, ${\mathcal {U}} {\mathcal {U}}^* = ({\overline{U}} \otimes U)(U^t \otimes U^*) = ({\overline{U}} U^t) \otimes (U U^*) = I_{m^2},$ that is ${\mathcal {U}}$ is a unitary matrix. Then observe that the equation (3) takes the form, $S(D_i){\mathcal {U}} x = 0$. Denoting $y = {\mathcal {U}} x$ we get, $S(D_i)y = 0, i=1,\dots , k$.

Note that y is a vector of order $m^2$. Setting

$$\begin{aligned} {\hat{y}}_j = (y_{(j - 1)m + 1} , y_{(j - 1)m + 2} , \dots , y_{jm})^t \in {\mathbb {R}}^m, \quad j= 1, \dots , m \end{aligned}$$

we obtain $y = ({\hat{y}}_1, {\hat{y}}_2, \dots {\hat{y}}_m)^t$. Suppose $D_i = {{\,\mathrm{diag}\,}}\{\lambda _1^{(i)}, \lambda _2^{(i)}, \dots , \lambda _m^{(i)}\}$. Then $I_m \otimes D_i = {{\,\mathrm{diag}\,}}\{D_i, D_i, \dots D_i\}$, a block diagonal matrix of order m, and $D_i \otimes I_m = {{\,\mathrm{diag}\,}}\{\lambda _1^{(i)} I_m, \lambda _2^{(i)} I_m, \dots \lambda _m^{(i)} I_m\}$. Observe that in each of the diagonal matrices $S(D_i)$ at least m diagonal entries are zero. They are at the position $1, m + 2, 2m + 3, \dots , m^2$ of the diagonal. Thus, $1, m + 2, 2m + 3, \dots , m^2$-th entries of the vector y may be arbitrary scalars and other entries of y chosen to be 0 provide a solution of $S(D_i)y=0, i=1,\dots , k$. Moreover, $\{{\hat{y}}_1, {\hat{y}}_2, \dots {\hat{y}}_m\}$ forms a set of linearly independent vectors. In particular, we may choose ${\hat{y}}_i = e_i$, the i-th column vector of the identity matrix $I_m$.

Finally

$$\begin{aligned} x={\mathcal {U}}^*y=(U^t\otimes U^*)y=\begin{bmatrix} \sum \nolimits _{j=1}^m u_{j1}U^*{\hat{y}}_j \\ \vdots \\ \sum \nolimits _{j=1}^m u_{jm}U^*{\hat{y}}_j \end{bmatrix}. \end{aligned}$$

Set $X_l=\sum _{j=1}^m u_{jl}U^*{\hat{y}}_j, l=1,\dots , m.$ Then, the matrix $X=[X_1 \, X_2 \,\dots \, X_m]$ for which ${{\,\mathrm{vec}\,}}(X)=x$ is a nonsingular matrix. Indeed we show that $\{X_1, \dots , X_m\}$ forms a set of linearly independent vectors as follows. Let $\alpha _1 X_1 + \alpha _2 X_2 + \dots + \alpha _m X_m =0$ for some scalars $\alpha _1,\dots ,\alpha _m.$ This implies

$$\begin{aligned} \left( \sum _{j=1}^{m} \alpha _ju_{j1}\right) {\hat{y}}_1 + \dots + \left( \sum _{j=1}^{m} \alpha _ju_{jm} \right) {\hat{y}}_m=0 \end{aligned}$$

which implies $\alpha _j=0, j=1,\dots , m$ since $\{{\hat{y}}_j : j=1,\dots ,m\}$ is a linearly independent set. This completes the proof. $\square$

Thus, it follows from the above theorem that for a partitioned graph G, if the blocks $A_{ij}, 1\le i,j\le n$ of its adjacency matrix (1) form a set of commuting normal matrices, then any GTPT equivalent graph of G, for example, $G^\tau$ is a cospectral mate of G. This calls for identifying structural properties of a partitioned graph for which this sufficient condition is met. Note that the specific structure of the partitions represented by $A_{i,i}$ (the diagonal blocks of $\mathbf{A }(G)$) and the structure of bipartite graphs constituted by the partitioned vertex sets of any two partitions say $C_i, C_j, i\ne j$ and edges between them determine the commuting normality property of $A_{i,j}, 1\le i,j\le n.$ We denote $\langle C_i,C_j\rangle$ for the bipartite subgraph of G whose adjacency matrix is given by

$$\begin{aligned} \begin{bmatrix} 0&\quad A_{i,j} \\ A_{i,j}^t&\quad 0 \end{bmatrix} \end{aligned}$$

when $i\ne j.$ If $i=j,$$\langle C_i,C_i\rangle$ represents the subgraph induced by the ith partition $C_i$ whose adjacency matrix is the diagonal block $A_{i,i}$ of $\mathbf{A }(G).$

A graph theoretic characterization of commuting normal blocks of a block matrix is devised in [5, 6] recently. Indeed we summarize the properties obtained in [5] in the following theorem.

Theorem 5

Let G be a partitioned graph with the partitions $C_i=\{v_{i,1}, v_{i,2}, \dots , v_{i,m}\}$, $i=1,\dots , n.$ For any bipartite graph $\langle C_i, C_j\rangle$, we define neighborhood index set of a vertex $v_{i,\alpha }$ in $C_i$ with respect to $C_j$ as

$$\begin{aligned} {{\,\mathrm{nbd}\,}}_{C_j}(v_{i,\alpha }) =\{\beta : v_{i,\alpha } \, \text{ and } \,\, v_{j,\beta } \, \text{ are } \text{ adjacent }\, \}\subseteq \{1,2,\dots ,m\} \end{aligned}$$

(5)

where $\alpha ,\beta \in \{1,2,\dots , m\}$ and $j\in \{1,2,\dots ,n\}.$ Then, the blocks of the adjacency matrix $\mathbf{A }(G)$ form a set of commuting normal matrices if the following conditions are satisfied.

• 1. (Commuting condition, Theorem 1, [5]) For any two graphs $\langle C_{i_1}, C_{j_1}\rangle ,$ and $\langle C_{i_2}, C_{j_2}\rangle ,$

  $$\begin{aligned} \left| {{\,\mathrm{nbd}\,}}_{C_{j_1}}(v_{i_1, \alpha }) \cap {{\,\mathrm{nbd}\,}}_{C_{i_2}}(v_{j_2, \beta })\right| = \left| {{\,\mathrm{nbd}\,}}_{C_{i_1}}(v_{j_1, \beta }) \cap {{\,\mathrm{nbd}\,}}_{C_{j_2}}(v_{i_2, \alpha })\right| \end{aligned}$$

  where $1\le \alpha , \beta \le m, 1\le i_1,i_2,j_1,j_2\le n.$

• 2. (Normality condition, Theorem 2, [5]) The number of common neighbors in $C_j$ of any pair of vertices $v_{i,\alpha }, v_{i,\beta }$ in $C_i, i\ne j$ is the same as the number of common neighbors in $C_i$ of the pair of vertices $v_{j,\alpha }, v_{j,\beta }$ in $C_j.$

Thus we have the following theorem.

Theorem 6

Let G be a partitioned graph which satisfies the commuting and normality conditions mentioned in Theorem 5. Then, G and $G^\tau$ are cospectral.

Proof

When the subgraphs $\langle C_\mu \rangle$, and $\langle C_\mu , C_{\nu } \rangle$ satisfy Theorem 5, there is an invertible matrix P such that $A^t_{i, j} = P^{-1}A_{i, j}P$, for all i and j as proved in Theorem 4 . Hence, we have

$$\begin{aligned} \mathbf{A }(G^\tau )&= \begin{bmatrix} A_{1,1}^t&\quad A_{1,2}^t&\quad \cdots&\quad A_{1,n}^t \\ A_{2,1}^t&\quad A_{2,2}^t&\quad \cdots&\quad A_{2,n}^t \\ \vdots&\quad \vdots&\quad \vdots&\quad \vdots \\ A_{n,1}^t&\quad A_{n,2}^t&\quad \cdots&\quad A_{n,n}^t \end{bmatrix} = \begin{bmatrix} P^{-1}A_{1,1}P&\quad P^{-1}A_{1,2}P&\quad \cdots&\quad P^{-1}A_{1,n}P \\ P^{-1}A_{2,1}P&\quad P^{-1}A_{2,2}P&\quad \cdots&\quad P^{-1}A_{2,n}P \\ \vdots&\quad \vdots&\quad \vdots&\quad \vdots \\ P^{-1}A_{n,1}P&\quad P^{-1}A_{n,2}P&\quad \cdots&\quad P^{-1}A_{n,n}P \end{bmatrix}\\&= \begin{bmatrix} P^{-1}&\quad 0&\quad \cdots&\quad 0 \\ 0&\quad P^{-1}&\quad \cdots&\quad 0 \\ \vdots&\quad \vdots&\quad&\quad \vdots \\ 0&\quad 0&\quad \cdots&\quad P^{-1} \end{bmatrix} \begin{bmatrix} A_{1,1}&\quad A_{1,2}&\quad \cdots&\quad A_{1,n} \\ A_{2,1}&\quad A_{2,2}&\quad \cdots&\quad A_{2,n} \\ \vdots&\quad \vdots&\quad \vdots&\quad \vdots \\ A_{n,1}&\quad A_{n,2}&\quad \cdots&\quad A_{n,n} \end{bmatrix} \begin{bmatrix} P&\quad 0&\quad \dots&\quad 0 \\ 0&\quad P&\quad \cdots&\quad 0 \\ \vdots&\quad \vdots&\quad&\quad \vdots \\ 0&\quad 0&\quad \cdots&\quad P \end{bmatrix}\\&= {\mathcal {P}}^{-1}\mathbf{A }(G){\mathcal {P}}\\ \text {where}~ {\mathcal {P}}&= {{\,\mathrm{diag}\,}}\{P, P, \dots P \}. \end{aligned}$$

This completes the proof. $\square$

Indeed we emphasize that the condition in Theorem 6 is sufficient but not necessary for cospectrality of graphs. This is evident from the following example.

Example 2

Consider the following pair of GTPT cospectral graphs:

Then,

Recall that any $2\times 2$ matrix is unitarily similar to its transpose (see Lemmas 2.4 and 3.3 in [8]). Let there be a matrix $P = \begin{bmatrix} a&\quad b \\ c&\quad d \end{bmatrix}$ such that

$$\begin{aligned} A_{1, 2}^t = P^{-1} A_{1, 2} P \Rightarrow \begin{bmatrix} 1&\quad 0 \\ 1&\quad 0 \end{bmatrix} = \begin{bmatrix} a&\quad b \\ c&\quad d \end{bmatrix}^{-1} \begin{bmatrix} 1&\quad 1 \\ 0&\quad 0 \end{bmatrix} \begin{bmatrix} a&\quad b \\ c&\quad d \end{bmatrix}, \\ A_{2, 1}^t = P^{-1} A_{2, 1} P \Rightarrow \begin{bmatrix} 1&\quad 1 \\ 0&\quad 0 \end{bmatrix} = \begin{bmatrix} a&\quad b \\ c&\quad d \end{bmatrix}^{-1} \begin{bmatrix} 1&\quad 0 \\ 1&\quad 0 \end{bmatrix} \begin{bmatrix} a&\quad b \\ c&\quad d \end{bmatrix}. \end{aligned}$$

Comparing entrywise we obtain $a = \frac{i}{\sqrt{2}}, b = \frac{i}{\sqrt{2}}, c = \frac{i}{\sqrt{2}}, d = \frac{-i}{\sqrt{2}}$. Thus $P = \frac{i}{\sqrt{2}}\begin{bmatrix} 1&\quad 1 \\ 1&\quad -1 \end{bmatrix}$. Hence, $\mathbf{A }(G^\tau )={\mathcal {P}}^*\mathbf{A }(G){\mathcal {P}}$, where ${\mathcal {P}}={{\,\mathrm{diag}\,}}\{P, P, P\}$. Consequently $\mathbf{A }(G)$, and $\mathbf{A }(G^\tau )$ are cospectral. Indeed, note that $A_{1,2}A_{2,1}\ne A_{2,1}A_{1,2}.$

A critical observation from the above example leads to a procedure of constructing cospectral graphs that violate the sufficient condition of Theorem 6 is given in the following theorem.

Theorem 7

Let A be a non-normal binary matrix of order m and let A be similar to its transpose. Consider a partitioned graph G on mn vertices with n partitions $\{C_1,\dots , C_n\}$ each of which contains m vertices. Assume that G has the following structural properties.

• 1. The induced subgraph of G defined by $C_i, 1\le i \le n$ is a graph with no edges.

• 2. The adjacency matrix corresponding to the bipartite graphs $\langle C_i \cup C_j\rangle$ is of the form

  $$\begin{aligned} \begin{bmatrix} 0_{m\times m}&\quad A_{i,j}\\ A_{i,j}^t&\quad 0_{m\times m}\end{bmatrix} \end{aligned}$$

  and $A_{i,j}\in \{A, I_m, 0_{m\times m}\}, i\ne j$ where $I_m$ is the identity matrix of order m,  $0_{m\times m}$ is the zero matrix of order m,  and at least for one pair of $(i,j), A_{i,j}=A.$

Then, the graphs G and $G^\tau$ are cospectral but the commuting normality property of blocks in $\mathbf{A }$ is not satisfied.

Proof

The proof follows from the fact that the matrix A is similar to its transpose.   $\square$

Here, we mention that construction of a non-normal binary matrix is easy. Indeed $r_i=c_i$ where $r_i$ is the sum of the entries of ith row and $c_i$ is the sum of entries of ith column of the matrix is a necessary condition for a binary matrix to be normal. Thus, any binary matrix violating this condition is an example of a non-normal matrix and the condition for similarity to its transpose can be found in [8]. In this context, we mention that if the blocks of the adjacency matrix $\mathbf{A }(G)$ are normal, then the degree sequence of G shall be same as the degree sequence of $G^\tau .$ This indicates a possibility that $G^\tau$ could be isomorphic to G. Whereas, for a non-normal off-diagonal block matrix of $\mathbf{A }(G)$, the degree sequence of G and $G^\tau$ need not be equal. Hence, Theorem 7 can provide a useful tool for generation of non-isomorphic cospectral graphs.

Obviously, Theorem 7 can be generalized in many ways. For instance, if the matrices $A_{i,j}\in \{A_l, I_m, 0_{m\times m}, l=1,\dots ,k\}$ such that there exists a nonsingular matrix X for which $X^{-1}A_lX=A_l^t$ and $A_l, l=1,\dots ,k$ form a set of non-normal and/or non-commutating matrices, then the graph $G^\tau$ is cospectral but need not be isomorphic to G.

3 Construction of cospectral graphs from GTPT equivalent cospectral graphs

In the following, we consider a partitioned graph G on mn vertices with partitions $C_i=\{v_{i,1}, v_{i,2}, \dots , v_{i,m}\}$, $i=1,\dots , n$ such that G and $G^\tau$ are cospectral. Denote the adjacency block matrix associated with the graph G as $\mathbf{A }(G)=[A_{ij}], 1\le i,j\le n.$ We develop procedures for construction of new cospectral graphs from GTPT equivalent cospectral graphs G and $G^\tau$ as follows.

Procedure 1

Let G be a partitioned graph which inherits the structural properties possessed by the commuting and normality conditions mentioned in Theorem 5. Construct a partitioned graph $H=(V(H), E(H))$ on km vertices with partitions $D_j, j=1,\dots ,k$ defined as follows:

• $V(H)=\bigsqcup _{p=1}^k D_p$ where $D_p\in \{C_1, C_2,\dots , C_n\}$ where $k\ge 2.$

• Generate edges between vertices of $D_p$ and $D_q, q\ne p$ such that the adjacency matrix corresponding to the bipartite graph $\langle D_p,D_q\rangle , 1\le p,q\le k$ is given by

  $$\begin{aligned} \begin{bmatrix} 0_{m\times m}&\quad D_{p,q}\\ D_{p,q}^t&\quad 0_{m\times m}\end{bmatrix} \end{aligned}$$

  such that $D_{p,q}\in \{I_{m}, 0_{m\times m}\} \cup \{ A_{i,j} | i\ne j, 1\le i,j\le n\}.$ Thus, either no vertex of $D_p$ is adjacent to any vertex of $D_q,$ or the lth vertex $v_{p,l}$ of $D_p$ is adjacent to lth vertex $v_{q,l}$ of $D_q$ for all $1\le l\le m$ only, or $\langle D_p,D_q\rangle =\langle C_i,C_j\rangle$ for some i and $j\ne i.$

Theorem 8

The partitioned graph H constructed from a partitioned graph G using Procedure-1 is a cospectral mate of the graph $H^\tau .$

Proof

The proof follows from the fact that the blocks of adjacency matrix associated with the graph H form a family of similar matrices with a common similarity matrix. $\square$

Observe that the crux behind the construction of the cospectral graphs H and $H^\tau$ in Procedure-1 is by adding/removing some copies of the existing partitions in G and adding/removing copies of some bipartite graphs between the existing partitions. We describe the next procedure for construction of cospectral graphs by adding new vertices in the existing partitions of G.

Procedure 2

Let G be a partitioned graph on mn vertices that inherit the structural properties possessed by the commuting and normality conditions mentioned in Theorem 5. Construct a partitioned graph $H=(V(H), E(H))$ on $(2m-1)n$ vertices with partitions $D_i, i=1,\dots ,n$ defined as follows:

• $V(H)=\bigsqcup _{i=1}^n D_i$ where $D_i=C_i \cup \, {\widehat{C}}_i$ where ${\widehat{C}}_i=\{v_{i,m}, v_{i,m+1}, \dots , v_{i,2m-1}\}.$ Note that $v_{i,j}, j=m+1,\dots ,2m-1, i=1,\dots , n$ are new vertices and $C_i \cap \, {\widehat{C}}_i=\{v_{i,m}\}.$

• Create an edge $(v_{i,l_2}, v_{j,l_2}), 1\le l_1,l_2\le m$ in H if and only if the vertices $v_{i,l_2}, v_{j,l_2}$ are adjacent in G,  $1\le i,j\le n.$

• Consider the map $f: \bigsqcup _{i=1}^n C_i \rightarrow \bigsqcup _{i=1}^n {\widehat{C}}_i$ defined by $f(v_{i,l})=v_{i,2m-l}, l=1, \dots , m, i=1,\dots ,n.$ Then define an edge between $f(v_{i,l_1})$ and $f(v_{j,l_2}), 1\le l_1,l_2\le m$ if and only if $v_{i,l_1}$ and $v_{j,l_2}$ are adjacent in G for all $i\ne j, 1\le i,j\le n.$

Some immediate observations about the graph H constructed by using Procedure 2 are as follows. Note that the vertex set of H can be written as $V(H)=\bigsqcup _{i=1}^n C_i\cup {\widehat{C}}_i$ and the induced subgraph generated by the vertex set $\sqcup _{i=1}^n C_i$ in H is G.

Theorem 9

The partitioned graph H constructed from a partitioned graph G using Procedure-2 is a cospectral mate of the graph $H^\tau .$

Proof

Consider the subgraph $\langle C_i, C_j \rangle$ of G. Then, the subgraph $\langle D_i, D_j \rangle$ of H contains all the edges of $\langle C_i, C_j \rangle$ and some additional edges that preserve the structural properties of $\langle C_i, C_j \rangle$. Let the matrix

$$\begin{aligned} \begin{bmatrix} 0_{2m-1\times 2m-1}&\quad B_{i,j}\\ B_{i,j}^t&\quad 0_{2m-1\times 2m-1}\end{bmatrix} \end{aligned}$$

in A(H) represent the adjacency relations of $\langle D_i, D_j \rangle$ and the k-th column of $B_{ij}$ is denoted by $b_{*k}^t$ for $k = 1, 2, \dots (2m - 1)$. Also let the k-th column of $A_{ij}$ is denoted by $a_{*k}^t$ for $k = 1, 2, \dots m$. Now, we observe that

$$\begin{aligned} b_{*k}^t = {\left\{ \begin{array}{ll} [a_{*k} \,\underbrace{0 \, 0 \, \dots 0}_{(m - 1)\text {-times}}]^t &{} ~\text {for}~ k = 1, 2, \dots (m - 1) \\ {[}a_{* m} \, a_{m - 1, m} \, a_{m - 2, m} \, \dots a_{1 ,m}]^t &{} ~\text {for}~ k = m\\ {[}\underbrace{0\, 0\, \dots 0}_{m\text {-times}} a_{m - 1, 2m - k}\, a_{m - 2, 2m - k}\, \dots a_{1, 2m - k}]^t &{} ~\text {for}~ k = (m + 1), (m + 2), \dots (2m - 1) \end{array}\right. } \end{aligned}$$

(6)

Note that due to our assumption on G,  there is a similarity matrix $P_a=[p_{xy}]$ such that $P_a A^t_{ij} = A_{ij}P_a$ for all i, j. Now, we show that there is a similarity matrix $P_b$ such that $P_b B^t_{ij} = B_{ij}P_b$ holds for all i, j,  and hence, the new graph H will be cospectral to $H^\tau .$ We proceed as follows.

Let the k-th columns of $P_a$ and $P_b$ be $p_{*k}^t$ and ${\tilde{p}}_{*k}^t$, respectively. Also the k-th row vector of $A_{ij}$ is $a_{k*}$ that becomes the k-th column vector of $A_{ij}^t$ after a transposition. Since $A_{ij}^t = P_a^{-1}A_{ij}P_a$, we obtain $a_{*k}^t = P_a^{-1}A_{ij}p_{*k}^t$. We define

$$\begin{aligned} {\tilde{p}}_{*k}^t = {\left\{ \begin{array}{ll} [p_{*k} \, \underbrace{0\, 0 \dots 0}_{(m - 1)\text {-times}}]^t &{} ~\text {for}~ k = 1, 2, \dots (m - 1) \\ {[}p_{*m} \, p_{m - 1, m}\, p_{m - 2, m}\, \dots p_{1 ,m}]^t &{} ~\text {for}~ k = m\\ {[}\underbrace{0\, 0\, \dots 0}_{ m\text {-times}} \, p_{m - 1, 2m - k}\, p_{m - 2, 2m - k}\, \dots p_{1, 2m - k}]^t &{} ~\text {for}~ k = (m + 1), (m + 2), \dots (2m - 1). \end{array}\right. } \end{aligned}$$

(7)

Now, it is a simple algebraic calculation to verify that $P_b b_{*k}^t = B_{ij}{\tilde{p}}_{*k}^t$ and $P_b$ is invertible. Hence, the proof. $\square$

The following example illustrates the relationship between $A_{ij}$ and $B_{ij}$ transparent.

Example 3

Consider the graph G of the example 2. Then, the graph H generated by applying Procedure2 on G is given by

In the Example 2, we calculated $A_{1,2} = \begin{bmatrix} 1&1 \\ 0&0 \end{bmatrix}$ and the block similarity matrix $P_a = \frac{i}{\sqrt{2}} \begin{bmatrix}1&1 \\ 1&-1 \end{bmatrix}$. In A(H), observe that the block $B_{1,2} = \begin{bmatrix} 1&1&0 \\ 0&0&0 \\ 0&1&-1 \end{bmatrix}$ and the similarity matrix $P_b = \frac{i}{\sqrt{2}} \begin{bmatrix}1&1&0\\ 1&-1&1 \\ 0&1&1\end{bmatrix}$.

We emphasize that Procedures 1 and 2 can be gainfully used to generate large cospectral graphs and hence compare to GM-switching the idea of GTPT equivalent graphs proves to be more efficient for producing cospectral graphs as almost no cospectral mate of a large graph can be obtained by GM-switching [11].

Now, we recall Example 1 which ensures that for two isomorphic (cospectral) graphs G and H the corresponding GTPT equivalent graphs $G^\tau$ and $H^\tau$ need not be cospectral. In the following, we introduce a method called alternative partitioning of a partitioned graph and develop a mechanism for constructing a cospectral GTPT equivalent graph from a given GTPT equivalent cospectral graph.

For the graph G with partitions $C_i=\{v_{i,1}, v_{i,2}, \dots , v_{i,m}\}$, $i=1,\dots , n,$ we define an alternative partitioning on G as $C'_j=\{v_{1,j}, v_{2,j}, \dots , v_{n,j}\}$, $j=1,\dots , m.$ Note that $\sqcup _{i=1}^n C_i = \sqcup _{j=1}^m C'_j.$ Defining these new partitions along with the exiting edges, an isomorphic copy of G is obtained that we call as the alternating partitioned graph of G and denote it by $G_{a}.$ Then we have the following theorem.

Theorem 10

Let G be a partitioned graph on mn vertices with n partitions. Then, $G^\tau$ and $G_a^\tau$ are isomorphic. Moreover, if G and $G^\tau$ are cospectral, then $G_a$ and $G_a^\tau$ are cospectral.

Proof

First we prove that $G^\tau$ and $G_a^\tau$ are isomorphic where the partitions of G are given by $C_i=\{v_{i,1}, v_{i,2}, \dots , v_{i,m}\}$, $i=1,\dots , n,$ and the partitions of $G_a$ are described as $C'_j=\{v_{1,j}, v_{2,j}, \dots , v_{n,j}\}$, $j=1,\dots , m.$ Define a bijective map $f: V(G^\tau ) \rightarrow V(G_a^\tau )$ as $f(v_{ij}) = v_{ji}$ for $i = 1, 2, \dots n$ and $j = 1, 2, \dots m$. Now we show that $(u,v)\in E(G^\tau )$ if and only if $(f(u),f(v))\in E(G_a^\tau )$ for any two vertices $u,v\in V(G^\tau ).$ We consider the following cases.

• 1. Case 1: Let there be an edge $(v_{ij}, v_{ik}) \in E(G)$ for some $j \ne k$. Then $(v_{ji}, v_{ki}) \in E(G_a)$ after the alternative partitioning. As GTPT does not change this edge, $(v_{ij}, v_{ik}) \in E(G^\tau )$ and $(v_{ji}, v_{ki}) \in E(G_a^\tau )$, that is, $(f(v_{ij}), f(v_{ik})) \in E(G_a^\tau )$. Further for any edge of the form $(v_{ji}, v_{ki}) \in E(G_a^\tau )$, $(f^{-1}(v_{ji}), f^{-1}(v_{ki})) = (v_{ij}, v_{ik}) \in E(G_a^\tau )$. The proof is similar for any edge $(v_{ij}, v_{kj}) \in E(G)$ for any $j \ne k.$

• 2. Case 2: Let $(v_{ij}, v_{kl}) \in E(G)$ for some $i \ne k$ and $j \ne l$. Then after alternative partitioning on G, $(v_{ji}, v_{lk}) \in E(G_a)$. After GTPT on G, and $G_a$ we have $(v_{il}, v_{kj}) \in E(G^\tau )$, and $(v_{jk}, v_{li}) \in E(G_a^\tau )$, respectively. As all the graphs are simple, $(v_{jk}, v_{li}) = (v_{li}, v_{jk}) = (f(v_{il}), f(v_{kj}))$. Further, for any edge of the form $(v_{jk}, v_{li}) \in E(G_a^\tau ),$$(f^{-1}(v_{jk}), f^{-1}(v_{li})) = (v_{il}, v_{kj}) \in E(G^\tau )$.

Combining Cases 1 and 2, we prove that $G^\tau$ and $G_a^\tau$ are isomorphic.

Let $\Lambda (X)$ denote the spectrum of a graph X. Then obviously $\Lambda (G)=\Lambda (G_a)$ and $\Lambda (G^\tau )=\Lambda (G_a^\tau )$ since G and $G^\tau$ are isomorphic to $G_a$ and $G_a^\tau$, respectively. Moreover, if G and $G^\tau$ are cospectral, that is, $\Lambda (G)=\Lambda (G^\tau )$ then obviously $\Lambda (G_a)=\Lambda (G_a^\tau ).$ This completes the proof. $\square$

4 Examples of non-isomorphic cospectral GTPT equivalent graphs

In order to investigate the efficiency of GTPT technique for constructing non-isomorphic cospectral graphs, we attempt to enumerate the number of non-isomorphic cospectral graphs that can be obtained from a few easily constructable partitioned graphs with the number of partitions at most 3. In some cases, we also employ the Procedures 1 and 2 for the same. Thus, in the following, we consider partitioned model graphs G with partitions $C_i=\{v_{i,1}, v_{i,2}, \dots v_{i,m}\}, i=1,\dots ,n, n\le 3$ and each $C_i$ contains $m\le 4$ number of vertices. We denote the path and cycle graphs on m vertices as ${\mathcal {P}}_m$ and ${\mathcal {C}}_m$, respectively. The number $\kappa$ of non-isomorphic cospectral graphs that can be obtained from each model graph is provided in the following tables. Each graph, say G, which is depicted in the following tables is non-isomorphic but cospectral to its corresponding GTPT equivalent graph $G^\tau$. When the number of such graphs is considerably huge for a given set of parameters m, n, we draw only a few prototype graphs. These graphs are generated by using NetworkX [21] which uses the algorithm stated in [1] for checking graph isomorphism. Note that in all the examples, the partitions are considered as the collection of vertices in each row or column as indicated by the numbers m.

First, we consider the following model graphs G having partitions $C_i, i=1,\dots , n, n\in \{2, 3\}$ with special structures and assign arbitrary edges to form $\langle C_i, C_j \rangle , i\ne j$ such that the ultimate graph G becomes cospectral and non-isomorphic to $G^\tau .$ We calculate the number of such graphs G possible for each fixed model.

• 1a. $n=2, m\in \{2,3,4\}.$ The partitions of G are as follows: $C_1$ is a graph with no edges, $C_2={\mathcal {P}}_m.$

• 1b. $n=2, m\in \{2,3,4\}.$ The partitions of G are as follows: $C_1$ is a graph with no edges, $C_2={\mathcal {C}}_m.$

Now we consider a few model graphs G that are used to generate graphs H for which H and $H^\tau$ are non-isomorphic and cospectral by applying Procedure 1 or 2 as described below. We calculate the number of non-isomorphic cospectral graphs that can be obtained for each of these model graphs G and draw a few of them in the following table when this number is large.

Examples using Procedure 1.

• 2. $n=3$ and $m\in \{2,3,4\}.$ The graph G consists of 3 partitions, $C_1, C_2, C_3$ such that the induced subgraph defined by the vertex set $C_1\cup C_2$ is a bipartite graph and $C_3$ is an isolated partition with no edges. Then, construct the graph H by following the Procedure 1 such that $V(H) = V(G)$ and $E(H) = E(G) \cup \{(v_{2,i}, v_{3,i}): i = 1, 2, \dots m\}.$

Examples using Procedure 2.

• 3a. Consider a partitioned graph G with $n=2, m\in \{2,3,4\}$ such that the partitions $C_1, C_2$ are graphs with no edges and arbitrary edges between the vertices of $C_1$ and $C_2.$ Consider the alternating partitioned graph $G_a$ and apply the Procedure 2 on $G_a$ by adding one vertex in each of the new partitions. Thus, the new partitioned graph H is obtained with $m=3, n\in \{2,3,4\}.$

• 3b. Consider a partitioned graph G with $n=2, m\in \{2,3,4\}$ such that the partitions $C_1$ is a graph with no edges, $C_2$ is the path ${\mathcal {P}}_m$ and arbitrary edges between the vertices of $C_1$ and $C_2.$ Consider the alternating partitioned graph $G_a$ and apply the Procedure 2 on $G_a$ by adding one vertex in each of the new partitions. Thus, the new partitioned graph H is obtained with $m=3, n\in \{2,3,4\}.$

• 3c. Consider a partitioned graph G with $n=2, m\in \{2,3,4\}$ such that the partitions $C_1$ is a graph with no edges, $C_2$ is the cycle ${\mathcal {C}}_m$ and arbitrary edges between the vertices of $C_1$ and $C_2.$ Consider the alternating partitioned graph $G_a$ and apply the Procedure 2 on $G_a$ by adding one vertex in each of the new partitions. Thus, the new partitioned graph H is obtained with $m=3, n\in \{2,3,4\}.$

Examples by applying combinations of Procedures 1, 2, alternate partitioning and/or adding new partitions.

• 4a. Consider a partitioned graph G with $n=2, m\in \{2,3,4\}$ with partitions $C_1, C_2$ such that $C_1$ is with no edges, $C_2={\mathcal {P}}_m,$ and arbitrary edges between the vertices of $C_1$ and $C_2.$ Then, we generate the alternating partitioned graph $G_a$ with partitions $C_1',\dots , C_m'.$ Following the Procedure 2, we add one vertex $v_{j}, j=1,\dots ,m$ to each of these new partitions and create edges. Finally, we link the vertices $v_j, j=1,\dots ,m$ to form a path ${\mathcal {P}}_m,$ and hence form the graph H such that it is cospectral with $H^\tau .$

• 4b. Consider a partitioned graph G with $n=2, m\in \{2,3,4\}$ with partitions $C_1, C_2$ such that $C_1={\mathcal {P}}_m=C_2$ and arbitrary edges between the vertices of $C_1$ and $C_2.$ Then, we generate the alternating partitioned graph $G_a$ with partitions $C_1',\dots , C_m'.$ Following the Procedure 2 we add one vertex $v_{j}, j=1,\dots ,m$ to each of these new partitions and create edges. Finally, we link the vertices $v_j, j=1,\dots ,m$ to form a path ${\mathcal {P}}_m,$ and hence form the graph H such that it is cospectral with $H^\tau .$

• 4c. Consider a partitioned graph G with $n=2, m\in \{2,3,4\}$ with partitions $C_1, C_2$ such that $C_1$ is with no edges, $C_2={\mathcal {C}}_m,$ and arbitrary edges between the vertices of $C_1$ and $C_2.$ Then, we generate the alternating partitioned graph $G_a$ with partitions $C_1',\dots , C_m'.$ Following the Procedure 2 we add one vertex $v_{j}, j=1,\dots ,m$ to each of these new partitions and create edges. Finally, we link the vertices $v_j, j=1,\dots ,m$ to form a path ${\mathcal {C}}_m,$ and hence form the graph H such that it is cospectral with $H^\tau .$

5 Conclusion and future work

We have identified classes of graphs for which the corresponding GTPT equivalent graphs are cospectral, and hence, it is established that GTPT approach can act as a novel method for construction of cospectral mates of a given graph. In contrast to the existing combinatorial approaches, thus we introduce a matrix function approach (known as partial transpose of a block matrix) for construction of cospectral graphs. This opens up a new idea of treating a graph on a composite number of vertices as a partitioned graph and identifying the properties of its partitions that guarantees to obtain cospectral mates of the given graph. We also developed two procedures to construct small and/or big GTPT equivalent cospectral graphs from a given GTPT equivalent cospectral graph. Finally, we produce several examples of non-isomorphic cospectral graphs using the GTPT approach and the procedures proposed in the paper.

We mention that the GTPT approach can be extended in many directions, in particular, for weighted graphs and construction of Laplacian cospectral graphs which we would like to investigate in future. Besides, it would be an interesting problem to determine properties of graphs that are invariant under GTPT.