Semimodularity and the Jordan–Hölder theorem in posets, with applications to partial partitions

Abstract

Lattice-theoretical generalizations of the Jordan–Hölder theorem of group theory give isomorphisms between finite maximal chains with same endpoints. The best one has been given by Czédli and Schmidt (after Grätzer and Nation), and it applies to semimodular lattices and gives a chain isomorphism by iterating up and down the perspectivity relation between intervals $[x\wedge y,x]$ and $[y,x\vee y]$ where x covers $x\wedge y$ and $x\vee y$ covers y. In this paper, we extend to arbitrary (and possibly infinite) posets the definitions of standard semimodularity and of the slightly weaker “Birkhoff condition”, following the approach of Ore (Bull Amer Math Soc 49(8):567–568, 1943). Instead of perspectivity, we associate tags to the covering relation, a more flexible approach. We study the finiteness and length constancy of maximal chains under both conditions and obtain Jordan–Hölder theorems. Our theory is easily applied to groups, to closure ranges of an arbitrary poset, and also to five new order relations on the set of partial partitions of a set (i.e. partitions of its subsets), which do not constitute lattices.

1 Introduction

In group theory, the Jordan–Hölder theorem states that in a finite group, all composition series (maximal series of subnormal subgroups) and all chief series (maximal series of normal subgroups) are isomorphic in the sense that they have the same length and their sequences of quotients of successive groups can be obtained from each other by permutation (that is, the sequences contain the same groups, with each one appearing the same number of times).

Naive lattice theory presents as analogue or “generalization” of it the so-called Jordan–Dedekind theorem  [2] due to Dedekind  [5], which states that in a modular lattice (i.e. satisfying the condition $a\le b \;\Rightarrow \;a \vee (x \wedge b) = (a \vee x) \wedge b$), in an interval of finite length all maximal chains will have the same length. Now normal subgroups of a group, ordered by inclusion, obviously constitute a modular lattice; thus, the Jordan–Dedekind theorem states here that in a group of finite normal length, all chief series have the same length.

In a lattice, write $\prec$ for the covering relation; then, the lattice is upper semimodular if it satisfies $a\wedge b \prec a \;\Rightarrow \;b \prec a \vee b$, and dually it is lower semimodular if it satisfies $b \prec a \vee b \;\Rightarrow \;a\wedge b \prec a$ [23]. Both conditions are more general than modularity. Then, the Jordan–Dedekind theorem holds also in a lower or upper semimodular lattice of finite length. Now the subnormal subgroups of a group with finite composition length, ordered by inclusion, constitute a lower semimodular lattice; hence, the Jordan–Dedekind theorem gives that all composition series have the same length.

However, we still have an impoverished version of the Jordan–Hölder theorem, since it lacks the part about the number of occurrences of each quotient in the series. Now Grätzer and Nation [10, 13] introduced the perspectivity relations in a lattice: given two elements x, y of a lattice, the two intervals $[x\wedge y,x]$ and $[y,x\vee y]$ are said to be perspective, $[x\wedge y,x]$ is up-perspective to $[y,x\vee y]$, and $[y,x\vee y]$ is down-perspective to $[x\wedge y,x]$. They showed that in an upper semimodular lattice of finite length, given two maximal chains (having thus the same length), there is a bijection from the set of successive intervals of the first chain to that of the second, obtained by composing an up-perspectivity followed by a down-perspectivity; for lower semimodularity, we have a down-perspectivity followed by an up-perspectivity. Then, Czédli and Schmidt [4] showed that the up and down sequence is unique. Now in both lattices of subnormal subgroups and of normal subgroups, two perspective intervals [A, B] and [C, D] give isomorphic quotient groups B / A and D / C; hence, we obtain here the full Jordan–Hölder theorem.

Although these results greatly improve on the usual Jordan–Dedekind theorem for modular lattices, we can nevertheless criticize their “ad hoc” nature and their lack of generality. First, it is not necessary to have a lattice, a poset (partially ordered set) suffices. Indeed, we can easily generalize semimodularity to posets, following the approach given by Ore  [15] for generalizing the slightly weaker Birkhoff condition  [23] or quadrilateral condition  [15]. Then, the result of Grätzer and Nation holds in a semimodular poset.

Next, we replace the “ad hoc” perspectivity relation by something more flexible in theory and more concrete in specific examples. We partition the covering relation $\prec$ into a set of tagged relations $\buildrel \! {\mathsf {h}} \! \over \prec$, each corresponding to a tag${\mathsf {h}}$. In practice, the tags are given by the concrete situation, for instance, for composition series in groups, $X \buildrel \! {\mathsf {h}} \! \over \prec Y$ means that the quotient Y / X is the simple group labelled ${\mathsf {h}}$. We will also consider several partial order relations on the set of partial partitions of a set (i.e. partitions of any subset), and here, $\pi _1 \buildrel \! {\mathsf {h}} \! \over \prec \pi _2$ will mean that $\pi _2$ is obtained from $\pi _1$ by a specific elementary transformation corresponding to the tag ${\mathsf {h}}$, say, $\buildrel \! {\mathsf {m}} \! \over \prec$ for merging two blocks, $\buildrel \! {\mathsf {i}} \! \over \prec$ for inflating a block by a point, or $\buildrel \! {\mathsf {s}} \! \over \prec$ for creating a new singleton block. In the case of a lattice, the tagged semimodularity condition will mean that for perspective intervals [a, b] and [c, d] such that $a \buildrel \! {\mathsf {h}} \! \over \prec b$ and $c \buildrel \! {\mathsf {k}} \! \over \prec d$, we must have ${\mathsf {h}} = {\mathsf {k}}$; in other words, each $\buildrel \! {\mathsf {h}} \! \over \prec$ will be a union of equivalence classes of projectivity, the transitive closure of perspectivity. Tags allow flexibility in results, as the partition of tagged relations can vary from the coarsest, namely the whole covering relation $\prec$, to the finest, that is, the set of projectivity equivalence classes on the set of covering pairs. Here the Jordan–Hölder theorem states that in a finite maximal chain between two endpoints, among the covering relations of the chain, each tag intervenes a constant number of times.

We will also consider the weaker Birkhoff (or quadrilateral) condition in posets. In the case of lattices, for upper semimodularity it takes the following form  [2]: if $a\wedge b \prec a$ and $a\wedge b\prec b$, then $a \prec a \vee b$ and $b \prec a \vee b$. When the poset or lattice has finite length, the Birkhoff condition is equivalent to semimodularity. In the case of a poset of infinite length, it is strictly weaker. We will analyse the relation of both conditions with the finiteness of maximal chains between two endpoints. The Birkhoff condition guarantees that two finite maximal chains of same endpoints have the same length, but it does not forbid having two maximal chains of same endpoints, one finite and the other infinite. Now semimodularity implies that given a finite maximal chain of given endpoints, every chain with the same endpoints will be included in a finite maximal chain with the same length; thus, finite and infinite maximal chains cannot coexist. An interesting fact is that besides the straightforward tagging of the Birkhoff condition (see Fig. 2), we can introduce a more flexible condition on tags, the skew-tagged Birkhoff condition (see Fig. 3), which is not compatible with projectivity; thus, the arguments of Grätzer and Nation do not apply in this case, but we can nevertheless obtain the Jordan–Hölder theorem.

Our results trivially apply to the two posets of composition and of chief series in a group; here, we do not need the fact that subnormal subgroups constitute a lattice  [24] in order to obtain the Jordan–Hölder theorem.

We apply them next to the poset of closure ranges (closure systems) in an arbitrary (possibly infinite) poset  [18]: it is lower semimodular.

However, the main application of our theory is to several partial order relations defined on the family of partial partitions of a set (i.e. partitions of any subset of that set) [16, 19]. Ore  [14] showed that the partitions of a set, ordered by refinement, constitute an upper semimodular lattice. The extension of this order relation to partial partitions (called the standard order in [19]) also constitutes an upper semimodular lattice [6]. In [19], we introduced five new order relations on partial partitions, obtained by restricting the standard order; they do not constitute lattices; then, we showed by combinatorial methods that in the finite case, the Jordan–Hölder theorem holds for the standard order and these five orders. Here we will show that these orders are all upper semimodular, and that those with a tagged covering satisfy the skew-tagged upper quadrilateral condition; this implies the Jordan–Hölder theorem.

Our work shows thus that lattice-theoretical methods devised in order to generalize the Jordan–Hölder theorem can be extended to posets that are neither finite nor lattices. Also, we have introduced some flexibility in them.

2 Tags, semimodularity and quadrilateral condition in a poset

Let a set P be partially ordered by $\le$, with covering relation $\prec$ ($x \prec y$ if $x<y$, but there is no m with $x<m<y$). For any $x \in P$, let $x^\downarrow = \{ y \in P \mid y \le x \}$ and $x^\uparrow = \{ y \in P \mid y \ge x \}$ be the down-set and up-set generated by x  [3]. For $x\le y$, define the interval$[x,y] = x^\uparrow \cap y^\downarrow = \{ m \in P \mid x \le m \le y \}$. A subset of P is a chain if it is totally ordered; given $C\subseteq P$ and $x,y\in P$ such that $x\le y$, C is a chain of endpoints x, y if C is a chain, $x,y\in C$ and $C\subseteq [x,y]$. Given a chain C and $a,b\in C$ with $a\le b$, let $C_a^b= C \cap [a,b]$; it is a chain of endpoints a, b. The length of a chain is its cardinal minus one. A maximal chain of endpoints x, y is a chain of endpoints x, y which is not included in a larger chain of endpoints x, y; when such a maximal chain is finite, it takes the form $x = c_0 \prec \cdots \prec c_n = y$ for some $n\ge 0$, then we call it a covering chain, and here n is the length of the chain. The length of an interval [x, y] is the supremum of lengths of all maximal chains of endpoints x, y. When P is a lattice or a semilattice, we write $\vee$ and $\wedge$ for the join and meet operations.

Let us now introduce tagging. Let H be a set of symbols called tags; they will be attached to coverings in the poset P. Let ${\mathcal {H}}= \{ \buildrel \! {\mathsf {h}} \! \over \prec \mid {\mathsf {h}} \in H \}$ be a partition of the binary relation $\prec$; this means (with & denoting a logical AND) that:

$$ \begin{aligned} \begin{array}{l} \forall \,{\mathsf {h}} \in H, ~ \forall \,x,y\in P, ~ x \buildrel \! {\mathsf {h}} \! \over \prec y \implies x \prec y ; \\ \forall \,{\mathsf {h}} \in H, ~ \exists \,x,y\in P, ~ x \buildrel \! {\mathsf {h}} \! \over \prec y ; \\ \forall \,x,y\in P, ~ x \prec y \implies \exists \,{\mathsf {h}} \in H, ~ x \buildrel \! {\mathsf {h}} \! \over \prec y ; \\ \forall \,{\mathsf {h}},{\mathsf {k}} \in H, ~ \forall \,x,y\in P, ~ \bigl [ x \buildrel \! {\mathsf {h}} \! \over \prec y ~ \& ~ x \buildrel \! {\mathsf {k}} \! \over \prec y \bigr ] \implies {\mathsf {h}} = {\mathsf {k}} . \end{array} \end{aligned}$$

Note that the second condition $\forall \,{\mathsf {h}} \in H, ~ \exists \,x,y\in P, x \buildrel \! {\mathsf {h}} \! \over \prec y$ (that all tags are used) is unnecessary; however, in practice it makes tagging easier to describe. When the binary relation $\prec$ is empty, H and ${\mathcal {H}}$ will necessarily be empty. Otherwise, there always exists the coarsest partition ${\mathcal {H}}= \{ \prec \}$; in other words, we take for H a singleton, and there is a unique tag, which can conveniently be written as a blank symbol.

All our definitions and results will be tagged, that is, they will depend on the partition ${\mathcal {H}}$, so they will be denoted with the prefix “${\mathcal {H}}$-”. The particular case with ${\mathcal {H}}= \{ \prec \}$ will give their non-tagged counterparts, for which the prefix “${\mathcal {H}}$-”will be removed.

2.1 Definitions of tagged semimodularity

We consider an arbitrary poset P; possibly it can be infinite, and its intervals can have infinite length.

Fig. 1

${\mathcal {H}}$-upper semimodularity. Here $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$ and $[b,u] \mathrel {_{{\mathcal {H}}}\!\!\searrow \!\!\!^{m}} [d,a]$. In our Hasse diagrams, dashed lines stand for the order $\le$ and plain lines for the covering relation $\prec$, with the letter h indicating the specialization $\buildrel \! {\mathsf {h}} \! \over \prec$

Definition 1

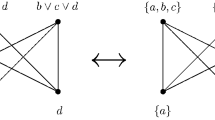
The poset P is ${\mathcal {H}}$-upper semimodular if for any ${\mathsf {h}} \in H$ and $m \in P$, given $a,b,d \in m^\downarrow$ such that $a \not \le b$, $d \buildrel \! {\mathsf {h}} \! \over \prec a$ and $d \le b$, there exists $u \in m^\downarrow$ such that $a \le u$ and $b \buildrel \! {\mathsf {h}} \! \over \prec u$, see Fig. 1.

Given ${\mathsf {h}} \in H$, $m\in P$ and $a,b,d,u \in m^\downarrow$ such that $a \not \le b$, $d \buildrel \! {\mathsf {h}} \! \over \prec a$, $d \le b$, $a \le u$ and $b \buildrel \! {\mathsf {h}} \! \over \prec u$, we say that the intervals [d, a] and [b, u] are ${\mathcal {H}}$-perspective under m, that [d, a] is ${\mathcal {H}}$-up-perspective under m to [b, u], that [b, u] is ${\mathcal {H}}$-down-perspective under m to [d, a], and we write $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$ and $[b,u] \mathrel {_{{\mathcal {H}}}\!\!\searrow \!\!\!^{m}} [d,a]$.

Note that we do not exclude the case where $b=d$; then, we can take $u=a$; thus, for $a,d \in m^\downarrow$ such that $d \prec a$, we have $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [d,a]$ and $[d,a] \mathrel {_{{\mathcal {H}}}\!\!\searrow \!\!\!^{m}} [d,a]$. When $d<b$, we necessarily have $a<u$.

For ${\mathcal {H}}= \{ \prec \}$, we remove the prefix “${\mathcal {H}}$-”, we just say that P is upper semimodular, and we write $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{}} [b,u]$ and $[b,u] \mathrel {_{}\!\!\searrow \!\!\!^{m}} [d,a]$. The property of ${\mathcal {H}}$-upper semimodularity weakens as the partition ${\mathcal {H}}$ is coarsened; in particular, upper semimodularity is weaker than ${\mathcal {H}}$-upper semimodularity for ${\mathcal {H}}\ne \{ \prec \}$.

When P is a lattice, $[a \not \le b ~ \& ~ d \buildrel \! {\mathsf {h}} \! \over \prec a ~ \& ~ d \le b]$ iff $d = a \wedge b \buildrel \! {\mathsf {h}} \! \over \prec a$, and $[a \not \le b ~ \& ~ b \buildrel \! {\mathsf {h}} \! \over \prec u ~ \& ~ a \le u]$ iff $b \buildrel \! {\mathsf {h}} \! \over \prec a \vee b = u$. Now we can always choose $m = a \vee b$, and then, $a,b,d,u \in m^\downarrow$. Therefore, the ${\mathcal {H}}$-upper semimodularity of P is equivalent to the tagged version of the usual definition of upper semimodularity in a lattice:

$$\begin{aligned} \forall \, {\mathsf {h}} \in H, ~ \forall \, a,b \in P, \quad a \wedge b \buildrel \! {\mathsf {h}} \! \over \prec a \implies b \buildrel \! {\mathsf {h}} \! \over \prec a \vee b . \end{aligned}$$

(1)

Moreover, we will say that $[a \wedge b,a]$ is ${\mathcal {H}}$-up-perspective to $[b,a \vee b]$ or that $[b,a \vee b]$ is ${\mathcal {H}}$-down-perspective to $[a \wedge b,a]$, without “under m”, and write $[a \wedge b,a] \mathrel {^{}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,a \vee b]$ or $[b,a \vee b] \mathrel {_{{\mathcal {H}}}\!\!\searrow \!\!\!^{}} [a \wedge b,a]$, without the superscript m, since we can take $m= a\vee b$ anyway.

There are some aspects of perspectivity which are simple in the case of a lattice, but generally more complicated when the poset is not a lattice. We introduce thus the following condition:

Definition 2

The poset P satisfies the ${\mathcal {H}}$-upper unicity if for any ${\mathsf {h}} \in H$ and $a,b,d \in P$ such that $a \not \le b$, $d \buildrel \! {\mathsf {h}} \! \over \prec a$ and $d \le b$, there is at most one $u \in P$ such that $a \le u$ and $b \buildrel \! {\mathsf {h}} \! \over \prec u$.

For ${\mathcal {H}}= \{ \prec \}$, we just say upper unicity. Note that the property of ${\mathcal {H}}$-upper unicity strengthens as the partition ${\mathcal {H}}$ is coarsened; in particular, upper unicity is stronger than ${\mathcal {H}}$-upper unicity for ${\mathcal {H}}\ne \{ \prec \}$.

From the above explanation, a join-semilattice satisfies upper unicity: if $a \not \le b$, $a \le u$ and $b \prec u$, then $u = a \vee b$; hence, it satisfies ${\mathcal {H}}$-upper unicity for any partition ${\mathcal {H}}$ of $\prec$. Upper unicity guarantees the following property of ${\mathcal {H}}$-perspectivity (the proof is elementary and left to the reader):

Lemma 3

Let the poset P be ${\mathcal {H}}$-upper semimodular and satisfying upper unicity. Then, for any $m \in P$, $\mathrel {^{m}\!\!\!\nearrow \!\!_{}}$ is included in $\mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}}$, that is, whenever $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{}} [b,u]$, we have $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$ (and similarly $\mathrel {_{}\!\!\searrow \!\!\!^{m}}$ is included in $\mathrel {_{{\mathcal {H}}}\!\!\searrow \!\!\!^{m}}$).

On the other hand, in the case of ${\mathcal {H}}$-upper semimodularity without upper unicity, we can have ${\mathsf {h}},{\mathsf {k}} \in H$ with ${\mathsf {h}} \ne {\mathsf {k}}$, $m\in P$ and $a,b,d,u,v \in m^\downarrow$ such that $a \not \le b$, $d \buildrel \! {\mathsf {h}} \! \over \prec a$, $d \le b$, $a \le u$, $a \le v$, $b \buildrel \! {\mathsf {h}} \! \over \prec u$ and $b \buildrel \! {\mathsf {k}} \! \over \prec v$. Here $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$ and $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{}} [b,v]$, but [d, a] is not${\mathcal {H}}$-up-perspective under m to [b, v].

Lemma 4

Let the poset P either be a join-semilattice or be ${\mathcal {H}}$-upper semimodular and satisfy ${\mathcal {H}}$-upper unicity. Then, the relations $\mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}}$ and $\mathrel {_{{\mathcal {H}}}\!\!\searrow \!\!\!^{m}}$ are transitive.

Proof

Let $[a_0,a_1] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b_0,b_1] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [c_0,c_1]$; thus, $a_0, a_1, b_0, b_1, c_0, c_1 \in m^\downarrow$, $a_1 \not \le b_0$, $b_1 \not \le c_0$, $a_0 \le b_0 \le c_0$, $a_1 \le b_1 \le c_1$, and for some ${\mathsf {h}} \in H$ we have $a_0 \buildrel \! {\mathsf {h}} \! \over \prec a_1$, $b_0 \buildrel \! {\mathsf {h}} \! \over \prec b_1$ and $c_0 \buildrel \! {\mathsf {h}} \! \over \prec c_1$.

If P is a join-semilattice, we have $b_1 = a_1 \vee b_0$, and as $b_0 \le c_0$, but $b_1 \not \le c_0$, we deduce that $a_1 \not \le c_0$. Now let P be ${\mathcal {H}}$-upper semimodular, satisfying ${\mathcal {H}}$-upper unicity, and suppose that $a_1 \le c_0$. Then $a_0, a_1, b_0 \in c_0^\downarrow$, and applying ${\mathcal {H}}$-upper semimodularity with $c_0$ in place of m, there is some $b_2 \in c_0^\downarrow$ such that $a_1 \le b_2$ and $b_0 \buildrel \! {\mathsf {h}} \! \over \prec b_2$; since $a_1 \not \le b_0$, $a_0 \buildrel \! {\mathsf {h}} \! \over \prec a_1$, $a_0 \le b_0$, $a_1 \le b_1, b_2$ and $b_0 \buildrel \! {\mathsf {h}} \! \over \prec b_1, b_2$, ${\mathcal {H}}$-upper unicity implies that $b_2 = b_1$, which contradicts the facts that $b_2 \le c_0$, but $b_1 \not \le c_0$. Therefore, we must have $a_1 \not \le c_0$.

Having $a_1 \not \le c_0$ in both cases, as $a_0 \le c_0$, $a_1 \le c_1$, $a_0 \buildrel \! {\mathsf {h}} \! \over \prec a_1$ and $c_0 \buildrel \! {\mathsf {h}} \! \over \prec c_1$, we get that $[a_0,a_1] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [c_0,c_1]$. Thus, $\mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}}$ is transitive. As $\mathrel {_{{\mathcal {H}}}\!\!\searrow \!\!\!^{m}}$ is the inverse relation, it is also transitive. $\square$

We now consider the tagged version of a slightly weaker version of semimodularity; following  [15] we call it the quadrilateral condition:

Fig. 2

${\mathcal {H}}$-upper quadrilateral condition

Definition 5

The poset P satisfies the ${\mathcal {H}}$-upper quadrilateral condition if for any ${\mathsf {h}},{\mathsf {k}} \in H$ and $m\in P$, given $a,b,d \in m^\downarrow$ such that $a \ne b$, $d \buildrel \! {\mathsf {h}} \! \over \prec a$ and $d \buildrel \! {\mathsf {k}} \! \over \prec b$, there exists $u \in m^\downarrow$ such that $a \buildrel \! {\mathsf {k}} \! \over \prec u$ and $b \buildrel \! {\mathsf {h}} \! \over \prec u$, see Fig. 2.

Here both $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$ and $[d,b] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [a,u]$. Note that we do not exclude the case where ${\mathsf {h}} = {\mathsf {k}}$. The non-tagged version of this definition was given in [15]. When P is a lattice, the ${\mathcal {H}}$-upper quadrilateral condition becomes equivalent to the tagged version of the classical Birkhoff condition  [2, 23]:

$$ \begin{aligned} \forall \, {\mathsf {h}},{\mathsf {k}} \in H, ~ \forall \, a,b \in P, \quad \bigl [ a \wedge b \buildrel \! {\mathsf {h}} \! \over \prec a ~ \& ~ a \wedge b \buildrel \! {\mathsf {k}} \! \over \prec b \bigr ] \implies \bigl [ a \buildrel \! {\mathsf {k}} \! \over \prec a \vee b ~ \& ~ b \buildrel \! {\mathsf {h}} \! \over \prec a \vee b \bigr ] .\nonumber \\ \end{aligned}$$

(2)

It is easily seen that applying (1) both for ${\mathsf {h}}$ and for ${\mathsf {k}}$ gives (2). We obtain a similar result in the case of a poset, by applying ${\mathcal {H}}$-upper semimodularity successively for ${\mathsf {h}}$, then for ${\mathsf {k}}$ (with u instead of m):

Proposition 6

Any ${\mathcal {H}}$-upper semimodular poset satisfies the ${\mathcal {H}}$-upper quadrilateral condition.

In a poset where all intervals have finite length, ${\mathcal {H}}$-upper semimodularity will be equivalent to the ${\mathcal {H}}$-upper quadrilateral condition, see Corollary 15. We now give a variant form of that condition:

Fig. 3

Skew-${\mathcal {H}}$-upper quadrilateral condition

Definition 7

The poset P satisfies the skew-${\mathcal {H}}$-upper quadrilateral condition if for any ${\mathsf {h}},{\mathsf {k}} \in H$ and $m\in P$, given $a,b,d \in m^\downarrow$ such that $a \ne b$, $d \buildrel \! {\mathsf {h}} \! \over \prec a$ and $d \buildrel \! {\mathsf {k}} \! \over \prec b$, there exist ${\mathsf {r}},{\mathsf {s}} \in H$ such that $\{ {\mathsf {h}}, {\mathsf {r}} \} = \{ {\mathsf {k}}, {\mathsf {s}} \}$, and $u \in m^\downarrow$ such that $a \buildrel \! {\mathsf {r}} \! \over \prec u$ and $b \buildrel \! {\mathsf {s}} \! \over \prec u$, see Fig. 3.

When ${\mathcal {H}}\ne \{ \prec \}$, the skew-${\mathcal {H}}$-upper quadrilateral condition is slightly more general than the ${\mathcal {H}}$-upper quadrilateral condition, but for ${\mathcal {H}}= \{ \prec \}$, the two are equivalent, and they are just Ore’s quadrilateral condition [15]. The condition $\{ {\mathsf {h}}, {\mathsf {r}} \} = \{ {\mathsf {k}}, {\mathsf {s}} \}$ gives 3 cases: (a) ${\mathsf {h}} = {\mathsf {k}} = {\mathsf {r}} = {\mathsf {s}}$; (b) ${\mathsf {h}} = {\mathsf {s}} \ne {\mathsf {k}} = {\mathsf {r}}$; (c) ${\mathsf {h}} = {\mathsf {k}} \ne {\mathsf {r}} = {\mathsf {s}}$. The first two correspond to the ${\mathcal {H}}$-upper quadrilateral condition, with $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$ and $[d,b] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [a,u]$; the third does not, and here we cannot use the perspectivity method of Grätzer and Nation. We will nevertheless obtain a Jordan–Hölder theorem by other means. In Sect. 3.3, we will describe two orders on partial partitions where this third case can arise, and this is our motivation for introducing the skew-${\mathcal {H}}$ quadrilateral condition.

Contrarily to modularity, semimodularity is not a self-dual concept. So all definitions given above have a dual, we will have the ${\mathcal {H}}$-lower semimodularity, quadrilateral condition and unicity, and up- or down-perspectivity will be above m, given that we will now have $a,b,d,u \in m^\uparrow$. For the ${\mathcal {H}}$-down- or up-perspectivity above m, we will write $\mathrel {_{m}\!\!\searrow \!\!\!^{{\mathcal {H}}}}$ and $\mathrel {^{{\mathcal {H}}}\!\!\!\nearrow \!\!_{m}}$.

It is easily seen that P is both ${\mathcal {H}}$-upper semimodular and ${\mathcal {H}}$-lower semimodular iff for any ${\mathsf {h}} \in H$, $m,n \in P$ with $n \le m$, and $a,b \in m^\downarrow \cap n^\uparrow$ with $a \not \le b$: there is $d \in n^\uparrow$ with $d \buildrel \! {\mathsf {h}} \! \over \prec a$ and $d \le b$ iff there is $u \in m^\downarrow$ such that $a \le u$ and $b \buildrel \! {\mathsf {h}} \! \over \prec u$. We will apply this in Sect. 3.3.

2.2 Finite maximal chains

We will consider the case where for $x<y$, there is a finite maximal chain of endpoints x, y (that is, a covering chain), and see what can be deduced about the length of other chains with endpoints x, y when the poset either is upper semimodular or satisfies the upper quadrilateral condition.

Given a chain C of endpoints x, y (where $x\le y$) and some $a \in C$, it is easily seen that C is a maximal chain of endpoints x, y if and only if $C_x^a = C \cap a^\downarrow$ and $C_a^y = C \cap a^\uparrow$ are both maximal chains of endpoints x, a and a, y, respectively.

Theorem 8

Let the poset P be upper semimodular. Let $x,y \in P$ such that $x \le y$ and let C be a maximal chain of endpoints x, y; if C is finite, then every chain of endpoints x, y is included in a finite maximal chain of endpoints x, y, having the same length as C.

Proof

We use induction on the length n of C. If $n=0$ or $n=1$, then there is only one chain of endpoints x, y. Now suppose that $n>1$ and the result holds for any length $<n$. Let D be a chain of endpoints x, y. In C, we have $x \prec c_1$. If $D {\setminus } \{x\} \subseteq c_1^\uparrow$, then the result follows by applying the induction hypothesis to $C' = C {\setminus } \{x\}$ (maximal chain of length $n-1$) and $D' = (D {\setminus } \{x\}) \cup \{c_1\}$, both with endpoints $c_1,y$. So we can assume that D has an element $z \ne x$ such that $c_1 \not \le z$; thus, $x< z < y$.

Fig. 4

Illustration of the proof of Theorem 8. For each maximal chain, its name is indicated to the left of it and its length to the right of it

Suppose first that $z \not \prec y$. See Fig. 4. By upper semimodularity, there exists $u \in y^\downarrow$ such that $c_1 < u$ and $z \prec u$; as $z \not \prec y$, we get $u<y$. By induction hypothesis with $C' = C {\setminus } \{x\}$ (maximal chain of length $n-1$) and $\{c_1,u,y\}$, both of the endpoints $c_1,y$, there are two maximal chains $E_1$ and $E_2$, respectively, of endpoints $c_1,u$ and u, y, and of lengths a and b, where $a+b = n-1$, $a \ge 1$ and $b \ge 1$. Now by induction hypothesis with the two chains of endpoints x, u, the maximal $\{x\} \cup E_1$ of length $1+a < n$, and $D_x^z \cup \{u\}$, we get a maximal chain $F_1$ of endpoints x, z containing $D_x^z$, and of length a. Then, the induction hypothesis applied to the two chains of endpoints z, y, the maximal $\{z\} \cup E_2$ of length $1+b < n$, and $D_z^y$, we get a maximal chain $F_2$ of endpoints z, y, containing $D_z^y$, and of length $1+b$. The concatenation $F_1 \cup F_2$ is a maximal chain of endpoints x, y, of length $a+1+b = n$, and containing D.

Suppose next that $x \not \prec z \prec y$. If there is some $z' \in D$ such that $x<z'<z$, we choose one; if there is no such $z' \in D$, then we choose any $z' \in P$ such that $x<z'<z$, and add it to D. We apply then the previous paragraph with $D \cup \{z'\}$ and $z'$ instead of D and z.

There remains the case where $x \prec z \prec y$. Applying the upper quadrilateral condition, we get $n=2$; then, both C and D are maximal chains of endpoints x, y and of length 2. $\square$

In this subsection and the next one, we will repeatedly use the following technical result, see also Figs. 5 and 6:

Lemma 9

Let P be a poset satisfying the ${\mathcal {H}}$-upper quadrilateral condition and let $n\ge 0$.

• 1. Let $m \in P$ and $a,b,d \in m^\downarrow$ such that $a \not \le b$, $d \prec a$, $d \le b$, and there is a covering chain $d = v_0 \prec \cdots \prec v_n = b$ of length n and of endpoints d, b. Then, there exists $u \in m^\downarrow$ such that $a\le u$, $b \prec u$, $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$, and there is a covering chain $a = w_0 \prec \cdots \prec w_n = u$ of length n and of endpoints a, u such that for $i = 1, \ldots , n$ we have $[v_{i-1},v_i] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [w_{i-1},w_i]$.

• 2. Let $x,y,z \in P$ such that $x \prec z \le y$, and there is a covering chain $x = v_0 \prec \cdots \prec v_{n+1} = y$ of length $n+1$ and of endpoints x, y such that $z \not \le v_n$. Then, $[x,z] \mathrel {^{y}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [v_n,v_{n+1}]$ and there is a covering chain $z = w_0 \prec \cdots \prec w_n = y$ of length n and of endpoints z, y such that for $i = 1, \ldots , n$ we have $[v_{i-1},v_i] \mathrel {^{y}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [w_{i-1},w_i]$.

Fig. 5

Illustration of Lemma 9, item 1, for $n=4$. The arrows indicate ${\mathcal {H}}$-up-perspectivity

Proof

1.   We use induction on n. The case $n=0$ is trivial. Assume now that $n>0$ and that the result is valid for $n-1$. For some ${\mathsf {h}}, {\mathsf {k}} \in H$ we have $d \buildrel \! {\mathsf {h}} \! \over \prec a$ and $d \buildrel \! {\mathsf {k}} \! \over \prec v_1$. As $a \ne v_1$, the ${\mathcal {H}}$-upper quadrilateral condition gives some $w_1 \in m^\downarrow$ such that $a \buildrel \! {\mathsf {k}} \! \over \prec w_1$ and $v_1 \buildrel \! {\mathsf {h}} \! \over \prec w_1$. Let $w_0 = a$; then, $[v_0,v_1] = [d,v_1] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [a,w_1] = [w_0,w_1]$. Now $w_1,v_1 \in m^\downarrow$, $v_1 \prec w_1$, $w_1 \not \le b$, and we have the covering chain $v_1 \prec \cdots \prec v_n = b$ of length $n-1$. Applying the induction hypothesis with $v_1$, $w_1$ and $n-1$ in place of a, d and n: there exists $u \in m^\downarrow$ such that $w_1\le u$, $b \prec u$, $[v_1,w_1] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$ and there is a covering chain $w_1 \prec \cdots \prec w_n = u$ (of length $n-1$ and of endpoints $w_1,u$) such that for $i = 2, \ldots , n$ we have $[v_{i-1},v_i] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [w_{i-1},w_i]$. As $[v_1,w_1] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$ and $v_1 \buildrel \! {\mathsf {h}} \! \over \prec w_1$, we have $b \buildrel \! {\mathsf {h}} \! \over \prec u$; as $d \buildrel \! {\mathsf {h}} \! \over \prec a$, $a \le u$ and $a \not \le b$, we get $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$.

Fig. 6

Illustration of Lemma 9, item 2, for $n=4$. The arrows indicate ${\mathcal {H}}$-up-perspectivity

2.   We apply item 1 with $m=y$, $d=x$, $a=z$ and $b=v_n$, and here we get $u = y = v_{n+1}$. $\square$

Proposition 10

Let the poset P satisfy the upper quadrilateral condition. Let $x,y,z \in P$ such that $x \le z \le y$, and there are two maximal chains of endpoints x, y and x, z, respectively, having respective lengths n and t. Then, $n \ge t$ and there exists a maximal chain of endpoints z, y, of length $n-t$.

Proof

Let $x = c_0 \prec \cdots \prec c_n = y$ be the maximal chain of endpoints x, y having length n. We use induction on t. If $t=0$, then the result trivially holds. Now let $t>0$ and suppose that the result holds for $t-1$. Let $x = d_0 \prec \cdots \prec d_t = z$ be the be the maximal chain of endpoints x, z having length t.

Since $d_1 \not \le c_0$, but $d_1 \le z \le y = c_n$, there is some $r \in \{ 0, \ldots , n-1\}$ such that $d_1 \not \le c_r$, but $d_1 \le c_{r+1}$. We apply item 2 of Lemma 9, with r, $d_0$, $d_1$ and $c_0, \ldots , c_{r+1}$ taking the place of n, x, z and $v_0, \ldots , v_{n+1} = y$: there is thus a covering chain $d_1 = w_0 \prec \cdots \prec w_r = c_{r+1}$ of length r and of endpoints $d_1,c_{r+1}$. Then, $d_1 = w_0 \prec \cdots \prec w_r = c_{r+1} \prec \cdots \prec c_n = y$ is a maximal chain of endpoints $d_1,y$, of length $n-1$. Now $d_1 \prec \cdots \prec d_t = z$ is a maximal chain of endpoints $d_1,z$, of length $t-1$. By induction hypothesis, we have $n-1 \ge t-1$; thus, $n \ge t$, and there is a maximal chain of endpoints z, y, of length $(n-1)-(t-1) = n-t$. $\square$

In particular, taking $z=y$, we deduce the following result, which was shown by Ore in the case of an interval of finite length [15]:

Corollary 11

If the poset P satisfies the upper quadrilateral condition, then any two finite maximal chains of the same endpoints have the same length.

As this result is self-dual, it is also valid for the lower quadrilateral condition. Now we show through two examples that with the upper quadrilateral condition, we cannot obtain a stronger result.

Example 12

1.   Let $P = \{ -n \mid n \in {\mathbb {N}}\} \cup \{-\infty ,\alpha \}$, with the order given by the numerical order on $\{ -n \mid n \in {\mathbb {N}}\}$, $-\infty < -n$ for every $n \in {\mathbb {N}}$, and $-\infty< \alpha < 0$ (it is illustrated in Fig. 1.21 of  [23]). Here the covering relation reduces to $-\infty \prec \alpha \prec 0$ and $-(n+1) \prec -n$ for every $n \in {\mathbb {N}}$. It is a complete lattice, it satisfies the upper quadrilateral (or Birkhoff) condition, but it is not upper semimodular. We have $-\infty \prec \alpha \prec 0$, a finite chain of endpoints -$\infty ,0$, as well as an infinite one, $P {\setminus } \{\alpha \}$. Note that the dual result of Proposition 10 does not hold, and we have an infinite descending covering chain $0 \succ -1 \succ -2 \succ \cdots$.

2.   Let $P = {\mathbb {Z}}\cup \{-\infty ,+\infty ,\alpha \}$, with the order given by the numerical order on ${\mathbb {Z}}$, $-\infty< z < +\infty$ for every $z \in {\mathbb {Z}}$, and $-\infty< \alpha < +\infty$. Here the covering relation reduces to $-\infty \prec \alpha \prec +\infty$ and $z-1 \prec z$ for every $z \in {\mathbb {Z}}$. It is a complete lattice, it satisfies both the upper and lower quadrilateral (Birkhoff) conditions, but it is neither upper nor lower semimodular. Then, $-\infty \prec \alpha \prec +\infty$ and $P {\setminus } \{\alpha \}$ are two maximal chains of endpoints -$\infty ,+\infty$, the first one finite, the second one infinite. Note that P contains infinite ascending and descending covering chains, $0 \prec 1 \prec 2 \prec \cdots$ and $0 \succ -1 \succ -2 \succ \cdots$. Thus, it satisfies neither the ascending nor the descending chain condition  [9].

We now define a restriction of the order, for which the quadrilateral condition gives semimodularity. Let $\buildrel \! {\mathsf {*}} \! \over \le$ be the reflexive and transitive closure of the covering relation $\prec$; in other words, for any $x,y \in P$, $x \buildrel \! {\mathsf {*}} \! \over \le y$ iff for some $n\ge 0$ there is a covering chain $x = c_0 \prec \cdots \prec c_n = y$ ($n=0$ when $x=y$).

Lemma 13

The relation $\buildrel \! {\mathsf {*}} \! \over \le$ is a partial order included in the order $\le$ and sharing with it the same covering relation $\prec$. The map $\le \;\mapsto \; \buildrel \! {\mathsf {*}} \! \over \le$ is idempotent, that is, $\buildrel \! {\mathsf {**}} \! \over \le$ coincides with $\buildrel \! {\mathsf {*}} \! \over \le$. The two orders $\le$ and $\buildrel \! {\mathsf {*}} \! \over \le$ coincide iff for any $x<y$ there is a finite maximal chain of endpoints x, y (for the order $\le$); this holds in particular if all intervals have finite length.

Proof

Since $\prec$ is included in $\le$, which is reflexive and transitive, the reflexive and transitive closure $\buildrel \! {\mathsf {*}} \! \over \le$ of $\prec$ will be included in $\le$; for $x \buildrel \! {\mathsf {*}} \! \over \le y$ and $y \buildrel \! {\mathsf {*}} \! \over \le x$ we have $x \le y$ and $y \le x$, so $y=x$, and $\buildrel \! {\mathsf {*}} \! \over \le$ is antisymmetric.

If $x \prec y$, then $x \buildrel \! {\mathsf {*}} \! \over \le y$ and there is no $z \in P$ with $x< z <y$, hence no $z \in P$ with $x \buildrel \! {\mathsf {*}} \! \over< z \buildrel \! {\mathsf {*}} \! \over < y$, hence y covers x for $\buildrel \! {\mathsf {*}} \! \over \le$. Conversely, let $x \buildrel \! {\mathsf {*}} \! \over < y$; we have $x = c_0 \prec \cdots \prec c_n = y$ for some $n>0$; if $n>1$, then $x = c_0 \buildrel \! {\mathsf {*}} \! \over< c_1 \buildrel \! {\mathsf {*}} \! \over < c_n = y$, so y does not cover x for $\buildrel \! {\mathsf {*}} \! \over \le$; therefore, if y covers x for $\buildrel \! {\mathsf {*}} \! \over \le$, then $n=1$ and $x \prec y$.

Since $\buildrel \! {\mathsf {*}} \! \over \le$ has the same covering relation as $\le$, the reflexive and transitive closure of that covering relation will be the same for both, that is, $\buildrel \! {\mathsf {**}} \! \over \le$ coincides with $\buildrel \! {\mathsf {*}} \! \over \le$.

Now $\le$ and $\buildrel \! {\mathsf {*}} \! \over \le$ coincide iff for any $x<y$ there is a covering chain $x = c_0 \prec \cdots \prec c_n = y$; it is a maximal chain of endpoints x, y; conversely, every finite maximal chain of endpoints x, y is a covering chain. If all intervals have finite length, then for $x<y$, there is a finite maximal chain of endpoints x, y. $\square$

Theorem 14

Write $(P,\le )$ and $(P,\buildrel \! {\mathsf {*}} \! \over \le )$ for the two posets of the set P with the orders $\le$ and $\buildrel \! {\mathsf {*}} \! \over \le$, respectively.

• 1. $(P,\le )$ satisfies the ${\mathcal {H}}$-upper quadrilateral condition iff it satisfies the ${\mathcal {H}}*$-upper condition: for any ${\mathsf {h}} \in H$ and $m,a,b,d \in P$ such that $a,b,d \le m$, $a \not \le b$, $d \buildrel \! {\mathsf {h}} \! \over \prec a$ and $d \buildrel \! {\mathsf {*}} \! \over \le b$, there exists $u \in P$ such that $u \le m$, $a \buildrel \! {\mathsf {*}} \! \over \le u$ and $b \buildrel \! {\mathsf {h}} \! \over \prec u$.

• 2. If $(P,\le )$ satisfies the ${\mathcal {H}}$-upper quadrilateral condition, then $(P,\buildrel \! {\mathsf {*}} \! \over \le )$ will be ${\mathcal {H}}$-upper semimodular.

• 3. In $(P,\buildrel \! {\mathsf {*}} \! \over \le )$, ${\mathcal {H}}$-upper semimodularity, the ${\mathcal {H}}*$-upper condition, and the ${\mathcal {H}}$-upper quadrilateral condition are equivalent.

Proof

1   Let $(P,\le )$ satisfy the ${\mathcal {H}}$-upper quadrilateral condition. Take ${\mathsf {h}} \in H$ and $m,a,b,d \in P$ such that $a,b,d \le m$, $a \not \le b$, $d \buildrel \! {\mathsf {h}} \! \over \prec a$ and $d \buildrel \! {\mathsf {*}} \! \over \le b$. There is a covering chain $d = v_0 \prec \cdots \prec v_n = b$. Applying item 1 of Lemma 9, there is some $u \in P$ such that $u \le m$$a\le u$, $b \prec u$, $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$, and there is a covering chain $a = w_0 \prec \cdots \prec w_n = u$. Thus, $a \buildrel \! {\mathsf {*}} \! \over \le u$, and as $d \buildrel \! {\mathsf {h}} \! \over \prec a$ and $[d,a] \mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [b,u]$, we get $b \buildrel \! {\mathsf {h}} \! \over \prec u$. Hence we get the ${\mathcal {H}}*$-upper condition.

Conversely, if $(P,\le )$ satisfies the ${\mathcal {H}}*$-upper condition, then applying it successively for $d \buildrel \! {\mathsf {h}} \! \over \prec a$, then for $d \buildrel \! {\mathsf {k}} \! \over \prec b$ (with u instead of m) will give the ${\mathcal {H}}$-upper quadrilateral condition.

2.   Now consider the ${\mathcal {H}}*$-upper condition in the special case where $a,b,d \buildrel \! {\mathsf {*}} \! \over \le m$. As $b \buildrel \! {\mathsf {*}} \! \over \le m$, $b \prec u$ and $u \le m$, Proposition 10 (with $x=b$, $z=u$ and $y=m$) implies that $u \buildrel \! {\mathsf {*}} \! \over \le m$. We get thus ${\mathcal {H}}$-upper semimodularity for $\buildrel \! {\mathsf {*}} \! \over \le$.

3.   Given that $\buildrel \! {\mathsf {**}} \! \over \le$ coincides with $\buildrel \! {\mathsf {*}} \! \over \le$ and that $\buildrel \! {\mathsf {*}} \! \over \le$ has the same covering relation $\prec$ as $\le$, for the order $\buildrel \! {\mathsf {*}} \! \over \le$, ${\mathcal {H}}$-upper semimodularity becomes identical with the ${\mathcal {H}}*$-upper condition; applying item 1 for $\buildrel \! {\mathsf {*}} \! \over \le$, the ${\mathcal {H}}*$-upper condition is equivalent to the ${\mathcal {H}}$-upper quadrilateral condition. $\square$

Combining Theorem 14 with Lemma 13, we obtain the extension to posets of the well-known fact that in lattices where intervals have finite length, upper semimodularity is equivalent to the upper Birkhoff condition:

Corollary 15

In a poset where all intervals have finite length, ${\mathcal {H}}$-upper semimodularity, the ${\mathcal {H}}*$-upper condition, and the ${\mathcal {H}}$-upper quadrilateral condition are equivalent.

Note that for intervals of infinite length, the converse of item 2 does not hold, and the ${\mathcal {H}}$-upper quadrilateral condition for $(P,\buildrel \! {\mathsf {*}} \! \over \le )$ is in general strictly weaker than the same condition for $(P,\le )$:

Example 16

Let $P = ({\mathbb {N}}\times \{0,1\}) \cup \{ \alpha , \omega \}$, with the order given by $(n,a) < (n',a)$ for any $a \in \{0,1\}$ and $n,n' \in {\mathbb {N}}$ such that $n<n'$, and $\alpha< (n,a) < \omega$ for all $a \in \{0,1\}$ and $n\in {\mathbb {N}}$. We take ${\mathcal {H}}= \{ \prec \}$ (no tags). For the order $\le$, the only possibility for $a,b,d,m \in P$ with $a,b,d \in m^\downarrow$, $a \ne b$, $d \prec a$ and $d \prec b$ is $d = \alpha$, $m = \omega$, $a= (0,0)$ and $b=(0,1)$ (or vice versa); then, there is no u with $a \prec u$ and $b \prec u$, so $(P,\le )$ does not satisfy the upper quadrilateral condition. Now for the order $\buildrel \! {\mathsf {*}} \! \over \le$, all covering chains are included in $P {\setminus } \{\omega \}$, so we cannot have $a,b,d \in m^\downarrow$ with $a \ne b$, $d \prec a$ and $d \prec b$; thus, $(P,\buildrel \! {\mathsf {*}} \! \over \le )$ satisfies the upper quadrilateral condition, and by item 3 it is upper semimodular.

2.3 Jordan–Hölder theorems

We have seen that when a poset satisfies the upper or lower quadrilateral condition, two finite maximal chains of the same endpoints have the same length. Now with tags, we will give Jordan–Hölder theorems for the two tagged versions of the upper quadrilateral condition, namely ${\mathcal {H}}$ and skew-${\mathcal {H}}$. Given two covering chains $x = c_0 \prec \cdots \prec c_n = y$ and $x = d_0 \prec \cdots \prec d_n = y$ of same length and same endpoints x, y, we will obtain a ${\mathcal {H}}$-isomorphism, that is, a bijection from $\{ [c_{i-1},c_i] \mid i = 1, \ldots , n \}$ to $\{ [d_{j-1},d_j] \mid j = 1, \ldots , n \}$ such that if $[c_{i-1},c_i]$ is mapped to $[d_{j-1},d_j]$, then for some ${\mathsf {h}} \in H$ we have $c_{i-1} \buildrel \! {\mathsf {h}} \! \over \prec c_i$ and $d_{j-1} \buildrel \! {\mathsf {h}} \! \over \prec d_j$. In fact, this bijection of intervals corresponds to a permutation $\pi$ of $\{ 1, \ldots , n \}$, with $[c_{i-1},c_i]$ being mapped to $[d_{\pi (i)-1},d_{\pi (i)}]$.

Write $\mathrel {^{m}\!\!\!\nearrow \nearrow \!\!_{{\mathcal {H}}}}$ and $\mathrel {_{{\mathcal {H}}}\!\!\searrow \searrow \!\!\!^{m}}$ for the transitive closures of $\mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}}$ and $\mathrel {_{{\mathcal {H}}}\!\!\searrow \!\!\!^{m}}$, respectively; these relations (defined on intervals [d, a] for $d \prec a$) are reflexive. By Lemma 4, if P is a join-semilattice or P is ${\mathcal {H}}$-upper semimodular and satisfies ${\mathcal {H}}$-upper unicity, $\mathrel {^{m}\!\!\!\nearrow \nearrow \!\!_{{\mathcal {H}}}}$ and $\mathrel {_{{\mathcal {H}}}\!\!\searrow \searrow \!\!\!^{m}}$ are just $\mathrel {^{m}\!\!\!\nearrow \!\!_{{\mathcal {H}}}}$ and $\mathrel {_{{\mathcal {H}}}\!\!\searrow \!\!\!^{m}}$.

In the case of the ${\mathcal {H}}$-upper quadrilateral condition, our result is a translation to posets of the one of Grätzer and Nation [10] in the case of lattices, and the proof is similar:

Theorem 17

Let the poset P satisfy the ${\mathcal {H}}$-upper quadrilateral condition, let $x,y \in P$ with $x \le y$, and let $x = c_0 \prec \cdots \prec c_n = y$ and $x = d_0 \prec \cdots \prec d_n = y$ be two covering chains of same length and same endpoints x, y. Then, there is a permutation $\pi$ of $\{ 1, \ldots , n \}$ such that for any $i = 1, \ldots , n$, there is an interval $P_i$ in $y^\downarrow$ with $[c_{i-1},c_i] \mathrel {^{y}\!\!\!\nearrow \nearrow \!\!_{{\mathcal {H}}}} P_i \mathrel {_{{\mathcal {H}}}\!\!\searrow \searrow \!\!\!^{y}} [d_{\pi (i)-1},d_{\pi (i)}]$. The map $[c_{i-1},c_i] \mapsto [d_{\pi (i)-1},d_{\pi (i)}]$ is an ${\mathcal {H}}$-isomorphism between the two covering chains.

Fig. 7

Left: illustration of the argument of Theorem 17. Middle: result of Theorem 17 for $n=3$. Right: an ${\mathcal {H}}$-substitution

Proof

We use induction on n. For $n=0$ or $n=1$, there is a unique chain of endpoints x, y. Suppose now that $n>1$ and that the result is true for $n-1$. As $c_1 \not \le x = d_0$ and $c_1 \le y = d_n$, there is some $k \in \{ 0, \ldots , n-1\}$ such that $c_1 \not \le d_k$ and $c_1 \le d_{k+1}$. Apply item 2 of Lemma 9 with $c_1, d_0, \ldots , d_{k+1}$ in place of $z, v_0, \ldots , v_{n+1}$. Then, $[c_0,c_1] \mathrel {^{d_{k+1}}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [d_k,d_{k+1}]$ and there is a covering chain $c_1 = e_0 \prec \cdots \prec e_k = d_{k+1}$ such that $[d_{i-1},d_i] \mathrel {^{d_{k+1}}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [e_{i-1},e_i]$ for $i = 1, \ldots , k$; see the left part in Fig. 7. As $d_{k+1} \le d_n = y$, we can replace $d_{k+1}$ by y in the perspectivities, so $[c_0,c_1] \mathrel {^{y}\!\!\!\nearrow \!\!_{{\mathcal {H}}}} [d_k,d_{k+1}]$ and $[e_{i-1},e_i] \mathrel {_{{\mathcal {H}}}\!\!\searrow \!\!\!^{y}} [d_{i-1},d_i]$ ($i = 1, \ldots , k$). We apply the induction hypothesis to the chains $x'= c_1 \prec \cdots \prec c_n = y$ and $x' = e_0 \prec \cdots \prec e_k = d_{k+1} \prec \cdots \prec d_n = y$: there is a bijection $\pi : \{ 2, \ldots , n \} \rightarrow \{ 1, \ldots n, \} {\setminus } \{k+1\}$ and for any $i = 2, \ldots , n$ there is an interval $P_i$ in $y^\downarrow$, such that $[c_{i-1},c_i] \mathrel {^{y}\!\!\!\nearrow \nearrow \!\!_{{\mathcal {H}}}} P_i$, and $P_i \mathrel {_{{\mathcal {H}}}\!\!\searrow \searrow \!\!\!^{y}} [e_{\pi (i)-1},e_{\pi (i)}]$ if $\pi (i) \le k$, but $P_i \mathrel {_{{\mathcal {H}}}\!\!\searrow \searrow \!\!\!^{y}} [d_{\pi (i)-1},d_{\pi (i)}]$ if $\pi (i) \ge k+2$. For $\pi (i) \le k$, as $[e_{\pi (i)-1},e_{\pi (i)}] \mathrel {_{{\mathcal {H}}}\!\!\searrow \!\!\!^{y}} [d_{\pi (i)-1},d_{\pi (i)}]$, we get $P_i \mathrel {_{{\mathcal {H}}}\!\!\searrow \searrow \!\!\!^{y}} [d_{\pi (i)-1},d_{\pi (i)}]$. Extending $\pi$ to a permutation $\pi$ of $\{ 1, \ldots n \}$ by $\pi (1) = k+1$, for $P_1 = [d_k,d_{k+1}]$ we have $[c_0,c_1] \mathrel {^{y}\!\!\!\nearrow \nearrow \!\!_{{\mathcal {H}}}} P_1 \mathrel {_{{\mathcal {H}}}\!\!\searrow \searrow \!\!\!^{y}} [d_{\pi (1)-1},d_{\pi (1)}]$. Hence, for $i = 1, \ldots , n$ we have $[c_{i-1},c_i] \mathrel {^{y}\!\!\!\nearrow \nearrow \!\!_{{\mathcal {H}}}} P_i \mathrel {_{{\mathcal {H}}}\!\!\searrow \searrow \!\!\!^{y}} [d_{\pi (i)-1},d_{\pi (i)}]$, and the map $[c_{i-1},c_i] \mapsto [d_{\pi (i)-1},d_{\pi (i)}]$ is an ${\mathcal {H}}$-isomorphism. $\square$

The result is illustrated in the middle part in Fig. 7 for $n=3$ (in the induction step from 2 to 3 we have $k=2$).

In the case of the skew-${\mathcal {H}}$-upper quadrilateral condition, we cannot use perspectivity and the method of Grätzer and Nation [10]. Our approach will be closer to the original one of Ore [15], see Theorem 4 there. Given a covering chain $x = c_0 \prec \cdots \prec c_n = y$, an ${\mathcal {H}}$-substitution replaces in it $c_j$ by $d_j$ for one $j \in \{ 1, \ldots , n-1 \}$, where there are ${\mathsf {h}}, {\mathsf {k}}, {\mathsf {r}}, {\mathsf {s}} \in H$ such that $\{ {\mathsf {h}}, {\mathsf {r}} \} = \{ {\mathsf {k}}, {\mathsf {s}} \}$, $c_{j-1} \buildrel \! {\mathsf {h}} \! \over \prec c_j \buildrel \! {\mathsf {r}} \! \over \prec c_{j+1}$ and $c_{j-1} \buildrel \! {\mathsf {k}} \! \over \prec d_j \buildrel \! {\mathsf {s}} \! \over \prec c_{j+1}$. See the right part in Fig. 7. We have then an ${\mathcal {H}}$-isomorphism from the first chain to the second, by map** $[c_{i-1},c_i]$ on itself for $i < j$ and for $i > j+1$; then: (a) $[c_{j-1},c_j]$ on $[c_{j-1},d_j]$ and $[c_j,c_{j+1}]$ on $[d_j,c_{j+1}]$ if ${\mathsf {h}} = {\mathsf {k}}$ and ${\mathsf {r}} = {\mathsf {s}}$; (b) $[c_{j-1},c_j]$ on $[d_j,c_{j+1}]$ and $[c_j,c_{j+1}]$ on $[c_{j-1},d_j]$ if ${\mathsf {h}} = {\mathsf {s}}$ and ${\mathsf {k}} = {\mathsf {r}}$.

Theorem 18

Let the poset P satisfy the skew-${\mathcal {H}}$-upper quadrilateral condition, let $x,y \in P$ with $x \le y$, and let $x = c_0 \prec \cdots \prec c_n = y$ and $x = d_0 \prec \cdots \prec d_n = y$ be two covering chains of same length and same endpoints x, y. Then, there is a sequence of ${\mathcal {H}}$-substitutions transforming the first chain into the second, giving thus an ${\mathcal {H}}$-isomorphism between the two.

Proof

As any ${\mathcal {H}}$-substitution provides an ${\mathcal {H}}$-isomorphism, a sequence of ${\mathcal {H}}$-substitutions will by composition give an ${\mathcal {H}}$-isomorphism between two chains. Thus, we only have to show that there is such a sequence of ${\mathcal {H}}$-substitutions.

We use induction on n. Again for $n=0$ or $n=1$, there is a unique chain of endpoints x, y. Suppose now that $n>1$ and that the result is true for $n-1$. If $c_1=d_1$, the result follows by applying the induction hypothesis to the two chains $x'= c_1 \prec \cdots \prec c_n = y$ and $x' = d_1 \prec \cdots \prec d_n = y$, then adding $x = c_0 = d_0$ at the head of each covering chain in the sequence of substitutions.

We assume thus that $c_1 \ne d_1$. For some ${\mathsf {h}},{\mathsf {k}} \in H$ we have $x \buildrel \! {\mathsf {h}} \! \over \prec c_1$ and $x \buildrel \! {\mathsf {k}} \! \over \prec d_1$. By the skew-${\mathcal {H}}$-upper quadrilateral condition, there exist ${\mathsf {r}},{\mathsf {s}} \in H$ such that $\{ {\mathsf {h}}, {\mathsf {r}} \} = \{ {\mathsf {k}}, {\mathsf {s}} \}$, and $e_2 \in y^\downarrow$ such that $c_1 \buildrel \! {\mathsf {r}} \! \over \prec e_2$ and $d_1 \buildrel \! {\mathsf {s}} \! \over \prec e_2$. By Proposition 10, there is a covering chain $e_2 \prec \cdots \prec e_n = y$ of length $n-2$ and endpoints $e_2,y$. By the above argument, there is a sequence of ${\mathcal {H}}$-substitutions transforming $x = c_0 \prec c_1 \prec c_2 \prec \cdots \prec c_n = y$ into $x = c_0 \prec c_1 \prec e_2 \prec \cdots \prec e_n = y$. Replacing $c_1$ by $d_1$ in the latter sequence is an ${\mathcal {H}}$-substitution transforming it into the chain $x = d_0 \prec d_1 \prec e_2 \prec \cdots \prec e_n = y$. Again, by the above argument, there is a sequence of ${\mathcal {H}}$-substitutions transforming $x = d_0 \prec d_1 \prec e_2 \prec \cdots \prec e_n = y$ into $x = d_0 \prec d_1 \prec d_2 \prec \cdots \prec d_n = y$. Concatenating all these successive ${\mathcal {H}}$-substitutions, we get the result. $\square$

3 Applications

We will describe here several particular types of posets, which satisfy one of the tagged upper or lower forms of semimodularity, having thus a Jordan–Hölder theorem. First we briefly consider the two posets of normal and of subnormal subgroups of a group: the first one is both ${\mathcal {H}}$-upper and lower semimodular, while the second one is ${\mathcal {H}}$-lower semimodular. Then, we will see that the poset of closure ranges of an arbitrary poset is ${\mathcal {H}}$-lower semimodular.

Now our main contribution here is the analysis of five new partial order relations on partial partitions, introduced in  [19], which do not constitute lattices, and for which Jordan–Hölder type properties had been shown in the finite case. We will see that each one is upper semimodular, and in the case of multiple tags, it satisfies the skew-${\mathcal {H}}$-upper quadrilateral property.

3.1 Normal and subnormal groups

Since the topic is well known, we will consider it briefly. More details can be found in Sect. 8.3 of  [23].

Let G be a group. Write $\le$ for the restriction of the inclusion relation to subgroups of G; for $A,B \le G$, write $A \vartriangleleft B$ if A is a normal subgroup of B. Let ${\mathcal {N}}(G)$ be the poset of normal subgroups of G, ordered by $\le$ (equivalently, by $\vartriangleleft$); then, ${\mathcal {N}}(G)$ is a lattice, with $A \wedge B = A \cap B$ and $A \vee B = AB$, and this lattice is modular: given $D,U,M \in {\mathcal {N}}(G)$ with $D \vartriangleleft U$, we have $(DM) \cap U = D(M \cap U)$. The covering relation $\prec$ on ${\mathcal {N}}(G)$ if given by $A \prec B$ iff $A \vartriangleleft B$ and B / A is a simple group. We attach to each covering $A \prec B$ a tag corresponding to the simple quotient group B / A. For $A,B \in {\mathcal {N}}(G)$, (AB) / B is isomorphic to $A/(A\cap B)$; thus, for any ${\mathsf {h}} \in H$ we get $A \cap B \buildrel \! {\mathsf {h}} \! \over \prec A \iff B \buildrel \! {\mathsf {h}} \! \over \prec AB$: the lattice is both ${\mathcal {H}}$-upper and ${\mathcal {H}}$-lower semimodular.

Now let $\vartriangleleft \!\vartriangleleft$ be the transitive closure of the relation $\vartriangleleft$; for $A \vartriangleleft \!\vartriangleleft B$ we say that A is a subnormal subgroup of B. Let ${\mathcal {S}}(G)$ be the poset of subnormal subgroups of G. It is easily seen that the two order relations $\le$ and $\vartriangleleft \!\vartriangleleft$ coincide on ${\mathcal {S}}(G)$, and that ${\mathcal {S}}(G)$, ordered by $\vartriangleleft \!\vartriangleleft$, is a meet-semilattice. It inherits the covering relation $\prec$ from ${\mathcal {N}}(G)$, with the tags corresponding to the simple quotient groups. A result by Wielandt  [24] states that in a group with finite composition length, the subgroup generated by two subnormal subgroups is subnormal; then, ${\mathcal {S}}(G)$ is a lattice [23]. But we will not require that we easily see that ${\mathcal {S}}(G)$ is an ${\mathcal {H}}$-lower semimodular poset.

Indeed, let ${\mathsf {h}} \in H$ and $M,A,B,U \in {\mathcal {S}}(G)$ such that $A,B,U \in M^\uparrow$, $B \not \le A$, $A \buildrel \! {\mathsf {h}} \! \over \prec U$ and $B \le U$. Then, $A \vartriangleleft U$, so B normalizes A; hence, $U = AB$. Let $D = A \cap B$; then, $D \in {\mathcal {S}}(G)$ and $D \in M^\uparrow$. Now $B/D = B/(A \cap B)$ is isomorphic to $(AB)/A = U/A$; hence, $D \buildrel \! {\mathsf {h}} \! \over \prec B$.

As ${\mathcal {S}}(G)$ is a meet-semilattice, it satisfies the ${\mathcal {H}}$-lower unicity; hence, ${\mathcal {H}}$-perspectivity is transitive by Lemma 4. We get the dual and transitive form of Theorem 17, with $\mathrel {_{m}\!\!\searrow \!\!\!^{{\mathcal {H}}}}$ and $\mathrel {^{{\mathcal {H}}}\!\!\!\nearrow \!\!_{m}}$ instead of $\mathrel {^{m}\!\!\!\nearrow \nearrow \!\!_{{\mathcal {H}}}}$ and $\mathrel {_{{\mathcal {H}}}\!\!\searrow \searrow \!\!\!^{m}}$. Thus, the Jordan–Hölder theorem holds in any interval having finite length and in particular in the whole ${\mathcal {S}}(G)$ if G has finite composition length.

3.2 Closure ranges

Let P be a poset. A closure map  [8, 9], or closure operator  [1, 18], on P is a map $\varphi : P \rightarrow P$ that is isotone ($x \le y \;\Rightarrow \;\varphi (x) \le \varphi (y)$), extensive ($x \le \varphi (x)$) and idempotent ($\varphi (\varphi (x)) = \varphi (x)$). Equivalently,

$$\begin{aligned} \forall \, x,y \in P, \qquad x \le \varphi (y) \iff \varphi (x) \le \varphi (y) . \end{aligned}$$

Note that some authors, following the tradition of topology, designate by “closure operator on X” a map acting on subsets of X; in our terminology, it is a closure map on the lattice ${\mathcal {P}}(X)$. The set $\Phi (P)$ of all closure maps on P can be ordered elementwise: $\varphi _1 \le \varphi _2$ iff $\forall \, x \in P$, $\varphi _1(x) \le \varphi _2(x)$.

A closure range  [8], or closure system  [18], on P is a subset S of P such that for any $x \in P$, $x^\uparrow \cap S$ is non-empty and has a least element  [1]. The set $\varSigma (P)$ of all closure ranges on P is ordered by inclusion.

For any closure map $\varphi$, the invariance domain, fixpoint set, or range of $\varphi$ is the set

$$\begin{aligned} {\mathsf {Inv}}(\varphi ) = \{ x \in P \mid \varphi (x) = x \} = \{ \varphi (x) \mid x \in P \} \end{aligned}$$

Then, the map $\varphi \mapsto {\mathsf {Inv}}(\varphi )$ is a bijection $\Phi (P) \rightarrow \varSigma (P)$; the inverse bijection associates with any closure range S the closure map $\varphi _S: x \mapsto$ least element of $x^\uparrow \cap S$. Now for any that two closure maps $\varphi _1$ and $\varphi _2$, we have $\varphi _1 \le \varphi _2 \iff {\mathsf {Inv}}(\varphi _1) \supseteq {\mathsf {Inv}}(\varphi _2)$; thus, this bijection $\Phi (P) \rightarrow \varSigma (P)$ is a dual isomorphism.

Under some restrictive conditions (e.g. P is a complete lattice, or it satisfies the ascending chain condition, or it is finite ..., see [1, 8, 18] for more details), $\varSigma (P)$ is closed under intersection; thus, it is a complete lattice; then, it is shown that this lattice is lower semimodular [8]. But as in [18], we will make no assumption on the poset P, so a priori $\varSigma (P)$ is only a poset. In that paper, we proved an ad hoc form of lower semimodularity for the poset $\varSigma (P)$; we relied on two important results (Corollary 2.4 and Proposition 2.5 there):

Proposition 19

For $S_0,S_1 \in \varSigma (P)$ such that $S_0 \subset S_1$, we have $S_0 \prec S_1$ (in $\varSigma (P)$) iff $S_1 {\setminus } S_0$ is a singleton.

Proposition 20

Let $S_1,S_2 \in \varSigma (P)$ such that $S_2 {\setminus } S_1$ is finite; then, $S_1 \cap S_2 \in \varSigma (P)$.

For any $x \in P$, we define the binary relation $\buildrel \! x \! \over \prec$ on $\varSigma (P)$ by $S_0 \buildrel \! x \! \over \prec S_1$ if $x \in S_1$ and $S_0 = S_1 {\setminus } \{x\}$. Then, we partition $\prec$ into

$$\begin{aligned} {\mathcal {H}}= \{ \buildrel \! x \! \over \prec \mid x \in P, ~ \exists \, S_0,S_1 \in \varSigma (P), ~ S_0 \buildrel \! x \! \over \prec S_1 \} . \end{aligned}$$

Proposition 21

The poset $\varSigma (P)$ is ${\mathcal {H}}$-lower semimodular.

Proof

Let $x \in P$ and $M,A,B,U \in \varSigma (P)$ such that $A,B,U \in M^\uparrow$, $B \not \subseteq A$, $A \buildrel \! x \! \over \prec U$ and $B \subseteq U$. We have $x \in U$ and $A = U {\setminus } \{x\}$; as $B \subseteq U$, but $B \not \subseteq A = U {\setminus } \{x\}$, we have $x \in B$. Thus, $A \cap B = B {\setminus } \{x\}$. As $B {\setminus } A = \{x\}$, Proposition 20 implies that $A \cap B \in \varSigma (P)$. We have $A \cap B \buildrel \! x \! \over \prec B$. As $A,B \in M^\uparrow$ for the inclusion order, we get $A \cap B \in M^\uparrow$. $\square$

Of course, we get a trivial version of the Jordan–Hölder theorem: given $S_0,S_1 \in \varSigma (P)$ such that $S_0 \subset S_1$ and $S_1 {\setminus } S_0$ is finite, a covering chain of endpoints $S_0,S_1$ is obtained by adding successively the elements of $S_1 {\setminus } S_0$ in some peculiar order, and each element is added exactly once.

For more properties of $\Phi (P)$ and $\varSigma (P)$, the reader is referred to  [8, 18].

3.3 Orders on partial partitions

We use here the terminology and notation of  [21]. Let E be any set. A partition of E is a set of mutually disjoint non-empty subsets of E, whose union gives E; a partial partition of E is a partition of any subset of E; in other words, a set of mutually disjoint non-empty subsets of E, but not necessarily covering E. The subsets of E belonging to a (partial) partition are called blocks.

Let us write $\varPi (E)$ for the set of all partitions of E and $\varPi ^*(E)$ for the set of all partial partitions of E. Write ${\varvec{\varnothing }}$ for the empty partial partition (with no block). Set ${\mathbf {1}}_\emptyset = {\mathbf {0}}_\emptyset = {\varvec{\varnothing }}$, while for any $A \in {\mathcal {P}}(E) {\setminus } \{\emptyset \}$, let ${\mathbf {1}}_A = \{A\}$ (the partition of A into a single block) and ${\mathbf {0}}_A = \bigl \{ \{p\} \mid p \in A \bigr \}$ (the partition of A into its singletons). The union of all blocks of a partial partition $\pi$ is called the support of $\pi$, written ${\mathsf {supp}}(\pi )$; thus, $\pi$ is a partition of ${\mathsf {supp}}(\pi )$; the background of $\pi$ is the complement of the support, ${\mathsf {back}}(\pi ) = E {\setminus } {\mathsf {supp}}(\pi )$.

Partitions are ordered by refinement  [14]: for $\pi _1,\pi _2 \in \varPi (E)$, we write $\pi _1 \le \pi _2$ if every block of $\pi _1$ is included in a block of $\pi _2$:

$$\begin{aligned} \pi _1 \le \pi _2 \iff \bigl [ \forall \, B\in \pi _1 , ~ \exists \, C\in \pi _2 , ~ B\subseteq C \bigr ] . \end{aligned}$$

(3)

Equivalently, every block of $\pi _2$ is a union of blocks of $\pi _1$. This order constitutes $\varPi (E)$ into a complete lattice with least element ${\mathbf {0}}_E$ and the greatest element ${\mathbf {1}}_E$.

The covering relation on $\varPi (E)$ is $\buildrel \! {\mathsf {m}} \! \over \prec$ defined by $\pi _1 \buildrel \! {\mathsf {m}} \! \over \prec \pi _2$ if $\pi _2$ is obtained by merging two blocks of $\pi _1$:

$$\begin{aligned} \pi _1 \buildrel \! {\mathsf {m}} \! \over \prec \pi _2 \iff \left[ \begin{array}{l} |\pi _1| \ge 2, ~ \exists \, C_1,C_2 \in \pi _1, ~ C_1 \ne C_2, \\ \pi _2 = \bigl ( \pi _1 {\setminus } \{ C_1,C_2 \} \bigr ) \cup \{ C_1 \cup C_2 \} \end{array} \right] . \end{aligned}$$

Ore  [14] showed that $\varPi (E)$ is upper semimodular:

$$\begin{aligned} \forall \, \pi _1,\pi _2 \in \varPi (E), \quad \pi _1 \wedge \pi _2 \buildrel \! {\mathsf {m}} \! \over \prec \pi _1 \implies \pi _2 \buildrel \! {\mathsf {m}} \! \over \prec \pi _1 \vee \pi _2 . \end{aligned}$$

(4)

Dras̆kovic̆ová  [6] introduced partial partitions of E under the name of partitions inE. By extending to $\varPi ^*(E)$ the order $\le$ defined in (3), then $\varPi ^*(E)$ is a complete lattice with least element ${\varvec{\varnothing }}$ and greatest element ${\mathbf {1}}_E$. Further properties of this order were given in [6, 7, 16, 17]. Note that for $\pi _1,\pi _2 \in \varPi ^*(E)$, when $\pi _1 \le \pi _2$, every block of $\pi _1$ is included in a block of $\pi _2$, but a block of $\pi _2$ is generally not a union of blocks of $\pi _1$. Hence, we do not use the word “refinement” for the order $\le$ on $\varPi ^*(E)$, and we call it the standard order  [19].

The relation $\buildrel \! {\mathsf {m}} \! \over \prec$ on $\varPi (E)$ extends naturally to $\varPi ^*(E)$. Now we define the relation $\buildrel \! {\mathsf {s}} \! \over \prec$ on $\varPi ^*(E)$ by $\pi _1 \buildrel \! {\mathsf {s}} \! \over \prec \pi _2$ if $\pi _2$ is obtained by adding a singleton block to $\pi _1$:

$$\begin{aligned} \pi _1 \buildrel \! {\mathsf {s}} \! \over \prec \pi _2 \iff \bigl [ {\mathsf {supp}}(\pi _1) \subset E, ~ \exists \, p \in {\mathsf {back}}(\pi _1), ~ \pi _2 = \pi _1 \cup \bigl \{ \{p\} \bigr \} \bigr ] . \end{aligned}$$

The following result was essentially proved in [6, 17]:

Proposition 22

The standard order on $\varPi ^*(E)$ has the covering relation $\buildrel \! {\mathsf {m}} \! \over \prec \cup \buildrel \! {\mathsf {s}} \! \over \prec$, and it is $\{\buildrel \! {\mathsf {m}} \! \over \prec ,\buildrel \! {\mathsf {s}} \! \over \prec \}$-upper semimodular:

$$\begin{aligned} \forall \, \pi _1,\pi _2 \in \varPi ^*(E), \quad \begin{array}{l} \pi _1 \wedge \pi _2 \buildrel \! {\mathsf {m}} \! \over \prec \pi _1 \implies \pi _2 \buildrel \! {\mathsf {m}} \! \over \prec \pi _1 \vee \pi _2 ; \\ \pi _1 \wedge \pi _2 \buildrel \! {\mathsf {s}} \! \over \prec \pi _1 \implies \pi _2 \buildrel \! {\mathsf {s}} \! \over \prec \pi _1 \vee \pi _2 . \end{array} \end{aligned}$$

(5)

Motivated by image analysis, we introduced in  [19] 5 new partial order relations on $\varPi ^*(E)$, then 3 more orders in [20] and 5 in  [21]. We proved by counting the number of blocks and the size of the support that when E is finite, all 13 orders satisfy the Jordan–Hölder theorem, namely that two maximal chains of same endpoints are ${\mathcal {H}}$-isomorphic. We will analyse here the five orders of  [19], and they are all included in the standard order. We will show that all five are upper semimodular, and that those with more than one tag satisfy the skew-${\mathcal {H}}$-upper quadrilateral condition; some of them are also lower semimodular, with the skew-${\mathcal {H}}$-lower quadrilateral condition. Hence, for these five orders, the Jordan–Hölder theorem will be a consequence of their upper semimodularity and of their skew-${\mathcal {H}}$-upper quadrilateral condition when $|{\mathcal {H}}|>1$.

Let us first introduce some terminology and notation. First, we have the relation $\buildrel \! {\mathsf {i}} \! \over \prec$ given by $\pi _1 \buildrel \! {\mathsf {i}} \! \over \prec \pi _2$ if $\pi _2$ is obtained by inflating one block of $\pi _1$ by exactly one point:

$$\begin{aligned} \pi _1 \buildrel \! {\mathsf {i}} \! \over \prec \pi _2 \iff \left[ \begin{array}{l} {\mathsf {supp}}(\pi _1) \subset E, ~ \pi _1 \ne {\varvec{\varnothing }}, ~ \exists \, p \in {\mathsf {back}}(\pi _1), \\ \exists \, B \in \pi _1, ~ \pi _2 = \bigl ( \pi _1 {\setminus } \{ B \} \bigr ) \cup \bigl \{ B \cup \{p\} \bigr \} \end{array} \right] . \end{aligned}$$

Next we have the relation $\buildrel \! {\mathsf {c}} \! \over \prec$ given by $\pi _1 \buildrel \! {\mathsf {c}} \! \over \prec \pi _2$ if $\pi _2$ is obtained by adding a block to $\pi _1$:

$$\begin{aligned} \pi _1 \buildrel \! {\mathsf {c}} \! \over \prec \pi _2 \iff \left[ \begin{array}{l} {\mathsf {supp}}(\pi _1) \subset E, ~ \exists \, B \subseteq {\mathsf {back}}(\pi _1), \\ B \ne \emptyset , ~ \pi _2 = \pi _1 \cup \{ B \} \end{array} \right] . \end{aligned}$$

The building order  [22] is the partial order relation $\Subset$ on $\varPi ^*(E)$ given by $\pi _1 \Subset \pi _2$ if every block of $\pi _2$ contains at least one block of $\pi _1$:

$$\begin{aligned} \pi _1\Subset \pi _2 \iff \bigl [ \forall \, C\in \pi _2 , ~ \exists \, B\in \pi _1 , ~ B\subseteq C \bigr ] . \end{aligned}$$

We then define the singularity relation by if every block of $\pi _2$ contains at most one block of $\pi _1$:

We can now describe the five orders introduced in  [19]; they are obtained by restricting the standard order and they do not constitute lattices. Their names correspond to the operations on blocks involved in growing a partial partition: inclusion, inflating, merging, inclusion–inflating and merging–inflating.

• 1. The inclusion order$\subseteq$: for $\pi _1 \subseteq \pi _2$, each block of $\pi _1$ is a block of $\pi _2$; thus, $\pi _2$ is obtained from $\pi _1$ by adding new blocks made of points in ${\mathsf {back}}(\pi _1)$. The covering relation is $\buildrel \! {\mathsf {c}} \! \over \prec$.

• 2. The inflating order$\buildrel \! {\mathsf {i}} \! \over \le$:

  

  In other words, the inclusion relation between blocks of $\pi _1$ and those of $\pi _2$ is a bijection. Here $\pi _2$ is obtained by inflating some blocks of $\pi _1$. The covering relation is $\buildrel \! {\mathsf {i}} \! \over \prec$.

• 3. The merging order$\buildrel \! {\mathsf {m}} \! \over \le$:

  $$ \begin{aligned} \pi _1 \buildrel \! {\mathsf {m}} \! \over \le \pi _2 \iff \bigl [ \pi _1 \le \pi _2 ~ \& ~ {\mathsf {supp}}(\pi _1) = {\mathsf {supp}}(\pi _2) \bigr ] . \end{aligned}$$

  In other words, $\pi _1$ and $\pi _2$ are two partitions of the same support, ordered by refinement. Here $\pi _2$ is obtained by merging some blocks of $\pi _1$. As $\varPi ^*(E)$ is the disjoint union of all $\varPi (A)$ for $A\in {\mathcal {P}}(E)$, the order $\buildrel \! {\mathsf {m}} \! \over \le$ is the disjoint union of the refinement orders on all $\varPi (A)$. The covering relation is $\buildrel \! {\mathsf {m}} \! \over \prec$.

• 4. The inclusion–inflating order$\buildrel \! {\mathsf {i}} \! \over \subseteq$:

  

  In other words, the inclusion relation between blocks of $\pi _1$ and those of $\pi _2$ is an injection. Here $\pi _2$ is obtained from $\pi _1$ by inflating some blocks and/or adding new blocks. The covering relation is $\buildrel \! {\mathsf {i}} \! \over \prec \cup \buildrel \! {\mathsf {s}} \! \over \prec$.

• 5. The merging–inflating order$\buildrel \! {\mathsf {mi}} \! \over \le$:

  $$ \begin{aligned} \pi _1 \buildrel \! {\mathsf {mi}} \! \over \le \pi _2 \iff \bigl [ \pi _1 \le \pi _2 ~ \& ~ \pi _1 \Subset \pi _2 \bigr ] . \end{aligned}$$

  In other words, the inclusion relation between blocks of $\pi _1$ and those of $\pi _2$ is a surjection. Here $\pi _2$ is obtained from $\pi _1$ by merging and/or inflating some blocks. The covering relation is $\buildrel \! {\mathsf {i}} \! \over \prec \cup \buildrel \! {\mathsf {m}} \! \over \prec$.

The inclusion, inflating, and merging orders are simple, they rely on a single operation for growth, and they have an elementary covering relation with exactly one tag (respectively, $\buildrel \! {\mathsf {c}} \! \over \prec$, $\buildrel \! {\mathsf {i}} \! \over \prec$ and $\buildrel \! {\mathsf {m}} \! \over \prec$); hence, we will consider the non-tagged version of semimodularity.

Proposition 23

The merging, inflating, and inclusion orders on $\varPi ^*(E)$, $\buildrel \! {\mathsf {m}} \! \over \le$, $\buildrel \! {\mathsf {i}} \! \over \le$ and $\subseteq$, are upper semimodular. The inflating and inclusion orders, $\subseteq$ and $\buildrel \! {\mathsf {i}} \! \over \le$, are also lower semimodular.

Proof

Let $\pi _m \in \varPi ^*(E)$. For the merging order $\buildrel \! {\mathsf {m}} \! \over \le$, $\pi _m^\downarrow$ is a sublattice of $\varPi ({\mathsf {supp}}(\pi _m))$, ordered by refinement, which is upper semimodular, see (4).

Consider next the inflating order $\buildrel \! {\mathsf {i}} \! \over \le$. Let $\pi _h, \pi _l \in \varPi ^*(E)$ such that $\pi _l \buildrel \! {\mathsf {i}} \! \over \le \pi _h$. We can write $\pi _h = \{ H_\imath \mid \imath \in I \}$ and $\pi _l = \{ L_\imath \mid \imath \in I \}$, where for each $\imath \in I$ we have $\emptyset \ne L_\imath \subseteq H_\imath$. Each element $\pi$ of the interval $[\pi _l,\pi _h]$ takes the form $\{ X_\imath \mid \imath \in I \}$, where $L_\imath \subseteq X_\imath \subseteq H_\imath$ for each $\imath \in I$. Let us define

$$\begin{aligned} \begin{array}{r} W = {\mathsf {supp}}(\pi _h) {\setminus } {\mathsf {supp}}(\pi _l) = \bigcup _{\imath \in I} (H_\imath {\setminus } L_\imath ) , \\ f: [\pi _l,\pi _h] \rightarrow {\mathcal {P}}(W) : \pi \mapsto {\mathsf {supp}}(\pi ) {\setminus } {\mathsf {supp}}(\pi _l) , \\ \{ X_\imath \mid \imath \in I \} \mapsto \bigcup _{\imath \in I} (X_\imath {\setminus } L_\imath ) . \end{array} \end{aligned}$$

(6)

It is easy to see that f is a bijection, whose inverse is the map ${\mathcal {P}}(W) \rightarrow [\pi _l,\pi _h] : Z \mapsto \{ L_\imath \cup (Z \cap H_\imath ) \mid \imath \in I \}$. Moreover, for $\pi _x,\pi _y \in [\pi _l,\pi _h]$, where $\pi _x = \{ X_\imath \mid \imath \in I \}$ and $\pi _y = \{ Y_\imath \mid \imath \in I \}$, we have $\pi _x \buildrel \! {\mathsf {i}} \! \over \le \pi _y$ iff for each $\imath \in I$ we have $X_\imath \subseteq Y_\imath$, iff $f(\pi _x) \subseteq f(\pi _y)$. Thus, f is an order isomorphism between $[\pi _l,\pi _h]$, ordered by $\buildrel \! {\mathsf {i}} \! \over \le$, and ${\mathcal {P}}(W)$, ordered by inclusion. Hence, $[\pi _l,\pi _h]$ inherits the upper and lower semimodularity of ${\mathcal {P}}(W)$.

Consider finally the inclusion order $\subseteq$. Let $\pi _h, \pi _l \in \varPi ^*(E)$ such that $\pi _l \subseteq \pi _h$. The interval $[\pi _l,\pi _h]$ consists of all partial partitions $\pi$ such that $\pi _l \subseteq \pi \subseteq \pi _h$. The map $\pi \mapsto \pi {\setminus } \pi _l$ is an isomorphism (for the inclusion order) $[\pi _l,\pi _h] \rightarrow {\mathcal {P}}(\pi _h {\setminus } \pi _l)$, so $[\pi _l,\pi _h]$ inherits the upper and lower semimodularity of ${\mathcal {P}}(\pi _h {\setminus } \pi _l)$. $\square$

The inclusion–inflating and merging–inflating orders are compound, they rely on two operations for growth, and their covering relation is double, involving two tags (the union of $\buildrel \! {\mathsf {i}} \! \over \prec$ with, respectively, $\buildrel \! {\mathsf {s}} \! \over \prec$ and $\buildrel \! {\mathsf {m}} \! \over \prec$); in this respect, they are like the standard order, see Proposition 22.

Proposition 24

The inclusion–inflating orders $\buildrel \! {\mathsf {i}} \! \over \subseteq$ is upper and lower semimodular, and it satisfies the $\{\buildrel \! {\mathsf {i}} \! \over \prec ,\buildrel \! {\mathsf {s}} \! \over \prec \}$-skew upper and lower quadrilateral conditions.

Proof

Let $\pi _h,\pi _l \in \varPi ^*(E)$ such that $\pi _l \buildrel \! {\mathsf {i}} \! \over \subseteq \pi _h$. We can write $\pi _h = \{ H_\imath \mid \imath \in I \}$, and $\pi _l = \{ L_\imath \mid \imath \in J \}$ for some $J \subseteq I$, where for $\imath \in J$ we have $\emptyset \ne L_\imath \subseteq H_\imath$ and for $\imath \in I {\setminus } J$ we have $H_\imath \ne \emptyset$; we set $L_\imath = \emptyset$ for $\imath \in I {\setminus } J$. Each element $\pi$ of the interval $[\pi _l,\pi _h]$ takes the form $\{ X_\imath \mid \imath \in K \}$ for some K with $J \subseteq K \subseteq I$, where $L_\imath \subseteq X_\imath \subseteq H_\imath$ for $\imath \in J$ and $\emptyset \ne X_\imath \subseteq H_\imath$ for $\imath \in K {\setminus } J$; we set $X_\imath = \emptyset$ for $\imath \in I {\setminus } K$. Thus, for all $\imath \in I$, $X_\imath = {\mathsf {supp}}(\pi ) \cap H_\imath$ and $L_\imath \subseteq X_\imath \subseteq H_\imath$; note, however, that the empty $L_\imath$ and $X_\imath$ are not blocks of $\pi _l$ and $\pi$. As with the inflating order in the preceding proof, we define W and f according to (6); then, f is a bijection, whose inverse is the map ${\mathcal {P}}(W) \rightarrow [\pi _l,\pi _h] : Z \mapsto \{ L_\imath \cup (Z \cap H_\imath ) \ne \emptyset \mid \imath \in I \}$. Now f is an order isomorphism between $[\pi _l,\pi _h]$, ordered by $\buildrel \! {\mathsf {i}} \! \over \subseteq$, and ${\mathcal {P}}(W)$, ordered by inclusion, and $[\pi _l,\pi _h]$ inherits from ${\mathcal {P}}(W)$ its upper and lower semimodularity, as above.

Write $\buildrel \! {\mathsf {i,s}} \! \over \prec$ for $\buildrel \! {\mathsf {i}} \! \over \prec \cup \buildrel \! {\mathsf {s}} \! \over \prec$, the covering relation of $\buildrel \! {\mathsf {i}} \! \over \subseteq$. Given $\pi ,\pi ' \in [\pi _l,\pi _h]$, with $X_\imath = {\mathsf {supp}}(\pi ) \cap H_\imath$ and $X'_\imath = {\mathsf {supp}}(\pi ') \cap H_\imath$ for all $\imath \in I$, then $\pi \buildrel \! {\mathsf {i,s}} \! \over \prec \pi '$ means that for a unique $\jmath \in I$ we have $X'_\jmath = X_\jmath \cup \{p\}$ for a point $p \in H_\jmath {\setminus } X_\jmath$, while $X'_\imath = X_\imath$ for all $\imath \ne \jmath$; now either $X_\jmath = \emptyset$ and $\pi \buildrel \! {\mathsf {s}} \! \over \prec \pi '$ (the singleton block $\{p\}$ is created), or $X_\jmath \ne \emptyset$ and $\pi \buildrel \! {\mathsf {i}} \! \over \prec \pi '$ (the block $X_\jmath$ is inflated by the point p).

Consider now a covering quadrilateral $\pi _0, \pi _a, \pi _b, \pi _1 \in [\pi _l,\pi _h]$, where $\pi _a \ne \pi _b$, $\pi _0 \buildrel \! {\mathsf {i,s}} \! \over \prec \pi _a \buildrel \! {\mathsf {i,s}} \! \over \prec \pi _1$ and $\pi _0 \buildrel \! {\mathsf {i,s}} \! \over \prec \pi _b \buildrel \! {\mathsf {i,s}} \! \over \prec \pi _1$. Given $X_\imath = {\mathsf {supp}}(\pi _0) \cap H_\imath$ ($\imath \in I$), then $\pi _1$ is obtained from $\pi _0$ in two possible ways: (a) for a unique $\jmath \in I$, add to $X_\jmath$ two points $p,q \in H_\jmath$; or (b) for two distinct $\jmath ,\ell \in I$, add to $X_\jmath$ a point $p \in H_\jmath$ and to $X_\ell$ a point $q \in H_\ell$. Then, in both covering chains $\pi _0 \buildrel \! {\mathsf {i,s}} \! \over \prec \pi _a \buildrel \! {\mathsf {i,s}} \! \over \prec \pi _1$ and $\pi _0 \buildrel \! {\mathsf {i,s}} \! \over \prec \pi _b \buildrel \! {\mathsf {i,s}} \! \over \prec \pi _1$, the number of occurrences of $\buildrel \! {\mathsf {s}} \! \over \prec$ is the number of times that for $\jmath$ or $\ell$ one goes from the empty set to a singleton block, in other words the number of occurrences of the empty set among $X_\jmath$ and $X_\ell$. Now in each covering chain the number of occurrences of $\buildrel \! {\mathsf {i}} \! \over \prec$ is the complement w.r.t. 2. Since $\pi _0, \pi _a, \pi _b, \pi _1 \in \pi _h^\downarrow$, this gives the $\{\buildrel \! {\mathsf {i}} \! \over \prec ,\buildrel \! {\mathsf {s}} \! \over \prec \}$-skew upper quadrilateral condition, and since $\pi _0, \pi _a, \pi _b, \pi _1 \in \pi _l^\uparrow$, this gives the $\{\buildrel \! {\mathsf {i}} \! \over \prec ,\buildrel \! {\mathsf {s}} \! \over \prec \}$-skew lower quadrilateral condition. $\square$

For the merging–inflating order, we use the following fact from Eq. (25) in Theorem 12 of  [19]:

$$ \begin{aligned} \forall \, \pi _0, \pi _1, \pi _2 \in \varPi ^*(E), \quad \bigl [ \pi _0 \le \pi _1 \le \pi _2 ~ \& ~ \pi _0 \buildrel \! {\mathsf {mi}} \! \over \le \pi _2 \bigr ] \implies \pi _1 \buildrel \! {\mathsf {mi}} \! \over \le \pi _2 . \end{aligned}$$

(7)

Next, we need the following preliminary result:

Lemma 25

Let $\pi _i \in \varPi ^*(E)$, $i \in I$, $I \ne \emptyset$, be a non-empty family of partial partitions of E, and let $\pi ^+$ be the supremum (complete join) of the $\pi _i$, $i \in I$, for the standard order. For any $\pi \in \varPi ^*(E)$:

• 1. If $\pi _i \buildrel \! {\mathsf {mi}} \! \over \le \pi$ for each $i \in I$, then $\pi ^+ \buildrel \! {\mathsf {mi}} \! \over \le \pi$.

• 2. If $\pi \buildrel \! {\mathsf {mi}} \! \over \le \pi _i$ for each $i \in I$, then $\pi _i \buildrel \! {\mathsf {mi}} \! \over \le \pi ^+$ for each $i \in I$.

Proof

By definition of the supremum, we have $\pi _i \le \pi ^+$ for each $i \in I$.

• 1. If for each $i \in I$ we have $\pi _i \buildrel \! {\mathsf {mi}} \! \over \le \pi$, then $\pi _i \le \pi$, and from the definition of the supremum, we get $\pi ^+ \le \pi$. Choose $i \in I$; we have $\pi _i \le \pi ^+ \le \pi$ and $\pi _i \buildrel \! {\mathsf {mi}} \! \over \le \pi$, so applying (7) with $\pi _0 = \pi _i$, $\pi _1 = \pi ^+$ and $\pi _2 = \pi$, we get $\pi ^+ \buildrel \! {\mathsf {mi}} \! \over \le \pi$.

• 2. The blocks of $\pi ^+$ are obtained by chaining overlap** blocks of the union of all $\pi _i$  [19]; thus, each block $A \in \pi ^+$ must contain a block $B \in \pi _i$ for at least one $i \in I$; as $\pi \buildrel \! {\mathsf {mi}} \! \over \le \pi _i$, $\pi \Subset \pi _i$, so B contains a block $C \in \pi$; hence $C \subseteq B \subseteq A$, and each block of $\pi ^+$ contains a block of $\pi$, that is, $\pi \Subset \pi ^+$. For any $i \in I$ we have $\pi \buildrel \! {\mathsf {mi}} \! \over \le \pi _i$, so $\pi \le \pi _i \le \pi ^+$; as $\pi \Subset \pi ^+$, we get $\pi \buildrel \! {\mathsf {mi}} \! \over \le \pi ^+$; applying (7) with $\pi _0 = \pi$, $\pi _1 = \pi _i$ and $\pi _2 = \pi ^+$, we get $\pi _i \buildrel \! {\mathsf {mi}} \! \over \le \pi ^+$ for each $i \in I$. $\square$

Proposition 26

The merging–inflating order $\buildrel \! {\mathsf {mi}} \! \over \le$ is upper semimodular, and it satisfies the $\{\buildrel \! {\mathsf {i}} \! \over \prec ,\buildrel \! {\mathsf {m}} \! \over \prec \}$-skew upper quadrilateral condition.

Proof

Write $\buildrel \! {\mathsf {i,m}} \! \over \prec$ for $\buildrel \! {\mathsf {i}} \! \over \prec \cup \buildrel \! {\mathsf {m}} \! \over \prec$, the covering relation of $\buildrel \! {\mathsf {mi}} \! \over \le$. Let $\pi _m, \pi _d, \pi _a, \pi _b \in \varPi ^*(E)$ such that $\pi _{a}, \pi _b \buildrel \! {\mathsf {mi}} \! \over \le \pi _{m}$, , $\pi _d \buildrel \! {\mathsf {i,m}} \! \over \prec \pi _a$ and $\pi _d \buildrel \! {\mathsf {mi}} \! \over \le \pi _b$. If we had $\pi _a \le \pi _b$, then we would get $\pi _d \le \pi _a \le \pi _b$ and $\pi _d \buildrel \! {\mathsf {mi}} \! \over \le \pi _b$, so (7) would give $\pi _a \buildrel \! {\mathsf {mi}} \! \over \le \pi _b$, a contradiction. Hence, $\pi _a \not \le \pi _b$. Let $\pi _u = \pi _a \vee \pi _b$, the join of $\pi _a$ and $\pi _b$ for the standard order. Applying Lemma 25 with the $\pi _i$, $i \in I$, being $\pi _a$ and $\pi _b$, we obtain $\pi _u \buildrel \! {\mathsf {mi}} \! \over \le \pi _m$ (by Item 1 with $\pi = \pi _m$) and $\pi _a, \pi _b \buildrel \! {\mathsf {mi}} \! \over \le \pi _u$ (by Item 2 with $\pi = \pi _d$). Let us show that $\pi _b \buildrel \! {\mathsf {i,m}} \! \over \prec \pi _u$. If $\pi _d \buildrel \! {\mathsf {m}} \! \over \prec \pi _a$, then in the standard order $\pi _a$ covers $\pi _d$ and $\pi _d \le \pi _b$; hence, $\pi _d = \pi _a \wedge \pi _b$, the meet of $\pi _a$ and $\pi _b$ for the standard order; hence, Proposition 22 gives $\pi _b \buildrel \! {\mathsf {m}} \! \over \prec \pi _a \vee \pi _b= \pi _u$. Assume now that $\pi _d \buildrel \! {\mathsf {i}} \! \over \prec \pi _a$; then, $\pi _a$ is obtained by adding to a block $D \in \pi _d$ a point $p \notin {\mathsf {supp}}(\pi _d)$. For some $B \in \pi _b$, we have $D \subseteq B$; as $\pi _a \not \le \pi _b$, $p \notin B$. There are two cases. First, if $p \notin {\mathsf {supp}}(\pi _b)$, then $\pi _u = \pi _a \vee \pi _b$ is obtained by adding the point p to the block B, so $\pi _b \buildrel \! {\mathsf {i}} \! \over \prec \pi _u$. Second, if $p \in {\mathsf {supp}}(\pi _b)$, then we have $p \in C$ for some block $C \in \pi _b$, where $C \ne B$; then, $\pi _u = \pi _a \vee \pi _b$ is obtained by merging the two blocks B and C, so $\pi _b \buildrel \! {\mathsf {m}} \! \over \prec \pi _u$. Thus, $\pi _b \buildrel \! {\mathsf {i,m}} \! \over \prec \pi _u$ in all cases. Therefore, $\buildrel \! {\mathsf {mi}} \! \over \le$ is upper semimodular.

Consider now the particular case where both $\pi _d \buildrel \! {\mathsf {i,m}} \! \over \prec \pi _a$ and $\pi _d \buildrel \! {\mathsf {i,m}} \! \over \prec \pi _b$. Interchanging $\pi _a$ and $\pi _b$ above, we get $\pi _a, \pi _b \buildrel \! {\mathsf {i,m}} \! \over \prec \pi _u$. We remark that for $\pi \buildrel \! {\mathsf {m}} \! \over \prec \pi '$, we have ${\mathsf {supp}}(\pi ) = {\mathsf {supp}}(\pi ')$, while for $\pi \buildrel \! {\mathsf {i}} \! \over \prec \pi '$, we have ${\mathsf {supp}}(\pi ) \subset {\mathsf {supp}}(\pi ')$ and $|{\mathsf {supp}}(\pi ') {\setminus } {\mathsf {supp}}(\pi )| = 1$. Thus, $|{\mathsf {supp}}(\pi _u) {\setminus } {\mathsf {supp}}(\pi _d)|$ is the number of occurrences of $\buildrel \! {\mathsf {i}} \! \over \prec$ in both covering chains $\pi _d \buildrel \! {\mathsf {i,m}} \! \over \prec \pi _a \buildrel \! {\mathsf {i,m}} \! \over \prec \pi _u$ and $\pi _d \buildrel \! {\mathsf {i,m}} \! \over \prec \pi _b \buildrel \! {\mathsf {i,m}} \! \over \prec \pi _u$, the number of occurrences of $\buildrel \! {\mathsf {m}} \! \over \prec$ being then the complement $2-|{\mathsf {supp}}(\pi _u) {\setminus } {\mathsf {supp}}(\pi _d)|$. Therefore, the $\{\buildrel \! {\mathsf {i}} \! \over \prec ,\buildrel \! {\mathsf {m}} \! \over \prec \}$-skew upper quadrilateral condition is satisfied. $\square$

It is well known that $\varPi (E)$, ordered by refinement, does not satisfy the lower quadrilateral condition. It follows that the merging and merging–inflating orders on $\varPi ^*(E)$, whose restriction to partitions is the refinement order, will not satisfy it.

4 Discussion, conclusion and perspectives

Semimodularity has been studied in depth in the case of lattices [23]; it takes several forms, which are usually equivalent in the case of lattices of finite length. We have analysed the generalization to posets of the two main forms of semimodularity, the standard one  [9, 23] and the one due to Birkhoff [2], called Birkhoff condition [23] or quadrilateral condition  [15]. In fact, [15] gave a definition for the Birkhoff condition in a poset, which for the first time allowed to obtain equal length for finite maximal chains with same endpoints; then, our definition of standard semimodularity in a poset follows the same approach. The two conditions are equivalent in a poset of finite length.

We have thoroughly analysed finite maximal chains (or covering chains) in a poset satisfying either semimodularity or the Birkhoff (quadrilateral) condition; in particular, we get that any two finite maximal chains of same endpoints have the same length.

In order to deal with isomorphism of quotients in composition series and chief series of finite groups, Grätzer and Nation  [10, 13] introduced the perspectivity relation between intervals, and the projectivity equivalence relation generated by it. Our approach based on tagging the covering relation is better adapted to concrete examples, but it is also more flexible: associating a tag to each equivalence class of projectivity; then, the upper/lower semimodularity and Birkhoff condition in a lattice give the ${\mathcal {H}}$-upper/lower semimodularity and quadrilateral condition, see Lemma 3. Now the skew-${\mathcal {H}}$-upper (or lower) quadrilateral condition describes a more general situation. We get the poset analogue of the isomorphism theorem of Grätzer and Nation [10], but also an isomorphism theorem for the skew-${\mathcal {H}}$-upper (or lower) quadrilateral condition.

Using the general framework of posets, instead of lattices, has applications in orders that do not constitute lattices, for instance, the set of closures ranges of an arbitrary poset  [18] and the five orders on partial partitions introduced in [19]. Moreover, the skew-${\mathcal {H}}$-upper quadrilateral condition allows to give the Jordan–Hölder theorem for the inclusion–inflating and merging–inflating orders, for which the perspectivity approach of Grätzer and Nation does not work.

Other definitions of semimodularity in a poset have been given in the literature (in particular in  [18]), and the most straightforward one consists in removing the condition that $a,b,d,u \in m^\downarrow$ in Definitions 1 and 5 (or the dual condition $a,b,d,u \in m^\uparrow$ for the lower versions). This leads to what we call the unbounded form of semimodularity or quadrilateral condition. The unbounded upper quadrilateral condition has been considered by several authors, in particular Ore  [15] called it the “weak quadrilateral condition”. The adjective “weak” is a misnomer, since the standard upper quadrilateral condition does not necessarily imply the unbounded one. Obviously when P has the greatest element max, taking $m=max$ in Definitions 1 and 5, our standard conditions imply the unbounded ones.

For an infinite poset without maximal elements, unbounded upper semimodularity does not guarantee equal length for finite maximal chains (i.e. covering chains) having the same endpoints:

Example 27

Consider ${\mathbb {N}}$ with the partial order $\sqsubseteq$ given by $x \sqsubseteq y$ iff $0 \le y-x \ne 1$. The covering relation $\prec$ is given by $x \prec y$ iff $y-x = 2$ or 3. The order $\sqsubseteq$ is the reflexive and transitive closure of the covering relation $\prec$ (that is, $\sqsubseteq$ coincides with $\buildrel ~{*}~ \over \sqsubseteq$ in the terminology at the end of Sect. 2.2). The poset has unbounded upper semimodularity: if $d \prec a$ and $d \sqsubseteq b$, then take $u = a+b-d$, so $a \sqsubseteq u$ and $b \prec u$. It does not satisfy the standard upper quadrilateral condition: for $a = d+2$, $b = d+3$ and $m = d+6$, $a,b,d \in m^\downarrow$, $a \ne b$, $d \prec a$ and $d \prec b$, but for $a \prec u$ and $b \prec u$ we must have $u=d+5$, so $u \not \sqsubseteq m$. The two covering chains $0 \prec 2 \prec 4 \prec 6$ and $0 \prec 3 \prec 6$ have the same endpoints, but different lengths.

When each element is bounded by a maximal element, and all intervals have finite length, it is possible to generalize the method used in Lemma 9 and Proposition 10 and obtain from the unbounded upper quadrilateral condition that any two finite maximal chains of the same endpoints have the same length (see also Theorem 5 in  [15]). This could be an interesting axis of research.

However, our main criticism against the unbounded version is that it leads to bizarre posets, and all examples that we saw in practice (see Sect. 3) satisfy the standard upper or lower quadrilateral condition.

Our work can lead to new directions of research. For instance, a deeper analysis could be made of chain transformations involved in the isomorphism of finite maximal chains, following the method of [15] and its extension in  [12]. Also, alternative definitions of semimodularity have been given in the case of lattices, taking a completely different form, in particular, those of Mac Lane [11] and Wilcox  [25]; they could be generalized to posets.

A disappointing fact is that the Jordan–Hölder theorem in a poset seems much more general than semimodularity or the quadrilateral condition. Indeed,  [20] introduced a new operation on partial partitions, block apportioning, which generalizes block merging. The three orders of  [20] and two of [21] are based on it, they satisfy the Jordan–Hölder theorem in the finite case, but we have checked that they do not satisfy either the upper or the lower quadrilateral condition, nor even some generalizations of it that we tried.