A novel flexible model for lot sizing and scheduling with non-triangular, period overlap** and carryover setups in different machine configurations

Abstract

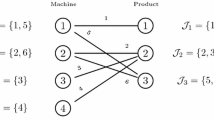
This paper develops and tests an efficient mixed integer programming model for capacitated lot sizing and scheduling with non-triangular and sequence-dependent setup times and costs incorporating all necessary features of setup carryover and overlap** on different machine configurations. The model’s formulation is based on the asymmetric travelling salesman problem and allows multiple lots of a product within a period. The model conserves the setup state when no product is being processed over successive periods, allows starting a setup in a period and ending it in the next period, permits ending a setup in a period and starting production in the next period(s), and enforces a minimum lot size over multiple periods. This new comprehensive model thus relaxes all limitations of physical separation between the periods. The model is first developed for a single machine and then extended to other machine configurations, including parallel machines and flexible flow lines. Computational tests demonstrate the flexibility and comprehensiveness of the proposed models.

Appendices

Appendix 1: MLOV-SM model

$$Minimise\;\mathop \sum \limits_{ijt} sc_{ij} y_{ijt} + \mathop \sum \limits_{it} h_{it} I_{it} + \mathop \sum \limits_{it} g_{it} B_{it}$$

(30)

$$I_{jt - 1} - B_{jt - 1} + x_{jt} - I_{jt} + B_{jt} = d_{jt} \quad\forall \,j, t$$

(31)

$$\mathop \sum \limits_{i} b_{i} x_{it} + \mathop \sum \limits_{ij} st_{ij} y_{ijt} + S_{t - 1} - S_{t} + slk_{t} = C_{t} \quad\forall \,t$$

(32)

$$x_{jt} \le UB_{jt} \times \left( {z_{jt} - \mathop \sum \limits_{i} OLS_{ijt} } \right)\quad\forall \,j,t$$

(33)

$$y_{jjt} = 0\quad\forall \,j,t$$

(34)

$$\mathop \sum \limits_{i} \alpha_{it} = 1\quad\forall \, t = 1, \ldots ,T + 1$$

(35)

$$\alpha_{{i_{o} t}} = 1\quad\forall \, t = 1$$

(36)

$$x_{jt}^{F} \le UB_{jt} \alpha_{jt} \quad\forall \,j,t$$

(37)

$$x_{jt}^{L} \le UB_{jt} \; \left( {\alpha_{j,t + 1} - \mathop \sum \limits_{i} OLS_{ijt} } \right)\quad\forall \,j,t$$

(38)

$$x_{jt}^{L} + x_{j,t + 1}^{F} \ge ml_{j} \alpha_{j,t + 1} \quad\forall \,j,t$$

(39)

$$x_{jt} - x_{jt}^{F} - x_{jt}^{L} \ge ml_{j} \left( {z_{jt} - \alpha_{jt} - \alpha_{j,t + 1} } \right) \quad\forall \,j,t$$

(40)

$$\alpha_{it} + \mathop \sum \limits_{j} y_{jit} = z_{it} \quad\forall \,i,t$$

(41)

$$\mathop \sum \limits_{j} y_{ijt} + \alpha_{i,t + 1} = z_{it} \quad\forall \,i,t$$

(42)

$$a_{ijt}^{k} \le y_{ijt} \quad\forall \,i,j,k,t$$

(43)

$$z_{it} \ge z_{it}^{bin} \quad\forall \,i,t$$

(44)

$$z_{it} \le ZUB_{i} z_{it}^{bin} \quad\forall \,i,t$$

(45)

$$\alpha_{kt} + \mathop \sum \limits_{i} a_{ikt}^{k} = z_{kt}^{bin} \quad\forall \,k,t$$

(46)

$$\alpha_{it} + \mathop \sum \limits_{j} a_{jit}^{k} \ge \mathop \sum \limits_{j} a_{ijt}^{k} \quad\forall \,k,i \ne k,t$$

(47)

$$a_{kjt}^{k} = 0\quad\forall \,k,j,t$$

(48)

$$S_{t} \le \mathop \sum \limits_{ij} st_{ij} OLS_{ijt} \quad\forall \,t$$

(49)

$$\mathop \sum \limits_{j} OLS_{ijt} \le \alpha_{i,t + 1} \quad\forall \,i,t$$

(50)

$$OLS_{ijt} \le y_{ijt} \quad\forall \,i,j,t$$

(51)

$$x_{jt} ,I_{jt} ,B_{jt} ,S_{t} ,slk_{t} ,x_{jt}^{F} , x_{jt}^{L} \quad Positive\,variables$$

$$z_{it} ,y_{ijt} \quad Integer\,variables$$

$$a_{ijt}^{k} ,\alpha_{it} ,z_{it}^{bin} ,OLS_{ijt} \quad Binary\,variables$$

Appendix 2: ML-PM model

$$Minimise\;\mathop \sum \limits_{ijmt} sc_{ijm} y_{ijmt} + \mathop \sum \limits_{it} h_{it} I_{it} + \mathop \sum \limits_{it} g_{it} B_{it}$$

(52)

$$I_{jt - 1} - B_{jt - 1} + \mathop \sum \limits_{m} x_{jmt} - I_{jt} + B_{jt} = d_{jt} \quad\forall \,j, t$$

(53)

$$\mathop \sum \limits_{i} b_{im} x_{imt} + \mathop \sum \limits_{ij} st_{ijm} y_{ijmt} + slk_{mt} = C_{mt} \quad\forall \,m,t$$

(54)

$$x_{jmt} \le UB_{jmt} \times z_{jmt}^{bin} \quad\forall \,j,m,t$$

(55)

$$y_{jjmt} = 0\quad\forall \,j,m,t$$

(56)

$$\mathop \sum \limits_{i} \alpha_{imt} = 1\; \forall \, m,t = 1, \ldots ,T + 1$$

(57)

$$\alpha_{{i_{om} mt}} = 1\quad\forall \,m,t = 1$$

(58)

$$x_{jmt}^{F} \le UB_{jmt} \alpha_{jmt} \quad\forall \,j,m,t$$

(59)

$$x_{jmt}^{L} \le UB_{jmt} \alpha_{jm,t + 1} \quad\forall \,j,m,t$$

(60)

$$x_{jmt}^{L} + x_{jm,t + 1}^{F} \ge ml_{j} \alpha_{mj,t + 1} \quad\forall \,j,m,t$$

(61)

$$x_{jmt} - x_{jmt}^{F} - x_{jmt}^{L} \ge ml_{j} \left( {z_{jmt} - \alpha_{jmt} - \alpha_{jm,t + 1} } \right)\quad\forall \,j,m,t$$

(62)

$$\alpha_{imt} + \mathop \sum \limits_{j} y_{jimt} = z_{imt} \quad\forall \,i,m,t$$

(63)

$$\mathop \sum \limits_{j} y_{ijmt} + \alpha_{im,t + 1} = z_{imt} \quad\forall \,i,m,t$$

(64)

$$a_{ijmt}^{k} \le y_{ijmt} \quad\forall \,i,j,k,m,t$$

(65)

$$z_{imt} \ge z_{imt}^{bin} \quad\forall \,i,m,t$$

(66)

$$z_{imt} \le ZUB_{im} z_{imt}^{bin} \quad\forall \,i,m,t$$

(67)

$$\alpha_{kmt} + \mathop \sum \limits_{i} a_{ikmt}^{k} = z_{kmt}^{bin} \quad\forall \,k,m,t$$

(68)

$$\alpha_{imt} + \mathop \sum \limits_{j} a_{jimt}^{k} \ge \mathop \sum \limits_{j} a_{ijmt}^{k} \quad\forall \,k,i \ne k,m,t$$

(69)

$$a_{kjmt}^{k} = 0\quad\forall \,k,j,m,t$$

(70)

$$x_{jmt} ,I_{jt} ,B_{jt} ,slk_{mt} ,x_{jmt}^{F} , x_{jmt}^{L} \quad Positive\,variables$$

$$z_{imt} ,y_{ijmt} \quad Integer\,variables$$

$$a_{ijmt}^{k} ,\alpha_{imt} ,z_{imt}^{bin} \quad Binary\,variables$$

Appendix 3: MLOV-PM model

$$Minimise\;\mathop \sum \limits_{ijmt} sc_{ijm} y_{ijmt} + \mathop \sum \limits_{it} h_{it} I_{it} + \mathop \sum \limits_{it} g_{it} B_{it}$$

(71)

$$I_{jt - 1} - B_{jt - 1} + \mathop \sum \limits_{m} x_{jmt} - I_{jt} + B_{jt} = d_{jt} \quad\forall j, t$$

(72)

$$\mathop \sum \limits_{i} b_{im} x_{imt} + \mathop \sum \limits_{ij} st_{ijm} y_{ijmt} + S_{m,t - 1} - S_{mt} + slk_{mt} = C_{mt} \quad\forall \,m,t$$

(73)

$$x_{jmt} \le UB_{jmt} \times \left( {z_{jmt} - \mathop \sum \limits_{i} OLS_{ijmt} } \right)\quad\forall \,j, m,t$$

(74)

$$y_{jjmt} = 0\quad\forall \,j, m,t$$

(75)

$$\mathop \sum \limits_{i} \alpha_{imt} = 1\quad\forall \; m,t = 1, \ldots ,T + 1$$

(76)

$$\alpha_{{i_{om} mt}} = 1\quad\forall \, m,t = 1$$

(77)

$$x_{jmt}^{F} \le UB_{jmt} \alpha_{jmt} \quad\forall \,j, m,t$$

(78)

$$x_{jmt}^{L} \le UB_{jt} \left( {\alpha_{jm,t + 1} - \mathop \sum \limits_{i} OLS_{ijmt} } \right)\quad\forall \,j, m,t$$

(79)

$$x_{jmt}^{L} + x_{jm,t + 1}^{F} \ge ml_{j} \alpha_{jm,t + 1} \quad\forall \,j, m,t$$

(80)

$$x_{jmt} - x_{jmt}^{F} - x_{jmt}^{L} \ge ml_{j} \left( {z_{jmt} - \alpha_{jmt} - \alpha_{jm,t + 1} } \right) \quad\forall \,j, m,t$$

(81)

$$\alpha_{imt} + \mathop \sum \limits_{j} y_{jimt} = z_{imt} \quad\forall \,i, m,t$$

(82)

$$\mathop \sum \limits_{j} y_{ijmt} + \alpha_{im,t + 1} = z_{imt} \quad\forall \,i, m,t$$

(83)

$$a_{ijmt}^{k} \le y_{ijmt} \quad\forall \,i,j,k, m,t$$

(84)

$$z_{imt} \ge z_{imt}^{bin} \quad\forall \,i, m,t$$

(85)

$$z_{imt} \le ZUB_{im} z_{imt}^{bin} \quad\forall \,i, m,t$$

(86)

$$\alpha_{kmt} + \mathop \sum \limits_{i} a_{ikmt}^{k} = z_{kmt}^{bin} \quad\forall \,k, m,t$$

(87)

$$\alpha_{imt} + \mathop \sum \limits_{j} a_{jimt}^{k} \ge \mathop \sum \limits_{j} a_{ijmt}^{k} \quad\forall \,k,i \ne k, m,t$$

(88)

$$a_{kjmt}^{k} = 0\quad\forall \,k,j, m,t$$

(89)

$$S_{mt} \le \mathop \sum \limits_{ij} st_{ijm} OLS_{ijmt} \quad\forall \, m,t$$

(90)

$$\mathop \sum \limits_{j} OLS_{jimt} \le \alpha_{im,t + 1} \quad\forall \,i, m,t$$

(91)

$$OLS_{ijmt} \le y_{ijmt} \quad\forall \,i,j, m,t$$

(92)

$$x_{jmt} ,I_{jt} ,B_{jt} ,S_{mt} ,slk_{mt} ,x_{jmt}^{F} , x_{jmt}^{L} \quad Positive\,variables$$

$$z_{imt} ,y_{ijmt} \quad Integer\,variables$$

$$a_{ijmt}^{k} ,\alpha_{imt} ,z_{imt}^{bin} ,OLS_{ijmt} \quad Binary\,variables$$

Appendix 4: ML-FFL model

$$Minimise\;\mathop \sum \limits_{ijemt} sc_{{ijm_{e} }} y_{{ijm_{e} t}} + \mathop \sum \limits_{it} h_{iet} I_{iet} + \mathop \sum \limits_{it} g_{it} B_{iEt}$$

(93)

$$I_{jE,t - 1} - B_{jE,t - 1} + \mathop \sum \limits_{{m_{E} }} x_{{jm_{e} t}} - I_{jEt} + B_{jEt} = d_{jt} \quad\forall \,j, t$$

(94)

$$I_{je,t - 1} + \mathop \sum \limits_{{m_{e} }} x_{{jm_{e} t}} - I_{jet} = \mathop \sum \limits_{{m_{e + 1} }} x_{{jm_{e + 1} ,t + 1}} \quad\forall \,j, t\,{\text{and}}\,e = 1, \ldots ,E - 1$$

(95)

$$B_{itE} \le BP \cdot d_{it} \quad\forall \,i,t$$

(96)

$$\mathop \sum \limits_{i} b_{{im_{e} }} x_{{im_{e} t}} + \mathop \sum \limits_{ij} st_{{ijm_{e} }} y_{{ijm_{e} t}} + slk_{{m_{e} t}} = C_{{m_{e} t}} \quad\forall \,e,m,t$$

(97)

$$x_{{jm_{e} t}} \le UB_{{jm_{e} t}} \times z_{{jm_{e} t}}^{bin} \quad\forall \,j,e,m,t$$

(98)

$$y_{{jjm_{e} t}} = 0\quad\forall \,j,e,m,t$$

(99)

$$\mathop \sum \limits_{i} \alpha_{{im_{e} t}} = 1\quad\forall \, e,m,t = 1, \ldots ,T + 1$$

(100)

$$\alpha_{{i_{{om_{e} }} m_{e} t}} = 1\quad\forall \,e,m,t = 1$$

(101)

$$x_{{jm_{e} t}}^{F} \le UB_{{jm_{e} t}} \alpha_{{jm_{e} t}} \quad\forall \,j,e,m,t$$

(102)

$$x_{{jm_{e} t}}^{L} \le UB_{{jm_{e} t}} \alpha_{{jm_{e} ,t + 1}} \quad\forall \,j,e,m,t$$

(103)

$$x_{{jm_{e} t}}^{L} + x_{{jm_{e} ,t + 1}}^{F} \ge ml_{j} \alpha_{{m_{e} j,t + 1}} \quad\forall \,j,e,m,t$$

(104)

$$x_{{jm_{e} t}} - x_{{jm_{e} t}}^{F} - x_{{jm_{e} t}}^{L} \ge ml_{j} \left( {z_{{jm_{e} t}} - \alpha_{{jm_{e} t}} - \alpha_{{jm_{e} ,t + 1}} } \right)\quad\forall \,j,e,m,t$$

(105)

$$\alpha_{{im_{e} t}} + \mathop \sum \limits_{j} y_{{jim_{e} t}} = z_{{im_{e} t}} \quad\forall \,i,e,m,t$$

(106)

$$\mathop \sum \limits_{j} y_{{ijm_{e} t}} + \alpha_{{im_{e} ,t + 1}} = z_{{im_{e} t}} \quad\forall \,i,e,m,t$$

(107)

$$a_{{ijm_{e} t}}^{k} \le y_{{ijm_{e} t}} \quad\forall \,i,j,k,e,m,t$$

(108)

$$z_{{im_{e} t}} \ge z_{{im_{e} t}}^{bin} \quad\forall \,i,e,m,t$$

(109)

$$z_{{im_{e} t}} \le ZUB_{{im_{e} }} z_{{im_{e} t}}^{bin} \quad\forall \,i,e,m,t$$

(110)

$$\alpha_{{km_{e} t}} + \mathop \sum \limits_{i} a_{{ikm_{e} t}}^{k} = z_{{km_{e} t}}^{bin} \quad\forall \,k,e,m,t$$

(111)

$$\alpha_{{im_{e} t}} + \mathop \sum \limits_{j} a_{{jim_{e} t}}^{k} \ge \mathop \sum \limits_{j} a_{{ijm_{e} t}}^{k} \quad\forall \,k,i \ne k,e,m,t$$

(112)

$$a_{{kjm_{e} t}}^{k} = 0\quad\forall \,k,j,e,m,t$$

(113)

$$x_{{jm_{e} t}} ,I_{jet} ,B_{jet} ,slk_{{m_{e} t}} ,x_{{jm_{e} t}}^{F} , x_{{jm_{e} t}}^{L} \quad Positive\,variables$$

$$z_{{im_{e} t}} ,y_{{ijm_{e} t}} \quad Integer\,variables$$

$$a_{{ijm_{e} t}}^{k} ,\alpha_{{im_{e} t}} ,z_{{im_{e} t}}^{bin} \quad Binary\,variables$$

Appendix 5: MLOV-FFL model

$$Minimise\;\mathop \sum \limits_{ijemt} sc_{{ijm_{e} }} y_{{ijm_{e} t}} + \mathop \sum \limits_{it} h_{iet} I_{iet} + \mathop \sum \limits_{it} g_{it} B_{iEt}$$

(114)

$$I_{jE,t - 1} - B_{jE,t - 1} + \mathop \sum \limits_{{m_{E} }} x_{{jm_{e} t}} - I_{jEt} + B_{jEt} = d_{jt} \quad\forall \,j, t$$

(115)

$$I_{je,t - 1} + \mathop \sum \limits_{{m_{e} }} x_{{jm_{e} t}} - I_{jet} = \mathop \sum \limits_{{m_{e + 1} }} x_{{jm_{e + 1} ,t + 1}} \quad\forall \,j, t\,{\text{and}}\,e = 1, \ldots ,E - 1$$

(116)

$$B_{itE} \le BP \cdot d_{it} \quad\forall \,i,t$$

(117)

$$\mathop \sum \limits_{i} b_{{im_{e} }} x_{{im_{e} t}} + \mathop \sum \limits_{ij} st_{{ijm_{e} }} y_{{ijm_{e} t}} + S_{{m_{e} ,t - 1}} - S_{{m_{e} t}} + slk_{{m_{e} t}} = C_{{m_{e} t}} \quad\forall \,e,m,t$$

(118)

$$x_{{jm_{e} t}} \le UB_{{jm_{e} t}} \times \left( {z_{{jm_{e} t}} - \mathop \sum \limits_{i} OLS_{{ijm_{e} t}} } \right)\quad\forall \,j,e,m,t$$

(119)

$$y_{{jjm_{e} t}} = 0\quad\forall \,j,e,m,t$$

(120)

$$\mathop \sum \limits_{i} \alpha_{{im_{e} t}} = 1\quad\forall \, e,m,t = 1, \ldots ,T + 1$$

(121)

$$\alpha_{{i_{{om_{e} }} m_{e} t}} = 1\quad\forall \,e,m,t = 1$$

(122)

$$x_{{jm_{e} t}}^{F} \le UB_{{jm_{e} t}} \alpha_{{jm_{e} t}} \quad\forall \,j,e,m,t$$

(123)

$$x_{{jm_{e} t}}^{L} \le UB_{{jm_{e} t}} \left( {\alpha_{{jm_{e} ,t + 1}} - \mathop \sum \limits_{i} OLS_{{ijm_{e} t}} } \right)\quad\forall \, j,e,m,t$$

(124)

$$x_{{jm_{e} t}}^{L} + x_{{jm_{e} ,t + 1}}^{F} \ge ml_{j} \alpha_{{m_{e} j,t + 1}} \quad\forall \,j,e,m,t$$

(125)

$$x_{{jm_{e} t}} - x_{{jm_{e} t}}^{F} - x_{{jm_{e} t}}^{L} \ge ml_{j} \left( {z_{{jm_{e} t}} - \alpha_{{jm_{e} t}} - \alpha_{{jm_{e} ,t + 1}} } \right)\quad\forall \,j,e,m,t$$

(126)

$$\alpha_{{im_{e} t}} + \mathop \sum \limits_{j} y_{{jim_{e} t}} = z_{{im_{e} t}} \quad\forall \,i,e,m,t$$

(127)

$$\mathop \sum \limits_{j} y_{{ijm_{e} t}} + \alpha_{{im_{e} ,t + 1}} = z_{{im_{e} t}} \quad\forall \,i,e,m,t$$

(128)

$$a_{{ijm_{e} t}}^{k} \le y_{{ijm_{e} t}} \quad\forall \,i,j,k,e,m,t$$

(129)

$$z_{{im_{e} t}} \ge z_{{im_{e} t}}^{bin} \quad\forall \,i,e,m,t$$

(130)

$$z_{{im_{e} t}} \le ZUB_{{im_{e} }} z_{{im_{e} t}}^{bin} \quad\forall \,i,e,m,t$$

(131)

$$\alpha_{{km_{e} t}} + \mathop \sum \limits_{i} a_{{ikm_{e} t}}^{k} = z_{{km_{e} t}}^{bin} \quad\forall \,k,e,m,t$$

(132)

$$\alpha_{{im_{e} t}} + \mathop \sum \limits_{j} a_{{jim_{e} t}}^{k} \ge \mathop \sum \limits_{j} a_{{ijm_{e} t}}^{k} \quad\forall \,k,i \ne k,e,m,t$$

(133)

$$a_{{kjm_{e} t}}^{k} = 0\quad\forall \,k,j,e,m,t$$

(134)

$$S_{{m_{e} t}} \le \mathop \sum \limits_{ij} st_{{ijm_{e} }} OLS_{{ijm_{e} t}} \quad\forall \, e,m,t$$

(135)

$$\mathop \sum \limits_{j} OLS_{{jim_{e} t}} \le \alpha_{{im_{e} ,t + 1}} \quad\forall \,i, e,m,t$$

(136)

$$OLS_{{ijm_{e} t}} \le y_{{ijm_{e} t}} \quad\forall \,i,j, e,m,t$$

(137)

$$x_{{jm_{e} t}} ,I_{jet} ,B_{jet} ,S_{{m_{e} t}} ,slk_{{m_{e} t}} ,x_{{jm_{e} t}}^{F} , x_{{jm_{e} t}}^{L} \quad Positive\,variables$$

$$z_{{im_{e} t}} ,y_{{ijm_{e} t}} \quad Integer\,variables$$

$$a_{{ijm_{e} t}}^{k} ,\alpha_{{im_{e} t}} ,z_{{im_{e} t}}^{bin} ,OLS_{{ijm_{e} t}} \quad Binary\,variables$$